Study of θϕ Networks via Zagreb Connection Indices
Abstract
:1. Introduction
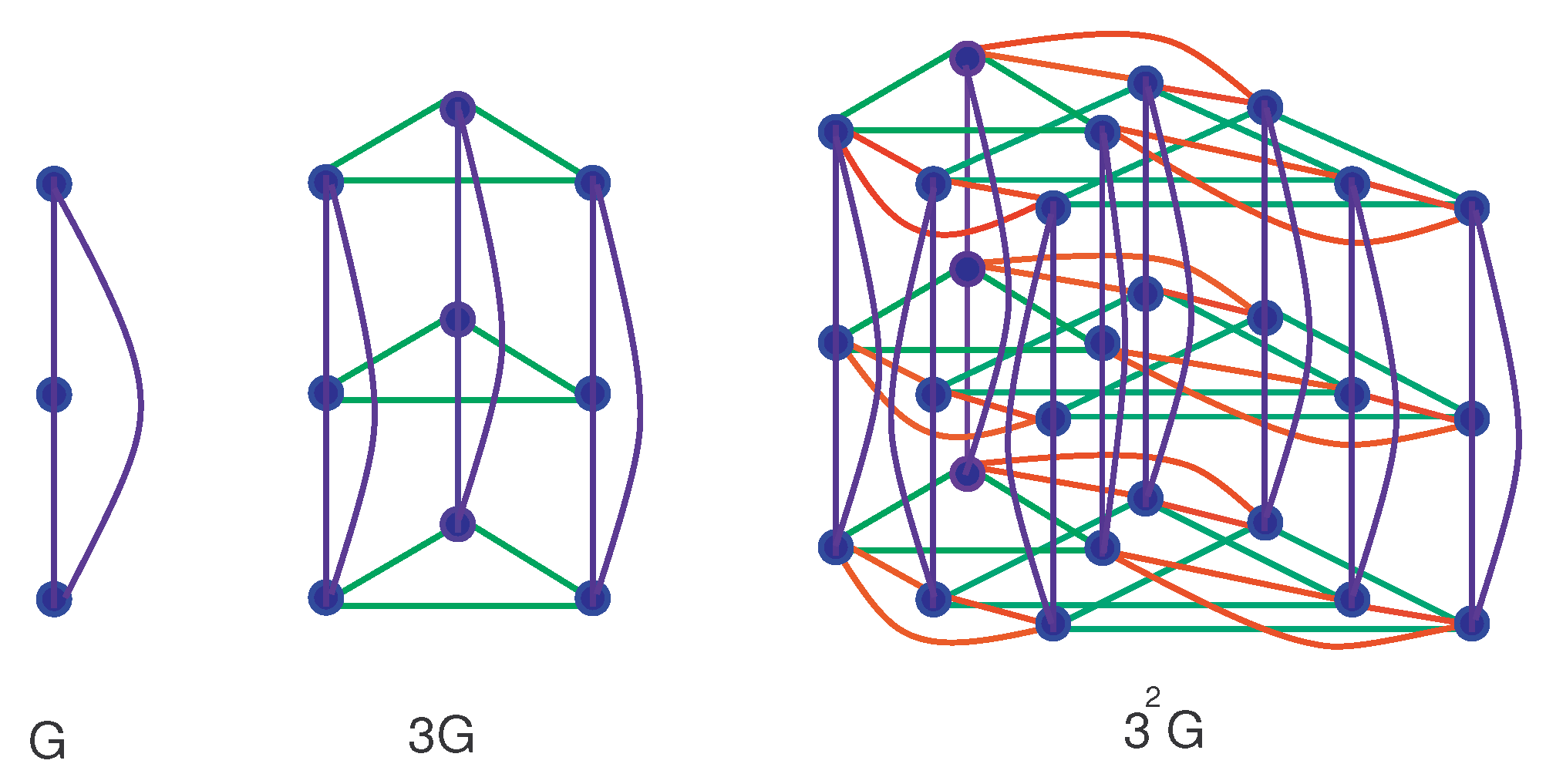
2. Materials and Methods
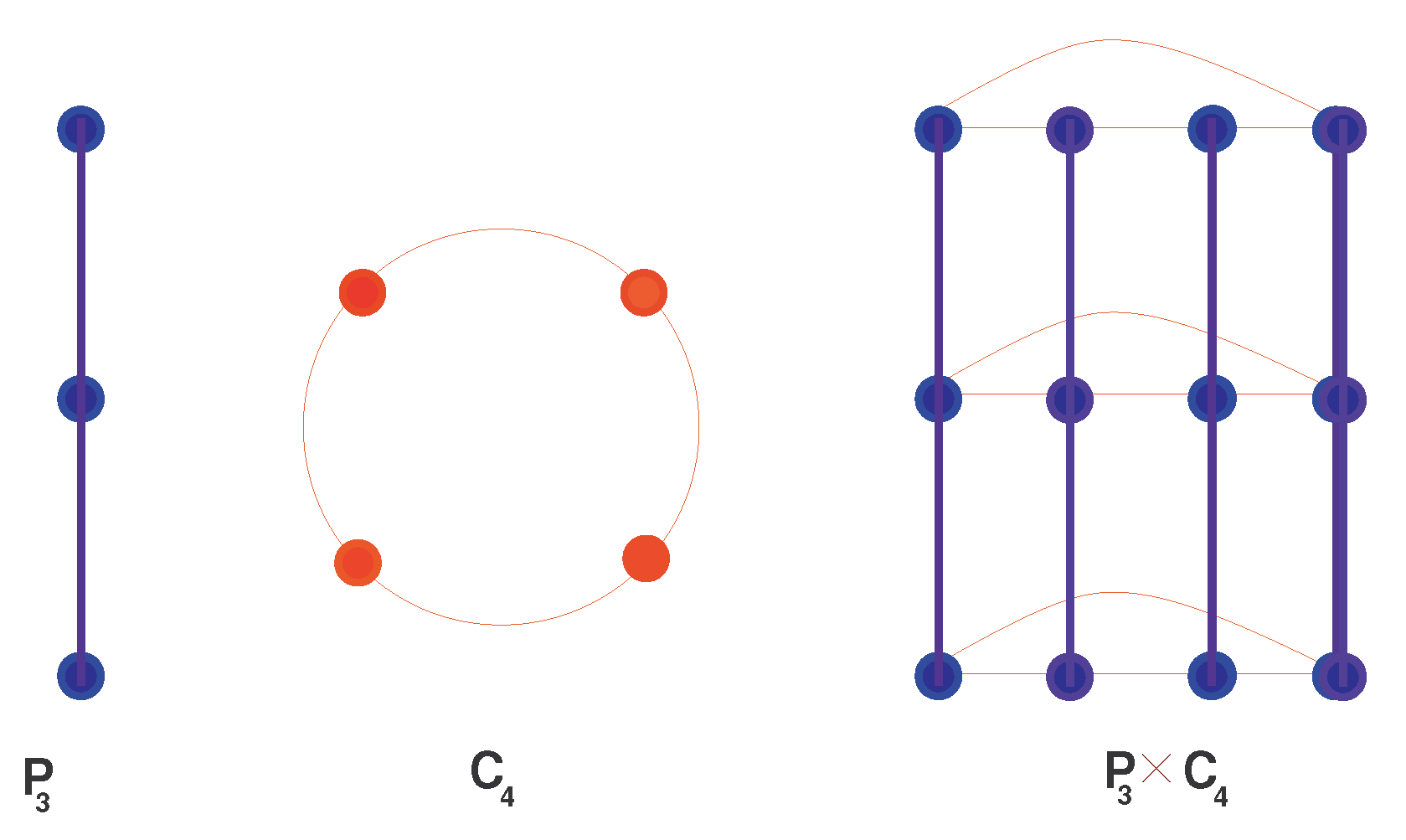
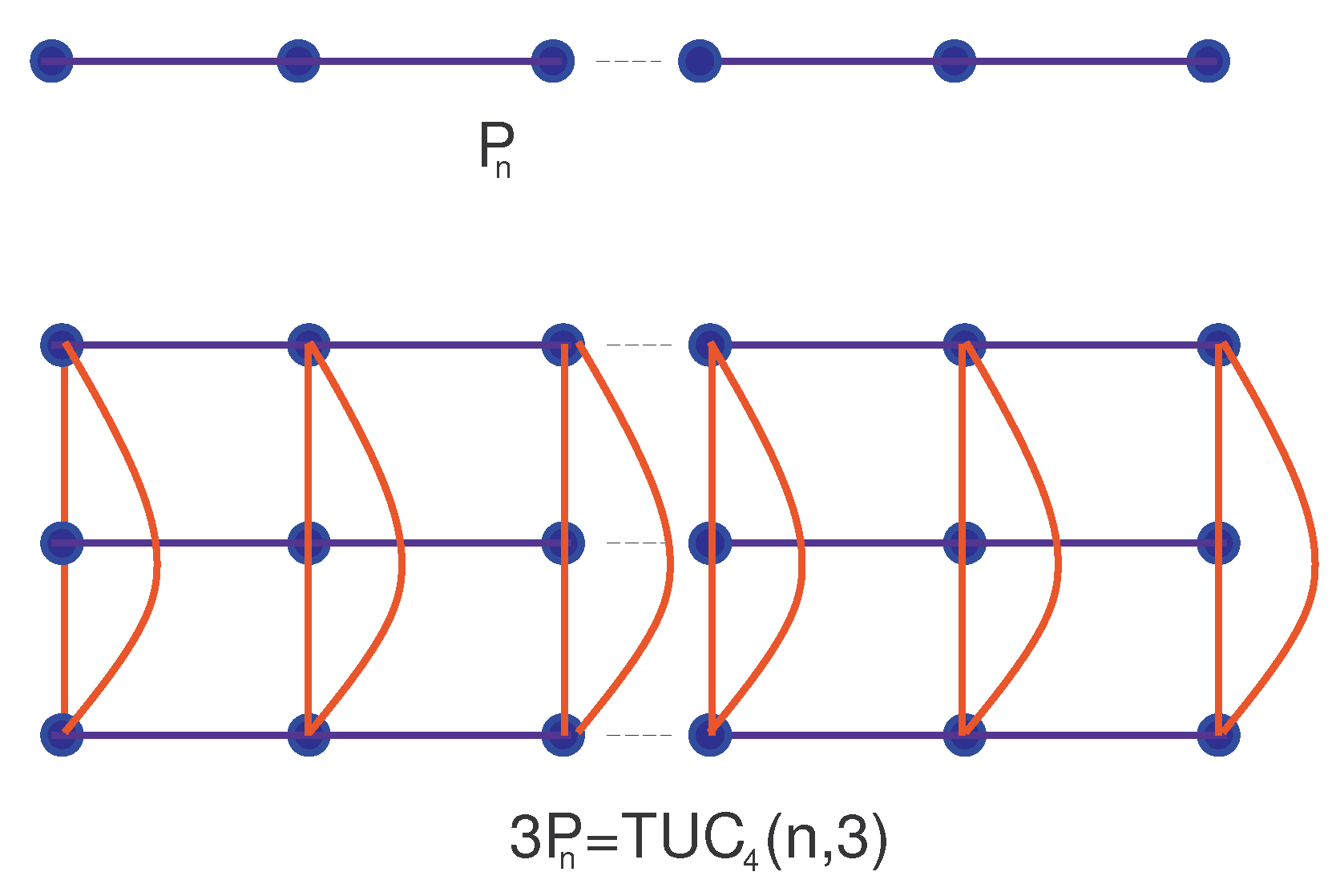
3. Network
Molecular Networks Formed by
Carbon Nanotube as
4. Main Results
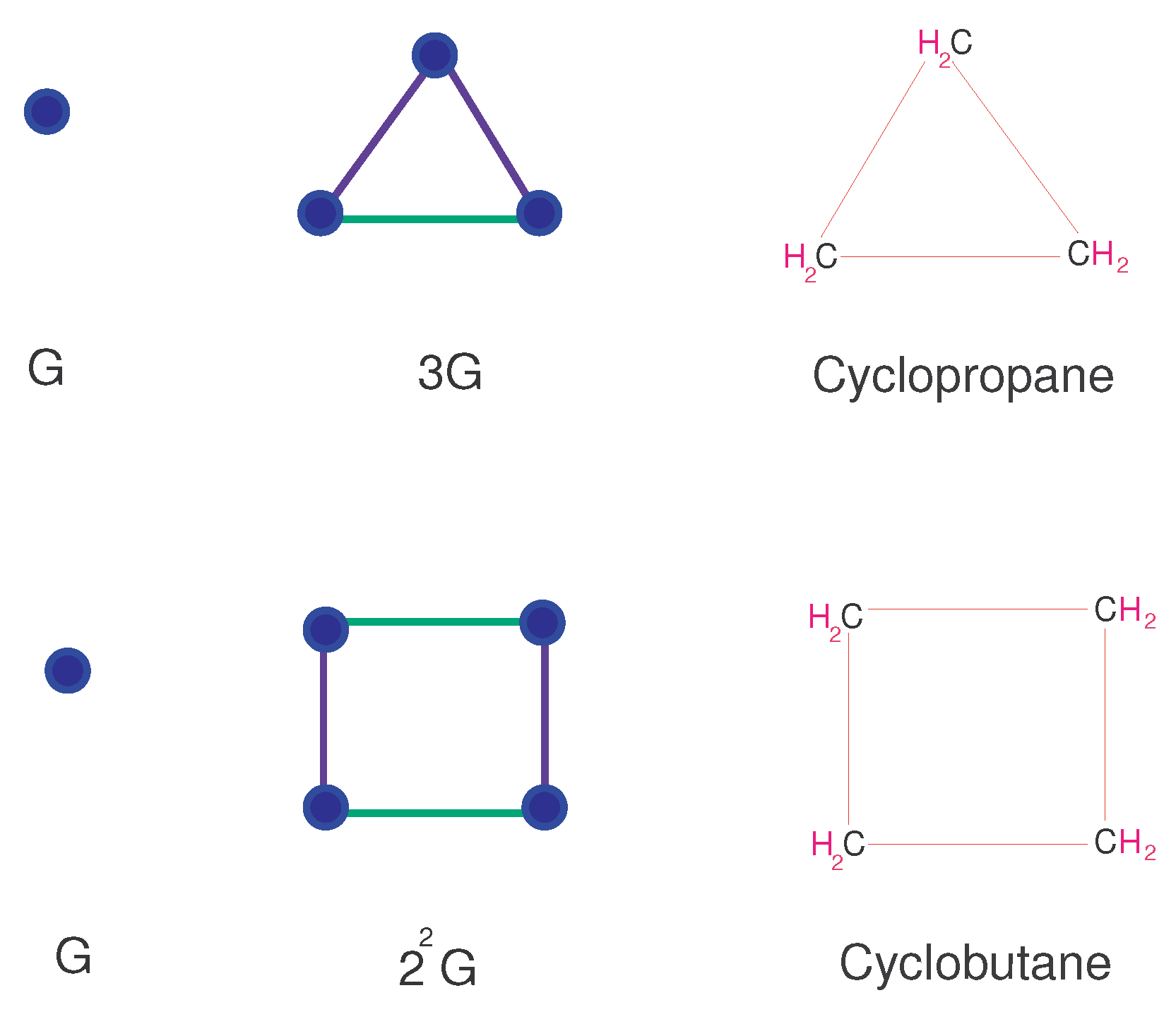
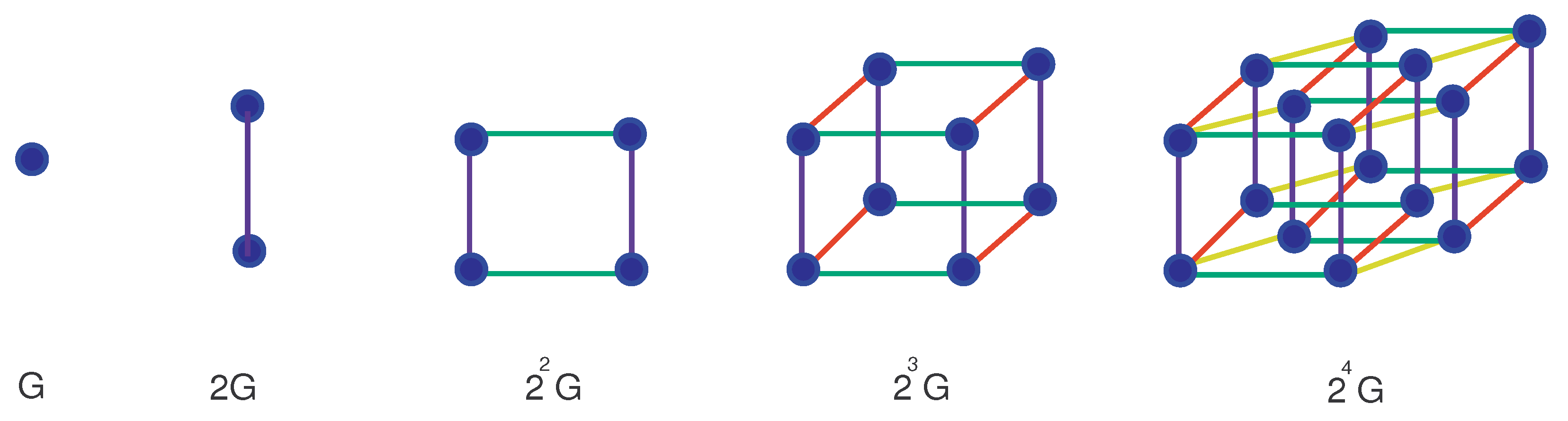
4.1. When Consist of Only One Vertex
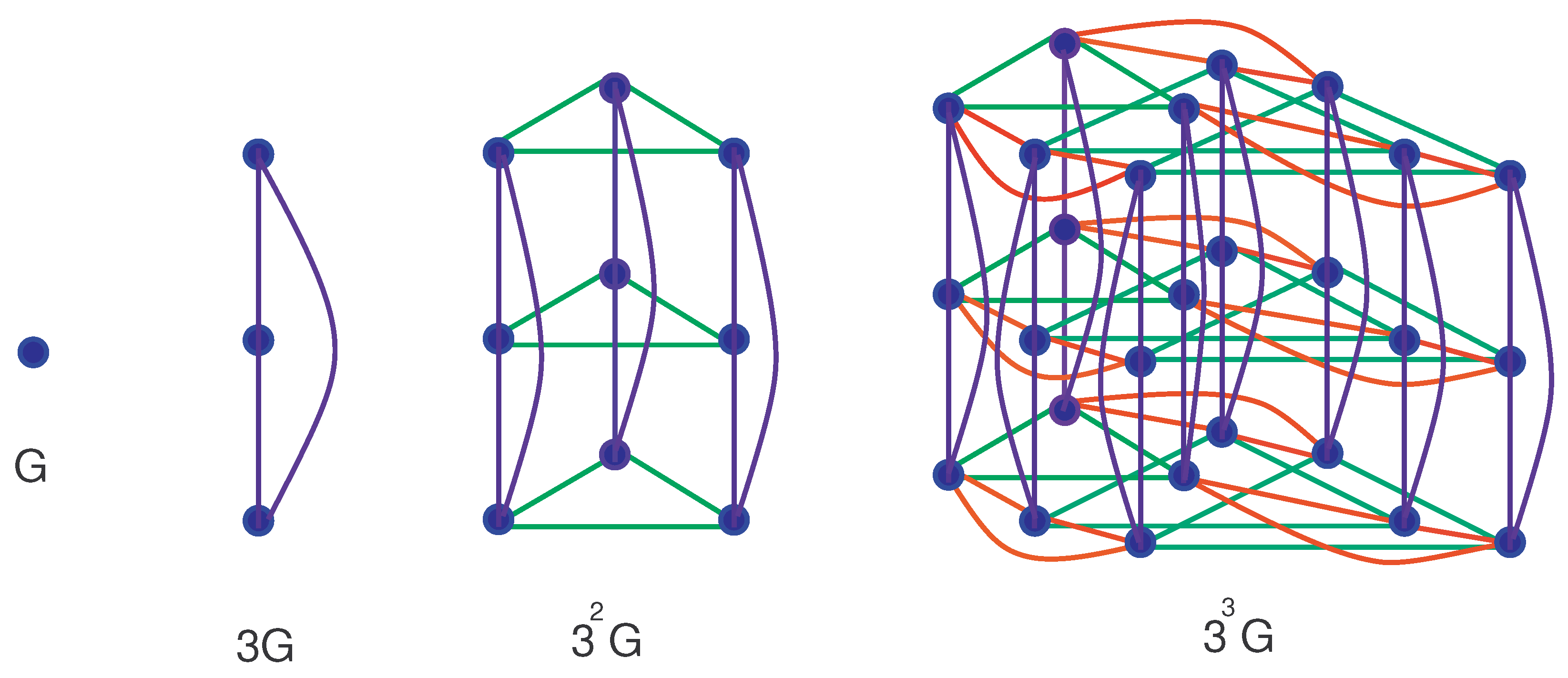
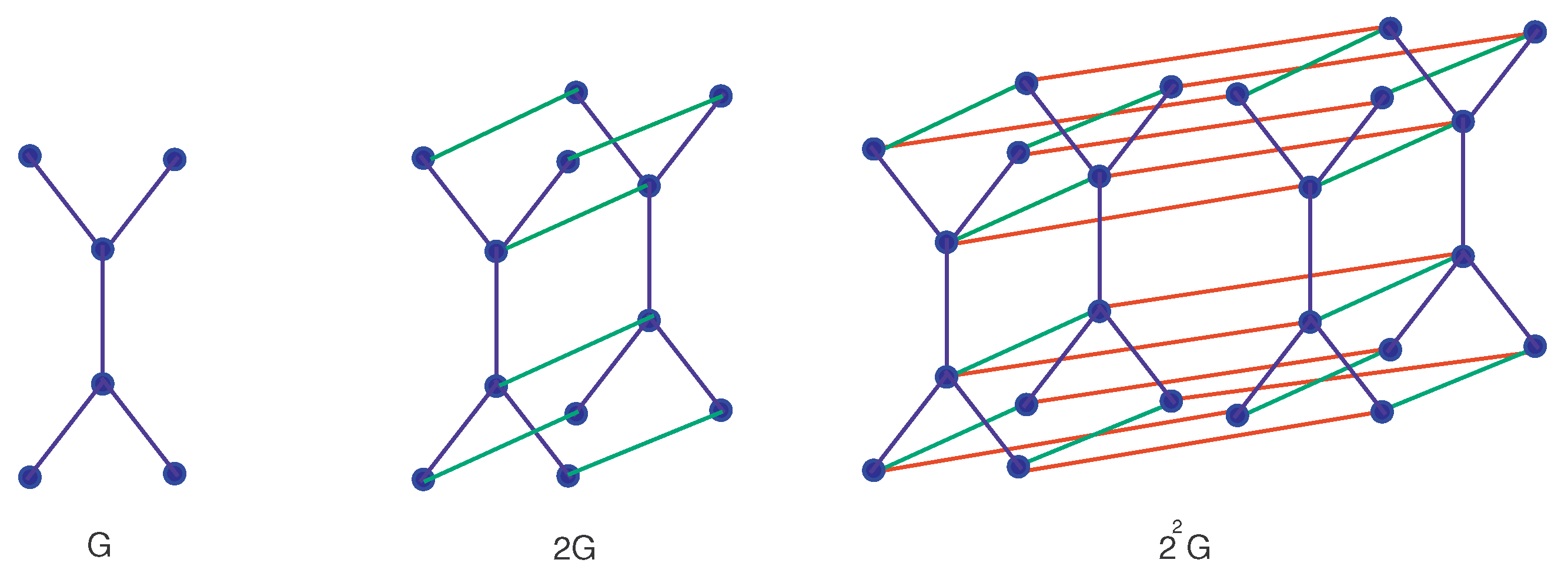
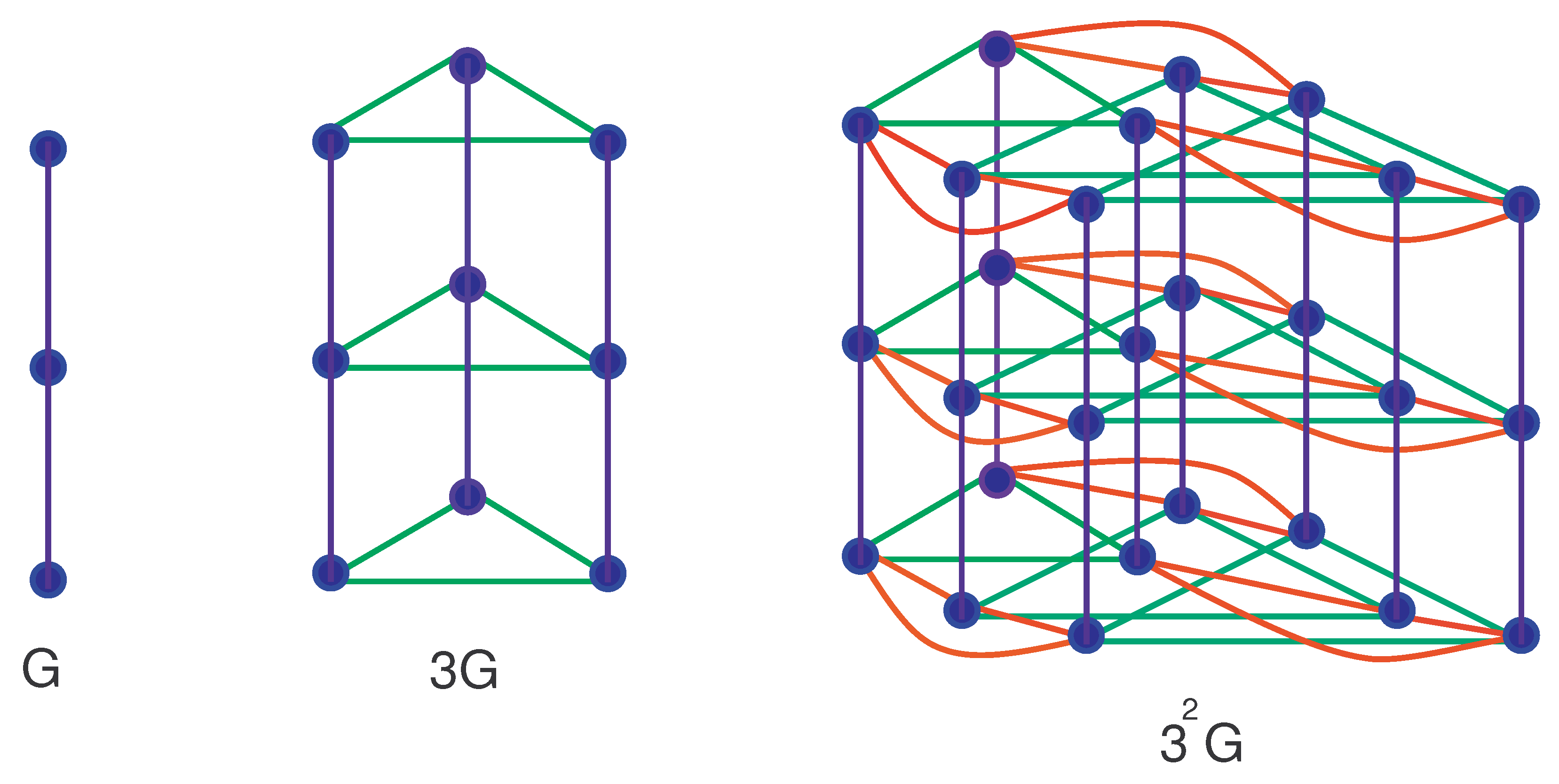
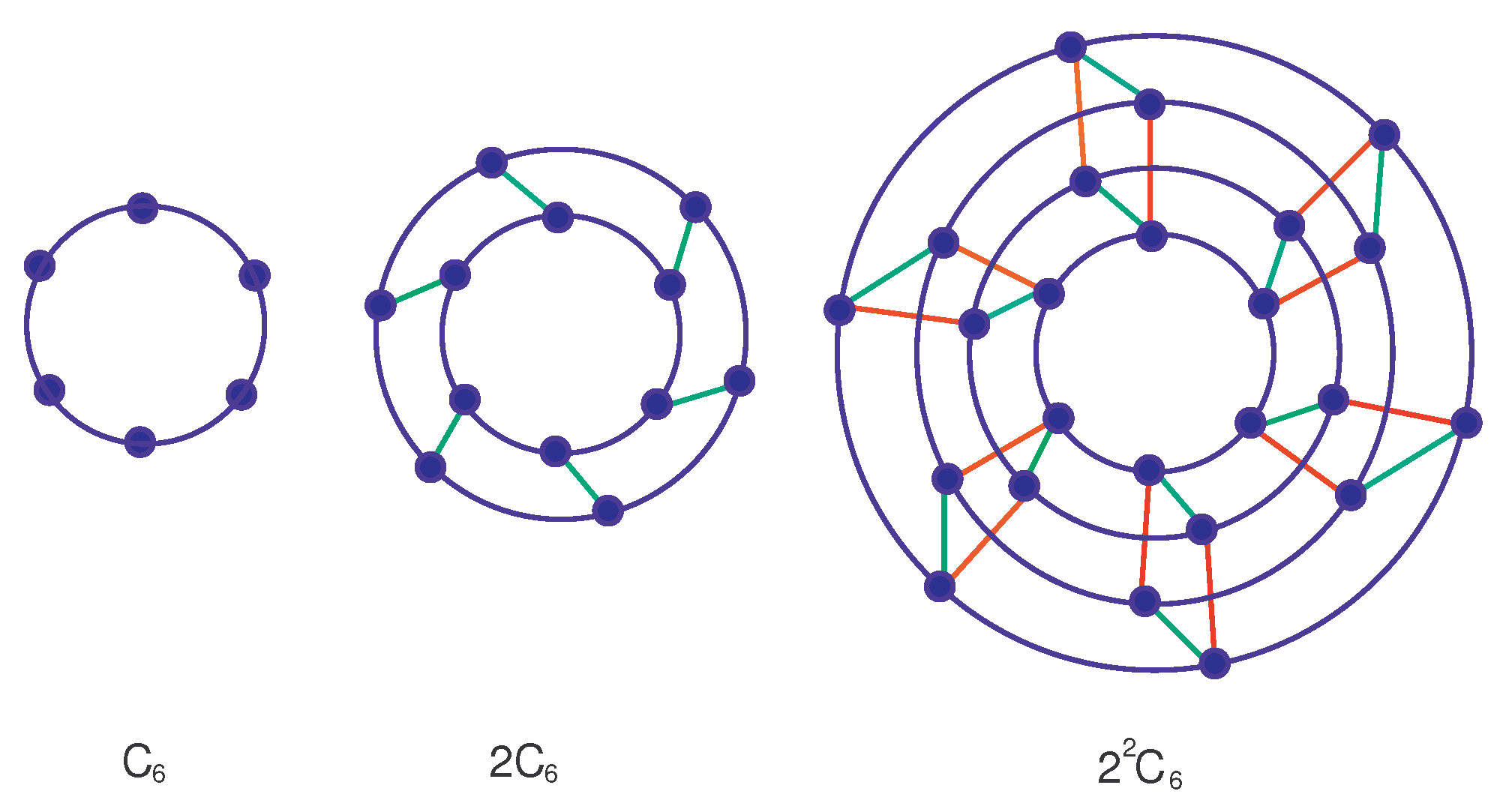
4.2. When Is Any -Vertex Simple Connected Graph
4.3. Applications of Computed Results as Zagreb Connection Indices of and
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feng, T.Y. A survey of interconnection networks. Computer 1981, 14, 12–27. [Google Scholar] [CrossRef]
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; Macmillan London: London, UK, 1976; Volume 290. [Google Scholar]
- Trinajstic, N. Chemical Graph Theory; Routledge: London, UK, 2018. [Google Scholar]
- Liu, J.B.; Shaker, H.; Nadeem, I.; Hussain, M. Topological aspects of boron nanotubes. Adv. Mater. Sci. Eng. 2018, 2018, 5729291. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, H.; Hussain, M.; Nazeer, W.; Chu, Y.M. Distance-based invariants of zigzag polyhex nanotube. In Mathematical Methods in the Applied Sciences; John Wiley and Sons Ltd.: New York, NY, USA, 2020. [Google Scholar]
- Rücker, G.; Rücker, C. On topological indices, boiling points, and cycloalkanes. J. Chem. Inf. Comput. Sci. 1999, 39, 788–802. [Google Scholar] [CrossRef]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Gutman, I.; Trinajstić, N. Graph theory and molecular orbitals. Total φ-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Hosoya, H.; Hosoi, K.; Gutman, I. A Topological Index for the total π-electron Energy. Theor. Chim. Acta 1975, 38, 37–47. [Google Scholar] [CrossRef]
- Ali, A.; Trinajstić, N. A novel/old modification of the first Zagreb index. Mol. Inform. 2018, 37, 1800008. [Google Scholar] [CrossRef]
- Manzoor, S.; Fatima, N.; Bhatti, A.A.; Ali, A. Zagreb connection indices of some nanostructures. Acta Chem. Iasi 2018, 26, 169–180. [Google Scholar] [CrossRef] [Green Version]
- Ducoffe, G.; Marinescu-Ghemeci, R.; Obreja, C.; Popa, A.; Tache, R.M. Extremal graphs with respect to the modified first Zagreb connection index. In Proceedings of the 2018 20th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC), Timisoara, Romania, 20–23 September 2018; pp. 141–148. [Google Scholar]
- Du, Z.; Ali, A.; Trinajstić, N. Alkanes with the first three maximal/minimal modified first Zagreb connection indices. Mol. Inform. 2019, 38, 1800116. [Google Scholar] [CrossRef]
- Basavanagoud, B.; Jakkannavar, P. Computing first leap Zagreb index of some nano structures. rn 2018, 55, 7. [Google Scholar]
- Ali, U.; Javaid, M.; Alanazi, A.M. Computing analysis of connection-based indices and coindices for product of molecular networks. Symmetry 2020, 12, 1320. [Google Scholar] [CrossRef]
- Ali, U.; Javaid, M.; Kashif, A. Modified Zagreb connection indices of the T-sum graphs. Main Group Met. Chem. 2020, 43, 43–55. [Google Scholar] [CrossRef]
- Cao, J.; Ali, U.; Javaid, M.; Huang, C. Zagreb connection indices of molecular graphs based on operations. Complexity 2020, 2020, 7385682. [Google Scholar] [CrossRef]
- Tang, J.H.; Ali, U.; Javaid, M.; Shabbir, K. Zagreb connection indices of subdivision and semi-total point operations on graphs. J. Chem. 2019, 2019, 9846913. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, M.; Saeed, M.; Javaid, M.; Hussain, M. Exact formula and improved bounds for general sum-connectivity index of graph-operations. IEEE Access 2019, 7, 167290–167299. [Google Scholar] [CrossRef]
- Asif, M.; Hussain, M.; Almohamedh, H.; Alhamed, K.M.; Alabdan, R.; Almutairi, A.A.; Almotairi, S. Study of Carbon Nanocones via Connection Zagreb Indices. Math. Probl. Eng. 2021, 2021, 5539904. [Google Scholar] [CrossRef]
- Asif, M.; Hussain, M.; Almohamedh, H.; Alhamed, K.M.; Almotairi, S. An Approach to the Extremal Inverse Degree Index for Families of Graphs with Transformation Effect. J. Chem. 2021, 2021, 6657039. [Google Scholar] [CrossRef]
- Fatima, N.; Bhatti, A.A.; Ali, A.; Gao, W. Zagreb connection indices of two dendrimer nanostars. Acta Chem. Iasi 2019, 27, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Ayache, A.; Alameri, A. Topological indices of the mk-graph. J. Assoc. Arab. Univ. Basic Appl. Sci. 2017, 24, 283–291. [Google Scholar]
- Afzal, F.; Naeem, M.; Chaudhry, F.; Afzal, D. Study of some topological invariants of subdivided mk graphs. Eurasian Chem. Commun. 2020, 2, 731–738. [Google Scholar]
- Javaid, M.; Ali, U.; Liu, J.B. Computing analysis for first zagreb connection index and coindex of resultant graphs. Math. Probl. Eng. 2021, 2021, 6019517. [Google Scholar] [CrossRef]
- Noureen, S.; Bhatti, A.A.; Ali, A. Extremal trees for the modified first Zagreb connection index with fixed number of segments or vertices of degree 2. J. Taibah Univ. Sci. 2020, 14, 31–37. [Google Scholar] [CrossRef] [Green Version]
- Noureen, S.; Bhatti, A.A.; Ali, A. Extremum modified first Zagreb connection index of-vertex trees with fixed number of pendent vertices. Discret. Dyn. Nat. Soc. 2020, 2020, 3295342. [Google Scholar] [CrossRef]
- Liu, J.B.; Raza, Z.; Javaid, M. Zagreb connection numbers for cellular neural networks. Discret. Dyn. Nat. Soc. 2020, 2020, 8038304. [Google Scholar] [CrossRef]
- Bataineh, M.S.; Raza, Z.; Sukaiti, M.E. On the zagreb connection indices of hex and honeycomb networks. J. Intell. Fuzzy Syst. 2021, 40, 4107–4114. [Google Scholar]
- Raza, Z. Zagreb connection indices for some benzenoid systems. Polycycl. Aromat. Compd. 2020, 1–14. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asif, M.; Kizielewicz, B.; Rehman, A.u.; Hussain, M.; Sałabun, W. Study of θϕ Networks via Zagreb Connection Indices. Symmetry 2021, 13, 1991. https://doi.org/10.3390/sym13111991
Asif M, Kizielewicz B, Rehman Au, Hussain M, Sałabun W. Study of θϕ Networks via Zagreb Connection Indices. Symmetry. 2021; 13(11):1991. https://doi.org/10.3390/sym13111991
Chicago/Turabian StyleAsif, Muhammad, Bartłomiej Kizielewicz, Atiq ur Rehman, Muhammad Hussain, and Wojciech Sałabun. 2021. "Study of θϕ Networks via Zagreb Connection Indices" Symmetry 13, no. 11: 1991. https://doi.org/10.3390/sym13111991
APA StyleAsif, M., Kizielewicz, B., Rehman, A. u., Hussain, M., & Sałabun, W. (2021). Study of θϕ Networks via Zagreb Connection Indices. Symmetry, 13(11), 1991. https://doi.org/10.3390/sym13111991







