Abstract
We present a new approach based on the notion of inertance for the simultaneous collisions without friction of a rigid solid. The calculations are performed using the screw (plückerian) coordinates, while the results are obtained in matrix form, and they may be easily implemented for different practical situations. One calculates the velocities after collision, the energy of lost velocities, and the loss of the kinetic energy. The general algorithm of calculation is described in the paper. The main assumption is that the normal velocities at the contact points vanish simultaneously. The coefficients of restitution at the contact points may be equal or not. Some completely solved applications are also presented, and the numerical results are discussed. The numerical values depend on which coefficient of restitution is used.
1. Introduction
The problem of the collision of rigid bodies is often met in the literature. The main problems may be described as follows. Most papers deal with the collision at one point, the collision being without [1,2,3,4,5,6,7,8,9,10,11,12,13,14] or with friction [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. Usually, the friction at the contact points is a Coulombian one [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43], but other types of friction may be also considered [44]. The unanimous accepted hypotheses for the collisions are [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49]: all the forces excepting the impact ones are neglected, there are two phases of collisions (compression and restitution), the rigid displacements vanish, and the tangential stiffness is infinite. Three different coefficients of restitution are used: Newton, Poisson, and energetic. It is proved [14,47] that in the in the case of the collision without friction the three coefficients of restitution have equal values, but this is not the singular case for their equality [43]. Researchers [30,31,39,40,41,43] have proved that in the case of collision with friction, the three coefficients of restitution may have different values. Moreover [43], there exists no relation between the values of the three coefficients of restitution and it is possible [43,47] that some certain coefficients of restitution may have values greater than 1 in the general case of collision with friction. The authors [30,31,40,41,42] have proved that the consideration of the Newton or Poisson variants may lead to inconsistent results. Generally, the authors consider that the best results in the study of collisions with friction are obtained using the energetic coefficient of restitution [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,39,40,41,42,43], but one may use some particular coefficients of restitution [38].
Most researchers deal with collision at one point, regardless of whether they discuss singular collision, multiple successive collisions, or collisions of particular kinematic chains. The approaches are based on classical mechanics and use of Lagrange’s or Kane’s equations. The simultaneous collision of a rigid solid at several points implies some difficulties concerning the distribution of velocities after the collision. This distribution must satisfy the Euler equation for the velocities of a rigid solid. Some aspects are discussed in [38,39,40,41] for some particular cases considering that at both points of collision, the coefficients of restitution are equal. The collision with friction may lead to complex mathematical problems concerning the cases of sticking and slipping of the rigid solid. It is proved that, in this situation, the contact point may move only on maximum four principal directions [43] resulting a system of polynomial equations [39,40,41] for which the solutions are obtained by numerical methods [49]. The phenomenon of jamb [24] is generally avoided in the references.
In our paper, we deal with screw coordinates [14,43,45,46,47,48,49]. The notion of inertance was introduced by Pandrea [13,48] and developed by Pandrea et al. [14,43,49].
Aside from the classical hypotheses at collision we added a supplementary one that states that the normal velocities at the contact points vanish simultaneously.
The paper is organized as follows: in Section 2, we present the case of the free rigid solid acted by two impulses at two different points; Section 3 and Section 4 are dedicated to the calculations of the velocities after collision, the energy of lost velocities, and the loss of kinetic energy; in Section 5, we highlight some particular cases; Section 6 describes the algorithm of calculation for the collision of the free rigid solid at two points; Section 7 is reserved for the presentation of four numerical applications, while in Section 8, we perform some discussions concerning the collision of the free rigid solid at two points; in Section 9, we discuss the general case of the collision at two points of the constrained rigid solid, and in Section 10, we calculate the velocities after collision; Section 11 is dedicated to the presentation of three numerical applications concerning the collision at two points of a rigid solid with constraints; in Section 12, we present the algorithm for the collision at two points of the rigid solid bounded by the surface of a certain equation, and in Section 13, we discuss an example; in Section 14, we present some general aspects concerning the collision with Coulombian friction; the paper ends with a Conclusion section.
2. The Case of the Free Rigid Solid
2.1. General Formulation of the Problem
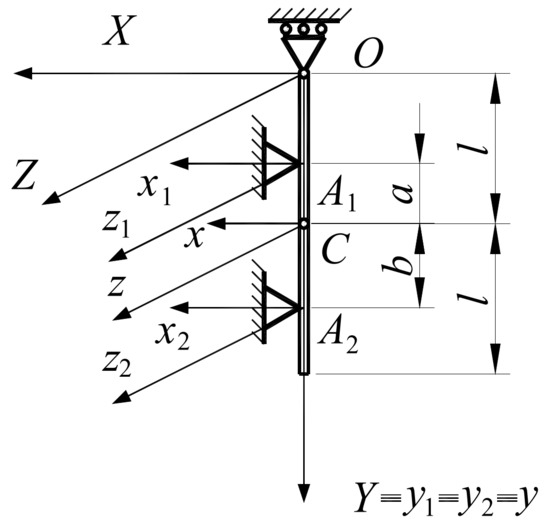
We have a rigid solid in general motion, and one considers the system of the central principal axes of inertia, being the center of weight. The kinematical parameters before the collision are (the velocity of the center of mass) and (the angular velocity) (Figure 1). The rigid solid collides normally at the points and , the collisions being without friction.
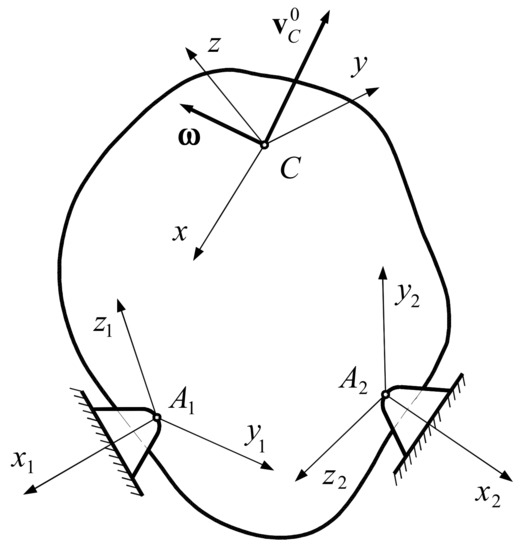
Figure 1.
The formulation of the problem.
One considers as known:
- -
- the mass and the central principal moments of inertia , , and for the rigid solid;
- -
- the restitution coefficients , , and , respectively, corresponding to the Newton, Poisson and energetic variants, respectively, defined by the relations , , and , respectively, are identical [14] in the case of a single collision without friction. In the previous expressions, represents the relative normal velocity after the collision at the contact point, is the relative normal velocity before the collision at the contact point, is the impulse in the phase of restitution, is the impulse corresponding to the phase of compression, represents the variation of the kinetic energy in the phase of restitution, and is the variation of the kinetic energy in the phase of compression;
- -
- the normal axes orientated to the outside of the rigid solid and at the collision points and , respectively;
- -
- the status of velocity and of the rigid solid before the collision.
One asks for (at the end of collision):
- -
- the velocity and the angular velocity ;
- -
- the velocities at the collision points;
- -
- the magnitudes and of the impulses at the points and , respectively;
- -
- the kinetic energy of the lost velocities;
- -
- the loss of kinetic energy.
One considers the cases of the Newton and Poisson variants.
The main hypothesis states that the normal velocities at the points and simultaneously vanish.
2.2. Notations
We use the following notations:
- -
- the components , , and , , of the angular velocities and , respectively;
- -
- the components , , and and , , and of the velocities and , respectively;
- -
- the screw (plückerian) coordinates of the velocities of the rigid solid
- -
- the coordinates , , and and , , and of the points and , respectively, relative to the reference frame ;
- -
- the director cosines of the axes of the local reference systems and and the rotational matrices and
- -
- the matrices , , , and defined by the relationswith ;
- -
- the matrices of the screw (plückerian) coordinates of the axes , , and , ,
- -
- the scalar values of the impulses and at the points and , respectively;
- -
- the matrix given by
- -
- the sign ∗ for the mixed product of two matrices in screw (plückerian) coordinates
- -
- the matrices of position and their inverseswhere ;
- -
- the components , , and and , , and of the velocities at the points and , respectively, components [48,49] given by relationswith ;
- -
- the matrix of inertia of the rigid solid and its inverse
2.3. Determination of the Impulses
The general theorems at collisions [13,14,48,49] may be put in the matrix relation
wherefrom it results in
Defining the inertances [13,14,43,48,49] by the relations
from the expression (11), one obtains
2.3.1. The Newton Model
For the Newton model [13,14,48,49], one may write
and from (13), it results in
The situation is captured in Figure 2.
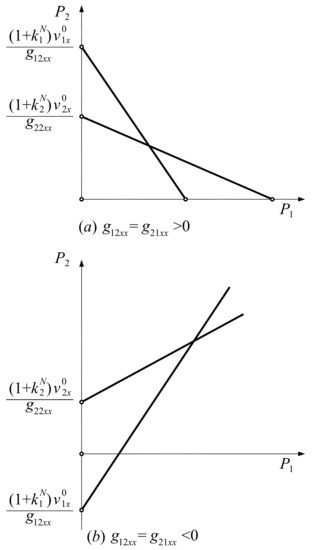
Figure 2.
(a) ; (b) .
For the planar collision, one has
with , .
It results in
The velocities after collision read
In addition, one has
Using the relations (15), one obtains the values of the impulses after collision for the Newton model
2.3.2. The Poisson Model
The impulses , , in the compression phase are obtained from the relations (13) imposing the conditions , ; it results in the system
with the solutions
The total impulses are deduced from the relations
3. Velocities after Collision
The matrix of the screw (plückerian) coordinates of the velocity at the point is deduced from the relation (11)
The tangential velocities at the point are
while the tangential velocities at the point read
The angles , , , between the tangential velocities and the axes , , before and after the collision are obtained from the expression
4. The Energy of Lost Velocities and the Loose of Kinetic Energy
The energy of lost velocities Ep [13,14,48,49] is defined by relation
Taking into account the expressions (10) and (11), one deduces
On the other hand,
and the relations (12) lead to
The loss of kinetic energy
is obtained by considering the expression (28), which successively reads
yielding
5. Particular Cases
5.1.
If the collision directions are perpendicular, and one of them passes through the center, then ; it results in the final impulses
for the Newton model, and
for the Poisson model, respectively.
5.2.
In this situation, one obtains
5.3. Planar Case
Let us return to the planar case, where we obtained the system
that is, a system of two linear equations with two unknowns.
Assuming that , , and , the system (40) becomes
where
The system (41) has a unique solution if and only if
The conditions (43) imply
If we consider that the rotational matrices are
then
and the relations (44) lead us to
No matter the value of ( or ), the relation (48) always holds true.
One may observe that the conditions and can be replaced by a weaker condition, namely
6. Algorithm of Calculation
The input data are:
- -
- mechanical and geometrical characteristics of the rigid solid (, , , , and );
- -
- the two points of collision and , that is the coordinates , , and , with , relative to the reference frame ;
- -
- the velocities and before collision;
- -
- the director cosines of the axes of the local systems , ;
- -
- the coefficients of restitution and .
One successively calculates:
- -
- the rotational matrices and using the expressions (2);
- -
- the matrices and , , using the formulae (3);
- -
- the matrices of screw coordinates , and , , using the relations (8);
- -
- the matrix given by (5);
- -
- the values , and , , using the formulae (8);
- -
- the matrix of inertia and its inverse with the aid of the expression (9);
- -
- the inertances , , using the formulae (12);
- -
- the impulses and :
- (a)
- for the Newton model using the relations (16),
- (b)
- for the Poisson model using the expression (18) and (19);
- -
- the velocities after the collision with the aid of the expressions (24)–(26);
- -
- the energy of lost velocities with the relation (28);
- -
- the loss of kinetic energy using the expression (34).
7. Numerical Applications
Example 1.
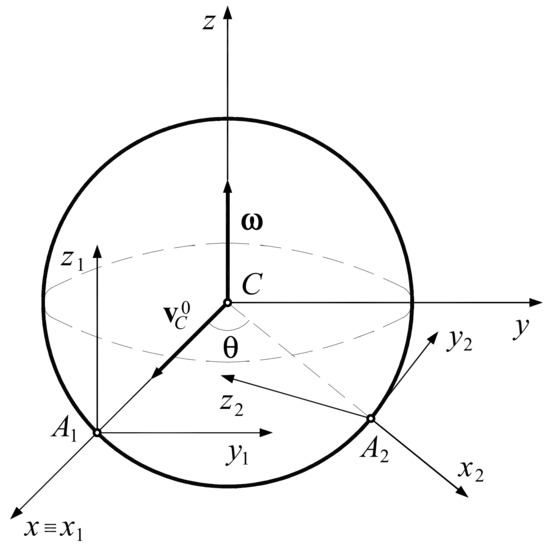
The collision of a sphere at two points (Figure 3).

Figure 3.
Example 1.
Due to the symmetry, we may choose the reference frames as shown in Figure 3. In addition: , , , , , , and , where is the radius of the sphere, and is the angle between the axis and the fixed axis , , , , and .
It results in the following
The Newton model yields
For the Poisson model, one obtains
The rest of results are identical to those obtained in the Newton case.
As numerical values, we consider , , , resulting in
Example 2.
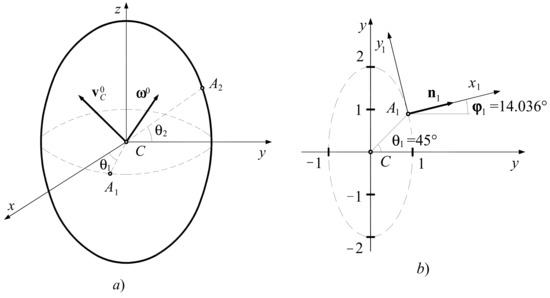
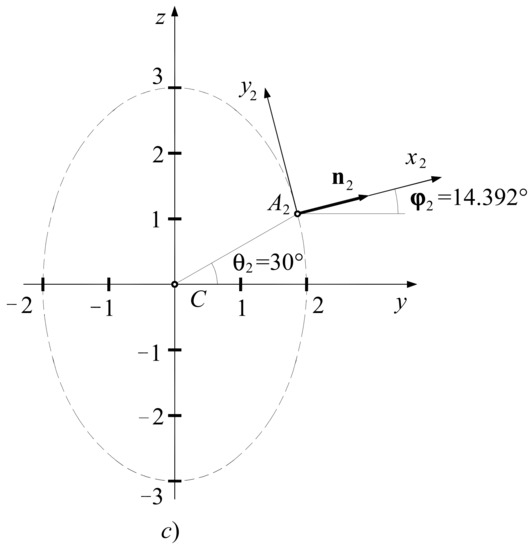
The collision of an ellipsoid at two points (Figure 4a).


Figure 4.
Example 2. (a) Formulation of the problem; (b,c) some calculations.
The equation of the ellipsoid is
One knows , , , .
The coordinates of point are obtained from the system
wherefrom (Figure 4b) , , .
Denoting the function , a vector which has the direction of the normal is given by
wherefrom , , , .
The rotational matrices read
For the coefficients of restitution, we choose the following values:
- -
- , (case 1);
- -
- , (case 2);
- -
- , (case 3);
- -
- , (case 4);
- -
- , (case 5).
The results are presented in Table 1.

Table 1.
Results for the numerical cases considered in Example 2.
The values obtained depend on which coefficient of restitution is used (Newton or Poisson). The same values result only if the coefficients of restitution at the points are equal (no matter their common value). This result is new, and it was not reported previously in the references.
Example 3.
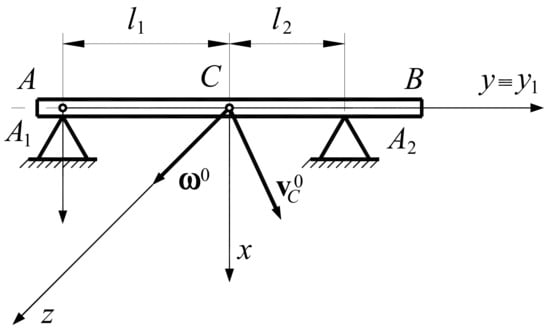
Planar collision of a bar at two points (Figure 5).

Figure 5.
Example 3.
One knows: , , , , , , , , , , and .
Proceeding analogically, one obtains:
- -
- for the Newton model:
- -
- for the Poisson model:
A classical subcase is that defined by , , and . Assuming now that , and , with the rest of the values remaining unchanged, the following results are obtained
- -
- for (regardless of the model (Newton or Poisson) used):
- -
- for (for both models (Newton and Poisson)):
- -
- for (both models):
One may observe that the results are identical, regardless of which coefficient of restitution is used. This is a particular case in which both coefficients of restitution at the two points are equal.
Example 4.
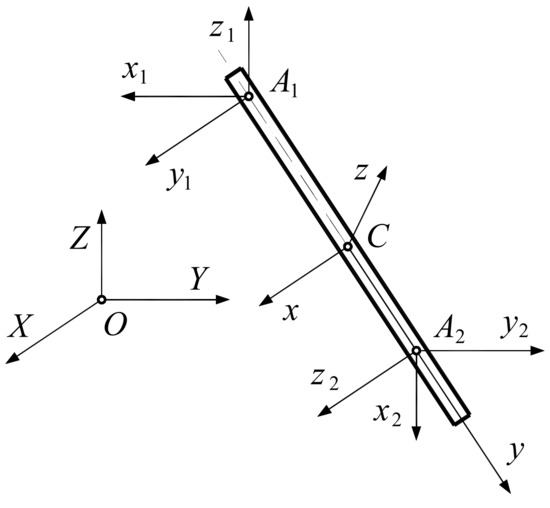
Spatial collision of a bar at two points (Figure 6).

Figure 6.
Example 4.
One knows:
- -
- the rotational matrix from the system to the system ,where , , ,
- -
- the mass of the bar ;
- -
- the dimensions ;
- -
- the central principal moments of inertia , and ;
- -
- the initial angular velocity , where , , and ;
- -
- the initial velocity of the center of mass , , with , , and ;
- -
- the coefficients of restitution:
- (i)
- , (case 1),
- (ii)
- , (case 2), and
- (iii)
- , (case 3).
It results in the following
The rotational matrices of the reference systems and relative to the reference system read
wherefrom
We impose and from the relations
one obtains
that is
It results in
- -
- for (both models, Newton and Poisson):
- -
- for , :
- -
- Newton model:
- -
- Poisson model:
- -
- for , (both model):
One may also observe that when the two coefficients of restitution at the two points are different, one does not obtain the same results using Newton or Poisson definitions.
8. Discussions
Recalling the relations (16), (18), and (19), one may ask for the determination of the situations in which the impulses given by the two models are equal, that is, and .
These equalities lead to the system
wherefrom
The previous relations become
Assuming that , (which is valid in the situation of single collision), the Equations (53) and (54) transform into the system
A first possibility is given by .
Taking into account that and , (there exist collisions at the points and ), the second possibility results.
From the expression
one gets
since , , , , for , it results
and, consequently, , .
If , , then the relations (16), (18), and (19) lead to
and since , , it yields , .
One may also question the compatibility of the systems (16) and (18).
To answer this question, we have to calculate the determinant
that is,
One may observe that if , which is equivalent to
then .
On the other hand, one has
Resulting in
Let us observe that if the two points and coincide (), then , , and , and it results in , , , , and Δ = 0; consequently, the formulae (68) cannot be applied. For the Newton model, we may use the first relation (15), which reads now
that is,
For the Poisson model, one has to use the first Equation (17), written as
wherefrom
The formulae (70) and (72) are identical to those obtained for the collision of a rigid solid with an impulse.
The conditions , , , imply the relations
which have the signification of real collisions at the points and .
When , taking into account the expression (59) and (60), the conditions (73) are equivalent to , and .
Remembering the relations (8), we obtain the conditions
which are the required conditions in this case.
The expressions (70) show that the model may be applied only if the initial data () and the matrices and (that is, the geometric positions of the two contact points) satisfy certain inequalities.
In the general case, one has to apply conditions (60), at which one has to add the expressions (62)–(67). These relations define the conditions which must be fulfilled by the initial data. If at least one of these the conditions is not satisfied, then it results that the problem is indeterminate.
More particular cases may be discussed, and some new particular conditions may be obtained.
9. Collision at Two Points of the Constrained Rigid Solid
Determination of the Impulses at the Collision Points
If the constraints’ space is described by the screw matrices of the directions of constraints , , being the number of constraints, and if the impulses have the scalar values , , …, , then [13,14,43,48,49] one may construct the matrix
while the general theorems at collision take the from
in which
The space of possible velocities is defined by the directions having the plückerian coordinates , , and by the matrix
the velocities along these directions having the scalar values , , …, and .
One obtains the relations
in which
Relation (76) becomes now
Multiplying the last relation by , taking into account [13,14,48,49] that
and denoting
one obtains
or, equivalently,
Considering now the inertances
the matrix Equation (85) leads to the system
For the Newton model, one has
wherefrom it results in the impulses and
From the expression (81), one obtains
and, by multiplication by and taking into account that [13,14,48,49]
it yields
wherefrom
10. Velocities after Collision
Knowing the impulses and (Equation (89)), from the matrix relation (85) one deduces , while the system (87) yields and .
Further on, using the inertances
from the matrix relation (85), one obtains the velocities
The energy of the lost velocities reads
while the variation of the kinetic energy is
11. Examples
Example 5.
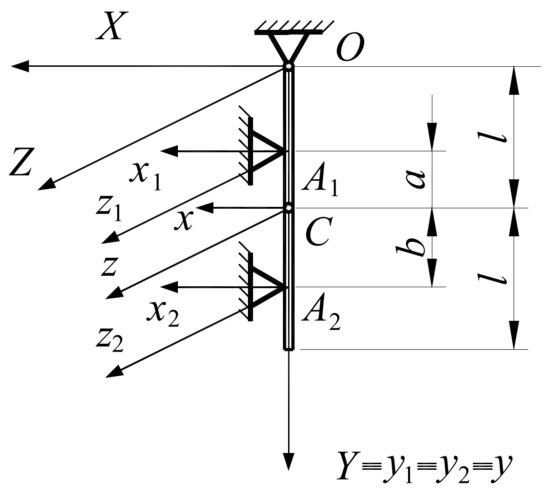
The homogeneous bar (Figure 7) collides with two obstacles at the points
and
.

Figure 7.
Example 5.
One knows: the mass of the bar, the dimensions , , , the coefficients of restitution and at the points and , respectively, and the initial distribution of velocities, , , , , , .
The only possible motion is the rotation about the axis, and because , one obtains
The constraints are:
- -
- displacement along the axis; since , the following results
- -
- displacement along the axis; we have , hence
- -
- displacement along the axis; , therefore
- -
- rotation about the axis;
- -
- rotation about the axis;
in conclusion
It is obvious that
We have
The system (88) is:
- -
- incompatible if the rank of the extended matrix
is equal to 2, that is either
or
The relation (98) leads to
wherefrom
Analogically, expression (99) offers
wherefrom one gets the same relation (100);
- -
- compatible if , that is
wherefrom
For instance, if , then it results in
Since and , one obtained, in this particular case, , .
Remark 1.
One may observe that
, and
The resulting condition (63) is a sufficient but not necessary one for the incompatibility of the system which gives the impulses.
Example 6.
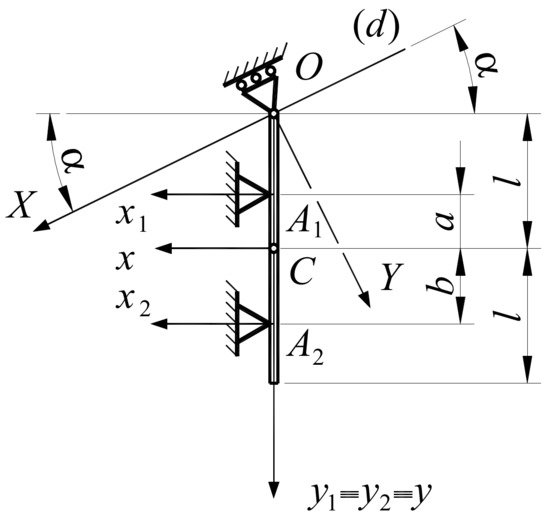
Let us modify the previous example assuming that the end of the bar can move along the
axis (Figure 8).

Figure 8.
Example 6.
In this situation, the bar may rotate about the axis,
and it may translate along the axis,
resulting in
Analogically, the constraints are:
- -
- the translation along the axis,
- -
- the translation along the axis,
- -
- the rotation about the axis,
- -
- the rotation about the axis,
one gets
A simple calculation offers
One obtains
Further on, for the simplicity of the calculation, we will consider that . It results in
As numerical values, we consider: , , , and . The simulations are performed in the following cases: (i) , ; (ii) , ; (iii) , ; (iv) , ; (v) , ; (vi) , ; (vii) , ; (viii) , ; (ix) , . The results are presented in Table 2.

Table 2.
Results for the numerical cases considered in Example 6.
Remark 2.
One may solve this example considering the rigid solid as a free one to obtain the same results.
Indeed, we have
The resulting values are the same for , and . Moreover, since
one obtains the same value for .
The coincidence of the results is explained by the fact that the motion is permitted along the directions on which there exist the impulses.
Example 7.
Let us assume that the only possibilities of motion for the bar are the rotation about the axis, and the displacement along the straight line
(Figure 9).

Figure 9.
Example 7.
The initial conditions are , , , , , and .
In this situation, we have
The simulations are performed for , , , , and the following cases: (i) , ; (ii) , ; and (iii) , . The results are given in Table 3 for , Table 4 for , and Table 5 for .

Table 3.
Results for the numerical cases considered in Example 7, .

Table 4.
Results for the numerical cases considered in Example 7, .

Table 5.
Results for the numerical cases considered in Example 7, .
12. Algorithm for the Collision at Two Points of the Rigid Solid Bounded by the Surface of Equation
The algorithm is as follows:
Inputs:
- -
- the geometric and mechanical parameters of the rigid solid;
- -
- the initial velocity of the center of weight ;
- -
- the coordinates , , and of the collision points , ;
- -
- the coefficients of restitution , .
- Step 1.
- Determination of the matrices and of the plückerian (screw) coordinates.One successively calculates
- Step 2.
- Determination of the matrices , , , and .One calculates:
- Step 3.
- Determination of the initial velocities in local coordinates at the contact points and .One calculates:
Remark 3.
One must obtain
and
.
- Step 4.
- Determination of the inertances.One uses the formulae:
- Step 5.
- Determination of the impulses.One obtains:
- Step 6.
- Determination of the velocities after collision.One calculates:
- Step 7.
- Determination of the energy of the lost velocities and the variation of the kinetic energy.One uses the formulae:
13. Example
Example 8.
Let us consider the sphere of equation
and mass
, which is collided at the points
and
(that is,
,
,
,
,
,
). One knows:
,
,
,
,
,
, and the coefficients of restitution
and
.
We have:
14. Collision with Coulombian Friction
14.1. General Aspects
In the case of collision with friction, one has to take into account the existence of the tangential impulses , which are situated in the planes (Figure 10). The scalar values of these impulses are , , while their senses are opposite to the tangential velocities . The scalar components of the tangential velocities read and , .
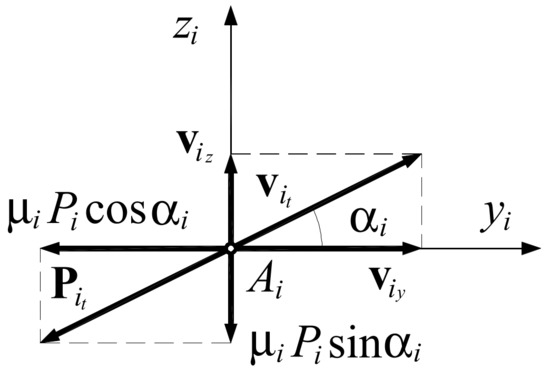
Figure 10.
Scalar components of impulse and velocity.
Consequently, the impulses at the points , , have the components , , and , where
14.2. Mathematical Model
Taking into account the components of the impulses, the general theorems [13,14,48,49] read
Using the notations:
one obtains
wherefrom
We denote by , , and , , the matrices of inertances,
These matrices are constant, each one having one row and three columns.
From the matrix relation (142), one deduces the system
The system has six non-linear equations with eight unknowns (, , , , , and ).
The non-linearity is given by the relations (137), (139), and (144).
We have to work with differentials, the system (144) becoming
15. Conclusions
This paper solves the problem of the simultaneous collision of a rigid solid at two points. The authors considered a supplementary hypothesis which states that the normal velocities at the contact points vanish simultaneously. The calculations are performed using the theory of the screw coordinates and the notion of inertances. We obtained the velocities after the collision, the energy of lost velocities, and the loss of kinetic energy. The problem is solved in both cases: free rigid solid and rigid solid with constraints. The coefficients of restitution are considered in the Newton and Poisson cases. We proved that in the general case, the results obtained using Newton and Poisson coefficients of restitution are different. In the case of the constrained rigid solid, we also deduced the expressions of the constraint impulses.
All the results are given in matrix form, and we present the algorithms of calculation in all possible situations. There are also cases of indetermination of the problem. The results are validated in some particular cases, proving that the problems may also be solved by classical methods.
Future works will be dedicated to the collision at several points of the rigid solid and to the case of the collisions with friction.
Author Contributions
Conceptualization, I.-B.D., N.P., and N.-D.S.; methodology, I.-B.D., N.P., and N.-D.S.; software, I.-B.D., N.P., and N.-D.S.; validation, I.-B.D., N.P., and N.-D.S.; formal analysis, I.-B.D., N.P., and N.-D.S.; investigation, I.-B.D., N.P., and N.-D.S.; resources, I.-B.D., N.P., and N.-D.S.; data curation, I.-B.D., N.P., and N.-D.S.; writing—original draft preparation, I.-B.D., N.P., and N.-D.S.; writing—review and editing, I.-B.D., N.P., and N.-D.S.; visualization, I.-B.D., N.P., and N.-D.S.; supervision, I.-B.D., N.P., and N.-D.S.; project administration, I.-B.D., N.P., and N.-D.S.; funding acquisition, I.-B.D., N.P., and N.-D.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shi, P. The Restitution Coefficient for a Linear Elastic Rod. Math. Comput. Model. 1998, 28, 427–435. [Google Scholar] [CrossRef]
- Shan, H.; Su, J.; Badiu, F.; Zhu, J.; Xu, L. Modeling and simulation of multiple impacts of falling rigid bodies. Math. Comput. Model. 2006, 43, 592–611. [Google Scholar] [CrossRef]
- Rossikhin, Y.A.; Shitikova, M.V. The analysis of the impact response of a thin plate via fractional derivative standard linear solid model. J. Sound Vib. 2011, 330, 1985–2003. [Google Scholar] [CrossRef]
- Chatterjee, A. On the Realism of Complementarity Conditions in Rigid Body Collisions. Nonlinear Dyn. 1999, 20, 159–168. [Google Scholar] [CrossRef]
- Dal Pont, S.; Dimnet, E. A theory for multiple collisions of rigid solids and numerical simulation of granular flow. Int. J. Solids Struct. 2006, 43, 6100–6114. [Google Scholar] [CrossRef][Green Version]
- Pazouki, A.; Mazhar, H.; Negrut, D. Parallel collision detection of ellipsoids with applications in large scale multibody dynamics. Math. Comput. Simul. 2012, 82, 879–894. [Google Scholar] [CrossRef]
- Rodgers, B.; Goyal, S.; Kelly, G.; Sheehy, M. The dynamics of multiple pair-wise collisions in a chain for designing optimal shock amplifiers. Shock Vib. 2009, 16, 99–116. [Google Scholar] [CrossRef]
- Cheng, Z.; Pellettiere, J.A.; Crandall, J.R.; Pilkey, W.D. Optimal occupant kinematics and crash pulse for automobile frontal impact. Shock Vib. 2009, 16, 61–73. [Google Scholar] [CrossRef]
- Batista, M. Self-induced jumping of a rigid body of revolution on a smooth horizontal surface. Int. J. Non-Linear Mech. 2008, 43, 26–35. [Google Scholar] [CrossRef]
- Mao, J.; Fu, Y. Dynamics of Periodic Impulsive Collision in Escapement Mechanism. Shock Vib. 2013, 20, 1001–1010. [Google Scholar] [CrossRef]
- Anisimov, A.V.; Zabaryanskii, S.F. Simulation of motion of a collection of rigid bodies, taking into account their collisions and joints. Cybern. Syst. Anal. 2005, 41, 500–508. [Google Scholar] [CrossRef]
- Kapoulitsas, G.M. On the collision of rigid bodies. Z. Angew. Math. Phys. ZAMP 1995, 46, 709–723. [Google Scholar] [CrossRef]
- Pandrea, N. About collisions of two solids with constraints. Rev. Romaine Sci. Tech. Sér. Méch. Appl. 2004, 49, 1–6. [Google Scholar]
- Pandrea, N.; Stănescu, N.D. A New Approach in the Study of Frictionless Collisions Using Inertances. Proc. Int. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 2144–2157. [Google Scholar] [CrossRef]
- Pfeiffer, F. On impacts with friction. Appl. Math. Comput. 2010, 217, 1184–1192. [Google Scholar] [CrossRef]
- Lankarani, H.M.; Fereira, M.F.O.S. Treatment of Impact with Friction in Planar Multibody Mechanical Systems. Multibody Syst. Dyn. 2001, 6, 203–227. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, C.; Chen, B. The numerical method for three-dimensional impact with friction of multi-rigid-body system. Sci. China Ser. G Phys. Math. Astron. 2006, 49, 102–118. [Google Scholar] [CrossRef]
- Yao, W.; Chen, B.; Liu, C. Energetic coefficient of restitution for planar impact in multi-rigid-body systems with friction. Int. J. Impact Eng. 2005, 31, 255–265. [Google Scholar] [CrossRef]
- Payr, M.; Glocker, C. Oblique Frictional Impact of a Bar: Analysis and Comparison of Different Impact Laws. Nonlinear Dyn. 2005, 41, 361–383. [Google Scholar] [CrossRef][Green Version]
- Nordmark, A.; Dankowicz, H.; Champneys, A. Discontinuity-induced bifurcations in systems with impacts and friction: Discontinuities in the impact law. Int. J. Non-Linear Mech. 2009, 44, 1011–1023. [Google Scholar] [CrossRef]
- Shen, Y.; Stronge, W.J. Painlevé paradox during oblique impact with friction. Eur. J. Mech. A Solids 2011, 30, 457–467. [Google Scholar] [CrossRef][Green Version]
- Marghitu, D.B.; Hurmuzlu, Y. Nonlinear Dynamics of an Elastic Rod with Frictional Impact. Nonlinear Dyn. 1996, 10, 187–201. [Google Scholar] [CrossRef]
- Battle, J.A. The Sliding Velocity Flow of Rough Collisions in Multibody Systems. J. Appl. Mech. 1996, 63, 804–809. [Google Scholar] [CrossRef]
- Battle, J.A.; Cardona, S. The Jamb (Self-Locking) Process in Three-Dimensional Collisions. J. Appl. Mech. 1998, 65, 417–423. [Google Scholar] [CrossRef]
- Battle, J.A. Termination conditions for three-dimensional inelastic collisions in multibody systems. Int. J. Impact Eng. 2001, 25, 615–629. [Google Scholar] [CrossRef]
- Brach, R.M. Friction, Restitution, and Energy Loss in Planar Collisions. J. Appl. Mech. 1984, 51, 164–170. [Google Scholar] [CrossRef]
- Brach, R.M. Rigid Body Collisions. J. Appl. Mech. 1989, 56, 133–138. [Google Scholar] [CrossRef]
- Brogliato, B. Kinetic quasi-velocities in unilaterally constrained Lagrangian mechanics with impacts and friction. Multibody Syst. Dyn. 2013, 32, 175–216. [Google Scholar] [CrossRef]
- Elkaranshawy, H.A. Rough collision in three-dimensional rigid multi-body systems. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2007, 221, 541–550. [Google Scholar] [CrossRef]
- Glocker, C. Energetic consistency conditions for standard impacts. Part I: Newton type inequality impact laws and Kane’s example. Multibody Syst. Dyn. 2013, 29, 77–117. [Google Scholar] [CrossRef]
- Glocker, C. Energetic consistency conditions for standard impacts. Part II: Poisson-type inequality impact laws. Multibody Syst. Dyn. 2014, 32, 445–509. [Google Scholar] [CrossRef]
- Keller, J.B. Impact with Friction. J. Appl. Mech. 1986, 53, 1–4. [Google Scholar] [CrossRef]
- Marghitu, D.B.; Hurmuzlu, Y. Three-Dimensional Rigid-Body Collisions with Multiple Contact Points. J. Appl. Mech. 1995, 62, 725–732. [Google Scholar] [CrossRef]
- Stronge, W.J. Rigid Body Collisions with Friction. Proc. R. Soc. A Math. Phys. Eng. Sci. 1990, 431, 169–181. [Google Scholar] [CrossRef]
- Tavakoli, A.; Gharib, M.; Hurmuzlu, Y. Collision of Two Mass Baton with Massive External Surfaces. J. Appl. Mech. 2012, 79, 051019. [Google Scholar] [CrossRef]
- Wang, Y.; Mason, M.T. Two-Dimensional Rigid-Body Collisions with Friction. J. Appl. Mech. 1992, 59, 635–642. [Google Scholar] [CrossRef]
- Yu, H.N.; Zhao, J.S.; Chu, F.L. An enhanced multi-point dynamics methodology for collision and contact problem. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 1203–1223. [Google Scholar] [CrossRef]
- Chatterjee, A.; Rodriguez, A.; Bowling, A. Analytic solution for the planar indeterminate impact problems using an energy constraint. Multibody Syst. Dyn. 2018, 42, 347–379. [Google Scholar] [CrossRef]
- Djerassi, S. Collision with friction; Part A: Newton’s hypothesis. Multibody Syst. Dyn. 2009, 21, 37–54. [Google Scholar] [CrossRef]
- Djerassi, S. Collision with friction; Part B: Poisson’s and Stronge’s hypotheses. Multibody Syst. Dyn. 2009, 21, 55–70. [Google Scholar] [CrossRef]
- Djerassi, S. Stronge’s hypothesis-based solution to the planar collision-with-friction problem. Multibody Syst. Dyn. 2010, 24, 493–515. [Google Scholar] [CrossRef]
- Flores, P.; Ambrósio, J.; Claro, J.C.P.; Lankarani, H.M. Influence of the contact-impact force model on the dynamic response of multi-body systems. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2006, 220, 21–34. [Google Scholar] [CrossRef]
- Pandrea, N.; Stănescu, N.D. A new approach in the study of the collisions with friction using inertances. Proc. Int. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 817–834. [Google Scholar] [CrossRef]
- Pennestrì, E.; Valentini, P.P.; Vita, L. Multibody dynamics simulation of planar linkages with Dahl friction. Multibody Syst. Dyn. 2007, 17, 321–347. [Google Scholar] [CrossRef]
- Yuan, M.S.C.; Freudenstein, F. Kinematic Analysis of Spatial Mechanisms by Means of Screw Coordinates. Part 1—Screw Coordinates. J. Eng. Ind. 1971, 93, 61–66. [Google Scholar] [CrossRef]
- Yuan, M.S.C.; Freudenstein, F.; Woo, L.S. Kinematic Analysis of Spatial Mechanisms by Means of Screw Coordinates. Part 2—Analysis of Spatial Mechanisms. J. Eng. Ind. 1971, 93, 67–73. [Google Scholar] [CrossRef]
- Brogliato, B. Nonsmooth Mechanics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Pandrea, N. Elements of the Mechanics of Solid Rigid in Plückerian Coordinates; The Publishing House of the Romanian Academy: Bucharest, Romania, 2000. [Google Scholar]
- Stănescu, N.D.; Munteanu, L.; Chiroiu, V.; Pandrea, N. Dynamical Systems. Theory and Applications; The Publishing House of the Romanian Academy: Bucharest, Romania, 2007. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).