Slow Invariant Manifold of Laser with Feedback
Abstract
1. Introduction
2. Slow–Fast Dynamical System
3. Stability Analysis
3.1. Fixed Points, Jacobian Matrix and Eigenvalues
3.2. Bifurcation Diagram
3.3. Numerical Computation of the Lyapunov Characteristic Exponents
4. Slow Invariant Manifold
5. Discussion
“Therefore, it is expected that they should not imply strong modifications of the slow-manifold shape which, as discussed above, is responsible for the observed dynamics.”
Author Contributions
Funding
Conflicts of Interest
References
- Al-Naimee, K.; Marino, F.; Ciszak, M.; Meucci, R.; Arecchi, F.T. Chaotic spiking and incomplete homoclinic scenarios in semiconductor lasers with optoelectronic feedback. New J. Phys. 2009, 11, 073022. [Google Scholar] [CrossRef][Green Version]
- Poincaré, H. Les Méthodes Nouvelles de la Mécanique Céleste; Gauthier-Villars: Paris, France, 1892; Volumes I–III. [Google Scholar]
- Andronov, A.A.; Chaikin, S.E. Theory of Oscillators, Moscow, I., English Translation; Princeton University Press: Princeton, NJ, USA, 1949. [Google Scholar]
- Levinson, N. A second-order differential equation with singular solutions. Ann. Math. 1949, 50, 127–153. [Google Scholar] [CrossRef]
- Tikhonov, A.N. On the dependence of solutions of differential equations on a small parameter. Mat. Sb. N.S. 1948, 31, 575–586. [Google Scholar]
- Wasow, W.R. Asymptotic Expansions for Ordinary Differential Equations; Wiley-Interscience: New York, NY, USA, 1965. [Google Scholar]
- Cole, J.D. Perturbation Methods in Applied Mathematics; Blaisdell: Waltham, MA, USA, 1968. [Google Scholar]
- O’Malley, R.E. Introduction to Singular Perturbations; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- O’Malley, R.E. Singular Perturbations Methods for Ordinary Differential Equations; Springer: New York, NY, USA, 1991. [Google Scholar]
- Fenichel, N. Persistence and Smoothness of Invariant Manifolds for Flows. Ind. Univ. Math. J. 1971, 21, 193–225. [Google Scholar] [CrossRef]
- Fenichel, N. Asymptotic stability with rate conditions. Ind. Univ. Math. J. 1974, 23, 1109–1137. [Google Scholar] [CrossRef]
- Fenichel, N. Asymptotic stability with rate conditions II. Ind. Univ. Math. J. 1977, 26, 81–93. [Google Scholar] [CrossRef]
- Fenichel, N. Geometric singular perturbation theory for ordinary differential equations. J. Diff. Eq. 1979, 31, 53–98. [Google Scholar] [CrossRef]
- Hirsch, M.W.; Pugh, C.C.; Shub, M. Invariant Manifolds; Springer: New York, NY, USA, 1977. [Google Scholar]
- Rossetto, B. Trajectoires lentes des syst‘emes dynamiques lents-rapides. In Analysis and Optimization of System; Springer: Berlin/Heidelberg, Germany, 1986; pp. 680–695. [Google Scholar]
- Rossetto, B. Singular approximation of chaotic slow-fast dynamical systems. In The Physics of Phase Space Nonlinear Dynamics and Chaos Geometric Quantization, and Wigner Function; Springer: Berlin/Heidelberg, Germany, 1987; pp. 12–14. [Google Scholar]
- Gear, C.W.; Kaper, T.J.; Kevrekidis, I.G.; Zagaris, A. Projecting to a slow manifold: Singularly perturbed systems and legacy codes. SIAM J. Appl. Dyn. Syst. Math. 2005, 4, 711–732. [Google Scholar] [CrossRef]
- Zagaris, A.; Gear, C.W.; Kaper, T.J.; Kevrekidis, Y.G. Analysis of the accuracy and convergence of equation-free projection to a slow manifold. ESAIM Math. Model. Num. 2009, 43, 757–784. [Google Scholar] [CrossRef]
- Maas, U.; Pope, S.B. Simplifying chemical kinetics: Intrinsic low-dimensional manifolds in composition space. Combust. Flame 1992, 8, 239–264. [Google Scholar] [CrossRef]
- Brøns, M.; Bar-Eli, K. Asymptotic analysis of canards in the EOE equations and the role of the inflection line. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1994, 445, 305–322. [Google Scholar]
- Rossetto, B.; Lenzini, T.; Ramdani, S.; Suchey, G. Slow fast autonomous dynamical systems. Int. J. Bifurc. Chaos 1998, 8, 2135–2145. [Google Scholar] [CrossRef]
- Ginoux, J.M.; Rossetto, B. Slow manifold of a neuronal bursting model. In Emergent Properties in Natural and Articial Dynamical Systems; Aziz-Alaoui, M.A., Bertelle, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 119–128. [Google Scholar]
- Ginoux, J.M.; Rossetto, B. Differential Geometry and Mechanics Applications to Chaotic Dynamical Systems. Int. J. Bif. Chaos 2006, 4, 887–910. [Google Scholar] [CrossRef]
- Ginoux, J.M.; Rossetto, B.; Chua, L.O. Slow Invariant Manifolds as Curvature of the Flow of Dynamical Systems. Int. J. Bif. Chaos 2008, 11, 3409–3430. [Google Scholar] [CrossRef]
- Ginoux, J.M. Differential Geometry Applied to Dynamical Systems; World Scientific Series on Nonlinear Science; Series A 66; World Scientific: Singapore, 2009. [Google Scholar]
- Ginoux, J.M.; Llibre, J. The flow curvature method applied to canard explosion. J. Phys. A Math. Theor. 2011, 44, 465203. [Google Scholar] [CrossRef]
- Ginoux, J.M. The Slow Invariant Manifold of the Lorenz-Krishnamurthy Model. Qual. Theory Dyn. Syst. 2014, 13, 19–37. [Google Scholar] [CrossRef]
- Ginoux, J.M. Slow Invariant Manifolds of Slow-Fast Dynamical Systems. Int. J. Bif. Chaos 2021, 31, 2150112-1-17. [Google Scholar] [CrossRef]
- Bender, C.M.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers; Springer: New York, NY, USA, 1999. [Google Scholar]
- Sandri, M. Numerical Calculation of Lyapunov Exponents. Math. J. 1996, 6, 78–84. [Google Scholar]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov Exponents from a Time Series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Ruelle, D. Ergodic Theory of Chaos and Strange Attractors. Rev. Mod. Phys. 1985, 57, 617–656. [Google Scholar] [CrossRef]
- Klein, M.; Baier, G. Hierarchies of Dynamical Systems. In A Chaotic Hierarchy; Baier, G., Klein, M., Eds.; World Scientific: Singapore, 1991. [Google Scholar]
- Ginoux, J.M.; Llibre, J.; Chua, L.O. Canards from Chua’s circuit. Int. J. Bif. Chaos 2013, 23, 1330010. [Google Scholar] [CrossRef]
- Ginoux, J.M.; Llibre, J. Canards Existence in FitzHugh-Nagumo and Hodgkin-Huxley Neuronal Models. Math. Probl. Eng. 2015, 2015, 342010. [Google Scholar] [CrossRef]
- Ginoux, J.M.; Llibre, J. Canards Existence in Memristor’s Circuits. Qual. Theory Dyn. Syst. 2016, 15, 383–431. [Google Scholar] [CrossRef]
- Ginoux, J.M.; Llibre, J.; Tchizawa, K. Canards Existence in The Hindmarsh-Rose Model. Math. Model. Nat. Phenom. 2019, 14, 1–21. [Google Scholar] [CrossRef]
- Darboux, G. Mémoire sur les équations différentielles algébriques du premier ordre et du premier degré. Bull. Sci. Math. Sér. 1878, 2, 60–96, 123–143, 151–200. [Google Scholar]
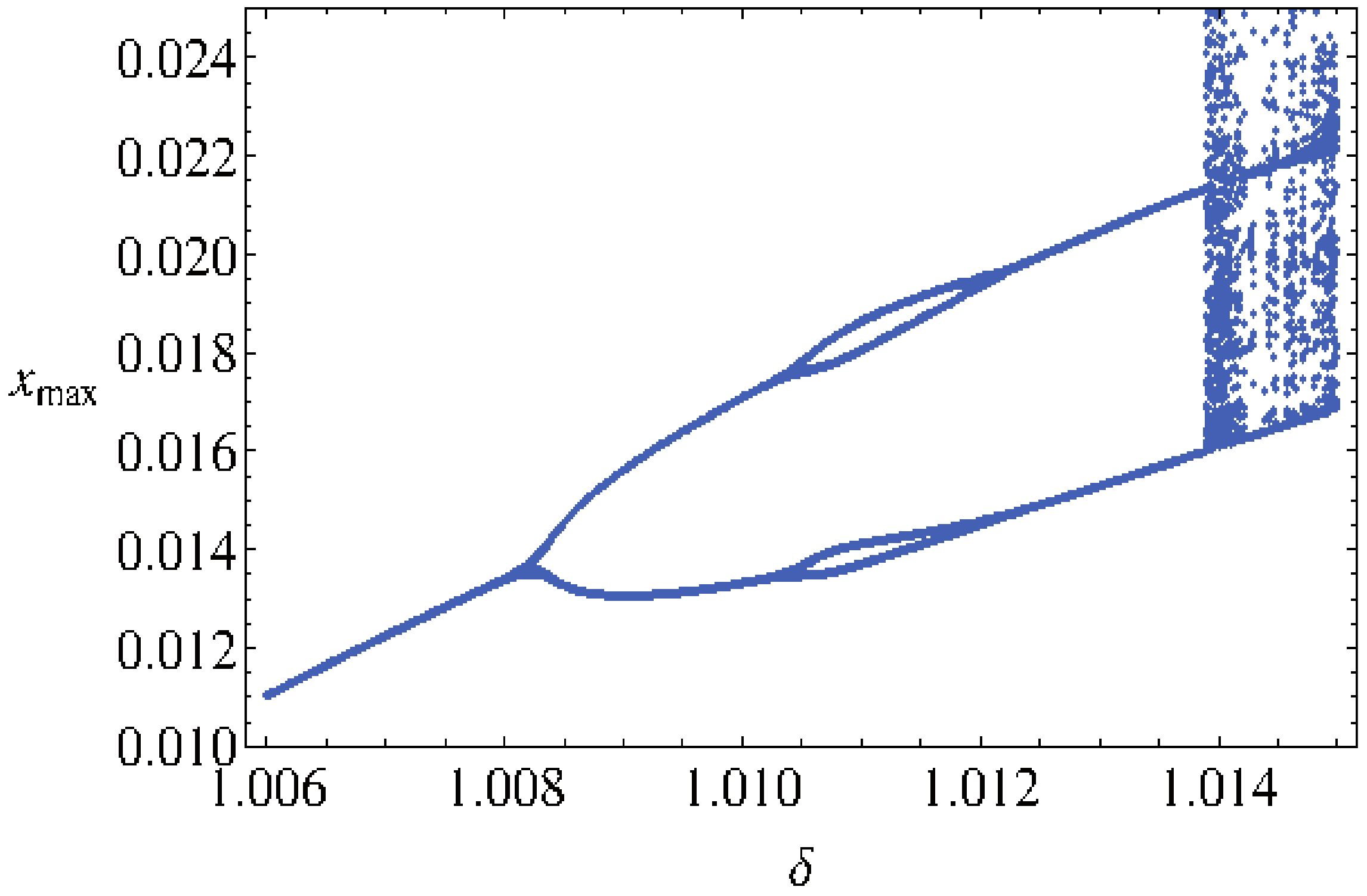
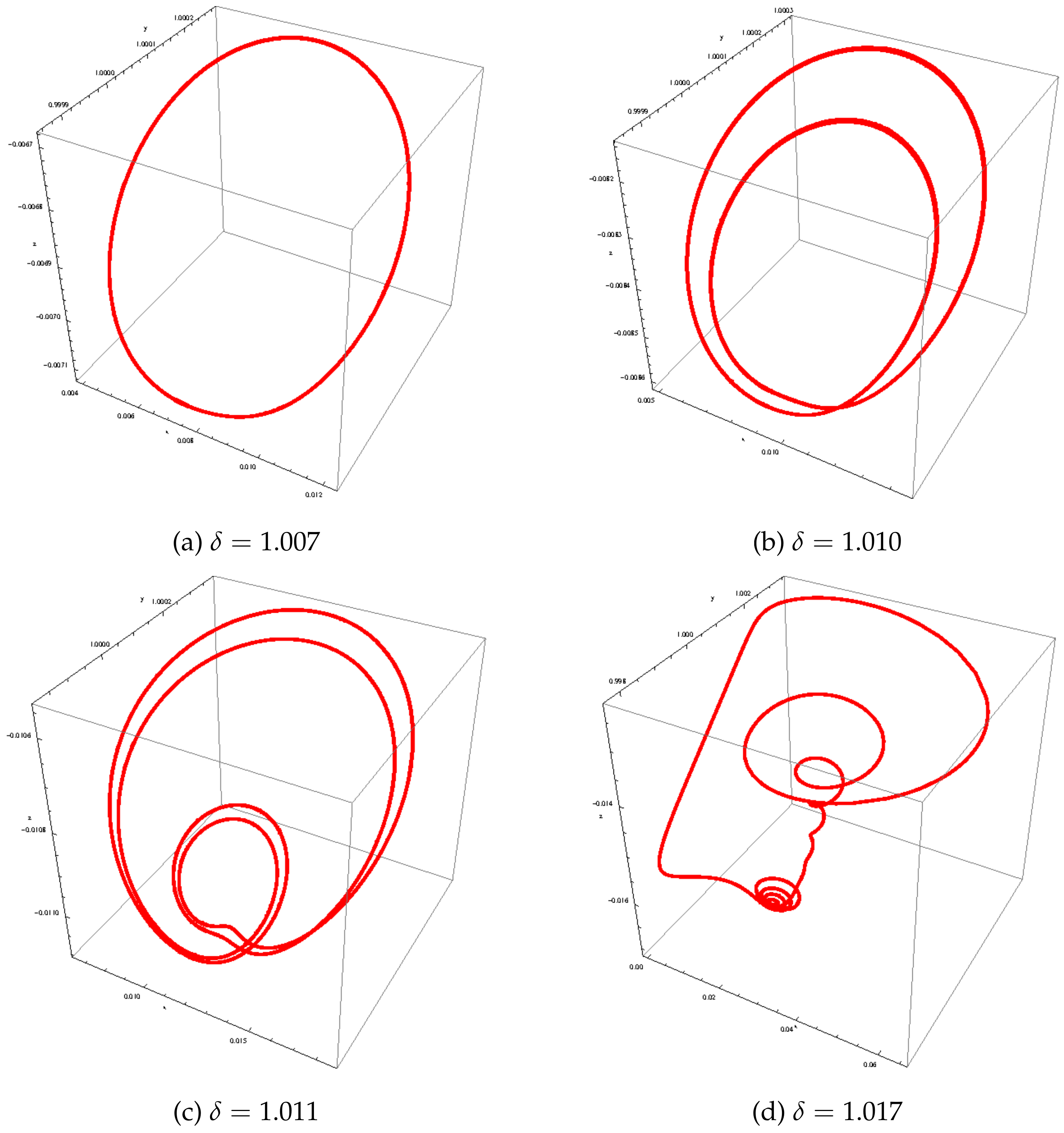


| LCE Spectrum | Dynamics of the Attractor | Hausdorff Dimension | |
|---|---|---|---|
| () | Limit cycle of period 1 | ||
| () | Limit cycle of period 2 | ||
| () | Limit cycle of period 4 | ||
| () | Limit cycle of period 2 | ||
| () | 2-Chaos |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ginoux, J.-M.; Meucci, R. Slow Invariant Manifold of Laser with Feedback. Symmetry 2021, 13, 1898. https://doi.org/10.3390/sym13101898
Ginoux J-M, Meucci R. Slow Invariant Manifold of Laser with Feedback. Symmetry. 2021; 13(10):1898. https://doi.org/10.3390/sym13101898
Chicago/Turabian StyleGinoux, Jean-Marc, and Riccardo Meucci. 2021. "Slow Invariant Manifold of Laser with Feedback" Symmetry 13, no. 10: 1898. https://doi.org/10.3390/sym13101898
APA StyleGinoux, J.-M., & Meucci, R. (2021). Slow Invariant Manifold of Laser with Feedback. Symmetry, 13(10), 1898. https://doi.org/10.3390/sym13101898






