Abstract
Physical principles for designing cellwise artificial materials with energy-absorbing/harvesting and wave guiding properties are discussed in the present work. We analyzed the evolution of waves in a one-dimensional lattice of 3D massive potential wells with light particles inside. The potential wells were coupled with elastic springs and represented soft-wall versions of the so-called stochastic billiards. A billiard could switch from repelling to the stadium type as the parameter of shape changed its sign from positive to negative. We found that certain shapes of the potential wells/containers provided a one-directional trend of the energy flow from the chain of containers into the chaotically moving light inclusions by increasing their total kinetic energy. As a result, propagating waves became trapped by giving rise to standing waves with chaotic mode shapes with decaying amplitudes.
1. Introduction
The effects of energy exchange and dissipation on both micro- and mesoscopic levels are of significant interest in different sections of physics and applied sciences developing artificial materials and molecular structures with desired targeted energy transfer properties [1]. In engineering, the number of publications dealing with vibrational energy harvesters [2] and absorbers [3,4] are growing exponentially. Note that concepts of energy absorption and vibration suppression are different. Whereas the classical area of vibration suppression usually deals with steady states of amplitude frequency response, the energy absorption is typically a nonstationary process that is triggered by usually impulsive type of initial perturbations. In the present work, we discuss some new physical principles for designing energy absorbing/harvesting metamaterials (generally, an artificial material with a specific property). We show that the corresponding mechanisms have quite interdisciplinary roots and analogs in mathematical theory of stochastic billiards and astrophysics. As a relatively simple illustrating model, we consider a lattice of elastically coupled massive potential wells representing 3D versions of the so-called soft wall stochastic billiards with light particles inside. As a preliminary insight into the matter, let us mention the related planar case of a single container attached to the base with a linearly elastic spring and including one or few non-interacting particles [5]. The model is described with Lagrangian.
where β and n are parameters controlling the container’s shape and the effective wall’s stiffness, respectively, and k is a small number of particles inside the potential well/container; see Figure 1a for details. Cases k = 1, 3, and 5 were considered for comparison reasons. A small k reduces the likelihood of collisions between the particles to enable us to ignore their interaction events in Lagrangian (1) and minimizing any statistical effects of large numbers.
In the rigid-body limit, , the contour V(x,y) = h resembles either dispersing [6] or stadium-type [7] billiards as the main geometrical parameter β switches its sign from positive to negative. The corresponding boundaries are shown in the upper part of Figure 1b for three different values of the parameter β with sample particle’ trajectories. It was shown that the light particles μ inside the ‘potential container’ M can absorb the energy from the oscillating container for quite a long period of time by delaying the Poincaré recurrence beyond any physically reasonable temporal intervals of the system. We emphasize that no phenomenological dissipation nor specific initial conditions were imposed. Nonetheless, the energy flow from the container (donor) to the inner particle (acceptor) appeared to have statistically irreversible trends whenever the dynamics of particle inside the potential well are chaotic. As mentioned above, Figure 1b gives three examples of chaotic trajectories inside containers of different shapes. The corresponding recurrence diagrams and energy responses of main oscillator versus the number of its cycles are shown below each of the three containers. A possible mechanism leading to the illustrated phenomena may associate with the so-called stochastic acceleration of cosmic particles as originally explained by E. Fermi [8] by their cyclic ‘elastic’ collisions against moving magmatic fields. According to his model, two types of collisions must be happening, namely, ‘head-on collisions’ with an energy gain and ‘overtaking collisions’ with an energy loss. Gain and loss, however, do not average out completely, because a head-on collision is slightly more probable than an overtaking collision due to the greater relative velocity. In our case, a chaotically moving particle should also have both types of collisions against the moving walls of its container. The physical nature of forces considered in cosmology is quite different, however. In our case, a naïve explanation is that chaotically moving particles collide with the container walls more often when the wall and particle move towards each other. As a result, particles should experience stronger pulses more frequently by gradually absorbing the kinetic energy from the container walls rather than losing it. Note that such interpretations are based on chaotic behaviors of individual particles. For that reason, let us summarize a comparison with the classical thermodynamic problem of energy transfer from a moving piston into a gas inside an adiabatic cylinder [9]. The main distinctive features are as follows:
- ○
- The problem of adiabatic piston essentially assumes the statistics of large numbers, namely, it deals with a gas of particles inside the adiabatic cylinder under the piston. Although the present work considers a chain of containers, it was shown earlier that the effect still develops, even if the model includes only one container with a single particle inside. The chaoticity of a particle was caused only by specific shapes of containers. This is why the effect of interest may happen or may not depends upon the container’s shape. Following the previous work [5], no statistics of large numbers are assumed in the current formulation as well, although the effect appeared to be enhanced by the dimension increase of the entire system.
- ○
- Further, it is essential for the classical adiabatic piston problem that the volume under a slowly moving piston is varying. As a result, the work done by the piston is simply transformed into the kinetic energy of particles. However, the gas releases its energy when the piston reverses its direction and the volume increases. In fact, neither of the above phases takes place in our case since the volume of containers remains fixed while containers oscillate as rigid bodies by changing the direction of motion.
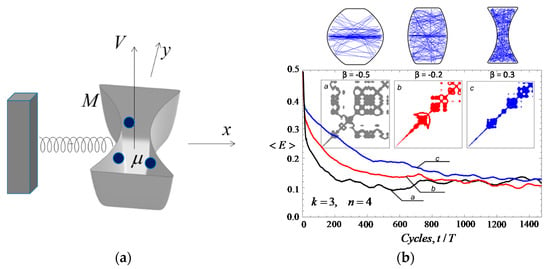
Figure 1.
Numerical evidence of the energy-absorbing properties of soft-wall stochastic billiards: (a) a potential container M is oscillating with small particles interacting with potential walls of different ‘stiffness’ and shapes; the container mass and spring stiffness are scaled to be unity, and , where k and m are the number of particles and their total mass, respectively. (b) Fifty points running average of the total energy of oscillating container with the corresponding recurrence diagrams, as defined in [10], for different container shapes shown at the top with sample chaotic particle’ trajectories, where T is the eigen period of oscillation of the container.
Finally, the idea of using the soft-wall version of billiards facilitates numerical simulations by letting us to avoid conditioning at collision times. More importantly, switching to the class of continuous systems provides the possibility for using the methodologies of nonlinear normal modes (NNMs) according to definitions [11]. As shown earlier [5], such tools reveal certain links between instabilities of NNMs and conditions of stochasticity of billiards. In the stiff-wall versions, the derivation of such conditions would require the designing of specific discrete maps in a technically quite complicated way.
2. Chain of 3D Soft-Wall Stochastic Billiards
In the present work, we generalize model (1) in order to consider the effects of wave propagation and dynamic interactions in one-dimensional lattices of 3D potential containers. By assigning the initial conditions as sine-waves propagating though the chain of containers, we found that the waves can be quickly destroyed as the interaction of inner particles with the container walls intensifies. Furthermore, varying the container shapes revealed the effect of a one-directional trend in the energy flow from the waves to inclusions increasing their total kinetic energy. Each container includes only one particle μ. After a proper scaling of parameters and variables, the model under consideration takes the following Lagrangian form,
where is the displacement of jth container, whose dynamics are constrained to be one-dimensional, whereas three-dimensional motions of particles are described with their relative displacements measured inside each container from its center of symmetry; the strength of coupling between containers is assumed to be unity, the stiffness of base springs is K, and all the potential wells of the chain are given by the same function.
The meaning of parameters in (3) is similar to the 2D case (1), although shapes described with relationship (3) possess more spatial symmetries compared to the planar case, as illustrated below in Figure 2. A mechanical analogy of the entire system (2) is represented by Figure 3. Finally, the assumption behind relationship (2) is that the potential wells (3) are localized with no effect on each other. Each inclusion is supposed to be trapped inside its own potential well, which is discussed below. The reason for describing the soft walls of a potential containers with relationship (3) employs the well-known property of power functions with high exponents. Namely, the dependence upon s is very weak within the interval while rapidly strengthening when crossing its boundaries . This dependence is obviously approaching the square well as . As a result, a small bead under the corresponding potential field would be moving almost freely inside the interval until it collides with a boundary.
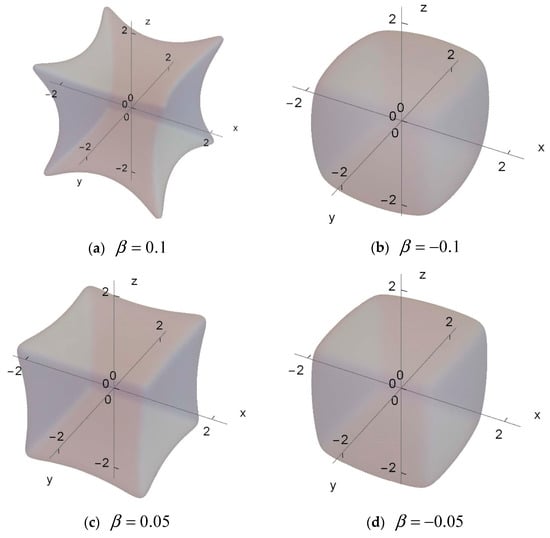
Figure 2.
Shapes of soft wall 3D billiards given by the level surface at and : (a,c) 3D dispersing boundaries; (b,d) 3D versions of stadium type billiards.
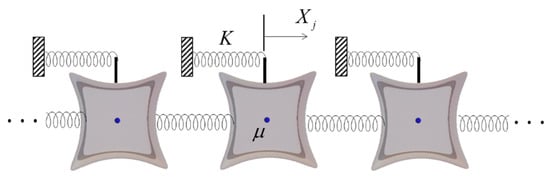
Figure 3.
Mass-spring chain model of soft-wall billiards with inclusions , where the potential wells are represented by the ‘top view’ of case (a) in Figure 2.
Under the condition n >> 1, a typical container shape can be visualized with the equipotential surface , which is shown in Figure 2 for different values of and the potential level . The shape’ symmetries reflect the evenness of function (3) with respect to each of its arguments. The term ‘soft wall’ means that the shape of container still depends upon the number h. However, within the considered range of total energies, qualitative changes of surfaces are insignificant due to the specific of power functions with high exponents. Therefore, images in Figure 2 can be viewed as a proper visualization the billiards boundaries. Possible high energy effects of topological changes, when inclusions may escape from the potential wells, will be discussed later in this text. As follows from the shape of the surface in Figure 2a,c, the inclusions interacting with potential walls are subjected to the repelling reaction forces. The only difference with the case of stiff wall dispersive billiards is that the impulsive reaction forces are still continuous in both temporal and spatial coordinates.
3. Discussion of Simulation Results
In order to characterize the energy flow from the ensemble of containers to their small inclusions, we use the following quantities:
The total energy of the ensemble of S containers per one container
The total energy of inclusions per one inclusion
where the mean values of kinetic and potential energies are given by, respectively,
and
The main goal of simulations was to obtain a numerical evidence of one-directional energy flows from the chain of massive containers to their inclusions. Such simulations were conducted with system (2) of S = 100 containers under the cyclical boundary conditions and the initial dynamic states corresponding to the propagating sine-wave, , , where and . The amplitude and wave number were assigned as A = 0.5 and k = 16, respectively. We also assumed that at t = 0 in order to keep the particles near their equilibrium states at the initial time while other initial coordinates of the particles were chosen as small random numbers within the interval generated as different for different containers. Other parameters were chosen as: K = 1.0, γ = 1.0, n = 6, and β = 0.1. The result of simulation is illustrated by Figure 4a and Figure 5a,c to show that the wave propagates through the chain of containers with almost no disturbance until the particles became involved in the dynamic process and developed interactions with the potential walls. As follows from the graphs, this occurred at about time units. Then, once the chaos in the particle motions was developed, the energy flow acquired a one-directional trend from the containers to the particles, which is clearly confirmed by Figure 4a,c. It is also seen from curves 2 and 3 that the collective energy of particles maintained mostly kinetic form since the potential energies of their interactions with the walls were spike-wise and chaotic. Due to the chaoticity of particles and thus incoherency of this process between different containers, the wave shape became irregular with the loss of the propagation property as follows from the wave contour lines in Figure 5a,c. Note that the plots are given for different time intervals in order to illustrate both short- and long-term dynamics. The loss of propagation appeared quite completed by the time . As seen from Figure 4b,d, obtained for the case , in contrast to the repelling case, there was only a minor energy flow from the containers to inclusions. Still, Figure 5b,d reveals that the wave switched to the standing vibration mode with chaotic amplitudes even faster. This occurred despite the irregular patterns emerging somewhat later (compare Figure 5a,b). Although both effects were caused by the interaction of inclusions with containers, the underlying mechanisms were quite different. The wave became trapped as soon as the interaction of inclusions with the container walls violated the translational symmetry of the chain of containers. However, this did not guarantee a one-directional trend in the energy exchange between containers and inclusions. Such a trend most likely associated with the Fermi type of acceleration of inclusions under a stronger chaoticity due to the stochastic billiard effect. The effect had a different physical nature and depended upon the geometry of container shapes. Namely, whereas the wave trapping may occur even in the case of one-dimensional ‘containers’, the stochastic acceleration required the inclusion dynamics to be strongly chaotic, which has the capacity to develop in two- or three-dimensional billiard-type containers with either repelling or specific ‘stadium type’ boundaries. Moreover, multidimensional containers provide additional degrees of freedom for absorbing the energy from the one-dimensional wave.
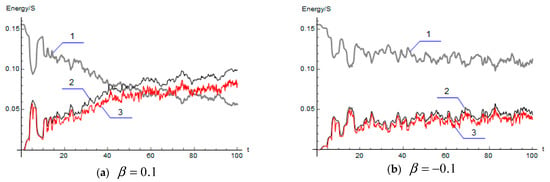
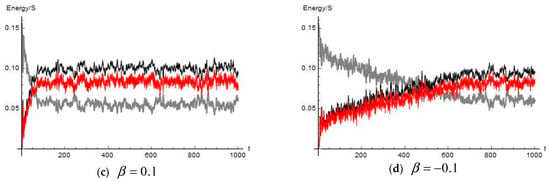
Figure 4.
The total energy per one cell under the initial conditions corresponding to the propagating sine wave: 1—containers, 2—particles, and 3—the kinetic energy particles; the corresponding evolution of wave shapes is illustrated below in Figure 5. (a,b) Short term response, and (c,d) tenfold increase of time range.
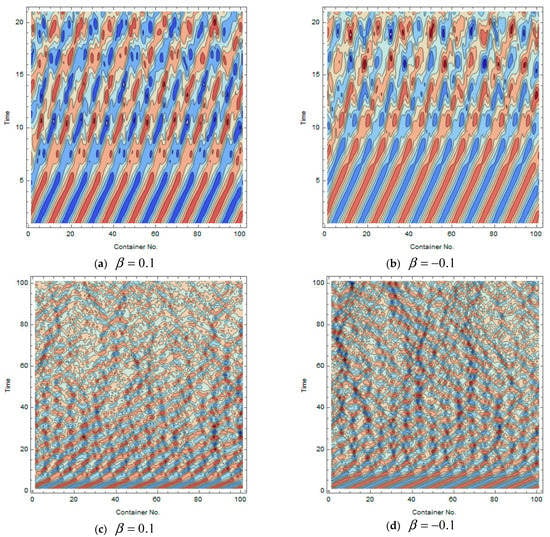
Figure 5.
Cancellation of the propagating wave due to almost irreversible energy transfer from the chain of containers into its inner particles: (a,b) short-term patterns of the displacement field; (c,d) long-term displacement field showing transition from the propagating wave to the chaotic dynamics of the chain of containers as their energy was absorbed by the inner particles as shown in Figure 4a,b.
The next series of simulations deals with the case of zero stiffness of base springs,. For comparison reasons, all other parameters are kept the same, in particular, . Figure 6a illustrates the energy flow, which appeared to be less intensive than that shown in Figure 4a,b for the case and thus required a much longer time to develop the same outcome. It was seen that the process reached some stationary phase within the time interval 200 < t < 300, in which most of the energy moved from the containers to the particles. The distribution was maintained then with minor fluctuations until the end of simulation interval at t = 2400. Moreover, the corresponding wave contours in Figure 7a,b showed that wave propagation property was maintained for a longer time interval compared to that in Figure 5. Eventually some standing modes with decaying chaotic amplitudes emerged as shown in Figure 6b and Figure 7b.
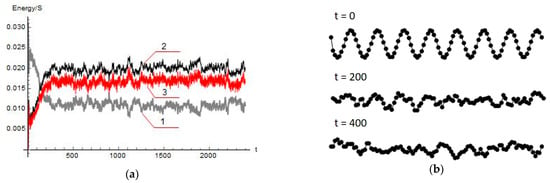
Figure 6.
Energy and wave shapes response at zero stiffness of base springs, K = 0: (a) time history of the total energy per one cell under the initial conditions corresponding to the propagating sine wave: 1—containers, 2—inner particles, and 3—the kinetic energy of particles interpreted as a structural temperature; (b) snapshots of the spatial wave profiles.
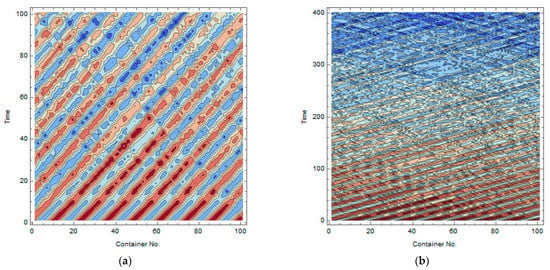
Figure 7.
Propagating wave patterns at zero stiffness of the foundation springs, K = 0, corresponding to the energy and wave profile trends of Figure 6: (a,b) short-term and long-terms patterns, respectively.
Further, the results of simulations showed that the container shapes may essentially affect the energy flow from containers to their inclusions. Figure 8 illustrates the ratio of the accumulated kinetic energy of inclusions by the end of run per the initial total energy of the system as a function of the parameter of containers shape . Three different executions under the same conditions with randomly chosen initial positions of inclusions showed a qualitatively similar result. The effect of energy absorption appeared to have a maximum at about . A more detailed numerical study showed that the maximum associated with the escape of inclusions from the potential containers through the channels shown in Figure 9 from two different viewpoints. It was seen that the topology of surface experienced qualitative change as the energy level h became large enough; see Figure 9 obtained for the case . The minimum potential barriers of escape were located on diagonals and depended upon the number , as shown in Figure 10. Note that escaping from the local potential well did not mean leaving the container since, at any distance from geometrical center, the inclusion still interacted with the container’ walls. Such a specific situation was due to a phenomenological nature of relationship (3) whose purpose was to approximate walls of some real container on either a macro- or mesoscopic scale. At the micro level, when the potential energy may be associated with molecular interactions, escapes from potential wells would mean that inclusions were gone from their cells.
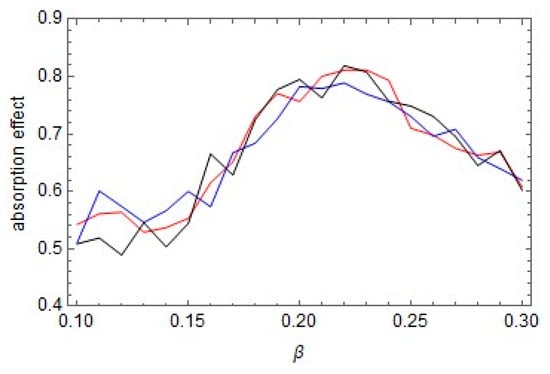
Figure 8.
Estimation of the energy-absorbing effect as a ratio of the accumulated kinetic energy of particles at final time per the initial total energy of the system, , as a function of the container shape, ; the ensemble of curves was obtained from three different simulations under random initial positions of particles.
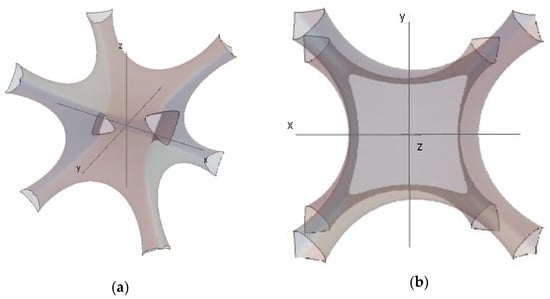
Figure 9.
Shapes of the potential surface at and h = 0.15 from different viewpoints: (a) diagonal view, (b) top view; the escape of particles from the potential well through the potential channels was possible.
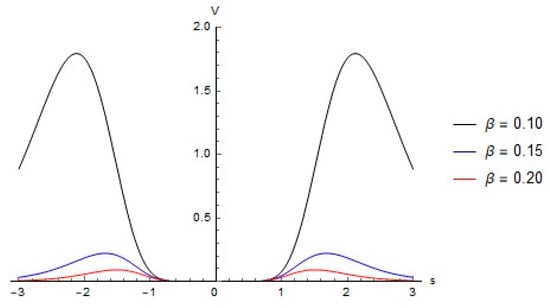
Figure 10.
Behavior of the potential energy along the diagonal at different values of the parameter .
4. Conclusions
The evolution of waves and specifics of energy exchange in a one-dimensional lattice of 3D massive potential wells/containers carrying light particles inside was analyzed in the present work. The containers were coupled with elastic springs and represented soft-wall versions of the so-called stochastic billiards. The billiards could switch from repelling to the stadium type as the parameter of shape changed its sign from positive to negative. We found that certain shapes of the potential wells provided a one-directional trend of the energy flow from the chain of containers into the chaotically moving light inclusions by gradually increasing their total kinetic energy. Furthermore, propagating waves became trapped by giving rise to standing waves with chaotic mode shapes with decaying amplitudes. However, it was found that the cancellation of wave propagation and its amplitude decay may have different physical causes. The energy outflow to the inclusions was likely due to their Fermi-type stochastic acceleration, whereas the wave trap was the outcome of the structural translational symmetry loss caused by spike-wise interactions of inclusions with container walls. Such observations offer certain guidelines for designing artificial energy absorbing/harvesting materials on micro-, macro-, and mesoscopic levels. The model may also be adapted as a phenomenological approach to the dynamic analyses of natural crystal structures.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Aubry, S.; Kopidakis, G.; Morgante, A.; Tsironis, G. Analytic conditions for targeted energy transfer between nonlinear oscillators or discrete breathers. Phys. B Condens. Matter 2001, 296, 222–236. [Google Scholar] [CrossRef] [Green Version]
- Cottone, F.; Vocca, H.; Gammaitoni, L. Nonlinear Energy Harvesting. Phys. Rev. Lett. 2009, 102, 080601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, T.; Seguy, S.; Berlioz, A. On the dynamics around targeted energy transfer for vibro-impact nonlinear energy sink. Nonlinear Dyn. 2016, 87, 1453–1466. [Google Scholar] [CrossRef] [Green Version]
- Vakakis, A.F.; Gendelman, O.V.; Bergman, L.A.; McFarland, D.M.; Kerschen, G.; Lee, Y.S. Nonlinear Targeted Energy Transfer in Mechanical and Structural Systems. In Internal Variables in Thermoelasticity; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 156. [Google Scholar] [CrossRef]
- Pilipchuk, V. Stochastic energy absorbers based on analogies with soft-wall billiards. Nonlinear Dyn. 2019, 98, 2671–2685. [Google Scholar] [CrossRef]
- Sinai, Y.G. Dynamical systems with elastic reflections: Ergodic properties of dispersing billiards. Russ. Math. Surv. 1970, 25, 137–189. [Google Scholar] [CrossRef]
- Bunimovich, L.A. Decay of correlations in dynamical systems with chaotic behaviour. Sov. Phys. JETP 1985, 62, 842–852. [Google Scholar]
- Fermi, E. On the Origin of the Cosmic Radiation. Phys. Rev. 1949, 75, 1169–1174. [Google Scholar] [CrossRef]
- Gislason, E.A. A close examination of the motion of an adiabatic piston. Am. J. Phys. 2010, 78, 995–1001. [Google Scholar] [CrossRef]
- Marwan, N. A historical review of recurrence plots. Eur. Phys. J. Spéc. Top. 2008, 164, 3–12. [Google Scholar] [CrossRef] [Green Version]
- Vakakis, A.F.; Manevich, L.I.; Mikhlin, Y.V.; Pilipchuk, V.N.; Zevin, A.A. Normal Modes and Localization in Nonlinear Systems; Wiley: New York, NY, USA, 1996. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).