1. Introduction
In the extensive literature of number theory we can find a systematic and extensive investigation of the ordinary Bernoulli, Euler, Genocchi and tangent polynomials and their corresponding numbers, as well as
q-extensions,
-extensions, and many generalizations. Many mathematicians have presented several interesting results of these general polynomial systems, including some explicit series representations in terms of the Hurwitz zeta function and generalized zeta function. Barnes [
1] introduced the generalized multiple Hurwitz zeta function. Choi and Srivastava [
2] defined and studied the multiple Hurwitz–Euler eta function. Hwang and Ryoo [
3,
4] introduced the multiple
-Hurwitz–Euler eta function and the multiple twisted
-
L function. Recently, He [
5] investigated some identities of symmetry for Carlitz-type
q-Bernoulli numbers and polynomials in a complex field. Kim et al. [
6] obtained several identities of symmetry for Carlitz-type
q-Euler numbers and polynomials in a complex field.
By
we denote the set of natural numbers and
Set
Note that if
, then
The binomial formulae are known as
and
Choi and Srivastava [
2] constructed the multiple Hurwitz–Euler eta function
defined by the following
r-ple series:
It is known that
can be continued analytically to be a whole complex
s-plane (see [
2]).
The ordinary Euler numbers
and polynomials
, together with their familiar generalizations
and Euler polynomials
of order
r, are usually defined by means of the following generating functions:
and
so that the ordinary Euler numbers
and polynomials
are given, respectively, by
Some interesting properties of the generalized
-Euler numbers and polynomials were first investigated by Ryoo [
7]. We begin by recalling here definitions of generalized
-Euler numbers and polynomials as follows. Let
r be a positive integer and let
be Dirichlet’s character with conductor
with
(mod 2).
Definition 1. For , the generalized -Euler numbers and polynomials related to χ are defined by means of the generating functionsandrespectively. The multiple
-Hurwitz–Euler eta functions of the
-extension of the multiple Hurwitz–Euler eta functions were constructed in [
3]. The aim of this paper is that a new generalization of the multiple
-Hurwitz–Euler eta function related to
is constructed and studied. The sections have the following contents. In
Section 2, Carlitz-type generalized higher-order
-Euler numbers and polynomials related to
are defined. We derive some of their relevant properties. In
Section 3, by using the complex integral and the Dirichlet character with conductor, we can also define the Dirichlet-type multiple
-
L function. That is, Dirichlet-type multiple
-
L functions are the generalization of multiple
-Hurwitz–Euler eta functions. In
Section 4, first, the summation is calculated by applying a new calculation technique using the Dirichlet character with conductor, and the symmetry of the Dirichlet-type multiple
-
L function is derived using the properties of the Dirichlet character. Specifically, if
is a trivial character (equal to 1 for all
n), then the results of [
3] are the same as our results. Next, we use this symmetric property for the Dirichlet-type multiple
-
L function to obtain a symmetric identity about Carlitz-type higher-order
-Euler numbers and polynomials related to
.
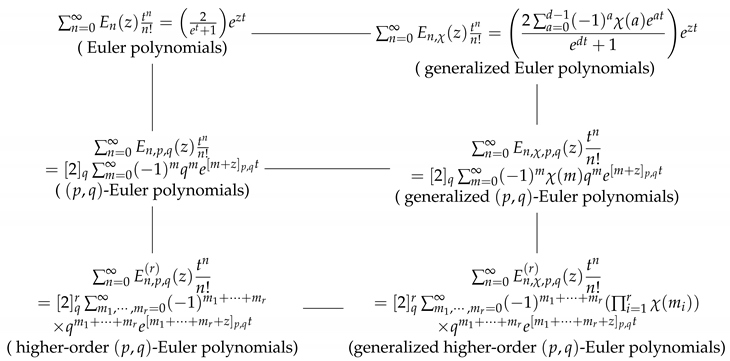
The following diagram shows the various types of Euler polynomials and generalized Euler polynomials. Those polynomials in the first and second rows of the diagram were studied by Hwang and Ryoo [
3,
4]; Ryoo, Kim and Jang [
8]; Ryoo [
7,
9]; Abramowitz and Stegun [
10]; and Yang and Qiao [
11]; and Srivastava [
12] and Y. Simsek [
13], respectively. The study of these has produced beneficial results in number theory. The best known in number theory is the one-variable zeta function, specifically the Riemann zeta function and its generalizations. Research on the multi-zeta function began to develop more intensively from the beginning of the 21st century (see [
1,
2,
14]). First, the Dirichlet-type multiple
-
L function is introduced as an important motive of this paper with the expansion of this research. We also establish symmetric identities for such functions and generalized higher-order
-Euler polynomials related to a Dirichlet character
in a complex field. Next, the motivation of this paper is to obtain some explicit properties and symmetric identities for Carlitz-type generalized higher-order
-Euler polynomials related to Dirichlet’s character
in the third row of the diagram.
![Symmetry 13 00095 i001 Symmetry 13 00095 i001]()
3. Dirichlet-Type Multiple -L Function
In this section, we construct the Dirichlet-type multiple
-
L-function. This function interpolates the generalized higher-order
-Euler polynomials related to
at negative integers. The multiple
-
L-function can be defined as follows (see [
3]):
Definition 4. For with , the multiple -L-function is defined by Note that if , then .
Definition 5. For with , the Dirichlet-type multiple -L-function is defined by Observe that if and is a trivial character (equal to 1 for all n), then . Note that if is a trivial character (equal to 1 for all n), .
Theorem 3. For , we havewhere . Proof. Applying the Mellin transformation to Equation (
5), and Definition 5, we obtain
This completes the proof of Theorem 3. □
The value of the Dirichlet-type multiple -L-function at negative integers is given explicitly by the following theorem:
Theorem 4. Let . Then we obtain Proof. Again, by using Equations (5) and (6), we have
For
, let us take
in Equation (
7). Then, by Equations (7) and (8), and Cauchy residue theorem, we obtain
Hence the proof is completed. □
4. Some Symmetric Identities for the Dirichlet-Type Multiple -L Function
In this section, we obtain some symmetric identities for the Dirichlet-type multiple -L function. Finally, we get symmetric identities for generalized higher-order -Euler polynomials related to using the symmetric properties for the Dirichlet-type multiple -L function .
Let with , . For and , we obtain certain symmetry identities for the multiple -L function.
Theorem 5. Let with , . Then we obtain Proof. Note that
for any
. In Definition 5, by substituting
for
z and replacing
q and
p with
and
, respectively, we derive the next result
Thus, from Equation (
9), we can derive the following equation.
By using the same method as in Equation (
10), we have
Therefore, the claimed result is obtained. □
Taking and if is a trivial character (equal to 1 for all n) in the above theorem, we have the following corollary.
Corollary 1. Let with . For and , we obtain If in Corollary 1, then we obtain the following corollary.
Corollary 2. Let with . For and , we obtain If and in Corollary 2, then we obtain the following corollary.
Corollary 3. Let with . For and , we obtain Let us take in Theorem 5. For and , we obtain certain symmetry identities for generalized higher-order -Euler polynomials.
Theorem 6. Let with , . For and , we obtain Proof. By Theorems 4 and 5, we obtain the following theorem. □
If is a trivial character (equal to 1 for all n) and taking in Theorem 6, we have the following corollary.
Corollary 4. Let with . For and , we obtain If
and
in Equation (
12), then we obtain the following corollary (see [
10]).
Corollary 5. Let with . For and , we obtain Hence we have the following theorem.
Theorem 7. Let with , . For and , we obtain For each integer , let The above sum are called the alternating generalized -power sums.
By using the same method as in Equation (
13), we have
Therefore, by Equations (13) and (14) and Theorem 6, we have the following theorem.
Theorem 8. Let with , . For and , we obtain By Theorem 8, we have the interesting symmetric identity for the generalized higher-order -Euler numbers related to .
Corollary 6. Let with , . For and , we obtain If in Corollary 6, then we obtain the following corollary.
Corollary 7. Let with , . For and , we obtainwhere If
is a trivial character (equal to 1 for all
n),
in Theorem 6, then we have the following theorem for Euler polynomials, which are symmetric in
a and
b (see [
11]).
Corollary 8. Let with , . Then we obtain 5. Conclusions and Future Directions
The motivation of this paper was to investigate some explicit identities for the generalized higher-order
-Euler polynomials
attached to
in the third row of the diagram at page 3. First, we defined the generalized higher-order
-Euler polynomials
related to
(see Definition 2). In order to obtain a symmetry identity for the generalized higher-order
-Euler polynomials
related to
, we constructed the Dirichlet-type multiple
-
L function (see Definition 5). In Theorem 5, we gave a symmetry identity for the Dirichlet-type multiple
-
L function
. Next, using the Dirichlet-type multiple
-
L-function
, we also obtained some symmetry identities for the generalized higher-order
-Euler polynomials
related to
(see Theorems 6 and 7). Finally, we also obtained the explicit identities related to the generalized higher-order
-Euler polynomials
related to
, the alternating generalized
-power sums (see Theorems 1, 2 and 8, and Corollaries 6 and 7). In particular, If we take
in all results of this article, then [
3] is the special case of our results. The Dirichlet character is the most important character in the algebra. Many mathematicians conduct research related to the Dirichlet character. In our paper, we wanted to generalize our known polynomial using this Dirichlet character, which has many applications in the algebra. We also want to further study the solution of equation
as an application. In our next research, we will draw distribution pictures of solutions of this equation using computer graphics and also investigate the symmetry of distribution pictures of the solutions, which may give clues about the properties of the solutions. Our referees mentioned that multi-zeta values have significant connections to arithmetic geometry. They also asked about the relation between arithmetic geometry and Carlitz q-analogues. Although we do not know how arithmetic geometry is related to Carlitz q-analogues, this is very helpful question. We have included reference 14 because it suggests several applications of special functions.