Abstract
Quantum search algorithms provide a way to speed up combinatorial search, and have found several applications in modern quantum technology. In particular, spatial search on graphs, based on continuous-time quantum walks (CTQW), represents a promising platform for the implementation of quantum search in condensed matter systems. CTQW-based algorithms, however, work exactly on complete graphs, while they are known to perform poorly on realistic graphs with low connectivity. In this paper, we put forward an alternative search algorithm, based on structuring the oracle operator, which allows one to improve the localization properties of the walker by tuning only the on-site energies of the graph, i.e., without altering its topology. As such, the proposed algorithm is suitable for implementation in systems with low connectivity, e.g., rings of quantum dots or superconducting circuits. Oracle parameters are determined by Hamiltonian constraints, without the need for numerical optimization.
1. Introduction
Structured databases, as opposed to unstructured ones, are characterized by the existence of a format or some form of organization, which make them searchable in a relational fashion. In turn, structured data are amenable to spatial search algorithms, i.e., algorithms taking into account the spatial organization of the dataset. Usually this is done using tools from graph theory, and exploiting the structure of links within the database. In this framework, quantum spatial search [1] is the problem of finding a marked element in a structured database using the quantum dynamics of a walker over a graph, as opposed to a classical one [2]. Quantum spatial search may be thus considered a generalization of the Grover search algorithm [3] to problems where some form of data structure is available.
Among the possible implementations, it has been shown [4] that continuous-time quantum walks (CTQWs) over graphs may provide exact solutions to the search problem for certain graph topologies, i.e., exact localization (with unit probability) of the walker on some given target state. Additionally, the time needed to have the walker localized may be of the order [5], where N is the size of the graph. This is largely outperforming any classical algorithm, where the searching time is at least of the order . Among the different graphs, the class of those achieving exact localization in a searching time includes the complete and the hypercube graphs of any size, and the d-dimensional lattice of any size for . Recently, the star graph has been added to this short list [6,7]. Quantum search based on CTQWs have received large attention in the recent years [8,9,10,11,12,13,14]. However, although the high connectivity and global symmetry of the graph have been proven not to be necessary for fast quantum search [15,16], CTQWs are known to perform poorly on realistic graphs with low connectivity, e.g., the ring graph [17].
Since the ring graph, and other similar graphs with low connectivity, may be of interest in view of possible implementations, a question arises on whether there exist alternative algorithms that make it possible to improve quantum search on simple graphs. In this paper, we address this problem and put forward an alternative search algorithm, based on structuring the oracle operator, which allows one to improve the localization properties of the walker by tuning only the on-site energies of the graph, i.e., without altering the topology of the graph itself. The proposed algorithm is thus suitable for implementation in systems with low connectivity, e.g., ring of quantum dots or superconducting circuits, and may be of interest for implementation of quantum search in condensed matter systems. As we will see in the following, the novel algorithm provides an overall faster strategy for quantum search, i.e., it increases the walker’s probability to reach a specific site, while decreasing the overall time needed to ensure the localization in that target. Besides quantum search, we foresee applications in the field of quantum probing [18].
The paper is structured as follows. In the next Section, we briefly review quantum spatial search on graphs and introduce notation. In Section 3 we discuss the use of a structured oracle to improve the searching performance of CTQW on ring graphs. Section 4 closes the paper with some concluding remarks.
2. Quantum Spatial Search on Graphs
In several systems of interest for condensed matter, the dynamics of particles or quasi-particle (excitations) may be effectively described using the concept of continuous-time quantum walks. In CTQW one assumes that the particle may reside only on a discrete set of sites, which replaces the continuum spatial domain. A graph structure thus naturally emerges, with the set of possible position states mapped to the vertex set V of some graph G. The presence of an edge connecting two sites of the graph means that the particle may tunnel between those two sites.
Quantum spatial search on graphs is usually implemented using quantum walkers with (dimensionless) Hamiltonians of the form
where L is the Laplacian matrix of the graph, is the so-called oracle operator, and is a tunable coupling, whose meaning and use will be discussed later. The Hilbert space of the walker is where N is the size of the graph, i.e., the number of vertices. The standard basis , is made of localized states, i.e., describing the walker sitting on a given site of the graph. The Laplacian is defined as where A is the adjacency matrix of the graph, i.e., a square matrix with elements , with iff the sites j and k are connected, i.e., the walkers may tunnel between the two sites, and zero otherwise. The matrix D is instead a diagonal matrix, known as the degree matrix of the graph, with elements , being the number of links originating from site j, i.e., the number of decay channels for a walker localized in j.
A quantum spatial search on graphs consists of preparing the walker in an initially delocalized state
which can be allowed to evolve according to the Hamiltonian in Equation (1). The goal is that of localizing, in the shortest time, the walker on a specific site , i.e., the target state encoding the solution of the search (here, for the sake of simplicity, we focus on the simple case of a unique solution, but our analysis can be straightforwardly extended to a general number M of solutions). The task of optimally design quantum spatial search on graph thus consists of looking for an oracle and a coupling quickly maximizing the localization probability
The figures of merit to assess whether quantum spatial search may be implemented on a given graph structure are therefore: (1) the maximum achievable value of the localization probability in Equation (3), and (2) the search time , i.e., the time needed to achieve the maximum of the localization probability . For the localization probability, the benchmark value is of course , whereas for the search time, the benchmark is given by the Grover (dimensionless) time , i.e., , taking into account the optimal value of .
For a complete graph of any size, quantum spatial search may be exactly implemented, i.e., we may achieve , with . This is obtained by choosing the oracle as the projector over the target . In turn, the Laplacian of the complete graph is given by , and the Hamiltonian in Equation (1) may be exactly diagonalized. The localization probability in Equation (3) may be thus written as
which is maximized, , for and . Results are of course independent on the specific choice of the target w, owing to the full symmetry of the complete graph.
Realistic physical structures, however, are not usually fully connected, and a question thus arises on whether it is possible to effectively implement quantum spatial search on graphs with lower connectivity, e.g., the paradigmatic example of the ring (cycle) graph. Using the same oracle , together with the Laplacian of the ring graph (boundary conditions: and ) the resulting search performance is rather poor, and degrades with N. For the sake of illustration, in Figure 1 we show the localization probability as a function of t for two ring graphs with and , and for different values of (chosen among those maximizing the localization probability for short time). Also for the ring graph we have full symmetry, and thus results do not depend on the choice of the target.
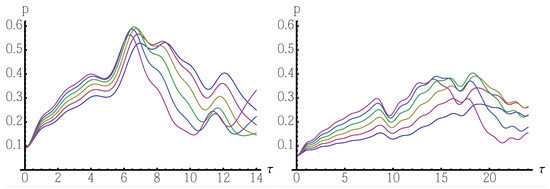
Figure 1.
Localization probability for ring graphs. The two panels show as a function of for two rings with (left) and (right), and for different values of (chosen among those maximizing the localization probability in the temporal range considered). From bottom to top (referring to the short time region, where the curves do not intersect) we have for in the left plot and for in the right one.
3. Quantum Search by Structured Oracles
In this Section we explore the possibility of using a structured oracle in order to improve the searching performance of CTQW on ring graphs. The idea is that of going beyond the simple projector structure, however without altering the topology of the graph. In other words, we allow ourselves to tune only the on-site energies of the graph by choosing an oracle operator (no longer a projector) that, in general, can be written in the form
where still refers to the unique solution of the search problem. In principle, the ability of a walker with Hamiltonian to localize at the target state may be assessed by diagonalizing the Hamiltonian , and then maximizing the probability by brute force. However, this task becomes quickly unfeasible as far as N increases, and an educated guess would be very much welcome.
In order to gain some insight into the problem, we start by considering the following three-site symmetric oracle operator
which is made of the usual oracle plus the projectors over the neighbouring sites. In particular, we analyze the effect of the sign and amplitude of the on-site energy on the localization probability of the ring graphs. Numerical evidence suggests that larger localization probabilities are obtained when is smaller than and with opposite sign. An illustrative example is reported in Figure 2, where we show the localization probability as a function of for the same graphs of Figure 1, i.e., two ring graphs with and . The black line in both panels denotes the localization probability , i.e., the result obtained without the additional terms in the oracle, and corresponding to the value of achieving maximum localization probability (i.e., for and for ).
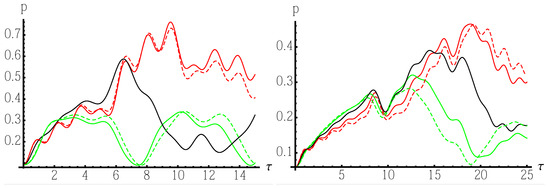
Figure 2.
Localization probability for ring graphs with a three-site symmetric oracle. The two panels show as a function of for two rings with and (left) and and (right), and for different values of (chosen among those leading to a localization probability larger than that for ). The red curves in both panels denote the results obtained for negative values of whereas the green ones are for positive values of . Solid lines in the left panel correspond to and dashed lines to . In the right panel we have (solid lines) and (dashed lines).
The red curves in both panels of Figure 2 denote the results obtained for negative values of , whereas the green ones are for positive values of . Solid lines in the left panel correspond to and dashed lines to . In the right panel we have (solid lines) and (dashed lines). As it is apparent from the plots, the inclusion of additional terms in the oracle is an effective strategy to achieve larger localization probability, although at later times. A systematic analysis for graphs of dimensions confirms that larger localization probabilities are obtained when is smaller than and with opposite sign. Another general feature that may be observed is that with the maximum value of the localization probability is achieved at later times.
A intuitive explanation of the behaviour of the walker goes as follows. The difference between the on-site energy of target and those of its neighbouring sites creates a barrier which slows down the walker. However, the same fact also leads to a trapping effect which allows the walker to localize more efficiently to the target.
Motivated by the above results and considerations, let us now consider a two-parameter structured oracle of the form
and try to optimize the performance by choosing suitable values of and c. Instead of using brute force numerical optimization, we set the values of the two parameters using the following argument. Since the evolution is unitary, the Hamiltonian is a constant of motion and we have for any integer k and any pair of initial and evolved states. In our case, the initial state is the fully delocalized state , and the desidred final state is the target . Since the localization is not exact, i.e., is not the exact final state of the evolution, we cannot hope that the all the equalities are satisfied. However, we may use these constraints to obtain suitable values of the oracle parameters. In particular, let us consider the value . Since for any Laplacian, and that from Equation (7), the equalities , and may be written as
Numerical counterexamples show that for a given n, the solutions of Equations (8) and (9) do not, in general, coincide the exact values found by numerical maximization of . However, they represent a suitable approximation and, as we will see in the following, they improve the localization probability, and the search time, in comparison to the case of a simple unstructured oracle. For these reasons, we refer to in Equation (7) with the parameters found by the Hamiltonian constraints Equations (8) and (9) as a pretty good oracle (PGO). The solutions of Equations (8) and (9), denoted by and , are reported in the left panel of Figure 3 as a function of N. The value of oscillates around the value (the oscillation amplitude decreases with N), whereas increases with N, approaching the limiting value from below. The corresponding localization probability, i.e.,
is reported, as a function of the graph size N, in the right panel of Figure 3, together with the localization probability obtained with an unstructured oracle. The improvement is apparent. In the range of N considered, the localization probability decreases as with an unstructured oracle and only as for a structured PGO.
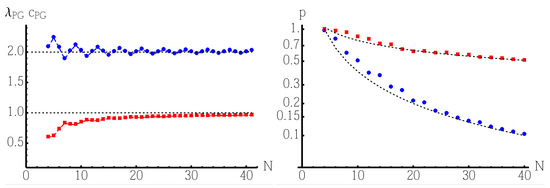
Figure 3.
(Left): The solutions of Equations (8) and (9), denoted by and , as a function of N. The two horizontal dashed lines denote the values and , respectively. (Right): The red squares denote the pretty good oracle (PGO) localization probability , defined in Equation (10), as a function of N. The blue circles denote the corresponding localization probability for an unstructured oracle. The upper and lower dashed curves correspond to the functions and , respectively.
Let us now address the performance of our structured PGO in terms of the search time. If one consider search algorithm where localization is not exact, i.e., the localization probability is not one, localization should be intended in statistical sense, i.e., obtained in average by repeating experiments. In this framework, a suitable figure of merit to compare different algorithms and regimes is given by the equivalent time
obtained by renormalizing time by the corresponding localization probability. In the two panels of Figure 4, we show the equivalent time of PGO compared to the corresponding equivalent time of an unstructured oracle for two ring graphs with sizes and .
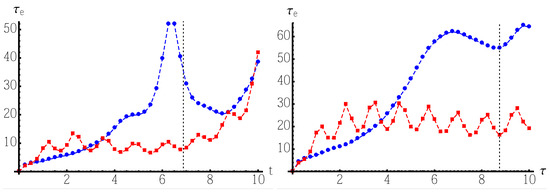
Figure 4.
The equivalent search time of Equation (11) for a structured PGO (red squares) and for an unstructured oracle (blue circles) as a function of the evolution time for two ring graphs with sizes (left) and (right). The vertical dashed line indicates the time at which the maximum PGO localization probability is obtained.
In both panels, the red squares denotes for our PGO, and the blue circles for an unstructured oracle. The vertical dashed line indicates the time at which the maximum PGO localization probability is obtained. The interpretation of the results reported in Figure 4 is the following: the equivalent time of PGO is not always lower than that of an unstructured oracle, but it becomes much smaller for times corresponding to the maximum localization probability. Overall, this means that despite the dynamics of the walker is slower with a PGO (see above), the gain in the localization probability make it convenient also in terms of the equivalent search time, which is closer to the Grover time compared to the corresponding quantity evaluated for an unstructured oracle.
Physical implementations of quantum search on graphs may require going beyond the projector structure, since acting on single sites may be difficult to implement. Our analysis shows that taking into account some modification of the on-site energies of the sites neighbouring the target one, it is still possible to obtain some effective improvement up to suitably control the phase and coupling of the different involved sites, as we highlighted in Equation (7).
4. Conclusions
In this paper, we have addressed spatial quantum search with quantum walks on graphs, and put forward an alternative search algorithm based on structuring the oracle operator. Our protocol allows one to improve the localization properties of the walker by tuning only the on-site energies of the graph, i.e., without altering its topology. In particular, we have analyzed the use of a structured oracle in order to improve the searching performance of CTQW on ring graphs, as a paradigmatic example of structure with low connectivity.
We have employed a two-parameter oracle operator and instead of using brute force numerical optimization, we have set the values of the two parameters using Hamiltonian constraints. The resulting oracle is not necessarily the optimal one, but it nevertheless provides improved performance compared to that of an unstructured oracle. We thus refer to our design as a pretty good oracle (PGO). We have considered ring graphs with size and, in the range of N considered, have found that the localization probability decreases as with an unstructured oracle and only as for a structured PGO.
The proposed algorithm is suitable for implementation in systems with low connectivity, e.g., ring of quantum dots or superconducting circuits, whereas characterization of oracle parameters may be achieved by quantum probing [19,20,21].
Author Contributions
M.G.A.P., C.B. and S.O. conceived and designed the experiments; M.G.A.P., C.B. and S.O. performed the experiments; M.G.A.P., C.B. and S.O. analyzed the data; M.G.A.P., C.B. and S.O. contributed reagents/materials/analysis tools; M.G.A.P., C.B. and S.O. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work received no funding.
Data Availability Statement
Data are available upon request.
Acknowledgments
MGAP is member of GNFM-IndAM.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aaronson, S.; Ambainis, A. Quantum search of spatial regions. In Proceedings of the 44th Annual IEEE Symposium on Foundations of Computer Science, Cambridge, MA, USA, 14 October 2003; pp. 200–209. [Google Scholar]
- Gualtieri, V.; Benedetti, C.; Paris, M.G.A. Quantum-classical dynamical distance and quantumness of quantum walks. Phys. Rev. A 2020, 102, 012201. [Google Scholar]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing—STOC ’96, Philadelphia, PA, USA, 11 May 1996; pp. 212–219. [Google Scholar]
- Farhi, E.; Gutmann, S. Quantum computation and decision trees. Phys. Rev. A 1998, 58, 915–928. [Google Scholar] [CrossRef]
- Childs, A.M.; Goldstone, J. Spatial search by quantum walk. Phys. Rev. A 2004, 70, 022314. [Google Scholar] [CrossRef]
- Cattaneo, M.; Rossi, M.A.C.; Paris, M.G.A.; Maniscalco, A.S. Quantum spatial search on graphs subject to dynamical noise. Phys. Rev. A 2018, 98, 052347. [Google Scholar] [CrossRef]
- Rossi, M.A.C.; Cattaneo, M.; Paris, M.G.A.; Maniscalco, S. Non-Markovianity is not a resource for quantum spatial search on a star graph subject to generalized percolation. Quantum Meas. Quantum Metr. 2018, 5, 40–49. [Google Scholar] [CrossRef]
- Novo, L.; Chakraborty, S.; Mohseni, M.; Neven, H.; Omar, Y. Systematic Dimensionality Reduction for Quantum Walks: Optimal Spatial Search and Transport on Non-Regular Graphs. Sci. Rep. 2015, 5, 13304. [Google Scholar] [CrossRef] [PubMed]
- Philipp, P.; Tarrataca, L.; Boettcher, S. Continuous-time quantum search on balanced trees. Phys. Rev. A 2016, 93, 032305. [Google Scholar] [CrossRef]
- Chakraborty, S.; Novo, L.; Ambainis, A.; Omar, Y. Spatial Search by Quantum Walk is Optimal for Almost all Graphs. Phys. Rev. Lett. 2016, 116, 100501. [Google Scholar] [CrossRef]
- Glos, A.; Krawiec, A.; Kukulski, R.; Puchała, Z. Vertices cannot be hidden from quantum spatial search for almost all random graphs. Quantum Inf. Process. 2018, 17, 81. [Google Scholar] [CrossRef]
- Wong, T.G. Spatial search by continuous-time quantum walk with multiple marked vertices. Quantum Inf. Process. 2016, 15, 1411–1443. [Google Scholar] [CrossRef]
- Agliari, E.; Blumen, A.; Mülken, O. Quantum-walk approach to searching on fractal structures. Phys. Rev. A 2010, 82, 012305. [Google Scholar] [CrossRef]
- Li, S.; Boettcher, S. Renormalization group for a continuous-time quantum search in finite dimensions. Phys. Rev. A 2017, 95, 032301. [Google Scholar] [CrossRef]
- Janmark, J.; Meyer, D.A.; Wong, T.G. Global Symmetry is Unnecessary for Fast Quantum Search. Phys. Rev. Lett. 2014, 112, 210502. [Google Scholar] [CrossRef]
- Meyer, D.A.; Wong, T.G. Connectivity is a Poor Indicator of Fast Quantum Search. Phys. Rev. Lett. 2015, 114, 110503. [Google Scholar] [CrossRef] [PubMed]
- Solenov, D.; Fedichkin, L. Continuous-time quantum walks on a cycle graph. Phys. Rev. A 2006, 73, 012313. [Google Scholar] [CrossRef]
- Benedetti, C.; Buscemi, F.; Bordone, P.; Paris, M.G.A. Quantum probes for the spectral properties of a classical environment. Phys. Rev. A 2014, 89, 032114. [Google Scholar] [CrossRef]
- Teklu, B.; Olivares, S.; Paris, M.G.A. Bayesian estimation of one-parameter qubit gates. J. Phys. B 2009, 42, 035502. [Google Scholar] [CrossRef]
- Tamascelli, D.; Olivares, S.; Benedetti, C.; Paris, M.G.A. Characterization of qubit chains by Feynman probes. Phys. Rev. A 2016, 94, 042129. [Google Scholar] [CrossRef]
- Troiani, F.; Paris, M.G.A. Probing molecular spin clusters by local measurements. Phys. Rev. B 2016, 94, 115422. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




