Lacunary Möbius Fractals on the Unit Disk

Abstract

Centered polygonal lacunary functions are a type of lacunary function that exhibit behaviors that set them apart from other lacunary functions, this includes rotational symmetry. This work will build off of earlier studies to incorporate the automorphism group of the open unit disk $\mathbb{D}$, which is a subgroup of the Möbius transformations. The behavior, dimension, dynamics, and sensitivity of filled-in Julia sets and Mandelbrot sets to variables will be discussed in detail. Additionally, several visualizations of this three-dimensional parameter space will be presented.

1. Introduction

In recent years, the current authors have been studying an interesting family of lacunary functions called centered polygonal lacunary functions [1,2]. The defining feature of lacunary functions is the fact that their power series have “gaps” (or “lacunae”) in the progression of powers and those gaps increase. Because of this, only certain monominal terms have non-zero coefficients in the power series. One simple example of such a series is $f\left(z\right)={\sum }_{n=1}^{\infty }{z}^{n^2}=z+z^4+z^9+z^{16}+\cdots$. The most distinctive feature of lacunary functions is that they exhibit a natural boundary [3,4,5]. The example above has a natural boundary at the unit circle and is analytic on the open unit disk. In general, if the function describing the gaps in the powers satisfies the criteria of Fabry’s gap theorem, then the function described by the power series will be lacunary and have a natural boundary at unit circle [3,4,5]. This implies that it will be impossible to analytically continue the function beyond the natural boundary.

The central focus of this work will be when the active powers in the Taylor series are described by the centered polygonal numbers [6,7,8],

$$C^{\left(k\right)}=\left\{\frac{k{n}^2-kn+2}{2}\right\},n\ge 1.$$

(1)

The centered polygonal numbers are a sequence of numbers arising from considering points on a polygonal lattice [6,7,8].

The family of lacunary functions generated by centered polygonal numbers are called centered polygonal lacunary functions. This family has particularly interesting features which are mainly due to the unusual symmetry present in this family, compared with arbitrary lacunary functions [1,2]. In a previous work the current authors explored some of the fractal character of the centered polygonal lacunary functions [2]. In that work both the “classical” Julia set, generated via direct iteration of the function, and a “phase-rotated” Julia set were explored. Phase-rotated Julia sets are created by introducing a constant phase factor each iteration.

The current work builds off the earlier study of phase-rotated Julia sets in a natural way. The domain of analyticity of the centered polygonal lacunary functions is the open unit disk, $\mathbb{D}$. Of course, a phase rotation maps $\mathbb{D}$ to $\mathbb{D}$, but the rotations are not the full automorphism group of $\mathbb{D}$. The automorphism group of $\mathbb{D}$ is the subgroup of Möbius transformations,

$$\mathcal{M}\left(z\right)=e^{i\theta }\frac{z-a}{\overline{a}z-1},$$

(2)

where $\theta \in \mathbb{R}$ and $a\in \mathbb{D}$ [3]. The current work offers a generalization to the previous work by introducing a Möbius transformation each iteration. These will be called lacunary Möbius fractals. This opens up a three-dimensional parameter space ($\theta$, Re$\left[a\right]$ and Im$\left[a\right]$) to explore and this results in some intricate and strikingly beautiful fractals in the form of filled-in Julia sets. Attendant with Julia sets are Mandelbrot sets. In this case, the full Mandelbrot set for a given centered polygonal lacunary function is three-dimensional. These Mandelbrot sets are explored along with two-dimensional subsets.

To be sure, Julia set and Mandelbrot set fractals capture the imagination. However they are not just visually fascinating, applications indeed abound. Within the past year, Xiang, Zhou, and Guo have employ a class of random fractals in the area of machine learning, specifically, generative adversarial networks [9]. In a recent review article, Yadav et al. discuss the control of Julia and Mandelbrot sets [10]. Incidentally, this review also has a good list of references to physical applications of Julia sets. Very recently, Abbas, Iqbal, and De la Sen have discussed the generation of Julia and Mandelbrot sets via fixed points [11]. In 2020, Kawahira has revised a the famous theorem by Tan [12] regarding the similarity between Mandelbrot sets and Julia sets at Misiurewicz points [13]. The lacunary Möbius fractals studied in the current work show global similarity between the Mandelbrot and Julia sets, albeit for different reasons. In the recent engineering literature, Nazeer and Kang intensely studied Jungck Mann orbits and fractal generating along with escape time algorithms for finite polynomials based on the concept of S-convexity [14,15,16]. Finally, one particularly interesting example is the recent work by Feijs, Toeters and collaborators on the exploration of a Mandelbrot set in a taxicab-based platform, which has inspired an application in the fashion industry [17,18].

Home-written Mathematica [19] code was utilized in this study. All computations were performed on Mathematica version 12.0. and distributed across 11 computers (four cores, Intel(R) Core(TM) i5-7500 CPU @ 3.40 GHz processor, 16 GB RAM, and a 64-bit Operating System, DELL COMPUTERS Round Rock, TX USA). More information and code snippets can be found in reference [2]. The one main modification to the Mathematica code compared to that used in reference [2]. A code snippet is included in Section 5.

2. Centered Polygonal Lacunary Functions

A given lacunary function is represented by a power series on $\mathbb{D}$ as

$$\sum _{n=1}^{\infty }{z}^{g\left(n\right)},$$

(3)

where $g\left(n\right)$ is the so-called gap function [3,4,5]. For the current work, the gap functions will be those which give the centered polygonal numbers, i.e.,

$$g_k\left(n\right)=\frac{k{n}^2-kn+2}{2}.$$

(4)

One can view lacunary functions as a limit of a sequence of functions, $f^{\left(k\right)}\left(z\right)={lim}_{N\to \infty }{f}_N\left(z\right)$. This sequence is denoted as

$$\mathfrak{L}(g;z)\equiv \left\{f_N^{\left(k\right)}\right\}=\left\{\sum _{n=1}^N{z}^{g_k\left(n\right)}\right\}.$$

(5)

As discussed in previous work [1,2], a particularly important and revealing way to consider members of $\mathfrak{L}(g;z)$ is in their polar form: $f_N^{\left(k\right)}\left(z\right)=R\left(z\right)e^{i\Phi \left(z\right)}$ and to focus on $R\left(z\right)=|f_N^{\left(k\right)}\left(z\right)|$. Figure 1 shows this representation. Specifically, the example of $|f_{16}^{\left(4\right)}\left(z\right)|$ is shown in a couple of ways in the left side of Figure 1 where it is plotted as a surface overlaying a contour plot. The unit circle is indicated with the black circle. The contour plots of $|f_N^{\left(k\right)}\left(z\right)|\le 1$ prove to be the most succinct and useful [1,2]. Contours plot of $|f_{16}^{\left(k\right)}\left(z\right)|$ for $k=1$, $k=2$, and $k=3$ are shown in the right-hand column of Figure 1.

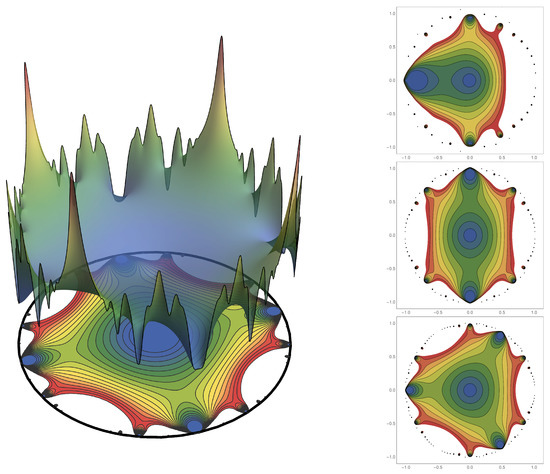
Figure 1. One nice way to present graphs of centered polygonal functions is shown on the right side column. The representation given here have been described in previous work [1,2]. The contour plot of the modulus is truncated at the unity level set (blue shading represents low values and red shading represents high values). The left side shows the example in which $k=4$ where a surface plot of $|f_{16}\left(z\right)|$ is shown above the contour plot as a guide to the interpretation of the contour plot. The unit circle is superimposed in black to guide the eye. The right column of panels show $|f_{16}\left(z\right)|$ for the cases of $k=1$, $k=2$, and $k=3$. The k-fold rotational symmetry of the the centered polygonal lacunary functions are clearly evident.

These contour plots expose an important property of centered polygonal based lacunary function. Centered polygonal lacunary functions display k-fold rotational symmetry (as seen in Figure 1). Dihedral mirror symmetry is also present. This manifests itself in powerful ways in the associated Julia sets and Mandelbrot set [1,2].

Jacobi $\vartheta$-Functions

It is noted here that the centered polygonal lacunary functions can be expressed as Jacobi $\vartheta$ functions [20]. To do this, one has

$$f_N^{\left(k\right)}\left(z\right)=\sum _{n=1}^N{z}^{\frac{k{n}^2-kn+2}{2}}=z\sum _{n=1}^N{\left(z^{\frac{k}{2}}\right)}^{n^2-n}.$$

(6)

Momentarily writing $w=z^{\frac{k}{2}}$ and completing the square gives

$$f_N^{\left(k\right)}\left(z\right)=z\sum _{n=1}^N{w}^{{\left(n-\frac{1}{2}\right)}^2}{w}^{-\frac{1}{4}}.$$

(7)

Setting $j=n-1$ and exploiting the symmetry in the dummy index, one obtains

$$f_N^{\left(k\right)}\left(z\right)=\frac{1}{2}z{w}^{-\frac{1}{4}}\sum _{j=-(N-1)}^{N-1}{w}^{{\left(j+\frac{1}{2}\right)}^2}.$$

(8)

Finally, letting $N\to \infty$, substituting back in for w and recognizing the second Jacobi $\vartheta$ function gives

$$f_{\infty }^{\left(k\right)}\left(z\right)=f\left(z\right)=\frac{1}{2}z{w}^{-\frac{1}{4}}\sum _{j=-\infty }^{\infty }{w}^{{\left(j+\frac{1}{2}\right)}^2}=\frac{1}{2}{z}^{\frac{8-k}{8}}{\vartheta }_2\left(0;z^{\frac{k}{2}}\right).$$

(9)

3. Iteration of Centered Polygonal Lacunary Functions

In order to maintain a limit in scope, this work will exclusively focus on the the fractal character of the filled-in Julia sets and their corresponding Mandelbrot sets [21,22,23]. Construction of a filled-in Julia set, of course, requires iteration [2]. The following notation is used to denote the number of iterations, j, the order of the partial summation N, and the primary symmetry, k. Classically, $f_N^{\left(k\right)}\left(z\right)$ iterated j times is written as

$${}^j{h}_N^{\left(k\right)}\left(z\right)\equiv f_N^{\left(k\right)}(\stackrel{j}{\overbrace{f_N^{\left(k\right)}(f_N^{\left(k\right)}(...f_N^{\left(k\right)}\left(z\right)))}}),$$

(10)

but for the lacunary Möbius fractals with parameters $\theta$ and a,

$${}^j{h}_N^{\left(k\right)}(z;\theta ,a)\equiv f_N^{\left(k\right)}(\stackrel{j}{\overbrace{\mathcal{M}(f_N^{\left(k\right)}(\mathcal{M}(f_N^{\left(k\right)}(...\mathcal{M}(f_N^{\left(k\right)}\left(z\right))))))}})).$$

(11)

4. Julia Sets and Mandelbrot Sets

A common and visually striking ways to show the fractal character of a complex function such as the classic example of $\eta \left(z\right)=z^2+c$ is to create its filled-in Julia set [21,22,23]. This is done by iterating the function, $\eta \left(\eta \right(\eta (\cdots \eta (z\left)\right)\cdots \left)\right))$ an infinite number of times. The appearance of the filled-in Julia set in this example is determined by the c. Since $c\in \mathbb{C}$, one regards the set of all filled-in Julia sets as parameterized by a two-dimensional space. A succinct representation of this collection of filled-in Julia sets is the Mandelbrot set [21,22,23]. In a recent work, Fowler and McGuinness derived expressions for measuring the size of the bulbs in the Mandelbrot set for $\eta$ [24].

4.1. Three-Dimensional and Two-Dimensional Mandelbrot Sets

For the case of the lacunary Möbius fractal as described in Equation (11) the parameter space is three-dimensional ($\theta$, Re$\left[a\right]$ and Im$\left[a\right]$). Throughout this work, a point in this space will be considered as an element of the Cartesian product $[0,2\pi )\times \mathbb{D}$. This means that the succinct representation by a Mandelbrot set is three-dimensional: one real angle and a complex Möbius parameter. There is one of these three-dimensional Mandelbrot sets for each value of k. The sets are labelled as ${\mathfrak{M}}_k$.

There are certainly some visually interesting representations of these sets, two of which are shown in Figure 2. where the specific example of ${\mathfrak{M}}_4$ is shown. Figure 2 collects three such representations of ${\mathfrak{M}}_4$. The top row and bottom right graphs are three different viewpoints of ${\mathfrak{M}}_4$ shown as a “surface-swarm” representation. In this representation, the Mandelbrot set is plotted with the transparency of its graph based how many points in a small region are not in the same set (${\mathfrak{M}}_4$ or its complement). For example, if a point is a member of ${\mathfrak{M}}_4$ and so are all its first, second, third, etc nearest neighbors in the lattice of sampled points, then that point will be plotted with very high transparency. The same is true if a point and its neighbors are in the complement of ${\mathfrak{M}}_4$. Conversely if the collection of nearby points in the sampling lattice differ, which is the case on the (fractal) surface of the Mandelbrot set, then the transparency is much lower. All this results in a smoothed out (because of the inherent averaging) outline of the surface of ${\mathfrak{M}}_4$. The bulk of the Mandelbrot set and the bulk of its complement are nearly see-through. The surface itself is then colored green if it faces the interior of the Mandelbrot set and colored blue if it faces the exterior of the Mandelbrot set. The surface-swarm representation gives a sense of complexity of the Mandelbrot set but is visually cluttered.

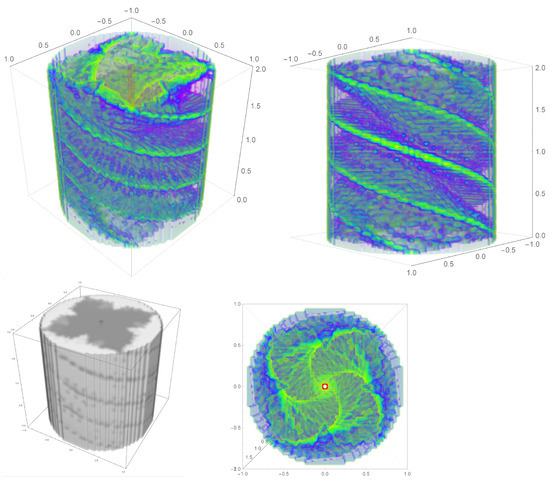
Figure 2. The “surface-swarm” (top row and bottom right) and “cylinder” (bottom left) graphical representation of ${\mathfrak{M}}_4$ for ${}^{25}{h}_{14}^{\left(4\right)}$. The sampling step size is 0.025 in each dimension. For the surface-swarm plots, the Mandelbrot set is colored based how many points in a small region are not in the same set, ${\mathfrak{M}}_4$ or its complement. The green (blue) gives the interior (exterior) side of the surface of ${\mathfrak{M}}_4$. (The red is an artifact of plotting and not physically relevant). For the cylinder graph, ${\mathfrak{M}}_4$ is colored dark grey and its complement is colored light grey. In all cases the plotted regions is $[0,2\pi )\times \mathbb{D}$. Note: the $\theta$-axis is in “units” of $\pi$.

In the interest of space, only ${\mathfrak{M}}_4$ is shown. The surface-swarm graphs for other values of k have a similar appearance. The main difference is in the number of green diagonal bands (seen best in the top right panel of Figure 2). The bands are caused be the fact that the Mandelbrot set extends to the edge of the unit disk in k places and these places twist through parameter for one full rotation. Thus, this results in k diagonal streaks of green across the face of the cylinder. Indeed there are four such streaks seen in Figure 2.

A second representation of ${\mathfrak{M}}_4$, called the “cylinder” representation, is shown in the bottom left of Figure 2. This is from the same viewpoint as the surface-swam graph in the top left of the figure. In this case the transparency of every plotted point is the same (unlike for the surface swarm). This results in the Mandelbrot set being dark grey in appearance and its complement being light gray. While much is lost here it helps to orient the eye to the parameter space of the Mandelbrot set.

In both of the representations, ${\mathfrak{M}}_4$ is in $[0,2\pi )\times \mathbb{D}$. It is clear from both representations that $\theta$ introduces a twisting in the structure of ${\mathfrak{M}}_4$. Beyond this observation, it will be more insight to consider subsets of ${\mathfrak{M}}_4$ that are obtains by taking planar slices of these graphs as shown in Figure 3.

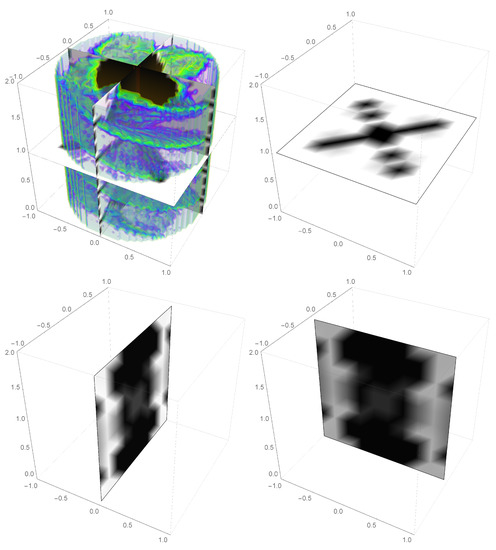
Figure 3. Examples of typical and useful two-dimensional subsets of ${\mathfrak{M}}_4$. The subsets arise from planar cuts in ${\mathfrak{M}}_4$. The resulting two-dimensional Mandelbrot sets can be explored in more detail and at much higher resolution to provide additional insight into lacunary Möbius fractals. Some of these subests are shown in Figure 4 and Figure 5. Members of the two-dimensional Mandelbrot set are colored black and members of the complement are colored white.

The three-dimensional Mandelbrot sets provide a general overview of the parameters space as a whole but they lack significant value in helping to understand the nature of the fractals. To get a more detailed picture of this one turns to the two-dimensional Mandelbrot sets which are two-dimensional subsets of ${\mathfrak{M}}_k$. Often these are slices of ${\mathfrak{M}}_k$ that are planes parallel to the three Cartesian planes. Figure 3 pictorially depicts the relationship between two-dimensional Mandelbrot sets and ${\mathfrak{M}}_4$. A number of these are explored subsequently.

Figure 4 shows two-dimensional Mandelbrot sets which are similar to the horizontal plane shown in Figure 3. These four slices occur at $\theta$ equal to every $\frac{2\pi }{3}$ from 0 to $\pi$. It is clear that the $\theta$ parameter introduces a twisting of the two-dimensional Mandelbrot set (which was also evident in ${\mathfrak{M}}_k$ itself as seen in Figure 2). One sees that the k-fold rotational symmetry persists upon the phase twisting, but a loss of the dihedral mirror symmetry that seen in the first column. The dihedral mirror symmetry is recovered at $\theta =\pi$. (It is noted that in this work $\theta$ differs by $\pi$ from that of reference [2].) Two main regions emerge as $\theta$ changes. There is a shrinking central region that appears to maintain a quasi-dihedral mirror symmetry. There is also the development of growing ”arms” off the tips of each lobe.

Figure 4. Two dimensional subsets of ${\mathfrak{M}}_k$ for $k=2$ (top row), $k=3$ (second row), $k=4$ (third row), and $k=6$ (bottom row). In the left most column $\theta =0$, $\theta =\frac{\pi }{3}$ in the second column, $\theta =\frac{2\pi }{3}$ in the third column, and $\theta =\pi$ in the right most column. The phase breaks the dihedral symmetry but maintains the k-fold rotational symmetry introduces. Other features of these two Mandelbrot sets are described in the text. Members of the two-dimensional Mandelbrot set are colored black and members of the complement are colored white. In all cases, ${}^{25}{h}_{14}^{\left(k\right)}$ with a sampling step size of 0.005 in both dimensions.

Two secondary features also emerge upon increasing $\theta$. One feature that is a bit unusual for Mandelbrot sets is the wispy fraying of the edges as it twists. This is most noticeable in the graphs shown in the second column of Figure 4. Another interesting feature is the emergence of “jets” spraying out from the nexus of the lobe and the arm regions. This is most noticeable in the third column of Figure 4. There is a lot of dynamicism in the filled-in Julia sets coming from the jets. Because of the inherit limit in scope and variety of behavior of the Julia sets, this jet is a an appropriate region to study in detail to understand the characteristics of the whole plane.

Like Figure 4 and Figure 5 shows slices of ${\mathfrak{M}}_k$ similar to the vertical planes shown in Figure 3. The examples $k=2$, 3, 4, and 6 are collected. The Re$\left[a\right]$-$\theta$ plane is shown across the top row and the Im$\left[a\right]$-$\theta$ plane is shown across the bottom row. As k increases, more arms extend out from the middle. Mirror plane symmetry about the Re$\left[a\right]=0$ and Im$\left[a\right]=0$ lines when k is even, but this mirror symmetry is broken when k is odd. There is a nexus point at $\theta =\pi$ and Re$\left[a\right]=0$ (or Im$\left[a\right]=0$). The two parts of the Mandelbrot set detach at that point when Re$\left[a\right]=0$ (or Im$\left[a\right]=0$) is not zero. One example of this is shown in the left panel of Figure 6.

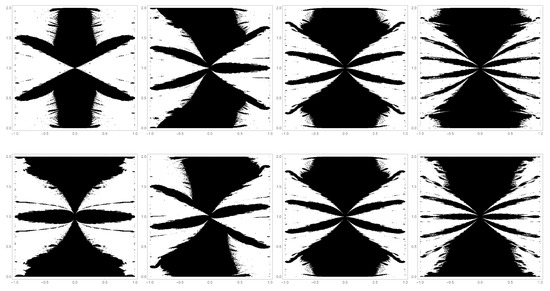
Figure 5. Two-dimensional subsets of ${\mathfrak{M}}_k$ for $k=2$ (leftmost column), $k=3$ (second column), $k=4$ (third column), and $k=6$ (rightmost column). The top row has $\theta$ as the ordinate (scaled by $\pi$) and Re$\left[a\right]$ as the abscissa and Im$\left[a\right]=0$. The second row has $\theta$ as the ordinate and Im$\left[a\right]$ as the abscissa and Re$\left[a\right]=0$. The features are these two-dimensional Mandelbrot sets are discussed in the texts. Members of the two-dimensional Mandelbrot set are colored black and members of the complement are colored white. In all cases, ${}^{25}{h}_{14}^{\left(k\right)}$ with a sampling step size of 0.005 in both dimensions.

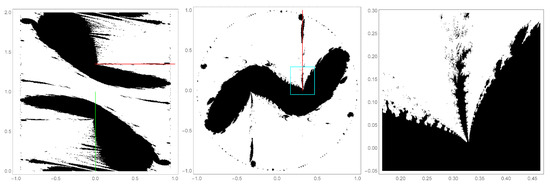
Figure 6. Two-dimensional subsets of ${\mathfrak{M}}_2$ that will serve as the primary exploration landscape for analysis of the associated filled in Julia sets. The red line indicates the path through parameter space, $\gamma =(1.35\pi ,0.315+iy)$. The green line indicates the path $\gamma =(\theta ,0.315+i0)$. The left panel shows a $\theta$-y plane slice of ${\mathfrak{M}}_2$ and the middle panel shows a x-y plane slice. The cyan-colored box in the middle graph indicate a blow-up window which is shown in the right panel. Note, in the graphs, $\theta$ is scaled by $\pi$. The jet structure emanating from the nexus of the main lobes of the Mandelbrot set is prominently featured. Members of the two-dimensional Mandelbrot set are colored black and members of the complement are colored white.

Figure 6 will play a central role for the remainder of this work, because it proves to be fertile ground to gain both qualitative and quantitative insight into the nature of lacunary Möbius fractals, specifically its filled-in Julia sets. The figure shows two slices of ${\mathfrak{M}}_2$ in the left ($x=0.315$ plane) and middle ($\theta =1.35\pi$ plane) panels. This particular part of ${\mathfrak{M}}_2$ exhibits some prominent jets that lie along convenient paths, for example $\gamma =(1.35\pi ,0.315+iy)$ which is marked as a red line in the figure. There is also a nice wispy fray region and, again, a convenient path cuts through it ($\gamma =(\theta ,0.315+i0)$, green line). Finally, the right panel of Figure 6 shows a blow-up of the region marked by the cyan-color box in the middle panel. This shows the intricate behavior of the jet region.

4.2. Filled-In Julia Sets

Each point, p, in ${\mathfrak{M}}_k$ represents a complete filled-in Julia set, ${\mathfrak{J}}_k\left(p\right)$. The diversity and intricacy of these filled-in Julia sets is stunning. We explore a number of these here. As a matter of notation a family of filled-in Julia sets arising from a path $\gamma$ through ${\mathfrak{M}}_k$ will be denoted as $\left\{{\mathfrak{J}}_k\left(\gamma \right)\right\}$. In practice, $\gamma$ will be discretized so the $i^{\mathrm{th}}$ member of $\left\{{\mathfrak{J}}_k\left(p\right)\right\}$ is ${\mathfrak{J}}_k\left({\gamma }_i\right)$.

It is also convenient to define the decretized “fill” of a filled-in Julia set $\mathcal{F}\left[{\mathfrak{J}}_k\left(p\right)\right]$, as the number of pixels in the unit disk that are zero (black in the figures). Note the the fill depends on the sampling rate of the filled-in Julia set.

It is particularly interesting to assess the filled-in Julia sets corresponding to points in the jets of the Mandelbrot sets. Because of the nature of the jets one might expect a wide range of diversity among the filled-in Julia sets. This is indeed the case and not only is there a diversity of shapes, the change in the global visual appearance of the filled-in Julia sets along a path $\gamma$ in ${\mathfrak{M}}_k$ is quite abrupt. As a concrete example, the filled-in Julia sets along a path that traverses the jet in ${\mathfrak{M}}_2$ (red line in Figure 6) is explored in detail. To begin, Figure 7 shows a sequence of 16 filled in Julia sets corresponding to points along $\gamma =(1.35\pi ,0.313x+iy)$, where y runs for the short range from 0 to $0.08$. The particular stretch of path through the jet is small but radically different filled-in Julia sets appear. In Figure 7, the Julia sets are read from left-to-right, top-to-bottom. Thus, for example, the left most Julia set in the second row is given from the point $(1.35\pi ,0.315+0.150i)$ in parameter space. The initial graph (point $(1.35\pi ,0.315+0i)$) consist of a relatively nondescript roughly three-lobed shape. The overall appearance changes very little across the top row. The second row marks the beginning of an abrupt transition to a rather elaborate (and beautiful) shape with many intricate clefts and protrusions.

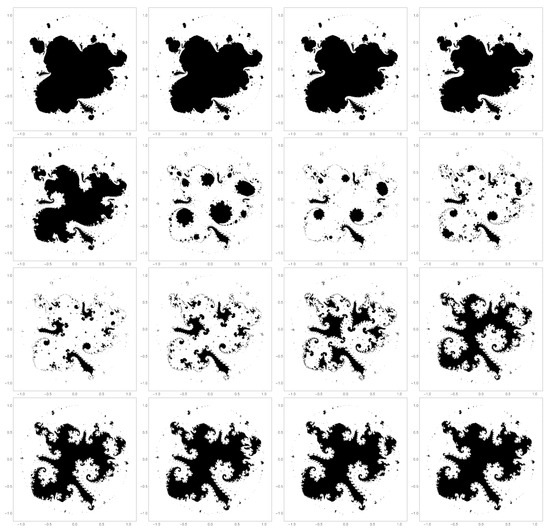
Figure 7. Filled-in Julia sets corresponding to equally spaced points in ${\mathfrak{M}}_2$ over the range shown in the inset of Figure 8 (0 to $0.08$) along the red path shown in Figure 6. The global form of filled-in Julia sets can change abruptly along this path. In all cases, ${}^{25}{h}_{14}^{\left(2\right)}$ with a sampling step size of 0.005 in both dimensions.

Interestingly, the transition is marked with a disappearance and reappearance of a large portion of the interior of the Julia set. There does appear to be some consistency in certain regions of $\mathbb{D}$ that are always in the complement of the filled-in Julia set. But other areas of $\mathbb{D}$ are very dynamic. Not only do certain points flicker in and out of the filled-in Julia set, but the size and shapes of the various connected domains differ significantly from on filled-in Julia set to the next, as can be seen in the third row of Figure 7.

4.3. Dynamicism of the Filled-In Julia Sets

In an effort to pull some quantitative understanding from the dynamic variability of the filled-in Julia sets just discussed, one can define a derivative of sorts to compare Julia sets alone a path in parameter space. This is accomplished by point-wise subtracting adjacent filled-in Julia sets from a collection alone a path. This is normalized by the fill of the initial filled-in Julia set. This a global analysis looking for total change so the sum of the absolute differences is taken. This will be referred to as the JS-derivative and is defined as,

$${\mathsf{\Delta }}_k\left({\gamma }_i\right)=\frac{|{\mathfrak{J}}_k\left({\gamma }_{i+1}\right)-{\mathfrak{J}}_k\left({\gamma }_i\right)|}{d·\mathcal{F}\left[{\mathfrak{J}}_k\left({\gamma }_i\right)\right]},$$

(12)

where $d\equiv |{\gamma }_{i+1}-{\gamma }_i|$ is the step size alone $\gamma$.

Figure 8 shows the JS-derivative for the path $\gamma =(1.35\pi ,0.313x+iy)$ (red line in Figure 6). It is important to explore the impact of N and j on the JS-derivative. The left graph of the Figure 8 shows and overlay of the JS-derivative for ${}^{25}{h}_8^{\left(2\right)}$ (brown curve) and ${}^{25}{h}_{20}^{\left(2\right)}$. This shows that the JS-derivative is relatively insensitive to the number of terms in the centered polygonal lacunary series. If fact, most of the data generated in this work used $N=14$. The corresponding JS-derivative curve for this case is nearly visually indistinguishable from the $N=20$ case (data not shown).

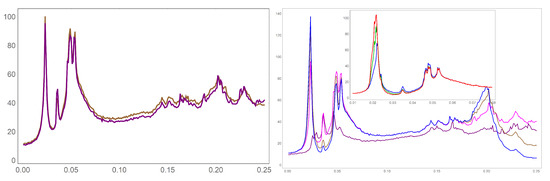
Figure 8. The effect of N (left) and j (right) on the JS-derivative. The abscissa for both graphs is y and the ordinate are in arbitrary units. The sampling step size is 0.001. Shown is ${\mathsf{\Delta }}_2(1.35\pi ,0.315+iy)$ (the red line in Figure 6). The left graph shows curves for $j=25$ and $N=8$ (brown) and $N=20$ (purple). The JS derivative is quite robust with changing values of N. The right graph shows curves for $N=14$ and $j=15$ (purple), $j=25$ (magenta), $j=35$ (brown), and $j=45$ (blue). The JS-derivatives are quite sensitive to changing values of j. Notably, some peaks have strong j dependence while others have very little j dependence. The inset in the right graph shows a higher resolution scan (step size 0.00025) of the region from $y=0.01$ to $0.08$ using higher values of j; $N=14$ and $j=45$ (blue), $j=60$ (green), $j=75$ (red). The higher resolution reveals structure in the sharp leftmost peak. Note: this peak is referred to as peak 1 in the body of the text.

The right graph of Figure 8 shows ${}^{15}{h}_{14}^{\left(2\right)}$ (purple curve), ${}^{25}{h}_{14}^{\left(2\right)}$ (magenta curve), ${}^{35}{h}_{14}^{\left(2\right)}$ (brown curve) and ${}^{45}{h}_{14}^{\left(2\right)}$ (blue curve). In contrast to N, the JS-derivative is quite sensitive to j, although one does see a convergence of the peak positions. Note the wild disparity of the JS-derivative on the right side of the graph is a result of the Julia sets being mostly “dust” at those parameters. The JS-derivative is unreliable in these conditions, thus care must be taken to visually inspect the filled-in Julia sets being evaluated.

Returning to the qualitative discussion of Figure 7, the behavior seen in sequence of Julia sets is captured by the JS-derivative in the form of the left most peak (referred to as peak 1). The non-descript roughly three lobed filled-in Julia sets are coming from the left side of peak 1. The largely white graphs of the last of the second row and start of the third row are coming from the peak itself. Finally, the intricate filled-in Julia sets are coming from the right of peak 1.

Figure 9 shows the JS-derivative for a path running through the wispy fray coming of the left side of the bottom lobe in Figure 6. The abscissa in the JS-derivative graph corresponds to the green line in Figure 6. Here $\gamma =(\theta ,0.315+0i)$ where $\theta$ runs from 0 to $\pi$. The figure also shows a few representative filled-in Julia sets. This sets are chosen from points that lie on opposite sides of a peak in the derivative spectrum. The sharp qualitative differences in the global appearance of the filled-in Julia sets occur on opposite sides of sharp JS-derivative peaks. Observationally, the filled-in Julia sets coming from the wispy fray region tend to be a bit less intricate that some of those arising from the jet region. They do, however, experience abrupt changes along a path in parameter space. One clearly sees many peaks in the JS-derivative. These correspond to moving in and out of the wisps of the fray in the Mandelbrot set.

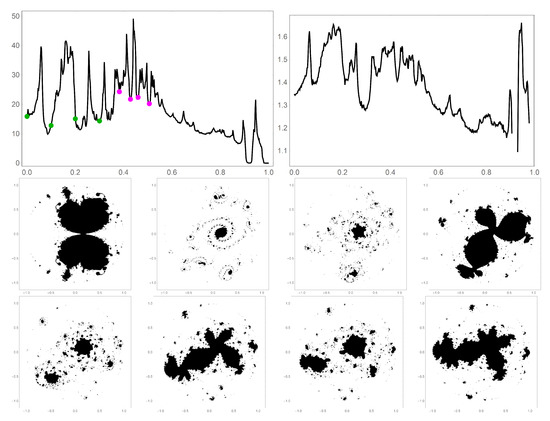
Figure 9. Derivative and dimension data for the green path in Figure 6 which runs through the wispy fray area of ${\mathfrak{M}}_2$. The sampling step size is 0.002 for both graphs. The abscissa for both graphs is $\theta$ (scaled by $\pi$) and the ordinate for the left graph is in arbitrary units while that for the right graph is fractal dimension. The second row is a sequence of filled-in Julia sets correspond to the green points (read left-to-right) in the JS-derivative graph ($\theta =0$, $0.1\pi$, $0.2\pi$ and $0.3\pi$). The third row is a sequence corresponding to the magenta points ($\theta =0.382\pi$, $0.428\pi$, $0.460\pi$ and $0.506\pi$).

4.4. Fractal Dimension

In this work, fractal dimension was calculated using a modified version of the Hausdorff dimension that was developed in reference [2] to which the reader is referred.

Figure 10 shows as plot of the fractal dimension of the Julia sets along the path $\gamma =(1.35\pi ,0.313x+iy)$ (red line in Figure 6). The left graph illustrates the j dependence on dimension. As with the JS-derivative the dimension is sensitive to j. And also as with the JS-derivative, the dimension behavior tends to converge. Note that the erratic behavior beginning a little beyond $y=0.2$ is due to the fact that the Julia sets are mostly dust in that region. The dimension calculation is unreliable for Julia sets of this type. The same ${}^j{h}_N^{\left(k\right)}$ with the same color scheme as right panel of Figure 8 is used. Like the JS-derivative, the dimension is relatively insensitive to N (data not shown). The dimension data for the path $\gamma =(\theta ,0.315+0i)$ (green line in Figure 6) is shown in the right panel of Figure 9.

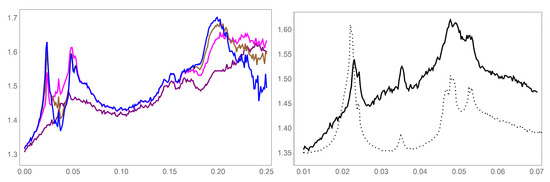
Figure 10. Dimension data for the same path through ${\mathfrak{M}}_2$ and parameters as in the right graph in Figure 8 ($N=14$ and $j=15$ (purple), $j=25$ (magenta), $j=35$ (brown), and $j=45$ (blue)). The dependence on j is evident. The right graph shows the dimension of ${}^{25}{h}_{14}^{\left(2\right)}$ over the range $0.01\le y\le 0.07$ (solid black curve). The dotted curve is a that of the JS-derivative (inset of Figure 8 and normalised to fit on the graph). Abrupt changes in JS-derivative appear to be correlated with abrupt changes in dimension.

The right panel of Figure 10 shows a blow-up on the region $0.1\le y\le 0.7$. This is compared to the JS-derivative over the same region (dotted curve). Perhaps not surprisingly, there appears to be a correlation between abrupt changes in the JS-derivative and abrupt changes in the dimension. They do, however, capture these abrupt change events differently to some degree. As a pair, the JS-derivative and the dimension information can provide insight into the nature of these transitions.

5. Code Snippets

The reader is directed to Section 8 of reference [2] for important Mathematica code snippets. Two additional main functions were needed to produce the fulled-in Julia sets and the three dimensional Mandelbrot sets.

The filled in Julia sets are produced via,

JSplotallMob[k_, m_, j_, s_, p1_, p2_] :=

 Module[{f},

 f[y_] := GF[p1 (y - p2)/(Conjugate[p2] y - 1), (k n^2 - k n + 2)/2,

 1, m]; ListDensityPlot[

  Flatten[Table[

   Table[{x, y, If[Abs[Nest[f, z, j]] > 2, 1, 0]}, {x, -1.1, 1.1,

    s}], {y, -1.1, 1.1, s}], 1], ColorFunction -> GrayLevel] //

 Quiet]

where the GF function is as in reference [2]:

GF[z_, g_, p1_, p2_] := Sum[z^g, {n, p1, p2}]

The three dimensional Mandelbrot sets are created via,

Madelbrot3D =

 Flatten[Table[

  Table[Table[{x, y, j,

   If[x^2 + y^2 > 1, 1,

    ManMobpt[1, 14, 25, Exp[I j Pi], x + I y ]]}, {x, -1,

   1, .025}], {y, -1, 1, .025}], {j, 0, 2, .025}], 2]

where,

ManMobpt[k_, m_, j_, p1_, p2_] :=

 Module[{f},

  f[y_] := GF[p1 (y - p2)/(Conjugate[p2] y - 1), (k n^2 - k n + 2)/2,

  1, m]; If[Abs[Nest[f, 0, j]] > 2, 1, 0] // Quiet]

6. Conclusions

This work serves as one natural extension of the work done on fractals arising from centered polygonal lacunary functions that was performed in reference [2]. This work included a fixed Möbius transformation at each iteration in the generation of the Julia set. This gave rise to a three dimensional parameter space and, consequently, a three dimensional Mandelbrot set.

The two interesting features of jet regions and wispy fray regions of the Mandelbrot set was the focus of the bulk of this work. The Julia sets associated with each point in the Mandelbrot set exhibited a great deal of diversity and dynamicism. This dynamicism was quantitatively captured to some degree by defining and employing the JS-derivative. Fractal dimension was also calculated for these Julia sets.