1. Introduction
The purpose of sensitivity analysis (SA) is to determine which of the inputs play more significant roles in reducing the uncertainty in the model output. It is useful because it can rank variables, simplify models, establish priorities for research, and so on [
1]. Generally, according to different analysis purposes, the available SA techniques can be classified into local SA (LSA) and global SA (GSA). GSA is a more widely used sensitivity analysis method because it does not rely on the choice of a nominal point and the information of the full distribution range is investigated.
In the past few decades, many GSA methods have been studied. Among them, two categories of methods are widely studied and employed: variance-based global sensitivity measures and moment-independent global sensitivity measures.
Variance-based global sensitivity measures, which are usually called Sobol’ indices, were proposed and developed by Sobol’ [
2], Iman [
3], Homma [
4], and Saltelli [
5]. Besides, there are several mature techniques available to solve the above indices, for instance, Monte Carlo simulation, quasi-Monte Carlo simulation, high-dimensional model representation (HDMR), Markovian integration [
6], and the surrogate-assisted method [
7,
8]. Variance-based global sensitivity measures have been widely applied in various fields such as the spray-drying process [
9], heap leaching [
10], the rainfall-runoff model [
11], and polymeric material [
12]. However, the variance is not fully representative of uncertainty, especially in some problems where higher moments have more of an effect. Cox [
13] and Huber [
14] pointed out that “mean-variance decision-making violates the principle that a rational decisionmaker should prefer higher to lower probabilities of receiving a fixed gain, all else being equal”.
To include the whole information of output distribution, moment-independent global sensitivity measures were proposed [
15]. In this regard, Chun’s method preliminarily needs some assumptions [
15]. Although the relative entropy-based method can show a ranking of relative importance, the value does not have an absolute physical meaning [
16]. Additionally, the delta index introduced by Borgonovo is the most popularly used among them [
17]. Cui [
18] extended the delta index to the failure probability to deal with reliability models. However, these methods have a relatively large computational cost due to the estimation of probability density functions.
There are other alternative GSA measures. Derivative-based global sensitivity measures were introduced by Kucherenko et al. [
19], which can serve as an upper bound on the Sobol’ total sensitivity index [
20]. Fort et al. proposed goal-oriented sensitivity indices, which depend on the quantity of interest [
21]. Kala proposed new quantile-oriented sensitivity indices based on measuring the distance between a quantile and the average value of the model output [
22]. Baroni et al. presented an effective strategy for combining variance- and distribution-based global sensitivity analysis [
23].
In this paper, we introduce a novel sensitivity measure based on probability weighted moments (PWMs). PWMs are popular in many science and engineering areas [
24]. PWMs are usually used to estimate parameters of a distribution. In contrast with classical moments, high-order PWMs can be accurately estimated from small samples. In addition, PWMs are fairly insensitive to outliers because they are linear combinations of samples [
25]. They can serve as constraints of the maximum entropy method to describe the distribution feature of the output, which are similar to classical moments [
26]. So, PWMs can reflect the influence of uncertainty and be applied in GSA as well.
The paper continues with a review of dominating global sensitivity measure systems in
Section 2.
Section 3 provides a brief introduction of probability weighted moments and their applications.
Section 4 proposes a new global sensitivity measure based on probability weighted moments.
Section 5 develops two numerical estimation methods, i.e., double-loop-repeated-set Quasi Monte Carlo (QMC) and double-loop-single-set QMC, for numerically estimating the presented measure.
Section 6 provides three numerical examples and one engineering example. Finally, conclusions are provided.
3. Probability Weighted Moments
The PWM of a random variable was formally defined by Greenwood et al. [
24] as:
where
are real numbers;
denotes the cumulative distribution function (CDF); and
is the inverse of the CDF (also called the quantile function). The two following forms of PWMs are commonly used:
Because these two forms can be converted to each other, we only consider Type 2 PWMs in the following equation. From an ordered random sample of size
N,
, unbiased estimates
of
can be obtained as [
26]:
where
are non-negative integers and the binomial coefficient is given as:
.
Equation (7) can also be written as:
From Equation (10), the PWM can be computed by multiplying each observed element by a weight coefficient that is proportional to its probability. Hence, probability weighted moments usually contain more information than classical moments. When comparing a first-order PWM with a first-order classical moment, the magnitudes of the observed elements of the former are adjusted according to probabilities before calculating the average value [
28]. A PWM is more robust because of the insensitivity to outliers and the required sample size is smaller.
For a non-negative random variable,
can be interpreted as moments of the inverse of the CDF [
26]. So, they can serve as constraints in the maximum entropy (MaxEnt) or the minimization cross-entropy [
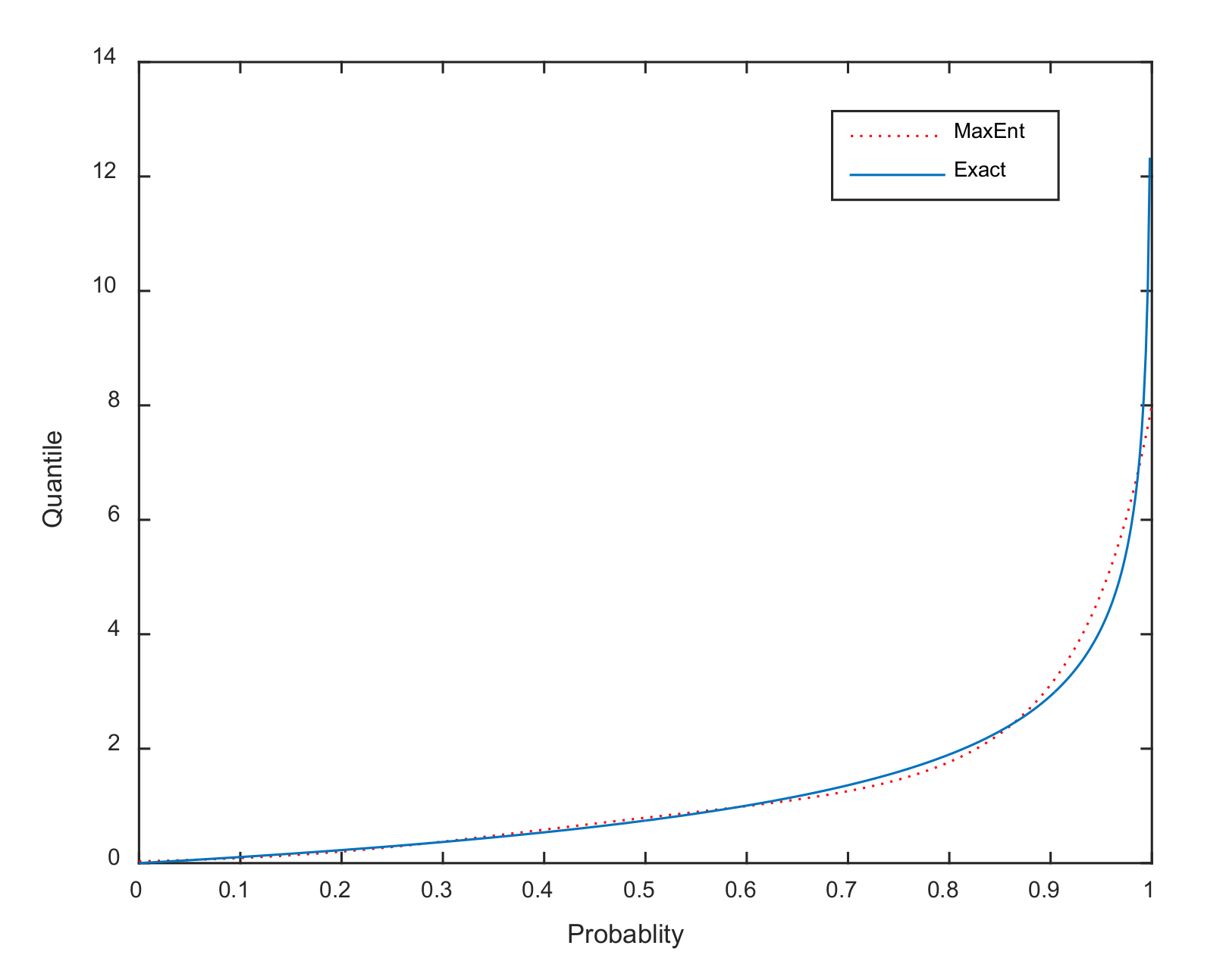
25] approach to estimate the inverse of the CDF. Generally, the estimation using the first four moments often produces an acceptable description. Taking the generalized Pareto distribution (GPD) as an example, its CDF and the inverse of the CDF are given in
Appendix A. In the case of
and
, the MaxEnt approximation combined with the first fourth-order PWMs of the Pareto quantile function is shown in
Figure 1.
4. Global Sensitivity Measure Based on Probability Weighted Moments
As stated above, not only does a probability weighted moment contain more information than conventional moments, but also it can be accurately estimated from small samples. So, we propose a new global sensitivity measure based on PWMs. It is defined as:
where
k denotes the order of the PWMs, and the maximal order is usually chosen as 4. Conditional PWMs
are computed with
at a fixed value and
over their full ranges.
is calculated over all possible
, since
is uncertain and its true value is unknown.
To scale the above-mentioned importance measure within the interval [0,1], the final form of the measure based on PWMs can be constructed:
where
n is the number of input variables.
The numerator in Equation (11) can be explained as the difference between the original PWM and the average of conditional PWMs. When the contribution of uncertainty from Xi to the difference is bigger, the main measure is bigger as well. Then, we can establish the following properties of the novel global sensitivity measure:
Property 1. .
Property 2. means the input variable Xi has no effect on the output.
Proof. When the computational model does not include Xi, the conditional distribution is equivalent to the distribution of . It is obvious that is also equivalent to the corresponding . So, Equation (11) is equal to 0 and . □
Property 3. denotes that only input Xi affects the output.
Proof. According to property 2, of all variables except is separately equal to 0. So, we can obtain by introducing the values of other variables into Equation (12). □
5. Numerical Estimation for Global Sensitivity Measures
Two numerical methods for estimating
indices are proposed in this section. Double-loop-repeated-set numerical estimators are presented in
Section 5.1 and double-loop-single-set numerical estimators are presented in
Section 5.2.
5.1. Double-Loop-Repeated-Set Numerical Estimators
The most direct method of estimating presented measures is to use the double-loop numerical estimation method. Equations (8) and (9) show the estimator of PWMs, so the key issue is how to estimate conditional PWMs. The main procedures are summarized as follows:
Step 1: Generate
N1 samples of the variable vector
by the joint PDF
and calculate the corresponding responses
as well as its
kth-order PWM. These samples can be generated by Monte Carlo sampling, Latin hypercube sampling, quasi-Monte Carlo simulation with sampling based on Sobol’ sequences [
29,
30], or other sampling techniques. Here, quasi-Monte Carlo simulation is recommended for higher and faster convergence.
Step 2: Generate N2 samples of the input variable Xi by its PDF and denote these samples as .
Step 3: The variable Xi should be fixed at individually and generate N3 samples of the remaining variables according to the joint PDF (all variables are independent in this paper). So, the conditional PWM of responses can be obtained, and this step needs to be repeated N2 times.
Step 4: Calculate the expectation of all conditional PWMs, i.e., , and can be easily obtained using Equation (11). After finishing the calculation of of all variables, the normalized versions also can be evaluated in Equation (12).
Step 5: Repeat Step 1–Step 4 under different orders of PWMs. As mentioned in
Section 3, we usually let
k = 1, 2, 3, and 4.
However, for estimating the presented measure of each individual input, the total number of sampled points is N1 + n × (N2 + N2 × N3). We denote it as double-loop-repeated-set QMC (DLRS QMC) because this method needs repeated sampling of inputs and outputs in each inner loop. It is obvious that the computational cost would be too heavy.
5.2. Double-Loop-Single-Set Numerical Estimators
We introduce another double-loop QMC method that needs only one set of samples of inputs and outputs for computing presented measures, which is denoted as double-loop-single-set QMC (DLSS QMC).
Step 1: Generate 2 ×
N1 samples of whole variables by the joint PDF
and assign half of these samples to a sample matrix
A:
Calculate the corresponding responses and estimate the kth-order PWM of .
Step 2: Matrix
B is generated by the remaining samples, which is:
Then, generate a new sample matrix
by assigning the (
p,
i)th component of
A to the
ith column of
B:
Step 3: Calculate the conditional PWM of responses , which is based on the sample matrix .
Steps 4 and 5 are identical to those for DLRS QMC.
The total number of sampled points is only (2 + n) × N1, contributing to a large reduction in sampling time compared to DLRS QMC. N1, N2, and N3 are in the same order of magnitude, which is not more than 4000 usually. Hence, to reduce the calculation cost, the following examples are all solved by the DLSS QMC method.
7. Conclusions
This paper introduced a novel global sensitivity measure based on PWMs. Since a PWM includes more information than a classical moment and can be accurately estimated from small samples, the new measure takes advantage of its properties. PWM-based measures can reflect the influence of input variables on output uncertainty when the output is obviously asymmetric. Subsequently, the double-loop-repeated-set QMC method and the double-loop-single-set QMC method were presented to estimate the new measure. The latter method is recommended because it needs fewer sample points. Three numerical examples were mainly used to compare the new measure with Sobol’ indices and the moment-independent delta index, thus demonstrating its advantages. Finally, an engineering example of a roof truss structure showed the possibility of realistic application. Besides, the measure can be used to analyze problems of groups of input factors.
There is still some further work that needs to be done. Detailed functions of influence factors of measures based on PWMs, i.e., PDFs and coefficients, should be found. From all the examples, the delta importance measure and presented measures often have the same ranking. So, it is possible to find a method to link them because they both identify the influence of the PDF.