Abstract
The theory of Generalized Bessel Functions is reviewed and their application to various problems in the study of electro-magnetic processes is presented. We consider the cases of emission of bremsstrahlung radiation by ultra-relativistic electrons in linearly polarized undulators, including also exotic configurations, aimed at enhancing the harmonic content of the emitted radiation. The analysis is eventually extended to the generalization of the FEL pendulum equation to treat Free Electron Laser operating with multi-harmonic undulators. The paper aims at picking out those elements supporting the usefulness of the Generalized Bessel Functions in the elaboration of the theory underlying the study of the spectral properties of the bremsstrahlung radiation emitted by relativistic charges, along with the relevant flexibility in accounting for a large variety of apparently uncorrelated phenomenolgies, like multi-photon processes, including non linear Compton scattering.
1. Introduction
The theory of Bessel Functions (BF) [1,2] is almost three hundred years old. Their systematic investigation started in the XIX-th century, within the context of astronomical studies. Actually, they had been suggested a century before by Daniel Bernoulli and Leonard Euler in their researches on string vibrations (see e.g., [3]).
These families of functions are characterized by a continuous variable and an index (not necessarily integer or real).
The Generalized Bessel Functions (GBF) [4] are an extension of the ordinary Bessel. They are multivariable, single or multi-index functions and the relevant studies were initially developed during the first years of the last century [5]. Their use in applications started many years later. During the sixties of XX-th century, Reiss rediscovered elementary examples of GBF while investigating problems in light-light and non-dipolar scattering [6,7]. More substantive applications started some years later and they have been employed in Classical/Quantum Electromagnetic Processes [8,9], laser physics [10], Sonar and Radar [11,12], Crystallography [13] … (For a partial list of references the reader is also addressed to [14]).
In the following, we denote the two variable-one index cylindrical GBF by . The most natural way of introducing these functions is through the associated generating function () and, in particular, by the use of Jacobi-Anger , which reads
and naturally leads to the associated integral representation
The definition in terms of an infinite series, involving products of ordinary Bessel
also follows from Equation (1). The special cases are obtained by keeping the values and ,
One of the characterizing features of BF theory are the so called recurrence relations, namely the relationships involving the nearest neighbor indices. The same holds for GBF, whose characteristic recurrences can be obtained from either Equations (1) and (2) and reads [4,5,6,7]
An idea of the relevant behaviour in space is offered by Figure 1. They offer a more complete idea of the relevant geometrical properties. The reflection property under the variable x, namely is evident from the plot of (the y-coordinate reflection does not lead to a simple relation involving the indices and will not be reported here (for the relative comments see [4,5,6,7])).
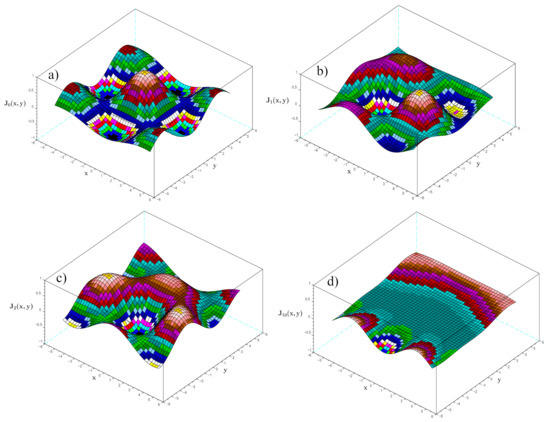
Figure 1.
3-D plots of generalized Bessel vs. (a) ; (b) ; (c) ; (d) .
The corresponding recurrence relations for the single variable case (say x), are obtained by setting . It is evident that the portion of recurrences associated with the y-variable, connects neighbor indices by steps of two. The list of properties is quite large, further identities will be discussed, whenever necessary, during the course of the paper, devoted to a description of their use in classical electro-magnetism. We will in particular deal with the theory of synchrotron radiation emission by ultra-relativistic charges in magnetic devices and the relevant outline is reported below.
In Section 2 we review the theory of radiation emission in linearly polarized undulators and discuss the reasons why the insurgence of “second order” non dipolar contributions in the electron trajectories, naturally leads to the expansion of the Lienard-Wiechert (L-W) integrals [15,16] in terms of GBF. This paper, even though summarizing results obtained in the past, is an attempt of developing a systematic description of how GBF can be succesfully exploited in the theory of electromagnetic processes. In particular in those regarding the emission by relativistic charged particles, moving in elaborated magnetic structure as well as in multiphotn ionizatio or in the elaboration of extended methods for the solution of Dirac-Volkov problem. The plane of the paper is given below.
In Section 2 we show how the use of GBF emerges through the study of the radion emitted by electrons in “ordinary” non dipolar structures.
In Section 3 the procedure is extended to “exotic” undulator devices [17], in which the electrons execute a non sinusoidal motion, with “higher order” non dipolar terms. The study of the emission process in these devices requires more general forms of GBF, involving more than two variables. Section 3 also deals with the relevant impact on the theory and the design of Free Electron Lasers (FEL) [18] with enhanced performances in terms of tunability [19].
Finally Section 4 contains a broader view to the problems touched in the previous parts and with the possibility of future upgrade of the mathematical tool and of the relevant applications.
Concluding comments are eventually contained in Section 5, where we address further discussions on the relevant usefulness as, e.g., in the study of physical problems including the non linear Compton scattering.
2. Bremsstrahlung Radiation in Linearly Polarized Undulators and Emergence of GBF
A magnetic undulator is a device of the type reported in Figure 2, exhibiting a structure provided by a double train of permanent magnets. Inside the open space the magnet arrangement determines a field directed along the vertical axis (y), with an oscillating periodicity along the z-axis, fixed by the magnet spatial disposition.
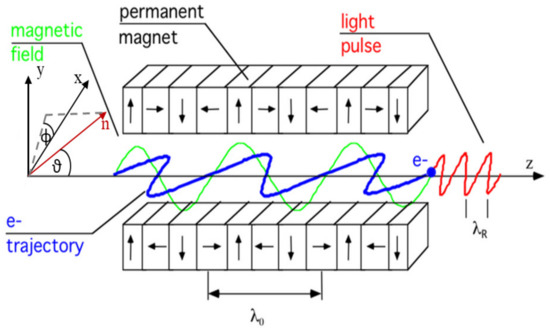
Figure 2.
Permanent magnet block arrangement in undulators (the arrow denotes the direction of the magnetization vector), on axis field distribution and electron beam trajectory (see, e.g., reference [20] for further comments on the undulator field distribution).
The Lorentz force, associated with the undulator field, impresses to the on axis injected electron-beam an oscillatory trajectory lying in the plane.
Without entering into further details concerning the effective field distribution, we note that on axis it can be cast in the simple form
where is the peak on axis field, the spatial oscillation period and N the number of periods constituting the entire undulator. Equation (6) is sufficient to evaluate the properties of the radiation emitted by the electrons, during their transit inside the undulator. The spectral properties of the emitted radiation are calculated through the L-W integral [15]
where are the trajectory and the velocity vector coordinates of the electrons, is the observation unit vector specified by
Since the electron motion assumed to be ultra-relativistic, the radiation is emitted mostly in the forward direction and therefore is of the order of (where is the electron relativistic factor). Hence the vector can be approximated as
The electrons equation of motion can be easily solved and at the lowest order in , thus getting (see Refs. [10,21,22,23] for the details of the computation)
with
The term oscillating at the frequency represents what we have (obscurely) defined second order non dipolar contribution. If we use the above expression for in the argument of the exponential appearing inside the L-W integral, we find
where
Expanding, in terms of two variable GBF, the second exponential in the first of Equation (12), we obtain
The variables , enter within the domain consistent with the GBF correct definition, therefore there no caveats for their use within the expansion of the L-W exponential.
It is evident that the evaluation of the harmonic content of the radiation emitted by energetic electrons in linearly polarized undulators, is complicated by the fact that the motion is not a simple oscillation (with period in the transverse direction, an extra modulation in the longitudinal (z-direction) arises which determines the breaking of the dipole approximation. It is accordingly evident that
and therefore the usual harmonic pattern is recovered.
The complete evaluation of the L-W integral requires a significant amount of boring algebra, involving the properties of GBF summarized in Equation (5), and can be found in [10] where the following expression is given
with
It is evident that the last identities state that the undulator spectrum consists of a series of harmonics centered at
For N very large, the harmonic spectral distribution, specified by , can be replaced by a Dirac function. The spectrum is therefore very narrow around around , and the arguments of the GBF in Equation (16) can be replaced by
The use of the further GBF identity
and the third of Equation (5) yields that the radiation emitted on axis ( as
where is the number of photons and the fine structure constant. According to the above relations the on axis photon spectrum consists of a series of peaks centered at odd harmonics (), with polarization directed along the direction.
It is evident that the radiation emitted in the forward direction by an electron with relativistic factor is characterized by a wavelength
and by the relevant harmonics
The tools allowing an extended tunability in these devices are the electron energy and the order of the harmonic. In an operating Synchrotron Radiation source or Free Electron Laser the first cannot be varied (except a modest range), while the use of the harmonics and/or “smart” rearrangement of the undulator configuration may allow a more significant extension of the radiated spectrum.
In the forthcoming section we discuss these aspects of the problem and present further elements aimed at corroborating the importance of the use of GBF in the study of bremsstrahlung processes in “exotic” undulator configurations.
3. Radiation Emission in Non Standard Undulator Structures and GBF
We have already underscored that the linearly polarized undulators are widely exploited in synchrotron radiation devices [24] and Free Electron Lasers [20]. The process of higher harmonic emission (in particular on axis) offers a useful tool to extend the relevant range of tunability. More advanced undulator schemes have been designed or suggested to enhance the performances of the emitted radiation, either in terms of tunability and polarization content.
About two decades ago, the use of bi-harmonic undulator (BHU) [17,18,19] has been proposed as a device allowing the enhancement of the harmonic generation in undulator driven Synchrotron-Radiation and FEL devices.
In the case of an undulator exhibiting a field with linear orthogonal polarization, specified by the vector
It is easily guessed that, in such a magnetic structure, the electron trajectory acquires a large number of non dipolar contributions of order larger than two.
This has a clear consequence in terms of complexity of the problem to be studied, in part mitigated by the use of the GBF, in forms even more general of the type discussed in the introductory section.
Before getting into more specific details, we note that the polarization content of the harmonics radiated in a BHU, with field vector distribution as in (24), exhibits two polarizations (along x and y), since the electron motion is ruled by two mutually orthogonal fields.
In dealing with this specific problem we should keep in mind that the spatial oscillation content of the field impresses an analogous modulation in the electron motion. In particular the electrons oscillate at the frequency
- along the x direction
- along y
- along z
The obvious consequence is that we will deal with L-W integrals containing an oscillating exponent of the type
we arrange the exponential as
and note that
with
or in integral form
The relevant recurrence identities eventually yield
The associated 3-D plots are shown in Figure 3 while in Figure 4 we have reported 2-D plots displaying their behavior vs. x for different values of y and viceversa. In Figure 3 the nature of GBF is more clearly displayed, along with the relevant symmetry property .
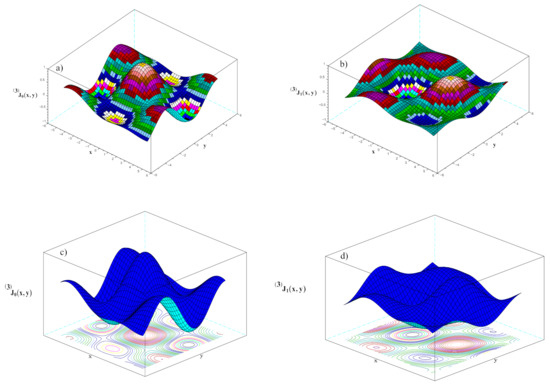
Figure 3.
3-D plots of (a) ; (b) ; with the respective contour plots (c) ; (d) .
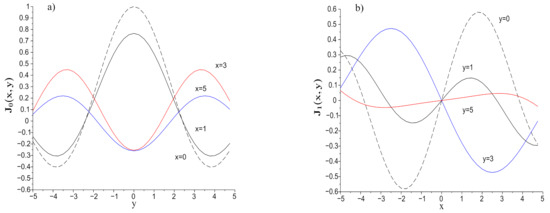
Figure 4.
(a) vs. y for different values of x (), (b) vs. x for different values of x ().
By taking advantage of the semi-group property of the exponential function, we break the exponential as
after setting and rearranging the indices, we end up with
with
where we have denoted by a variable GBF, whose properties are reported in references [25,26,27,28,29].
Regarding the harmonics radiated on axis, owing to the fact that the variables corresponding to are vanishing, we obtain the following expression for the spectral photon number
where
with
The last relations is an extension of Equation (21) and includes the richer harmonic content in terms of harmonic and of polarization content ( stand for the polarization along the transverse directions x and y).
The discussion of this section has reinforced the idea, we wanted to convey, that the GBFs are a very effective tool to treat radiation problems in “non trivial” magnetic structures. The forthcoming concluding sections contains further elements stressing the relevant flexibilities in applications.
4. GBF and Electromagnetic Processes: Concluding Remarks
In the previous section we have discussed the case of a BHU whose field in the x direction exhibits a spatial period of that along the y-axis. In the introductory part of this section, we consider a more general example. This slightly more cumbersome example is aimed at stressing the reliability of the method. The magnetic field we consider is
where h is an integer and d is a numerical factor, smaller or larger than unit and not necessarily an integer.
The spectral content of the on axis emitted radiation is fairly rich [17,18,19] and the order of the harmonics depend on the polarization of the emitted harmonics, we have indeed
The derivation of the FEL evolution equations involves a rather awkward algebra, certainly mildly alleviated by the use of multi-variable Bessel functions.
If we follow the procedure we have outlined in the previous sections we end up with the following amplitudes for x and y polarizations
with
where is a GBF defined through the
The case of allows the study of undulator radiation exhibiting on axis either even and odd harmonics, the first of which have alternate polarizations and relatively large intensities.
As anticipated the formalism we have outlined is also effective to study Free Electron Laser (FEL) devices operating with BHU.
Quantities of crucial importance, as e.g., the gain or the efficiency, can be expressed in terms of GBF.
Within this context the so called Pierce parameter [30] accounting either for the FEL growth and efficiency, writes, in the case of an undulator exhibiting the field vector reported in Equation (24), as it follows
where J is the beam current density. Accordingly the gain length (namely the field intensity growth per unit length) reads
It is not necessary to go into further technicalities to appreciate the usefulness and the flexibility of the formalism. We have just scratched on the surfaces and omitted other important applications, which will be just mentioned below.
One interesting use of GBF emerges in studies associated with laser matter interaction. Here we like to quote an interesting interplay between Physics and Mathematics, appearing within such a context and regarding the “physical origin” of the recursion relation. The argument has been suggested by Loetstedt and Jentschura [31].
To this aim we consider the Klein-Gordon equation regarding the interaction of a spinless particle with an external laser electromagnetic field, which in the notation of reference [31] and in natural units () writes
with the vector potential A specified by
with the polarization vector and
Expanding Equation (44), taking into account that and , we find
The relevant solution can therefore be written as
with
and unspecified for the moment. If we plug (48) into (47) we obtain the following condition, to be satisfied by in order that be a solution of the Klein-Gordon Equation (47)
where
which, after multiplying by and integrating between , yields the condition
The recurrence in Equation (52) is the same as the first of Equation (4), thus allowing the identification of with . The normalization of the wave function follows from the generating function, which yields
This form of , which is that of the Volkov solution of Dirac equation, allows interesting speculations on the possibility of getting general solution of the quantum relativistic spin particles equation in a linearly polarized electro-magnetic wave. This aspect of the problem goes beyond the scope of the paper and the interested reader is addressed to the already quoted reference [31].
Before concluding the paper, we like to mention the example of multi-photon ionization [32]. In this type of processes, unlike what happens in ordinary photoelectric effect, many small photons are transformed into a “big one”. In Figure 5 we have reported a multi-photon process in which many identical photons add up coherently to reach the level of ionization threshold.
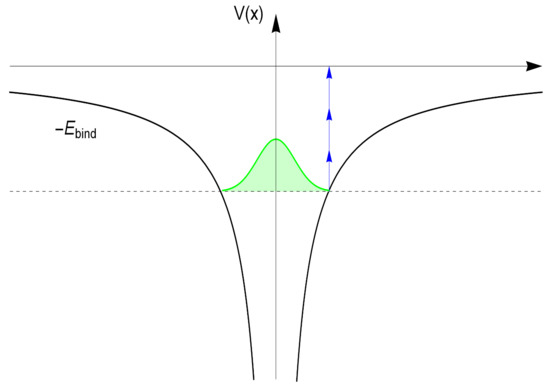
Figure 5.
Schematic illustration of the multi-photon ionization process.
Within this context a central role are played by the dressed Volkov states, accounting, as already mentioned before, for the electron states in a laser wave.
In mathematical terms, the problem is treated by considering an electron subject to a laser wave in terms of the Volkov (Schroedinger) states
with the electron momentum and the laser vector potential. After computing the wave function the transition rates between a bound electronic and Volkov states are computed.
Without mentioning any further detail we note that the transition rates of these processes can be written as [32,33]
where
with the peak laser electric field, the laser angular frequency and the ionization potential.
Furthermore
In this case too, the pivotal mathematical quantity is a two variable Bessel.
The examples discussed in the paper offer a limited, albeit effective scenario, of the usefulness of GBF in electromagnetic process. We hope that this review will provide the stimulus for a deeper study.
5. Final Comments
This article has gone through decades of theory of Bessel Functions of generalized type and relevant use in applications. We have noted that they harbored within a mathematical context, at the beginning of the last century and only later found applications in physical problems.
The book of by Appèl and Kampè dé Fèeriét [5] yields a very illuminating view of their developments (along with applications to astronomy) during the first two decades of XX-th century.
In our discussion we have, for reasons of brevity, ignored important aspects of their use in Quantum Optics. We have excluded many and also more recent applications concerning, e.g., that relevant to light beams with angular momentum [34]. Within this context, an important field of investigation is provided by the study of the emission of twisted photons by classical currents [35], in which the use of GBF plays a significant role in the simplification of the associated computations.
An interesting view to the use of GBF in electromagnetic processes (classical and not) is offered by the references [36,37], which yield a general discussion on the problem which can be treated also in terms of GBF including those of fundamental nature like laser assisted bremsstrahlung [38] and double non linear Compton Scattering [38].
This last point offers the possibility of getting a closer link with the matter relevant to higher order harmonic operation in Free Electron laser device. In particular it has been pointed in reference [39], reporting theoretical predictions on triple Compton scattering, that their experimental check is within the parameters range of the X-FEL facility [40].
Within this respect, we like to stress that the cross section of processes like 2 or 3 photon Compton scattering, could be enhanced if the scattering occurs inside the multi-harmonic FEL light generated with the previously quoted harmonic generation magnification. The optimization of the parameters for this type of experiments require a massive use of the GBF formalism, as it will be discussed in a forthcoming paper.
Author Contributions
Conceptualization, G.D., E.D.P., E.S.; methodology, G.D., E.D.P., E.S.; validation, G.D., E.D.P., S.L., E.S.; formal analysis, G.D., E.D.P., S.L., E.S.; data curation, G.D., E.D.P., S.L., E.S. writing–original draft preparation, G.D., E.D.P., E.S.; writing–review and editing, E.D.P., S.L.; supervision, G.D., E.D.P., S.L., E.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The work of S. Licciardi was supported by an Enea Research Center individual fellowship.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bessel, F.W. Analytische Auflösung der Keplerschen Aufgabe. Abh. Preuß. Akad. Wiss. Berlin 1819, XXV, 49–55. [Google Scholar]
- Watson, G.N. A Treatise on the Theory Bessel Functions, 2nd ed.; Cambridge University Press: Cambridge, UK, 1966. [Google Scholar]
- Cannon, J.T.; Dostrovsky, S. The Evolution of Dynamics: Vibration Theory from 1687 to 1742, 1st ed.; Springer: New York, NY, USA, 1981; pp. 53–69. Available online: https://link.springer.com/bookseries/626 (accessed on 28 December 2020).
- Dattoli, G.; Torre, A. Theory and Application of Generalized Bessel Functions, 1st ed.; Aracne Editrice: Roma, Italy, 1996. [Google Scholar]
- Appell, P.; Kampé de Fériet, J. Fonctions Hypergéométriques et Hypersphériques:Polynome d’Hermite; Gauthier-Villars: Paris, France, 1926. [Google Scholar]
- Reiss, H.R. Theoretical methods in quantum optics: S-matrix and Keldysh techniques for strong-field processes. Prog. Quantum Electron. 1992, 16, 1–71. [Google Scholar] [CrossRef]
- Reiss, H.R. Absorption of light by light. Prog. Quantum Electron. 1962, 3, 59–67. [Google Scholar] [CrossRef]
- Nikishov, A.; Ritus, V. Quantum processes in the field of a plane electromagnetic wave and in a constant field 1. Sov. Phys. JETP 1964, 19, 529–541. [Google Scholar]
- Avetissian, H.K. Relativistic Non Linear Electrodynamics. The QED Vacuum and Matter in Super-Strong Radiation Fields, 2nd ed.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Dattoli, G.; Renieri, A.; Torre, A. Lectures on Free Electron Laser and related Topics, 1st ed.; World Scientific: Singapore, 1990. [Google Scholar]
- Hague, D.A.; Buck, J.R. The generalized sinusoidal frequency-modulated waveform for active sonar. IEEE J. Ocean. Eng. 2017, 42, 109–123. [Google Scholar]
- Hague, D.A.; Kuklinski, P. Waveform design using multi-tone feedback frequency modulation. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar]
- Paciorek, W.A.; Chapuis, G. Generalized Bessel functions in incommensurate structure analysis. Acta Crystallogr. Sect. A Found. Crystallogr. 1994, 50, 194–203. [Google Scholar] [CrossRef]
- Kuklinski, P.; Hague, D.A. Properties of Generalized Bessel Functions. arXiv 2020, arXiv:1908.11683v6. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Hofman, A. Characteristic of Synchrotron Radiation; CERN: Geneva, Switzerland, 1990; Available online: https://cds.cern.ch/record/375972/files/p1.pdf (accessed on 28 December 2020).
- Asakawa, M.; Mima, K.; Nakai, S.; Imasaki, K.; Yamanaka, C. Higher harmonic generation in a modified wiggler magnetic field. Nucl. Instrum. Meth. A 1992, 318, 538–545. [Google Scholar] [CrossRef]
- Dattoli, G.; Giannessi, L.; Ottaviani, P.L.; Freund, H.P.; Milton, S.; Biedron, S. Two Harmonic Undulators and Harmonic Generation in high gain free electron lasers. Nucl. Instrum. Meth. A 2002, 495, 48–57. [Google Scholar] [CrossRef]
- Dattoli, G.; Doria, A.; Sabia, E.; Artioli, M. Charged Beam Dynamics, Particle Accelerators and Free Electron Lasers, 1st ed.; IOP-Institute of Physics Publishing: Bristol, UK, 2017. [Google Scholar]
- Onuki, H.; Ellaume, P. Undulators, Wigglers and Their Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Alferov, D.F.; Yu, A.; Bashmakov, A.; Bessonov, E.G. Undulator Radiation. Sov. Phys. Tech. Phys. 1974, 18, 1336. [Google Scholar]
- Colson, W.B. Free Electron Laser Theory. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1977. [Google Scholar]
- Kim, K.J. Characteristics of synchrotron radiation. AIP Conf. Proc. 1989, 184, 565–632. [Google Scholar]
- Ciocci, F.; Dattoli, G.; Torre, A.; Renieri, A. Insertion devices for Synchrotron Radiation and Free Electron Lasers, 1st ed.; World Scientific: Farrer Road, Singapore, 2000. [Google Scholar]
- Dattoli, G.; Giannessi, L.; Mezi, L.; Torre, A. Theory of generalized bessel functions. Il Nuovo Cimento B (1971–1996) 1990, 105, 327–348. [Google Scholar] [CrossRef]
- Dattoli, G.; Torre, A.; Lorenzutta, S.; Maino, G.; Chiccoli, C. Theory of generalized bessel functions-II. Il Nuovo Cimento B (1971–1996) 1991, 106, 21–51. [Google Scholar] [CrossRef]
- Dattoli, G.; Giannessi, L.; Mari, M.; Richetta, M.; Torre, A. Linear undulator brightness: Exact analytical treatment. J. Math. Phys. 1992, 33, 1200–1207. [Google Scholar] [CrossRef]
- Dattoli, G.; Maino, G.; Chiccoli, C.; Lorenzutta, S.; Torre, A. A unfied point of view on the theory of generalized bessel functions. Comput. Math. Appl. 1995, 30, 113–1254. [Google Scholar] [CrossRef]
- Dattoli, G.; Chiccoli, C.; Lorenzutta, S.; Maino, G.; Richetta, M.; Torre, A. Generating functions of multivariable generalized bessel functions and jacobi-elliptic functions. Comput. Math. Appl. 1992, 33, 25–36. [Google Scholar] [CrossRef]
- Saldin, E.; Schneidmiller, E.V.; Yurkov, M.V. The Physics of Free Electron Lasers; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Lötstedt, E.; Jentschura, U.D. Recursive algorithm for arrays of generalized Bessel functions: Numerical access to Dirac-Volkov solutions. Phys. Rev. E 2009, 79, 026707. [Google Scholar] [CrossRef]
- Milonni, P.W.; Sundaram, B. I Atoms in Strong Fields: Photoionization and chaos. Prog. Opt. 1993, 31, 1–137. [Google Scholar]
- Reiss, H.R. Effect of an intense electromagnetic field on a weakly bound system. Phys. Rev. A 1980, 22, 1786–1813. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light. Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef]
- Bogdanov, O.V.; Kazinski, P.O.; Lazarenko, G.Y. Probability of emission of twisted photons by classical currents. arXiv 2017, arXiv:1712.06140v3. [Google Scholar]
- Jentschura, U.D. Advanced Electrodynamics: Green Functions, Regularization, Multipole Decomposition; World Scientific: Hackensack, NJ, USA, 2017. [Google Scholar]
- Jentschura, U.D. Fundamental Constants Theory and Experiments. Available online: http://web.mst.edu/~jentschurau/files/jentschura_talk.pdf (accessed on 28 December 2020).
- Lotstedt, E.; Jentschura, U.D. Triple Compton effect: A photon splitting into three upon collision with a free electron. Phys. Rev. Lett. 2012, 108, 233201. [Google Scholar] [CrossRef] [PubMed]
- Lötstedt, E.; Jentschura, U.D.; Keitel, C.H. Evaluation of laser-assisted bremsstrahlung with Dirac-Volkov propagators. Phys. Rev. Lett. 2007, 98, 043002. [Google Scholar] [CrossRef] [PubMed]
- Rossbach, J.; Schneider, J.R.; Wurth, W. 10 years of pioneering X-ray science at the Free-Electron Laser FLASH at DESY. Phys. Rep. 2019, 808, 1–74. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).