Dynamic Cost Ant Colony Algorithm to Optimize Query for Distributed Database Based on Quantum-Inspired Approach
Abstract
1. Introduction
2. Preliminaries
2.1. Ant Colony Optimization
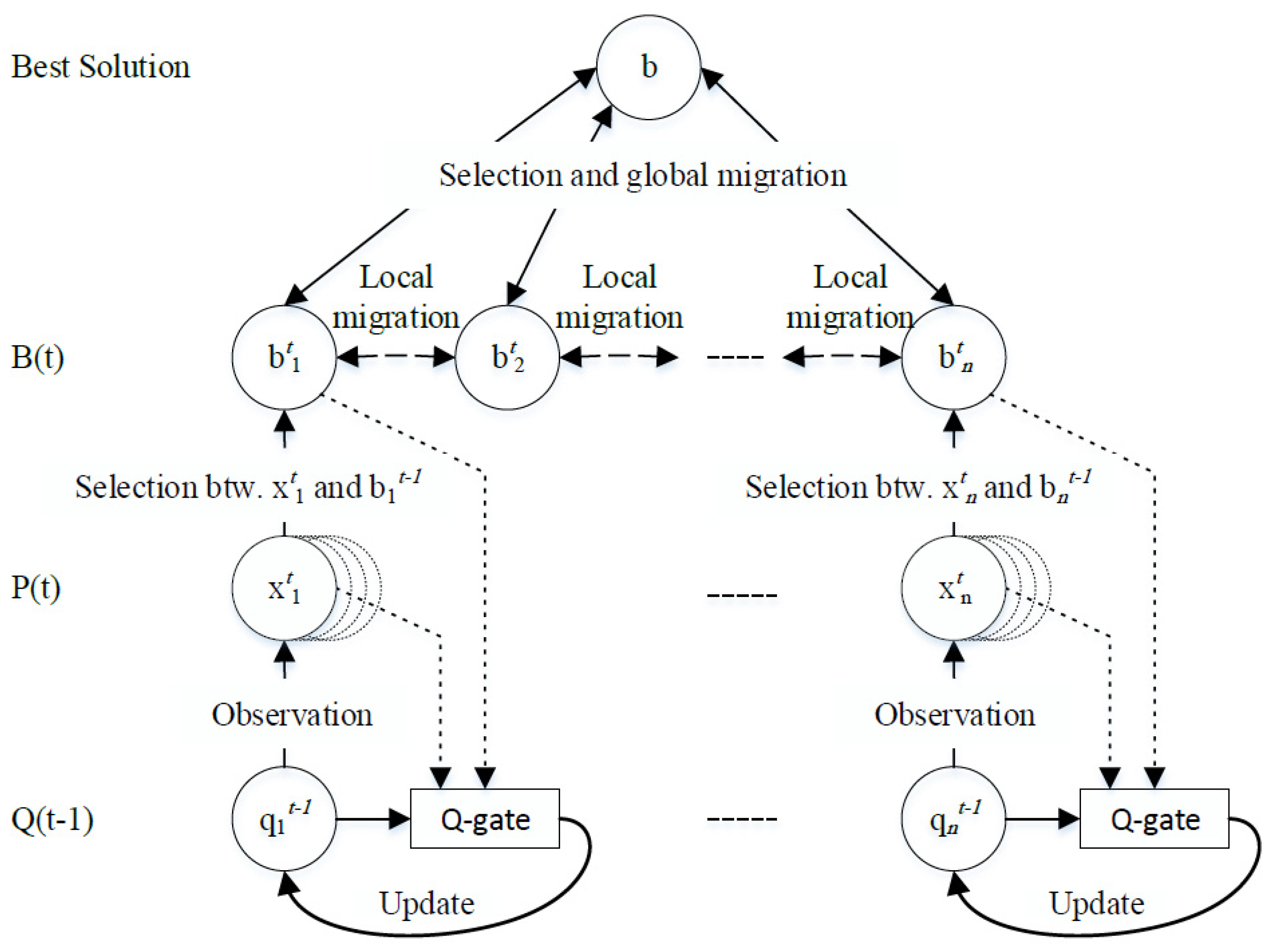
2.2. Quantum-Inspired Evolutionary Algorithms
2.3. Problem Definition
3. Related Work
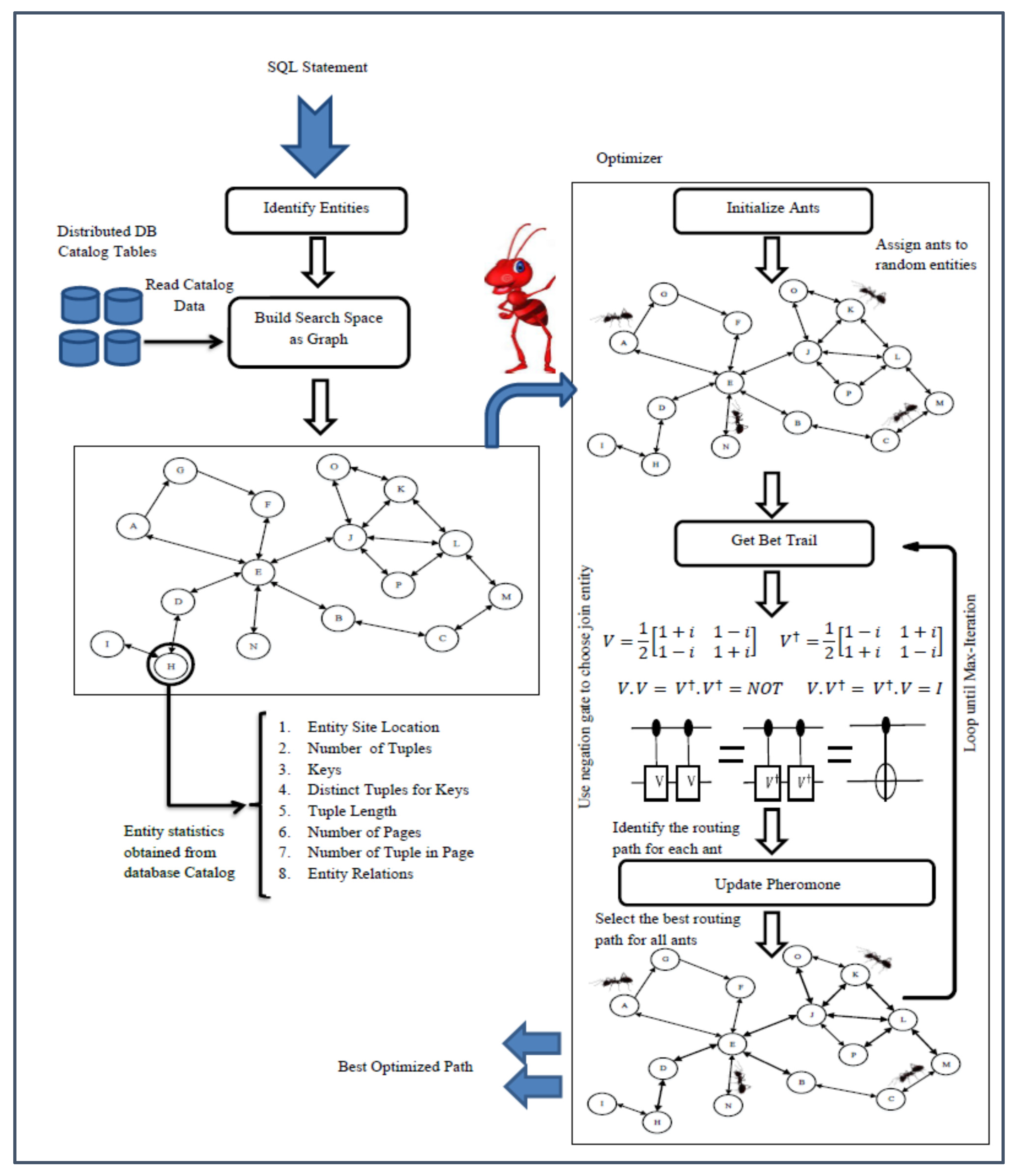
4. The Proposed Technique
4.1. Cost Model
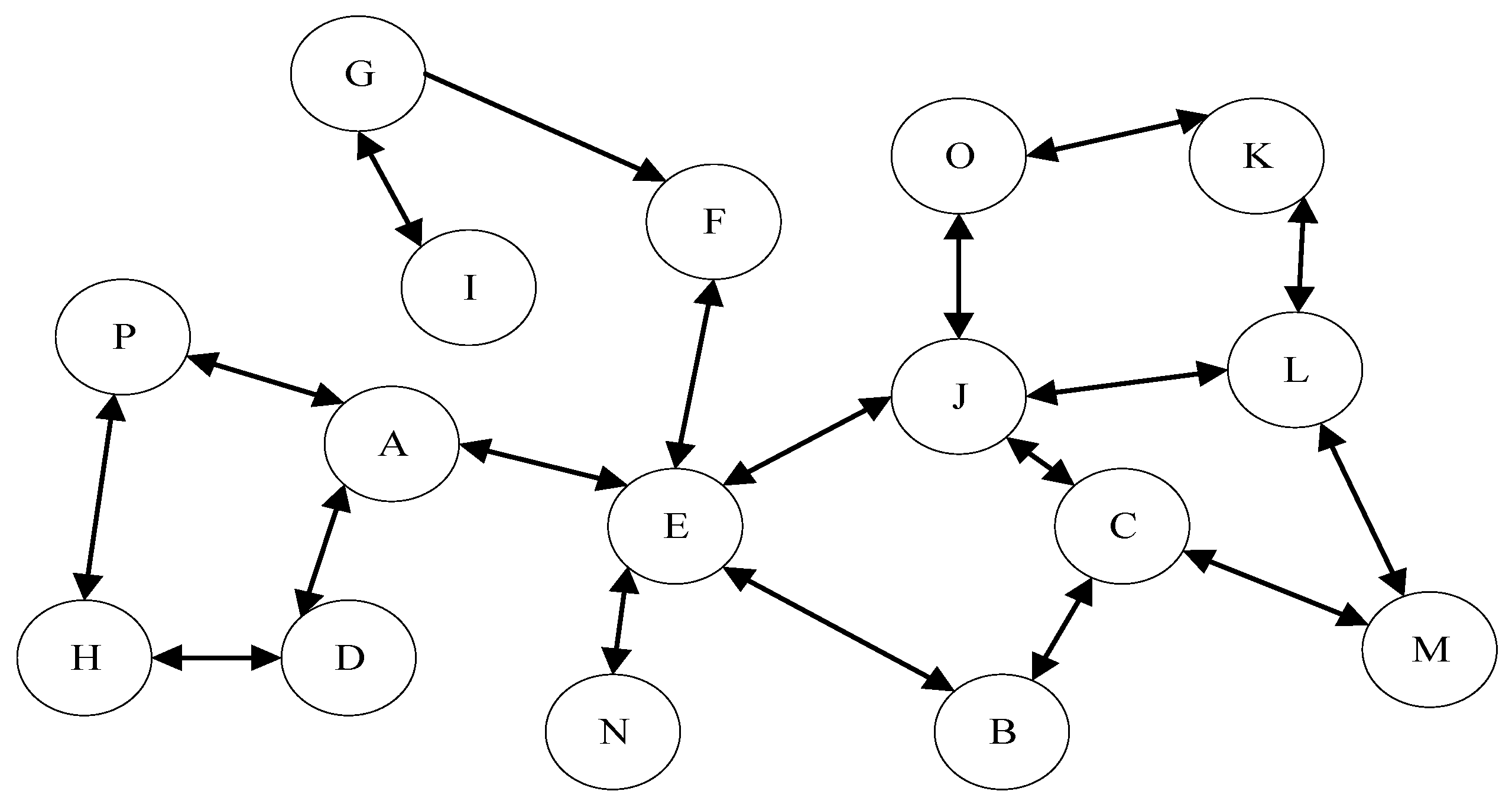
4.2. Build Search Space
4.3. Search Strategy
| Algorithm 1. QIACO |
| (1) Max-Iteration, Ant-Numbers // (step 1) |
| (2) . // (step1) |
| (3) = [1/sqrt(2); 1/sqrt(2)] // (step 1) |
| (4) |
| (5) Loop (cycle < Max-Iteration) |
| (6) |
| (7) StartEntity = random beginning entity // (step2) |
| (8) Loop (ant < Ant-Numbers) |
| partialStep = NegationGate(ant, StartEntity) // (step 3) |
| NextEntity = ChooseNextEnity (partialStep) // (step 4) |
| CalculateCost(StartEntity, NextEntity) // (step 5) |
| StartEntity = NextEntity |
| (9) EndLoop // (step 6) |
| (10) Identify best trail for ants. // (step 7) |
| (11) Modify the pheromones. // (step 8) |
| (12) EndLoop // (step 9) |
| (13) Identifybest trail for the solution |
| Algorithm 2. Partial Negation Gate |
| Function NegationGate(antX, currentEntity) |
| (1) QGate = [0 1;1 0] |
| (2) For (entity = 1 to Number-of-Entities) |
| If entity is visited then |
| partialStep[entity] = ; very small value |
| continue |
| End IF |
| cost = CalcCost(currentEntity, entity) |
| ph = GetPheromone(currentEntity, entity) |
| partialStep[entity] = |
| (3) End For |
| (4) Return partialStep[entity] |
4.4. Limitation
- This algorithm uses the total query time calculated for distributed query optimization as the model’s cost.
- The algorithm applies for non-replicated entities.
| Algorithm 3. Choose Next Enity |
| Function ChooseNextEnity(partialStep) |
| NRV= NormalizeVictore(partialStep) |
| SelectedEntity = RouletteWheel(NRV) Return SelectedEntity |
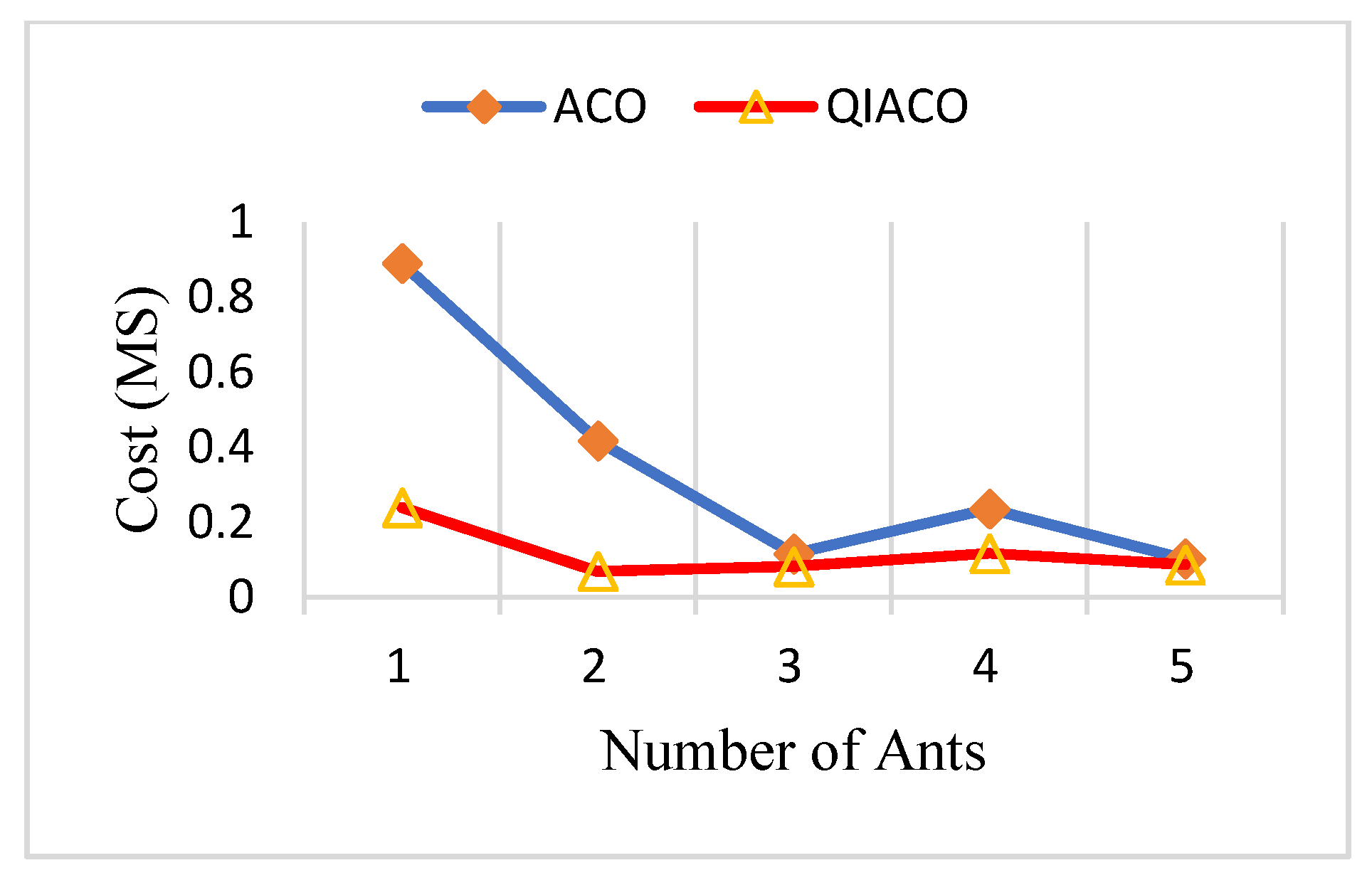
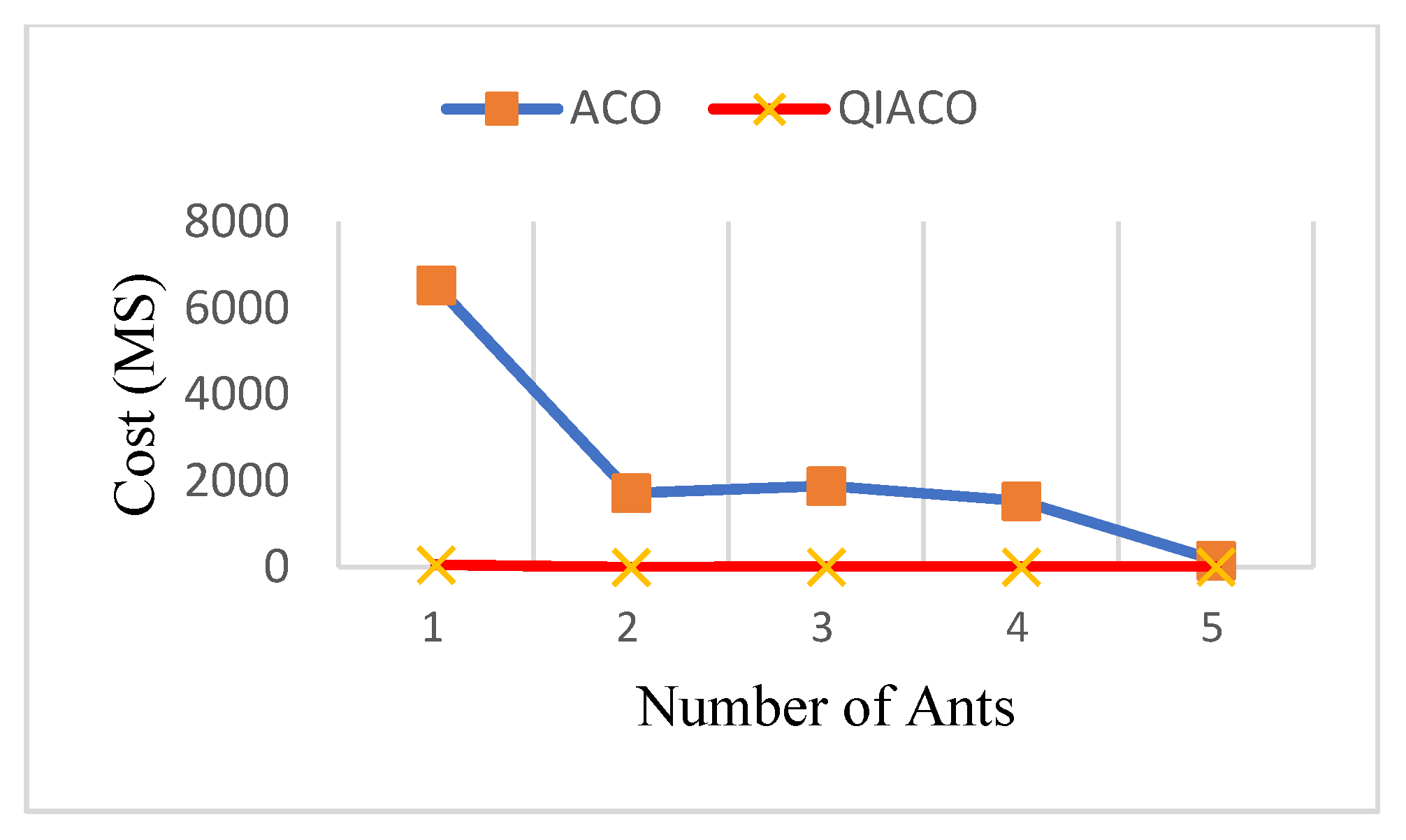
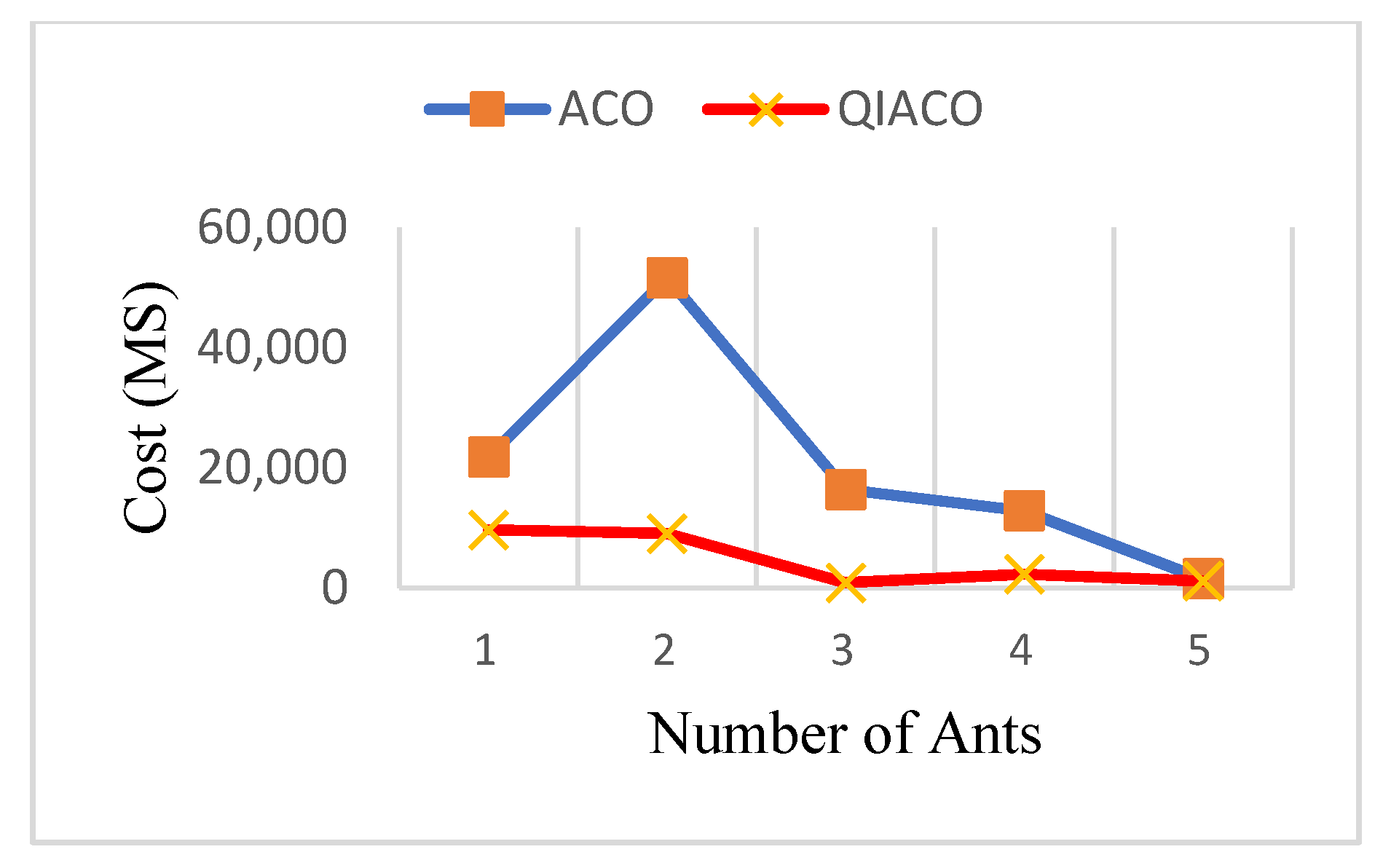
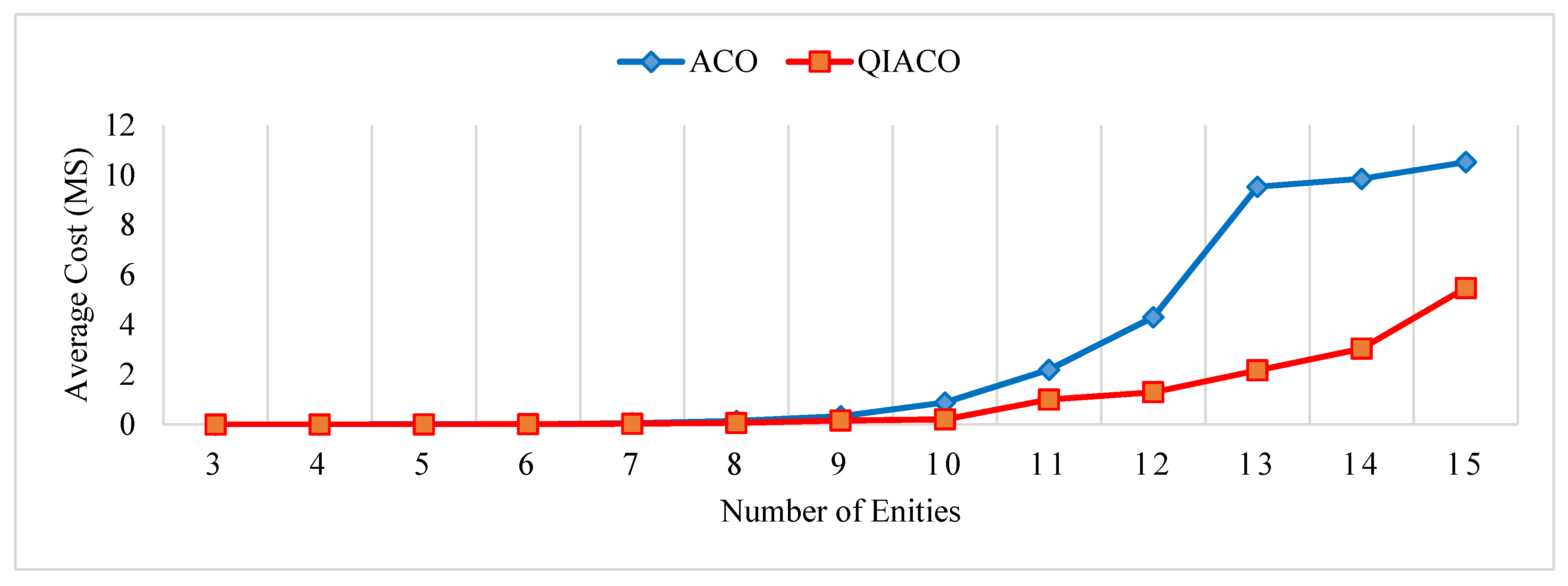
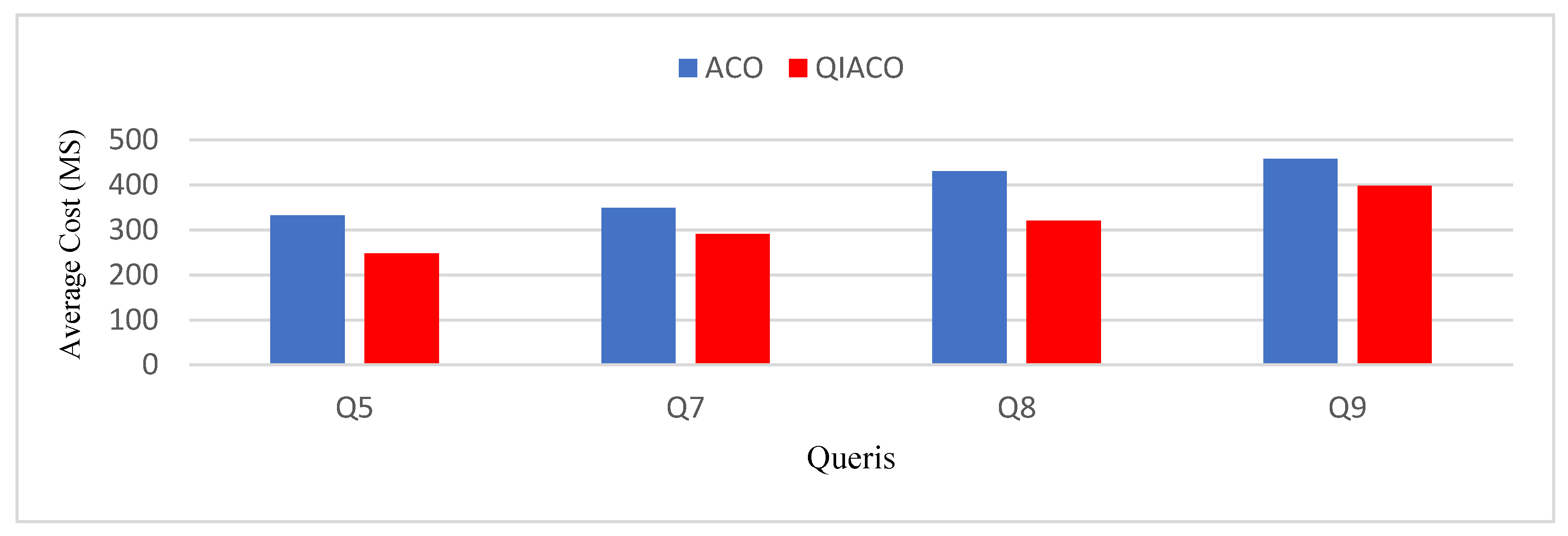
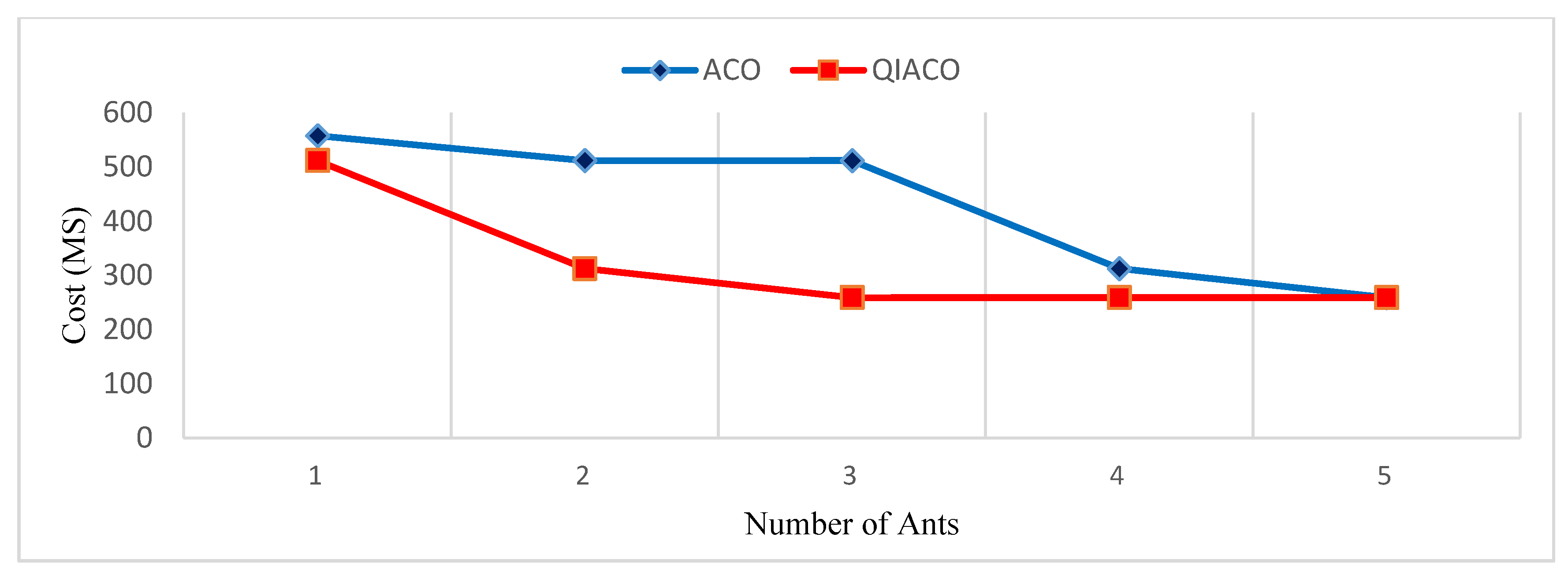
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ramakrishnan, R. Databases Management Systems, 3rd ed.; McGraw-Hill Inc.: New York, NY, USA, 2003. [Google Scholar]
- Tiwari, M.P.; Chande, S.V. Query Optimization Strategies in Distributed Databases. Int. J. Adv. Eng. Sci. 2013, 3, 23–29. [Google Scholar]
- Dokeroglu, T.; Cosar, A. Dynamic Programming with Ant Colony Optimization Metaheuristic for Optimization of Distributed Database Queries. In Proceedings of the 26th International Symposium on Computer and Information, London, UK, 26–28 September 2011; pp. 107–113. [Google Scholar]
- Sharma, M.; Gurvinder, S.; Rajinder, S. A Review of Different Cost-based Distributed Query Optimizers. Prog. Artif. Intell. 2019, 8, 45–62. [Google Scholar] [CrossRef]
- Hameurlain, A.; Morvan, F. Evolution of Query Optimization Methods. Lect. Note Comput. Vis. 2009, 5740, 211–242. [Google Scholar]
- Chen, M.; Yu, P. Using Join Operations as Reducers in Distributed Query Processing. Proceedings of 2nd International Symposium on Databases in Parallel and Distributed System, Dublin, Ireland, 2–4 July 1990. [Google Scholar]
- Pramanik, S.; Vineyard, D. Optimizing join queries in distributed databases. IEEE Trans. Softw. Eng. 1988, 14, 1319–1326. [Google Scholar] [CrossRef]
- Raipurkar, A.; Bamnote, G.R. Query Processing in Distributed Database through Data Distribution. Int. J. Adv. Res. Comput. Commun. Eng. 2013, 2, 1134–1139. [Google Scholar]
- Kossmann, D.; Konrad, S. Iterative dynamic programming: A new class of query optimization algorithms. ACM Trans. Database Syst. 2000, 25, 43–82. [Google Scholar] [CrossRef]
- Ioannidis, Y.E.; Younkyung, K. Randomized Algorithms for Optimizing Large Join Queries. ACM Sigmod Rec. 1990, 19, 312–321. [Google Scholar] [CrossRef]
- Horng, J.T.; Cheng-Yan, K.; Baw-Jhiune, L. A Genetic Algorithm for Database Query Optimization. In Proceedings of the First IEEE Conference on Evolutionary Computation, Orlando, FL, USA, 27–29 June 1994; pp. 432–444. [Google Scholar]
- Sevinc, E.; Cosar, A. An Evolutionary Genetic Algorithm for Optimization of Distributed Database Queries. Comput. J. 2010, 54, 717–725. [Google Scholar] [CrossRef]
- Ristè, D.; Da Silva, M.P.; Ryan, C.A.; Cross, A.W.; Córcoles, A.D.; Smolin, J.A.; Gambetta, J.M.; Chow, J.M.; Johnson, B.R. Demonstration of quantum advantage in machine learning. NPJ Quantum Inf. 2017, 3, 16. [Google Scholar] [CrossRef]
- Kuo, S.; Yao-Hsin, C.; Chi-Yuan, C. Quantum-inspired algorithm for cyber-physical visual sur-veillance deployment systems. Comput. Netw. 2017, 117, 5–18. [Google Scholar] [CrossRef]
- Mohsin, S.A.; Darwish, S.M.; Younes, A. Dynamic Cost Ant Colony Algorithm for Optimize Distributed Database Query. In Proceedings of the Artificial Intelligence and Computer Vision (AICV2020), Cairo, Egypt, 8–10 April 2020. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stützle, T. Ant Colony Optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Dorigo, M.; Stuzle, T. Ant Colony Optimization; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Han, K.H.; Kim, J.H. Quantum-inspired evolutionary algorithm for a class of combinatorial optimization. IEEE Trans. Evol. Comput. 2002, 6, 580–593. [Google Scholar] [CrossRef]
- Narayan, A.; Chellapilla, P. A novel quantum evolutionary algorithm for quadratic knap-sack problem. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 1388–1392. [Google Scholar]
- Kaye, P.; Laflamme, R.; Mosca, M. An Introduction to Quantum Computing; Oxford University Press: New York, NY, USA, 2007. [Google Scholar]
- Rana, M.S.; Mohammad, K.S.; Shohel, A. Distributed Database Problems, Ap-proaches and Solutions—A Study. Int. J. Mach. Learn. Comput. 2018, 8, 472–476. [Google Scholar]
- Steinbrunn, M.; Moerkotte, G.; Kemper, A. Heuristic and Randomized Optimization for the Join-Ordering Problem. Int. J. Very Large Data Bases 1997, 6, 191–208. [Google Scholar] [CrossRef]
- Zhou, Z. Using Heuristics and Genetic Algorithms for Largescale Database Query Optimization. J. Inf. Comput. Sci. 2007, 2, 261–280. [Google Scholar]
- Ban, W.; Jiming, L.; Jichao, T.; Shiwen, L. Query optimization of distributed database based on par-allel genetic algorithm and max-min ant system. In Proceedings of the 8th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 12–13 December 2015; Volume 2, pp. 581–585. [Google Scholar]
- Li, N.; Liu, Y.; Dong, Y.; Gu, J. Application of Ant Colony Optimization Algorithm to Multi-Join Query Optimization. In Proceedings of the 3rd International Symposium on Intelligence Computation and Applications, Berlin/Heidelberg, Germany, 19–21 December 2008. [Google Scholar]
- Golshanara, L.; Rankoohi, S.M.T.R.; Shah-Hosseini, H. A multi-colony ant algorithm for optimizing join queries in distributed database systems. Knowl. Inf. Syst. 2014, 39, 175–206. [Google Scholar] [CrossRef]
- Zhang, G. Quantum-inspired evolutionary algorithms: A survey and empirical study. J. Heuristics 2011, 17, 303–351. [Google Scholar] [CrossRef]
- Chmiel, W.; Kwiecień, J. Quantum-Inspired Evolutionary Approach for the Quadratic Assignment Problem. Entropy 2018, 20, 781. [Google Scholar] [CrossRef]
- Darwish, S.M.; Shendi, T.A.; Younes, A. Quantum-inspired genetic programming model with application to predict toxicity degree for chemical compounds. Expert Syst. 2019, 36, e12415. [Google Scholar] [CrossRef]
- Dey, S.; Bhattacharyya, S.; Maulik, U. New quantum inspired meta-heuristic techniques for multi-level colour image thresholding. Appl. Soft Comput. 2016, 46, 677–702. [Google Scholar] [CrossRef]
- Tiwari, P.; Chande, S.V. Optimal Ant and Join Cardinality for Distributed Query Optimization Using Ant Colony Optimization Algorithm. In Proceedings of the 2nd International Symposium on Emerging Trends in Expert Applications and Security, Singapore, 17–18 February 2018. [Google Scholar]
- Younes, A. Reading a single qubit system using weak measurement with variable strength. Ann. Phys. 2017, 380, 93–105. [Google Scholar] [CrossRef][Green Version]
- Duan, H. Ant colony optimization: Principle, convergence and application. In Handbook of Swarm Intelligence; Springer: Berlin/Heidelberg, Germany, 2011; pp. 373–388. [Google Scholar]
- Kazharov, A.A.; Kureichik, V.M. Ant colony optimization algorithms for solving transportation problems. J. Comput. Syst. Sci. Int. 2010, 49, 30–43. [Google Scholar] [CrossRef]
- James, M. Test Run—Ant Colony Optimization. Msdn Mag. 2012, 27, 2. Available online: https://docs.microsoft.com/en-us/archive/msdn-magazine/2012/february/test-run-ant-colony-optimization (accessed on 30 December 2020).
- Deshpande, A.; Hellerstein, J.M. Decoupled query optimization for federated database systems. In Proceedings of the 18th International Conference on Data Engineering, San Jose, CA, USA, 26 February–1 March 2002; pp. 716–727. [Google Scholar]






| Parameter | Description | Value |
|---|---|---|
| Pheromone influence factor | 3 | |
| The influence of heuristic | 2 | |
| Pheromone evaporation rate | 0.02 | |
| Q | Constant used while pheromone update | 2 |
| Max-Iteration | Varies with the number of entities | - |
| Ant-Numbers | Varies with the number of entities | - |
| Table Name | Number of Tuples | Tuple Size | Table Name | Number of Tuples | Tuple Size |
|---|---|---|---|---|---|
| Lineitem | 6,000,000 | 120 | orders | 1,500,000 | 100 |
| Partsupp | 800,000 | 140 | Part | 200,000 | 160 |
| Customer | 150,000 | 180 | supplier | 10,000 | 160 |
| Nation | 25 | 120 | region | 5 | 120 |
| Site | Tables |
|---|---|
| 1 | supplier, partsupp |
| 2 | orders, lineitem |
| 3 | nation, region, customer |
| 4 | Part |
| No. of Entity | ACO | QIACO | Perform-ance % | ||||||
|---|---|---|---|---|---|---|---|---|---|
| No. of Iterations | Worst Cost | Average Cost | Best Cost | No. of Iterations | Worst Cost | Average Cost | Best Cost | ||
| 5 | 100 | 0.01341 | 0.01304 | 0.01239 | 100 | 0.01138 | 0.01138 | 0.01138 | 12.73 |
| 10 | 100 | 0.88999 | 0.352626 | 0.10301 | 100 | 0.23963 | 0.11929 | 0.06968 | 66.17 |
| 15 | 300 | 6538.64340 | 2367.65590 | 158.82610 | 100 | 58.25450 | 18.66170 | 2.34710 | 99.21 |
| 20 | 300 | 51,574.72700 | 20,818.50940 | 1506.29500 | 100 | 9689.55970 | 4627.87840 | 890.40500 | 77.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohsin, S.A.; Younes, A.; Darwish, S.M. Dynamic Cost Ant Colony Algorithm to Optimize Query for Distributed Database Based on Quantum-Inspired Approach. Symmetry 2021, 13, 70. https://doi.org/10.3390/sym13010070
Mohsin SA, Younes A, Darwish SM. Dynamic Cost Ant Colony Algorithm to Optimize Query for Distributed Database Based on Quantum-Inspired Approach. Symmetry. 2021; 13(1):70. https://doi.org/10.3390/sym13010070
Chicago/Turabian StyleMohsin, Sayed A., Ahmed Younes, and Saad M. Darwish. 2021. "Dynamic Cost Ant Colony Algorithm to Optimize Query for Distributed Database Based on Quantum-Inspired Approach" Symmetry 13, no. 1: 70. https://doi.org/10.3390/sym13010070
APA StyleMohsin, S. A., Younes, A., & Darwish, S. M. (2021). Dynamic Cost Ant Colony Algorithm to Optimize Query for Distributed Database Based on Quantum-Inspired Approach. Symmetry, 13(1), 70. https://doi.org/10.3390/sym13010070






