Connecting (Anti)Symmetric Trigonometric Transforms to Dual-Root Lattice Fourier–Weyl Transforms
Abstract
1. Introduction
2. Dual-Root Lattice Fourier–Weyl Transforms
2.1. Root and Weight Lattices
2.2. Discrete Fourier–Weyl Transforms
3. (Anti)symmetric Trigonometric Transforms
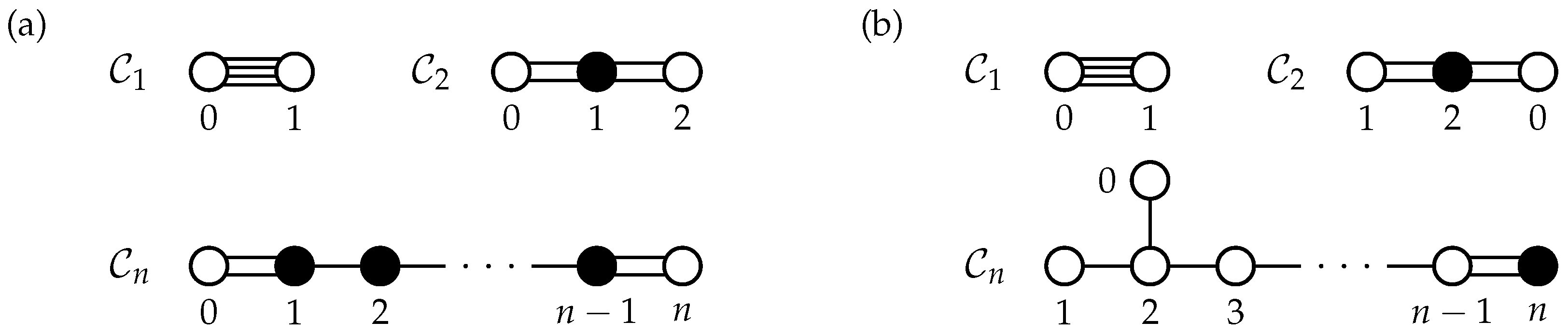
3.1. Point and Label Sets
3.2. Discrete Trigonometric Transforms
4. Connecting Label and Point Sets
4.1. Sets of Labels
4.2. Sets of Points
5. Connecting Normalization and Weight Functions
5.1. Normalization Functions
- (i)
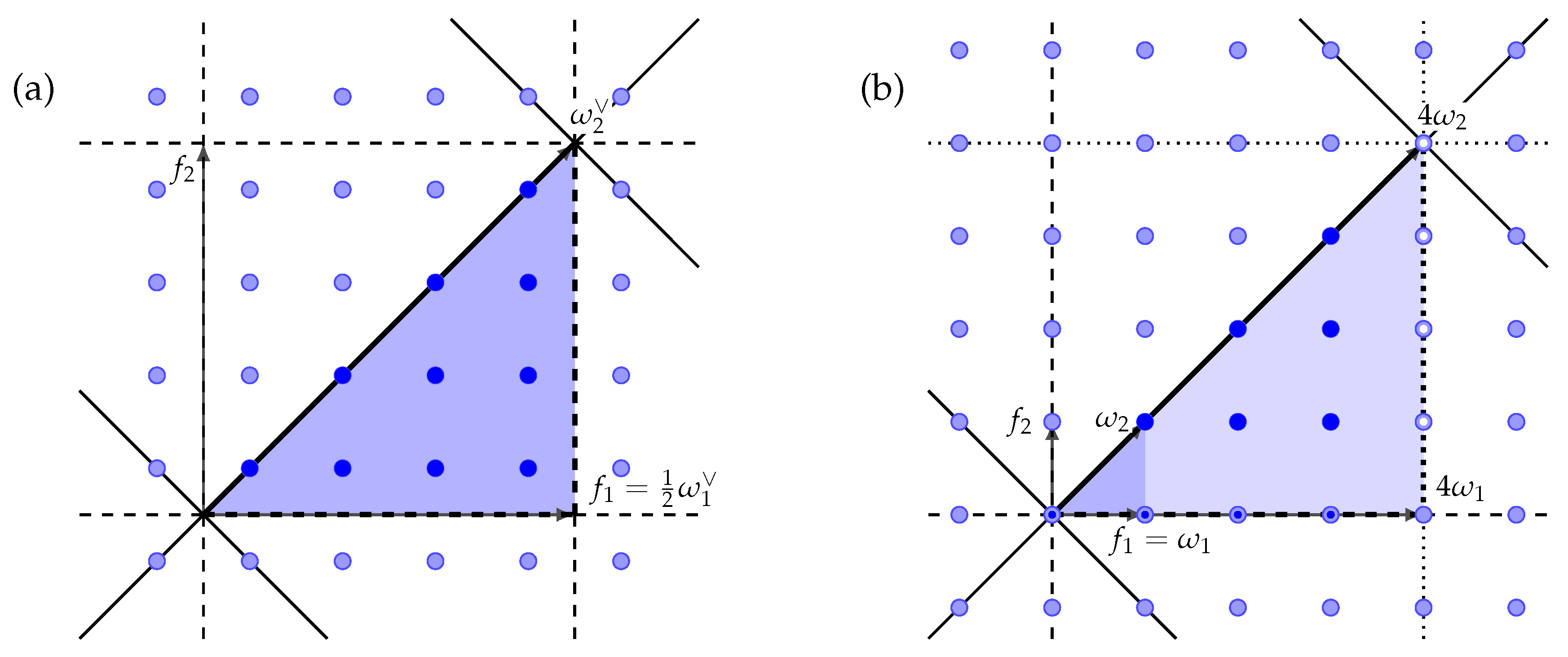
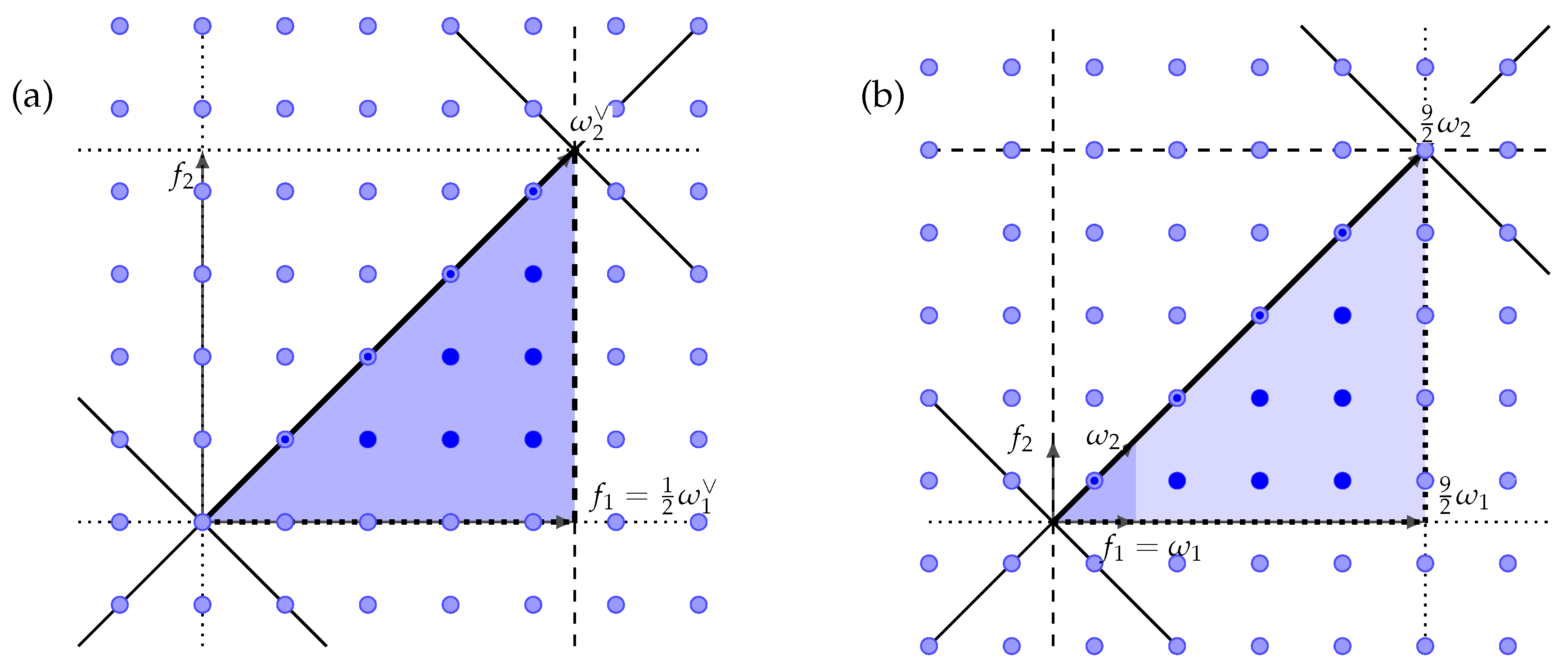
- If the magnified Kac coordinates satisfy for all that andthen the Fourier–Weyl normalization functions reduce toand equivalence conditions (70) force the relationsThe explicit forms of the Fourier–Weyl label sets (10) and (11) admit equality (71) only for the cases and . Moreover, according to the ranges of the magnified Kac coordinates (8) and (9), the cases and admit condition (71) only for M even and odd and correspond in Table 3 to the symmetric cosine transforms of the types I and VII, respectively. Similarly, the symmetric sine transforms are identified to be of the types II and VIII and Table 2 together with restrictions (72) yield
- (ii)
- Suppose that there is exactly one connected component of the subgraph associated with the extended dual Dynkin diagram formed by the nodes corresponding to the zero coordinates , and the only zero coordinates are of the form , . The Dynkin diagram of is according to Figure 2 of type for and of type , otherwise. Thus, the value of Fourier–Weyl normalization functions are derived from Table 1 and defining relation (17) asIn this case, equivalence conditions (70) lead to the following restrictions on , ,As discussed above, condition (71) is attained only for the symmetric cosine functions of types I and VII and for the symmetric sine functions of types II and VIII. Therefore, it follows from Table 2 and restrictions (77) that
- (iii)
- If the only connected component is associated with the only zero magnified Kac coordinates of the form for , , the Dynkin diagram of corresponds, from Figure 2, to type . According to Table 1, the Fourier–Weyl normalization function is evaluated asand defining relation (17) implies that the value of depends on whether the first two Kac coordinates coincide. The restrictions on the parameters , are deduced from equivalence conditions (70) asAssuming that the equality holds, step (i) guarantees that the equivalent condition (71) is achieved only for the symmetric cosine functions of types I and VII and for the symmetric sine functions of types II and VIII. Therefore, Table 2 together with restrictions (81) assures that the values of trigonometric normalization functions are in this case given by (73). Otherwise, the trigonometric normalization functions are for any type of transform evaluated asIn both cases, it follows from restrictions (81) and definition (30) that
- (iv)
- If the only connected component is associated with the only zero magnified Kac coordinates of the form for , the Dynkin diagram of is according to Figure 2 of type for , of type for and of type otherwise. Therefore, it results from Table 1 thatand the Fourier–Weyl normalization function depends, from defining relation (17), on the values of the first two Kac coordinates. Equivalence conditions (70) in this case guarantee the following restrictions:Because is attained according to the ranges of the last magnified Kac coordinate (9) only if and , Table 3 admits only the symmetric cosine transforms of the types and . Step (i) guarantees that the possible transforms reduce to the type if the equality is valid. Therefore, it follows from Table 2 and restrictions (85) that the trigonometric normalization functions are, for , evaluated as
- (v)
- Assuming that the only zero magnified Kac coordinates are of the form leads to the Dynkin diagram, denoted by , consisting of two connected components of type . Thus, it follows from Table 1 and defining relations (18) and (17) that the Fourier–Weyl normalization functions are evaluated asThe following restrictions on the coordinates , are derived from equivalence conditions (70),Step (i) guarantees that the condition is attained only for the symmetric cosine transforms of the types and for the symmetric sine transforms of the types . Table 2 and restrictions (91) produce that the values of the trigonometric normalization functions are given by
- (vi)
- Supposing that the subgraph of nodes associated with the zero Kac coordinates is formed by several connected components, then it combines blocks of nodes corresponding to the cases studied in steps (ii)–(v). Note that, if the block of two connected components from step (v) occurs, the total number of connected components equals . Denoting by the value of the Fourier–Weyl normalization function (76), (80), (84) or (89) given by the step identified with the block , defining relation (18) validates the identityAs in the previous steps, the value of depends on whether the first two Kac coordinates are equal or not. If and denote the value of trigonometric normalization functions (73), (78), (82), (86), (87), or (92) corresponding to the step of the block , the definition of trigonometric normalization functions and steps (ii)–(v) imply thatDenoting by the value of the trigonometric normalization function (79), (83), (88) or (93) depending on the step associated with the block , it follows from definition (30) that
5.2. Weight Functions
- (i)
- Suppose that there is exactly one connected component of the subgraph of the extended Dynkin diagram formed by the nodes corresponding to the zero coordinates , and the only zero coordinates are of the form , . The Dynkin diagram of is according to Figure 2 of type . Thus, the value of the Fourier–Weyl weight function is deduced from Table 1 and defining relation (20) asIn this case, equivalence conditions (98) force the following restrictions on , ,The ranges of the first magnified Kac coordinate (12) and (13) admit the equalityonly for the cases and . Furthermore, according to the explicit forms of the Fourier–Weyl point sets (15), the cases and permit condition (101) only for M even and odd and correspond in Table 3 to the symmetric cosine transforms of the types and , respectively. Similarly, the symmetric sine transforms are identified to be of the types and and Table 2, defining relation (30) and restrictions (100) validate
- (ii)
- If the only connected component is associated with the only zero magnified Kac coordinates of the form for , , the Dynkin diagram of corresponds from Figure 2 to type . Thus, the value of Fourier–Weyl weight function is derived from Table 1 and defining relation (20) asIn this case, restrictions on , are deduced from equivalence conditions (98) asAccording to Table 2, defining relation (30) and restrictions (105), the trigonometric weight functions are evaluated for any type of transform as
- (iii)
- If the only connected component is associated with the only zero magnified Kac coordinates of the form , , the Dynkin diagram of is of type . Therefore, the value of Fourier–Weyl weight function results from Table 1 and defining relation (20) asEquivalence conditions (98) in this case guarantee the following restrictions on , ,The ranges of the magnified Kac coordinates (14) together with explicit forms of the Fourier–Weyl point sets (15) admit the condition only for the cases and that correspond according to Table 3 to the symmetric cosine transforms of the types and for M even and and for M odd. Table 2, defining relation (30), and restrictions (109) imply that the values of the trigonometric weight functions are given by
- (iv)
- Suppose that the subgraph of nodes associated with the zero Kac coordinates is formed by several connected components , then each , identifies with one of the connected components from steps (i)–(iii). Denoting by the value of the Fourier–Weyl weight function (99), (104) or (108) given by the step corresponding to , defining relation (20) validates the identityIf and denote the value of trigonometric weight functions (102), (106) or (110) corresponding to the step of the component , the definition of trigonometric weight functions and steps (i)–(iii) imply thatDenoting by , the value of the trigonometric weight function (103), (107) or (111) depending on the step associated with the component , it follows from definition (30) that
6. Unitary Matrices of Discrete Transforms
6.1. Type II
6.2. Type VII
7. Conclusions
- The presented link of the generalized root-lattice Fourier–Weyl transforms related to the crystallographic series to the (anti)symmetric trigonometric transforms provides significant advantages for the further development and method transfer in both directions. The analogous form of the label and point sets in the trigonometric approach enables embedding of both transform sets by a common choice of the basis (35). Besides comparison of the label and point sets in Theorems 1 and 2, the more challenging evaluation of the weight and normalization functions relies on the Coxeter–Dynkin diagrams counting algorithms [14]. The achieved results of the extended (dual) Coxeter–Dynkin diagram analysis in Theorems 3 and 4 demonstrate feasible explicit forms of the Fourier–Weyl weight and normalization functions that are independent on Lie theory. Formulation of similarly directly structured final forms encoding the , and transforms poses an open problem.
- The family of 32 cubature formulas for multivariate numerical integration belongs to the class of the Chebyshev polynomial methods that are obtained utilizing the present (anti)symmetric trigonometric transforms [9,10]. Among the cubature formulas of this family, eight types lead to the Gaussian rules with the highest precision. Migration of the multivariate Chebyshev polynomials [5] via the functional substitution (36) together with the Chebyshev nodes and weight functions conversions straightforwardly generates cubature formulas in the Lie theoretical setting [8,26]. Such direct comparison indicates the presence of other Gaussian rules attached to the generalized root-lattice Fourier–Weyl transforms of the remaining crystallographic root systems. The presented correspondence between the discrete transforms allows for further research pertaining to the Lebesgue constant estimates of the polynomial cubatures in both frameworks.
- Defined by relations analogous to the trigonometric symmetrizations (31)–(34), the multivariate antisymmetric and symmetric exponential functions represent distinct variants of the induced special functions [40]. A similar form of the point and label sets of the discrete Fourier transforms associated with the (anti)symmetric exponential functions and the present root-lattice Fourier–Weyl transforms signals the existence of novel types of orbit functions and induced discrete transforms attached to all crystallographic root systems. Successful interpolation tests demonstrated for both 2D and 3D cases [2,41] of the (anti)symmetric exponential Fourier transforms suggest the transforms’ significant application potential. Moreover, the one-parameter variable position of the point sets relative to the triangular fundamental domain of the (anti)symmetric exponential functions [2] reveals different types of admissible shifts of the Weyl (sub)group invariant lattices [4,18].
- The research toward unique types of symmetrized multivariate exponential functions, invariant with respect to the even subgroups of the Weyl groups, produces the even orbit functions [42] together with the ten types of the even dual weight lattice Fourier–Weyl transforms [43]. Taking into account the alternating subgroup of the permutation group , the trigonometric adaptation of the functions results in both alternating trigonometric and exponential functions as well as the associated discrete Fourier transforms [44,45]. According to the currently assembled correspondence between the functions and discrete transforms, the link between the alternating trigonometric functions and the series functions is expected. Even though their existence is strongly indicated by the presently obtained connection, the exact forms of the (dual) root-lattice Fourier–Weyl transforms have not yet been derived for any case. The (dual) root-lattice Fourier–Weyl transforms along with their ties to the alternating trigonometric and exponential functions deserve further study.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Klimyk, A.; Patera, J. (Anti)symmetric multivariate trigonometric functions and corresponding Fourier transforms. J. Math. Phys. 2007, 48, 093504. [Google Scholar] [CrossRef]
- Hrivnák, J.; Patera, J. Two-dimensional symmetric and antisymmetric generalizations of exponential and cosine functions. J. Math. Phys. 2010, 51, 023515. [Google Scholar] [CrossRef]
- Hrivnák, J.; Motlochová, L. Dual-root lattice discretization of Weyl orbit functions. J. Fourier Anal. Appl. 2019, 25, 2521–2569. [Google Scholar] [CrossRef]
- Czyżycki, T.; Hrivnák, J.; Motlochová, L. Generalized Dual-Root Lattice Transforms of Affine Weyl Groups. Symmetry 2020, 12, 1018. [Google Scholar] [CrossRef]
- Hrivnák, J.; Motlochová, L. On connecting Weyl-orbit functions to Jacobi polynomials and multivariate (anti)symmetric trigonometric functions. Acta Polytech. 2016, 56, 283–290. [Google Scholar] [CrossRef]
- Klimyk, A.; Patera, J. Orbit functions. SIGMA 2006, 2, 006. [Google Scholar]
- Klimyk, A.; Patera, J. Antisymmetric orbit functions. SIGMA 2007, 3, 023. [Google Scholar] [CrossRef]
- Moody, R.V.; Motlochová, L.; Patera, J. Gaussian cubature arising from hybrid characters of simple Lie groups. J. Fourier Anal. Appl. 2014, 20, 1257–1290. [Google Scholar] [CrossRef]
- Hrivnák, J.; Motlochová, L. Discrete transforms and orthogonal polynomials of (anti)symmetric multivariate cosine functions. SIAM J. Numer. Anal. 2010, 51, 073509. [Google Scholar] [CrossRef]
- Brus, A.; Hrivnák, J.; Motlochová, L. Discrete Transforms and Orthogonal Polynomials of (Anti)symmetric Multivariate Sine Functions. Entropy 2018, 20, 938. [Google Scholar] [CrossRef]
- Britanak, V.; Rao, K.; Yip, P. Discrete Cosine and Sine Transforms: General Properties, Fast Algorithms and Integer Approximations; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Hrivnák, J.; Motlochová, L.; Patera, J. Two-dimensional symmetric and antisymmetric generalizations of sine functions. J. Math. Phys. 2010, 51, 073509. [Google Scholar] [CrossRef]
- van Diejen, J.F.; Emsiz, E. Discrete Fourier transform associated with generalized Schur polynomials. Proc. Am. Math. Soc. 2018, 146, 3459–3472. [Google Scholar] [CrossRef]
- Hrivnák, J.; Patera, J. On discretization of tori of compact simple Lie groups. J. Phys. A Math. Theor. 2009, 42, 385208. [Google Scholar] [CrossRef]
- Hrivnák, J.; Motlochová, L.; Patera, J. On discretization of tori of compact simple Lie groups II. J. Phys. A Math. Theor. 2012, 45, 255201. [Google Scholar]
- Li, H.; Xu, Y. Discrete Fourier analysis on fundamental domain and simplex of Ad lattice in d-variables. J. Fourier Anal. Appl. 2010, 16, 383–433. [Google Scholar]
- Hrivnák, J.; Walton, M.A. Weight-Lattice Discretization of Weyl-Orbit Functions. J. Math. Phys. 2016, 57, 083512. [Google Scholar] [CrossRef]
- Czyżycki, T.; Hrivnák, J. Generalized discrete orbit function transforms of affine Weyl groups. J. Math. Phys. 2014, 55, 113508. [Google Scholar] [CrossRef]
- Strang, G. The discrete cosine transform. SIAM Rev. 1999, 41, 135–147. [Google Scholar] [CrossRef]
- Wen, W.; Kajínek, O.; Khatibi, S.; Chadzitaskos, G. A Common Assessment Space for Different Sensor Structures. Sensors 2019, 19, 568. [Google Scholar] [CrossRef]
- Moody, R.V.; Patera, J. Orthogonality within the families of C-, S-, and E-functions of any compact semisimple Lie group. SIGMA 2006, 2, 076. [Google Scholar] [CrossRef]
- Hrivnák, J.; Myronova, M.; Patera, J. Central Splitting of A2 Discrete Fourier–Weyl Transforms. Symmetry 2020, 12, 1828. [Google Scholar] [CrossRef]
- Berens, H.; Schmid, H.J.; Xu, Y. Multivariate Gaussian cubature formulae. Arch. Math. 1995, 64, 26–32. [Google Scholar] [CrossRef]
- Heckman, G.; Schlichtkrull, H. Harmonic Analysis and Special Functions on Symmetric Spaces; Academic Press Inc.: San Diego, CA, USA, 1994. [Google Scholar]
- Koornwinder, T.H. Two-variable analogues of the classical orthogonal polynomials. Theory Appl. Spec. Funct. 1975, 435–495. [Google Scholar]
- Moody, R.V.; Patera, J. Cubature formulae for orthogonal polynomials in terms of elements of finite order of compact simple Lie groups. Adv. Appl. Math. 2011, 47, 509–535. [Google Scholar] [CrossRef]
- Hrivnák, J.; Motlochová, L.; Patera, J. Cubature formulas of multivariate polynomials arising from symmetric orbit functions. Symmetry 2016, 8, 63. [Google Scholar] [CrossRef]
- Hrivnák, J.; Motlochová, L. Discrete cosine and sine transforms generalized to honeycomb lattice. J. Math. Phys. 2018, 59, 063503. [Google Scholar] [CrossRef]
- Hrivnák, J.; Motlochová, L. Graphene Dots via Discretizations of Weyl-Orbit Functions. In Lie Theory and Its Applications in Physics, Varna, Bulgaria, June 2019; Dobrev, V., Ed.; Springer: Singapore, 2020; pp. 407–413. [Google Scholar]
- Cserti, J.; Tichy, G. A simple model for the vibrational modes in honeycomb lattices. Eur. J. Phys. 2004, 25, 723–736. [Google Scholar] [CrossRef][Green Version]
- Güçlü, A.D.; Potasz, P.; Korkusinski, M.; Hawrylak, P. Graphene Quantum Dots; Springer: Berlin, Germany, 2014. [Google Scholar]
- Drissi, L.B.; Saidi, E.H.; Bousmina, M. Graphene, Lattice Field Theory and Symmetries. J. Math. Phys. 2011, 52, 022306. [Google Scholar] [CrossRef]
- Siddeq, M.M.; Rodrigues, M.A. DCT and DST Based Image Compression for 3D Reconstruction. 3D Res. 2017, 8, 5. [Google Scholar] [CrossRef]
- Çapoğlu, I.R.; Taflove, A.; Backman, V. Computation of tightly-focused laser beams in the FDTD method. Opt. Express 2013, 21, 87–101. [Google Scholar] [CrossRef]
- Crivellini, A.; D’Alessandro, V.; Bassi, F. High-order discontinuous Galerkin solutions of three-dimensional incompressible RANS equations. Comput. Fluids 2013, 81, 122–133. [Google Scholar] [CrossRef]
- Young, J.C.; Gedney, S.D.; Adams, R.J. Quasi-Mixed-Order Prism Basis Functions for Nyström-Based Volume Integral Equations. IEEE Trans. Magn. 2012, 48, 2560–2566. [Google Scholar] [CrossRef]
- Chernyshenko, D.; Fangohr, H. Computing the demagnetizing tensor for finite difference micromagnetic simulations via numerical integration. J. Magn. Magn. Mater. 2015, 381, 440–445. [Google Scholar] [CrossRef]
- Bourbaki, N. Groupes et Algèbres de Lie, Chapiters IV, V, VI; Hermann: Paris, France, 1968. [Google Scholar]
- Humphreys, J.E. Reflection Groups and Coxeter Groups; Cambridge Studies in Advanced Mathematics 29; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Klimyk, A.U.; Patera, J. (Anti)symmetric multivariate exponential functions and corresponding Fourier transforms. J. Phys. A Math. Theor. 2007, 40, 10473–10489. [Google Scholar] [CrossRef]
- Bezubik, A.; Hrivnák, J.; Patera, J.; Pošta, S. Three–variable symmetric and antisymmetric exponential functions and orthogonal polynomials. Math. Slovac. 2017, 67, 427–446. [Google Scholar] [CrossRef]
- Klimyk, A.U.; Patera, J. E-orbit functions. SIGMA 2008, 4, 002. [Google Scholar]
- Hrivnák, J.; Juránek, M. On E-Discretization of Tori of Compact Simple Lie Groups. II. J. Math. Phys. 2017, 58, 103504. [Google Scholar] [CrossRef]
- Klimyk, A.U.; Patera, J. Alternating multivariate trigonometric functions and corresponding Fourier transforms. J. Phys. A Math. Theor. 2008, 41, 145205. [Google Scholar] [CrossRef]
- Klimyk, A.; Patera, J. Alternating Group and Multivariate Exponential Functions. In Groups and Symmetries, From Neolithic Scots to John McKay; Harnad, J., Winternitz, P., Eds.; American Mathematical Society: Providence, RI, USA, 2009; pp. 233–246. [Google Scholar]
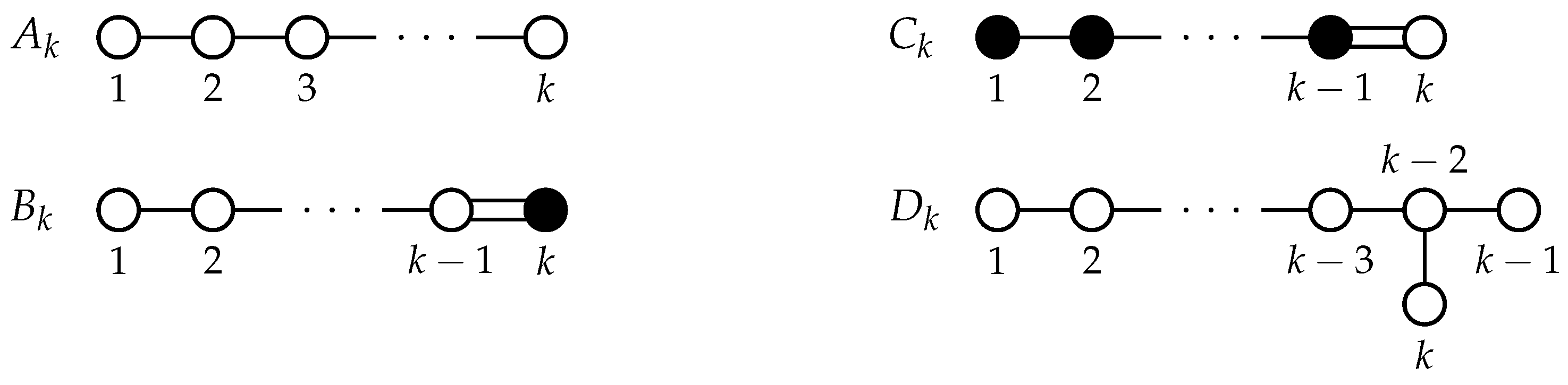

| ⋆ | ||||||||
|---|---|---|---|---|---|---|---|---|
| I | 1 | |||||||
| II | 1 | 1 | ||||||
| III | ||||||||
| IV | 1 | 1 | ||||||
| V | 1 | |||||||
| VI | 1 | |||||||
| VII | 1 | |||||||
| VIII | 1 |
| I | 0 | 0 | 0 | 0 | ||
| II | 0 | 0 | ||||
| III | 0 | 0 | ||||
| IV | ||||||
| V | 0 | 0 | 0 | 0 | ||
| VI | 0 | 0 | ||||
| VII | 0 | 0 | ||||
| VIII | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brus, A.; Hrivnák, J.; Motlochová, L. Connecting (Anti)Symmetric Trigonometric Transforms to Dual-Root Lattice Fourier–Weyl Transforms. Symmetry 2021, 13, 61. https://doi.org/10.3390/sym13010061
Brus A, Hrivnák J, Motlochová L. Connecting (Anti)Symmetric Trigonometric Transforms to Dual-Root Lattice Fourier–Weyl Transforms. Symmetry. 2021; 13(1):61. https://doi.org/10.3390/sym13010061
Chicago/Turabian StyleBrus, Adam, Jiří Hrivnák, and Lenka Motlochová. 2021. "Connecting (Anti)Symmetric Trigonometric Transforms to Dual-Root Lattice Fourier–Weyl Transforms" Symmetry 13, no. 1: 61. https://doi.org/10.3390/sym13010061
APA StyleBrus, A., Hrivnák, J., & Motlochová, L. (2021). Connecting (Anti)Symmetric Trigonometric Transforms to Dual-Root Lattice Fourier–Weyl Transforms. Symmetry, 13(1), 61. https://doi.org/10.3390/sym13010061





