Abstract
An extremely fast exponential expansion of the Universe is typical for the stable version of the inflationary model, based on the anomaly-induced action of gravity. The total amount of exponential e-folds could be very large, before the transition to the unstable version and the beginning of the Starobinsky inflation. Thus, the stable exponential expansion can be seen as a pre-inflationary semiclassical cosmological solution. We explore whether this stable phase could follow after the bounce, subsequent to the contraction of the Universe. Extending the previous consideration of the bounce, we explore both stable expansion and the bounce solutions in the models with non-zero cosmological constant and the presence of background radiation. The critical part of the analysis concerns stability for small perturbations of the Hubble parameter. It is shown that the stability is possible for the variations in the bounce region, but not in the sufficiently distant past in the contraction phase.
1. Introduction
The importance of singularities in general relativity is partially based on the fact that they are unavoidable [1,2,3,4] and, therefore, indicate to the limits of applicability of the theory. The common belief is that, by properly extending general relativity, one arrives at the singularity-free theory. In particular, the cosmological singularities (see, e.g., [5] and references therein) led to various theoretical developments, such as, e.g., exploration of -type models with simplified form of quantum corrections [6,7], string cosmology [8], different versions of cyclic universe (see, e.g., [9]), quantum cosmology (see, e.g., [10,11,12]) and, in general, the interest in the bouncing models (see [13,14] for reviews and many references). Typically, bouncing models require fundamentally new assumptions, such as the especially designed non-localities (see, e.g., [15,16]) or introducing a scalar field with specially adjusted features (or a modified -type gravity, see, e.g., [17]). One of the most economical ways to avoid singularity is the assume a relevant positive curvature of the space section of the spacetime manifold [18] in the very early Universe.
The natural question is whether one can achieve the cosmological solutions with bounce with the minimal set of, or even without any, additional assumptions. The proposal of this type was done in the paper [19]. In the present paper, we elaborate the same idea in more detail and consider it from the modern perspective of the effective field theory framework.
Even without quantum gravity, the consistent treatment near the singularity requires taking into account the back reaction of the quantum matter fields on the classical gravitational background. In general, the derivation of the semiclassical corrections to the gravitational action is an unsolved problem, except for an extreme UV, where at least the one-loop effects are controlled by the logarithmic divergences, admitting a simple and elegant description in terms of conformal anomaly [20,21,22] and anomaly-induced effective action [23,24]. It was suggested that these quantum corrections may be sufficient to provide a bouncing solution [19], without additional assumptions. In the present work, we elaborate this proposal in detail. First, we extend the information about the bounce solution by including the large cosmological constant and the background radiation. These aspects of the model are relevant because a huge cosmological constant may be generated in the UV by symmetry restoration, while an intensive creation of matter from the vacuum is expected in the region of bounce, when the Universe leaves the de Sitter-type contraction phase. The second important point is the generalization of the phase diagrams for unstable [25,26] and stable [27,28] phases, in the presence of the cosmological constant. Finally, we explore the stability of the approximately exponential expansion and contraction with respect to the small perturbations of the conformal factor of the metric. Taken together, these new results extend our general understanding of the possibility of the bounce due to the semiclassical contributions to the gravitational action.
The paper is organized as follows. In Section 2, we briefly review the anomaly and induced action, and describe the derivation of the 00 component of the gravitational equations in the presence of radiation from the conservation law. In Section 3, we derive the particular de Sitter-like solutions from the 00 equations with semiclassical correction and formulates the detailed conditions of their stability. These conditions can be applied to both expanding and contracting phases. In Section 4, we present the phase diagrams with the cosmological constant for stable and unstable versions of the theory, and also give new examples of the bounce, including with the background radiation or cosmological constant. Section 5 is devoted to the stability analysis of the contracting case, clarifying the status of the bounce solutions. Finally, in Section 6, we draw our conclusions and also discuss general perspectives of solving the problem of cosmological singularities using quantum corrections.
The definitions of geometric quantities, used below, included the signature of the metric, the curvature tensor , and the scalar curvature .
2. Anomaly-Induced Action and the Early Universe
In the very early epoch of the Universe, the typical energy scale is very high. Different models of particle physics give different estimates for the upper bounds of the masses of the particles, but usually these upper bounds are of the order of magnitude, or below, the GUT scale , that is a few orders below the Planck scale . The Friedmann equation, based on general relativity, predicts an unbounded growth of the Hubble parameter near the beginning of time , and the singularity emerges with . Thus, in the region close to the spacetime singularity, the gravitational field is so intensive, that all real particles can be regarded massless. The same concerns the virtual particles, which are interacting with the strong gravitational background. Thus, the relevant quantum effects in the vicinity of cosmological singularity may be limited by the effects of massless fields, which is, in fact, the simplest case.
It is a natural hypothesis that the fundamental theory of particle physics possesses the asymptotic freedom in the UV, including in the vicinity of the singularity. Furthermore, for fermion and vector fields, the masslessness implies local conformal invariance. This is a natural feature from the perspective of quantum theory. The point is that, free massless particles have a vanishing trace of the energy-momentum tensor. Demanding the field-particles duality in the description of quantum matter, we arrive at the condition for the trace of the dynamical energy-momentum tensor,
On the other hand, (1) is the Noether identity for the local conformal symmetry
where is the conformal weight for the matter fields (scalars, fermions and vectors, , correspondingly. If the Noether identity (1) is satisfied, the action S does not depend on the conformal factor . For the scalar field, the symmetry (2) imposes an additional condition on the value of the nonminimal parameter of interaction with the scalar curvature, such that the Lagrangian of this field (we write down the Lagrangian for a single real scalar, for simplicity), becomes
Furthermore, it is sufficient to choose the action of vacuum to satisfy the local conformal symmetry (2), without jeopardizing the renormalizability of the theory. Taking the power counting arguments into account, this means that the part of the vacuum action, which is the subject of an infinite renormalization in the UV, has the form
where the integrand of the Gauss-Bonnet topological term and the square of the Weyl tensor are
respectively. Action (4) satisfies the Noether identity (2) at the classical level. On the top of this, the classical action of vacuum may include the non-conformal part, e.g., the Einstein-Hilbert term with the cosmological constant , and the term,
Finally, , and are the parameters of the vacuum action. The renormalization of the parameters and generates the anomalous violation of the Noether identity (2). The main idea of the corresponding inflationary model is to use the anomaly, or the anomaly-induced action of gravity, to arrive at the cosmological solution which replaces the usual Friedmann-Lemaître solution of general relativity.
Consider the particle physics theory with real scalars (a complex scalar counts as two real scalars), Dirac spinors, and massless vector fields. The beta functions for the parameters are as follows:
where we introduced the useful notations for the coefficients , and . At the quantum level, for free matter fields, the Noether identity (2) is violated by the anomaly in the vacuum sector,
Here is the renormalized quantum correction to the classical action (4) plus the contribution to the radiation term, . One has to include the background radiation term because in the early Universe there may be radiation. The radiation term is conformal invariant and can be kept together with term in the derivation of anomaly-effective action . The general form of the beta function is
where and are multiplicities of charged fermions and scalars.
Solving Equation (9) with respect to is a relatively simple exercise, described in many papers (e.g., in the first original works [23,24]), the review [29], book [30] and the forthcoming textbook [31]). Here we need just the simplest version of the solution, which can be obtained directly from the two relations
and
In these relations, we use the conformal parametrization of the metric (2). is the fourth-order, Hermitian, conformal invariant operator [32,33,34] acting on a conformal invariant, dimensionless scalar field,
The general solution for the anomaly-induced effective action is (In this paper, we deal only with the dynamics of the conformal factor. Thus, this simplest non-covariant solution is equivalent to the nonlocal covariant one [23,24] and to the local covariant with two auxiliary fields [35].) [23,24]
where and . The first term in the solution (13) is an arbitrary conformal invariant functional, , which plays the role of an integration constant for Equation (9). There is no regular method for deriving in the explicit form. However, in the known physical applications it is usually considered insignificant. E.g., for the background cosmological solutions (not for perturbations), this functional is irrelevant because an isotropic and homogeneous metric has the form
As usual, the conformal time is related to the cosmic time t by the formula . Thus, is obviously independent of the conformal factor .
The form of Equations (9) and (13) demonstrates that the term in the anomaly contributes to the covariant local term in the induced action. The coefficient of this term is regularization-dependent [22,36]. This dependence was explored in detail in [37], where it was shown, in particular, that it is equivalent to modifying the finite term in the classical non-conformal action (5).
In contrast to the term in the action (4), the term affects the equation for the conformal factor . Therefore, it is important to fix the value of by some physical conditions. In the literature, there are two main choices for such a condition. The most important one is , providing the consistent inflationary model of Starobinsky [25,26,38]. The large magnitude of this coefficient, compared to the beta function (8), makes the quantum contributions to the term completely irrelevant. Another interesting choice is , such that the particle contents , , in (8) becomes an important issue. In what follows, we shall follow this option and discuss how the choice of the particle contents defines the stability of the cosmological solutions.
The basis of the cosmological model for the early Universe is the total action, including (5), (4), matter and the quantum corrections described by (13)
Let us remember that the matter corresponds to the pure radiation, its action is conformal invariant and thus, it does not affect the dynamical equation We shall see how the radiation density appears in the first integral of this equation.) for .
Taking variational derivative with respect to , we arrive at the equation of motion in the form
where the traces of the equations of motion for the corresponding terms in the action, are
where or for different space geometries.
Equation (16) represents the trace of the equations of motion, and can be used for analytical and numerical study of the system. However, it is more useful to derive 00-component using the conservation law for each of the components , and ,
In what follows, we shall use the notations and general approach of the previous works, e.g., [39,40]. Let us stress that this consideration implies that we omit the conformal invariant functional in the purely gravitational part of the expression (13). This approximation is necessary here, because all the information we have, comes from the anomaly and reflects only the trace of the equations of motion. From Equation (20), follows that
with the general solution defined by
In these expressions we have changed from conformal time to the cosmological time t, from to and used the definition of Planck mass . One of the advantages of the 00-component of the equations of motion compared to the trace is that, in the expression (25), we can include the classical radiation term. Since the corresponding term is conformal, it was hidden in the trace of Equation (16).
3. De Sitter-Like Solutions and Their Stability
Now we are in the position to write the dynamical equation for in the form
where the are defined in Equations (23)–(25). Most of the further discussion will be based on this equation. For the sake of brevity, we restrict our attention to the case.
It is most economical to write the purely gravitational part of the equation in terms of the Hubble parameter . In this way we get
As the first step, consider the equation without the radiation term. Looking for the solution with a constant H, we meet a biquadratic equation
with the following four solutions [41]:
It is clear that the solutions with the positive H correspond to expanding, and the ones with the negative H, to contracting Universes. From Equation (7) follows that for any particle contents of the underlying theory, such that the is always real. Consider the sign in the parenthesis, taking and for the definiteness. Taking into account that , we get the two approximate solutions:
The first one, , is the classical de Sitter solution where the anomaly-induced terms play no role. The second solution, , is the solution corresponding to the equilibrium between quantum, anomaly-induced part and the classical part, of Equation (27). This solution cannot be obtained in the approach when the quantum part is treated a small perturbation. On the other hand, it can be derived from different approaches to quantum corrections in curved spacetime [42,43].
Let us consider the stability of these solutions. Our purpose is to explore the asymptotic stability, and, owing to the exponential time dependence of , it is important to perform variation of or , instead of [41]. For the variation of , without the radiation term in (27) and in the linear approximation, we obtain
For a constant , such as the ones in (30), this equation boils down to
In the case of extreme inflationary solution with in (30), we have and then the solution of (32) has the form
where
Since we always have , for there are no eigenvalues with the positive real part hence there are no growing modes and the solution with is stable [19,25,26]. Using the equation for the trace, one can show that in the model with the same solution is unstable.
It is instructive to consider the stability of the classical solution with . In this case the equation for linear perturbation has the form
and the eigenvalues in (33) are
Obviously, for there is a Planck order positive eigenvalue and hence a very fast growing mode. For there are oscillations with the frequency of the Planck order of magnitude, suppressed by a relatively slow damping. Qualitatively, the results for the stability are the same as derived earlier from the trace Equation (16) in [41].
The anomaly-induced action (13) includes the semiclassical corrections to the gravitational action which are certain, in the sense they do not depend on the way we intend to quantize gravity, use string theory, etc. Thus, we have to correctly interpret the stability results, formulated above. The Starobinsky model of inflation [25,36] is based on the unstable version and requires especially chosen initial conditions. As we have mentioned above, the phenomenological consistency requires adding a classical term with in the action (5). On the other hand, the stable version is free from the restrictions on the initial conditions.
As we just discussed, without the classical term, the stability is defined by the sign of c and this sign depends on the particle contents, according to Equation (8). The stability of solution is achieved for . This inequality holds for the minimal standard model of particle physics (MSM) with , and , but does not hold for supersymmetric extensions, such as MSSM, or for the “doubled” standard model with , and . In what follows, we shall use the last version for the numerical analysis, but one has to remember that there is no real difference between the behavior of different models with . Let us note that the case, which occurs for the supersymmetric Yang-Mills theory [44], gives an unstable solution with .
It is clear that, in the late Universe, there should be either , or a sufficiently large classical , as otherwise flat space would be unstable. (As we already mentioned above, these two possibilities are equivalent [22,36,37].) Thus, using the advantage of the stable version at the beginning of inflation, requires the scheme of transition between stable and unstable particle contents. One of the possibilities for such a transition is related to the low-energy decoupling of the heavy degrees of freedom beyond the MSM, e.g., the s-particles in the case of MSSM [45]. A possible explanation of this decoupling is based on the slowing down exponential expansion with owing to the masses of the quantum s-particles [41,46]. It turns out that the process of slowing down inflation takes a long while and, as a result, the observable effects of inflation come from the very last 60–70 e-folds out of much greater rate of inflation.
The next question regarding this transition is how to provide the sufficiently large coefficient at the physically relevant, last 60–70, e-folds. This problem has been addressed in [28] and will not be discussed here. Instead of this, in the rest of the paper, we shall discuss the beginning of the exponential phase and, in particular, whether it could follow after the bounce from a contracting phase.
4. Phase Diagrams
Before starting the analysis of stability of the special solutions with respect to the small perturbations, let us complete the previous section by considering the phase diagrams for the Equation (27). Without the radiation term the equation is
We shall follow the analysis of the original paper by Starobinsky [25,26], and also the ones in [27,28] for the stable case. The main difference with these publications is that we include the cosmological constant term. As before, we restrict the main attention to the flat-space case. Indeed, there are no strong arguments of why the space curvature could be important in the very early Universe.
On the other hand, the cosmological constant may be relevant in the vicinity of the cosmological singularity because its value may be dramatically different from the one in the late Universe. The reason is that, in the last case, the observed value of the vacuum energy density is a sum of the vacuum term and the contribution , induced from the symmetry breaking in the matter fields sector, e.g., from the spontaneous breaking in the Higgs potential [47] (see also [48]). In the early epoch, this symmetry can be (and most likely is) restored owing to the high temperature or/and high curvature effects. As a result, the acquires the value which is typical for the corresponding phase transition. E.g., in case of the electroweak phase transition, this value is about 56 orders of magnitude greater than the one in the present Universe, but still negligibly small compared to the Planck scale in the vicinity of the singularity. However, in the case of the possible GUT-scale phase transition the difference between and , may be just a few orders, and in the case of the Planck-scale phase transition the two quantities may be of the same order of magnitude. In what follows we consider the last two possibilities.
Indeed, the reduction can be achieved by a simpler transformation , but the resulting equation is more complicated. Equation (37) can be elaborated using (38) as
In this way, we arrive at
Inserting these relations in (40), we obtain
Taking , defined in (29), we can write
where we used an abbreviation .
The analogous formula from [28] can be reproduced in the limit . Using (44), we arrive to the phase diagrams for the two different values of , as shown in Figure 1 for the stable and in Figure 2 for the unstable versions of the theory (All numerical calculations and plots were done using Wolfram’s Mathematica [49].).
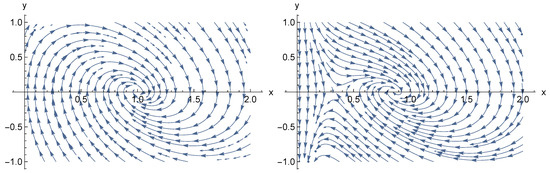
Figure 1.
Phase diagram for Equation (44) with the MSSM particle contents. In the left plot we choose and in the right plot, .
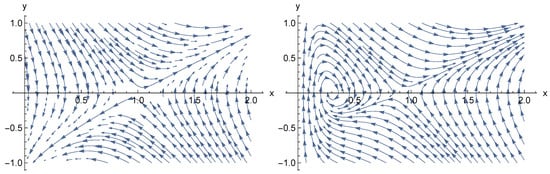
Figure 2.
Phase diagram for Equation (44) with the MSM particle contents, corresponding to the unstable exponential solution. In the left plot there is and in the right plot, .
One can easily note that small cosmological constant does not produce essential modifications compared to the previously known diagrams [25,26,27]. At the same time, the cosmological constant of the Planck order of magnitude, greatly transforms the phase diagram of the stable case making it qualitatively similar to the one of the unstable case with a small cosmological constant. This feature suggests a new mechanism of transition between the stable and unstable phases (different from the one described in [28,45,46]) and perhaps deserves further investigation in the future.
Imposing the special initial conditions at , one can arrive at the bounce solutions, with the exponential [for a(t)] expansion after the exponential contraction, and the smooth transition between these two phases. The basic example of this sort is shown in Figure 3 for the model with zero cosmological constant. It is important that we cannot set , as otherwise the solution is .
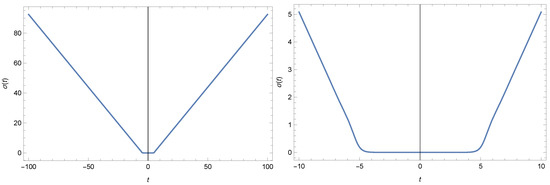
Figure 3.
Solution without radiation for the MSSM particles contents and hence . The initial conditions are , , and . On the left plot we show the interval in the Planck units and on the right plot the interval is ten times smaller.
Let us present more details concerning the bounce solutions, based on the numerical analysis. Figure 4 demonstrates the result of the small variations of initial conditions. Here we still keep zero cosmological constant. These plots clearly show that the bounce survives such a small changes. However, we have found that larger modifications may exclude the bounce solutions.
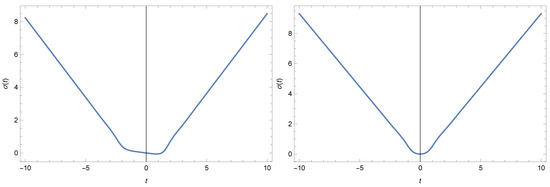
Figure 4.
Numerical solution for the conformal factor with the small variation in the initial conditions at . The left plot shows the behavior of the conformal factor under variations of and . In this case, the initial conditions become , , and . In the right plot, the variation was performed as , so that the new initial conditions are , , and . In both cases the bounce solution is maintained.
Another two relevant aspects concern the choice of initial conditions. As we already know, changing these conditions, one can produce the solutions without bounce. It is especially important, that these conditions are imposed in the vicinity of the minimum of the curve. This point is in the past for the expansion region , but, at the same time, it is in the future for the region where we meet a contraction. In the next section, we shall elaborate on the qualitative sense of this restriction.
The next step is to switch on the cosmological constant. As we have mentioned above, in the region close to singularity the magnitude of the corresponding density may be either a few (even many, actually) orders of magnitude smaller than , or even of the same order of magnitude as , if the Universe is approaching singularity after the corresponding phase transition. The example of the corresponding plots is shown in Figure 5. We can observe that the bounce may hold even for a relatively large cosmological constant. In fact, the cosmological constant of the given range does not change, qualitatively, the behavior near the singularity, even though the phase diagram gets modified. Let us note, without going into detail, that qualitatively the same situation with bounce holds for the space geometry.
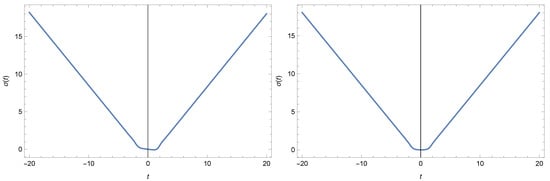
Figure 5.
Numerical solution for the conformal factor with the non-zero cosmological constant density. In the left graph, we consider and the initial conditions , , and . In the right plot, the value is larger, and the initial conditions are , , and .
The last example of the numerical analysis is included to illustrate the bounce in the presence of radiation. This is an important aspect to explore, because in the region close to the bounce, the solution is rapidly deviating from de Sitter and, as a consequence, there is an intensive creation of particles and radiation from the vacuum (see, e.g., [50,51,52,53] and references therein). Thus, there may be a large amount of radiation in the vicinity of the bounce, and this should be taken into account. However, since we use the equation for the trace (16), the classical radiation is not “visible” for the equation. On the other hand, we can still model the presence of radiation with the anomalous contribution, and the result of this is shown in Figure 6.
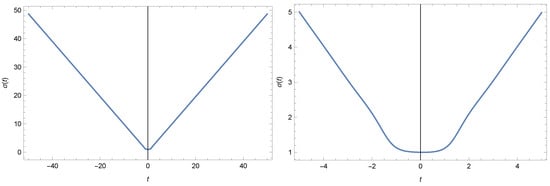
Figure 6.
Numerical solution for the conformal factor in the presence of the anomalous radiation term. Here, we use the value and the following initial conditions: , , , and . In the left plot, we show the range in Planck units and in the right plot the range is ten times smaller. One can observed that, even considering the quantum contribution to radiation, the bounce solution is still present.
5. Bounce and the Stability Analysis
It is interesting to explore the stability of the bounce solutions with respect to small perturbations of initial conditions. The analysis can be easily done analytically using the previous results (33) and (34) for the exponential behavior.
According to Equation (29), there are two pairs of solutions, corresponding to each of the values (30) with positive and negative signs. The “pre-inflationary” exponential expansion corresponds to the value of . Then, from the diagrams in Figure 4, Figure 5 and Figure 6, follows that the contraction phase corresponds to the change of sign .
Starting from this point, we can address the issue of stability in the linear contracting regime using the eigenvalues (34) of the solution (33) for small perturbations. Since we assume that in Equation (5) is zero, the value of c should be defined from quantum contribution (8). It is easy to see that for the MSSM particle contents, when . Then the real parts of both roots in Equation (34) are defined by the sign of . In the expansion phase, , and both roots have negative real parts. On the contrary, in case of contraction, we have and the solution is unstable under small perturbations of . Thus, the stable bounce due to the anomaly-induced semiclassical corrections is impossible.
A natural and important question is how it happened that we meet the bounce solutions as shown in the plots above, if the bounce can not be stable? As we discussed in the previous section, there is no strong dependence on the initial conditions in these solutions. The numerical analysis shows that the bounce survives small variations of these conditions, which is typical for the stable case. We know that typically, for the linearly unstable solutions, one has to expect that the solution of the desired type can be achieved only for an absolutely precise fine-tuning of the initial conditions.
The answer to this question is as follows. Indeed, the stability or instability depend on the way we interpret the dynamics of the system or, in other words, depends on our viewpoint. Defining the initial conditions at the bounce point and choosing sufficiently small, we are exploring the contraction phase by looking backward in time t. In this case, for the contraction there is a negative t and therefore a positive product . Then Equation (33) tells us that the contraction phase is stable. However, if we look forward in time, that is choose the initial point at some point near the same decreasing line, the solution is unstable.
It is worth noting that the situation in many other bounce models (see, e.g., the review [13]) is different. In these models there is a typical relation , such that the sign of the product does not change in the transition between the expansion and contraction phases, when we consider the dynamics forward in time. (We are grateful to Nelson P. Neto for this explanation.)
6. Conclusions and Discussions
It is quite natural to expect that the anomaly-induced semiclassical corrections to the gravitational action cure the cosmological singularity. Qualitatively, the reason for this expectation is that the theory with fourth and higher derivatives has a natural cut-off. In the fourth-derivative theory [54] this cut-off is the Planck mass divided by the dimensionless parameter of the relevant coefficient of the fourth-derivative term. From the dimensional arguments follows that, in the the cosmological case, the higher derivative terms should modify the dynamics of the conformal factor of the metric and remove the singularity.
For example, in the Newtonian singularity case, i.e., for a point-like static mass source, many types of higher derivative terms remove singularity in the modified Newtonian potential. This occurs starting from the simplest fourth-derivative theory with the action composed by (5) and (4) terms [55]. The same is true for the local (see, e.g., [56,57]) and nonlocal [58] higher derivative models. It is worthwhile to note that the detailed analysis of the Newtonian and especially black hole cases is more complicated (see, e.g., [59,60,61,62] and further references therein).
In cosmology, the basic four-derivative action (5) and (4) does not remove singularity because the term, contributing with the ghost degree of freedom to the spin-2 sector of the theory, equals zero on the cosmological background. Then, the term alone cannot help removing singularity because it does not produce a massive unphysical ghost.
At this point, it becomes clear that the cosmological case is more complicated, especially because the situation with singularity can not be reduced to the analysis of the flat space propagator, as it is in the Newtonian singularity case. Taking these considerations into account, one can expect that the anomaly-induced term (13) may remove singularity and promote bounce since it introduces a more complete form of dynamics to the conformal factor . This sort of intuitive arguments should be carefully verified by direct calculations. In the previous sections, we saw that the bounce solutions in this model really take place. On the other hand, these solutions are unstable if we define the initial conditions sufficiently far backward in the contraction regime and look forward in time. In this respect, the anomaly-induced model is different from the models with nonlocal form factors, where the bounce solutions can be found [15,16].
It would be certainly interesting to obtain a stable bounce solutions from the semiclassical or quantum gravity corrections, derived in a consistent way. One of the options is to explore higher-loop semiclassical corrections in the initially conformal model, which are expected to give higher than linear powers of logarithms in the UV form factors and, therefore, stronger non-linear -dependence in the effective action (see, e.g., [63]). This possibility represents an interesting proposal for a possible future work.
Author Contributions
Both authors contributed equally to this manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Authors is grateful to N.-P. Neto and A.A. Starobinsky for useful discussions. C.W. is grateful to Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—CAPES (Brazil) for supporting this Ph.D. project. The work of I.Sh. was partially supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico—CNPq (Brazil) under the grant 303635/2018-5. I.Sh. was also supported in parts by Russian Ministry of Science and High Education, project No. FEWF-2020-0003.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Penrose, R. Gravitational collapse and space-time singularities. Phys. Rev. Lett. 1965, 14, 57. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational collapse: The role of general relativity. Riv. Nuovo Cimento 1969, 1, 252. [Google Scholar]
- Hawking, S.W. Occurrence of singularities in open universes. Phys. Rev. Lett. 1965, 15, 689. [Google Scholar] [CrossRef]
- Hawking, S.W. Singularities in the Universe. Phys. Rev. Lett. 1966, 17, 443. [Google Scholar] [CrossRef]
- Borde, A.; Guth, A.H.; Vilenkin, A. Inflationary space-times are incompletein past directions. Phys. Rev. Lett. 2003, 90, 151301. [Google Scholar] [CrossRef]
- Gurovich, V.T.; Starobinsky, A.A. Quantum effects and regular cosmological models. Sov. Phys. JETP 1979, 50, 844. [Google Scholar]
- Müller, D.; Ricciardone, A.; Starobinsky, A.A.; Toporensky, A. Anisotropic cosmological solutions in R + R2 gravity. Eur. Phys. J. 2018, C78, 311. [Google Scholar] [CrossRef]
- Gasperini, M.; Veneziano, G. The Pre-big bang scenario in string cosmology. Phys. Rept. 2003, 373, 212. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Turok, N. Cosmic evolution in a cyclic universe. Phys. Rev. D 2002, 65, 126003. [Google Scholar] [CrossRef]
- Acacio de Barros, J.; Pinto-Neto, N.; Sagioro-Leal, M.A. The Causal interpretation of dust and radiation fluids nonsingular quantum cosmologies. Phys. Lett. 1998, A241, 229. [Google Scholar] [CrossRef]
- Pinto-Neto, N.; Fabris, J.C. Quantum cosmology from the de Broglie-Bohm perspective. Class. Quant. Grav. 2013, 30, 143001. [Google Scholar] [CrossRef]
- Casadio, R. Quantum gravitational fluctuations and the semiclassical limit. Int. J. Mod. Phys. 2000, D9, 511. [Google Scholar] [CrossRef]
- Novello, M.; Bergliaffa, S.E.P. Bouncing cosmologies. Phys. Rept. 2008, 463, 127. [Google Scholar] [CrossRef]
- Battefeld, D.; Peter, P. A Critical review of classical bouncing cosmologies. Phys. Rept. 2015, 571, 1–66. [Google Scholar] [CrossRef]
- Biswas, T.; Koshelev, A.S.; Mazumdar, A.; Vernov, S.Y. Stable bounce and inflation in non-local higher derivative cosmology. JCAP 2012, 8, 24. [Google Scholar] [CrossRef]
- Koshelev, A.S. Stable analytic bounce in non-local Einstein-Gauss-Bonnet cosmology. Class. Quant. Grav. 2013, 30, 155001. [Google Scholar] [CrossRef][Green Version]
- Saidov, T.; Zhuk, A. Bouncing inflation in nonlinear R2 + R4 gravitational model. Phys. Rev. 2010, D81, 124002. [Google Scholar]
- Ellis, G.F.R.; Maartens, R. The emergent universe: Inflationary cosmology with no singularity. Class. Quant. Grav. 2004, 21, 223. [Google Scholar] [CrossRef]
- Fabris, J.C.; Pelinson, A.M.; Shapiro, I.L. Anomaly induced effective action for gravity and inflation. Grav. Cosmol. 2000, 6, 59. [Google Scholar]
- Deser, S.; Duff, M.J.; Isham, C. Nonlocal conformal anomalies. Nucl. Phys. 1976, B111, 45. [Google Scholar] [CrossRef]
- Duff, M.J. Observations On Conformal Anomalies. Nucl. Phys. 1977, B125, 334. [Google Scholar] [CrossRef]
- Duff, M.J. Twenty years of the Weyl anomaly. Class. Quant. Grav. 1994, 11, 1387. [Google Scholar] [CrossRef]
- Riegert, R.J. A non-local action for the trace anomaly. Phys. Lett. 1984, B134, 56. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Tseytlin, A.A. Conformal anomaly in Weyl theory and anomaly free superconformal theories. Phys. Lett. 1984, B134, 187. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. 1980, B91, 99. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Nonsingular Model of the Universe with the Quantum-Gravitational De Sitter Stage and its Observational Consequences. In Proceedings of the Second Seminar “Quantum Gravity”, Moscow, Russia, 13–15 October 1982; pp. 58–72. [Google Scholar]
- Pelinson, A.M.; Shapiro, I.L.; Takakura, F.I. Stability issues in the modified Starobinsky model. Nucl. Phys. B Proc. Suppl. 2004, 127, 182. [Google Scholar] [CrossRef]
- Netto, T.d.P.; Pelinson, A.M.; Shapiro, I.L.; Starobinsky, A.A. From stable to unstable anomaly-induced inflation. Eur. Phys. J. 2016, C76, 544. [Google Scholar] [CrossRef]
- Shapiro, I.L. Effective action of vacuum: Semiclassical approach. Class. Quant. Grav. 2008, 25, 103001. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Odintsov, S.D.; Shapiro, I.L. Effective Action in Quantum Gravity; IOP Publishing: Bristol, UK, 1992. [Google Scholar]
- Buchbinder, I.L.; Shapiro, I.L. Introduction to Quantum Field Theory with Applications to Quantum Gravity; Oxford University Press: Oxford, UK, to be published.
- Fradkin, E.S.; Tseytlin, A.A. Asymptotic freedom on extended conformal supergravities. Phys. Lett. 1982, B110, 117. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Tseytlin, A.A. One-loop beta function in conformal supergravities. Nucl. Phys. 1982, B203, 157. [Google Scholar] [CrossRef]
- Paneitz, S. A Quartic Conformally Covariant Differential Operator for Arbitrary Pseudo-Riemannian Manifolds; MIT Preprint; MIT: Cambridge, MA, USA, 1983. [Google Scholar]
- Shapiro, I.L.; Jacksenaev, A.G. Gauge dependence in higher derivative quantum gravity and the conformal anomaly problem. Phys. Lett. 1994, B324, 286. [Google Scholar] [CrossRef]
- Birell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Asorey, M.; Gorbar, E.V.; Shapiro, I.L. Universality and ambiguities of the conformal anomaly. Class. Quant. Grav. 2004, 21, 163. [Google Scholar] [CrossRef]
- Starobinsky, A.A. The perturbation spectrum evolving from a nonsingular initially de-Sitter cosmology and the microwave background anisotropy. Sov. Astron. Lett. 1983, 9, 302. [Google Scholar]
- Fischetti, M.V.; Hartle, J.B.; Hu, B.L. Quantum effects in the early universe. I. Influence of trace anomalies on homogeneous, isotropic, classical geometries. Phys. Rev. 1979, D20, 1757. [Google Scholar] [CrossRef]
- Pelinson, A.M.; Shapiro, I.L. On the scaling rules for the anomaly-induced effective action of metric and electromagnetic field. Phys. Lett. 2011, B694, 467. [Google Scholar] [CrossRef]
- Pelinson, A.M.; Shapiro, I.L.; Takakura, F.I. On the stability of the anomaly-induced inflation. Nucl. Phys. 2003, B648, 417. [Google Scholar] [CrossRef]
- Dowker, J.S.; Critchley, R. Effective Lagrangian and energy-momentum tensor in de Sitter space. Phys. Rev. 1976, D13, 3224. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Tseytlin, A.A. One loop effective potential in gauged O(4) supergravity. Nucl. Phys. 1984, B234, 472. [Google Scholar] [CrossRef]
- Henningson, M.; Skenderis, K. The Holographic Weyl anomaly. JHEP 1998, 7, 23. [Google Scholar] [CrossRef]
- Shapiro, I.L. The graceful exit from the anomaly-induced inflation: Supersymmetry as a key. Int. J. Mod. Phys. 2002, D11, 1159. [Google Scholar] [CrossRef]
- Shapiro, I.L.; Solà, J. Massive fields temper anomaly-induced inflation: The clue to graceful exit? Phys. Lett. 2002, B530, 10. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 1, 61. [Google Scholar] [CrossRef]
- Shapiro, I.L.; Solà, J. Scaling behavior of the cosmological constant: Interface between quantum field theory and cosmology. JHEP 2002, 2, 6. [Google Scholar] [CrossRef]
- Mathematica; Version 12.1; Wolfram Research, Inc.: Champaign, IL, USA, 2020.
- Parker, L. Particle creation in expanding universes. Phys. Rev. Lett. 1968, 21, 562. [Google Scholar] [CrossRef]
- Parker, L. Quantized fields and particle creation in expanding universes. Phys. Rev. 1969, 183, 1057. [Google Scholar] [CrossRef]
- Zeldovich, Y.B.; Starobinsky, A.A. Rate of particle production in gravitational fields. JETP Lett. 1977, 26, 252. [Google Scholar]
- Dobado, A.; Maroto, A.L. Particle production from nonlocal gravitational effective action. Phys. Rev. 1999, D60, 104045. [Google Scholar] [CrossRef]
- Stelle, K.S. Renormalization of higher derivative quantum gravity. Phys. Rev. 1977, D16, 953. [Google Scholar] [CrossRef]
- Stelle, K.S. Classical gravity with higher derivatives. Gen. Rel. Grav. 1978, 9, 353. [Google Scholar] [CrossRef]
- Accioly, A.; Giacchini, B.L.; Shapiro, I.L. Low-energy effects in a higher-derivative gravity model with real and complex massive poles. Phys. Rev. D 2017, 96, 104004. [Google Scholar] [CrossRef]
- Giacchini, B.L. On the cancellation of Newtonian singularities in higher-derivative gravity. Phys. Lett. 2017, B766, 306. [Google Scholar] [CrossRef]
- Tseytlin, A.A. On singularities of spherically symmetric backgrounds in string theory. Phys. Lett. 1995, B363, 223. [Google Scholar] [CrossRef]
- Giacchini, B.L.; de Paula Netto, T. Weak-field limit and regular solutions in polynomial higher-derivative gravities. Eur. Phys. J. 2019, C79, 217. [Google Scholar] [CrossRef]
- Giacchini, B.L.; de Paula Netto, T. Effective delta sources and regularity in higher-derivative and ghost-free gravity. JCAP 2019, 7, 013. [Google Scholar] [CrossRef]
- Burzillà, N.; Giacchini, B.L.; Netto, T.D.; Modesto, L. Newtonian Potential in Higher-Derivative Quantum Gravity. arXiv 2012, arXiv:2012.06254. [Google Scholar]
- Burzillà, N.; Giacchini, B.L.; Netto, T.D.; Modesto, L. Higher-order regularity in local and nonlocal quantum gravity. arXiv 2012, arXiv:2012.11829. [Google Scholar]
- Hamada, K.J. Diffeomorphism invariance demands conformal anomalies. arXiv 2020, arXiv:2010.06771. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).