A Fuzzy-Based Optimization Technique for the Energy and Spectrum Efficiencies Trade-Off in Cognitive Radio-Enabled 5G Network

Abstract

In 5G systems, enhancing the energy efficiency (EE) and spectrum efficiency (SE) is a significant task that is capable of fulfilling the demand of future wireless networks and providing Quality of Service (QoS) provisioning, such as high throughput with low power consumption. In the present work, a look-up table enabled a fuzzy-based approach to investigate the SE and EE issues in 5G networks and obtained an efficient symmetrical trade-off between them to enhance the system’s overall performance. We completed simulations in NS-2.31 software version 2.31, and MATLAB is used to visualize the results. The proposed model achieved maximum values of EE and SE of 0.92 bit/J/Hz with a sensing time τ_s(LUT) = 20 ms. Furthermore, optimizing the sensing time and the secondary user (SU) transmission power, yielded a maximum EE and provided a QoS provisioned cognitive radio-enabled 5G network.

1. Introduction

Since the inception of mobile communication networks over recent decades and with the advancement of mobile communication, the focus for research has been on achieving better connectivity, anytime anywhere, seamless connectivity, less complexity and minimum latency, while providing high-speed network services. The optimization of critical design parameters, namely spectrum efficiency (SE); energy efficiency (EE); and energy harvesting (EH) are in massive demand for future prospective wireless networks, specifically the 5G cognitive radio networks (5G-CRN) by 2021 [1,2,3,4,5]. Although in most regions, different countries face the severe problem of spectrum scarcity, there are still many regions where spectrum inefficiency is also a vital issue in the case of spectrum utilization. Thus, a tremendous amount of work is required to achieve the enhancement of spectrum efficiency techniques. Energy efficiency is another potential design parameter for the next-generation wireless networks, because of limited battery power availability in mobile devices and its inefficient utilization, as well as global environment concerns [6,7,8,9]. Practically speaking, methods that enhance the spectral efficiency, lead to a decrease in energy efficiency and vice versa. The main challenge in 5G systems is to obtain high spectral efficiency while utilizing minimal amount of energy for mobile devices. This problem is rectified by introducing an optimal trade-off between SE and EE while providing quality of service (QoS) provisioning in a 5G-CRN. Another challenge is to reduce the outage probability and provide secure, guaranteed communication. The deployment of mobile communication technologies also overcomes these challenges and meet the targets [1,2,3,4,5,6,7,8,9,10].

Cognitive radio is a concept that guarantees effective utilization of the radio spectrum through dynamic spectrum access and provides a solution to SE issues [4]. The secondary user (SU) practically does not perform sensing and accessing operations simultaneously. The SU first senses the spectrum, and only if the channel is vacant, does the SU then transmit the data. Therefore, additional sensing energy is used before the actual start of every transmission frame of data. Therefore, energy efficiency is a key issue in cognitive radio enabled networks [3,4,5]. To overcome this issue, co-operative sensing using a look-up table (LUT) performs a vital role in spectrum sensing, which is explained in subsequent sections. Researchers have paid more and more attention towards the co-operative spectrum sensing (CSS) method over the last 5–8 years because it gives good spectrum efficiency capabilities [4,5,6]. Moreover, the sensing capability of a single user is reduced by the presence of multipath fading and shadowing [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28].

Detection of the primary user (PU) with consistent spectrum detection and data transmission is currently required and hence, a vital topic of research nowadays in cognitive radio networks [7,8,9,10,11,12,13]. Gao, Y. et al. proposed the sensing-power trade-off problem in a multi-input/multi-output cognitive radio system [7]. In [8], Stotas et al. designed a novel receiver architecture; they also developed a frame structure to overcome the issues of the sensing-throughput trade-off in CRNs and were able to achieve spectrum sensing and transmission simultaneously [9]. Tang et al. investigated the effect of PU data transmission on the sensing–transmission trade-off in the co-operative cognitive radio model [10]. They also optimized the sensing and transmission power allocation while achieving maximum throughput. Jhao et al. explained maximum throughput by minimizing sensing time with the low probability of detection [11]. Liang et al. demonstrated the effect of the secondary user’s power that is utilized for data transmission on energy efficiency [12]. In contrast, the EE design of advanced channel sensing in a cognitive radios (CR)-network was proposed by [13].

Although extensive work has been carried out on the sensing–throughput trade-off in [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. Ref. [15] considered the SE–EE simultaneously. In other words, the proposed work listed in the literature did not consider energy-efficient models as well; most of the researchers did not even address energy constraints while considering other research objectives. As most sensing devices (energy detector, cyclostationary and matched filter) work with minimum energy requirements, this leads to a critical issue for researchers in an attempt to minimize energy consumption [16,17,18,19]. The detailed survey clearly shows an enormous scope of development of an efficient technique that jointly considers spectrum sensing, transmission, and spectrum handoff for energy-efficient 5G-CRN (problem P₁). Second, EE-CRNs provide a greater spectrum for wireless portable devices while consuming less energy [20]. EE policies are becoming more critical to achieving green communication because of traditional grid-powered or replaceable battery-powered devices which emit 2% of the total CO₂. Ref. [21] developed an efficient sensing time optimization algorithm, which we have modified using the concept of a look-up table and then used it throughout the study. Due to this severe issue, recently researchers have focused on developing energy harvesting wireless communication systems (LUT). On the other hand, an LUT-incorporated EH system with spectrum and energy efficiencies is yet to be explored (problem P₂) [22,23,24,25,26,27,28,29,30,31,32,33,34].

Highlights of this Investigation

The highlights of this investigation are summarized as follows:

• In a traditional CSS, a large amount of time is consumed while reporting, which contributes little to the sensing performance and hence makes the system inefficient. Therefore, we have designed a novel super frame with a look-up table for reporting and hence, the ability to further reduced the sensing time. The LUT updates regularly and thus acts as a sensing database for other SUs connected in co-operative communication.
• To enhance the EE using CSS the sensing time and transmission power were jointly considered when optimizing EE under PU transmission constraints. We derived an optimized co-operative sensing model by maximizing the EE under QoS provisioning while optimizing the sensing time using an LUT. Another problem of CR with QoS provisioning is formulated, i.e., satisfying the SE requirements under the constraint of maximizing EE. For this issue, we analyzed the effect of the spectrum efficiency on the energy efficiency. The literature shows that for different SEs, different values of the sensing time are required. To overcome this problem, we optimized the LUT incorporated EH systems to obtain a trade-off between the sensing time and power utilized during transmission under EE Constraints with QoS provisioning.
• We further implemented a fuzzy-based selection switch in the proposed system to optimize sensing time to provide a symmetrical trade-off between the EE and the SE for 5G-CRN networks

2. Materials and Methods

2.1. Network Models

A look-up table based co-operative spectrum sensing technique was proposed to obtain the optimal time to achieve reasonable spectral and the energy efficiencies of a cognitive-enabled 5G network. The look-up table played a vital role in minimizing the sensing time and improving the time for data transmission and hence enhanced the system’s overall spectral efficiency. As we know, a CR does not have the facility to sense and transmit data simultaneously, giving a wide scope for co-operative spectrum sensing.

2.2. Primary Network Model

Consider a primary network that has the rights to access the spectrum allocated by the Federal Communications Commission (FCC) with bandwidth W.

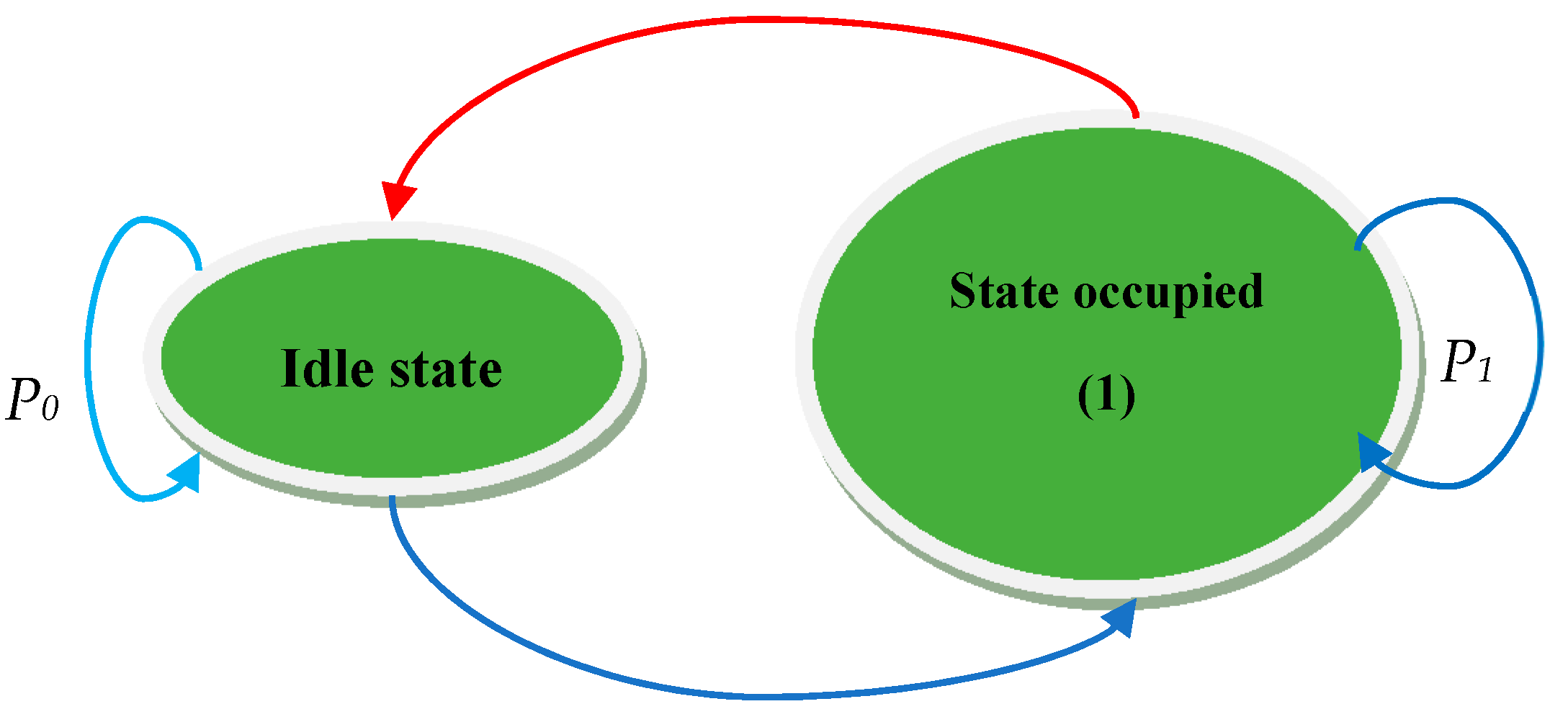
The PU makes use of a slotted communication protocol with sensing time ${\tau }_s$ within time frame T, which is a function of Ch_i with Ch_i = 0 (for the channel in idle state) and Ch_i = 1 (for an occupied channel). The state diagram of the primary spectrum utilization is shown in Figure 1. In this model, the spectrum in state ”0” corresponds to idle with probability P₀, and it transits from state ”0” to ”1” with probability (1 − P₀). Conversely, if the spectrum is in state ”1” with probability P₁ is moving towards state ”0”, with probability (1 − P₁). Therefore the steady-state probability in two cases is ${\Phi }_0\left(P_{0,}{P}_1\right)=\frac{1-P_1}{2-\left(P_1+P_0\right)}$ and ${\Phi }_1\left(P_{0,}{P}_1\right)=\frac{1-P_0}{2-\left(P_1+P_0\right)}$ respectively.

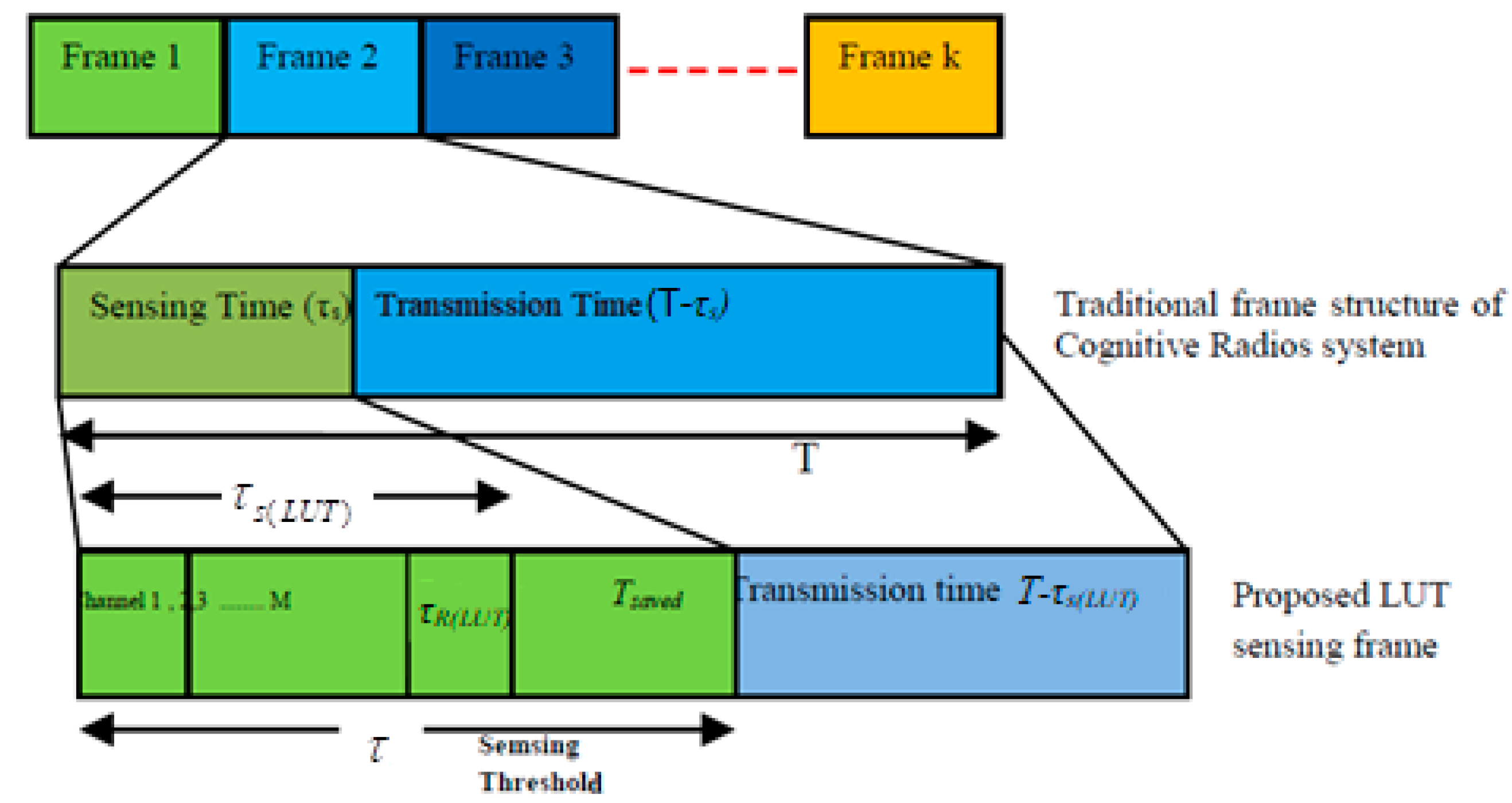
Let ${\tau }_s$ be the sensing time used for a fixed sensing frame and (T − τ_s) be the transmission frame with total frame time duration in T. The modified sensing time ${\tau }_{s(LUT)}$ is the suggested LUT time that is exploited for co-operative sensing, as shown in Figure 2. Let δ_min be the minimum time frame for SUs to sense the spectrum and τ_R(LUT) be the reporting time to the cognitive radios base station ${\tau }_{R\left(LUT\right)}<<{\tau }_{s(LUT)}$:- for example. for T = 20 ms, the reporting time for the maximum τ_R(LUT) = 0.1 ms [15,21].

$$T_{saved}={\tau }_{}-({\tau }_{s(LUT)}+{\tau }_{R\left(LUT\right)})$$

(1)

We review some foundation ideas of Wang et al. [15] that will be utilized throughout this study.

Let

$$\begin{gathered} C_i=0:\mathrm{the}\mathrm{current}\mathrm{state}\mathrm{of}\mathrm{the}i\mathrm{th}\mathrm{channel}\mathrm{is}\mathrm{vacant} \\ {C}_i=1:\mathrm{the}\mathrm{current}\mathrm{state}\mathrm{of}\mathrm{the}i\mathrm{th}\mathrm{channel}\mathrm{is}\mathrm{occupied} \end{gathered}$$

Similarly

$$\begin{gathered} {\widehat{C}}_i=0:\mathrm{during}\mathrm{sensing},\mathrm{the}i\mathrm{th}\mathrm{channel}\mathrm{sensed}\mathrm{as}\mathrm{vacant} \\ {\widehat{C}}_i=1:\mathrm{the}i\mathrm{th}\mathrm{channel}\mathrm{is}\mathrm{perceived}\mathrm{as}\mathrm{occupied}\mathrm{during}\mathrm{sensing}. \end{gathered}$$

$P_D\mathrm{and}{P}_{FA}$ is a function of LUT enabled sensing time which are termed as the detection probability and false alarm respectively. Mathematically

$$P_D=P(C_i=0|C_i=0)\mathrm{or}P(C_i=1|C_i=1)$$

(2)

This means that the probability of sensing a channel is 100%, i.e., the channel is genuinely sensed in the right spectrum. In contrast

$$P_{FA}=P({\widehat{C}}_i=0|C_i=1)\mathrm{or}P({\widehat{C}}_i=1|C_i=0)$$

(3)

Equation (3) signifies that the channel sensing is not accurate, and the probability of a false alarm is at a maximum. We can calculate P_D and P_FA using the following relations:

$$P_D=Q\left(\frac{1}{\sqrt{2\gamma +1}}\left(Q^{-1}\left(P_{FA}\right)-\sqrt{{\tau }_{s(LUT)}{f}_s\gamma }\right)\right)$$

(4)

$$P_{FA}=Q\left(\sqrt{2\gamma +1}\left(Q^{-1}\left(P_D\right)+\sqrt{{\tau }_{s(LUT)}{f}_s\gamma }\right)\right)$$

(5)

where $Q(x)$ is probability Gaussian function, f_s is the sampling frequency, and γ denotes the average power consumed

$${\tau }_s\left(\mathrm{minimum}\right)=\frac{1}{{\gamma }^2{f}_s}{\left(Q^{-1}\left(\stackrel{⌢}{P_{FA}}\right)-Q^{-1}\left(\stackrel{⌢}{P_D}\right)\sqrt{2\gamma +1}\right)}^2$$

(6)

where ${\tau }_s\left(\mathrm{minimum}\right)$ is the minimum value of sensing time to facilitate the condition of target probability of detection and target probability of false alarm.

2.3. Problem Formulation

From Equations (4) and (5) we can calculate the average SE using [12] as

$${\eta }_{S{E}_1}=\frac{T-{\tau }_{s(LUT)}-{\tau }_{R(LUT)}}{T}{R}_1{\pi }_i(1-P_{fa})$$

(7)

where π_i is the probability that the spectrum is vacant $R_1={\log }_2(1+\frac{P_t{h}_s}{{\sigma }_s^2})$, P_t is the power utilized by the SU during transmission, h_s is the CR link gain, and ${\sigma }^2{}_s$ denotes the power due to unwanted signals (noise). During miss detection (i.e., the spectrum falsely detected as vacant), the probability is calculated as ${\pi }_i(1-P_d)$ and hence the average SE, in this case, using [12] is as follows:

$${\eta }_{S{E}_2}=\frac{T-{\tau }_{s(LUT)}-{\tau }_{R(LUT)}}{T}{R}_2{\pi }_j(1-P_d)$$

(8)

where π_i is the probability of vacant spectrum $R_2={\log }_2(1+\frac{P_t{h}_s}{P_{PU}{h}_{PU}+{\sigma }_s{}^2})$, P_PU is the power utilized by the PU during transmission, and h_PU denotes PU gain. Hence the average value of the spectral efficiency is calculated as follows:

$${\eta }_{SE}={\eta }_{S{E}_1}+{\eta }_{S{E}_2}$$

(9)

However, the energy efficiency of a 5G-CRN is obtained using

$${\eta }_{EE}=\frac{{\eta }_{SE}}{\gamma }$$

(10)

where

$$\gamma =\frac{1}{T}\left\{N(P_s+P_c){\tau }_{s(LUT)}+({\mathrm{P}}_R+P_c){\tau }_{R(LUT)}\times (T-{\tau }_{s(LUT)}-{\tau }_{R(LUT)})\left[{\pi }_i(1-P_{fa})+{\pi }_j(1-P_d)\right]\right\}$$

(11)

where P_s is the sensing power and P_c is the power consumed by the circuit. During reporting to the LUT stage, the average power consumption is ${\tau }_{R(LUT)}N({\mathrm{P}}_R+P_c)$, where ${\mathrm{P}}_R$ is the power consumed during reporting to the cognitive radio-base station(CR-BS).

The problem was to optimize the sensing time using a look-up table (τ_s(LUT)) as well as the SUs power (P_t) use such that the energy efficiency will be maximized under the constraint that the primary user’s rights are always protected, i.e.,

$$Opt\left[{\tau }_{s(LUT)},P_t\right]=\max \left[{\eta }_{EE}\right]$$

(12)

such that the probability of detection (P_d) ≤ threshold detection probability ($\widehat{P_d}=0.9$).

2.4. Solution to the Problem

We have designed a system to monitor the sensing time using the LUT concept. The proposed method first states the optimization problem (Problem P₁). Then an optimal solution of P₁ is provided by achieving a sensing time that provides maximum energy efficiency for a given transmission power of the SUs (Problem P₁). To achieve this, we took a partial derivative of the energy efficiency w.r.t the sensing time using LUT.

$$\frac{\partial {\eta }_{EE}}{\partial {\tau }_{s(LUT)}}=\frac{1}{{\gamma }^2}(\gamma \frac{\partial {\eta }_{SE}}{\partial {\tau }_{s(LUT)}}-{\eta }_{SE}\frac{\partial \gamma }{\partial {\tau }_{s(LUT)}})$$

(13)

Let

$$\begin{array}{ll}{f}_1({\tau }_{s(LUT)})& =T^2(\gamma \frac{\partial {\eta }_{SE}}{\partial {\tau }_{s(LUT)}}-{\eta }_{SE}\frac{\partial \gamma }{\partial {\tau }_{s(LUT)}})\\ & =-N{\pi }_i(T-N{\tau }_{R(LUT)})(P_s+P_c)[R_1(1-P_{ fa})-N{\pi }_0{\tau }_{R(LUT)}{R}_2(1-\stackrel{⌢}{P_d})(P_R+P_c)\\ & +R_2((1-\stackrel{⌢}{P_d})-N{\pi }_i{\tau }_{R(LUT)}{R}_1\left[1-P_{ fa}(T-{\tau }_{s(LUT)}-N{\tau }_{R(LUT)})\frac{d{P}_{ fa}}{d{\tau }_{s(LUT)}}\right](P_R+P_c)\\ & -{\pi }_i{\pi }_0{(T-{\tau }_{s(LUT)}-N{\tau }_{R(LUT)})}^2(1-\stackrel{⌢}{P_d})(P_R+P_t)(R_1-R_2)\frac{d{P}_{ fa}}{d{\tau }_{s(LUT)}},\end{array}$$

(14)

where

$$\begin{array}{l}\frac{d{P}_{ fa}}{d{\tau }_{s(LUT)}}=N{(P_{fa})}^{N-1}\frac{d{p}_{fa}}{d{\tau }_{s(LUT)}}=-N{(P_{fa})}^{N-1}\frac{\gamma }{4}\sqrt{\frac{f_s}{\pi {\tau }_{s(LUT)}}}{e}^{\frac{-1}{2}{\theta }^2}\\ \mathrm{and}\\ \theta =Q(P_{fa})\end{array}$$

(15)

Then

$$\begin{gathered} \frac{\partial {\eta }_{EE}}{\partial {\tau }_{s(LUT)}}=0\to f_1({\mathsf{\tau }}_{\mathrm{s}\left(\mathrm{LUT}\right)})=0 \\ \mathrm{Obviously}{\lim }_{{\tau }_{s(LUT)}\to 0}{f}_1({\tau }_{s(LUT)})=\infty \mathrm{and}{\lim }_{{\tau }_{s(LUT)}\to T-{\tau }_{s(LUT)}}{f}_1({\tau }_{s(LUT)})<0 \end{gathered}$$

.

The second-order partial derivative of $f_1({\tau }_{s(LUT)})$(14) w.r.t τ_s(LUT) is equal to

$$\begin{array}{ll}\frac{\partial f_1({\tau }_{s(LUT)})}{\partial {\tau }_{s(LUT)}}& =T^2(\gamma \frac{{\partial }^2{\eta }_{SE}}{\partial {\tau }^2{}_{s(LUT)}}-{\eta }_{SE}\frac{{\partial }^2\gamma }{\partial {\tau }^2{}_{s(LUT)}})\\ & =N{\pi }_i{R}_1\left\{{\tau }_{R(LUT)}(P_s+P_c)[R_1(1-P_{ fa}+{\tau }_{R(LUT)}(P_R+P_c)\times (1-\stackrel{⌢}{P_d})(P_t+P_c)(R_1-R_2)\right\}\\ & \times \left[2\frac{d{P}_{ fa}}{d{\tau }_{s(LUT)}}-(T-{\tau }_{s(LUT)}-N{\tau }_{R(LUT)})\frac{d^2{P}_{ fa}}{d{\tau }^2{}_{s(LUT)}}\right],\\ \mathrm{where}& \\ & \frac{d^2{P}_{ fa}}{d{\tau }^2{}_{s(LUT)}}=N(N-1)p_f{}^{N-2}{\left(\frac{d{P}_{ fa}}{d{\tau }_{s(LUT)}}\right)}^2+(N)p_f{}^{N-1}\frac{d^2{P}_{ fa}}{d{\tau }^2{}_{s(LUT)}}\end{array}$$

(16)

Thus $\frac{\partial f_1({\tau }_{s(LUT)})}{\partial {\tau }_{s(LUT)}}$ < 0, where $f_1({\tau }_{s(LUT)})$ decreases with ${\tau }_{s(LUT)}$. For a particular value of P_t, there must be one unique value of ${\tau }_{s(LUT)}’$ for which $f_1({\tau }_{s(LUT)})$ = 0.

Therefore, $\frac{\partial {\eta }_{EE}}{\partial {\tau }_{s(LUT)}}\ge 0for{\tau }_{s(LUT)}\in (0,{\tau }_{s(LUT)}’)\mathrm{and}\frac{\partial {\eta }_{EE}}{\partial {\tau }_{s(LUT)}}\le 0\mathrm{for}{\tau }_{s(LUT)}\in ({\tau }_{s(LUT)}’,T-N{\tau }_{R(LUT)})$.

Hence there must be a unique value of the sensing time using the LUT (${\tau }_{s(LUT)}$) that maximizes the system’s energy efficiency. Similarly, the effect of the transmission power on the energy efficiency for a given sensing time should be calculated for a given optimization problem (Problem P₂). Where an optimal solution of P₂ is found by taking the second-order partial derivative of the energy efficiency w.r.t the transmission power.

$$\frac{\partial {\eta }_{EE}}{\partial P_t}=\frac{1}{{\gamma }^2}(\gamma \frac{\partial {\eta }_{SE}}{\partial P_t}-{\eta }_{SE}\frac{\partial \gamma }{\partial P_t})$$

(17)

Let

$$\begin{array}{ll}{f}_2(P_t)& =T^2(\gamma \frac{\partial {\eta }_{SE}}{\partial P_t}-{\eta }_{SE}\frac{\partial \gamma }{\partial P_t})\\ & =\frac{C_1}{\ln 2}N(T-{\tau }_{s(LUT)}-N{\tau }_{R(LUT)})\left[{\tau }_{s(LUT)}(P_s+P_c)+{\tau }_{R(LUT)}(P_R+P_c)\right]\\ & +{(T-{\tau }_{s(LUT)}-N{\tau }_{R(LUT)})}^2\left[{\pi }_i(1-P_{fa})+{\pi }_0(1-\stackrel{⌢}{P_d})\right]\left[\frac{C_1}{\ln 2}(P_t+P_c)-C_2\right],\\ \mathrm{where}& \\ & C_1={\pi }_i(1-P_{fa})\frac{f_2{}_s}{{\sigma }^2{}_s+P_t{h}_s}+{\pi }_0(1-\stackrel{⌢}{P_d})\frac{f_2{}_s}{P_{PU}{h}_{PU}+P_t{h}_s+{\sigma }^2{}_s}\\ \mathrm{and}& \\ & C_2={\pi }_i(1-P_{fa})lo{g}_2\left(1+\frac{P_t{h}_s}{{\sigma }^2{}_s}\right)+{\pi }_0(1-\stackrel{⌢}{P_d})lo{g}_2\left(1+\frac{P_t{h}_s}{P_{PU}{h}_{PU}+{\sigma }^2{}_s}\right)\end{array}$$

(18)

Then $\frac{\partial {\eta }_{EE}}{\partial P_t}=0\to f_2(P_t)=-\infty$ Obviously ${\lim }_{P_t\to 0}{f}_2(P_t)>0\mathrm{and}{\lim }_{P_t\to \infty }{f}_2(P_t)=-\infty$.

The first partial derivative of $f_2(P_t)$(18) w.r.t $P_t$ to find out the unique value of P_t for which the energy efficiency is a maximum is equal to:

$$\begin{array}{ll}\frac{\partial f_2(P_t)}{\partial P_t}& =T^2(\gamma \frac{{\partial }^2{\eta }_{SE}}{\partial P_t{}^2}-{\eta }_{SE}\frac{{\partial }^2\gamma }{\partial P^2{}_t})\\ & =-\frac{C_3}{\ln 2}(T-{\tau }_{s(LUT)}-N{\tau }_{R(LUT)})\left\{N{\tau }_{R(LUT)}(P_s+P_c)+{\tau }_{R(LUT)}(P_R+P_c)\right\}\\ & -\frac{C_3}{\ln 2}(T-{\tau }_{s(LUT)}-N{\tau }_{R(LUT)})\left\{\left[{\pi }_i(1-P_{fa})+{\pi }_0(1-\stackrel{⌢}{P_d})\right](P_t+P_c)(T-{\tau }_{s(LUT)}-N{\tau }_{R(LUT)})\right\},\end{array}$$

(19)

where $C_3={\pi }_i(1-P_{fa}){\left(\frac{f_2{}_s}{{\sigma }^2{}_s+P_t{h}_s}\right)}^2+{\pi }_0(1-\stackrel{⌢}{P_d}){\left(\frac{f_2{}_s}{P_{PU}{h}_{PU}+P_t{h}_s+{\sigma }^2{}_s}\right)}^2$. Hence, $\frac{\partial f_2(P_t)}{\partial P_t}<0,f_2(P_t)$ decreases with P_t. For a particular value of P_t, there must be one unique value of $P_t{}^{†}$ for which $f_2(P_t)=0$. Therefore $\frac{\partial {\eta }_{EE}}{\partial P_t}\ge 0\mathrm{for}{P}_t\in (0,P_t{}^{\text{†}})\mathrm{and}\frac{\partial {\eta }_{EE}}{\partial P_t}<0for{P}_t\in (P_t{}^{†},\infty )$. Therefore the energy efficiency of the cognitive radio network ${\eta }_{EE}$ has one optimal value of $P_t$ that maximizes ${\eta }_{EE}$.

3. Energy Efficiency-Spectrum Efficiency Trade-Off

The quality of service should be guaranteed for secondary users, while practical applications are considered. We aimed to maximize the EE while satisfying SE constraints. First, we can find out the effect of ${\eta }_{SE}$ with respect to ${\tau }_{s(LUT)}$. From Equation (9), ${\eta }_{SE}={\eta }_{S{E}_1}+{\eta }_{S{E}_2}$. The first partial derivative w.r.t ${\tau }_{s(LUT)}$ is:

$$\frac{\partial {\eta }_{SE}}{\partial {\tau }_{s(LUT)}}=-\frac{{\pi }_i{R}_1}{T}\left[1-P_{ fa}(T-{\tau }_{s(LUT)}-N{\tau }_{R(LUT)})\frac{d{P}_{ fa}}{d{\tau }_{s(LUT)}}\right]-{\pi }_0{R}_2(1-\stackrel{⌢}{P_d})$$

(20)

where $\frac{d{P}_{ fa}}{d{\tau }_{s(LUT)}}$ can be calculated from Equation (15), although we have the following conditions to be satisfied, i.e., ${\lim }_{{\tau }_{s(LUT)}\to 0}\frac{\partial {\eta }_{SE}}{\partial {\tau }_{s(LUT)}}=\infty \mathrm{and}{\lim }_{{\tau }_{s(LUT)}\to T-N{\tau }_{R(LUT)}}\frac{\partial {\eta }_{SE}}{\partial {\tau }_{s(LUT)}}<0$.

From limits, it is clear that ${\eta }_{SE}$ increases and is a decreasing function of sensing time in the case of an immense amount of sensing time. Therefore, there should be one unique value of sensing time, that satisfies the condition of maximizing SE. It can be calculated by applying a double partial derivative of ${\eta }_{SE}$ w.r.t the sensing time:

$$\frac{{\partial }^2{\eta }_{SE}}{\partial {\tau }^2{}_{s(LUT)}}=\frac{{\pi }_i{R}_1}{T}\left[2\frac{d{P}_{ fa}}{d{\tau }_{s(LUT)}}-(T-{\tau }_{s(LUT)}-N{\tau }_{R(LUT)})\frac{d^2{P}_{ fa}}{d{\tau }^2{}_{s(LUT)}}\right]$$

(21)

where $\frac{d^2{P}_{ fa}}{d{\tau }^2{}_{s(LUT)}}$ can be evaluated from Equation (15). We can obtain that $\frac{{\partial }^2{\eta }_{SE}}{\partial {\tau }^2{}_{s(LUT)}}<0$, therefore, SE is an intrusive function of the sensing time. By equating $\frac{\partial {\eta }_{SE}}{\partial {\tau }_{s(LUT)}}=0$, we can get a unique sensing time value, which will generate maximum SE to satisfy the spectrum efficiency. We set the sensing efficiency greater than or equal to SE threshold $(\widehat{{\eta }_{SE}})$.

4. LUT Enabled Energy Harvested Optimization in 5G-CRN

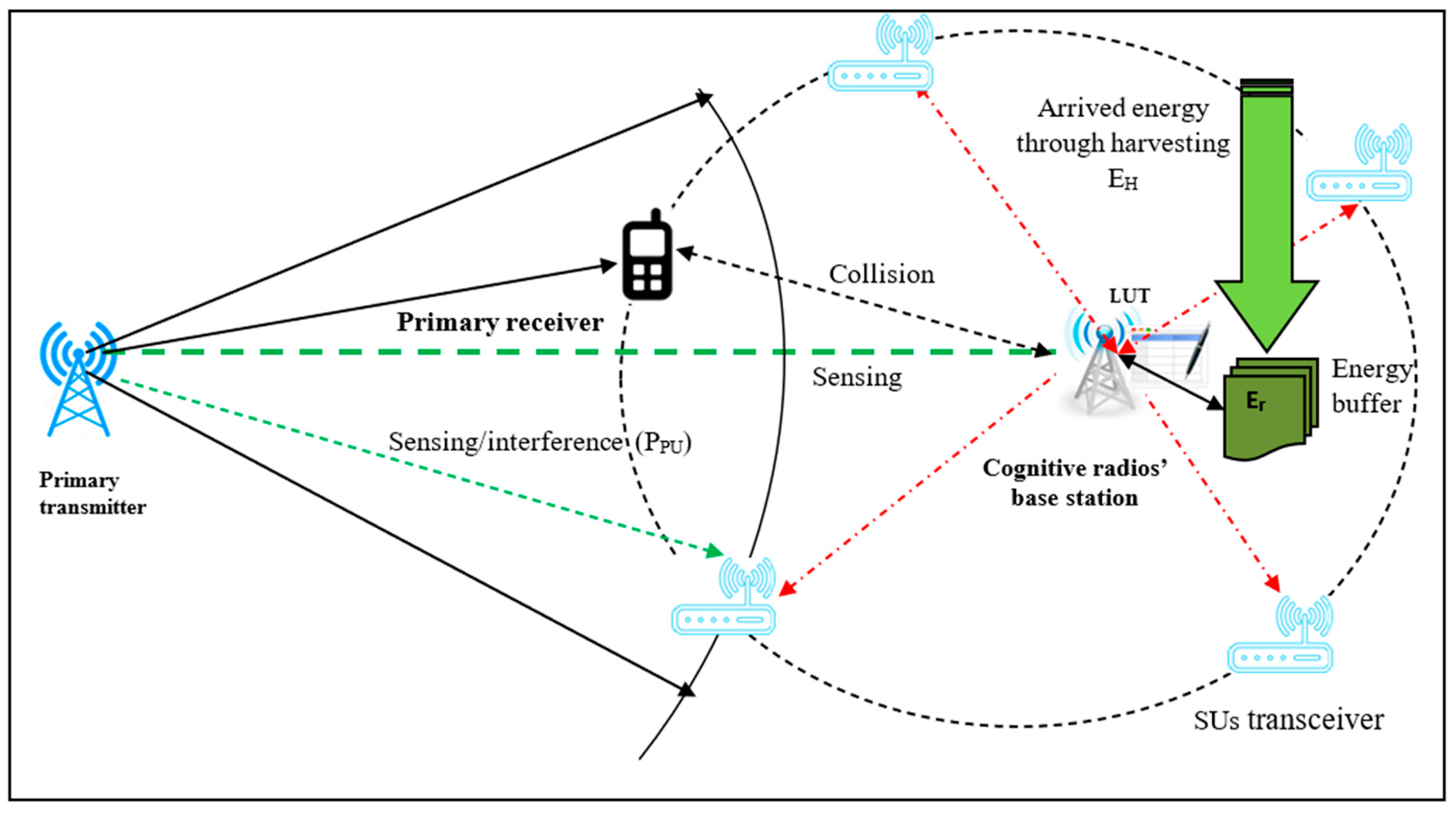
The energy-harvesting 5G-secondary system merged with the look-up table is as shown in Figure 3. The method comprises a primary transceiver and cognitive-based multiple transceivers. The presence of PUs is accomplished with the help of spectrum sensing. The LUT regularly updates the status of every channel. The energy harvesting concept is used, which acts as a cushion by storing the energy in the cognitive radio’s battery. To overcome a flooding situation, the capacity of these batteries is assumed to be infinite. Furthermore, energy leakage from this stored energy tank is zero.

E_H represents the energy stored in the buffer_, if the energy utilized when sensing is $(P_S{\tau }_{s(LUT)})$$P_T(T-{\tau }_{s(LUT)})$. M is the number of available channels, and N is the number of SUs. The Algorithm 1 for the sensing energy minimization is shown below.

Algorithm1: Look-up-table-based minimization of the sensing energy (LUT-MSE)

Pre-requisites: PD, M, N, Signal to noise ratio of primary users (SNRPUs), T, SUs sensing frame (δmin)

Step 1: Remaining transmission time [n] = T − ${\tau }_{s(LUT)}$ Ɐn

Step 2: for Chi = 1 to M do

Step 3: Sorting of all SUs sensing channels data in terms of decreasing SNRPUs.

Step 4: Start sensing for M channels by N SUs, for SNR = 0, k = 1

Step 5: while sensing < δmin do

Step 6: update LUT = index [k]

Step 7: For each SU monitor ${\tau }_{s(LUT)}$ calculate PD by applying step 3

Step 8: if ${\tau }_{s(LUT)}<\mathrm{total}\mathrm{time}\mathrm{remained}\left[\mathrm{n}\right]$ then

Step 9: if $\mathrm{total}\mathrm{time}\mathrm{remained}\left[\mathrm{n}\right]=\mathrm{total}\mathrm{time}\mathrm{remained}\left[\mathrm{n}\right]-{\tau }_{s(LUT)}$ then

Step 10: Increment the LUT [index] = LUT [index + 1]

Step 11: end if

Step 12: k = k + 1

Step 13: end while

Step 14 end for

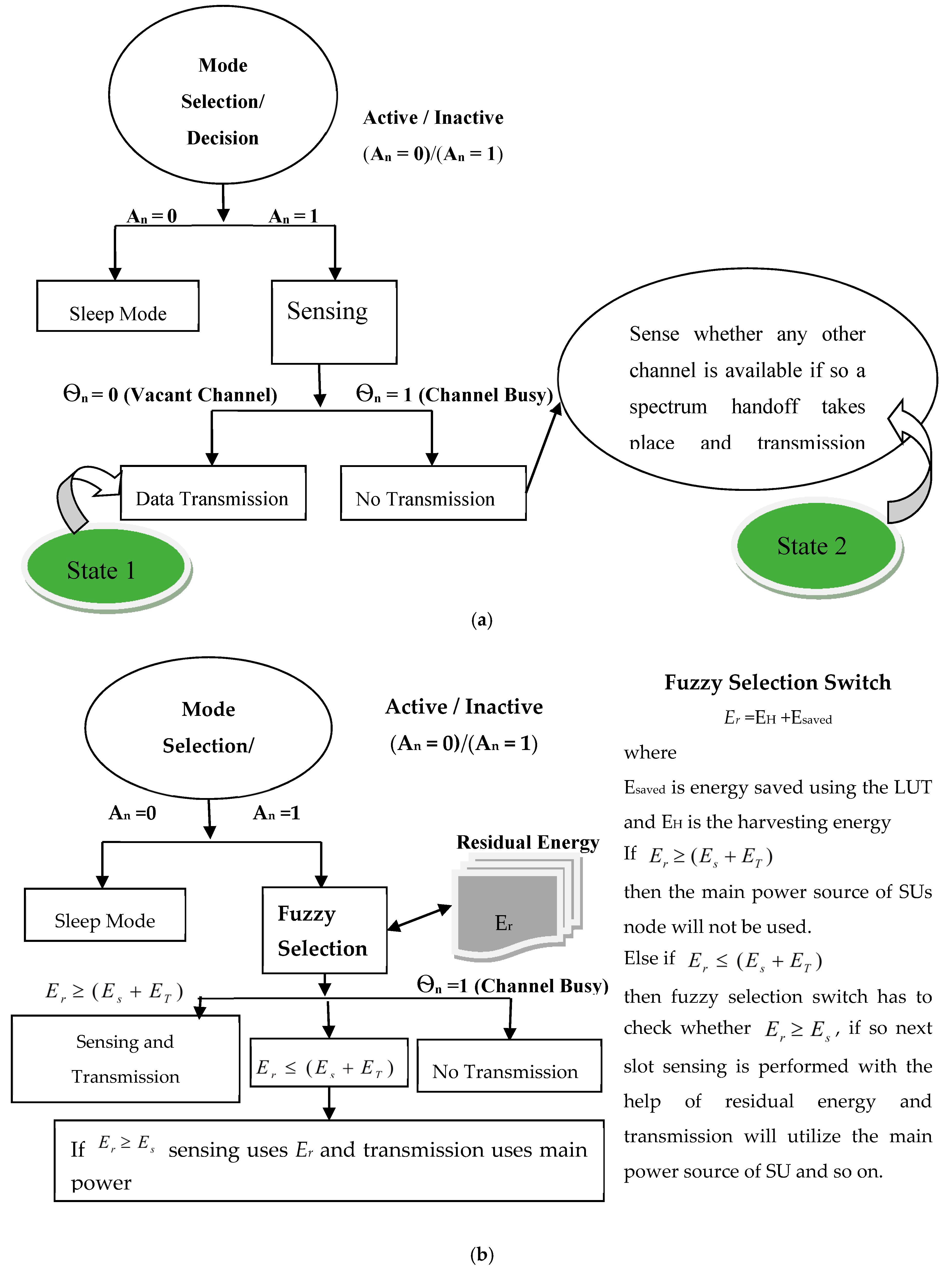
Conventionally, the radio is off at the initial level, i.e., the radio is not active (A_n = 0), thereby saving energy. Sensing of the channel starts immediately when the radio comes into “on” mode (A_n = 1) as shown in Figure 4a. While sensing if the channel is found to be busy and another channel near it is found to be idle, handoff occurs immediately to that idle channel, leading to the system’s good throughput.

The transmitter of the cognitive radio utilizes accessing through the greedy spectrum, and the remaining energy is used for the consecutive frame.

$$\begin{array}{cc}\hfill A_n\in 0& \left(\mathrm{radios}\mathrm{remain}\mathrm{inactive}\mathrm{due}\mathrm{to}\mathrm{insufficient}\mathrm{residual}\mathrm{energy}\right)\hfill \\ \hfill 1& \left(\mathrm{sensing}+\mathrm{transmission}\mathrm{takes}\mathrm{place}\right)\hfill \end{array}$$

(22)

such that

$$\begin{array}{cc}\hfill A_n=1,& E_r\ge P_S{\tau }_{s(LUT)}+P_T(T-{\tau }_{s(LUT)})\hfill \\ \hfill 0,& E_r<P_S{\tau }_{s(LUT)}+P_T(T-{\tau }_{s(LUT)}),\hfill \end{array}$$

(23)

where the total residual energy is equal to the Harvested energy

$$E_r=E_H$$

(24)

By using the LUT-based model, less energy is utilized during the sensing period and hence saves energy (E_Saved). Furthermore, the LUT incorporated EH model also saves E_.H. energy also, as shown in Figure 4b. Therefore, the total energy saved (residual energy) in a fixed frame (T), depending upon the amount of residual energy E_r = E_H +E_saved is left in the battery unit of the SUs. $P_s{\tau }_s$ helps in the calculation of the energy and the power used in sensing. Therefore minimizing ${\tau }_s$ will lead to overcoming two problems, namely less energy consumption while sensing and maximizing the transmission time, which improves the throughput of the system.

In the conventional approach, if E_r < E_s + E_T, then the whole E_r was left unutilized. Here we have proposed a novel fuzzy-based approach that will decide whether the residual energy is utilized for next slot sensing, transmission, or both. The fuzzy switch regularly checks whether the consumption of energy in sensing and transmitting is always less than the residual energy

$$E_r \ge (E_s+E_T)$$

(25)

As per Equation (25), if the amount of energy needed for sensing and transmitting is less than the residual energy, the Sus’ node power will not be used, and it will be saved for sensing the consecutive slot. Else if

$$E_r\le (E_s+E_T)$$

(26)

the fuzzy switch evaluates $E_r \ge E_s$, and if it is satisfied, the energy will be used in sensing, and energy will be saved in this way the main power is used for transmitting till the last transmission of data is complete.

5. Results

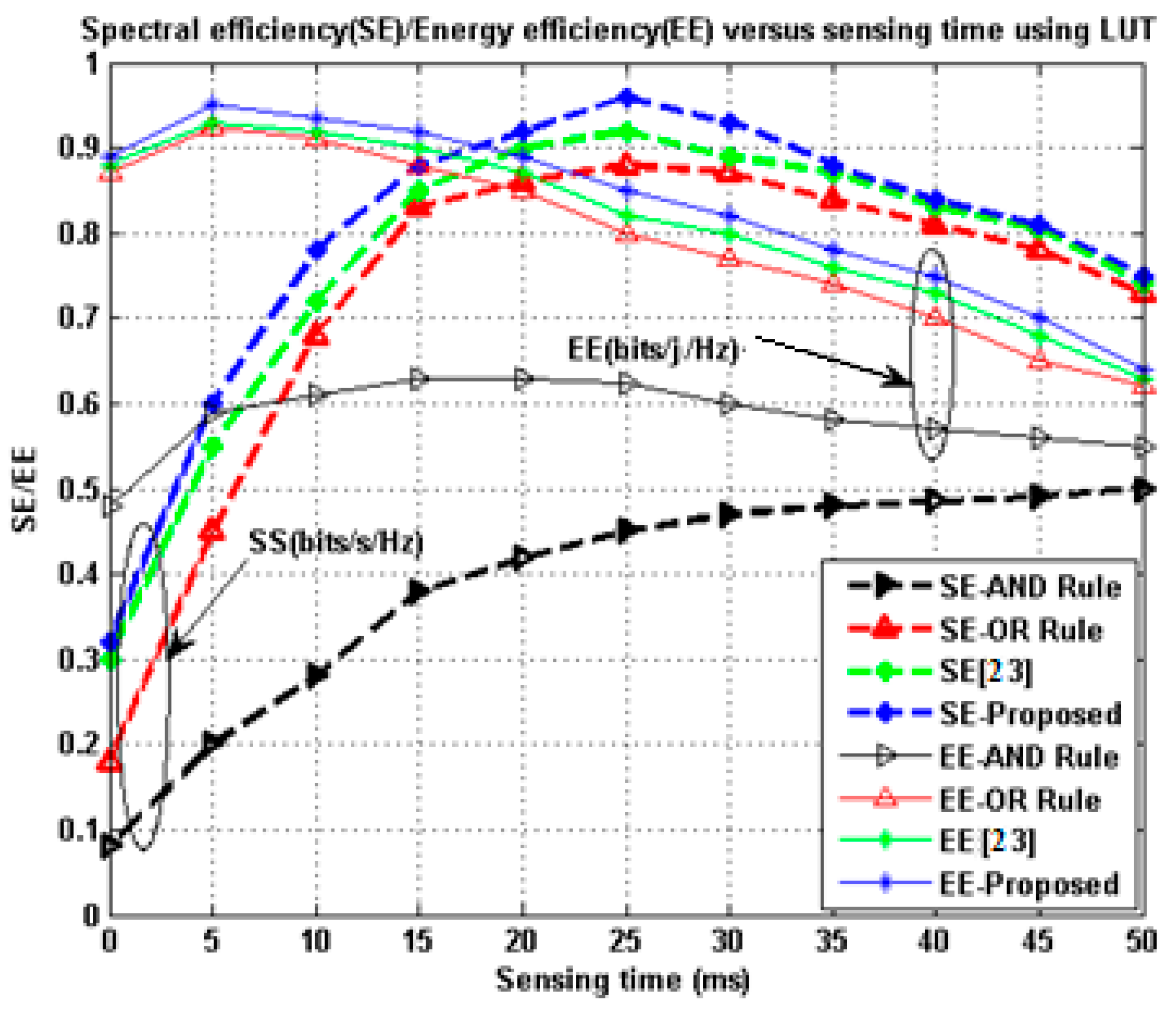
Investigations of the energy efficiency enhancement were carried out using a NS-2.31 simulator under a cognitive radio cognitive network (CRCN) environment. The effect of the sensing time on the SE and EE using different fusion rules can be observed in Figure 5. The EE and SE maximization can never co-exist, therefore, after the diligent trade-off, the optimal value of the EE and the SE is reported as 0.92 bit/J/Hz at sensing time ${\tau }_{s(LUT)}$ = 20 ms.

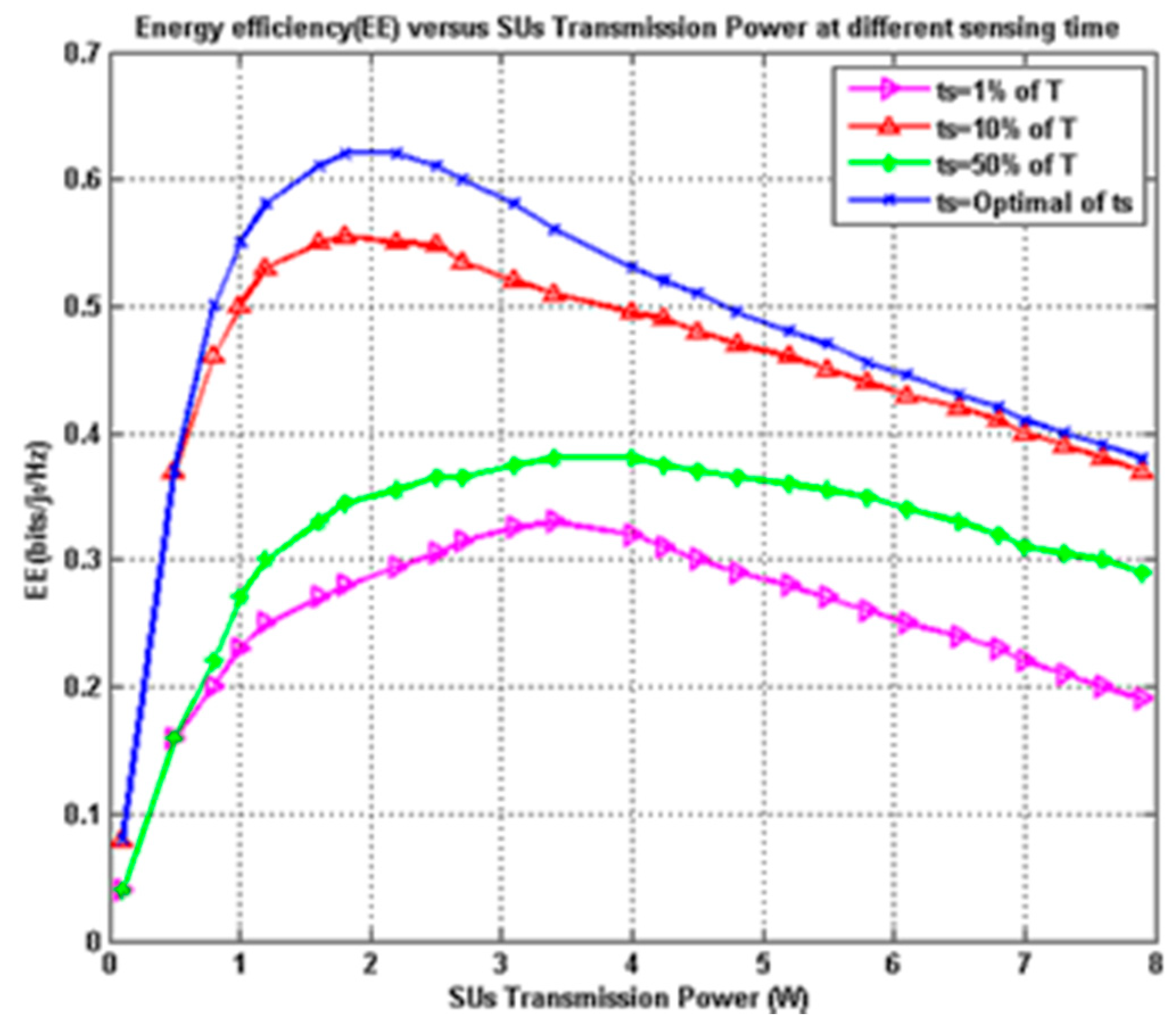
Figure 6 depicts the variation in energy efficiency w.r.t. the transmission power of SUs at different sensing time. By optimizing the sensing time, the energy efficiency of 63% was observed at a transmission power of 2 W.

To enhance the energy efficiency of the system ${\tau }_{s(LUT)}$ should be optimized using a neuro-fuzzy energy-aware unequal clustering scheme (NFEAUCS) algorithm for CSS in the near future.

Figure 7 shows the EE relation concerning sensing time using a LUT under different SU transmission power levels. We considered different solutions to provide EE i.e., P_t = 25%, 50%, 75% of P_t(max) and optimal transmission power. Figure 7 shows that the optimal value for the transmission power at ${\tau }_{s(LUT)}=3$ ms yielded a maximum energy efficiency of 58–60%.

Figure 8 shows the effect of the SU transmission power, signal to noise ratio of SUs, and sensing time on the energy efficiency. We considered six different sensing time cases as follows: 10%, 50%, and optimal sensing time. We also considered transmission powers as follows: 10%, 50%, and 100% of P_t(max) and optimal power. Solutions 1, 2, and 4 gave the worst EE since the time and power were fixed whereas, for solutions 3 and 5, the EE increased with an increase in the signal-to-noise ratio (SNR), but was almost constant for higher SNR (SNR > 4 dB) values. In solution 6, joint optimization (optimal τ_s(LUT) and optimal P_t) gave better results for low and high SNR, and reached a mark of 88% at the optimal sensing time and transmission power.

6. Conclusions

A 5G-CRN network’s effectiveness depends upon its lifetime, energy consumption, and the achieved throughput of information transmitted. As far as we know, no one has yet proposed an algorithm using LUT incorporated energy harvesting CRN to optimize SE and EE, and to provide an improved throughput system. The proposed method used in this study can take advantage of a look-up table and the energy harvesting concepts. Simulations were performed, and the results showed that adopting the new technique reduced the energy consumption and improved the spectrum efficiency resulting in an improved normalized achievable throughput. From the results of the simulations, we found that the proposed method outperformed existing methods. Energy-saving, energy consumption, the EE/SE trade-off, and achievable throughput regarding the sensing time of the proposed method were calculated using the energy efficiency and spectrum efficiency w.r.t. decision threshold(M). The proposed model achieved a maximum EE and SE, which was 0.92 bit/J/Hz at ${\tau }_{s(LUT)}$ = 20 ms. A further, optimal value of sensing time (typically 3 ms) was achieved, which yielded 58–60% EE.

On the other hand, 2 W for the transmission power of the SUs was the optimal power to achieve an EE of approximately 66%. Finally, we achieved a maximum energy efficiency (88%) by jointly optimizing the sensing time and optimizing the SU transmission power. This system can be used in the various real-time applications for the acquisition of data from pervasive networks. The proposed method is also helpful in telemedicine systems. The main drawback of the system is that we assumed the battery capacity to be infinite, which is an impractical scenario. This work can be further extended by taking finite batter capacity and using higher-level optimization techniques and soft computing techniques, such as NFEAUCS algorithm in the near future.