Abstract
The real world can be characterized as a complex network sto in symmetric matrix. Community discovery (or community detection) can effectively reveal the common features of network groups. The communities are overlapping since, in fact, one thing often belongs to multiple categories. Hence, overlapping community discovery has become a new research hotspot. Since the results of the existing community discovery algorithms are not robust enough, this paper proposes an effective algorithm, named Two Expansions of Seeds (TES). TES adopts the topological feature of network nodes to find the local maximum nodes as the seeds which are based on the gravitational degree, which makes the community discovery robust. Then, the seeds are expanded by the greedy strategy based on the fitness function, and the community cleaning strategy is employed to avoid the nodes with negative fitness so as to improve the accuracy of community discovery. After that, the gravitational degree is used to expand the communities for the second time. Thus, all nodes in the network belong to at least one community. Finally, we calculate the distance between the communities and merge similar communities to obtain a less- undant community structure. Experimental results demonstrate that our algorithm outperforms other state-of-the-art algorithms.
1. Introduction
Many complex systems exist in the form of networks in the real world, such as social networks [1,2], traffic networks [3,4], network sparsification [5] and protein interaction networks [6,7]. These complex systems can be characterized as complex networks sto in symmetric matrix for analysis and research. Entities in the complex network are represented by nodes, and the relationships between the entities are represented by edges [8,9]. Many researches based on complex networks have been investigated, such as social computing [10], network computation [11], and community discovery [12]. The community structure (module or cluster) is an important feature of a complex network, which means that the network is composed of several communities. The connections between the nodes in the community are very close, while the connections between the communities are relatively sparse [13]. The purpose of community discovery (or community detection [14]) is to mine community structures in a complex network. Community discovery can reveal the universal features of a complex network and help in understanding its topology accurately, which provides guidance for the use and transformation of the network and promotes the practical application of the network. Hence, community discovery has become one of the hotspots of complex network research [15] and various researches have been investigated, such as disjoint community detection [16,17], overlapping community detection [18], and multiobjective community detection [19].
Early researches on community discovery mainly focused on nonoverlapping communities, which assumed that each node belongs to only one community and there is no overlap of any two communities. Many representative algorithms have been proposed, such as the graph-partitioning-based method [20], label-propagation-based method [21], clustering method [22,23], and optimization method [24,25]. However, in the real world, things often have the characteristics of diversity. One thing often belongs to multiple categories and there may be overlap between communities. Therefore, overlapping community discovery has become a new research hotspot in recent years. Researches on overlapping community discovery can be divided into two categories: global-network-information-based and local-network-information-based methods.
The methods based on global network information aim to find the community structure in the whole network by optimizing a certain global objective function using whole connection information, which mainly include the link-based method [26,27] and the clique percolation method [28]. These methods can get better results in community discovery, but they have high time complexity and are not suitable for large-scale complex networks with numerous nodes. The methods based on local information aim to find the community structure starting from a node in the network by optimizing a certain local objective function using local connection information, which mainly include the label propagation method [29,30] and the local community expansion method [31,32]. Since the process of community discovery is only related to the local information in the network, the time complexity is low. Thus, these methods are suitable for large-scale complex networks. However, their disadvantage is that when the parameters of the algorithms change slightly, the results of community discovery change remarkably.
To tackle this problem, this paper proposes an overlapping community discovery method based on Two Expansions of Seeds (TES). The main features of this method are that the topological feature of the network (node degree centrality) is used to define the gravitational degree and the local maximum node is taken as the seed. The reason is that the greater the gravitational degree of the node, the greater its influence and the stronger its information transmission ability in the network is, which is beneficial for robust community discovery. Then, the seed is expanded by the greedy strategy based on the fitness function. When new nodes are added to the community, the community structure may be changed, thereby, there may be nodes with negative fitness. To avoid such nodes, this paper adopts the community cleaning strategy. After the expansion based on the fitness function, a community can cover most of the nodes in the network, but there are still a small number of nodes that cannot be assigned to any community because of the uction of community fitness. To solve this problem, this paper uses a gravitational function to expand the nodes that are not included in any community for the second time. Thus, all nodes belong to at least one community. Finally, by calculating the distance between communities and merging similar communities, we effectively uce the undant communities. The main contributions of this paper are as follows:
- We propose an overlapping community discovery algorithm named TES.
- TES employs the gravitational degree to find the local maximum nodes as the seeds and expands these seeds by the greedy strategy.
- Experimental results verify that our algorithm has better performance than other competitive algorithms.
The rest of this paper is organized as follows: Section 2 briefly summarizes the related work. Section 3 proposes our algorithm, named TES, which is composed of three parts: seed selecting, twice node expanding, and overlapping community merging. Section 4 reports the performance of TES. We draw the conclusion in Section 5.
2. Related Work
In this section, we will briefly review the categories of the overlapping community discovery methods first. Then, we will introduce the methods of local community optimization and expansion in detail and analyze the shortcomings of the-state-of-the-art algorithms. This paper aims to deal with the problem of unreasonable seed selection for local community optimization and expansion.
The overlapping community discovery methods can be divided into four categories: link-based method, clique percolation method, label-propagation-based method, and local-community-optimization-and-expansion-based method.
- The link-based method converts the cluste objects into network edges (or links) and deals with these edges by nonoverlapping partitions. Since a node is usually a vertex of multiple edges, if these edges belong to different linked communities, the node is an overlapping node. The LINK algorithm [27] is representative of this method. In addition, k-means was employed to expand seeds twice in dynamic community detection [33].
- The clique percolation method considers that a community is composed of a number of fully connected subgraphs. defined as a clique, and an adjacent clique forms a community. Since a node may belong to more than one clique, it is an overlapping node. However, the algorithm has higher constraints on interconnected conditions and depends on the selection of parameter k. The CPM algorithm [28] is representative of this method.
- The label-propagation-based method assigns a unique label to each node during initialization; updates the label and its membership by iteration; and finally, assigns the nodes with the same label to the same community. Apparently, if a node has multiple labels, the node is an overlapping node. The COPRA algorithm [29] is a representative of this method.
- The local-community-optimization-and-expansion-based method starts from the local communities, expands the communities gradually based on the optimization function, and forms cross-regions between multiple extensions, thus finding overlapping community nodes. The representative algorithms are LFM [31] and GCE [32]. In addition to the above algorithms, there are some classical methods, such as the semisupervised learning method [34]; deep learning method [35]; and the CONGA algorithm [36], which splits the clone node by itself and adds a virtual edge between the split nodes to find the overlapping nodes.
Among the abovementioned methods, the fourth one—local community optimization and expansion—becomes more and more popular. For example, the research in [21] found that taking the local maximum node defined by the degree centrality as the seed can discover higher quality communities and avoid instability at the same time. The research in [37] was about two methods to define the node influence: the community structure of social networks and the influence-based measure of node intimacy center, and took the nodes with great influence as the seeds. The EAGLE algorithm took the largest clique in the network as the seed and igno the second largest one, which has high time complexity [38]. Another paper [39] selected a group of nodes as seeds that were closely connected in the network, namely, an Egonet (hawk-eye network), but this method is more suitable for networks with a large global clustering coefficient. A seed set expansion method based on graph partitioning was proposed in [40] to find a group of nodes with low conductivity, and the node closest to the cluster was taken as a seed. The online social network (OSN) algorithm, as a multilever community discovery algorithm, combined user interests and cohesiveness to coarsen the initial network and found an initial community assignment using stochastic inference in the coarsest network [41]. All these methods use the local topology information of the network to optimize the local optimization function to find the community structure in the network. It does not need to know the global topology of the network, and shows certain advantages in large-scale networks. Therefore, seed selection is the foundation of this kind of method, which will affect the quality of community structure mining. The LFM algorithm [31] and the DEMON algorithm [32] expand the community by random seed selection, which inevitably causes the instability of community discovery. The GCE algorithm improved the LFM algorithm by mining k-cliques as the seed through the classic Bron–Kerbosch algorithm in the network [42]. In this method, cliques are fixed, but the seed selection depends on the selection of parameter k, which can easily cause the problem of low network coverage.
To solve the problem of unreasonable seed selection for local community optimization and expansion, this paper proposes an overlapping community discovery algorithm based on two expansions of seeds. A node with the local maximum gravitational degree defined by degree centrality is taken as a seed. This method has the advantages of a high-quality community and robust results, but the disadvantage is that these communities cannot cover the whole network. To overcome this problem, the communities are expanded for the second time to ensure that each node belongs to at least one community.
3. Proposed Method
In this section, we propose the TES algorithm, which is composed of three parts. The first part employs the gravitational degree defined by the network topological feature (degree centrality) to find the local maximum nodes as the seeds. The second part expands these seeds by the greedy strategy based on the fitness function. Then, the communities are expanded for the second time based on the gravitational function. The third part calculates the distance between the communities and merges the similar communities to get the final communities.
3.1. Seed Selection
In actual networks, some nodes are usually closely connected with other nodes, called central nodes, which contribute greatly to information transmission. They are usually scatte across the whole network and located in regions where the nodes are more closely connected. This is consistent with the fact that the nodes in a community are closely connected, while the connections between communities are sparse. Hence, the central nodes can be taken as the seeds. The centrality of a node reflects its centrality and importance in the network [43]. Inspi by the gravitational relationships in the dynamic social network [44], this paper proposes a gravitational degree based on degree centrality to measure the influence of the central nodes on other nodes.
Newton’s law of universal gravitation holds that any two particles are attracted by a force in the direction of the line between them. The gravitation is proportional to the product of their masses and inversely proportional to the square of their distance, as shown in Equation (1).
where g is the gravitational constant, and are the masses of two particles, and r is the distance between two particles.
In this paper, a network is represented by an undirected graph , where is a set of n vertices and is a set of m edges.
Definition 1.
Node centrality is the degree of a node, denoted by .
Definition 2.
If there is an edge between nodes and , then node is a neighbor of node . All neighbors of node are denoted by .
Definition 3.
To measure the similarity between nodes and , this paper employs the Jaccard similarity coefficient [45], denoted by .
Definition 4.
The distance between node and its neighbor is .
Definition 5.
The gravitation of node to its neighbor is .
Using the node degree to measure the quality of a node can reflect the ability of information transmission to its neighbor. The gravitational degree of to its neighbor is directly proportional to the node degree and inversely proportional to the distance between them.
Definition 6.
The gravitational degree of node is the sum of its gravitation to all nodes in the network.
The greater the gravitational degree of node , the greater its influence on the network. The stronger the information transmission ability of a node, the more likely it is to become a seed node.
An illustrative example is shown as follows:
Example 1.
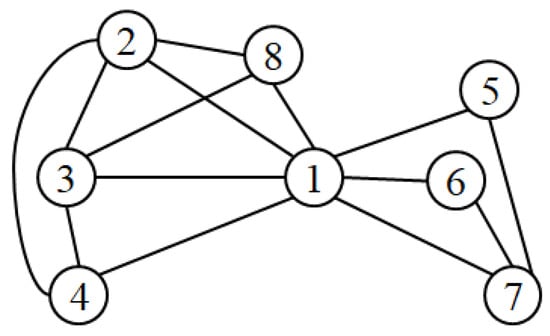
In Figure 1, node has 7 neighbors, i.e., = {2, 3, 4, 5, 6, 7, 8}. Node has 3 neighbors, i.e., = {1, 2, 3}. Thus, node centrality of nodes and are = 7 and = 3, respectively. and are {2, 3} and {1, 2, 3, 4, 5, 6, 7, 8}, respectively. Thus, and . Hence, ; .

Figure 1.
An illustrative network with 8 nodes and 14 edges.
Definition 7.
If the gravitational degree of a node is no less than that of all its neighbors, the node will be called the local maximum degree node of the network.
The local maximum node has a large gravitational degree and strong information transmission ability. Most of them are scatte in the network. Therefore, this paper selects the local maximum nodes as the seeds. The seed selection algorithm is shown in Algorithm 1. First, all nodes are marked as 0 and the gravitational degree of each node is calculated. The node with the largest gravitational degree is put into the seed set. Then, the node with the local maximum degree is marked as 1, and the node and its neighbors are moved out of the vertex set. Search for the next seed iteratively until all nodes have been marked and moved out of the vertex set.
| Algorithm 1 GetSeed. |
| Require: network ; |
| Ensure: seed set S; |
|
3.2. Community Discovery
For each seed in seed set S, this paper iteratively adds its neighbors to the community to discover natural communities. There are many ways to expand the community, including the minimum one norm [20], the label propagation method [29], and the fitness function method [31,42]. This paper employs the fitness function method since it can provide good results on real datasets.
Definition 8.
Community C is a subset of V. For community C in network , its neighbor is defined as
Definition 9.
For community C in network , its fitness is defined as
where and are the sum of the degrees of the nodes that are inside and outside community C, respectively. and , where is the number of edges inside community C. is an adjustment parameter.
in the fitness function is the resolution parameter, which can adjust the scale of the community discove. The smaller is, the greater the influence of . This will lead to a rapid increase of after adding node to community C. Therefore, community C can accept more nodes. When tends to be 0, the community may expand to cover the entire network. On the contrary, the larger is, the smaller the impact of . This will lead to the tiny increase of after adding node . Therefore, a small community is formed. When , . The more sparse the connection between community C and outside is, the smaller is and the larger is, which can reflect the local connection density of community C.
Example 2.
In Figure 1, suppose community C is composed of nodes 5, 6, and 7. = {1} since node 1 connects with community C. Node 8 does not belong to since it does not connect with community C. Suppose there is an edge between nodes 5 and 8, node 8 belongs to . is 4 since the degrees of nodes 5, 6, and 7 in community C are 1, 1, and 2, respectively, and 1 + 1 + 2 = 4. Another method is to count the number of edges in community C. There are 2 edges in community C, thus, . Similarly, .
Definition 10.
The fitness of node can be obtained as follows:
The disadvantage of this method is that although most of nodes can be assigned to the corresponding communities, some nodes fail to be assigned, thus resulting in low network coverage. Therefore, this paper expands the nodes that have not been assigned to the community for the second time. This is in accordance with the actual situation. For example, in a social network, everyone has friends and belongs to a circle of friends [37]. This paper assumes that each node belongs to at least one community. A gravitational function is defined by the ratio of the gravitation between nodes and the gravitational degree of nodes. The gravitation of node is the sum of the gravitational degrees between node and its neighbors. The more neighbors of node the community C contains, the greater the gravitation between the community and node is. The gravitational function is given as follows:
Definition 11.
The gravitation of community C to node is measu by the gravitational degree, and the gravitational function is
When the seed set is found in the first stage, the seed is expanded by the greedy strategy, that is, the local objective function of the community is maximized by adding node to the temporal community or deleting it from the community. We will show the principle of the algorithm as follows: We put a seed into temporal community C first. Then, we calculate the fitness of all its neighbors and add the maximum fitness neighbor into C, as shown in lines 3–7 of Algorithm 2. After adding the maximum fitness neighbor, the structure of the community will be changed. At this time, the fitness of each node for the new temporary community should be updated. If a node has a negative fitness, it will be removed from the community, as shown in lines 9–14 of Algorithm 2. Iterate the above expansion until the fitness decreases when any node is added. We store temporal community C into community set and remove these nodes from the network.
Obviously, when a community is expanded, the fitness of the nodes in the community and the neighbors need to be recalculated. To solve this problem, we adopt the following steps. If there is an edge between and , then is 1; otherwise, it is 0. The initials of and are 0. If node is added into the community, we adopt Equations (10) and (11). If node is removed from the community, we adopt Equations (12) and (13).
Example 3.
In Figure 1, according to Example 2, community C ={5, 6, 7}. Let node 1 be added into community C. According to Equation (10), , since when node 1 is added, there are three edges that are added into community C. According to Equation (11), . Let node 5 be removed from community C. According to Equation (12), , since there is one edge in community C that connects with node 5. According to Equation (13), .
Equation (8) is used to update the community fitness. In this way, we only need to know the degree of node and calculate of the nodes which are both in community C and neighbors of . To further speed up the calculation, we store and , which will be updated when temporal community C adds a new node or removes a node, as shown in lines 7–8 and 11–12 of Algorithm 2.
| Algorithm 2 GetNaturalcoms. |
| Require: network , seed set S, and parameter ; |
| Ensure: community set ; |
|
Finally, we expand nodes for the second time. If a node does not belong to any community, the node is merged into the community with the greatest gravitation, as shown in Algorithm 3.
| Algorithm 3 ExpandingSecond. |
| Require: node set V, and community set ; |
| Ensure: community set ; |
|
3.3. Merging Overlapping Communities
In a nonoverlapping community, a node belongs to only one community [46], while a node may belong to multiple communities in an overlapping community. Therefore, there may be similarities between two communities. When a certain similarity is reached, the excessive overlapping phenomenon will occur, resulting in a undant community [47]. Hence, after discovering the communities, this paper defines a measure of community distance which is used to discover and merge the overlapping communities to simplify the community structure.
Definition 12.
The distance between communities and is
In this paper, is the threshold of the distance parameter. If , communities and are merged into one community since they overlap excessively. The Merge_Overlap algorithm is shown in Algorithm 4.
To avoid invalid calculations, we adopt the principle of inverted index to prune invalid detection of overlapping communities. Therefore, set is used to store the communities in which node belongs. An illustrative example is shown as follows:
Suppose we have 3 communities: , , and . We know that , , and . To obtain the overlapping community of , we calculate = since . Therefore, communities and are two overlapping communities. It is not necessary to calculate the distance between communities and . Therefore, the inverted index is an effective pruning strategy.
According to the above example, we should create set at first, as shown in lines 1–7 of Algorithm 4. Apparently, if the number of elements in is greater than 1, it indicates that node belongs to multiple communities and is an overlapping node. We determine whether the communities in overlap or not, as shown in lines 8–19 of Algorithm 4.
To sum up, Algorithm 5 presents the overlapping community discovery algorithm based on two expansions of seeds.
| Algorithm 4 MergeOverlap. |
| Require: network , community set , and parameter ; |
| Ensure: the new community set ; |
|
| Algorithm 5 TES. |
| Require: network , parameter , and parameter ; |
| Ensure: community set , community set to which the node belongs; |
|
3.4. Theoretical Analysis
The space complexity and time complexity of TES are and , respectively, where k, n, and m are the number of seeds, nodes, and edges in G, respectively. The reason is shown as follows:
The space complexity of network G is . The space complexity of all neighbors of each node is since each edge should be calculated. Thus, the time complexity of of each node is also . Further, the space complexity and time complexity of , , and are also . Obviously, the time complexity of of each node is and the space complexity of is . Hence, the time complexity of lines 2–5 in Algorithm 1 is . Since each node will be checked once, the time complexity of lines 6–13 is . Therefore, both the space complexity and time complexity of Algorithm 1 are .
Suppose we find k seeds, where . When a node is added into or removed from a community, no more than n edges are checked. Thus, the time complexity of Equations (10)–(13) are . Hence, the time complexity of Equations (7)–(9) are also . A node can be assigned into no more than k communities. Therefore, the time complexity of Algorithm 2 is .
Suppose there are t nodes which are expanded twice, where . Each node will be added into each community once. Thus, the time complexity of lines 3–5 is . Therefore, the time complexity of Algorithm 3 is .
Obviously, the time complexity of lines 1–7 of Algorithm 4 is since there are k communities and n nodes. Similarly, the time complexity of lines 8–19 of Algorithm 4 is also .
Apparently, each community has no more than n nodes. Thus, the space complexities of these communities are . Hence, the space complexities of Algorithms 2, 3, and 4 are .
Since , the time complexity of TES is and the space complexity of TES is .
4. Experimental Results and Analysis
4.1. Baseline Methods
To verify the performance of TES, three state-of-the-art algorithms are selected: CONGA [36], COPRA [29], and LFM [31]. In addition, the TES algorithm has three key steps: searching for seeds, discovering communities based on two expansions, and merging overlapping communities. The two expansions of communities include the first expansion of the community based on the fitness function and the second expansion of the community based on the gravitational function. The community expansion based on the fitness function includes community cleaning. To verify the reasonability of these parts, four comparative algorithms—TES_Seed, TES_Unclean, TES_Fitness, and TES_Unmerge—are constructed, and their specific descriptions are shown in Table 1.

Table 1.
Comparative algorithms.
4.2. Benchmark Datasets
In this paper, we compare the performance of the TES algorithm on five real network datasets. The real network datasets are shown in Table 2.

Table 2.
Real network datasets.
4.3. Evaluation Criteria
To evaluate the performance of the proposed algorithm, this paper employs extended modularity [38] and overlapping modularity [53] as the evaluation criteria.
The main idea of modularity (Q) is that if a subgraph is a community, the number of edges of its internal nodes is greater than that of a randomly generated subgraph [54]. Unfortunately, the Q function can only be used to evaluate nonoverlapping communities. To evaluate the overlapping community structure, extend modularity () was proposed based on the Q function [38]. The function is shown as Equation (15).
where m is the total number of edges of the network, K is the number of communities discove, is the degree of node , is the number of communities to which node belongs, and A is the adjacency matrix of the network. If there is an edge between and , then ; otherwise, .
Overlapping modularity () is another method to evaluate the structure of overlapping communities [53], as shown in Equation (16):
where m is the total number of edges of the network, A is the adjacency matrix of the network, is the strength of an edge which belongs to community C, is the in-degree of node j, and is the out-degree of node i.
and are both in the interval [0,1]. The greater they are, the better the community discovery results will be.
4.4. Parameter Selection
The selection of parameters will affect the results of community discovery. The TES algorithm has two parameters, and . According to Equation (7), is a special value. According to Equation (14), is in the range of (0,1). Thus, we select in the range of [0.8, 1.5] and in the range of [0.1, 0.9], and the step is 0.1. is employed to evaluate the performance. The experimental results are shown in Figure 2 and Figure 3.
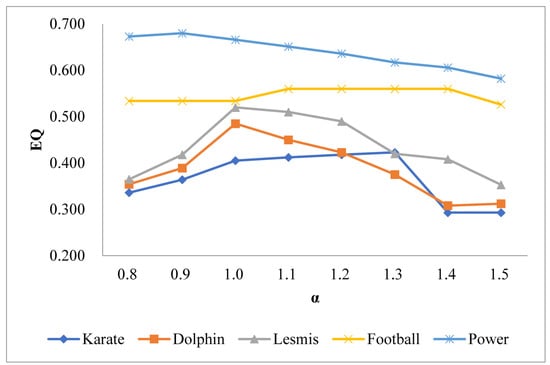
Figure 2.
Comparison of extend modularity () with different on real networks.
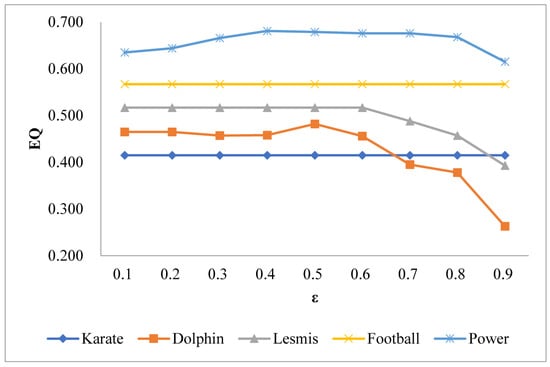
Figure 3.
Comparison of with different on real networks.
Figure 2 and Figure 3 show the trend of along with the increase of parameters and , respectively. In general, the influence of on community discovery is greater than that of . In Figure 2, it can be seen that with the increase of , increases first and then decreases. For different networks, the maximum is obtained with different . The maximum values are achieved at on the Karate and Football networks, on the Dolphin and Lesmis networks, and on the Power network. From Figure 3, it can be seen that has little influence on the Karate network and the Football network, but has the greatest impact on the Dolphin network. values of the Dolphin and Lesmis networks are not significantly changed when . However, when , decreases rapidly as increases. All five networks obtain the maximum when .
In conclusion, for five real networks, when and for the Karate and Football networks, and for the Dolphin and Lesmis networks, and and for the Power network, the optimal community discovery results can be achieved. Therefore, in the rest of this paper, TES selects the above parameters for different networks.
4.5. Performance Evaluation
4.5.1. Module Performance Evaluation
In this subsubsection, we verify that each module has an effect on the improvement of the proposed algorithm. The experiments are carried out on five real networks, and evaluation criteria is selected to evaluate the influence of each module on the TES algorithm. The parameters of TES_Seed, TES_Unclean, TES_Fitness, and TES_Unmerge are the same as those of TES. The experimental results are shown in Table 3. The coverage rates of the nodes with only one expansion and two expansions are calculated, respectively. Therefore, TES_Fitness with one expansion and TES with two expansions are selected. The coverage rates of the two algorithms are reported in Table 4.

Table 3.
Comparison of .

Table 4.
Comparison of the coverage rate.
From Table 3, it can be seen that all four parts of the TES algorithm have impacts on the TES algorithm and have different influence on different networks. Therefore, TES outperforms the other four algorithms. For example, TES gets 0.675 on Power dataset, which is larger than that obtained by the other four algorithms. According to Equation (15), we know that the greater is, the better the community discovery results will be. The reasons are as follows: It should be noticed that the results of TES_Seed in Table 3 are not robust. The reason is that TES_Seed randomly selects the seed to expand, resulting in different community discovery results. Thus, the results are different even under the same parameters. Hence, the results of TES_Seed in Table 3 are the average value of 20 times. After the first community expansion based on the fitness function, TES_Unclean does not clean the community. When the community structure changes, there may be negative fitness nodes in the community, which will effect the quality of the community discovery results. TES_Unmerge has the most significant impact on the algorithm, which proves that excessive overlapping between communities has a great impact on community structure.
TES_Fitness expands the community based on the seeds only once, which leads to the decrease of and affects the coverage rate of network nodes. From Table 4, we know that the coverage rate of TES_Fitness are all less than 1. The reason is as follows: For complex networks with fewer nodes, the coverage rate of the nodes can be high with only one expansion. However, with the increase of the nodes, the network scale becomes larger and larger, and the coverage rate with only one expansion becomes lower and lower. After two expansions of the community, the TES algorithm can cover all nodes in the network completely, and a high coverage rate of 1.00 can be achieved for a large network such as Power.
Hence, we can safely say that the four parts of the TES algorithm are all very important. The community discovery result is robust since the local maximum node is selected as the seed based on the gravitational degree. Community cleaning can avoid negative fitness nodes when the community structure changes. The natural community can significantly increase the coverage rate of the network nodes through two expansions, and the merging of the overlapping communities can deal with undant communities effectively. The four parts can effectively improve the quality of community discovery.
4.5.2. Algorithm Performance Evaluation
To report the performance of the TES algorithm, this paper selects three state-of-the-art algorithms: the CONGA algorithm, based on the splitting method for overlapping community discovery; the COPRA algorithm, based on the label propagation method; and the LFM algorithm, based on local community optimization and expansion. The parameter of CONGA is community number c, which needs to be determined according to the modularity degree function. The parameter of COPRA is the label length v, which is from 2 to 8 with steps of 1. The parameter of LFM is the resolution parameter , which is from 0.8 to 1.5 with steps of 0.1. For each algorithm, we select the best results as the final results shown in Figure 4 and Figure 5.
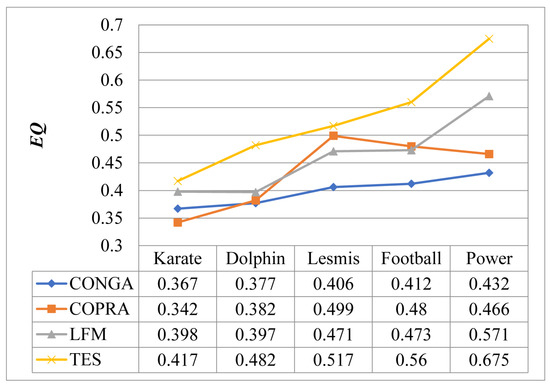
Figure 4.
Comparison results of on different networks.
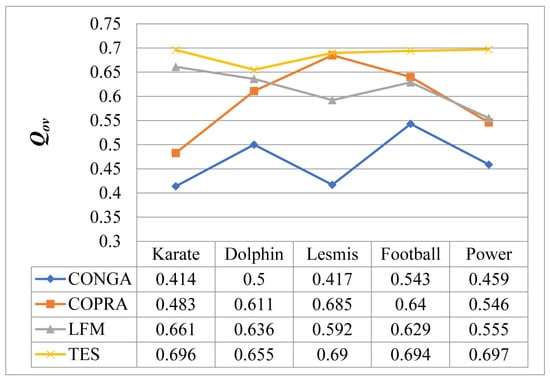
Figure 5.
Comparison results of overlapping modularity () on different networks.
From Figure 4 and Figure 5, TES outperforms all three competitive algorithms since both and obtained by TES are better than those of the other three algorithms on the five datasets. For example, from Figure 4, we know that of TES is 0.417 on the Karate network, while the other three algorithms are all less than 0.4. Similarly, of TES is 0.697 on the Power network, while the other three algorithms are all less than 0.56. As we know, the greater and are, the better the community discovery results will be. Hence, the community discovery results of TES are significantly improved compa with the other three algorithms. The reason is that the natural community discovery is based on local community optimization, and the expansion is only related to the local topology structure of the network, not the global topology of the whole network. Although the LFM algorithm is based on local community optimization, and values achieved by the LFM algorithm are lower than that of the COPRA algorithm on the Lesmis and Football networks, but higher than that of the COPRA algorithm on the other three networks. The reason is that the LFM algorithm randomly selects seeds, meaning that the community structure discove is not robust.
In summary, TES has better performance than all competing algorithms.
4.6. Case Study
To further clarify the performance of TES, the Karate network is employed to show the community discovery results. Figure 6 shows the community discovery results obtained by the TES algorithm. The seeds are nodes 1, 17, 26, and 34, and four communities are obtained. Node 10 is the overlapping node of the grey and yellow communities.
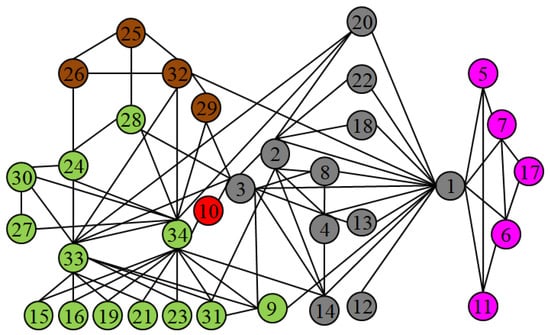
Figure 6.
Community discovery result by TES algorithm on the Karate network. The seeds are nodes 1, 17, 26, and 34, and four communities are obtained. Node 10 is the overlapping node of the gray and yellow communities.
It can be seen from Figure 6 that the TES algorithm finds four communities, while the CONGA and COPRA algorithms both discover two communities and the LFM algorithm discovers five communities. Compa with the CONGA and COPRA algorithms, the partition of the network by TES algorithm is more detailed. For example, community {5,6,7,11,17} is closely related to node 1, but the nodes inside community {5,6,7,11,17} have stronger connection relationship with each other. The TES algorithm can mine small communities in large-scale communities, mainly because in the first part of the algorithm, the center node with strong information transmission ability is taken as the seed. Although the LFM algorithm discovers five communities, the seed does not have centrality since the LFM algorithm randomly selects seeds. The expanded community structure locality is poor, and a community is included in another community. The reason for this kind of situation is that the LFM algorithm does not detect the merged undant community, which illustrates the importance of detecting overlapping community in the TES algorithm.
5. Conclusions
In this paper, we propose an overlapping community discovery algorithm, named TES, which has three parts. In the first part, the local maximum node is taken as the seed based on the gravitational degree. The second part discovers the natural community by two expansions. The community is expanded based on the fitness function. After adding a new node, the community is cleaned. The second expansion is based on the gravitational function. The third part examines and merges the overlapping communities. To verify the reasonability of these parts, four comparative algorithms, TES_Seed, TES_Unclean, TES_Fitness, and TES_Unmerge, are proposed. Besides these four algorithms, three state-of-the-art algorithms: CONGA, COPRA, and LFM, are employed. Experimental results on five real networks report that TES outperforms all these competitive algorithms.
Author Contributions
Conceptualization, Y.L. and Y.W.; methodology, Y.L. and J.H.; validation, J.H., Y.L. and Y.W.; investigation, R.L.; writing—original draft preparation, J.H.; writing—review and editing, Y.L. and Y.W.; supervision, Y.W. and R.L.; funding acquisition, R.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The National Social Science Fund of China under grant number 18BGL191.
Informed Consent Statement
Informed written consent was obtained from the authors for publication of this paper.
Data Availability Statement
Data was obtained from http://www-personal.umich.edu/mejn/netdata/.
Conflicts of Interest
The authors declare that there is no conflict of interest regarding the publication of this article.
References
- Gu, K.; Wang, L.; Yin, B. Social community detection and message propagation scheme based on personal willingness in social network. Soft Comput. 2019, 23, 6267–6285. [Google Scholar] [CrossRef]
- He, J.; Liu, H.; Zheng, Y.; Tang, S.; He, W.; Du, X. Bi-labeled LDA: Inferring interest tags for non-famous users in social network. Data Sci. Eng. 2020, 5, 27–47. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Zhu, H.; Li, J.; Yan, W.; Wu, Y. IBAS: Index based A-star. IEEE Access 2018, 6, 11707–11715. [Google Scholar] [CrossRef]
- Dolgorsuren, B.; Xu, W.; Khan, K.U.; Jeong, B.S.; Lee, Y.K. SP2: Spanner construction for shortest path computation on streaming graph. In Proceedings of the Sixth International Conference on Emerging Databases: Technologies, Applications, and Theory, Jeju Island, Korea, 17–19 October 2016; pp. 43–50. [Google Scholar]
- Batjargal, D.; Khan, K.U.; Lee, Y.K. EM-FGS: Graph sparsification via faster semi-metric edges pruning. Appl. Intell. 2019, 49, 3731–3748. [Google Scholar] [CrossRef]
- Wu, Y.; Tong, Y.; Zhu, X.; Wu, X. NOSEP: Nonoverlapping sequence pattern mining with gap constraints. IEEE Trans. Cybern. 2018, 48, 2809–2822. [Google Scholar] [CrossRef]
- Hai, M.; Li, H.; Ma, Z.; Gao, X. Algorithm for detecting communities in complex networks based on Hadoop. Symmetry 2019, 11, 1382. [Google Scholar] [CrossRef]
- Shi, Q.; Shan, J.; Yan, W.; Wu, Y.; Wu, X. NetNPG: Nonoverlapping pattern matching with general gap constraints. Appl. Intell. 2020, 50, 1832–1845. [Google Scholar] [CrossRef]
- Wu, Y.; Shen, C.; Jiang, H.; Wu, X. Strict pattern matching under non-overlapping condition. Sci. China Inf. Sci. 2017, 60, 012101. [Google Scholar] [CrossRef]
- Bu, Z.; Li, H.J.; Zhang, C.; Cao, J.; Li, A.; Shi, Y. Graph k-means based on leader identification, dynamic game and opinion dynamics. IEEE Trans. Knowl. Data Eng. 2019. [Google Scholar] [CrossRef]
- Li, H.J.; Bu, Z.; Wang, Z.; Cao, J.; Shi, Y. Enhance the performance of network computation by a tunable weighting strategy. IEEE Trans. Emerg. Top. Comput. Intell. 2018, 2, 214–223. [Google Scholar] [CrossRef]
- Chen, D.; Fu, Y.; Shang, M. An efficient algorithm for overlapping community detection in complex networks. In Proceedings of the WRI Global Congress on Intelligent Systems, Xiamen, China, 19–21 May 2009; pp. 244–247. [Google Scholar]
- Atzmueller, M.; Doerfel, S.; Mitzlaff, F. Description-oriented community detection using exhaustive subgroup discovery. Inf. Sci. 2016, 329, 965–984. [Google Scholar] [CrossRef]
- Geng, X.; Lu, H.; Sun, J. Network structural transformation-based community detection with autoencoder. Symmetry 2020, 12, 944. [Google Scholar] [CrossRef]
- Chen, J.; Liu, M.; Liu, X. Research on of overlapping community detection algorithm based on tag influence. Clust. Comput. 2019, 22, 6669–6679. [Google Scholar] [CrossRef]
- Fortunato, S.; Hric, D. Community detection in networks: A user guide. Phys. Rep. 2016, 659, 1–44. [Google Scholar] [CrossRef]
- Javed, M.A.; Younis, M.S.; Latif, S.; Qadir, J.; Baig, A. Community detection in networks: A multidisciplinary review. J. Netw. Comput. Appl. 2018, 108, 87–111. [Google Scholar] [CrossRef]
- Xie, J.; Kelley, S.; Szymanski, B.K. Overlapping community detection in networks: The state-of-the-art and comparative study. ACM Comput. Surv. 2013, 45, 1–35. [Google Scholar] [CrossRef]
- Guerrero, M.; Gil, C.; Montoya, F.G.; Alcayde, A.; Baños, R. Multi-objective evolutionary algorithms to find community structures in large networks. Mathematics 2020, 8, 2048. [Google Scholar] [CrossRef]
- Li, Y.; He, K.; Kloster, K.; Bindel, D.; Hopcroft, J. Local spectral clustering for overlapping community detection. ACM Trans. Knowl. Discov. Data 2018, 12, 17. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, S.; Chen, G.; Yu, Z. Overlapping community discovery based on node hierarchy and label propagation gain. Pattern Recognit. Artif. Intell. 2015, 28, 289–298. [Google Scholar]
- Liu, H.; Ling, H.; Jian, J.; Chen, L. Overlapping community discovery algorithm based on hierarchical agglomerative clustering. Int. J. Pattern Recognit. Artif. Intell. 2015, 32, 1850008. [Google Scholar] [CrossRef]
- Xu, M.; Li, Y.; Li, R.; Zou, F.; Gu, X. EADP: An extended adaptive density peaks clustering for overlapping community detection in social networks. Neurocomputing 2019, 337, 287–302. [Google Scholar] [CrossRef]
- Guerrero, M.; Baños, R.; Gil, C.; Montoya, F.G.; Alcayde, A. Evolutionary algorithms for community detection in continental-scale high-voltage transmission grids. Symmetry 2019, 11, 1472. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Wang, X.; Zhao, Y.; Lu, X.; Liu, D. Community detection based on differential evolution using social spider optimization. Symmetry 2017, 9, 183. [Google Scholar] [CrossRef]
- Sun, H.; Liu, J.; Huang, J.; Wang, G.; Jia, X.; Song, Q. LinkLPA: A link-based label propagation algorithm for overlapping community detection in networks. Comput. Intell. 2017, 33, 308–331. [Google Scholar] [CrossRef]
- Ahn, Y.; Bagrow, J.; Lehmann, S. Link communities reveal multiscale complexity in networks. Nature 2010, 466, 761. [Google Scholar] [CrossRef]
- Palla, G.; Derenyi, I.; Farkas, I.; Vicsek, T. Uncovering the overlapping community structure of complex networks in nature and society. Nature 2005, 435, 814–818. [Google Scholar] [CrossRef] [PubMed]
- Gregory, S. Finding overlapping communities in networks by label propagation. New J. Phys. 2010, 12, 2011–2024. [Google Scholar] [CrossRef]
- Kianian, S.; Khayyambashi, M.; Movahhedinia, N. Semantic community detection using label propagation algorithm. J. Inf. Sci. 2015, 42, 166–178. [Google Scholar] [CrossRef]
- Lancichinetti, A.; Fortunato, S.; Kertész, J. Detecting the overlapping and hierarchical community structure of complex networks. New J. Phys. 2008, 11, 19–44. [Google Scholar] [CrossRef]
- Coscia, M.; Rossetti, G.; Giannotti, F.; Pedreschi, D. DEMON: A local-first discovery method for overlapping communities. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 615–623. [Google Scholar]
- Cheraghchi, H.S.; Zakerolhosseini, A. Toward a novel art inspi incremental community mining algorithm in dynamic social network. Appl. Intell. 2017, 46, 409–426. [Google Scholar] [CrossRef]
- Yang, L.; Cao, X.; He, D.; Wang, C.; Wang, X.; Zhang, W. Modularity based community detection with deep learning. In Proceedings of the International Joint Conference on Artificial Intelligence, New York, NY, USA, 9–15 July 2016; pp. 2252–2258. [Google Scholar]
- Yang, L.; Cao, X.; Jin, D.; Wang, X.; Meng, D. A unified semi-supervised community detection framework using latent space graph regularization. IEEE Trans. Cybern. 2017, 45, 2585–2598. [Google Scholar] [CrossRef] [PubMed]
- Gregory, S. An algorithm to find overlapping community structure in networks. In In Proceedings of the European Conference on Principles and Practice of Knowledge Discovery in Databases, Warsaw, Poland, 17–21 September 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 91–102. [Google Scholar]
- Maryam, H.; Kamran, Z.; Ahmad, R. A community-based approach to identify the most influential nodes in social networks. J. Inf. Sci. 2017, 43, 204–220. [Google Scholar]
- Shen, H.; Cheng, X.; Cai, K.; Hu, M. Detect overlapping and hierarchical community structure in networks. Phys. A Stat. Mech. Appl. 2009, 388, 1706–1712. [Google Scholar] [CrossRef]
- Gleich, D.; Seshadhri, C. Vertex neighborhoods, low conductance cuts, and good seeds for local community methods. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 597–605. [Google Scholar]
- Whang, J.; Gleich, D.; Dhillon, I. Overlapping community detection using seed set expansion. In Proceedings of the 22nd ACM International Conference on Information Knowledge Management, San Francisco, CA, USA, 27 October–1 November 2013; pp. 2099–2108. [Google Scholar]
- Su, C.; Guan, X.; Du, Y.; Wang, Q.; Wang, F. A fast multi-level algorithm for community detection in directed online social networks. J. Inf. Sci. 2018, 44, 392–407. [Google Scholar] [CrossRef]
- Lee, C.; Reid, F.; Mcdaid, A.; Hurley, N. Detecting highly overlapping community structure by greedy clique expansion. In Proceedings of the fourth SNA-KDD Workshop on Social Network Mining and Analysis, Washington, DC, USA, 25 July 2010. [Google Scholar]
- Cai, G.; Wang, R.; Liu, G. Hierarchical overlapping community discovery algorithm based on node purity. In Proceedings of the International Conference on Intelligent Information Processing, Haikou, Hainan, China, 14–15 July 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 248–257. [Google Scholar]
- Liu, J.; Du, Y.J.; Li, Q.; Fu, C. Social community evolution by combining gravitational relationship with community structure. Intell. Data Anal. 2018, 22, 1143–1161. [Google Scholar] [CrossRef]
- Li, Y. A new vertex similarity metric for community discovery: A distance neighbor model. In Asian Conference on Intelligent Information and Database Systems; Springer: Berlin/Heidelberg, Germany, 2011; pp. 228–237. [Google Scholar]
- Wu, Y.; Zhu, C.; Li, Y.; Guo, L.; Wu, X. NetNCSP: Nonoverlapping closed sequential pattern mining. Knowl. Based Syst. 2020, 196, 105812. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, G.; Nan, Y.; Zeng, Q. Semi-supervised local expansion method for overlapping community detection. Comput. Res. Dev. 2016, 53, 1376–1388. [Google Scholar]
- Zachary, W.W. An information flow model for conflict and fission in small groups. J. Anthropol. Res. 1997, 33, 452–473. [Google Scholar] [CrossRef]
- Lusseau, D.; Schneider, K.; Boisseau, O.J.; Haase, P.; Slooten, E.; Dawson, S.M. The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations. Behav. Ecol. Sociobiol. 2003, 54, 396–405. [Google Scholar] [CrossRef]
- Knuth, D.E. The Stanford GraphBase: A Platform for Combinatorial Computing; ACM Press: New York, NY, USA, 1993. [Google Scholar]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of small-world networks. Nature 1998, 93, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Nicosia, V.; Mangioni, G.; Carchiolo, V.; Malgeri, M. Extending the definition of modularity to directed graphs with overlapping communities. J. Stat. Mech. Theory Exp. 2009, 3, 3166–3168. [Google Scholar] [CrossRef]
- Newman, M.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).