Abstract
As a symmetrical structure in track system, the dynamic properties of recycled composite sleepers are important factors affecting the vibration characteristics of track structure. To study the viscoelastic dynamic properties of the composite sleeper, dynamic mechanical analysis (DMA) tests of a composite sleeper at −5 to 30 °C and 1–60 Hz were first carried out, and then the time-temperature superposition (TTS) and the Williams–Landel–Ferry (WLF) formula were used to predict the dynamic properties of a composite sleeper at a wider frequency range. Finally, the generalized Maxwell model was adopted to characterize the dynamic properties of the composite sleeper, which provides parameters and theoretical models for dynamic analysis. The research results show that the composite sleeper has obvious viscoelasticity. Its modulus is large at low temperature or high frequency. On the contrary, the modulus is small at high temperature or low frequency. Under the test conditions, its complex modulus ranges from 1500 to 2700 MPa. The loss factor is in the range of 0.08–0.13. Using the generalized Maxwell model (n = 4), which can better reflect the dynamic properties of the composite sleeper.
1. Introduction
In recent years, due to the rapid development of high-speed railways in China, various types of track structures have been applied. Although ballastless tracks are more commonly used, in some special areas, such as active fracture zones and areas with severe ground subsidence, ballasted tracks should be used [1]. Among the ballasted tracks, the most widely used sleeper is the prestressed concrete sleeper, which has the advantages of stable structure and high vertical and horizontal resistance of the ballast bed. However, due to its excessive rigidity, it is easy to cause the ballast bed to powder and increase its required maintenance. At present, the recently developed recycled composite sleeper, which is made from waste rubber, plastics, fibers, and additives (hereinafter referred to as a composite sleeper), is considered the optimal sleeper. In addition, because most of its components are reused waste, the composite sleeper has economic and social benefits. It is widely used in the United States, Australia, and Europe, but less so in China [2]. The composite sleeper has good elasticity and damping, and its track structure has vibration reduction characteristics. Its vibration reduction effect will affect the further promotion and application of the composite sleeper. However, the dynamic properties of the composite sleeper (such as elastic modulus and loss factor) are the prerequisite for analyzing the vibration reduction characteristics of the track structure. Therefore, it is necessary to clarify the dynamic properties of the composite sleeper.
The composite sleeper is composed of polymer materials such as rubber and plastic, and has viscoelastic properties. Its dynamic properties change with temperature, loading frequency, and loading amplitude. Elastic modulus and damping are the most important parameters that affect its vibration characteristics. At present, the related research on the composite sleeper mostly relates to its material composition [3,4], bending performance [5], and fatigue characteristics [6]. The dynamic properties of composite and other sleepers are usually assumed to be constant, which is an inaccurate assumption when analyzing the vibration characteristics of track structures. Therefore, it is necessary to carry out research on the dynamic properties of the composite sleeper to provide effective parameters for accurately analyzing the vibration characteristics of the composite sleeper track structure.
To date, numerous studies have been carried out on the testing of dynamic properties of viscoelastic materials, such as asphalt pavements [7,8,9,10,11] and magnetorheological elastomers [12,13,14]. Regarding track structures, most researchers have also examined their viscoelastic materials [15,16,17]. Wei Kai [18,19] adopted a universal testing machine and a thermostat to design and test the dynamic properties of the fastener pads commonly used in China’s high-speed railways and applied the time-temperature superposition (TTS) and Williams–Landel–Ferry (WLF) formula to predict the dynamic properties with a wider frequency range. The Fractional Derivative Kelvin–Voigt model was adopted to characterize the fastener rubber pad and based on the vehicle-track coupling dynamic model, the vibration characteristics of the track and vehicle were analyzed considering the viscoelasticity of the fastener pads. Thompson [20,21] designed a laboratory method to test the dynamic stiffness of fastener rubber pads with a test frequency range of 100 to 1000 Hz. Li [22] tested three different types of railpads, and obtained dynamic properties in a frequency range with different preloads and different temperatures. He also tested the aging railpad and found that its elastic modulus and damping were reduced. Finally, he adopted the Prony series material model to characterize the dynamic properties of the railpad. Jie Zhou et al. [23] tested the dynamic modulus of the asphalt concrete waterproof layer (ACWL) laid on the high-speed railway subgrade, and used the generalized Maxwell model for characterization. A 3D model of the vehicle-track structure was established, and the influence of the ACWL on the vibration of the track structure was calculated. The above research indicates that the viscoelastic materials used in the track structure are mainly fastener rubber pads, asphalt concrete, etc. Viscoelasticity is mainly studied using dynamic mechanical analysis (DMA) to test dynamic properties, and the time-temperature superposition is used to predict the viscoelasticity of a wider frequency range. A suitable constitutive model is then selected to characterize the viscoelasticity, making the theoretical analysis more accurate and reasonable.
It can be seen from Figure 1 that the sleeper and its track structure are symmetrical structures. Due to the viscoelasticity of the composite sleeper, it is unreasonable to assume that its dynamic properties as constants. To clarify the dynamic properties of the composite sleeper, the DMA method was used to test the dynamic properties of the composite sleeper at different temperatures and different frequencies (Section 2). Then, the time-temperature superposition and WLF formula were applied to predict the dynamic properties at a wider frequency range (Section 3). On this basis, the generalized Maxwell model was used to characterize the dynamic properties, which provides effective parameters for accurately analyzing the vibration characteristics of the composite sleeper track structure (Section 4).
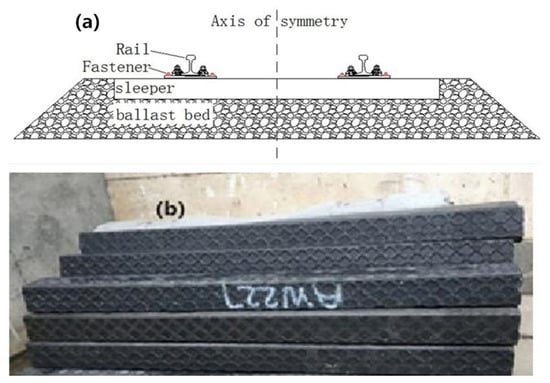
Figure 1.
Structure: (a) schematic diagram of track structure, (b) composite sleepers.
2. A Test for the Dynamic Properties of Composite Sleeper
2.1. Test Method and Equipment
Viscoelastic materials have the properties of both elastic and viscous materials, their dynamic properties (such as modulus and damping) are affected by temperature, loading frequency, and loading. To obtain these dynamic properties of the composite sleeper, dynamic mechanical analysis (DMA) is used.
As a viscoelastic material, when the composite sleeper is subjected to periodic loads, it will produce periodic stress and strain. The strain is not synchronized with the stress, and the strain lags behind by a phase angle δ. The phase angle depends on the material’s damping properties. For an ideal elastic material, the phase angle is zero, and the stress and strain is perfectly synchronized. For an ideal viscous material, the phase angle is 90°. The composite sleeper is a viscoelastic material, its phase angle is between zero and 90°, as shown in Figure 2. The composite sleeper is subjected to periodic load, and the stress and strain time history curve formulas are as follows:
where is the stress amplitude (MPa), is the strain amplitude (dimensionless), is the circular frequency of the periodic load (rad/s), t is the time (s), and is the phase angle of the strain behind the stress (rad).
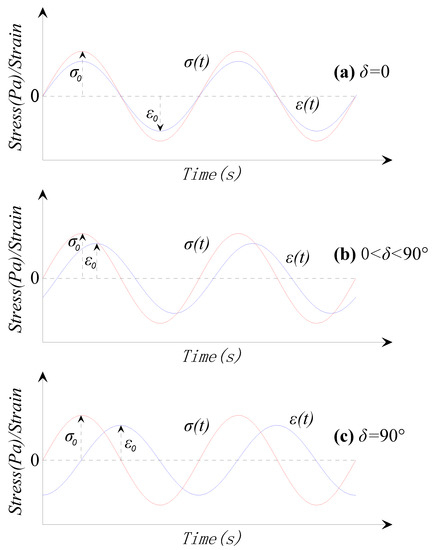
Figure 2.
Stress/strain time history curve: (a) Ideal elastic materials, (b) viscoelastic materials, (c) ideal viscous materials.
According to the theory of viscoelasticity [22,24], the stress of a viscoelastic material can be expressed as follows [25]:
where is the storage modulus (MPa), and is the loss modulus (MPa). The storage modulus is related to the elastic energy, and the loss modulus is related to the energy consumed by internal movement [22,25]. According to Formulas (1) to (3):
where is the loss factor, reflecting the damping properties of the material, and is the complex modulus (MPa). According to the above description, the periodic load is applied to the composite sleeper, the stress–strain time history curve can be obtained, and the elastic modulus and loss factor of the composite sleeper can be calculated by the above formulas.
For the DMA test, we used a Q800 dynamic mechanical analyzer produced by American TA Company, as shown in Figure 3. The test temperature range of the Q800 is −150 to 600 °C the frequency range is 0.01–200 Hz, and the maximum loading force is 18 N. The analyzer is mainly composed of two parts, the controller and the actuator. The controller can set the loading parameters by operating the computer, using the temperature scan or frequency scan loading method. The actuator contains a magnetic drive motor, low friction air bearing, temperature cabinet, etc., which can ensure the test accuracy. The specimen was placed in the temperature cabinet, as shown in the Figure 3b, the specimen was fixed with a splint clamp. During the loading process, the bottom cap remains unchanged, the loading rod connects to the top cap and moves downward synchronously to make the specimen stressed. Considering that the modulus of composite sleepers is much smaller than that of concrete sleepers, significant compression deformation will occur at the support when subjected to a train load. Therefore, the compression modulus of composite sleepers was tested.

Figure 3.
TA Q800 dynamic mechanical analyzer: (a) Overview, (b) test loading arrangement.
2.2. Process
It can be seen from the above that when a periodical load is applied to a viscoelastic material, the stress and strain curve will have a phase angle. Through the stress, strain curve and phase angle, the dynamic properties of the viscoelastic material can be obtained. The viscoelastic material also has temperature-dependent characteristics; that is, if the external environment temperature changes, the dynamic properties of the viscoelastic material will change accordingly. The TA Q800 dynamic mechanical analyzer can be used to apply periodic loads of different frequencies and temperatures to viscoelastic materials. Therefore, in order to obtain the dynamic characteristics of the composite sleeper, the test process will be formulated according to the service state of the composite sleeper and test conditions.
Three sets of composite sleeper specimens were tested. The fixture of the Q800 requires the specimen diameter to be less than 30 mm, and the upper and lower surfaces were smooth and flat. Therefore, the composite sleeper was cut into specimens with a diameter of 20 mm and a thickness of 7 mm, as shown in Figure 4. Considering the test conditions, the pre-pressure on the specimen was 6 N, the loading amplitude was 4 N (that is, the load range was 2–10 N), the test temperatures were −5, 0, 5, 10, 15, 20, 25, and 30 °C, and the test frequencies were 1, 3, 5, 10, 30, and 60 Hz.

Figure 4.
Specimens.
2.3. Test Results
Combining the test and the above formula, the dynamic properties of the composite sleeper can be obtained. As shown in Figure 5, taking a set of test specimen as an example, the dynamic properties at different temperatures and different frequencies can be seen from the figure. The composite sleeper exhibits obvious viscoelasticity. Under low temperature or high frequency excitation, the modulus is larger. At the same frequency, the lower the temperature, the larger the complex modulus and storage modulus of the composite sleeper; the loss modulus is also obvious from −4.5 to 15.4 °C. At the same frequency above 20.3 °C, the loss modulus is closer. Above 15.4 °C at the same frequency, as the temperature increases, the loss factor gradually increases, and below 10.1 °C, the loss factor is closer. At the same temperature, as the loading frequency increases, the complex modulus and storage modulus of the composite sleeper gradually increase, the loss modulus also shows an increasing trend, and the change in the loss factor is smaller. This is because the loss factor is the ratio of the loss modulus to the storage modulus, both of which gradually increase, thus, the loss factor fluctuates in the range of 0.08 to 0.13. It can also be seen from the Figure 5b,c that the loss modulus is about 1/12 to 1/7 of the storage modulus, which is relatively small. The main factor affecting the complex modulus is the storage modulus. The dynamic properties of the composite sleepers vary with temperature and loading frequency. Therefore, when analyzing the vibration characteristics of the composite sleeper track, the sleeper dynamic properties are taken as constants, which will obviously affect the calculation accuracy. It can be concluded that it is necessary to consider the viscoelasticity of the composite sleeper.
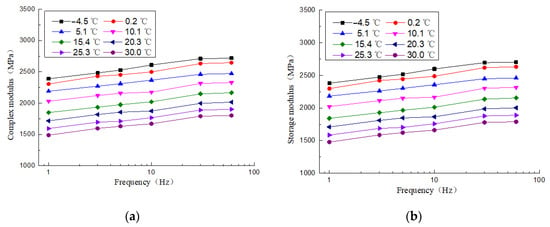
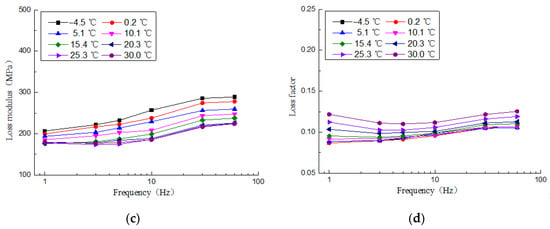
Figure 5.
A set of viscoelastic parameters of recycled composite sleepers: (a) Complex modulus, (b) storage modulus, (c) loss modulus, (d) loss factor.
Taking the 15 °C test condition as an example, the comparison of dynamic properties of the three sets of composite sleeper specimens is shown in Figure 6. It can be seen that the dynamic properties of the three sets of specimens at different frequencies are relatively close. However, differences also exist, which indicates that the modulus of the composite sleeper is discrete, due mainly to internal and external factors. The internal cause is mainly the uneven distribution of the internal components of the recycled composite sleeper. Furthermore, bubbles arise during processing that affect its modulus. The external cause is mainly due to the inevitable error in the test process. For example, although the temperature was set to 15 °C, the temperature would fluctuate slightly when different specimens were tested at different frequencies. Due to these factors, the dynamic properties of the composite sleeper fall within a certain range.
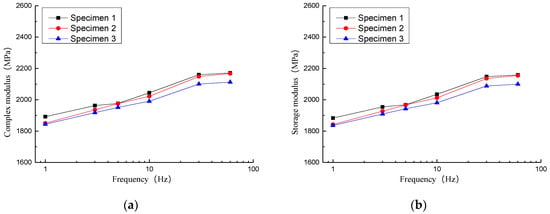
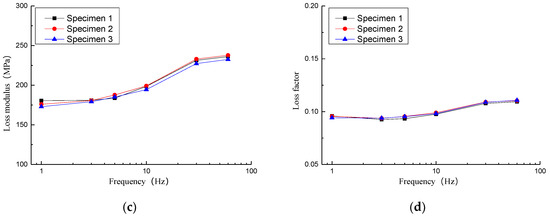
Figure 6.
Viscoelastic parameters of three groups of recycled composite sleepers at 15 °C: (a) Complex modulus, (b) storage modulus, (c) loss modulus, (d) loss factor.
3. Prediction of the Untested Dynamic Properties of the Composite Sleeper
3.1. Time-Temperature Superposition (TTS) and Williams–Landel–Ferry (WLF) Formula
Based on the DMA test data, the time-temperature superposition (TTS) and the Williams–Landel–Ferry (WLF) formula can be adopted to predict the untested dynamic properties of the composite sleeper. According to the TTS, the modulus of the material with density tested at temperature T and loading frequency f can be converted to the modulus of reference temperature T0, frequency f0, and density [22]. The calculations are shown in Formulas (8) and (9):
In the formula, is the conversion factor, which can be calculated using the WLF formula:
In the formula, C1 and C2 are constants, which are related to the reference temperature and material type.
The density at the reference temperature T0 can be calculated by the following formula:
where is the volume expansion coefficient, which has a value of 4.8 × 10−4/k.
3.2. Predicted Results
According to the above description, the dynamic properties of the composite sleeper can be predicted in a wider frequency range. Taking 15 °C as the reference temperature, Figure 7 shows the master curve of the dynamic properties of the composite sleeper at 15 °C. It can be seen from the Figure 7a–d that each modulus increases as the frequency increases, each modulus and loss factor are approximately linear with the frequency in the logarithmic coordinate system, and the slopes at different temperatures are relatively close. The complex modulus and the storage modulus have an excellent linear relationship with the frequency. The loss modulus is discrete in different frequency bands, and the slope is relatively low. Because the storage modulus and loss modulus both increase with the increase in frequency, the loss factor changes little at different frequencies, and both fluctuate in the range of 0.08–0.13. The predicted dynamic properties again show that the modulus of the composite sleepers is not constant and changes with frequency. Analysis of the vibration characteristics of the composite sleeper track will yield inaccuracies if the sleeper dynamic properties are considered to be constant.
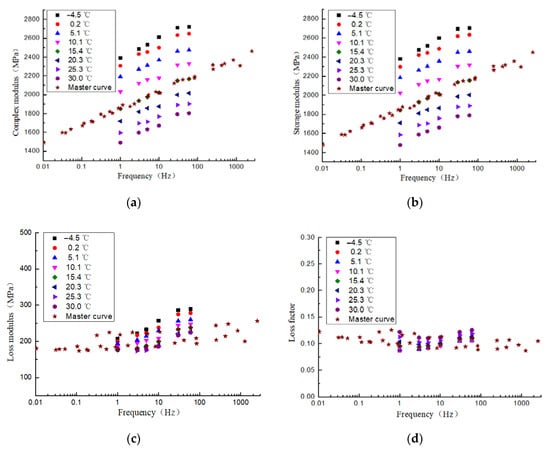
Figure 7.
Master curve of viscoelastic parameters of the composite sleeper at 15 °C: (a) Complex modulus, (b) storage modulus, (c) loss modulus, (d) loss factor.
4. Modeling Frequency-Dependent Composite Sleeper Properties
4.1. Generalized Maxwell Model
The dynamic properties of viscoelastic materials are usually characterized by a model composed of springs and dashpots. Commonly used are the Kelvin model, Maxwell model, Burgers model, and generalized Maxwell model, etc. as shown in Figure 8. According to the literature [22], it is recommended to use the generalized Maxwell model to characterize the composite sleeper. Thus, the vibration characteristics of the composite sleeper can be appropriately reflected in the theoretical analysis of the composite sleeper track. The generalized Maxwell model relaxation modulus is:
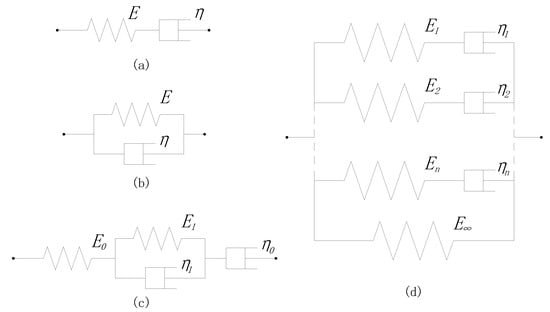
Figure 8.
Common models: (a) Maxwell model, (b) Kelvin–Voigt model, (c) Burgers model, (d) generalized Maxwell model.
In the frequency domain, the storage modulus and loss modulus of the material can be expressed as [22]:
where is the modulus of the parallel spring, is the modulus of the term i, is the relaxation time constant, n is the total number of parallel Maxwell models, is the circular frequency (rad/s), and is the frequency (Hz). The higher the value of n in the generalized Maxwell model, the better the model can characterize the dynamic properties.
4.2. Model Characterization Results
Based on the composite sleeper DMA test data and the master curve of the dynamic properties predicted by the TTS and the WLF formula, the least squares method was used to iteratively solve for the relevant parameters of the model. Taking the condition of 15 °C as an example, Figure 9 shows the fitting curve of the dynamic properties of the composite sleeper using the generalized Maxwell model. In the generalized Maxwell model, n has the values of 1 and 4. The parameters of the model are shown in Table 1 and Table 2.
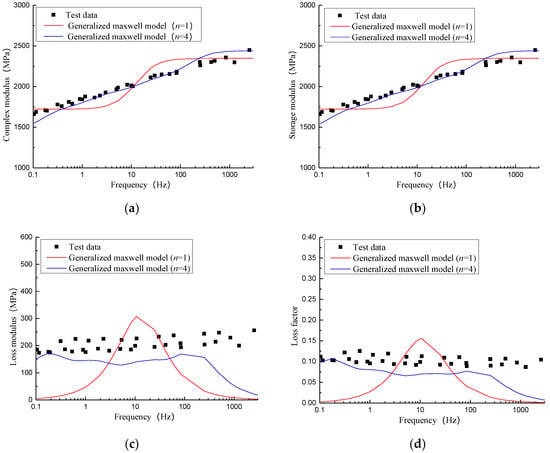
Figure 9.
Fitting curve of viscoelastic parameters of composite sleeper at 15 °C: (a) Complex modulus, (b) storage modulus, (c) loss modulus, (d) loss factor.

Table 1.
Generalized Maxwell model parameters (n = 1).

Table 2.
Generalized Maxwell model parameters (n = 4).
It can be seen from Figure 9 that the generalized Maxwell model is used to characterize the dynamic properties of the composite sleeper at different frequencies. Both n = 1 and n = 4 can better characterize the complex modulus and storage modulus, however, the accuracy of the characterization of the loss modulus and loss factor is lower. It can be seen from Figure 9c,d that when n = 1, the loss modulus and loss factor of the composite sleeper all show a trend of first increasing and then decreasing with the increase of frequency. The maximum value appears at 10 Hz. The fitting effect is better in the frequency range of 3–8 Hz and 30–60 Hz. In most frequency ranges, the fitting effect of loss modulus and loss factor is not ideal, and they are all less than the test value. When n = 4, the loss modulus and loss factor represented by the generalized Maxwell model in the frequency range below 500 Hz are satisfactory. In the frequency range above 500 Hz, the loss modulus and loss factor represented by the generalized Maxwell model are significantly reduced, and the accuracy of the fitting is not ideal. In the high frequency range, the generalized Maxwell model no longer works. Considering the overall results, the effect of using the generalized Maxwell model to characterize the dynamic properties of the composite sleeper is still significantly better than when considering the properties to be constant.
5. Discussion
This study used the DMA test, the time-temperature superposition (TTS), and the Williams–Landel–Ferry (WLF) formula to obtain the dynamic properties of the composite sleeper in a wide frequency range. The parameters are temperature-dependent and frequency-dependent. Compared with the previous consideration of the composite sleeper parameters as constants, the dynamic properties of the composite sleeper is described more accurately. In addition, based on the DMA test and the time-temperature superposition, the generalized Maxwell model was used to characterize the dynamic properties of the composite sleeper. By defining composite sleepers as the generalized Maxwell model, frequency-dependent modulus and damping can be considered in the vibration reduction analysis of track structure models.
This study is limited by its limited test conditions. The dynamic properties of the actual composite sleeper are also affected by the loading rate and loading amplitude. As the train approaches and passes the sleeper, the load on the sleeper increases, which affects the sleeper’s dynamic properties. In future research, the dynamic parameters of composite sleepers that are more in line with actual conditions should be studied based on the changes in train load.
In the future, theoretical analysis and experimental research on the vibration reduction characteristics of composite sleeper ballasted track can be carried out, and the accuracy of the generalized Maxwell model can also be verified.
6. Conclusions
To study the dynamic properties of the composite sleeper, DMA tests were used, and the dynamic properties of a wider frequency range were predicted according to the time-temperature superposition (TTS) and Williams–Landel–Ferry (WLF) formula. Finally, the generalized Maxwell model was used to characterize the dynamic properties of the composite sleeper. The main conclusions are as follows:
(1) The composite sleeper has viscoelastic behavior, and its elastic modulus has a certain degree of dispersion. The test shows that the range of the composite modulus of the composite sleeper under test conditions (temperature range −5 to 30 °C and loading frequency range of 1–60 Hz) is 1500–2700 MPa, and the loss factor is in the range of 0.08–0.13.
(2) By the Time-Temperature Superposition (TTS) and WLF formula, the dynamic properties of the composite sleeper is predicted at 15 °C. The modulus and loss factor are approximately linear with the frequency in the logarithmic coordinate system. On the whole, the modulus clearly increase with increasing frequency, the loss factor changes little at different frequencies.
(3) Using the generalized Maxwell model, n = 1 and n = 4 can better characterize the complex modulus and storage modulus of the composite sleeper, but the accuracy of the loss modulus and loss factor characterization is relatively low. In the frequency range above 500 Hz, the loss modulus and loss factor represented by the generalized Maxwell model are significantly reduced, and the accuracy of the fitting is not ideal. However, considering the overall results, the effect of using the generalized Maxwell model to characterize the dynamic properties of the composite sleeper is significantly better than when considering the properties to be constant.
Author Contributions
Conceptualization, Z.Z., Y.G. and C.L.; methodology, Z.Z. and C.L.; software, Z.Z. and Y.G.; formal analysis, Z.Z. and Y.G.; investigation, Z.Z. and C.L.; data curation, Z.Z.; writing—original draft preparation, Z.Z.; writing—review and editing, Y.G. and C.L.; visualization, Z.Z.; supervision, C.L.; funding acquisition, C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 51778543 and Chengdu-Lanzhou Railway Special Project, grant number CLRQT-2016-006.
Acknowledgments
The authors express gratitude to Rongshan Yang and Wei Qi for their valuable suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- National Railway Administration of the People’s Republic of China. TB/10621-2014 Code for Design of High Speed Railway; China Railway Press: Beijing, China, 2014. [Google Scholar]
- Haibin, D. Study on the Vertical Dynamic Behavior of Recycled Plastic Composite Crosstie Ballast Structure. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2017. [Google Scholar]
- Ferdous, W.; Manalo, A.; Van Erp, G.; Aravinthan, T.; Kaewunruen, S.; Remennikov, A. Composite railway sleepers—Recent developments, challenges and future prospects. Compos. Struct. 2015, 134, 158–168. [Google Scholar] [CrossRef]
- Manalo, A.; Aravinthan, T.; Karunasena, W.; Ticoalu, A. A review of alternative materials for replacing existing timber sleepers. Compos. Struct. 2010, 92, 603–611. [Google Scholar] [CrossRef]
- Lotfy, I.; Farhat, M.; Issa, M.A.; Al-Obaidi, M. Flexural behavior of high-density polyethylene railroad crossties. Proc. Inst. Mech. Eng. Part. F 2016, 230, 813–824. [Google Scholar] [CrossRef]
- Lotfy, I.; Issa, M.A. Evaluation of the longitudinal restraint, uplift resistance, and long-term performance of high-density polyethylene crosstie rail support system using static and cyclic loading. Proc. Inst. Mech. Eng. Part. F 2017, 231, 1–15. [Google Scholar] [CrossRef]
- Shan, L.; Xu, Y.; He, H.; Ren, N. Optimization criterion of viscoelastic response model for asphalt binders. Constr. Build. Mater. 2016, 113, 553–560. [Google Scholar] [CrossRef]
- Liyan, S.; Tan, Y.; Zhang, H.; Xu, Y. Analysis of Linear Viscoelastic Response Function Model for Asphalt Binders. J. Mater. Civ. Eng. 2016, 28, 4016010. [Google Scholar]
- Delgadillo, R.; Bahia, H.U.; Lakes, R. A nonlinear constitutive relationship for asphalt binders. Mater. Struct. 2012, 45, 457–473. [Google Scholar] [CrossRef]
- Specht, L.; Babadopulos, L.; Di Benedetto, H.; Sauzeat, C.; Soares, J. Application of the theory of viscoelasticity to evaluate the resilient modulus test in asphalt mixes. Constr. Build. Mater. 2017, 149, 648–658. [Google Scholar] [CrossRef]
- Gudmarsson, A.; Ryden, N.; Di Benedetto, H.; Sauzeat, C. Complex modulus and complex Poisson’s ratio from cyclic and dynamic modal testing of asphalt concrete. Constr. Build. Mater. 2015, 88, 20–31. [Google Scholar] [CrossRef]
- Sun, T.; Gong, X.; Jiang, W.; Li, J.; Xu, Z.; Li, W.H. Study on the damping properties of magnetorheological elastomers based on cis-polybutadiene rubber. Polym. Test. 2009, 27, 520–526. [Google Scholar] [CrossRef]
- Kallio, M.; Lindroos, T.; Aalto, S.; Jarvinen, E.; Karna, T.; Meinander, T. Dynamic compression testing of a tunable spring element consisting of a magnetorheological elastomer. Smart Mater. Struct. 2007, 16, 506–514. [Google Scholar] [CrossRef]
- Liao, G.; Gong, X.; Xuan, S. Magnetic Field-Induced Compressive Property of Magnetorheological Elastomer under High Strain Rate. Ind. Eng. Chem. Res. 2013, 52, 8445–8453. [Google Scholar] [CrossRef]
- Fenander, Å. Frequency Dependent Stiffness and Damping of Railpads. Proc. Inst. Mech. Eng. Part. F 1997, 211, 51–62. [Google Scholar] [CrossRef]
- Maes, J.; Sol, H.; Guillaume, P. Measurements of the dynamic railpad properties. J. Sound Vib. 2006, 293, 557–565. [Google Scholar] [CrossRef]
- Zhu, S.; Cai, C.; Spanos, P.D. A nonlinear and fractional derivative viscoelastic model for rail pads in the dynamic analysis of coupled vehicle-slab track systems. J. Sound Vib. 2015, 335, 304–320. [Google Scholar] [CrossRef]
- Wei, K.; Yang, Q.; Dou, Y.; Wang, F.; Wang, P. Experimental investigation into temperature- and frequency-dependent dynamic properties of high-speed rail pads. Constr. Build. Mater. 2017, 151, 848–858. [Google Scholar] [CrossRef]
- Wei, K.; Wang, P.; Yang, F.; Xiao, J. The effect of the frequency-dependent stiffness of rail pad on the environment vibrations induced by subway train running in tunnel. Proc. Inst. Mech. Eng. Part F 2016, 230, 697–708. [Google Scholar] [CrossRef]
- Thompson, D.J.; Verheij, J.W. The Dynamic Behaviour of Rail Fasteners at High Frequencies. Appl. Acoust. 1997, 52, 1–15. [Google Scholar] [CrossRef]
- Thompson, D.J.; van Vliet, W.J.; Verheij, J.W. Developments of the indirect method for measuring the high frequency dynamic stiffness of resilient elements. J. Sound Vib. 1998, 213, 169–188. [Google Scholar] [CrossRef]
- Oregui, M.; de Man, A.X.; Woldekidan, M.F.; Li, Z.; Dollevoet, R. Obtaining railpad properties via dynamic mechanical analysis. J. Sound Vib. 2016, 363, 460–472. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, X.; Fu, Q.; Xu, G.; Cai, D. Dynamic Responses of Asphalt Concrete Waterproofing Layer in Ballastless Track. Appl. Sci. 2019, 9, 375. [Google Scholar] [CrossRef]
- Christensen, R.M. Theory of Viscoelasticity, 2nd ed.; DOVER PUBN INC: New York, NY, USA, 2010. [Google Scholar]
- Menard, K. Dynamic Mechanical Analysis, 2nd ed.; Taylor & Francis: Abingdon, UK, 2008. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).