Color Revolution: A Novel Operator for Imperialist Competitive Algorithm in Solving Cloud Computing Service Composition Problem
Abstract
1. Introduction
1.1. Literature Review
2. Problem and Algorithm Description
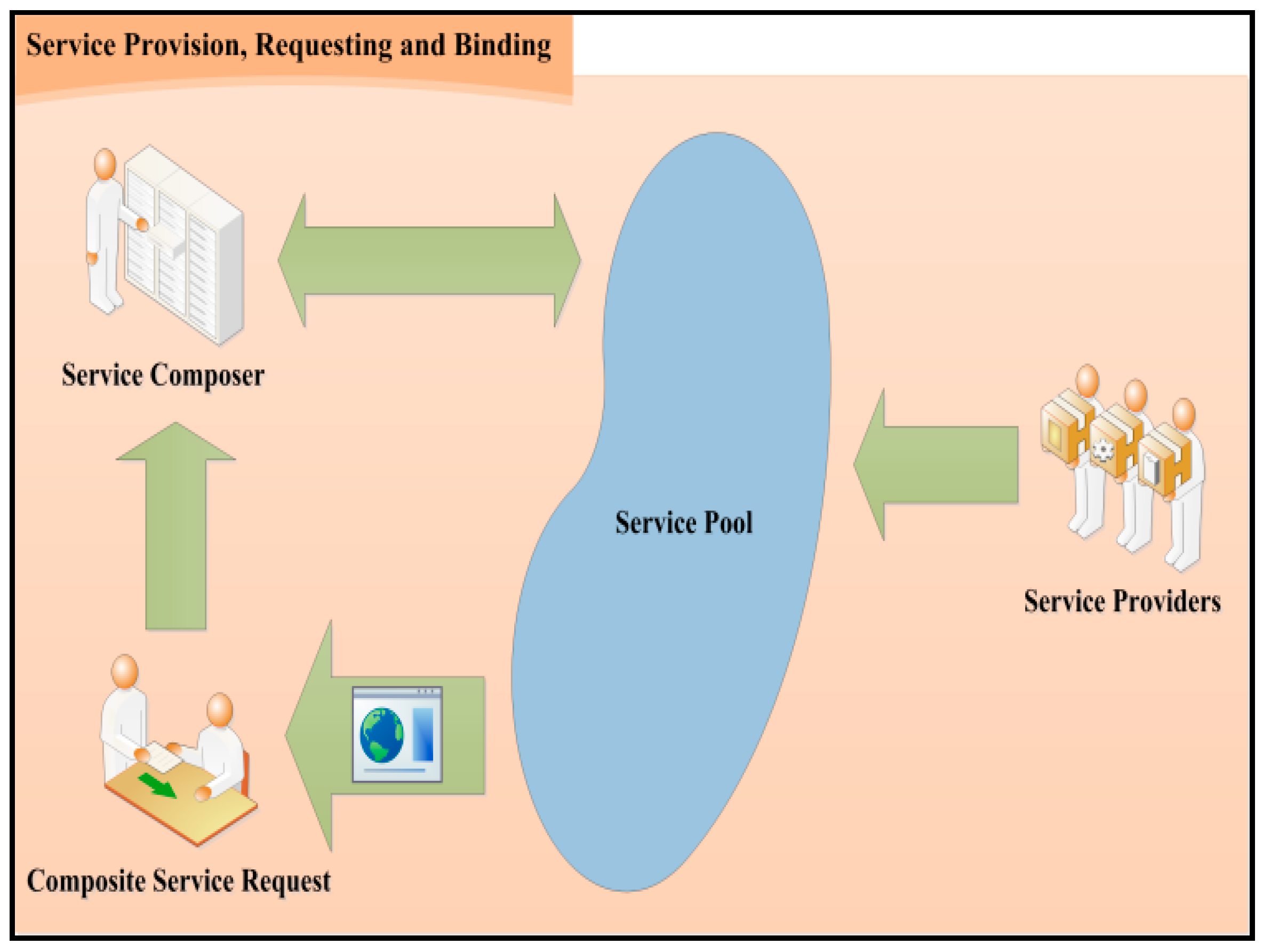
2.1. Service Time-Cost Optimization in Cloud Computing Service Composition (STCOCCSC)
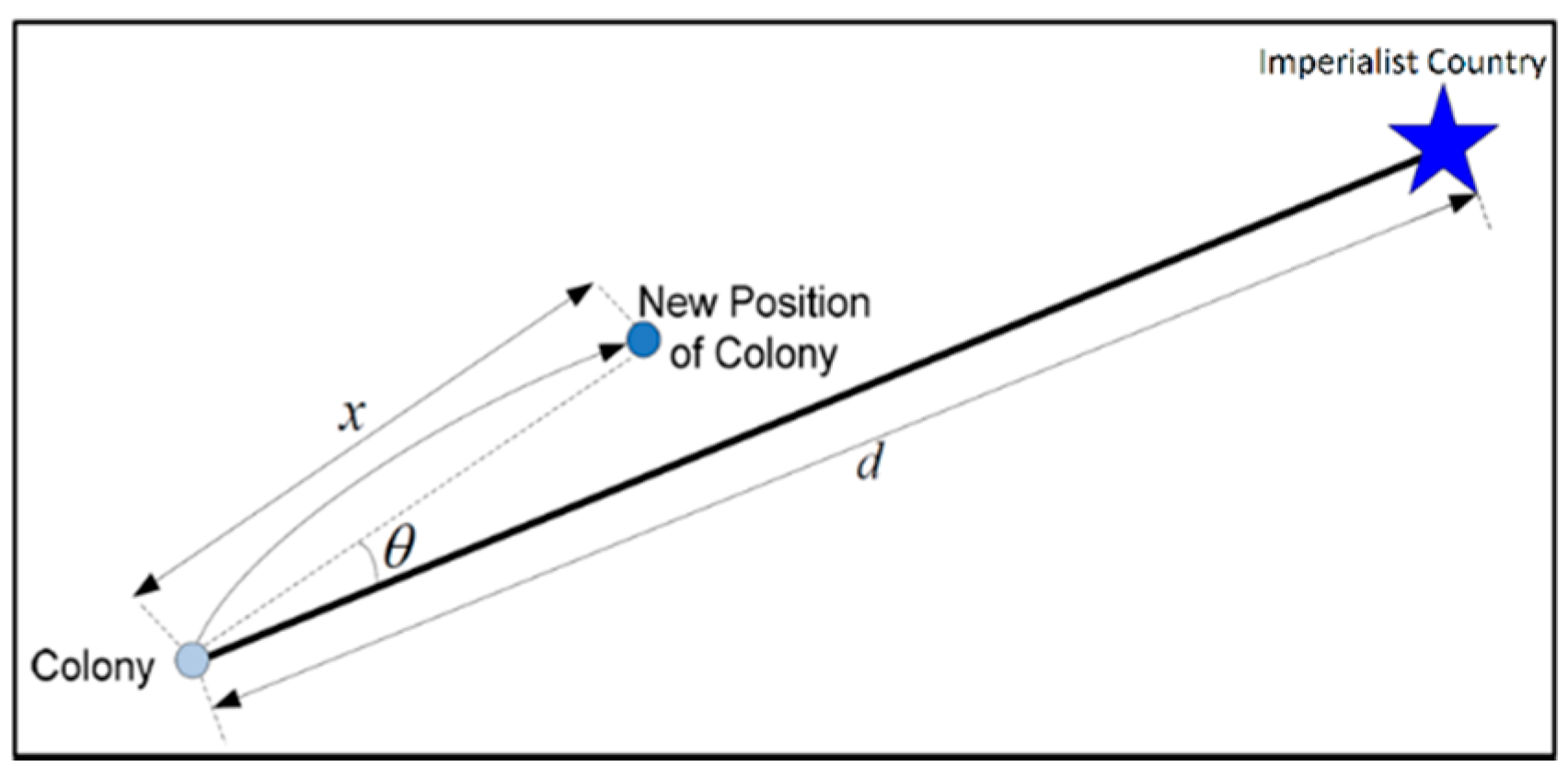
2.2. Imperialist Competitive Algorithm (ICA)
3. Imperialist Competitive Algorithm with the Color Revolution Operator (ICACRO)
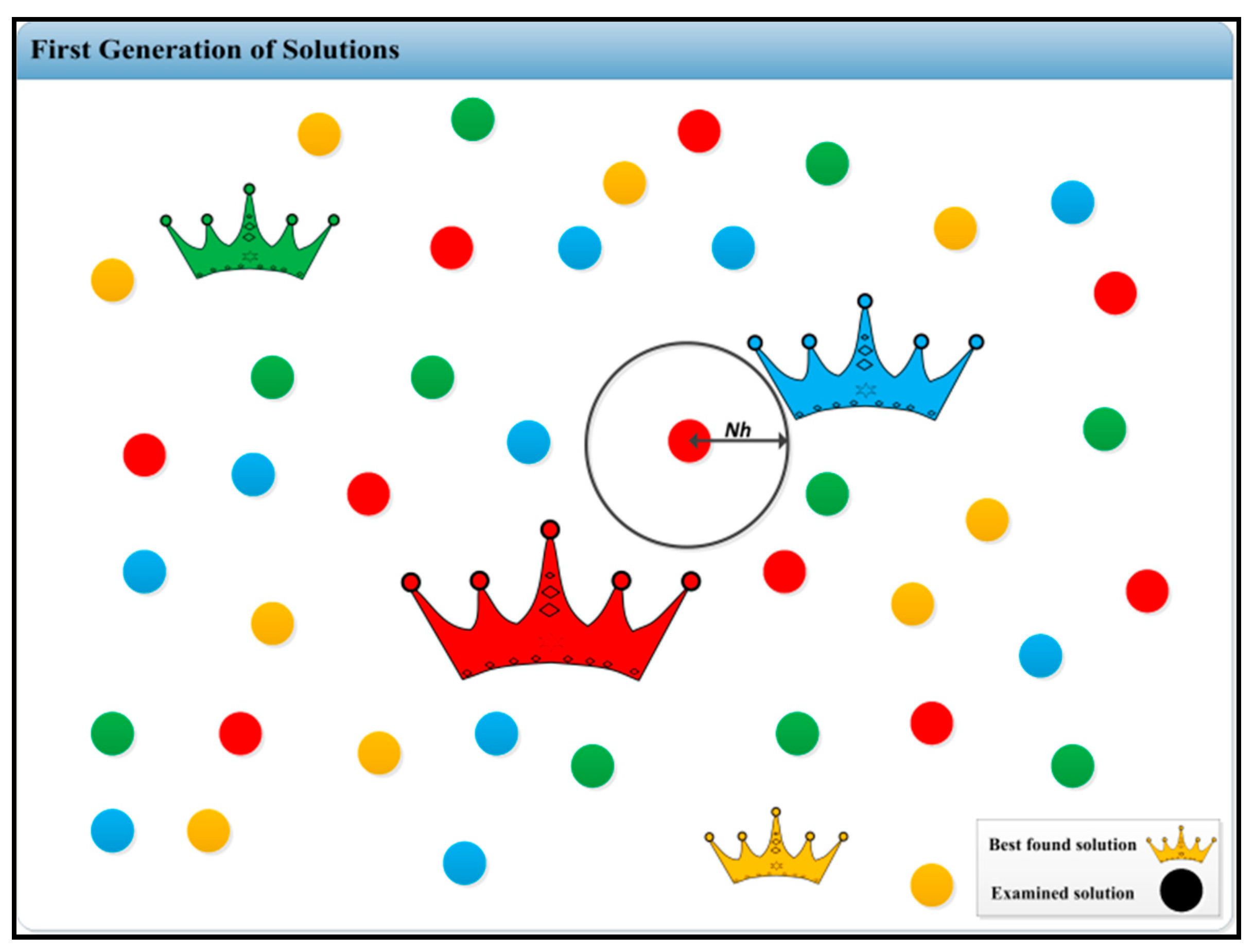
3.1. Color Revolution Operator (CRO)
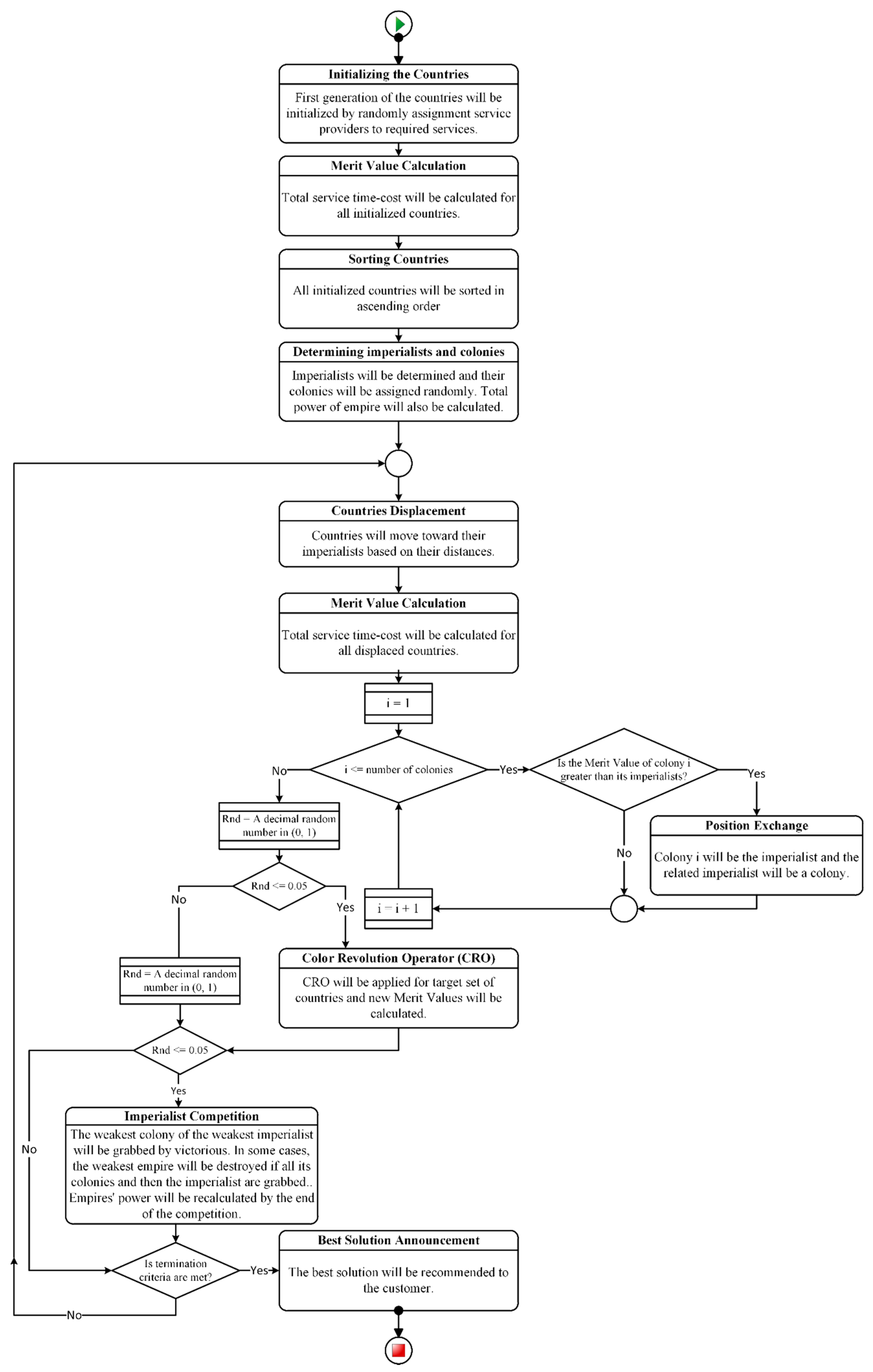
3.2. ICA with CRO (ICACRO)
4. Experimental Design
4.1. ICACRO Implementation and Execution
4.2. Definitions
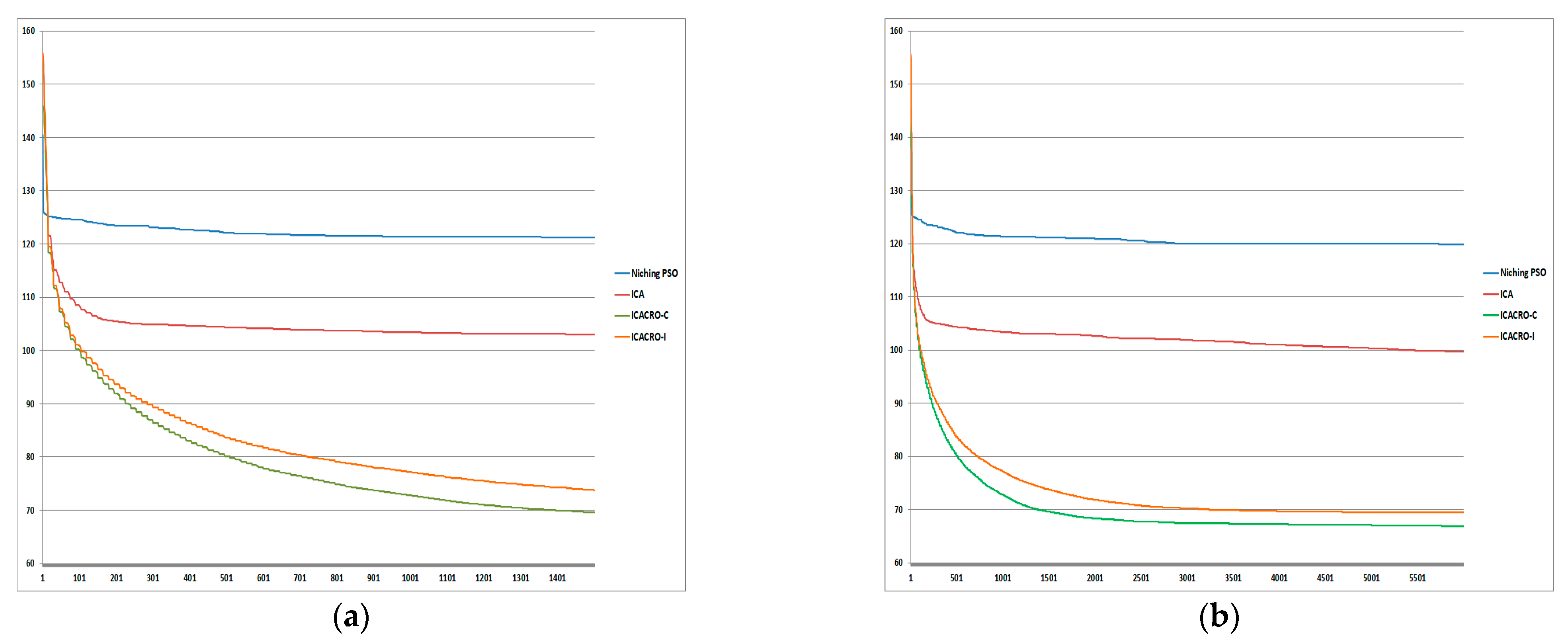
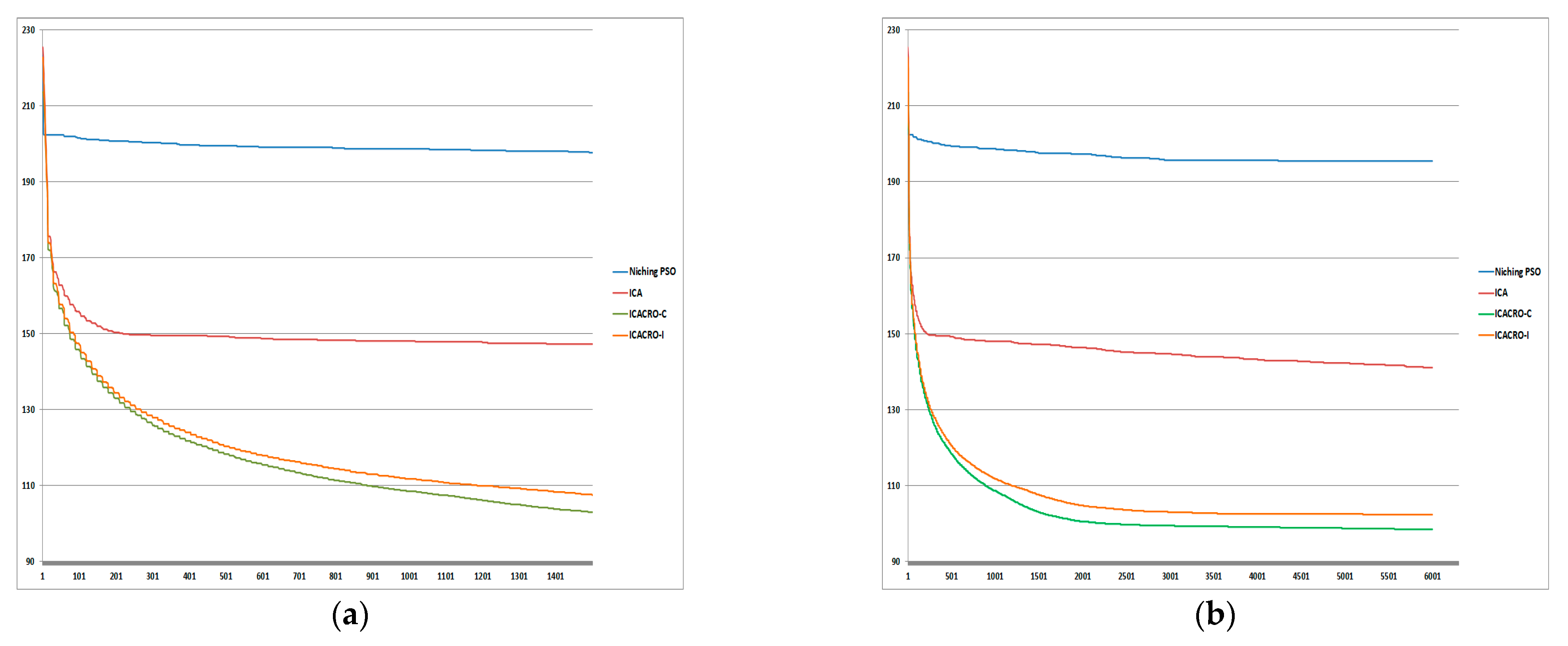
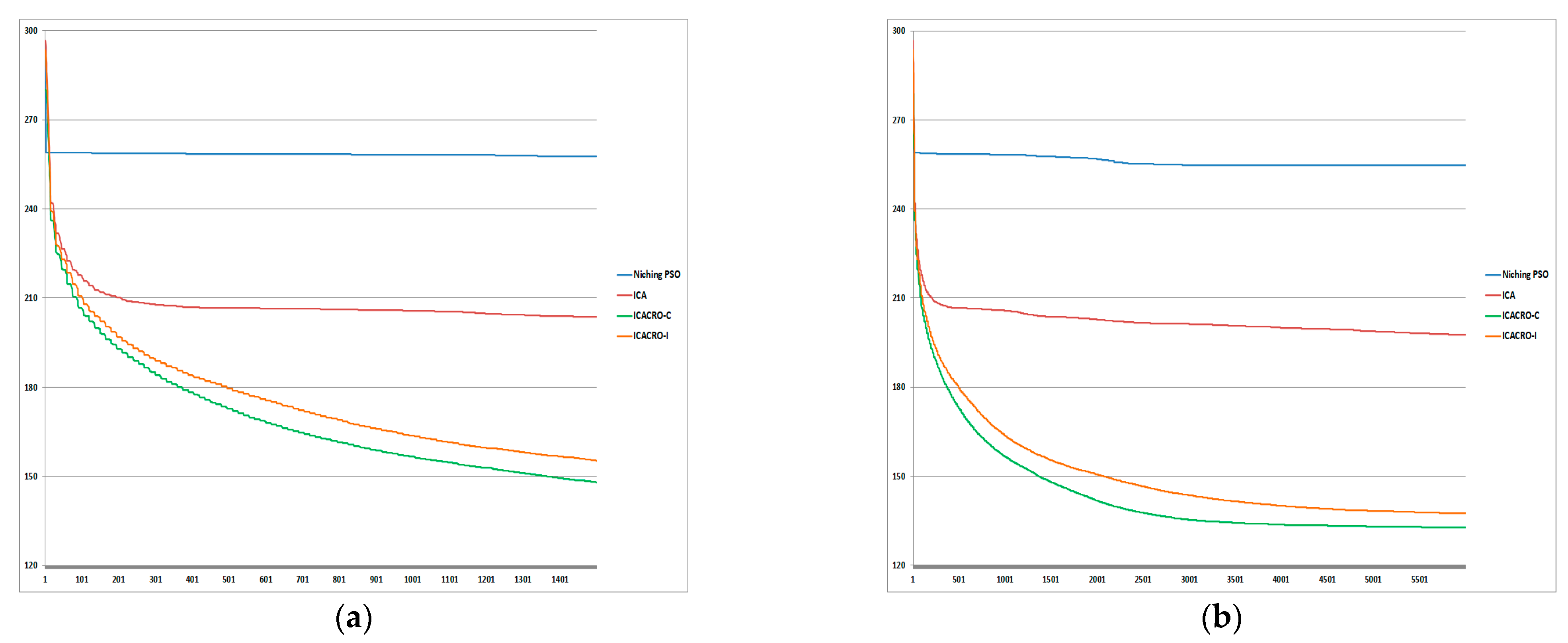
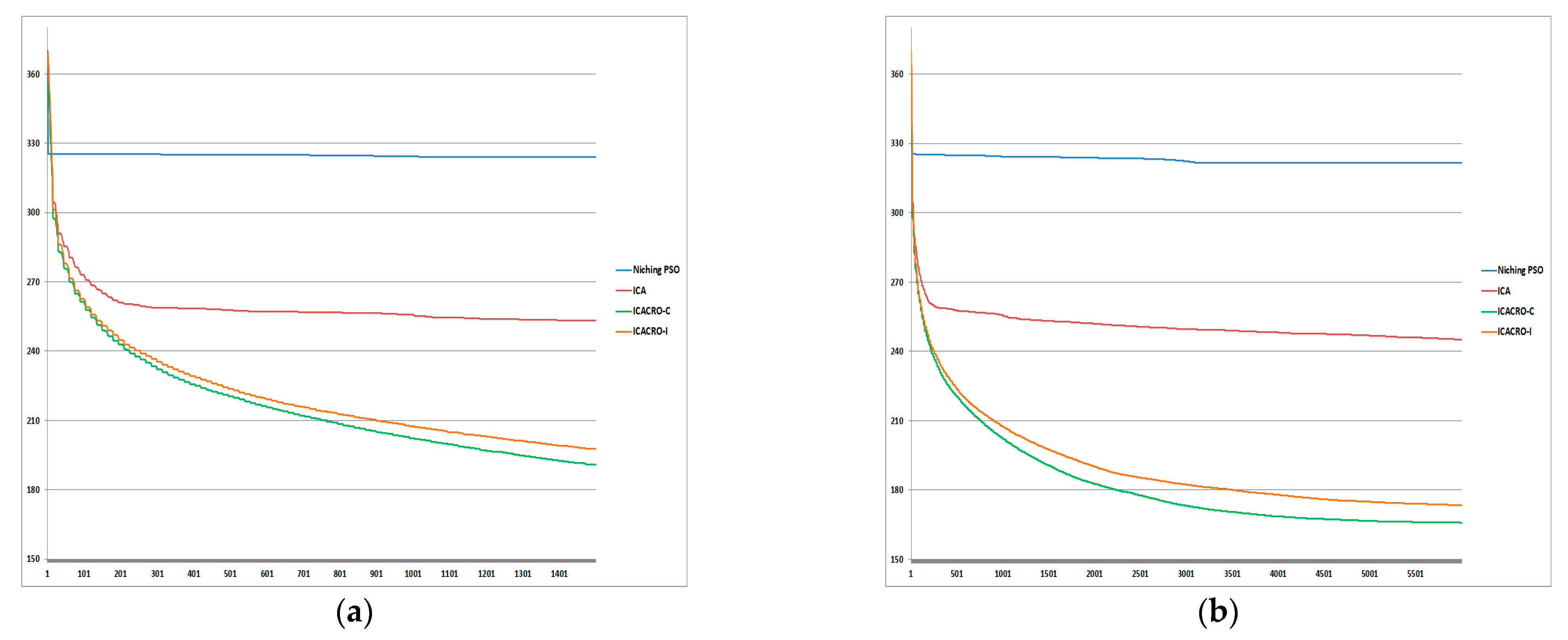
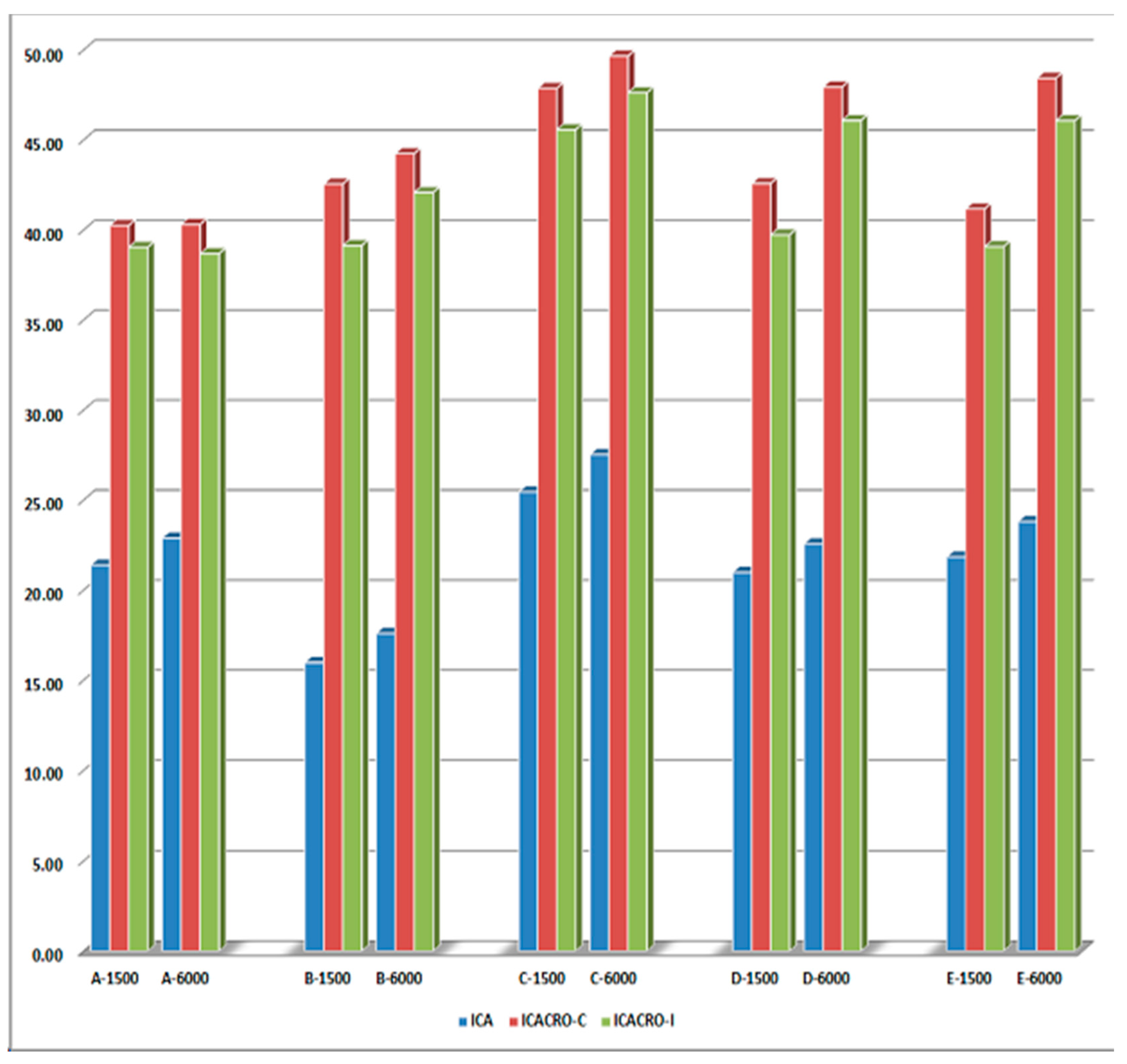
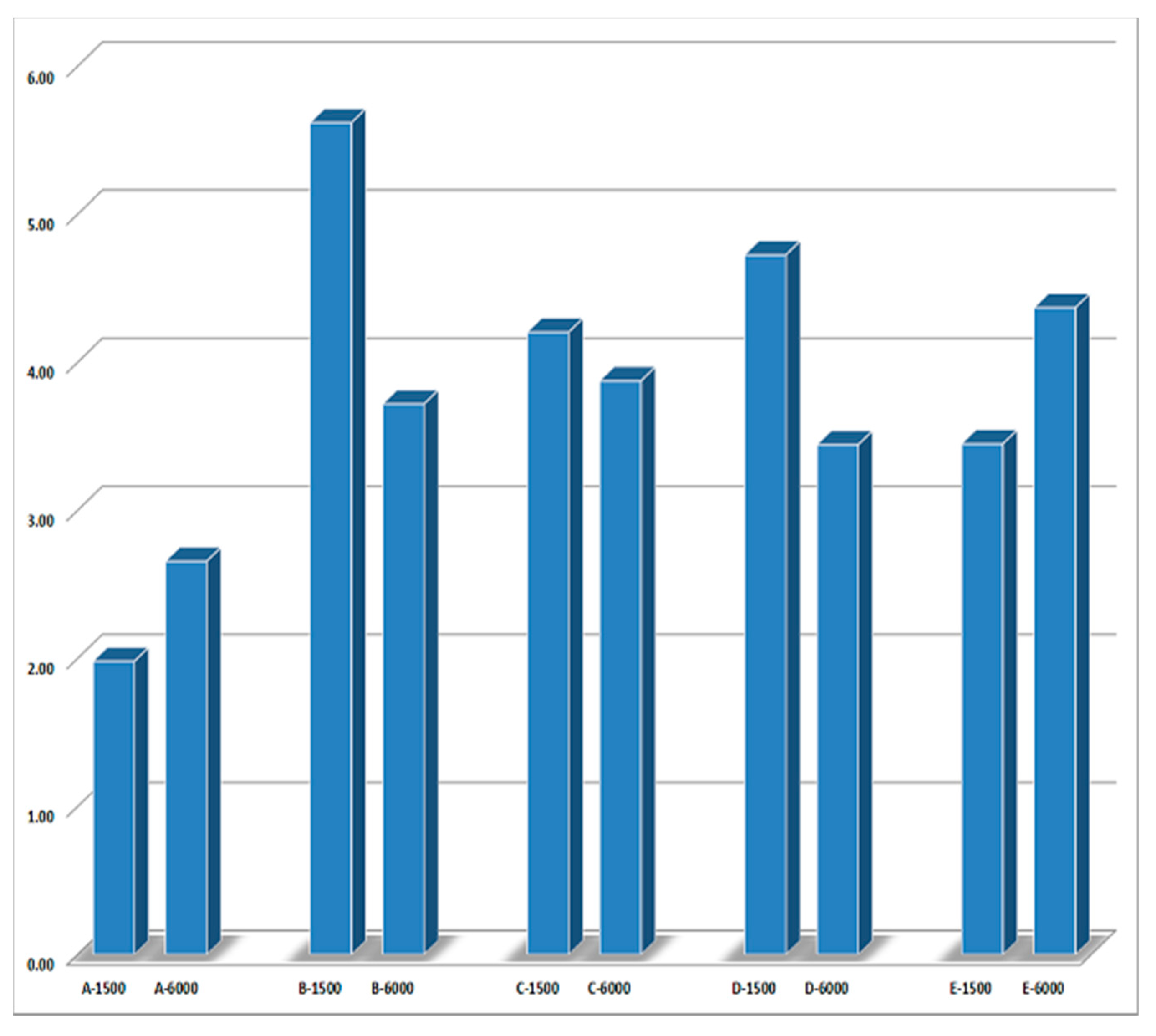
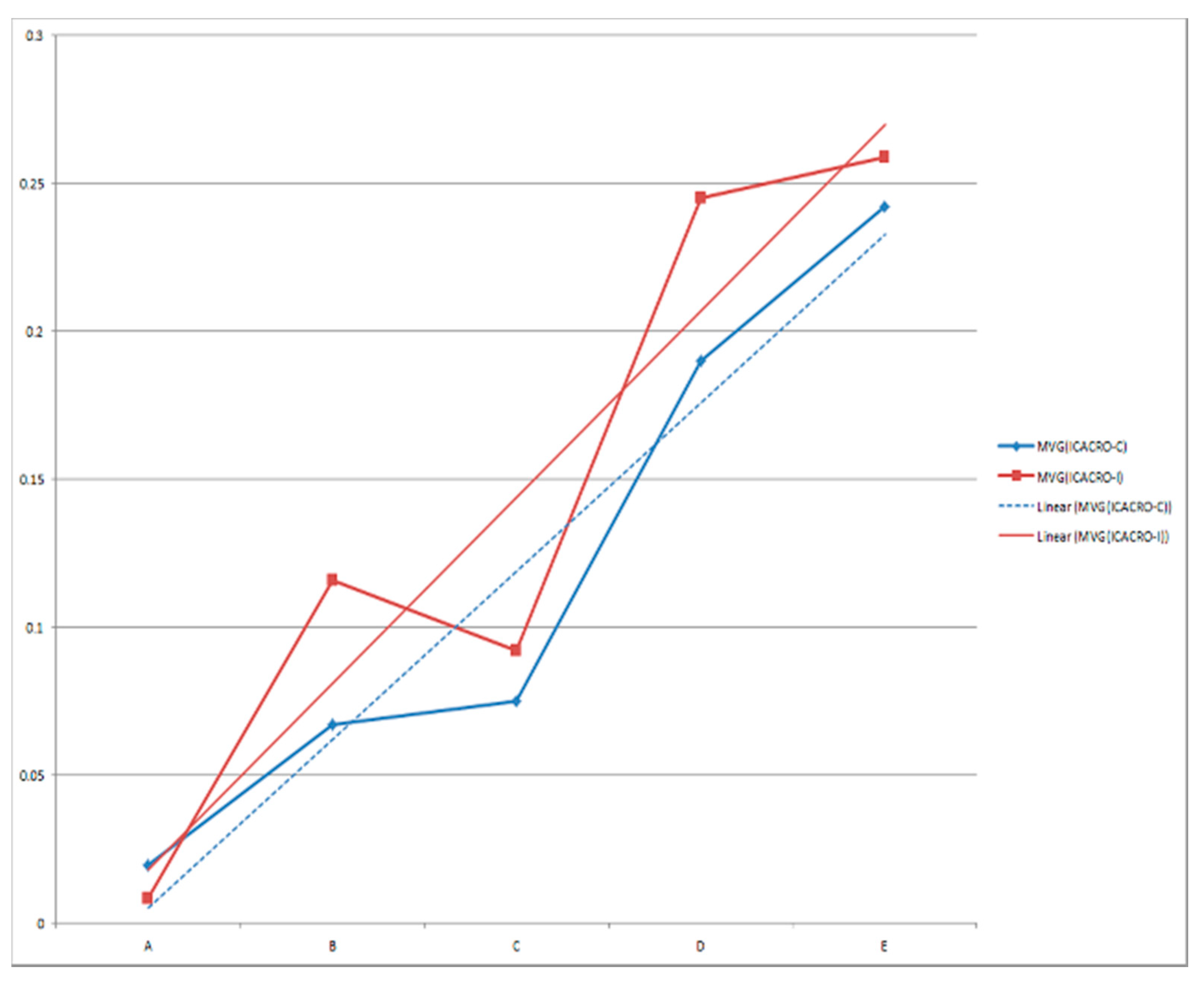
5. Comparison of Results and Discussion
5.1. ICACRO-C or ICACRO-I?
5.2. Fps or Fs?
5.3. Performance Statistical Test
6. Conclusions and Directions for Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hamdaqa, M.; Tahvildari, L. Cloud Computing Uncovered: A Research Landscape. Adv. Comput. 2012, 86, 41–85. [Google Scholar] [CrossRef]
- Mell, P.; Grance, T. The NIST Definition of Cloud Computing; National Institute of Standards and Technology, U.S. Department of Commerce: Gaithersburg, MA, USA, 2011; pp. 1–7.
- Vaquero, L.M.; Rodero-Merino, L.; Caceres, J.; Lindner, M. A break in the clouds: Towards a cloud definition. Comput. Commun. Rev. 2008, 39, 50–55. [Google Scholar] [CrossRef]
- Jula, A.; Sundararajan, E.; Othman, Z. Cloud computing service composition: A systematic literature review. Expert Syst. Appl. 2014, 41, 3809–3824. [Google Scholar] [CrossRef]
- Ding, S.; Yang, S.; Zhang, Y.; Liang, C.; Xia, C. Combining QoS prediction and customer satisfaction estimation to solve cloud service trustworthiness evaluation problems. Knowl. Based Syst. 2014, 56, 216–225. [Google Scholar] [CrossRef]
- Yousefipour, A.; Rahmani Amir, M.; Jahanshahi, M. Energy and cost-aware virtual machine consolidation in cloud computing. Softw. Pract. Exp. 2018, 48, 1758–1774. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, W.; Zhang, X.; Zhai, H. Dynamic Service Selection Based on Adaptive Global QoS Constraints Decomposition. Symmetry 2019, 11, 403. [Google Scholar] [CrossRef]
- Lu, P.; Zhang, L.; Liu, X.; Yao, J.; Zhu, Z. Highly efficient data migration and backup for big data applications in elastic optical inter-data-center networks. IEEE Netw. 2015, 29, 36–42. [Google Scholar] [CrossRef]
- Fei, T.; Yuanjun, L.; Lida, X.; Lin, Z. FC-PACO-RM: A Parallel Method for Service Composition Optimal-Selection in Cloud Manufacturing System. IEEE Trans. Ind. Inform. 2013, 9, 2023–2033. [Google Scholar] [CrossRef]
- Yu, T.; Lin, K.-J. Service selection algorithms for composing complex services with multiple qos constraints. In Proceedings of the Third International Conference on Service-Oriented Computing, Amsterdam, The Netherlands, 12–15 December 2005; pp. 130–143. [Google Scholar]
- Anselmi, J.; Ardagna, D.; Cremonesi, P. A QoS-based selection approach of autonomic grid services. In Proceedings of the 2007 Workshop on Service-Oriented Computing Performance: Aspects, Issues, and Approaches, Monterey, CA, USA, 25 June 2007; pp. 1–8. [Google Scholar]
- Li, J.; Zheng, X.-L.; Chen, S.-T.; Song, W.-W.; Chen, D. An efficient and reliable approach for quality-of-service-aware service composition. Inf. Sci. 2014, 269, 238–254. [Google Scholar] [CrossRef]
- Mijumbi, R.; Serrat, J.; Gorricho, J.; Bouten, N.; Turck, F.D.; Boutaba, R. Network Function Virtualization: State-of-the-Art and Research Challenges. IEEE Commun. Surv. Tutor. 2016, 18, 236–262. [Google Scholar] [CrossRef]
- Ocampo, A.F.; Gil-Herrera, J.; Isolani, P.H.; Neves, M.C.; Botero, J.F.; Latré, S.; Zambenedetti, L.; Barcellos, M.P.; Gaspary, L.P. Optimal Service Function Chain Composition in Network Functions Virtualization. In Proceedings of the 11th IFIP WG 6.6 International Conference on Autonomous Infrastructure, Management, and Security, Zurich, Switzerland, 10–13 July 2017; pp. 62–76. [Google Scholar]
- Wang, M.; Cheng, B.; Li, B.; Chen, J. Service Function Chain Composition and Mapping in NFV-Enabled Networks. In Proceedings of the 2019 IEEE World Congress on Services (SERVICES), Milan, Italy, 8–13 July 2019; pp. 331–334. [Google Scholar]
- Wada, H.; Suzuki, J.; Yamano, Y.; Oba, K. A Multiobjective Optimization Framework for SLA-Aware Service Composition. IEEE Trans. Serv. Comput. 2012, 5, 358–372. [Google Scholar] [CrossRef]
- Hayyolalam, V.; Pourhaji Kazem, A.A. A systematic literature review on QoS-aware service composition and selection in cloud environment. J. Netw. Comput. Appl. 2018, 110, 52–74. [Google Scholar] [CrossRef]
- Jula, A.; Othman, Z.; Sundararajan, E. A Hybrid Imperialist Competitive-Gravitational Attraction Search Algorithm to Optimize Cloud Service Composition. In Proceedings of the 2013 IEEE Workshop on Memetic Computing (MC), Singapore, 15–19 April 2013; pp. 37–43. [Google Scholar]
- Wang, Z.-S.; Lee, J.; Song, C.G.; Kim, S.-J. Efficient Chaotic Imperialist Competitive Algorithm with Dropout Strategy for Global Optimization. Symmetry 2020, 12, 635. [Google Scholar] [CrossRef]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the IEEE Congress on Evolutionary Computation, CEC 2007, Singapore, 25–28 September 2007; pp. 4661–4667. [Google Scholar]
- Zibin, Z.; Yilei, Z.; Lyu, M.R. Distributed QoS Evaluation for Real-World Web Services. In Proceedings of the 8th IEEE International Conference on Web Services (ICWS 2010), Miami, FL, USA, 5–10 July 2010; pp. 83–90. [Google Scholar]
- Kofler, K.; ul Haq, I.; Schikuta, E. A Parallel Branch and Bound Algorithm for Workflow QoS Optimization. In Proceedings of the ICPP 2009, International Conference on Parallel Processing, Vienna, Austria, 22–25 September 2009; pp. 478–485. [Google Scholar]
- Moura, L.D.; Bjørner, N. Satisfiability modulo theories: Introduction and applications. Commun. ACM 2011, 54, 69–77. [Google Scholar] [CrossRef]
- Worm, D.; Zivkovic, M.; van den Berg, H.; van der Mei, R. Revenue maximization with quality assurance for composite web services. In Proceedings of the 2012 5th IEEE International Conference on Service-Oriented Computing and Applications (SOCA 2012), Taipei, Taiwan, 17–19 December 2012; pp. 1–9. [Google Scholar]
- Shangguang, W.; Qibo, S.; Fangchun, Y. Towards Web Service selection based on QoS estimation. Int. J. Web Grid Serv. 2010, 6, 424–443. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, W.; Luo, J.; Zheng, X. A novel two-phase approach for QoS-aware service composition based on history records. In Proceedings of the 2012 5th IEEE International Conference on Service-Oriented Computing and Applications (SOCA 2012), Taipei, Taiwan, 17–19 December 2012; pp. 1–8. [Google Scholar]
- Qi, Y.; Bouguettaya, A. Efficient Service Skyline Computation for Composite Service Selection. IEEE Trans. Knowl. Data Eng. 2013, 25, 776–789. [Google Scholar] [CrossRef]
- Hossain, M.S.; Hassan, M.M.; Al Qurishi, M.; Alghamdi, A. Resource Allocation for Service Composition in Cloud-Based Video Surveillance Platform; IEEE: New York, NY, USA, 2012; pp. 408–412. [Google Scholar] [CrossRef]
- Zeng, C.; Guo, X.A.; Ou, W.J.; Han, D. Cloud Computing Service Composition and Search Based on Semantic. In Lecture Notes in Computer Science; Jaatun, M.G., Zhao, G., Rong, C., Eds.; Springer: Berlin, Germany, 2009; Volume 5931, pp. 290–300. [Google Scholar]
- Huang, J.; Liu, Y.; Yu, R.; Duan, Q.; Tanaka, Y. Modeling and Algorithms for QoS-Aware Service Composition in Virtualization-Based Cloud Computing. IEICE Trans. Commun. 2013, 96, 10–19. [Google Scholar] [CrossRef]
- Zhou, X.; Mao, F. A Semantics Web Service Composition Approach Based on Cloud Computing. In Proceedings of the 2012 Fourth International Conference on Computational and Information Sciences (ICCIS 2012), Chongqing, China, 17–19 August 2012; pp. 807–810. [Google Scholar]
- Karim, R.; Chen, D.; Miri, A. An End-to-End QoS Mapping Approach for Cloud Service Selection. In Proceedings of the 2013 IEEE Ninth World Congress on Services (SERVICES), Santa Clara, CA, USA, 28 June–3 July 2013; pp. 341–348. [Google Scholar]
- Barzegar, S.; Davoudpour, M.; Meybodi, M.R.; Sadeghian, A.; Tirandazian, M. Formalized learning automata with adaptive fuzzy coloured Petri net; an application specific to managing traffic signals. Sci. Iran. 2011, 18, 554–565. [Google Scholar] [CrossRef]
- Zhao, H.; Gao, W.; Deng, W.; Sun, M. Study on an Adaptive Co-Evolutionary ACO Algorithm for Complex Optimization Problems. Symmetry 2018, 10, 104. [Google Scholar] [CrossRef]
- Jaddi, N.S.; Alvankarian, J.; Abdullah, S. Kidney-inspired algorithm for optimization problems. Commun. Nonlinear Sci. Numer. Simul. 2017, 42, 358–369. [Google Scholar] [CrossRef]
- He, J.; Lin, G.M. Average Convergence Rate of Evolutionary Algorithms. IEEE Trans. Evol. Comput. 2016, 20, 316–321. [Google Scholar] [CrossRef]
- Vesterstrom, J.; Thomsen, R. A comparative study of differential evolution, particle swarm optimization, and evolutionary algorithms on numerical benchmark problems. In Proceedings of the IEEE Congress on Evolutionary Computation, CEC 2004, Portland, OR, USA, 19–23 June 2004; pp. 1980–1987. [Google Scholar]
- Bäck, T.; Fogel, D.B.; Michalewicz, Z. Handbook of Evolutionary Computation; IOP Publishing Ltd.: Bristol, UK, 1997; p. 988. [Google Scholar]
- Naseri, N.K.; Sundararajan, E.A.; Ayob, M.; Jula, A. Smart Root Search (SRS): A Novel Nature-Inspired Search Algorithm. Symmetry 2020, 12, 2025. [Google Scholar] [CrossRef]
- Knuth, D.E. The Art of Computer Programming, Volume 4A: Combinatorial Algorithms, Part 1; Pearson Education: Tamil Nadu, India, 2011. [Google Scholar]
- Abonyi, J.; Akerkar, R.; Alavi, A.H.; Arango, C.; Aydogdu, I.; Brest, J.; Cai, X.; Cordeiro, J.; Cortés, P.; Costa, K.A.P.; et al. List of Contributors. In Swarm Intelligence and Bio-Inspired Computation; Yang, X.-S., Cui, Z., Xiao, R., Gandomi, A.H., Karamanoglu, M., Eds.; Elsevier: Oxford, UK, 2013; pp. xv–xviii. [Google Scholar] [CrossRef]
- Zhang, X.; Dou, W. Preference-Aware QoS Evaluation for Cloud Web Service Composition Based on Artificial Neural Networks. In Web Information Systems and Mining; Wang, F., Gong, Z., Luo, X., Lei, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6318, pp. 410–417. [Google Scholar]
- Wu, Q.; Zhang, M.; Zheng, R.; Lou, Y.; Wei, W. A QoS-Satisfied Prediction Model for Cloud-Service Composition Based on a Hidden Markov Model. Math. Probl. Eng. 2013, 2013, 7. [Google Scholar] [CrossRef]
- Lie, Q.; Yan, W.; Orgun, M.A. Cloud Service Selection Based on the Aggregation of User Feedback and Quantitative Performance Assessment. In Proceedings of the 2013 IEEE International Conference on Services Computing (SCC), Santa Clara, CA, USA, 28 June–3 July 2013; pp. 152–159. [Google Scholar]
- Ye, Z.; Zhou, X.; Bouguettaya, A. Genetic Algorithm Based QoS-Aware Service Compositions in Cloud Computing. In Database Systems for Advanced Applications; Yu, J., Kim, M., Unland, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6588, pp. 321–334. [Google Scholar]
- Klein, A.; Ishikawa, F.; Honiden, S. Towards network-aware service composition in the cloud. In Proceedings of the 21st International Conference on World Wide Web, Lyon, France, 16–20 April 2012; pp. 959–968. [Google Scholar]
- Ludwig, S.A. Clonal selection based genetic algorithm for workflow service selection. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation (CEC), Brisbane, QLD, Australia, 10–15 June 2012; pp. 1–7. [Google Scholar]
- Wang, S.G.; Sun, Q.B.; Zou, H.; Yang, F.C. Particle Swarm Optimization with Skyline Operator for Fast Cloud-based Web Service Composition. Mob. Netw. Appl. 2013, 18, 116–121. [Google Scholar] [CrossRef]
- Liao, J.X.; Liu, Y.; Wang, J.Y.; Zhu, X.M. Service Composition Based on Niching Particle Swarm Optimization in Service Overlay Networks. KSII Trans. Internet Inf. Syst. 2012, 6, 1106–1127. [Google Scholar] [CrossRef]
- Wang, Y.W. Application of Chaos Ant Colony Algorithm in Web Service Composition Based on QoS; IEEE Computer Soc: Los Alamitos, CA, USA, 2009; pp. 225–227. [Google Scholar] [CrossRef]
- Yang, Y.; Mi, Z.; Sun, J. Game theory based iaas services composition in cloud computing environment. Adv. Inf. Sci. Serv. Sci. 2012, 4, 238–246. [Google Scholar]
- Jula, A.; Othman, Z.; Sundararajan, E. Imperialist competitive algorithm with PROCLUS classifier for service time optimization in cloud computing service composition. Expert Syst. Appl. 2015, 42, 135–145. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2011; p. 696. [Google Scholar]
- Bahrami, H.; Faez, K.; Abdechiri, M. Imperialist Competitive Algorithm Using Chaos Theory for Optimization (CICA). In Proceedings of the 2010 12th International Conference on Computer Modelling and Simulation (UKSim), Brisbane, Australia, 24–26 March 2010; pp. 98–103. [Google Scholar]
- Zarandi, M.H.F.; Zarinbal, M.; Ghanbari, N.; Turksen, I.B. A new fuzzy functions model tuned by hybridizing imperialist competitive algorithm and simulated annealing. Application: Stock price prediction. Inf. Sci. 2013, 222, 213–228. [Google Scholar] [CrossRef]
- Zherebkin, M. In search of a theoretical approach to the analysis of the ‘Colour revolutions’: Transition studies and discourse theory. Communist Post-Communist Stud. 2009, 42, 199–216. [Google Scholar] [CrossRef]
- Marples, D.R. Color revolutions: The Belarus case. Communist Post-Communist Stud. 2006, 39, 351–364. [Google Scholar] [CrossRef]
- Jula, A.; Nilsaz, H.; Sundararajan, E.; Othman, Z. A new dataset and benchmark for cloud computing service composition. In Proceedings of the 2014 5th International Conference on Intelligent Systems, Modelling and Simulation, Langkawi, Malaysia, 27–29 January 2014; pp. 83–86. [Google Scholar]
- Liao, J.X.; Liu, Y.; Zhu, X.M.; Xu, T.; Wang, J.Y. Niching Particle Swarm Optimization Algorithm for Service Composition. In 2011 IEEE Global Telecommunications Conference; IEEE: Houston, TX, USA, 2011. [Google Scholar]
- Abdi, H. Greenhouse-Geisser Correction. Encyclopedia of Research Design; SAGE Publications, Inc.: Thousand Oaks, CA, USA, 2010; pp. 545–549. [Google Scholar] [CrossRef]
- Nakagawa, S. A farewell to Bonferroni: The problems of low statistical power and publication bias. Behav. Ecol. 2004, 15, 1044–1045. [Google Scholar] [CrossRef]
- Cabin, R.; Mitchell, R. To Bonferroni or not to Bonferroni: When and how are the questions. Bull. Ecol. Soc. Am. 2000, 81, 246–248. [Google Scholar] [CrossRef]
- Holm, S. A Simple Sequentially Rejective Multiple Test Procedure. Scand. J. Stat. 1979, 6, 65–70. [Google Scholar] [CrossRef]







| STCOCCSC | ICA | Optimization |
|---|---|---|
| Composite Service (CS) | Country | Solution |
| Merit Value (MV) | Power of Country | Objective Function |
| Problem A | Problem B | Problem C | Problem D | Problem E | |
|---|---|---|---|---|---|
| ICACRO-C Best result after 1500 iterations (Cfps) | 34.53 | 69.63 | 103.02 | 147.96 | 190.64 |
| ICACRO-C Best result after 6000 iterations (Cfs) | 34.15 | 66.94 | 98.49 | 132.70 | 165.87 |
| ICACRO-C 1500-iteration execution time (CfpsT) | 6.5 s | 13.4 s | 20.2 s | 26.8 s | 34.4 s |
| ICACRO-C 6000-iteration execution time (CfsT) | 25.7 s | 53.5 s | 80.4 s | 107 s | 136.6 s |
| ICACRO-I Best result after 1500 iterations (Ifps) | 35.23 | 73.78 | 107.54 | 155.29 | 197.45 |
| ICACRO-I Best result after 6000 iterations (Ifs) | 35.08 | 69.50 | 102.39 | 137.41 | 173.46 |
| ICACRO-I 1500-iteration execution time (IfpsT) | 5.9 s | 12.2 s | 18.7 s | 24.5 s | 31.1 s |
| ICACRO-I 6000-iteration execution time (IfsT) | 23.5 s | 49.1 s | 74.6 s | 97.5 s | 123.8 s |
| Cfps—Cfs | 0.38 | 2.69 | 4.53 | 15.26 | 24.77 |
| Ifps—Ifs | 0.15 | 4.28 | 5.15 | 17.88 | 23.99 |
| CfsT—CfpsT | 19.2 s | 40.1 s | 60.2 s | 80.2 s | 102.2 s |
| IfsT—IfpsT | 17.6 s | 36.9 s | 55.9 s | 73 s | 92.7 s |
| df | Mean Square | F | Sig. | ||
|---|---|---|---|---|---|
| Problem A | Between Groups | 1.234 | 1654453.748 | 1064352.466 | <0.001 |
| Error | 7400.915 | 1.554 | |||
| Problem B | Between Groups | 1.079 | 9596518.233 | 258544.375 | <0.001 |
| Error | 6473.570 | 37.117 | |||
| Problem C | Between Groups | 1.082 | 31014381.517 | 441298.360 | <0.001 |
| Error | 6493.645 | 70.280 | |||
| Problem D | Between Groups | 1.052 | 46227282.898 | 199913.106 | <0.001 |
| Error | 6309.354 | 231.237 | |||
| Problem E | Between Groups | 1.040 | 72555514.778 | 195415.062 | <0.001 |
| Error | 6239.068 | 371.289 | |||
| (I) Algorithm | (J) Algorithm | Mean Difference (J—I) | Std. Error | Sig. | |
|---|---|---|---|---|---|
| Problem A | ICACRO-C | Niching PSO | −22.836 | 0.018 | <0.001 |
| ICACRO-I | Niching PSO | −22.037 | 0.019 | <0.001 | |
| ICA | Niching PSO | −12.575 | 0.009 | <0.001 | |
| ICACRO-C | ICA | −10.261 | 0.015 | <0.001 | |
| ICACRO-I | ICA | −9.462 | 0.016 | <0.001 | |
| ICACRO-C | ICACRO-I | −0.798 | 0.002 | <0.001 | |
| Problem B | ICACRO-C | Niching PSO | −50.116 | 0.089 | <0.001 |
| ICACRO-I | Niching PSO | −47.144 | 0.088 | <0.001 | |
| ICA | Niching PSO | −18.518 | 0.026 | <0.001 | |
| ICACRO-C | ICA | −31.598 | 0.072 | <0.001 | |
| ICACRO-I | ICA | −28.626 | 0.071 | <0.001 | |
| ICACRO-C | ICACRO-I | −2.972 | 0.01 | <0.001 | |
| Problem C | ICACRO-C | Niching PSO | −92.806 | 0.127 | <0.001 |
| ICACRO-I | Niching PSO | −89.269 | 0.121 | <0.001 | |
| ICA | Niching PSO | −51.471 | 0.044 | <0.001 | |
| ICACRO-C | ICA | −41.335 | 0.098 | <0.001 | |
| ICACRO-I | ICA | −37.798 | 0.091 | <0.001 | |
| ICACRO-C | ICACRO-I | −3.537 | 0.009 | <0.001 | |
| Problem D | ICACRO-C | Niching PSO | −111.665 | 0.221 | <0.001 |
| ICACRO-I | Niching PSO | −104.956 | 0.218 | <0.001 | |
| ICA | Niching PSO | −53.594 | 0.061 | <0.001 | |
| ICACRO-C | ICA | −58.071 | 0.178 | <0.001 | |
| ICACRO-I | ICA | −51.362 | 0.174 | <0.001 | |
| ICACRO-C | ICACRO-I | −6.709 | 0.019 | <0.001 | |
| Problem E | ICACRO-C | Niching PSO | −139.396 | 0.293 | <0.001 |
| ICACRO-I | Niching PSO | −132.027 | 0.27 | <0.001 | |
| ICA | Niching PSO | −71.467 | 0.086 | <0.001 | |
| ICACRO-C | ICA | −67.928 | 0.225 | <0.001 | |
| ICACRO-I | ICA | −60.56 | 0.2 | <0.001 | |
| ICACRO-C | ICACRO-I | −7.369 | 0.026 | <0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jula, A.; Sundararajan, E.A.; Othman, Z.; Naseri, N.K. Color Revolution: A Novel Operator for Imperialist Competitive Algorithm in Solving Cloud Computing Service Composition Problem. Symmetry 2021, 13, 177. https://doi.org/10.3390/sym13020177
Jula A, Sundararajan EA, Othman Z, Naseri NK. Color Revolution: A Novel Operator for Imperialist Competitive Algorithm in Solving Cloud Computing Service Composition Problem. Symmetry. 2021; 13(2):177. https://doi.org/10.3390/sym13020177
Chicago/Turabian StyleJula, Amin, Elankovan A. Sundararajan, Zalinda Othman, and Narjes Khatoon Naseri. 2021. "Color Revolution: A Novel Operator for Imperialist Competitive Algorithm in Solving Cloud Computing Service Composition Problem" Symmetry 13, no. 2: 177. https://doi.org/10.3390/sym13020177
APA StyleJula, A., Sundararajan, E. A., Othman, Z., & Naseri, N. K. (2021). Color Revolution: A Novel Operator for Imperialist Competitive Algorithm in Solving Cloud Computing Service Composition Problem. Symmetry, 13(2), 177. https://doi.org/10.3390/sym13020177









