Data for Beryllium–Hydrogen Charge Exchange in One and Two Centres Models, Relevant for Tokamak Plasmas

Abstract

Data on the cross section and kinetic rate of charge exchange (CX) between the bare beryllium nucleus, the ion Be(+4) and the neutral hydrogen atom are of great interest for visible-range high-resolution spectroscopy in the ITER tokamak because beryllium is intended as the material for the first wall in the main chamber. Here an analysis of available data is presented, and the data needs are formulated. Besides the active probe signal produced by the CX of the diagnostic hydrogen neutral beam with impurity ions in plasma, a passive signal produced by the CX of impurity ions with cold edge plasma is also important, as it shows in observation data from the JET (Joint European Torus) tokamak with an ITER-like beryllium wall. Data in the range of a few eV/amu to ~100 eV/amu (amu stands for the atomic mass unit) needed for simulations of level populations for principal and orbital quantum numbers in the emitting beryllium ions Be(+3) can be obtained with the help of two-dimensional kinetic codes. The lack of literature data, especially for data resolved in orbital quantum numbers, has instigated us to make numerical calculations with the ARSENY code. A comparison of the results obtained for the one-centre Coulomb problem using an analytic approach and for the two-centre problem using numerical simulations is presented.

1. Introduction

The use of beryllium as a material for the first wall in the main chamber of the ITER tokamak requires detailed data on the cross sections of elementary atomic processes involving beryllium. Although such processes have been studied in detail, there are still types of processes for which the databases are not complete enough in the parameter ranges of interest. Such a process is the charge exchange of bare beryllium ions with hydrogen ions and its isotopes, which plays an important role in optical diagnostics of plasma in the visible spectral range. The charge exchange process can be written in the following general form:

A^z+ + B⁰(n_B) → A^(z−1)+(n,l) + B⁺

(1)

It plays an important role for the Charge eXchange Recombination Spectroscopy (CXRS) diagnostics that Russia will supply to the ITER [1], as well as for other diagnostics of the Active Beam Spectroscopy type as a process that strongly affects the background signal (for more information, see, e.g., [2]). For such diagnostics, a diagnostic beam of neutral atoms is injected into the plasma. The plasma ion A^z+ interacts with a neutral atom B⁰ in a state with the principal quantum number n_B from the diagnostic beam and captures an electron from it. Usually, an electron is captured in an excited state A^(z−1)+(n,l), where n, l are the principal and orbital quantum numbers, respectively. The excitation relaxes by the emission of radiation, which is collected by the optical system and delivered to the spectrometers.

The CXRS diagnostics measures important plasma parameters, such as impurity concentration and distribution, ion temperature, and plasma rotation velocity profiles. For reliable interpretation of measurements, predictive modelling of the plasma emission spectra is necessary, which, in particular, requires information on the cross sections of the charge exchange reaction (1).

Besides the active signal produced by the CX of diagnostic neutral hydrogen beam with impurity ions in the plasma, the passive signal produced by the CX of impurity ions with atoms in the cold edge plasma is also important, as follows from the available observational data from the JET (Joint European Torus) tokamak with ITER-like beryllium wall (see, e.g., comments and references in [2]).

This paper is focused on data on the cross section of charge exchange of bare beryllium nuclei with neutral atoms of hydrogen isotopes:

Be⁴⁺ + H⁰(n_H) → Be³⁺(n,l) + H⁺

(2)

(Herein parentheses are the quantum numbers of the state of an atom or ion). We present (i) an overview of the data available in the literature and databases, and (ii) new data recently calculated using the ARSENY code [3,4], in the range from a few eV/amu to ~1000 eV/amu (amu stands for the atomic mass unit) especially the data resolved in orbital quantum numbers, which are needed for modelling the level populations of emitting beryllium ions Be(+3) with the help of two-dimensional, in principal and orbital quantum numbers, kinetic codes.

The following transitions of the hydrogen-like beryllium ion Be IV between the states with certain principal quantum numbers will be used to implement CXRS diagnostics on the ITER: 4658.42 Å (6–5 transition) and 4685.4 Å (8–6 transition). Therefore, it is important to have data for charge exchange cross sections at high levels that contribute to the spectral transitions used for measurements.

A comparison of the results obtained for the one-centre Coulomb problem using the analytical approach [5] and the two-centre problem using numerical simulations [6,7,8,9,10,11,12,13,14,15,16] is presented.

2. Materials and Methods

One and Two Centres Symmetry Problems in CXRS

The problem of charge exchange recombination of a neutral hydrogen atom on a nucleus with a charge Z, which is a classic example of the evolution of atomic states between two Coulomb centres, was considered within the framework of the one-centre model. The charge exchange process here is due to the intersection of quasi-molecular terms in the system of repulsive centres. The transition probability was determined by the exchange matrix element at the intersection points and was calculated by the Landau-Zener method (see [17]). The further evolution of the recharged states between two points of convergence and scattering of nuclei occurred under the action of an electric field created by a recharged nucleus moving along a classical trajectory. This field, varying in magnitude and direction, caused a mixing of the initially degenerate one-centre states with respect to orbital angular momenta (the effect of rotation of the internuclear axis). Thus, the initially populated state with a principal quantum number n of the order of Z^2/3 due to charge exchange from the ground state of the hydrogen atom, which possessed zero orbital angular momentum, turned out to be strongly mixed over states with other orbital angular momenta due to the effects of the rotation of the internuclear axis. These effects led to the population of states with predominantly large orbital angular momenta. This phenomenon was observed already in the first experiments on CXRS [18] of carbon nuclei, where the increase in the luminescence at the transition from the initially populated state n = 4 to the nearest level n = 3 did not occur, while the intensity of the 3–2 radiative transition increased noticeably. This is evidently explained by the selection rules for the radiation cascade between excited states with the maximum orbital momenta. Of course, transitions between the levels n = 4 and n = 2 are possible for different values of the orbital angular momentum due to the mixing of states with different orbital angular momenta in collisions with plasma ions. However, the predominance of radiative transitions with a decrease in the orbital angular momentum over similar transitions with an increase in it correlates well with the observed effect.

The one-centre model is attractive due to the ability to follow the above effects analytically. This possibility is due to the symmetry of the Coulomb field in the one-centre problem. This symmetry makes it possible to construct the exact evolution of atomic states under the action of the ZR⁻² Coulomb force acting on the degenerate one-centre states of the target atom. This force has the same decay law with distance R as the centrifugal energy of an electron. This makes it possible to construct “dynamic” terms of the system evolving under the action of the indicated forces, parametrically depending on the relative velocity of the nuclei [5].

Thus, we can speak of the charge exchange transition directly into these dynamic terms, which directly take into account the effects of the rotation of the internuclear axis.

However, further analysis showed that the charge exchange process, especially at low energies, is extremely sensitive to the structure of electronic terms, and the one-centre approximation becomes insufficient. In this regard, numerous calculations have been performed on the two-centre basis of wave functions. These calculations use a more general symmetry of the two-centre Coulomb problem associated with the separation of variables in hyperspherical coordinates. In view of the complex nature of the dependence of the terms on the internuclear distance, the corresponding calculations are carried out by numerical methods.

In this work, we present the results of such calculations for the charge exchange of atomic hydrogen in the ground and first excited states on the nuclei of beryllium, which is the main impurity element of the planned thermonuclear tokamak reactor. At the same time, a comparison is made both with the results of calculations in the one-centre model and with two-centre models among themselves. Such a comparison allows one to judge the limits of applicability of models based on the use of one- and two-centre symmetries of the Coulomb field.

For the calculation of the charge exchange cross sections for slow collisions, the ARSENY code, based on the method of hidden crossings, is used [3]. In the adiabatic approximation, radial inelastic transitions occur in the regions of the closest approach of potential curves and are decomposed into a sequence of individual two-level transitions via hidden crossings. Electronic energies are the eigenvalues of the two-centre Coulomb problem [4], which is separable in the prolate spheroidal coordinates and is solved for the complex internuclear distance R.

In the adiabatic theory, the charge exchange transitions occur at the internuclear distances where the electronic wave function changes rapidly. This happens when the non-adiabatic coupling has its maximum. Transitions caused by the radial coupling take place in the hidden crossings (branch points) at complex internuclear separation R, where the electronic energies of two states are equal. Hidden crossings arise when the full-dimensional classical trajectory of the electron collapses into an unstable periodic orbit. They are invisible on the plot of the adiabatic potential curves at the real value of the adiabatic parameter R and require direct calculation in the complex R-plane.

Rotational coupling, associated with the rotation of the internuclear axis in close collisions, induces transitions between electronic states, which are degenerate in the limit of the united atom. The potential curves of these states have an exact crossing at complex R values (Re(R) = 0). Since the scattering angle depends on the reduced mass, the trajectories of the heavy particles in the reactions with H, D and T are different. This, in turn, leads to a difference in the corresponding cross sections.

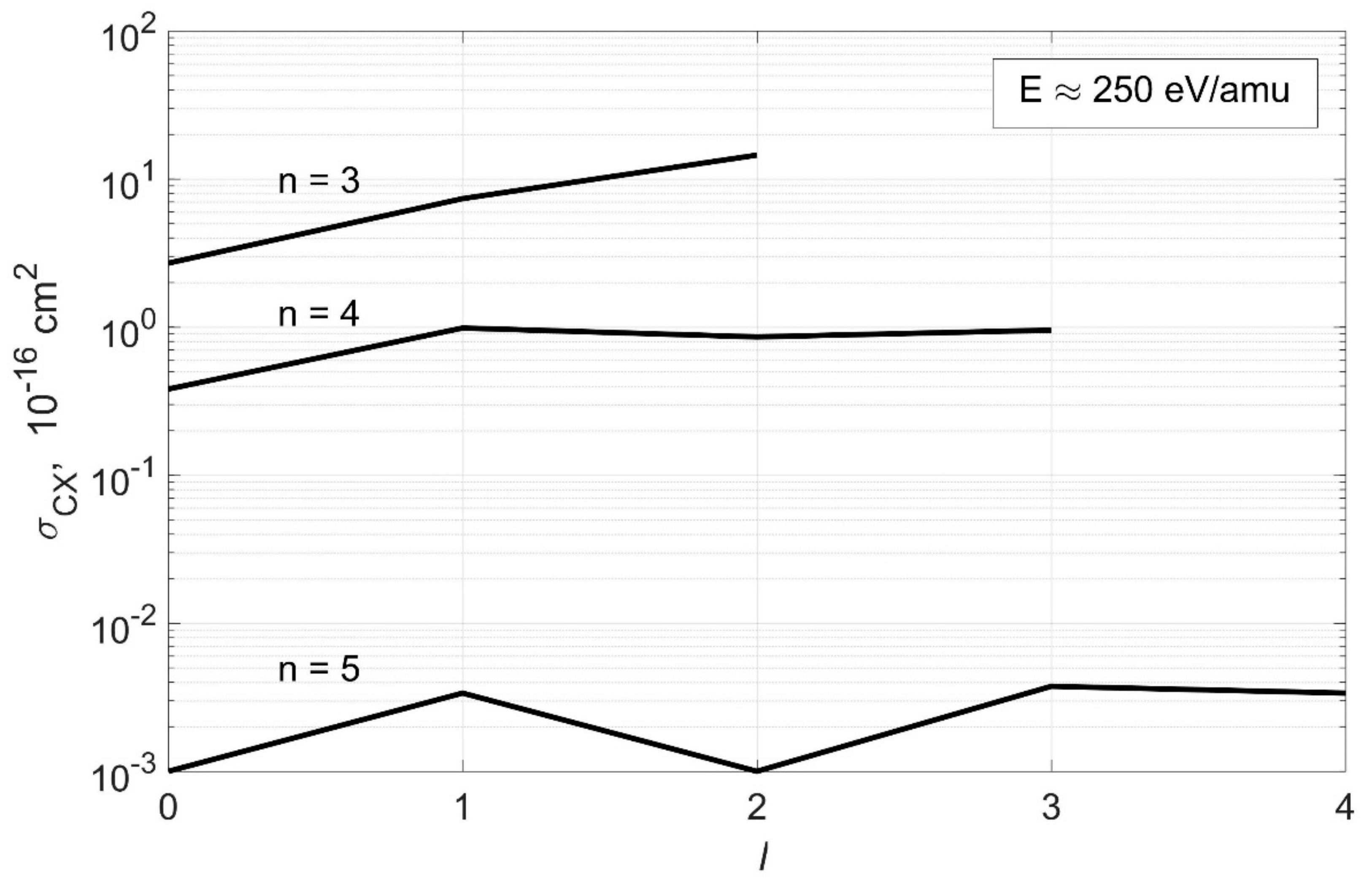
3. Results

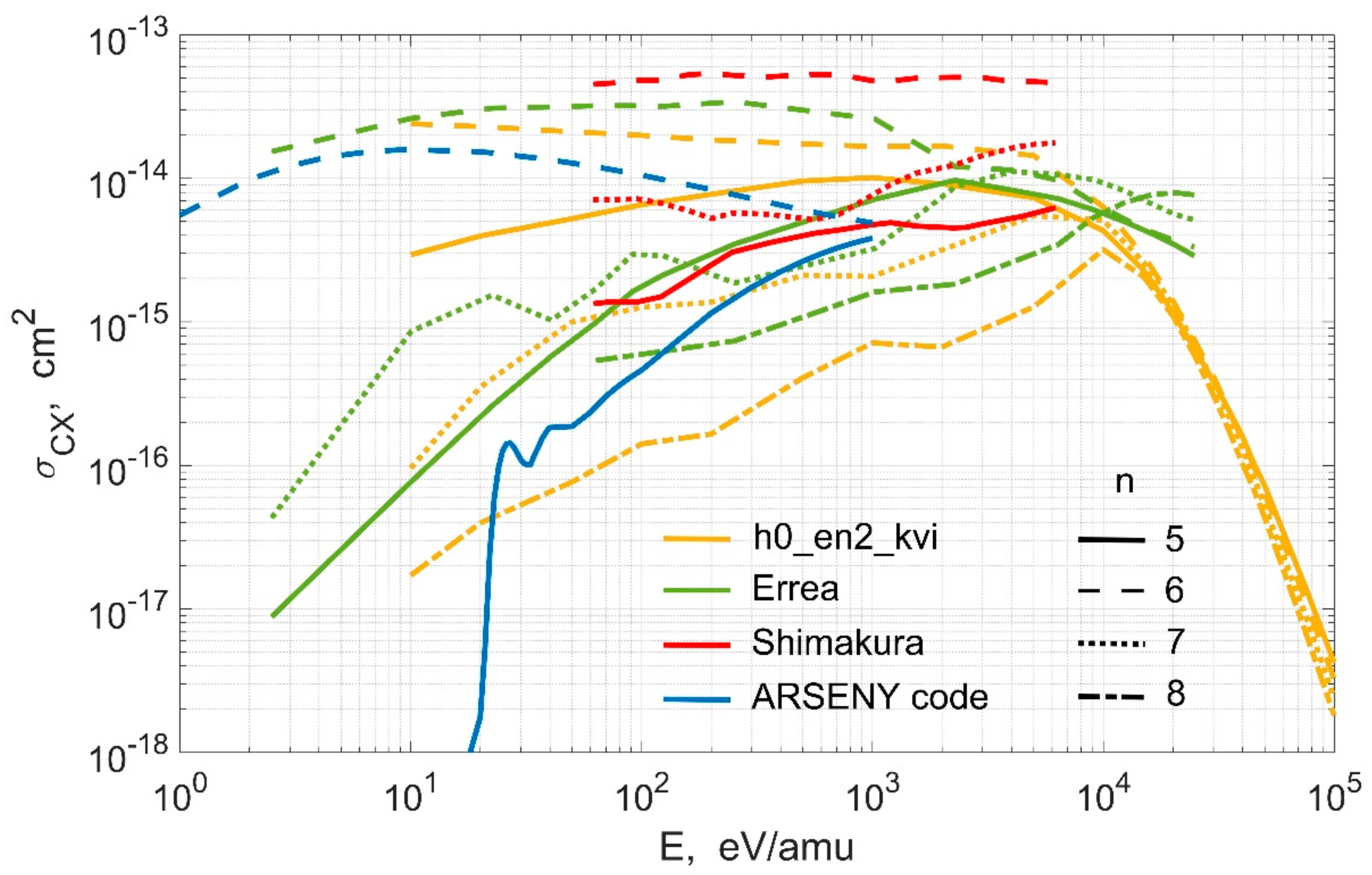
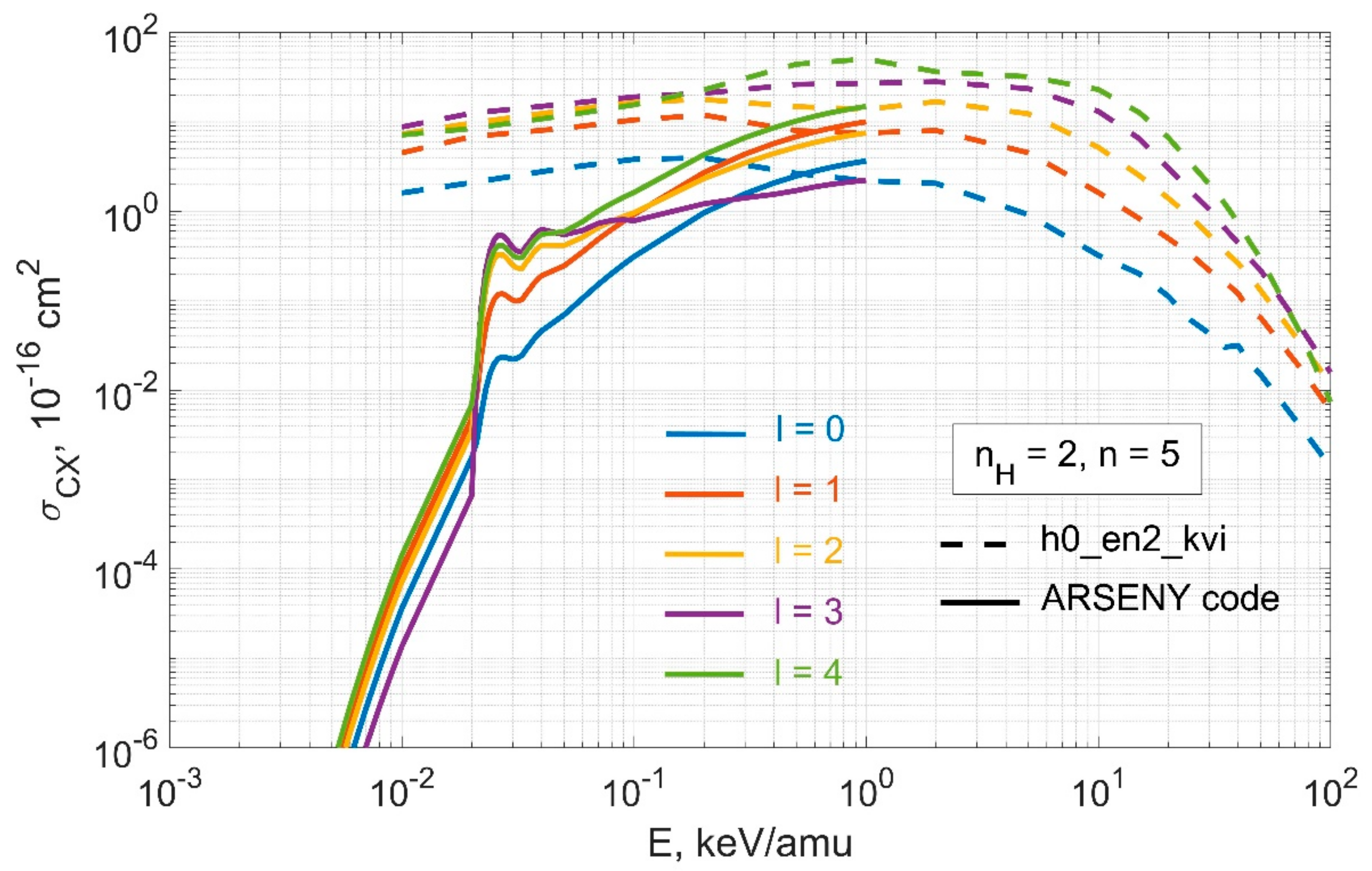
3.1. A Brief Review of the Data Available in OPEN-ADAS

The figures in this section show the data for the cross sections for reaction (2), taken from the OPEN-ADAS database [6,7], and their comparison with cross sections from various sources, depending on the relative velocity v and the collision energy E, expressed in units of eV/amu (amu stands for the atomic mass unit). Collision energy E = 2.5 eV/amu corresponds to the relative velocity of colliding particles v ≈ 0.01 a.u. (1 a.u. ≈ 2.188 10⁶ m/s); collision energy E = 1 keV/amu corresponds to v ≈ 0.2 a.u.

Figure 1 shows a comparison of the data on the charge exchange cross sections for hydrogen in the ground state, taken from the OPEN-ADAS database [6,7], paper [8], with calculations within the one-centre model [5].

The curve names (“ory” and “old”) in the legend in Figure 1 refer to the filename in OPEN-ADAS [6,7] from which the data were taken. The files in OPEN-ADAS have names such as qcx#h0_*#be4.dat, where instead of * are the words specified in the legend. Thus, if the curve is labeled “ory” in the legend, it means that it is plotted from the data from the qcx#h0_ory#be4.dat file. The green curves (solid for the population of the atomic level with principal quantum number n = 3 and dotted for the population of level with n = 4) show the data from Errea 1998 [8], where the results for cross sections at low collision energies are available. The yellow curve shows the result of calculations within the one-centre model [5] for populating at the level of n = 3.

From Figure 1, one can see that the data available in OPEN-ADAS cover the region of medium and high collision energies, while data for low energies are not available.

Figure 2 presents a comparison of the data from the OPEN-ADAS database for charge exchange cross sections for hydrogen in the ground and excited states.

Figure 2 shows that the charge exchange cross sections for hydrogen in the excited state are higher than those for hydrogen in the ground state. In the first case, the largest cross section corresponds to the charge exchange with the population of level with the principal quantum number n = 6, in the second—the level with n = 3.

Figure 3, Figure 4, Figure 5 show the data from the qcx#h0_en2_kvi#be4.dat file from OPEN-ADAS for charge exchange from excited hydrogen with a population of levels with different n and l. In Figure 3, one can see a comparison of these data with cross sections from several other sources, while Figure 4 and Figure 5 show a detailed l-resolved comparison with calculations with the ARSENY code.

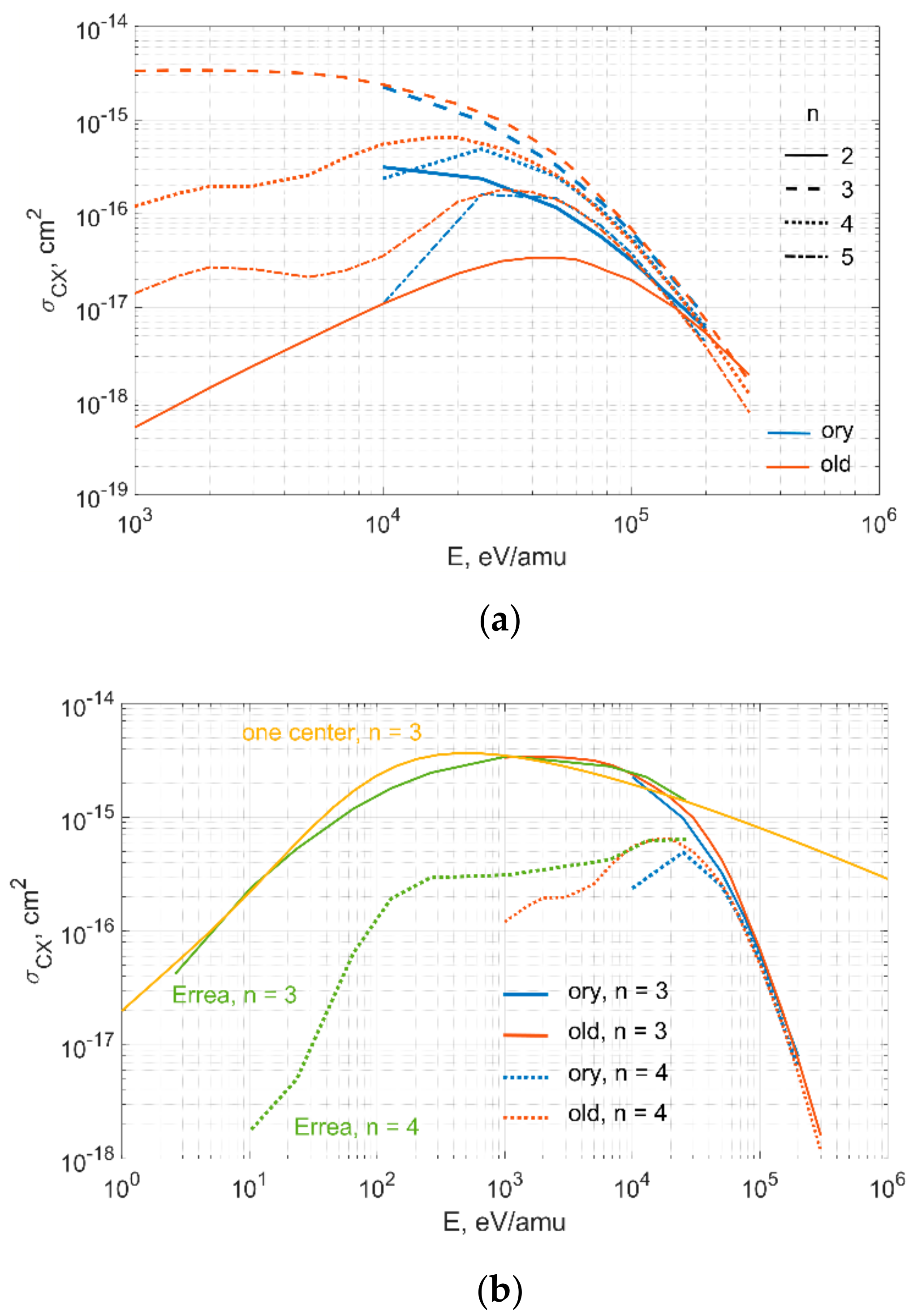
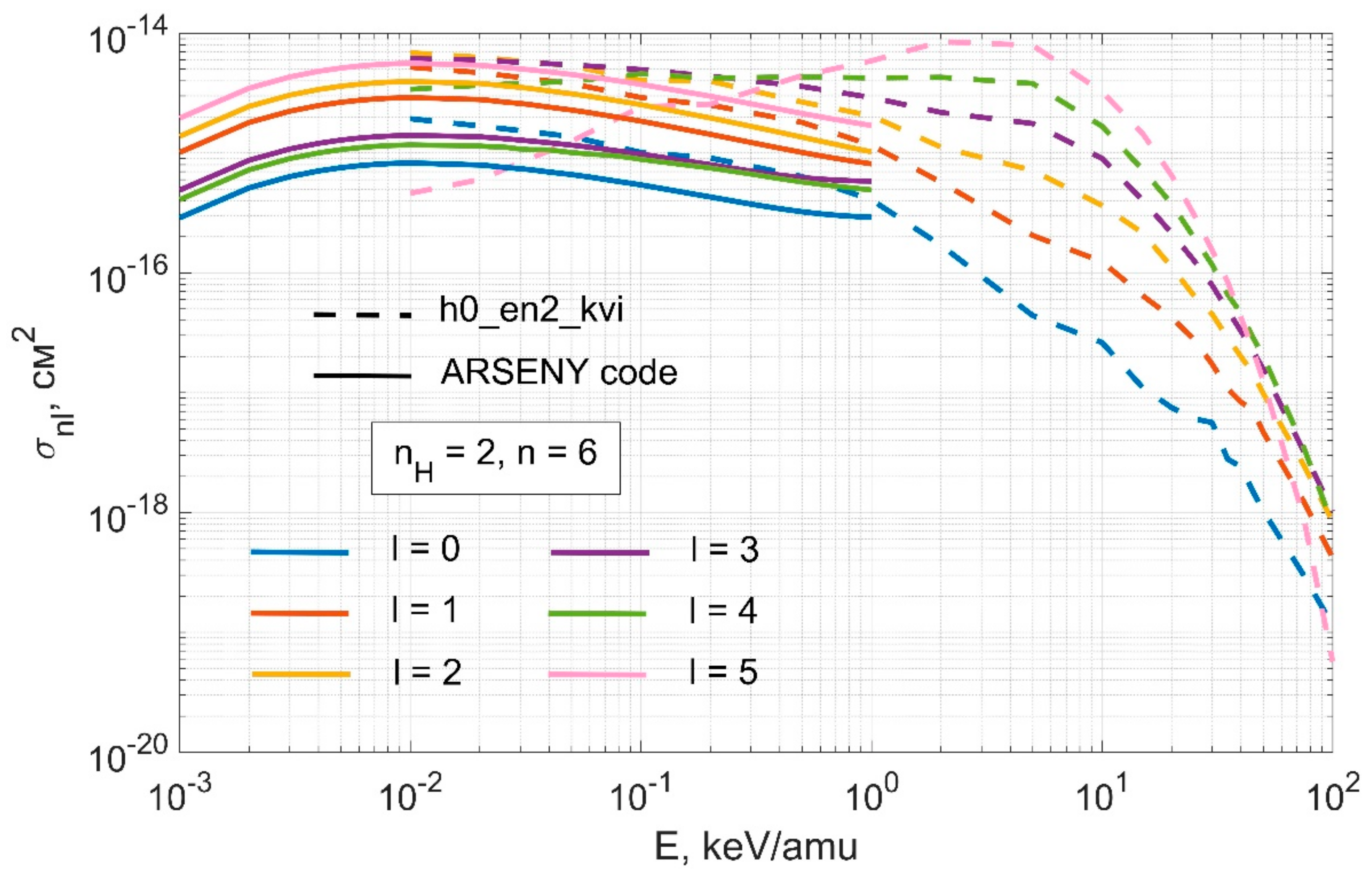
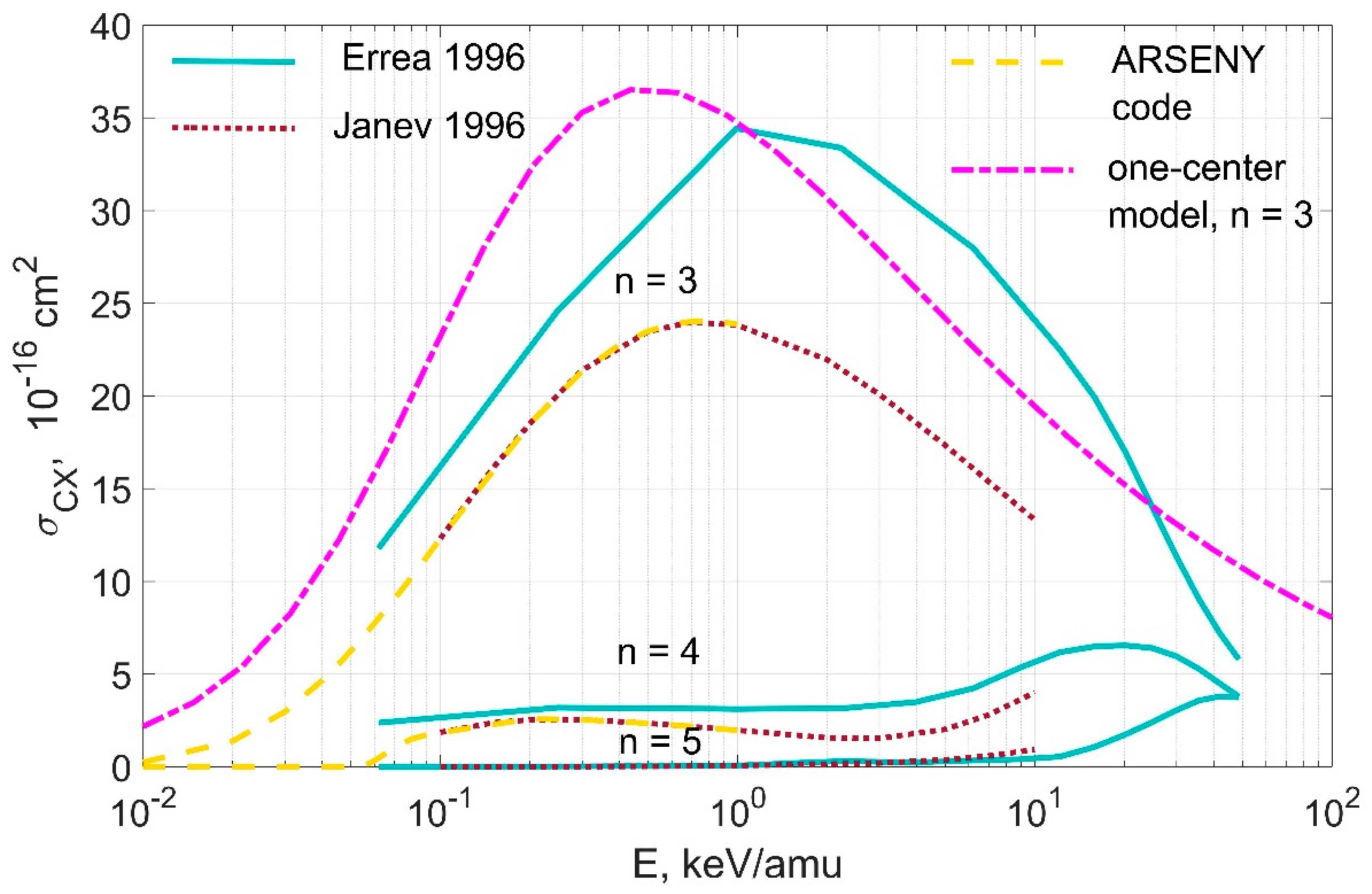
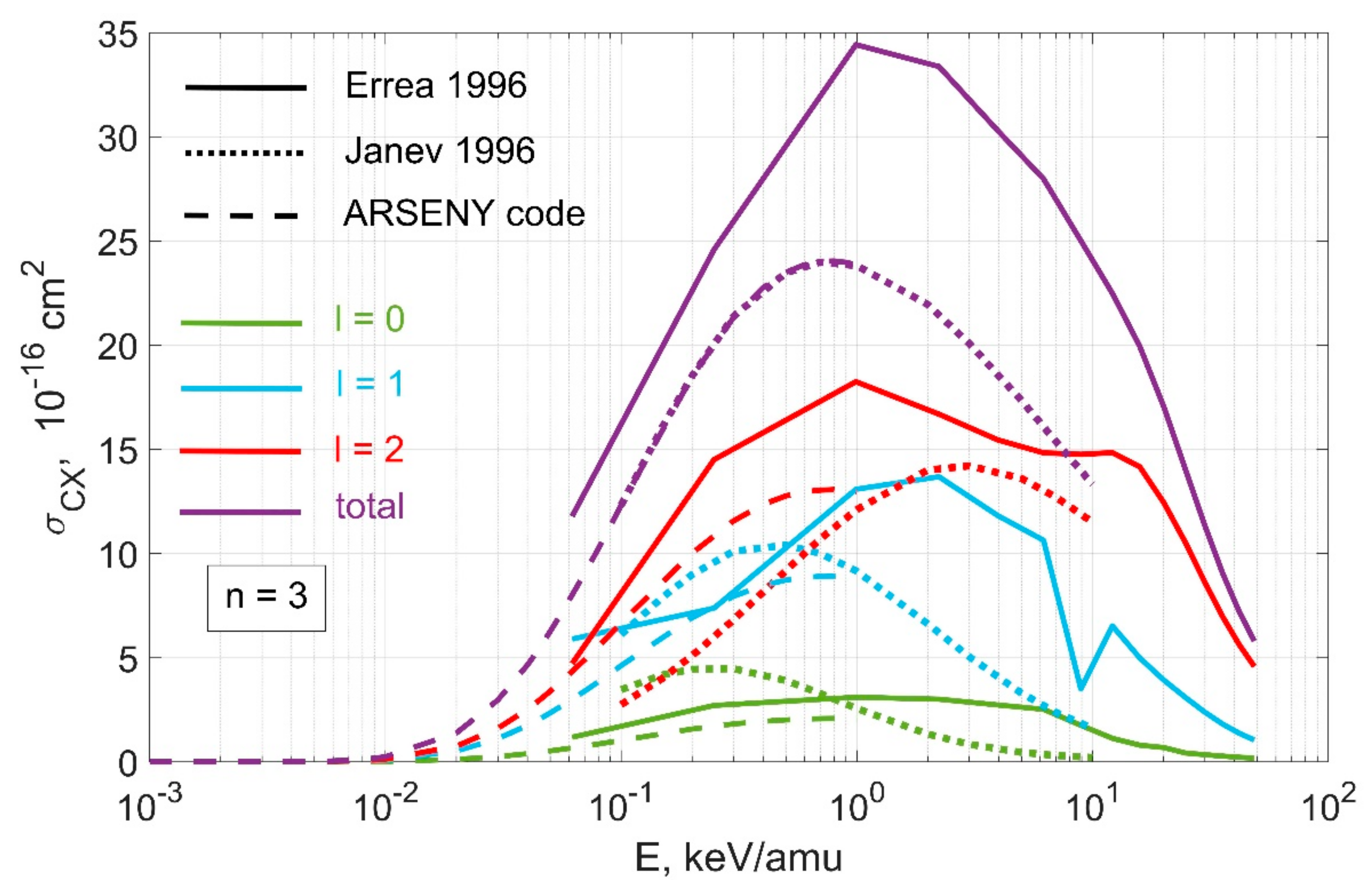
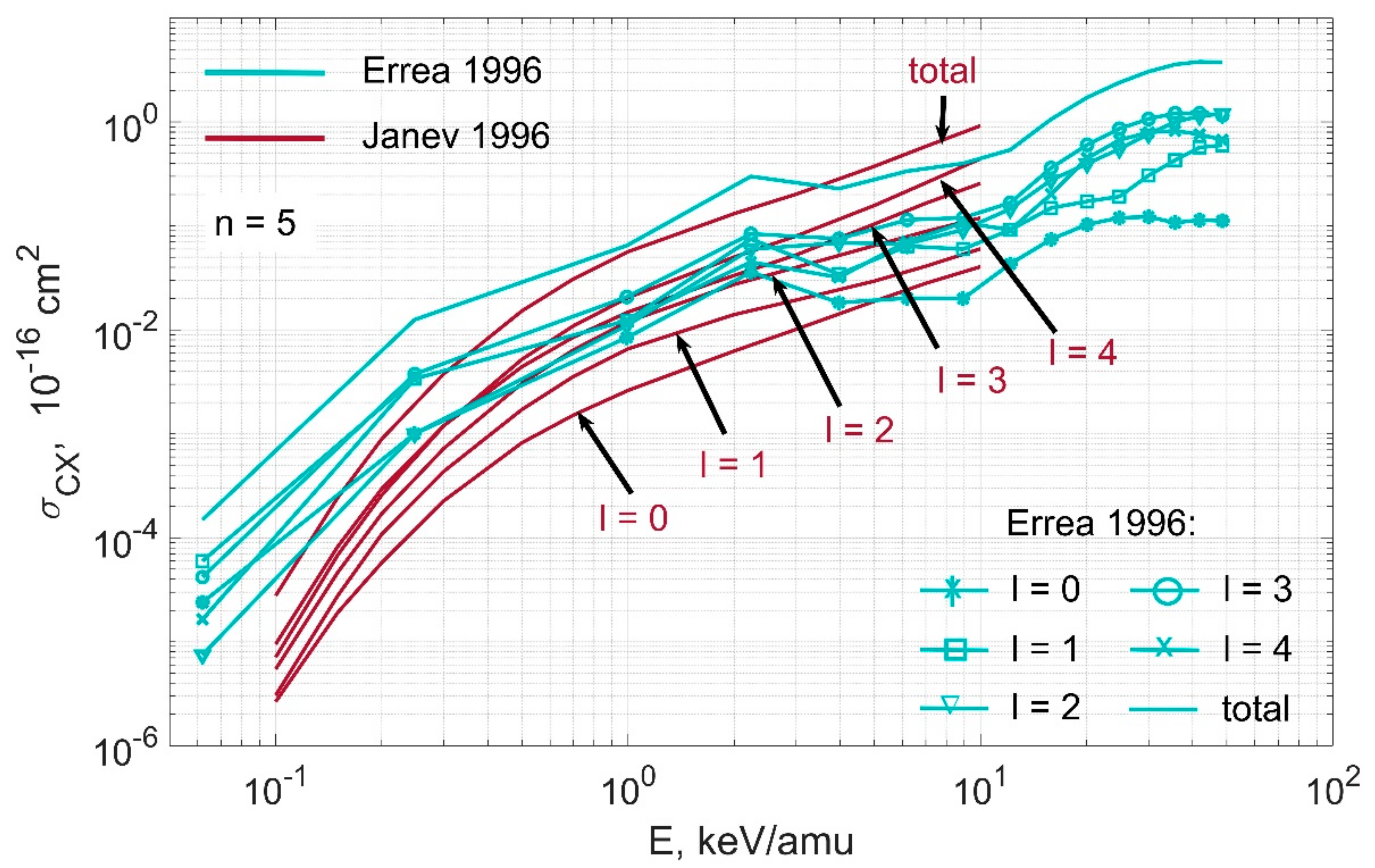
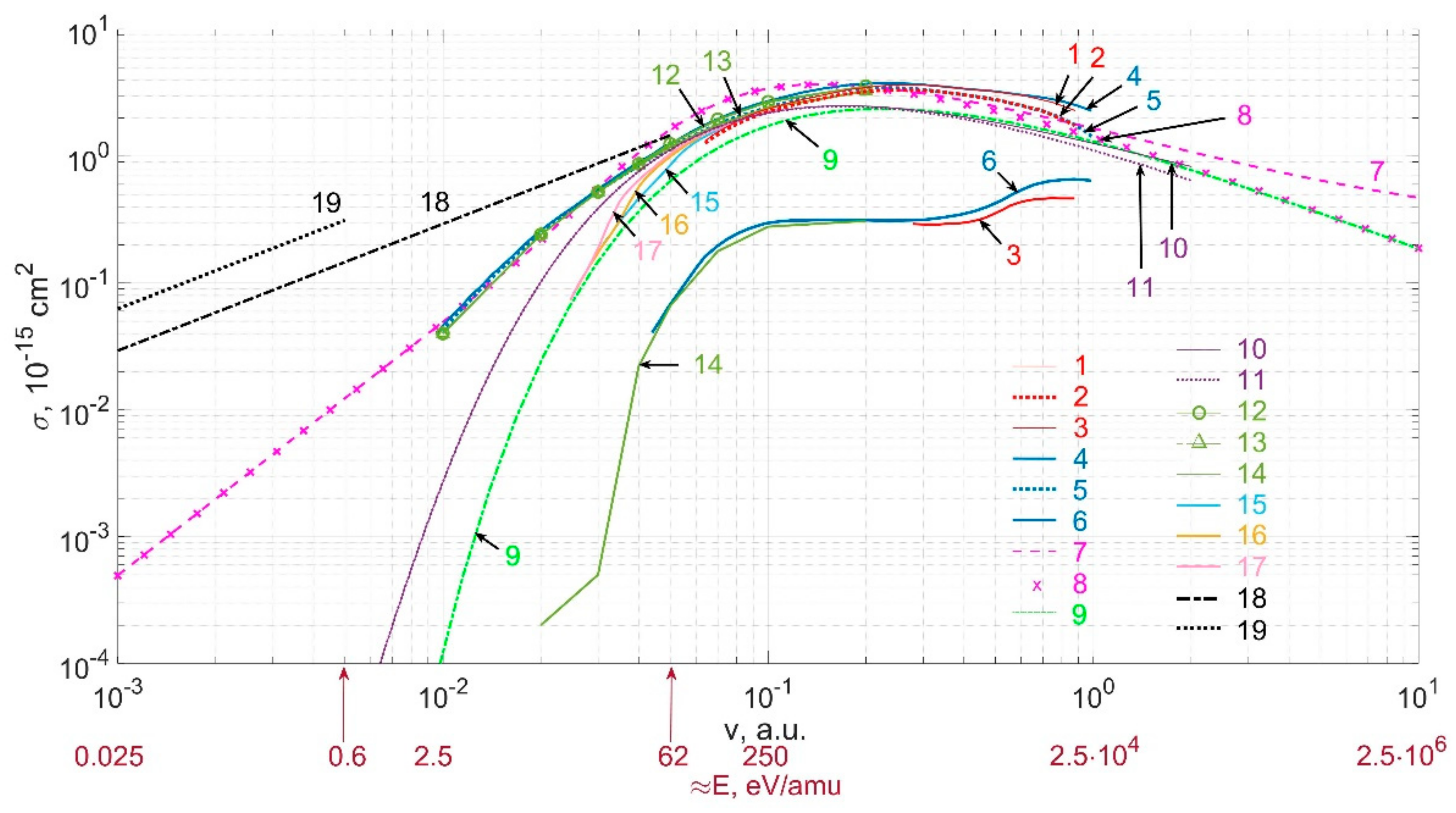
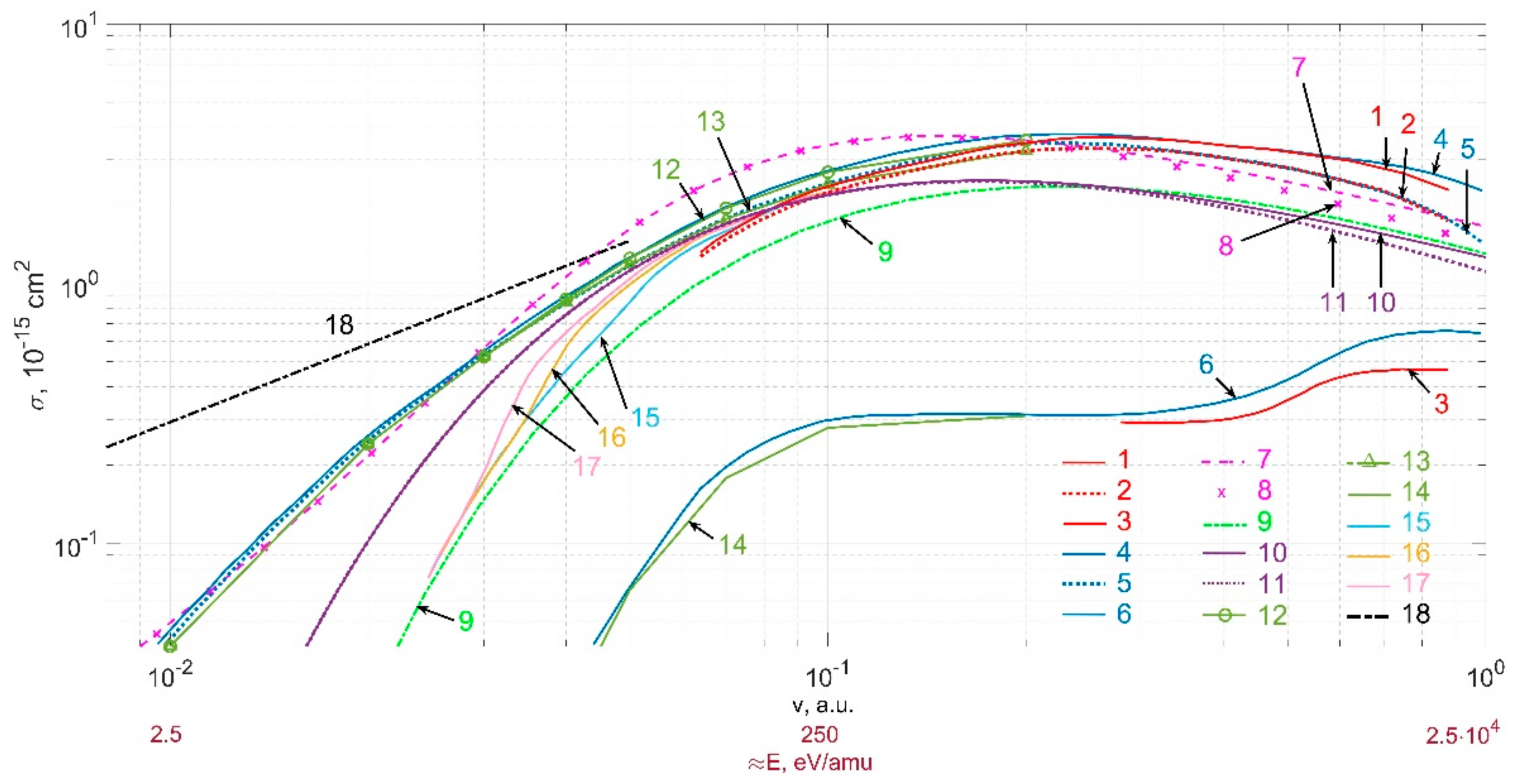
3.2. Comparison of Cross Sections from Special Issue of Physical Scripta

Figure 6, Figure 7, Figure 8, Figure 9 below show the comparison of charge exchange cross sections for reaction (2), taken from [10] and [11]. Figure 10 shows the dependence of charge exchange cross sections for reaction (2) on the orbital quantum number l for different values of the principal quantum number n.

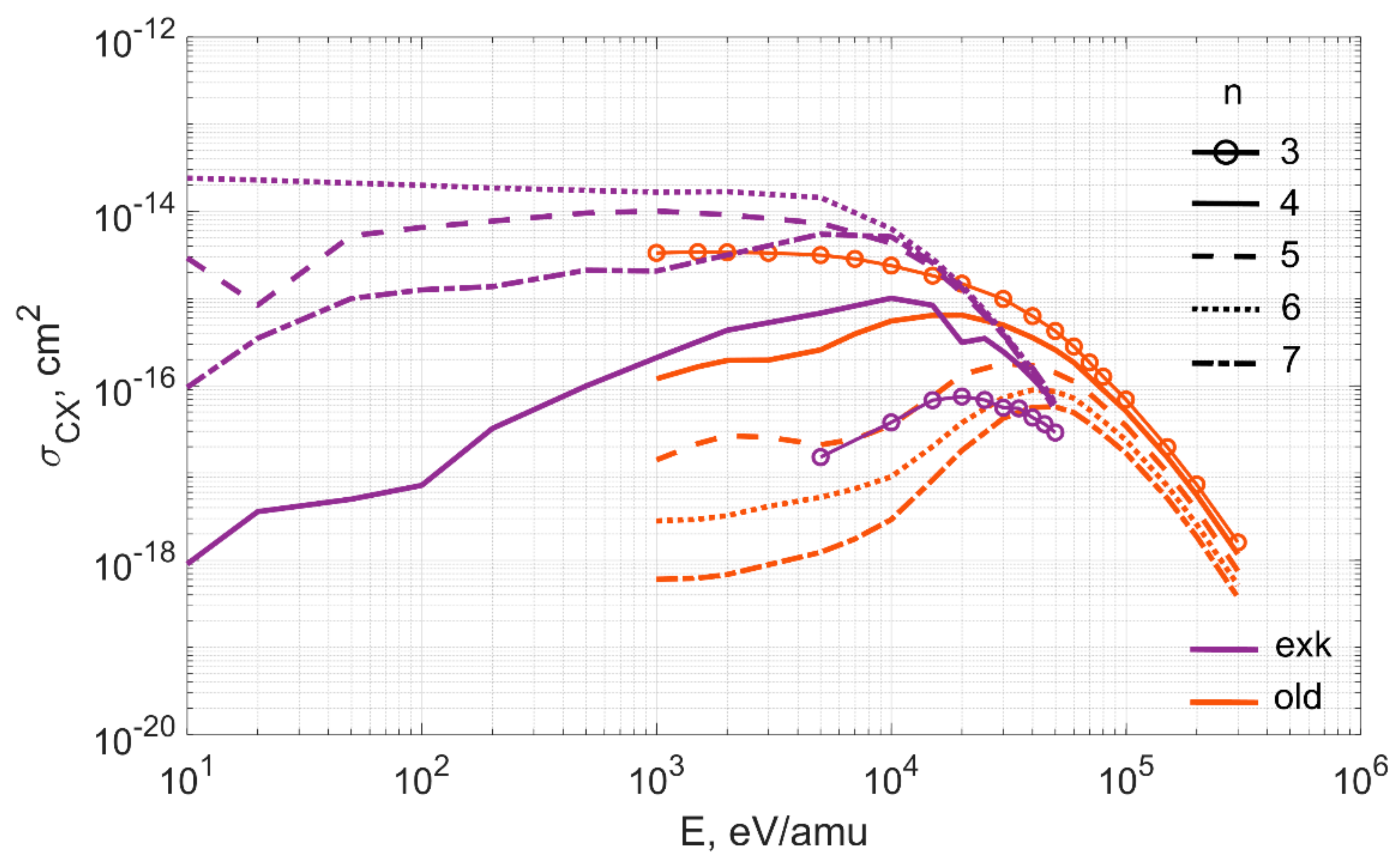
3.3. A Survey of Data on Cross Sections from Various Sources

It can be seen from the Figures in previous subsections that in the range of collision energies below 100 eV/amu, there is practically no data resolved in orbital quantum numbers l.

Figure 11 and Figure 12 show a comparison of the charge exchange cross sections calculated by various methods for reaction (2), taken from various sources.

The notations of the curves in Figure 11 and Figure 12 are as follows. Curves 1, 2 and 3 stand for the calculation [12] of the total cross section and partial cross sections for n = 3 and n = 4, respectively, using 21-state atomic-orbital expansion. Curves 4, 5 and 6 stand for the calculation [8] of the total cross section and partial cross sections for n = 3 and n = 4, respectively, using molecular expansion with semiclassical and quantal calculations for 96- and 17-state basis sets. Curves 7 and 8 stand for our calculations of the total cross section and partial cross section for n = 3, respectively, in the frame of the Landau-Zener model with rotation taken into account [5], while curve 9 is the same but without rotation taken into account [5]. Curves 10 and 11 stand for the total cross section and partial cross section for n = 3, respectively, according to the Kronos database [13]; the model is described in [14]. Curves 12, 13 and 14 stand for the calculation [15] of the total cross section and partial cross sections for n = 3 and n = 4, respectively, using the hyperspherical close-coupling (HSCC) approach. Curve 15 stands for the calculation [16] for hydrogen; curve 16 stands for the calculation [16] for deuterium Be⁴⁺ + D⁰(1s) → Be³⁺(n) + D⁺ (for more details on the isotopic effect see, e.g., [19] or review [20]); the curve 17 stands for the calculation [16] for tritium: Be⁴⁺ + T⁰(1s) → Be³⁺(n) + T⁺; calculations were performed in the framework of the adiabatic theory of transitions in slow collisions using the ARSENY code, based on the hidden crossings method. The curve 18 stands for low velocities asymptotic (2.18) in [5] with |b₊(R)/b₋(R)| = 1, n = 3, Z = 4, R₀ = R_{n = 3}, where R_n is defined by (2.2) in [5]; V is defined by (1.1) in [5].

4. Discussion

In the lack of experimental data, special attention must be paid to the accuracy and reliability of calculations. The most reliable are the results obtained using the atomic/molecular orbital method or their variations. One of the drawbacks of calculations by the Landau-Zener model is the impossibility of calculating the cross sections for charge exchange with the population of levels with the principal quantum number n ≥ Z, where Z is the ion charge.

Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 in Section 3.1 show the data for the cross section for reaction (2) taken from the OPEN-ADAS database [6,7] and their comparison both with each other and with the cross sections from several other sources. Figure 1 also shows the calculations within the one-centre model [5], while Figure 4 and Figure 5 show a detailed l-resolved comparison with calculations using the ARSENY code [3,4].

Section 3.2 is devoted to a comparison of the cross sections from [10,11], calculations in the framework of the one-centre model, and calculations using the ARSENY code are presented there as well.

Figure 11 and Figure 12 in Section 3.3 show a survey of data for cross sections, taken from various sources with different models and approaches used for calculations.

It can be seen from Section 3 that in the literature and existing databases (e.g., OPEN-ADAS [6,7]), most of the available information on the charge exchange cross sections covers the range of energies of interest primarily for calculating the active signal of the Charge eXchange Recombination Spectroscopy (CXRS), i.e., for diagnostic beams with energies of tens and hundreds of keV. At the same time, for estimates of the passive charge exchange signal (see, e.g., the recently proposed algorithm [21]), when the energy of neutral atoms coming from the wall is in the range from few eV to tens or hundreds of eV, the data are not enough, especially for l-resolved data. Therefore, for the charge exchange reactions of interest, additional theoretical calculations of the cross sections may be necessary, which are needed for simulations of level populations of the emitting beryllium ions Be³⁺ using two-dimensional, in principal and orbital quantum numbers, kinetic codes, such as the nl-KINRYD code [22].

5. Conclusions

An analysis of the available data on the cross sections of the charge exchange reaction of bare beryllium nuclei on hydrogen isotopes was carried out. The dependence of the cross sections on the relative nuclear energy, which are selective both in the principle and orbital momentum quantum numbers, were presented in a wide range of relative energies that are relevant for the CXRS diagnostics of the beryllium impurity, the main component of the plasma facing materials in the thermonuclear tokamak-reactor ITER. The charge exchange cross sections from the first excited energy states of hydrogen were presented as well. The approaches based on one- and two-centres Coulomb symmetry were discussed in detail. A comparison was made of a number of modern approaches to simulations of charge exchange cross sections. It was shown that there was a lack of data in the region of low (below 100 eV/amu) collision energies for beryllium, which is now reduced due to calculations using the ARSENY code. However, there is still a lack of data in the entire space of states (populations of other states in beryllium, and other impurities, such as carbon), which is of interest for modelling the passive charge exchange signal of the CXRS diagnostic of impurities in the ITER tokamak and other thermonuclear fusion facilities.