Abstract
The present paper concerns the general solution for finite plane strain pure bending of incompressible, orthotropic sheets. In contrast to available solutions, the new solution is valid for inhomogeneous distributions of plastic properties. The solution is semi-analytic. A numerical treatment is only necessary for solving transcendent equations and evaluating ordinary integrals. The solution’s starting point is a transformation between Eulerian and Lagrangian coordinates that is valid for a wide class of constitutive equations. The symmetric distribution relative to the center line of the sheet is separately treated where it is advantageous. It is shown that this type of symmetry simplifies the solution. Hill’s quadratic yield criterion is adopted. Both elastic/plastic and rigid/plastic solutions are derived. Elastic unloading is also considered, and it is shown that reverse plastic yielding occurs at a relatively large inside radius. An illustrative example uses real experimental data. The distribution of plastic properties is symmetric in this example. It is shown that the difference between the elastic/plastic and rigid/plastic solutions is negligible, except at the very beginning of the process. However, the rigid/plastic solution is much simpler and, therefore, can be recommended for practical use at large strains, including calculating the residual stresses.
1. Introduction
Sheet metal forming processes usually include bending. A brief review of typical sheet metal forming processes that incorporate bending is provided in [1]. The process of bending is also an essential test for identifying material properties, for example [2,3,4,5,6,7,8,9,10]. Theoretical analyses of the bending process are necessary for interpreting test results.
An exact rigid perfectly plastic solution for finite pure plane strain bending and plane strain bending under tension of sheets has been found in [11]. This solution has been adopted in [12] for deriving a closed form expression for strain at any fiber. This paper has concluded that the basic assumptions made in [11] are plausible. The solution [11] has been extended to many material models. Of primary interest for the present paper are solutions for anisotropic materials and inhomogeneous sheets. A brief review of such solutions is given below.
Elastic and plastic anisotropy is a typical property of many metallic and non-metallic materials [13,14,15,16]. A solution for pure plane strain bending of anisotropic sheets has been derived in [17]. The model adopted incorporates the Bauschinger effect and strain hardening. Plastic anisotropy is described by Hill’s quadratic yield criterion [11]. It has been found that the effect of plastic anisotropy on the bending moment is rather significant. Papers [18,19] present an analysis of elastic/plastic bending of orthotropic sheets. Elastic properties are isotropic, and plastic yielding obeys Hill’s quadratic yield criterion [11]. A more detailed review of solutions for plane strain bending of anisotropic sheets is provided in [20]. An extension of the solutions above has been proposed in [21] where tension/compression asymmetry of plastic properties has been considered. All these solutions are for homogeneous sheets.
Several solutions are available for piecewise homogenous sheets. The pure bending of bonded laminated metals under plane strain conditions has been considered in [22,23]. Different rigid plastic material models have been adopted in these papers. Elastic properties have been taken into consideration in [24]. This paper emphasizes the prediction of springback. The distribution of residual stresses in bilayer sheets after bending has been found in [25]. A simplified solution for bending and subsequent unloading of bilayer sheets has been proposed in [26].
Different methods have been employed to get the solutions above. A unified approach for analyzing finite pure plane strain bending has been developed in [27]. The approach applies to a broad class of incompressible materials. In particular, the corresponding solutions for anisotropic and bilayer sheets have been found in [28] and [29], respectively.
In many cases, the through-thickness distribution of material properties in sheets is non-uniform but, in contrast to [22,23,24,25,26], is described by continuous functions [30]. Using the approach [27], the pure bending of isotropic elastic/plastic functionally graded sheets has been analyzed in [31]. The present paper extends this solution to anisotropic sheets. In addition, a rigid/plastic model is considered. The general solution involves quite an arbitrary through-thickness distribution of plastic properties. The numerical example is based on the experimental data presented in [32]. In the case of the rigid/plastic solution, the prediction of residual stresses can be made using the methodology proposed in [33] and further developed and discussed in [34]. According to this methodology, for computing residual stresses in a deformation process, the elasticity is neglected during the process’s loading phase. It is shown that the solution for purely elastic unloading is not valid even for a relatively large inside radius.
2. Statement of the Problem
A metallic sheet is bent under plane strain conditions by two couples M, as shown in Figure 1. The initial shape of the sheet in the planes of flow is a rectangular of thickness H and width 2L.
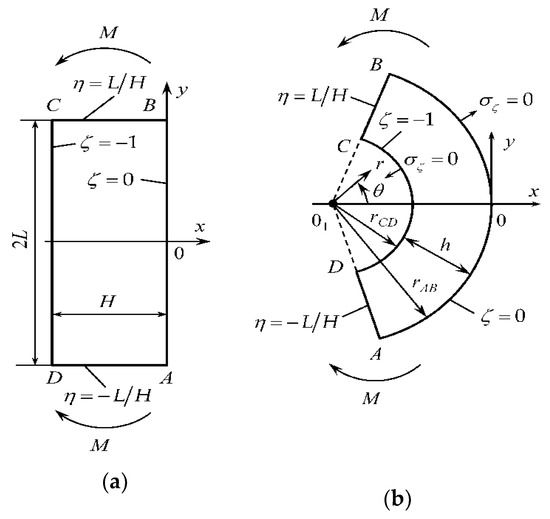
Figure 1.
Schematic diagram of the pure bending process: (a) initial configuration, (b) intermediate and final configurations.
Curves AB and CD are circular arcs, and AD and BC are straight throughout the process of deformation (except the initial instant when AB and CD are straight). It has been shown in [27] that the following equations describe the transformation of the initial shape into the shape after any amount of strain:
Here are Eulerian Cartesian coordinates and are Lagrangian coordinates. Additionally, a is a time-like variable such that at the initial instant and s is a function of a. The latter should be found from the solution. The x-axis is an axis of symmetry of the process. The Cartesian coordinate system’s origin is situated at the intersection of the axis of symmetry and curve AB. At the initial instant,
This condition is satisfied if
at . It is convenient to introduce a plane polar coordinate system with the origin at and . It follows from (1) that
It is seen from (2) and Figure 1 that on curve AB and on curve CD throughout the process of deformation. The radii of circular arcs AB and CD are determined from (4) as
respectively. The transformation (1) satisfies the equation of incompressibility.
Let and be the normal stresses referred to the Lagrangian coordinate system. This coordinate system is orthogonal, and the normal stresses and are the principal stresses. The principal axes of anisotropy coincide with the x—and y—axes at the initial instant. Then, according to the model proposed in [35], the principal anisotropy axes coincide with the and coordinate curves throughout the process of deformation. Under plane strain conditions, the anisotropic yield criterion proposed in [11] reads
Here T is the shear yield stress with respect to the and coordinate curves, and c is expressed through the yield stresses in the principal anisotropy axes’ directions [11]. Both T and c depend on . It is convenient to represent T as where is constant with the dimensions of stress. Then, Equation (6) becomes
where
The transformation equations between the and coordinate systems in (1) satisfy the flow rule associated with the yield criterion (7).
Let and be the principal components of the total strain rate tensor. This tensor is the sum of the elastic and plastic strain rate tensors. Then,
The superscript e denotes the elastic portion of the strain rate components and the superscript p the plastic portion. The elastic portion is related to the stress components as
Here the superimposed dot denotes the convected derivative, is the hydrostatic stress and G is the shear modulus of elasticity. Since the material is incompressible, . Then, Equation (10) becomes
The only stress equilibrium equation which is not identically satisfied in the polar coordinate system is
It is evident from (4) that and . Therefore, Equation (12) becomes
The boundary conditions are
for (or ) and (or ).
The bending moment is determined as
3. General Solution
Using (1), one can immediately find the total principal strains as
Using (4), one transforms Equation (13) to
and Equation (15) to
It is worthy of note that if in (7), as follows from [11].
3.1. Purely Elastic Solution
In the case of the purely elastic solution, and in (11). The solution of Equations (11) and (17) supplemented with the equation of strain compatibility is [36]
Here and C is constant.
3.2. Solution in Plastic Regions Where
In this case, the yield criterion (7) becomes
Substituting this equation into (17) leads to
One integrates this equation to get
Here is a dummy variable of integration and
at . Equations (20) and (22) combine to give
3.3. Solution in Plastic Regions Where
In this case, the yield criterion (7) becomes
Substituting this equation into (17) leads to
One integrates this equation to get
where
at . Equations (25) and (27) combine to give
4. Initiation of Plastic Yielding
The entire sheet is elastic at the beginning of the process. In this case, the solution (19) is valid in the range . Therefore, this solution should satisfy the boundary conditions in Equation (14). Then,
Eliminating C between these equations yields
Solving this equation for s and then using any of the equations in (30), one gets
Substituting (32) into (19) supplies the principal stresses’ through-thickness distribution at any value of a. This solution is valid if the yield criterion is not violated in the range . Equations (7) and (19) combine to give
where
If is a monotonically increasing or decreasing function of its argument, then the yield criterion may violate at , or , or and simultaneously. The corresponding conditions are
Here the upper sign corresponds to monotonically increasing functions, and the lower sign to monotonically decreasing functions.
Let and be the values of a and s, respectively, that correspond to plastic yielding initiation. These values are readily found from (32) and (35) if the function is prescribed. In particular, if the distribution of material properties is symmetric relative to the surface , then and it follows from the third case in (35) that . The latter equation coincides with (31). Therefore, if the distribution of material properties is symmetric relative to the surface , then the initiation of plastic yielding occurs at and simultaneously.
If the has a local minimum or maximum, then one should consider the possibility of the initiation of plastic yielding at such points, in addition to the points and . The initiation of plastic yielding at where occurs if
Here . Using (19) and (34), one transforms Equation (36) to
or
Here . The equations in (37) combine to give
Then, Equation (32) supplies as a function of . One can replace a and s in the second equation in (37) with and , respectively, to arrive at the equation for . This equation should be solved numerically. Then, is readily determined from (39).
One applies the same procedure to (38) for determining , , and . In particular,
If and , then .
In what follows, it is assumed that .
5. Rigid Plastic Solution
For many applications, it is possible to assume that the inelastic behavior is dominant and to neglect the elastic response [37,38]. In this case, the general solution given in Section 3 simplifies. There are two plastic regions throughout the process of deformation. The inequality is valid in one of these regions, and the inequality in the other. The neutral line separates the plastic regions. The stress is discontinuous across the neutral line.
Let be the neutral line. It has been shown in [27] that
The solution (27) is valid in the region . This solution should satisfy the boundary condition (14) at . Then, and in (27), and this equation becomes
Consequently, Equation (29) becomes
The solution (22) is valid in the region . This solution should satisfy the boundary condition (14) at . Then, and in (22), and this equation becomes
Consequently, Equation (24) becomes
The stress must be continuous across the neutral line. Then, Equations (41), (42) and (44) combine to give
Since W is a known function of its argument, this equation is an ordinary differential equation for determining s as a function of a. However, its form is non-standard. To develop a numerical method for solving (46), it is advantageous that one considers the initial instant separately. The distribution of the stress at the initial instant is illustrated in Figure 2. The stress vanishes everywhere.
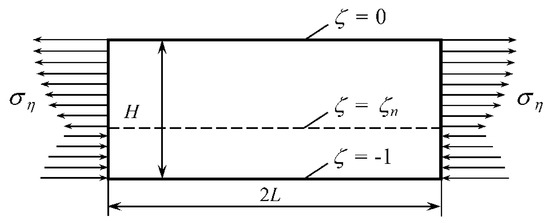
Figure 2.
Distribution of the stress ση at the initial instant.
Then, it follows from (7) that
In the case of pure bending, equilibrium demands
Substituting (47) into (48) and using (41) yields
This equation should be solved for . In general, a numerical method should be used. However, in some cases, an analytic solution is available. For example, if W is constant then at the initial instant. If the distribution of material properties is symmetric relative to the central plane of the sheet, then is an even function of Z where and . In this case, Equation (49) becomes
Integrating gives
where is the anti-derivative of . Therefore, is an odd function of Z and . Then, it follows from (51) that
at the initial instant.
Using (47), the bending moment at the initial instant is determined as
If the distribution of material properties is symmetric relative to the central plane of the sheet, then Equation (53) becomes
Here Equation (52) has been taken into account.
Assume that one needs to find the solution of (46) at . Let the interval be subdivided into an arbitrary number of small segments by the points . The values of s and at are denoted as and , respectively. It is convenient to choose these points a constant distance apart. Let the value of , , and be known. Then, . The value of can be approximated as
Equation (46) at becomes
One can eliminate in (56) using (55). The resulting equation contains one unknown, . This equation should be solved numerically. Then, is readily determined from (55). Having found and , one can apply the procedure above to find the solution at . This procedure should be repeated until becomes equal to . It remains to find the input data for the first step. It is evident that and . It follows from (3) that . The solution of (49) supplies . However, if the distribution of material properties is symmetric relative to the central plane of the sheet, then , as follows from (52).
6. Unloading
Consider purely elastic unloading. Variations of the shape are neglected during this stage of the process. At the end of loading, , , and . The corresponding values of the inside and outside radii are denoted as and , respectively. The distribution of and at is denoted as and . All the quantities introduced above can be calculated using the solution given in the previous sections.
The general solution for the increment of the principal stresses from the configuration corresponding to is independent of the solution at loading. Therefore, one may adopt the solution for the plane strain bending under tension provided in [36] assuming the tensile force vanishes. In our nomenclature, this solution reads
where . Equation (4), in which a should be replaced with and s with , supplies the dependence of r on . The distribution of residual stresses is given by
After calculating the residual stresses, it is necessary to verify that the yield criterion is not violated in the range . The corresponding condition follows from (7) in the form
7. Practical Example
The through-thickness distribution of the coefficients involved in Hill’s quadratic yield criterion [11] has been experimentally determined in rolled sheets of Al-Mg-Si alloy in [32]. The distribution is symmetric relative the central plane of the sheets. In our nomenclature, Table 1 represents the results from [32]. It is seen from this table that the function W is non-monotonic in each half of the sheet. This discrete function is approximated to the following continuous function:

Table 1.
Through-thickness distribution of W.
It is worthy to note that the experimental data were first approximated by an even function of and then Equation (60) was derived. The numerical solution has been found using the general solutions described in Section 3, Section 4, Section 5 and Section 6 and (60). In all calculations, .
It has been found that . Two plastic regions initiate in the vicinity of the inside and outside surface almost simultaneously and quickly propagate to the corresponding stress-free surface. This stage of the process is very short and is not significant for bending at large strains. The solution with three regions (two plastic regions and an elastic region between them) starts at . At , the plastic region adjacent to the surface (plastic region 1) occupies the domain and the plastic region adjacent to the surface (plastic region 2) occupies the domain . The elastic region occupies the domain . Thus and are the elastic/plastic boundaries. Both and depend on a.
The distribution of and in plastic region 1 follows from (22) and (24), and in plastic region 2 from (27) and (29). Using the boundary conditions in (14), one finds that , ,, and . The stresses and must be continuous across the elastic/plastic boundaries. This requirement is equivalent to the requirement that and are continuous across the elastic/plastic boundaries. Using (19), (20), (22), (24), (25), (27) and (29), one can represent the latter as
One can eliminate C between the first two equations. In the resulting equation, and can be eliminated using the third and fourth equations. Then,
Moreover, the third and fourth equations in (61) can be solved for a and s. As a result,
One can now eliminate a and s in (62) using (63). The resulting equation contains the two unknowns, and . A numerical solution of this equation supplies the dependence of on . Having found this dependence, a and s are readily calculated from (63) giving , , and s as functions of a in implicit form. Then, C is determined from the first equation in (61). It has been found that and at . It is more informative to use as a time-like variable instead of a. Equation (5) allows one to replace a with with no difficulty. The variation of and with is depicted in Figure 3. It is seen from this figure that the thickness of the elastic region decreases with very quickly. In particular, this thickness is less than 0.8% of the sheet’s initial thickness when (e.g., the inside radius of the sheet is 25 times larger than the sheet’s initial thickness). The through-thickness distribution of and at is shown in Figure 4 and Figure 5, respectively. In these figures, X is the dimensionless distance from the inside surface of the sheet defined as
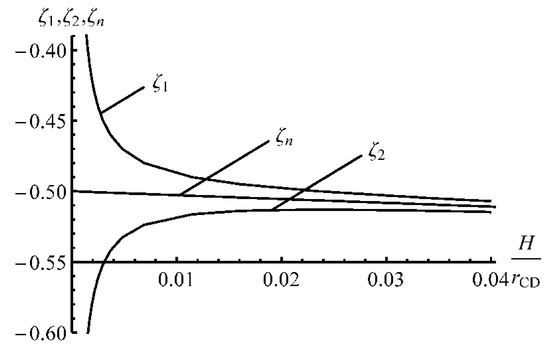
Figure 3.
Variation of the locations of the elastic/plastic boundaries and the neutral line with H/rCD at the beginning of the process.
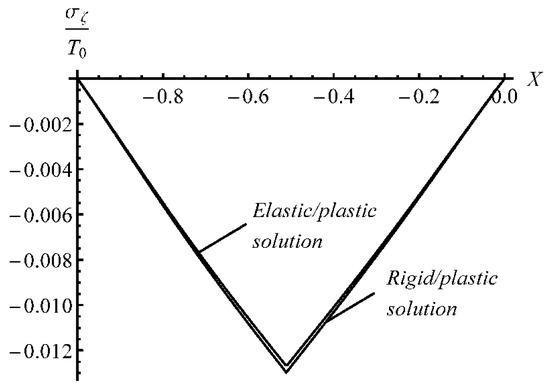
Figure 4.
Distribution of the stress σζ at H/rCD = 0.04 found using the elastic/plastic and rigid/plastic solutions.
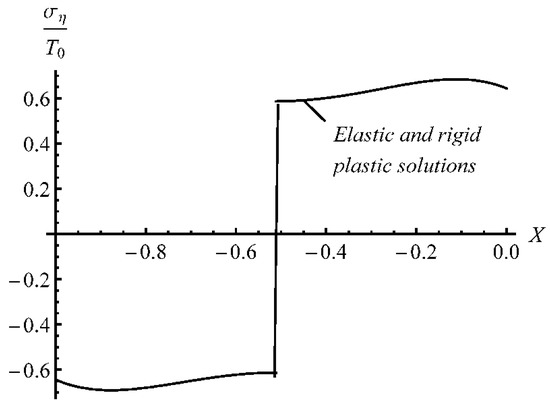
Figure 5.
Distribution of the stress ση at H/rCD = 0.04 found using the elastic/plastic and rigid/plastic solutions.
Using the numerical procedure described in Section 5, s and have been found as functions of a. Then, Equation (5) has been used to replace a with . The dependence of on in the range is depicted in Figure 3. It is seen from this figure that the neutral line found from the rigid/plastic solution is located between the two elastic/plastic boundaries found from the elastic/plastic solution.
The dependence of on in the range is shown in Figure 6. It is seen from this figure that the location of the neutral line changes very quickly at the beginning of the process but gradually at large . The through-thickness distribution of and at is shown in Figure 4 and Figure 5, respectively. It is seen from Figure 4 that the difference between the elastic/plastic and rigid/plastic solutions is insignificant. The difference is most considerable near the neutral line in the rigid/plastic solution, and the rigid/plastic solution predicts a slightly higher value of than the elastic/plastic one. The difference between the elastic/plastic and rigid/plastic solutions is invisible in Figure 5. The through-thickness distribution of and at several stages of the process found by means of the rigid/plastic solution is shown in Figure 7 and Figure 8, respectively. The maximum value of significantly increases as the deformation proceeds.
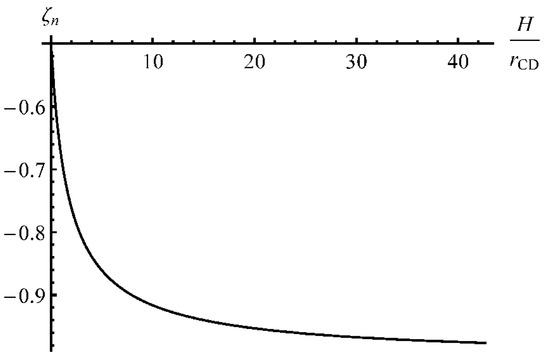
Figure 6.
Variation of the location of the neutral line with H/rCD.
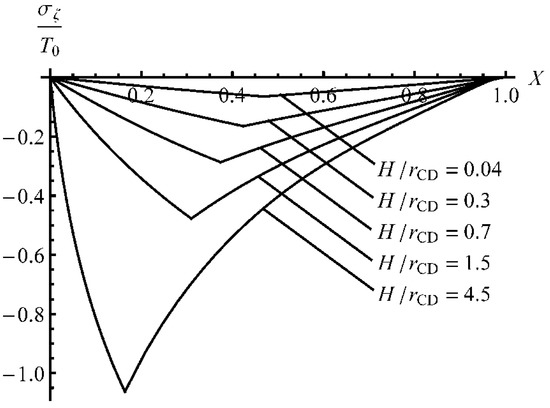
Figure 7.
Distribution of the stress σζ at several stages of the process.
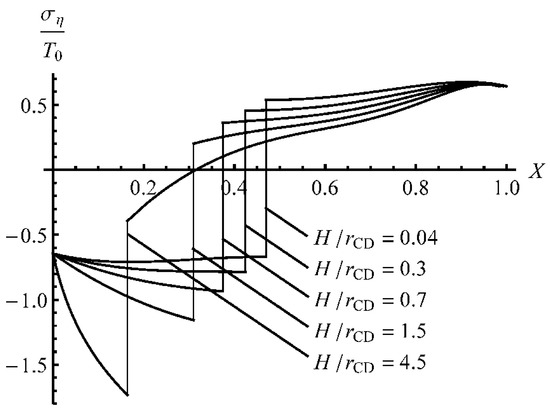
Figure 8.
Distribution of the stress ση at several stages of the process.
The distribution of has a weak local maximum in the vicinity of the outside surface, which may affect bendability. Having found the stress solution, one can calculate the bending moment using (18). The variation of the dimensionless bending moment with is depicted in Figure 9. It is seen from this figure that the dimensionless bending moment changes very quickly at the beginning of the process but gradually at large . Its value attains a local minimum around .
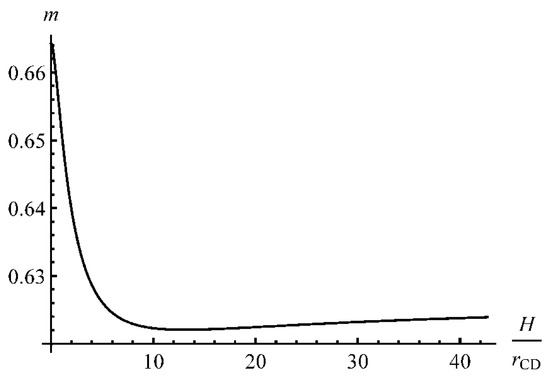
Figure 9.
Variation of the dimensionless bending moment with H/rCD.
The procedure described in Section 6 has been applied to calculate the distribution of residual stresses. The methodology proposed in [34] has been adopted. Figure 4 and Figure 5 justify the validity of this methodology. These calculations have shown that inequality (59) is not satisfied with relatively large values of , requiring consideration of reversed yielding. In particular, even if , inequality (59) is not satisfied at a narrow region near the neutral line.
8. Conclusions
A general semi-analytic solution for finite pure plane strain bending of a sheet made of incompressible material has been found. A distinguished feature of this solution is that the sheet is plastically anisotropic and inhomogenous. No restriction of the through-thickness distribution of plastic properties is imposed. Both elastic/plastic and rigid/plastic models have been considered. It has been shown that the difference between the elastic/plastic and rigid/plastic solutions is negligible, except at the very beginning of the process. Since the rigid/plastic solution is much simpler than the elastic/plastic one, it is recommended to use rigid/plastic models at large strains. It is possible even if residual stresses should be calculated. In this case, the methodology proposed in [34] can be adopted. The numerical example uses real material properties provided in [32]. The through-thickness distribution of these properties is symmetric relative to the center line of the original sheet. The through-thickness stress distributions are illustrated in Figure 4, Figure 5, Figure 7 and Figure 8. It is seen from Figure 5 and Equation (18) that the difference between the bending moment found using the elastic/plastic and rigid/plastic solutions is negligible if , at least.
An advantage of the general solution is that it is valid for an arbitrary distribution of material properties. Therefore, in conjunction with experimental data, this solution can be readily used for identifying these properties.
It is crucial to predict springback in bending followed by unloading accurately [39]. The solution for purely elastic unloading is not valid for all cases considered, and it is necessary to consider the appearance of reversed yielding. The latter will be the subject of a subsequent investigation.
Author Contributions
Conceptualization, S.A.; writing, Y.-M.H.; formal analysis, E.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was made possible by the grants RFBR-19-51-52003 (Russia), MOST 108-2923-E-110-002-MY3 (Taiwan), and AAAA-A20-120011690136-2 (Russia).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ikumapayi, O.M.; Akinlabi, E.T.; Madushele, N.; Fatoba, S.O. A brief overview of bending operation in sheet metal forming. In Advances in Manufacturing Engineering; Lecture Notes in Mechanical Engineering; Emamian, S., Awang, M., Yusof, F., Eds.; Springer: Singapore, 2020; pp. 149–159. [Google Scholar] [CrossRef]
- Yoshida, F.; Urabe, M.; Toropov, V.V. Identification of material parameters in constitutive model for sheet metals from cyclic bending tests. Int. J. Mech. Sci. 1998, 40, 237–249. [Google Scholar] [CrossRef]
- Brown, J.A.; Vendra, L.J.; Rabiei, A. Bending properties of al-steel and steel-steel composite metal foams. Met. Mater. Trans. A 2010, 41, 2784–2793. [Google Scholar] [CrossRef]
- Murphey, T.W.; Peterson, M.E.; Grigoriev, M.M. Large strain four-point bending of thin unidirectional composites. J. Spacecr. Rockets 2015, 52, 882–895. [Google Scholar] [CrossRef]
- Capilla, G.; Hamasaki, H.; Yoshida, F.; Suzuki, T.; Okamura, K. Determination of the anisotropic hardening of sheet metals at large strain from stretch bending test. Key Eng. Mater. 2016, 725, 677–682. [Google Scholar] [CrossRef]
- Capilla, G.; Hamasaki, H.; Yoshida, F. Determination of uniaxial large-strain workhardening of high-strength steel sheets from in-plane stretch-bending testing. J. Mater. Process. Technol. 2017, 243, 152–169. [Google Scholar] [CrossRef]
- Nie, D.; Lu, Z.; Zhang, K. Mechanical properties and microstructure evolution during bending–unbending deformation of pure titanium sheet. J. Mater. Eng. Perform. 2018, 27, 705–713. [Google Scholar] [CrossRef]
- Alves, M.M.; Abreu, L.M.; Pereira, A.B.; De Morais, A.B. Determination of bilinear elastic-plastic models for an acrylic adhesive using the adhesively bonded 3-point bending specimen. J. Adhes. 2019, 1–16. [Google Scholar] [CrossRef]
- Somà, A.; Saleem, M.M. Elastic–plastic characterization of microstructures through pull-in 4 point bending test. J. Micromech. Microeng. 2019, 29, 025004. [Google Scholar] [CrossRef]
- Trzepieciński, T. Effect of the plastic strain and drawing quality on the frictional resistance of steel sheets. Acta Metallurgica Slovaca 2020, 26, 42–44. [Google Scholar] [CrossRef]
- Hill, R. The Mathematical Theory of Plasticity; Clarendon Press: Oxford, UK, 1950. [Google Scholar]
- Yeh, G.C.K. Large plastic strains in sheet-bending. Int. J. Non-Linear Mech. 1971, 6, 393–399. [Google Scholar] [CrossRef]
- Habraken, A.M. Modelling the plastic anisotropy of metals. Arch. Comput. Meth. Eng. 2004, 11, 3–96. [Google Scholar] [CrossRef]
- Szymczyk, M.; Nowak, M.; Sumelka, W. Numerical study of dynamic properties of fractional viscoplasticity model. Symmetry 2018, 10, 282. [Google Scholar] [CrossRef]
- Yu, F.; Liu, Y. DFT Calculations of the structural, mechanical, and electronic properties of TiV alloy under high pressure. Symmetry 2019, 11, 972. [Google Scholar] [CrossRef]
- Lu, W.; Zhu, Z.; Que, X.; Zhang, C.; He, Y. anisotropic constitutive model of intermittent columnar jointed rock masses based on the cosserat theory. Symmetry 2020, 12, 823. [Google Scholar] [CrossRef]
- Tan, Z.; Persson, B.; Magnusson, C. Plastic bending of anisotropic sheet metals. Int. J. Mech. Sci. 1995, 37, 405–421. [Google Scholar] [CrossRef]
- Chakrabarty, J.; Lee, W.B.; Chan, K.C. An analysis of the plane-strain bending of an orthotropic sheet in the elastic/plastic range. J. Mater. Process. Tech. 2000, 104, 48–52. [Google Scholar] [CrossRef]
- Chakrabarty, J.; Lee, W.B.; Chan, K.C. An exact solution for the elastic/plastic bending of anisotropic sheet metal under conditions of plane strain. Int. J. Mech. Sci. 2001, 43, 1871–1880. [Google Scholar] [CrossRef]
- Yu, T.X.; Zhang, L.C. Plastic Bending: Theory and Applications; World Scientific: Singapore, 1996; 572p. [Google Scholar] [CrossRef]
- Ahn, K. Plastic bending of sheet metal with tension/compression asymmetry. Int. J. Solids Struct. 2020, 204–205, 65–80. [Google Scholar] [CrossRef]
- Verguts, H.; Sowerby, R. The pure plastic bending of laminated sheet metals. Int. J. Mech. Sci. 1975, 17, 31–51. [Google Scholar] [CrossRef]
- Majlessi, S.A.; Dadras, P. Pure plastic bending of sheet laminates under plane strain condition. Int. J. Mech. Sci. 1983, 25, 1–14. [Google Scholar] [CrossRef]
- Yuen, W.Y.D. A generalised solution for the prediction of springback in laminated strip. J. Mater. Process. Tech. 1996, 61, 254–264. [Google Scholar] [CrossRef]
- Joudaki, J.; Sedighi, M. A closed-form analytical solution for residual stresses due to the bending of bilayer sheets. Arch. Appl. Mech. 2020, 90, 1349–1361. [Google Scholar] [CrossRef]
- Kagzi, S.A.; Gandhi, A.H.; Dave, H.K.; Raval, H.K. An analytical model for bending and springback of bimetallic sheets. Mech. Adv. Mater. Struct. 2015, 23, 80–88. [Google Scholar] [CrossRef]
- Alexandrov, S.; Kim, J.-H.; Chung, K.; Kang, T.-J. An alternative approach to analysis of plane-strain pure bending at large strains. J. Strain Anal. Eng. 2006, 41, 397–410. [Google Scholar] [CrossRef]
- Alexandrov, S.; Hwang, Y.-M. The bending moment and springback in pure bending of anisotropic sheets. Int. J. Solids Struct. 2009, 46, 4361–4368. [Google Scholar] [CrossRef]
- Alexandrov, S.; Kien, N.D.; Manh, D.V.; Grechnikov, F.V. Plane strain bending of a bimetallic sheet at large strains. Struct. Eng. Mech. 2016, 58, 641–659. [Google Scholar] [CrossRef]
- Elishakoff, I.; Pentaras, D.; Gentilini, C. Mechanics of Functionally Graded Material Structures; World Scientific: Singapore, 2016; 340p. [Google Scholar] [CrossRef]
- Alexandrov, S.; Wang, Y.-C.; Lang, L. A theory of elastic/plastic plane strain pure bending of FGM sheets at large strain. Materials 2019, 12, 456. [Google Scholar] [CrossRef]
- Kitamura, K.; Terano, M. Determination of local properties of plastic anisotropy in thick plate by small-cube compression test for precise simulation of plate forging. CIRP Ann. 2014, 63, 293–296. [Google Scholar] [CrossRef]
- Zienkiewicz, O.; Jain, P.; Oñate, E. Flow of solids during forming and extrusion: Some aspects of numerical solutions. Int. J. Solids Struct. 1978, 14, 15–38. [Google Scholar] [CrossRef]
- Lee, Y.; Dawson, P.R. Obtaining residual stresses in metal forming after neglecting elasticity on loading. ASME. J. Appl. Mech. 1989, 56, 318–327. [Google Scholar] [CrossRef]
- Collins, I.F.; Meguid, S.A. On the influence of hardening and anisotropy on the plane-strain compression of thin metal strip. ASME J. Appl. Mech. 1977, 44, 271–278. [Google Scholar] [CrossRef]
- Alexandrov, S.; Manabe, K.; Furushima, T. A general analytic solution for plane strain bending under tension for strain-hardening material at large strains. Arch. Appl. Mech. 2011, 81, 1935–1952. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Godbole, P.N. Flow of plastic and visco-plastic solids with special reference to extrusion and forming processes. Int. J. Numer. Methods Eng. 1974, 8, 25. [Google Scholar] [CrossRef]
- Druyanov, B.; Nepershin, R. Problems of Technological Plasticity; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Le, H.; Vu, D.; Doan, P.; Le, K. Effect of springback in DP980 advanced high strength steel on product precision in bending process. Acta Metall. Slovaca 2019, 25, 150–157. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).