Discrete-Time Pole-Region Robust Controller for Magnetic Levitation Plant
Abstract
1. Introduction
2. Preliminaries and Problem Formulation
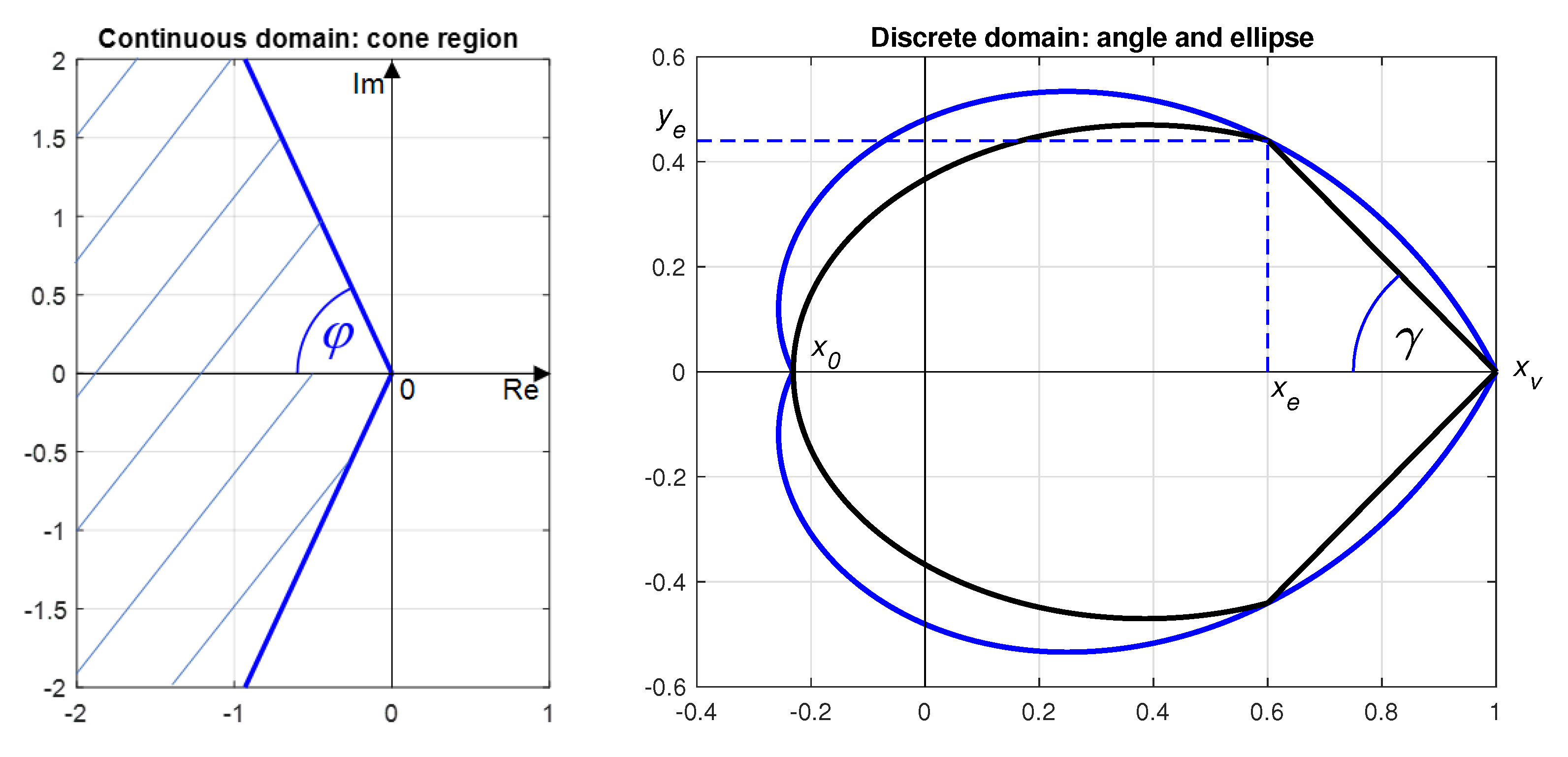
2.1. Regions
- Open left-half plane of the complex plane, (continuous-time systems),
- Interior of the unit circle, (discrete-time systems),
- Shifted left-half plane of the complex plane corresponding to stability degree ,(continuous-time systems),
- Interior of the circle centered in [0,0] with radius corresponding to stability degree , (discrete-time systems),
- Interior of the convex cone with vertex angle , corresponding to the relative damping (given by a ratio of the imaginary and real part of the complex pole in continuous-time systems)
2.2. Performance Evaluation
3. Magnetic Levitation Plant
4. Robust Controller Design for Magnetic Levitation
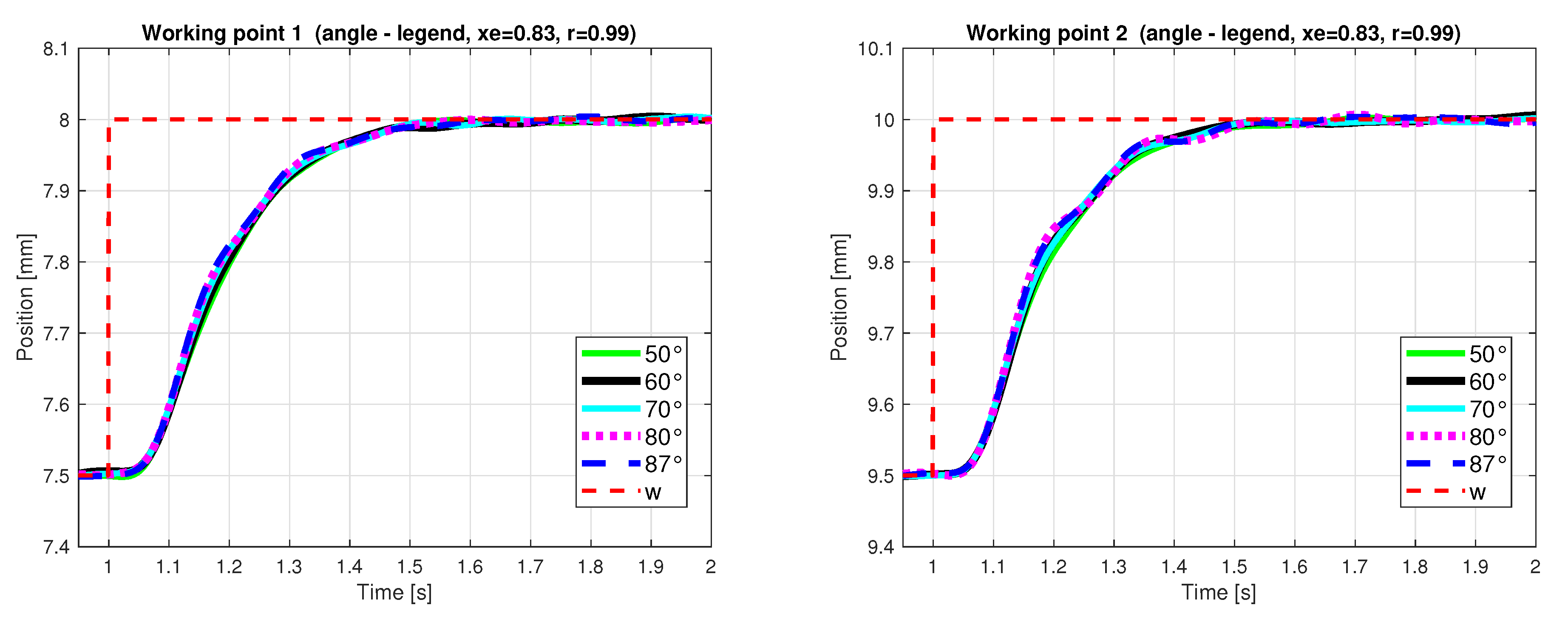
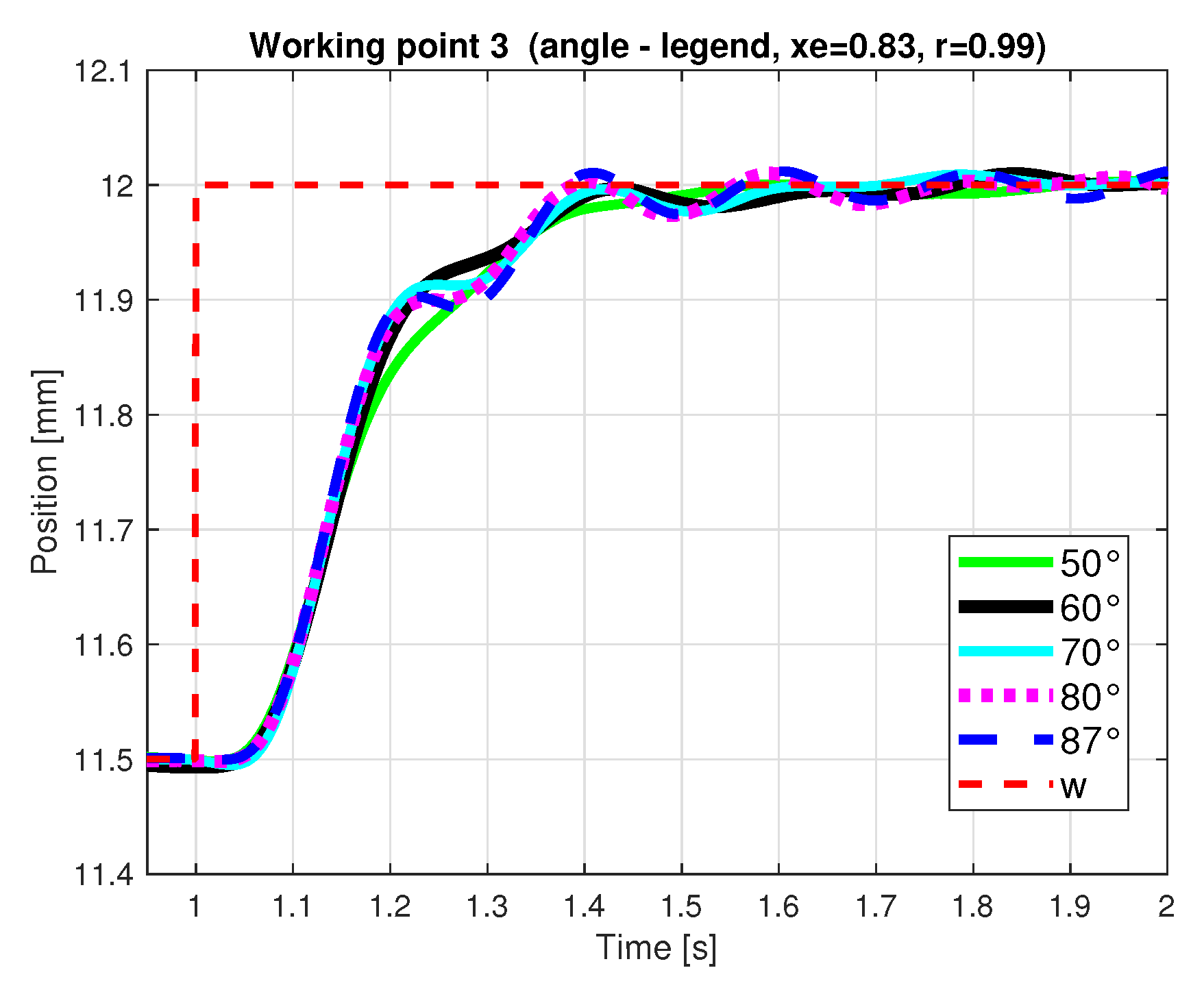
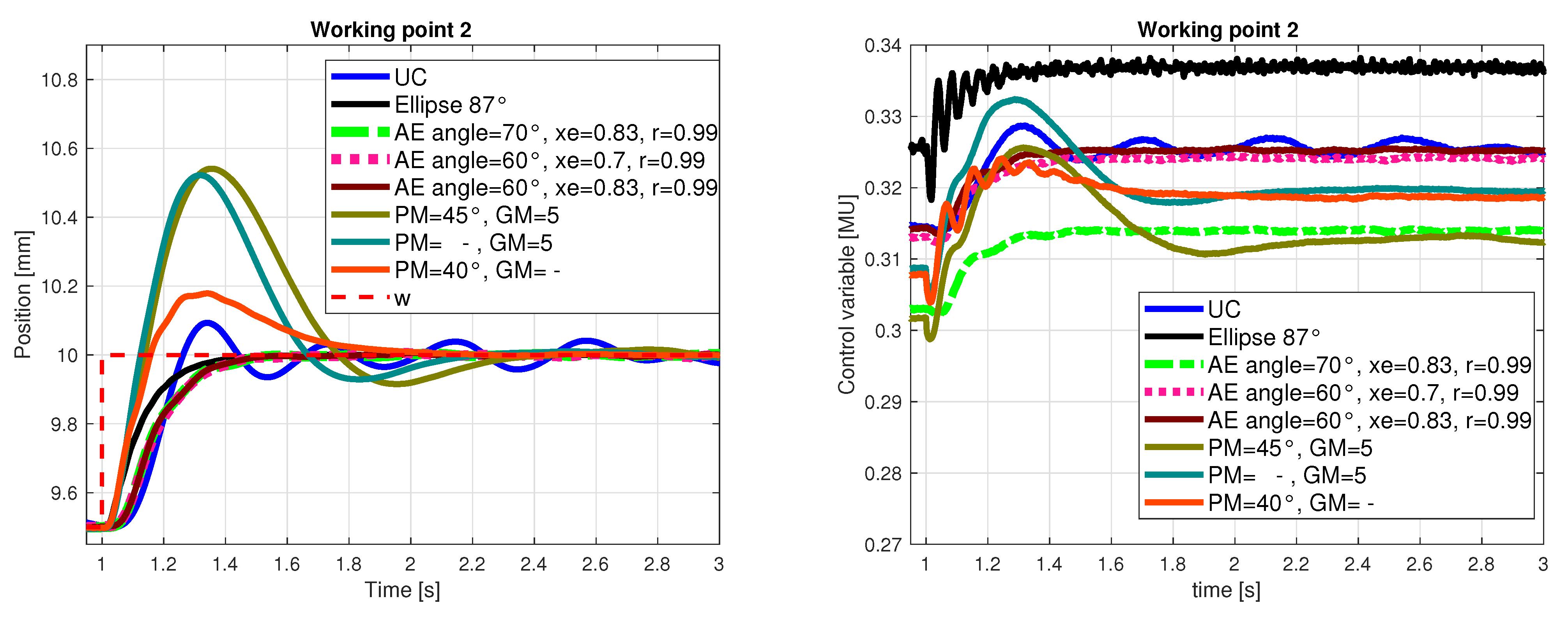
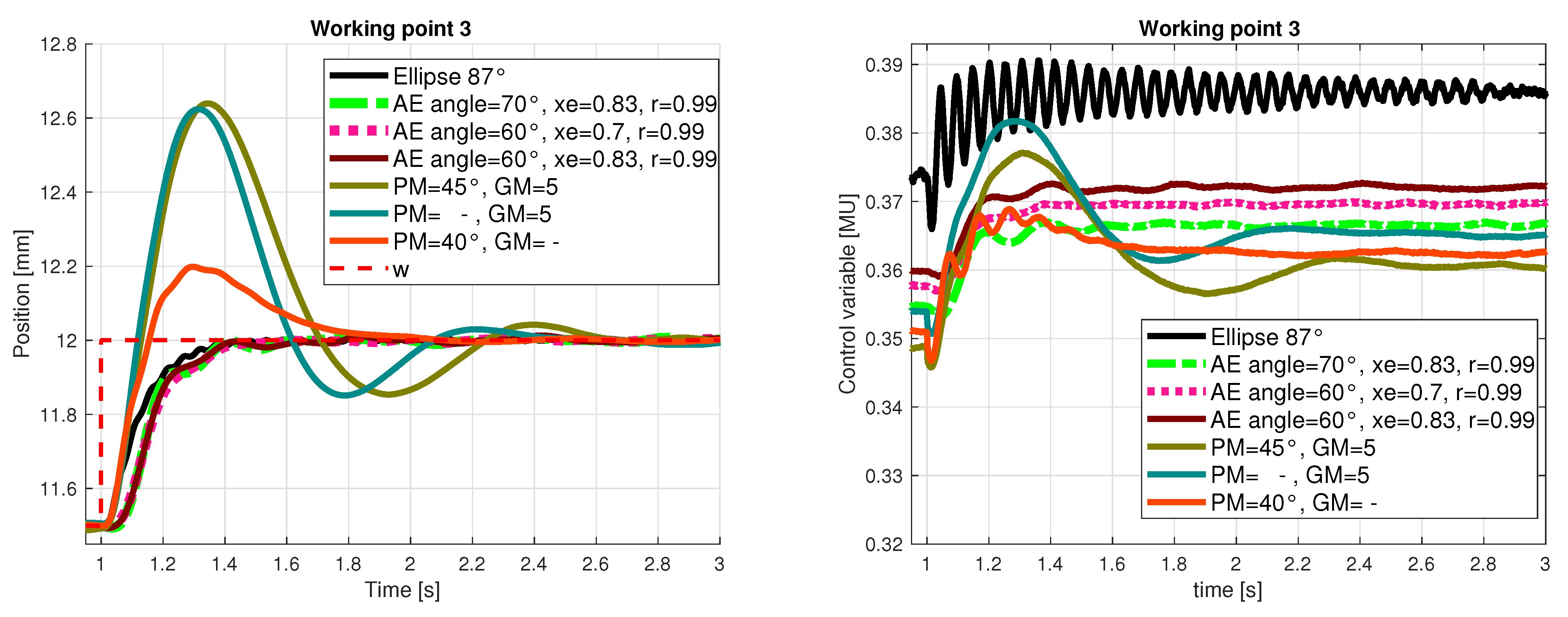
- The influence of AE domain design parameters: , , and r (defining the stability degree), is systematically analyzed and evaluated on a real laboratory magnetic levitation plant. For each parameter, we design several controllers, measure their step responses for three working points (Table 2) and assess their closed-loop performance using performance measures IAE, TV0 a TV1 (described in Section 2.2), the corresponding analysis of design parameters influence on CL performance is presented. Based on the above performance measures, the best controller is chosen.
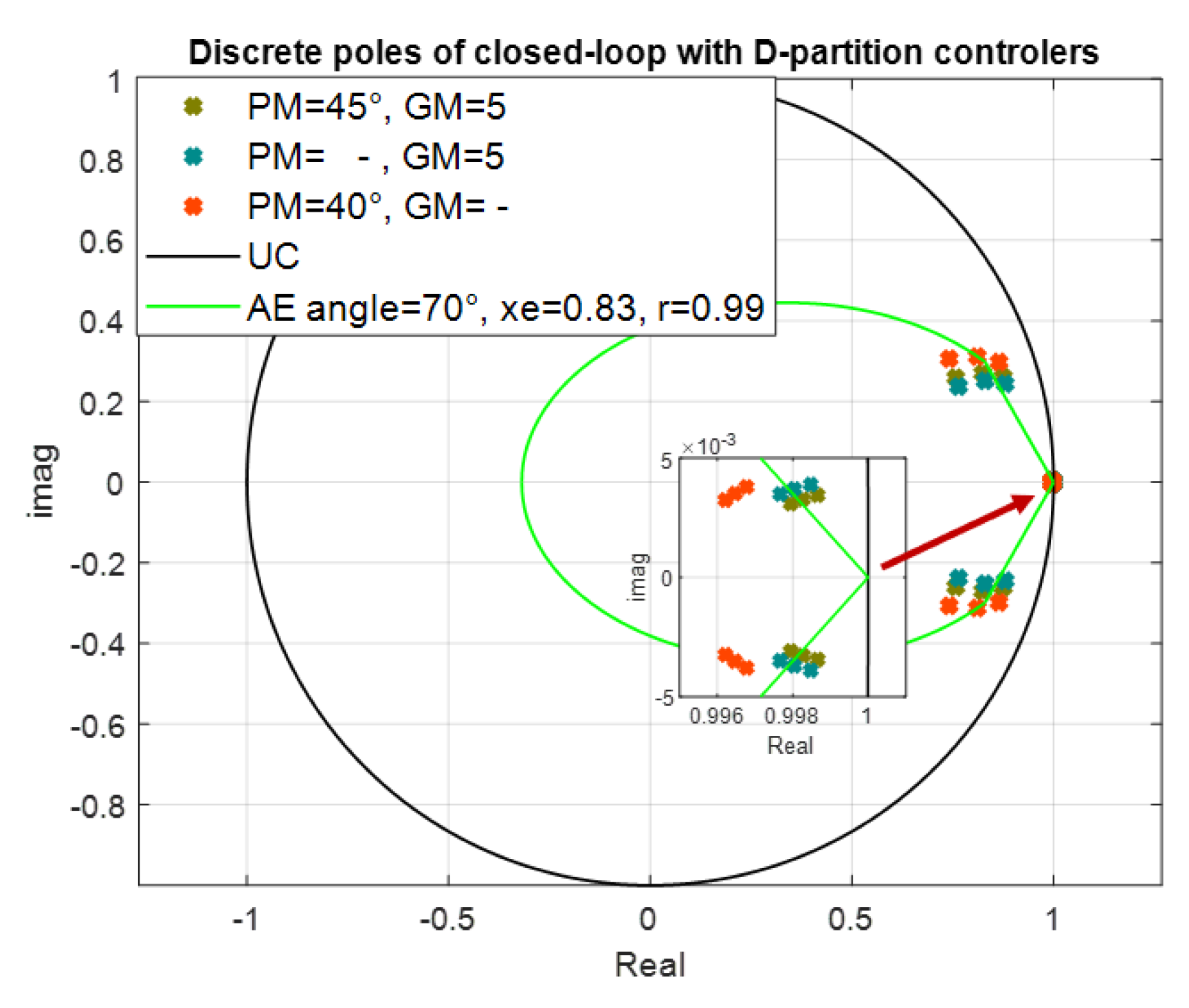
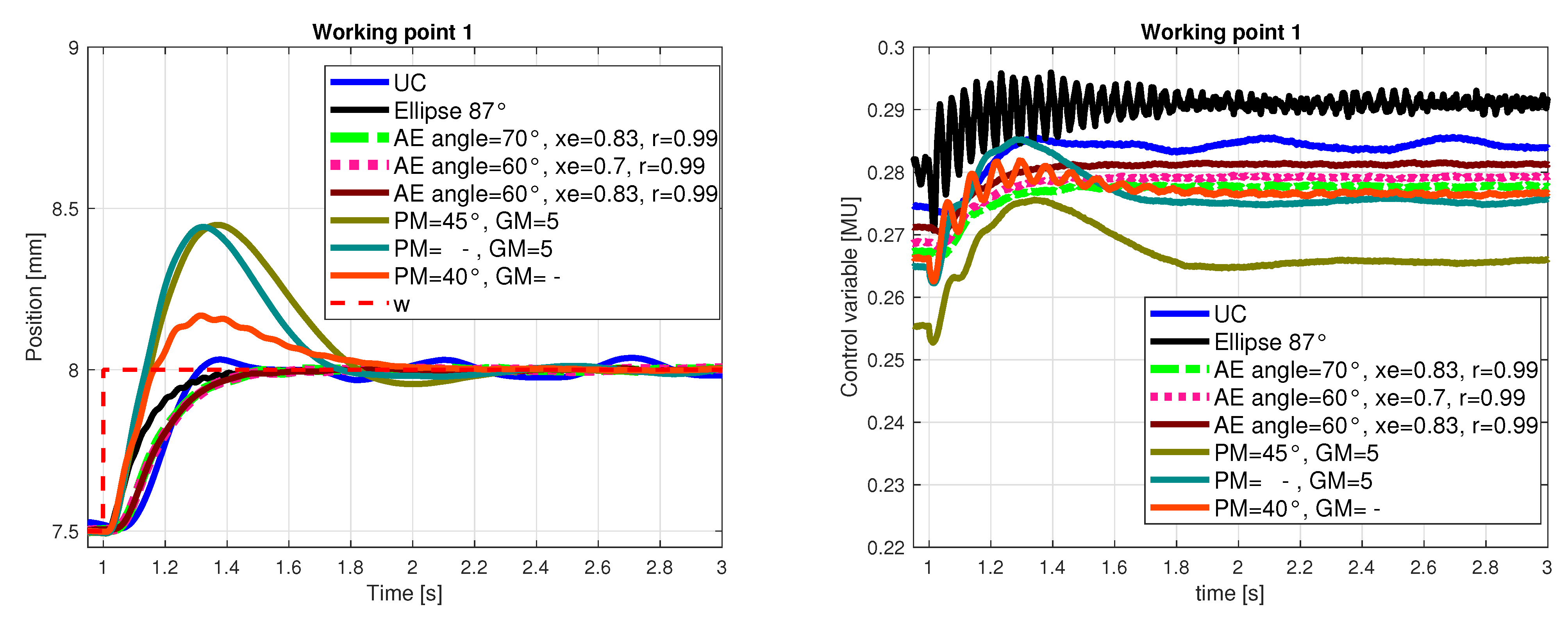
- Superior controllers received for the AE region are then compared with robust controllers received by alternative approaches: simple robust stability controller placing the poles into a unit circle (UC), [29]; ellipse approximation for the prescribed damping , [23] and with robust continuous-time controllers based on the D-partition approach, [22]; three representative controllers with the smallest overshoot were chosen from the latter approach.
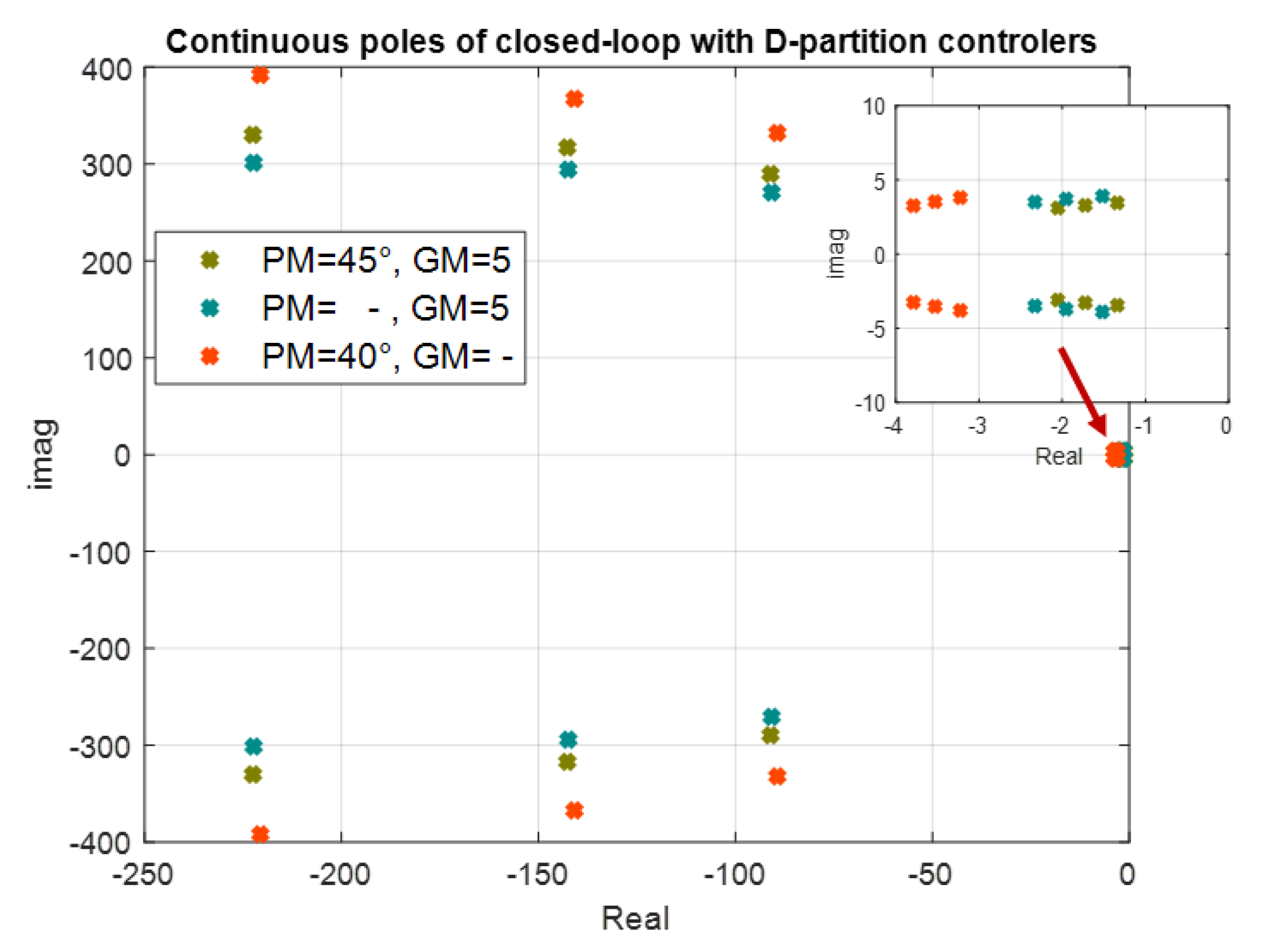
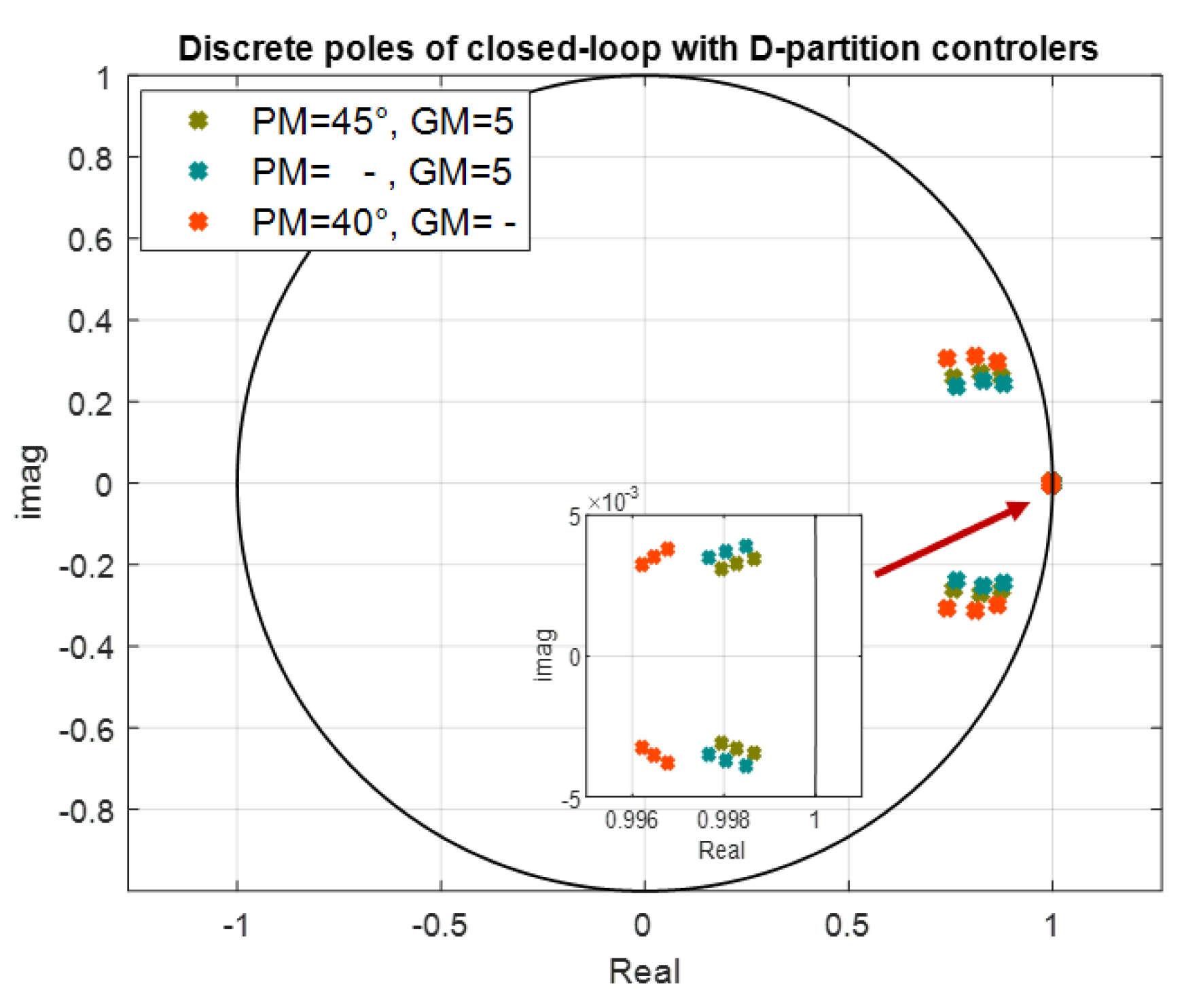
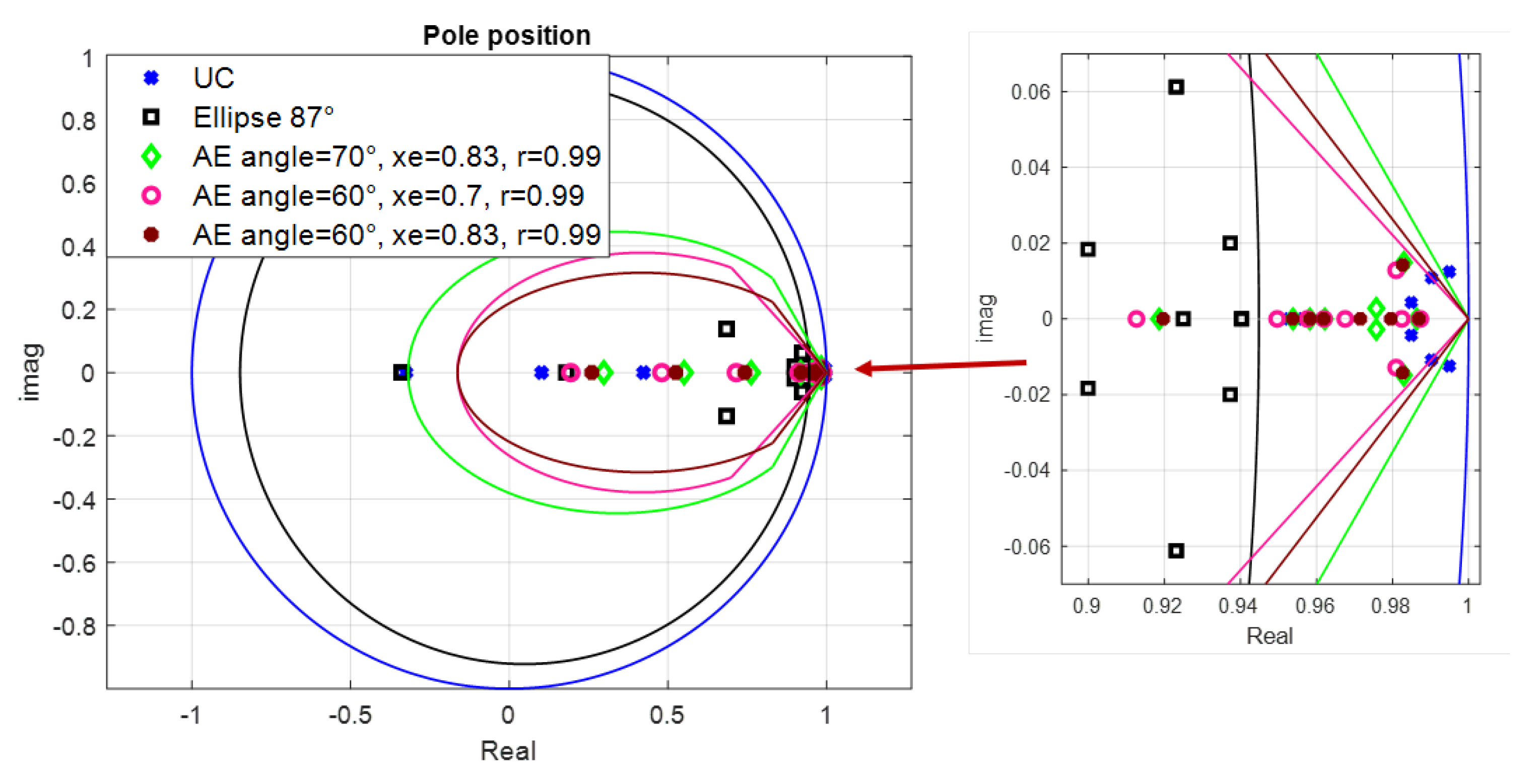
- The last subsection is devoted to analysis of the closed-loop pole position. The prescribed poles are confronted with the obtained closed-loop poles for linearized system; to enable comparison with the continuous-time controller (based on D-partition method), the continuous-time closed-loop poles are recalculated to the corresponding discrete-time ones.
4.1. Discrete-Time Robust Pole-Placement State Feedback Controller Design Based on LMI Solution
4.2. Discrete-Time Robust Pole-Placement Controller Design Using AE Approximation
4.2.1. Design Results for Damping Angle Parameter Changes
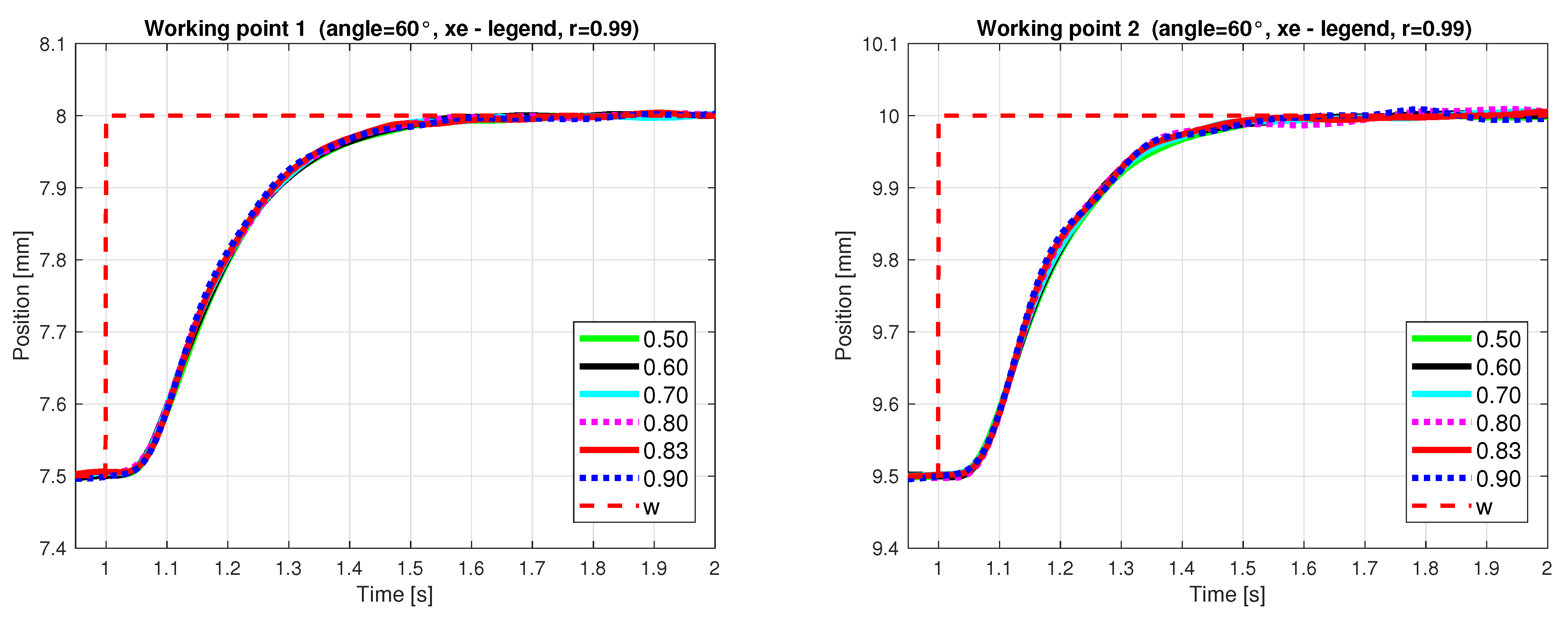
4.2.2. Design Results for Intersection Parameter Changes
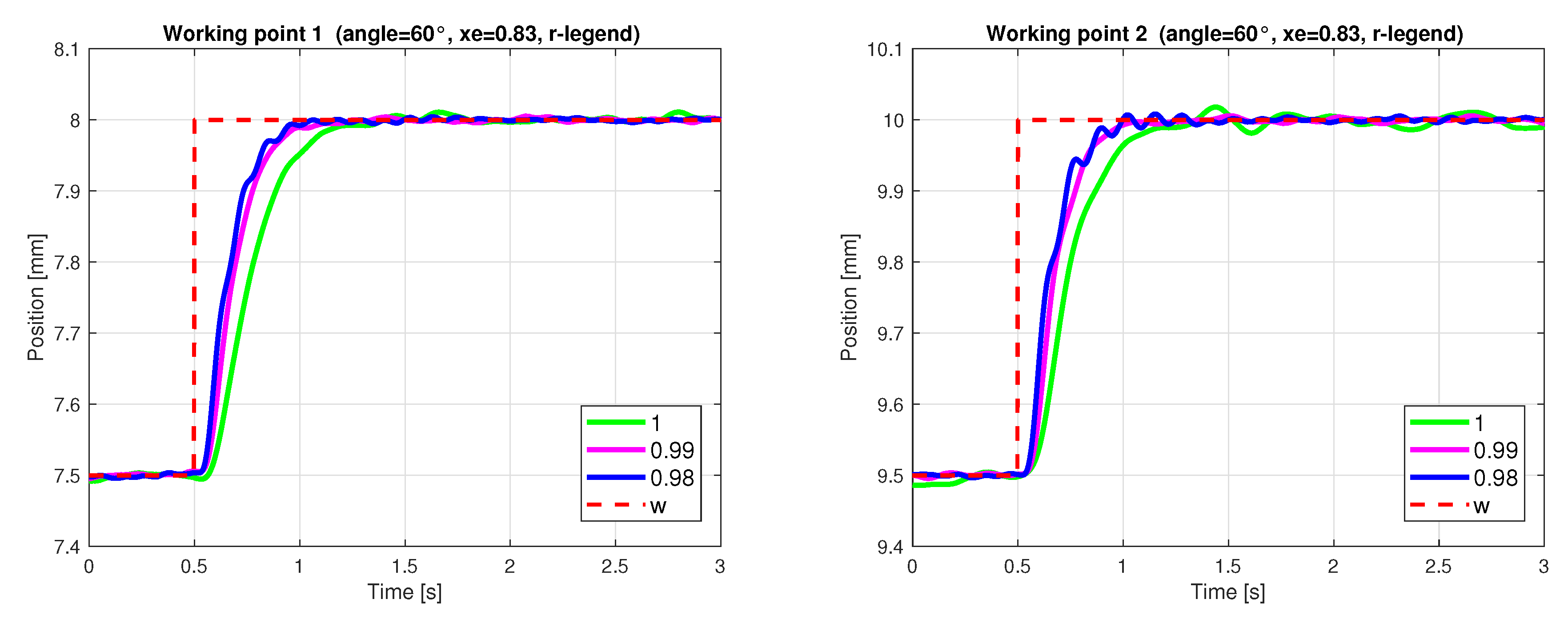
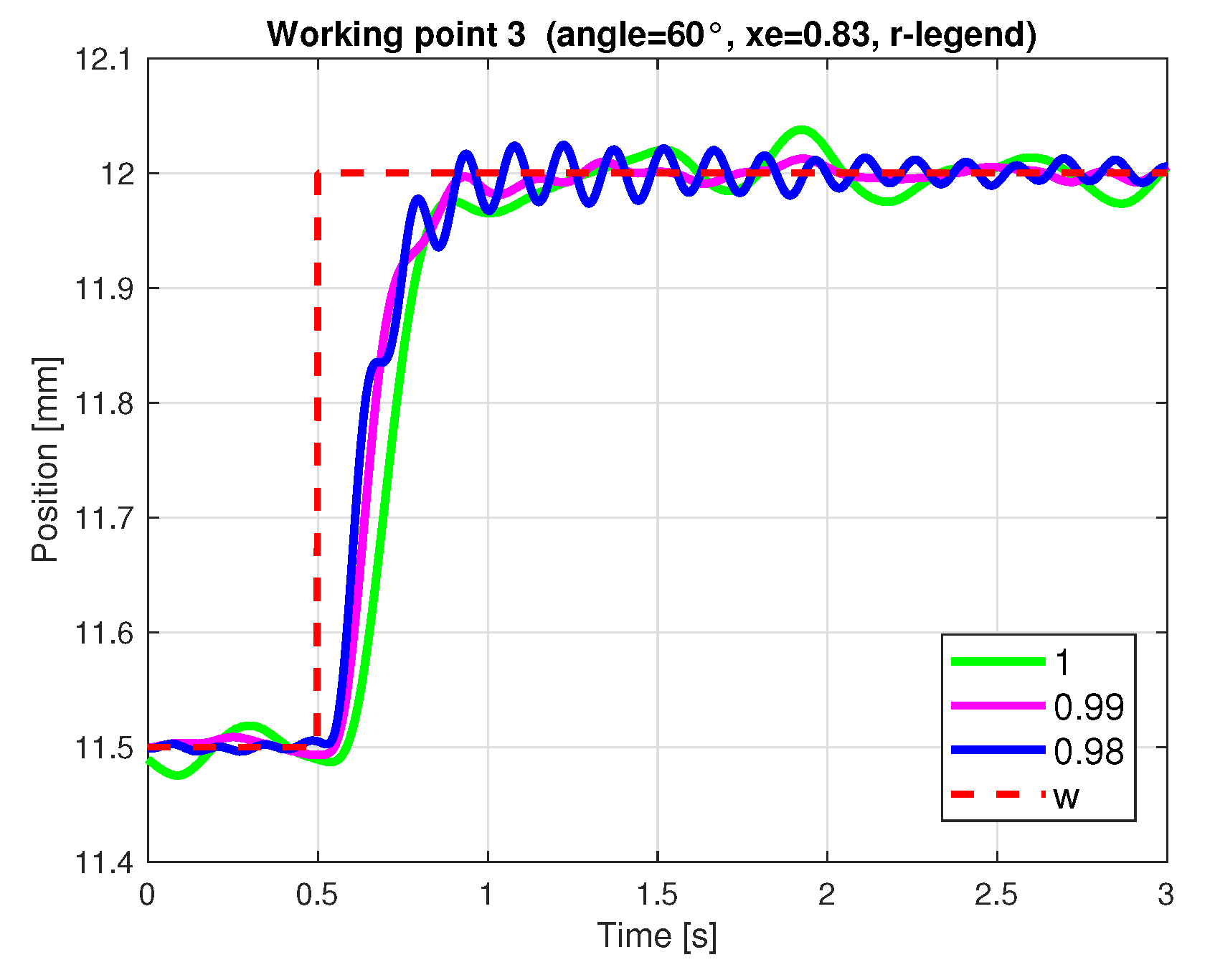
4.2.3. Design Results for Changing Stability Degree Radius r
4.3. Comparison of Robust Controllers: AE with Other Convex Approximations and Continuous-Time Controllers
- Stabilizing controllers (closed-loop poles in unit circle), [29]
- Pole-placement controllers for the prescribed relative damping, based on ellipse inner approximation of the non-convex cardioid domain, [23]
- Continuous-time robust controllers based on D-partition, [22].
4.4. Closed-Loop Pole Analysis
- Tunable parameters: corresponding to relative damping, intersection of inner AE approximation and cardioid , stability degree represented by radius r—as shown in Section 4.2.1, Section 4.2.2 and Section 4.2.3;
- AE region basically includes the neigbourhood of the stability border, namely critical point [1, 0] and simultaneously provides the prescribed relative damping, which prevents oscillations; this feature appears as rather advantageous in magnetic levitation control as can be seen from the results presented in this section, where the corresponding closed-loop performance is quantified by IAE and Total Variance measures; as can be seen from Figure 14 and Figure 15 some of the closed-loop poles for magnetic levitation are inherently in the neighbourhood of stability border—point [1, 0]; since the realizable control variable has a limited value, the stability degree and damping can be shifted only slightly (not too far from stability border);
- The application on a real inherently nonlinear and unstable magnetic levitation plant shows the great application potential of the proposed AE region for discrete-time pole-placement controller design;
- The AE region is described by LMIs, which significantly simplifies the robust controller design for systems described in state space by an uncertain linear polytopic system and converts it to an LMI solution.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Petersen, I.R.; Tempo, R. Robust control of uncertain systems: Classical results and recent developments. Automatica 2014, 50, 1315–1335. [Google Scholar] [CrossRef]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; 0-89871-334-X; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Ebihara, Y.; Peaucelle, D.; Arzelier, D. S-Variable Approach to LMI-Based Robust Control; Communications and Control Engineering; Springer: London, UK, 2015. [Google Scholar]
- Chilali, M.; Gahinet, P.; Apkarian, P. Robust pole placement in LMI regions. IEEE Trans. Autom. Control 1999, 44, 2257–2270. [Google Scholar] [CrossRef]
- Chestnov, V.N.; Alexandrov, V.A.; Rezkov, I.G. Discrete-Time Control Based on Pole Placement by Engineering Performance Indices for SISO systems. In Proceedings of the 2019 27th Mediterranean Conference on Control and Automation (MED), Akko, Israel, 1–4 July 2019; pp. 362–367. [Google Scholar] [CrossRef]
- Voßwinkel, R.; Pyta, L.; Schrödel, F.; Mutlu, İ.; Mihailescu-Stoica, D.; Bajcinca, N. Performance boundary mapping for continuous and discrete time linear systems. Automatica 2019, 107, 272–280. [Google Scholar] [CrossRef]
- Sahoo, P.; Goyal, J.; Ghosh, S.; Naskar, A. New results on restricted static output feedback H∞ controller design with regional pole placement. IET Control Theory Appl. 2019, 13, 1095–1104. [Google Scholar] [CrossRef]
- Behrouz, H.; Mohammadzaman, I.; Mohammadi, A. Robust static output feedback design with pole placement constraints for linear systems with polytopic uncertainties. Trans. Inst. Meas. Control 2019. [Google Scholar] [CrossRef]
- Peaucelle, D.; Arzelier, D.; Bachelier, O.; Bernussou, J. A new robust D-stability condition for real convex polytopic uncertainty. Syst. Control Lett. 2000, 40, 21–30. [Google Scholar] [CrossRef]
- Oliveira, R.C.L.F.; de Oliveira, M.C.; Peres, P.L.D. Robust state feedback LMI methods for continuous-time linear systems: Discussions, extensions and numerical comparisons. In Proceedings of the IEEE International Symposium on Computer-Aided Control System Design (CACSD), Denver, CO, USA, 28–30 September 2011; pp. 1038–1043. [Google Scholar] [CrossRef]
- Khatibi, H.; Karimi, A.; Longchamp, R. Robust pole placement of systems with polytopic uncertainty via convex optimization. In Proceedings of the 2007 European Control Conference (ECC), Kos, Greece, 2–5 July 2007; pp. 204–210. [Google Scholar] [CrossRef]
- Botto, M.A.; Babuška, R.; da Costa, J.S. Discrete-time robust pole-placement design through global optimization. In Proceedings of the 15th IFAC World Congress, Barcelona, Spain, 21–26 August 2002. [Google Scholar]
- Wisniewski, V.L.; Yoshimura, V.L.; Assunção, E.; Teixeira, M.M.C. Regional pole placement for discrete-time systems using convex approximations. In Proceedings of the 2017 25th Mediterranean Conference on Control and Automation (MED), Valletta, Malta, 3–6 July 2017; pp. 655–659. [Google Scholar] [CrossRef]
- Krokavec, D.; Filasová, A. A new D-stability area for linear discrete-time systems. Arch. Control Sci. 2019, 29, 5–23. [Google Scholar]
- Rosinová, D.; Holič, I. LMI approximation of pole-region for discrete-time linear dynamic system. In Proceedings of the 15th International Carpathian Control Conference: ICCC 2014, Velké Karlovice, Czech Republic, 28–30 May 2014; pp. 497–502. [Google Scholar]
- Rosinová, D.; Hypiusová, M. LMI pole regions for a robust discrete-time pole placement controller design. Algorithms 2019, 12, 167. [Google Scholar] [CrossRef]
- Wang, D.; Meng, F.; Meng, S. Linearization Method of Nonlinear Magnetic Levitation System. Math. Probl. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Mahapatro, K.; Rane, M.; Suryawanshi, P. Robust uncertainty compensation in MagLev by using extended state observer. In Proceedings of the 2016 International Conference on Computing Communication Control and automation (ICCUBEA), Pune, India, 12–13 August 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Ma’arif, A.; Cahyadi, A.; Wahyunggoro, O. CDM Based Servo State Feedback Controller with Feedback Linearization for Magnetic Levitation Ball System. Int. J. Adv. Sci. Eng. Inf. Technol. 2018, 8, 930–937. [Google Scholar] [CrossRef]
- Abdulwahhab, O.W. Design of an adaptive state feedback controller for a magnetic levitation systems. Int. J. Electr. Comput. Eng. 2020, 10, 4782–4788. [Google Scholar] [CrossRef]
- Balko, P.; Rosinová, D. Modeling of magnetic levitation system. In Proceedings of the 21st International Conference on Process Control, Štrbské Pleso, Slovakia, 6–9 June 2017. [Google Scholar]
- Hypiusová, M.; Kozáková, A. Robust PID Controller Design for the Magnetic Levitation System: Frequency Domain. In Proceedings of the 21st International Conference on Process Control, Štrbské Pleso, Slovakia, 6–9 June 2017. [Google Scholar]
- Hypiusová, M.; Rosinová, D. Discrete-time Robust LMI Pole Placement for Magnetic Levitation. In Proceedings of the Cybernetics and Informatics, Lazy pod Makytou, Slovakia, 31 January–3 February 2018. [Google Scholar]
- Rosinová, D.; Hypiusová, M. Robust Pole Placement DR—Regions for Discrete-time Systems. In Proceedings of the 22nd International Conference on Process Control, Štrbské Pleso, Slovakia, 11–14 June 2019. [Google Scholar]
- Available online: https://www.researchgate.net/project/Robust-pole-placement-in-discrete-time-D-R-regions (accessed on 14 January 2021).
- Shinskey, F.G. How good are Our Controllers in Absolute Performance and Robustness. Meas. Control 1990, 23, 114–121. [Google Scholar] [CrossRef]
- Huba, M. Performance measures, performance limits and optimal PI control for the IPDT plant. J. Process. Control 2013, 23, 500–515. [Google Scholar] [CrossRef]
- Magnetic Levitation System 2EM—User’s Manual; Inteco Ltd.: Krakow, Poland, 2008.
- deOliveira, M.; Bernussou, J.; Geromel, J. A new discrete-time robust stability condition. Syst. Control Lett. 1999, 37, 261–265. [Google Scholar] [CrossRef]


| Parameters | Values | Units |
|---|---|---|
| m | 0.023 | kg |
| g | 9.81 | m/s |
| 0.017521 | H | |
| 0.0058231 | m | |
| 1.4142 × 10 | ms | |
| 4.5626 × 10 | m | |
| −0.4 | A | |
| 4.4 | A | |
| 0.03884 | A | |
| 0.00498 | MU |
| WP | ||||||
|---|---|---|---|---|---|---|
| WP1 | 0.008 | 0.7697 | −0.0233 | 0.8300 | −0.0098 | 0.7479 |
| WP2 | 0.010 | 0.9139 | −0.0187 | 0.7492 | −0.0124 | 1.1036 |
| WP3 | 0.012 | 1.0852 | −0.0146 | 0.6391 | −0.0154 | 1.5878 |
| AE Angle-Legend, xe = 0.83, r = 0.99 | WP | yIAE | uTV1 | yTV0 |
|---|---|---|---|---|
| angle = 50° | 1 | 0.2183 | 0.4413 | 1.4318 |
| 2 | 0.2130 | 0.2937 | 1.3766 | |
| 3 | 0.2161 | 0.3528 | 1.4955 | |
| mean(WP) | 0.2158 | 0.3626 | 1.4346 | |
| stdev(WP) | 0.0027 | 0.0743 | 0.0595 | |
| angle = 60° | 1 | 0.2171 | 0.4512 | 1.3684 |
| 2 | 0.2205 | 0.3479 | 1.4046 | |
| 3 | 0.2084 | 0.3942 | 1.3992 | |
| mean(WP) | 0.2153 | 0.3978 | 1.3907 | |
| stdev(WP) | 0.0063 | 0.0517 | 0.0195 | |
| angle = 70° | 1 | 0.2090 | 0.3321 | 1.4828 |
| 2 | 0.2048 | 0.2607 | 1.3848 | |
| 3 | 0.2070 | 0.2798 | 1.6814 | |
| mean(WP) | 0.2069 | 0.2909 | 1.5164 | |
| stdev(WP) | 0.0021 | 0.0370 | 0.1511 | |
| angle = 80° | 1 | 0.2069 | 0.2842 | 1.4586 |
| 2 | 0.2048 | 0.2206 | 1.5102 | |
| 3 | 0.2192 | 0.5039 | 2.3119 | |
| mean(WP) | 0.2103 | 0.3363 | 1.7602 | |
| stdev(WP) | 0.0077 | 0.1487 | 0.4785 | |
| angle = 87° | 1 | 0.2063 | 0.2839 | 1.4710 |
| 2 | 0.2075 | 0.2365 | 1.5319 | |
| 3 | 0.2102 | 0.2742 | 1.8276 | |
| mean(WP) | 0.2080 | 0.2649 | 1.6102 | |
| stdev(WP) | 0.0020 | 0.0250 | 0.1907 |
| AE Angle = 60°, xe-Legend, r = 0.99 | WP | yIAE | uTV1 | yTV0 |
|---|---|---|---|---|
| xe = 0.5 | 1 | 0.2171 | 0.4512 | 1.3684 |
| 2 | 0.2205 | 0.3479 | 1.4046 | |
| 3 | 0.2084 | 0.3942 | 1.3992 | |
| mean(WP) | 0.2153 | 0.3978 | 1.3907 | |
| stdev(WP) | 0.0063 | 0.0517 | 0.0195 | |
| xe = 0.6 | 1 | 0.2172 | 0.4154 | 1.3803 |
| 2 | 0.2066 | 0.3369 | 1.3082 | |
| 3 | 0.2026 | 0.3795 | 1.3976 | |
| mean(WP) | 0.2088 | 0.3773 | 1.3620 | |
| stdev(WP) | 0.0075 | 0.0393 | 0.0474 | |
| xe = 0.7 | 1 | 0.2119 | 0.3719 | 1.3759 |
| 2 | 0.2090 | 0.2802 | 1.3482 | |
| 3 | 0.2013 | 0.3230 | 1.4352 | |
| mean(WP) | 0.2074 | 0.3250 | 1.3864 | |
| stdev(WP) | 0.0055 | 0.0459 | 0.0444 | |
| xe = 0.8 | 1 | 0.2114 | 0.3137 | 1.4014 |
| 2 | 0.2292 | 0.2743 | 1.5324 | |
| 3 | 0.2221 | 0.2924 | 1.6088 | |
| mean(WP) | 0.2209 | 0.2935 | 1.5142 | |
| stdev(WP) | 0.0090 | 0.0197 | 0.1049 | |
| xe = 0.83 | 1 | 0.2139 | 0.3092 | 1.4245 |
| 2 | 0.2073 | 0.2491 | 1.3739 | |
| 3 | 0.2169 | 0.3049 | 1.6605 | |
| mean(WP) | 0.2127 | 0.2877 | 1.4863 | |
| stdev(WP) | 0.0049 | 0.0335 | 0.1530 | |
| xe = 0.9 | 1 | 0.2124 | 0.2964 | 1.4170 |
| 2 | 0.2108 | 0.2485 | 1.4673 | |
| 3 | 0.2099 | 0.2781 | 1.7917 | |
| mean(WP) | 0.2110 | 0.2743 | 1.5587 | |
| stdev(WP) | 0.0013 | 0.0242 | 0.2034 |
| AE Angle = 60°, xe = 0.83, r-Legend | WP | yIAE | uTV1 | yTV0 |
|---|---|---|---|---|
| r = 1 | 1 | 0.3115 | 0.2214 | 1.5068 |
| 2 | 0.3141 | 0.1801 | 1.6399 | |
| 3 | 0.3371 | 0.2035 | 2.2280 | |
| mean(WP) | 0.3209 | 0.2017 | 1.7916 | |
| stdev(WP) | 0.0141 | 0.0207 | 0.3838 | |
| r = 0.99 | 1 | 0.2139 | 0.3092 | 1.4245 |
| 2 | 0.2073 | 0.2491 | 1.3739 | |
| 3 | 0.2169 | 0.3049 | 1.6605 | |
| mean(WP) | 0.2127 | 0.2877 | 1.4863 | |
| stdev(WP) | 0.0049 | 0.0335 | 0.1530 | |
| r = 0.98 | 1 | 0.1818 | 0.4030 | 1.5000 |
| 2 | 0.1815 | 0.3205 | 1.6506 | |
| 3 | 0.2090 | 0.4176 | 3.0320 | |
| mean(WP) | 0.1907 | 0.3803 | 2.0608 | |
| stdev(WP) | 0.0158 | 0.0523 | 0.8444 |
| Discrete Controller | ||||
|---|---|---|---|---|
| UC | 106.7382 | 2.4693 | −0.6172 | 0.3527 |
| Ellipse: angle = 87° | 952.3722 | 9.7547 | −0.6533 | 26.8816 |
| AE: angle = 70°, xe = 0.83, r = 0.99 | 91.5534 | 1.9303 | −0.2448 | 0.5237 |
| AE: angle = 60°, xe = 0.7, r = 0.99 | 110.4822 | 2.3323 | −0.3093 | 0.6308 |
| AE: angle = 60°, xe = 0.83, r = 0.99 | 96.5089 | 2.0400 | −0.2677 | 0.5406 |
| Continuous Controller | P | I | D |
|---|---|---|---|
| D-partition: PM = 45°, GM = 5 | 33.2660 | 61.0400 | 4.5320 |
| D-partition: PM = -, GM = 5 | 33.3380 | 69.0000 | 4.0220 |
| D-partition: PM = 40°, GM = - | 58.1155 | 141.3250 | 5.8074 |
| Controller | WP | yIAE | uTV1 | yTV0 |
|---|---|---|---|---|
| UC | 1 | 0.3333 | 0.4767 | 2.6340 |
| 2 | 0.3922 | 0.3602 | 3.8896 | |
| 3 | 11.9563 | 5.0270 | 166.3964 | |
| mean(WP) | 4.2272 | 1.9546 | 57.6400 | |
| Ellipse: angle = 87° | 1 | 0.1380 | 3.0493 | 2.0134 |
| 2 | 0.1343 | 1.6811 | 1.3212 | |
| 3 | 0.1364 | 1.9510 | 1.6248 | |
| mean(WP) | 0.1362 | 2.2271 | 1.6532 | |
| AE angle = 70°, xe = 0.83, r = 0.99 | 1 | 0.2090 | 0.3321 | 1.4828 |
| 2 | 0.2048 | 0.2607 | 1.3848 | |
| 3 | 0.2070 | 0.2798 | 1.6814 | |
| mean(WP) | 0.2069 | 0.2909 | 1.5164 | |
| AE angle = 60°, xe = 0.7, r = 0.99 | 1 | 0.2119 | 0.3719 | 1.3759 |
| 2 | 0.2090 | 0.2802 | 1.3482 | |
| 3 | 0.2013 | 0.3230 | 1.4352 | |
| mean(WP) | 0.2074 | 0.3250 | 1.3864 | |
| AE angle = 60°, xe = 0.83, r = 0.99 | 1 | 0.2139 | 0.3092 | 1.4245 |
| 2 | 0.2073 | 0.2491 | 1.3739 | |
| 3 | 0.2169 | 0.3049 | 1.6605 | |
| mean(WP) | 0.2127 | 0.2877 | 1.4863 | |
| D-partition: PM = 45°, GM = 5 | 1 | 0.4940 | 0.4158 | 3.3857 |
| 2 | 0.5453 | 0.3323 | 3.6695 | |
| 3 | 0.6657 | 0.3684 | 4.7647 | |
| mean(WP) | 0.5684 | 0.3722 | 3.9400 | |
| D-partition: PM = - , GM = 5 | 1 | 0.4349 | 0.3978 | 3.3848 |
| 2 | 0.4557 | 0.2932 | 3.5281 | |
| 3 | 0.5505 | 0.3223 | 4.3085 | |
| mean(WP) | 0.4804 | 0.3377 | 3.7405 | |
| D-partition: PM = 40°, GM = - | 1 | 0.2251 | 0.6747 | 2.0834 |
| 2 | 0.2278 | 0.4505 | 1.9199 | |
| 3 | 0.2450 | 0.4846 | 2.0367 | |
| mean(WP) | 0.2326 | 0.5366 | 2.0133 |
| Discrete Contholler | [°] | |
| UC | 0.9950 | 68 |
| Ellipse: angle = 87° | 0.9403 | 39 |
| AE: angle = 70°, xe = 0.83, r = 0.99 | 0.9864 | 41 |
| AE: angle = 60°, xe = 0.7, r = 0.99 | 0.9873 | 34 |
| AE: angle = 60°, xe = 0.83, r = 0.99 | 0.9869 | 39 |
| Continuous Controller | Continuous Domain | [°] | Discrete Domain | [°] |
|---|---|---|---|---|
| Real Stability Degree | Real Stability Degree | |||
| D-partition: PM = 45°, GM = 5 | 1.3388 | 73 | 0.9987 | 69 |
| D-partition: PM = -, GM = 5 | 1.5169 | 71 | 0.9985 | 69 |
| D-partition: PM = 40°, GM = - | 3.2248 | 75 | 0.9968 | 66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hypiusová, M.; Rosinová, D. Discrete-Time Pole-Region Robust Controller for Magnetic Levitation Plant. Symmetry 2021, 13, 142. https://doi.org/10.3390/sym13010142
Hypiusová M, Rosinová D. Discrete-Time Pole-Region Robust Controller for Magnetic Levitation Plant. Symmetry. 2021; 13(1):142. https://doi.org/10.3390/sym13010142
Chicago/Turabian StyleHypiusová, Mária, and Danica Rosinová. 2021. "Discrete-Time Pole-Region Robust Controller for Magnetic Levitation Plant" Symmetry 13, no. 1: 142. https://doi.org/10.3390/sym13010142
APA StyleHypiusová, M., & Rosinová, D. (2021). Discrete-Time Pole-Region Robust Controller for Magnetic Levitation Plant. Symmetry, 13(1), 142. https://doi.org/10.3390/sym13010142






