Abstract
In this paper, heat transfer and entropy of steady Williamson nanofluid flow based on the fundamental symmetry is studied. The fluid is positioned over a stretched flat surface moving non-uniformly. Nanofluid is analyzed for its flow and thermal transport properties by consigning it to a convectively heated slippery surface. Thermal conductivity is assumed to be varied with temperature impacted by thermal radiation along with axisymmetric magnetohydrodynamics (MHD). Boundary layer approximations lead to partial differential equations, which are transformed into ordinary differential equations in light of a single phase model accounting for -water and -water nanofluids. The resulting ODEs are solved via a finite difference based Keller box scheme. Various formidable physical parameters affecting fluid movement, difference in temperature, system entropy, skin friction and Nusselt number around the boundary are presented graphically and numerically discussed. It has also been observed that the nanofluid based on -water is identified as a superior thermal conductor rather than -water based nanofluid.
1. Introduction
The study of nanofluid flow and heat transfer has gained importance in the current era due to its significant importance in engineering applications. In many processes, nanofluids are used as a coolant in several industrial refrigeration systems and used in the process of oil extraction, computer processors, car radiators and thermal solar collectors, etc. Nanofluids are solid additive enriched fluids with enhanced thermal transport abilities. The heat transfer characteristics of ordinary fluids have been improved by nanofluids. The innovative idea of construction of nanofluids was practically implemented by Choi and Eastman [1,2,3]. The prominent nanoparticles used are made up of metals (, carbides or oxides with water and ethylene glycol as base fluids. Experimental studies have shown that the concentration, scale, form and composition of nanoparticles have a substantial effect on the thermal capability of traditional fluids (Lomascolo et al. [4]). The increase in thermal conductivity is in fact due to nanoparticles, but the improvement and efficacy of heat transfer depends mainly on the shape of the material and the composition of the scattered particles.
The study of nanofluids over a stretching surface has gained much interest. Sakiadis [5] initiated the concept of boundary layer flow over a stretching surface. Hakeem et al. [6] pondered over the impact of MHD on the 2nd order partial slip flow of thermally radiating nanofluids over sheets that can either shrink or stretch. In their work, they implemented the analytical hyper-geometric function and numerical shooting techniques and concluded that the skin drag is highest for alumina-water and lowest for silver-water nanofluids in both cases of stretching and shrinking sheets. In addition, their research involves increasing the values of the magnetic parameter that disappear in the lower branch solution of the shrinking sheet. Khalil et al. [7] performed a study on dual convection fluid flow and concluded that in a magnetized thermally stratified medium, the fluid velocity is an increasing function of mixed convection parameters but inverse trends are seen towards the magnetic field parameter. In [8], Usman et al. modeled Newtonian nanofluid flow manifested with thermal radiation and heat generation in the form of coupled differential equations. They concluded that the temperature depicts the uplift for thermal radiation. The effect of Lorentz forces and viscous dissipation of micropolar nanofluid that passes through a stretching surface using the mathematical model of Buongiorno has been investigated by Hsiao [9]. With the elevation of Eckert and Prandtl numbers, the increase in thermal profile has been observed. In addition, to enhance the values for these numbers, the rate of heat transfer is also increased. Another study related to the impact of an unsteady MHD flow over a horizontal stretching sheet on its thermal and solutal transfer in the presence of heat generation/absorption was analyzed and enlightened by Mukhopadhyay [10]. By introducing the uniform stress that was first studied by Crane [11], the sheet contains an incompressible flow. Ishak et al. [12] considered a KBM solution of MHD fluid flow over a stretched surface. The concept of the slip effect was created by Dorrepaal [13]. In [14], Noghrehabadi et al. reprised the partial slip condition on the heat transfer rate across a stretching sheet of nanofluids. Computational analysis of forced convection of nanofluids in terms of power law was done by Farhan et al. [15]. Recently, the same authors [16] analyzed the heat transfer of the MHD power law for nanofluid flow passing through an annular cavity. Sharma et al. [17] evaluated the slip effect of -water nanofluid on the heat transfer rate across a stretching sheet. Though its effects of viscous dissipation are often minimal, their impacts are more important when the viscosity of the fluid is very high. Notable contributions regarding thermal and solutal diffusion nanofluids in different physical situations are presented by [18,19,20,21,22,23,24,25,26,27].
Across most of the above research, Newtonian nanofluid models are proposed for convective transfer, but in the real world, nanofluids do not respond as Newtonian fluids, hence it is more likely to fit the non-Newtonian fluid framework for the nanofluid analysis. Hussain et al. [28] performed an analysis of the MHD flow and heat transfer of ferrofluid in a channel with non-symmetrical cavities. They investigated and addressed the thermal transport properties of ferrofluid in the non-symmetric cavity in the channel with the magnetic field enforced on it. Ibrahim and Negera [29] carried out the analysis based on numerical computation of the two-dimensional upper convected Maxwell (UCM) with the effect of magnetohydrodynamics and heat transfer through quite a linear flexible surface. Their work has shown that the indicated mass transfer parameter reduces the velocity, temperature and concentration profiles by using the Keller-box approach. In [30], Patel et al. addressed the heat transport phenomenon of micropolar nanofluid on the stretching/shrinking sheet through the use of the Brinkman nanofluid model. The Homotopy analysis approach was used to investigate the effect of significant physical parameters on thermal transmission. Their study yielded that micro-rotation and velocity fields minimize mass transfer parameters with an increased magnetic field in the stretching scenario. Ghobadi and Hassankolaei [31] addressed the two-dimensional Carreau nanofluid under the influence of Lorentz forces and nonlinear thermal radiation. They noted that fluid motion decreases by the increase in the local Weissenberg and Hartman numbers of shear thinning fluids, but increases by rising the local Weissenberg number of shear thickening fluids. Aziz et al. [32] analyzed the implications of a partial slippery and heated surface on Maxwell nanofluid over a stretching sheet using the Keller box method (KBM). The entropy production is associated with heat transfer, magnetic field, viscous dissipation, heat and mass transfer. Very recent studies on non-Newtonian nanofluids can be found in [33,34,35,36,37,38,39,40,41,42] and references therein.
The primary concern of this study is to study Williamson nanofluid’s steady two-dimensional boundary layer flow due to various non-uniform velocities of a stretching surface. In this regard the findings of the work done by Jamshed and Aziz [43] have been extended and analyzed the steady case. In the present study, the Tiwari and Das model [44] is considered. The fluid, velocity and temperature are considered the same as in the Tiwari and Das model (single phase model). The benefit of a single step model is that since we neglect the slip frameworks, the model becomes simple and can be solved easily by a numerical technique. However, the drawback of this approach is that in certain situations, the numerical results vary from those obtained by the experiments. The volume concentration of nanoparticles in this model volume varies from 3% to 20%. With the use of a similarity transformation, basic fundamental PDEs are achieved and converted into nonlinear and coupled ODEs and finally the Keller box scheme is used to obtain the numerical solution of the problem. The graphical and tabular representation of numerical results sheds light on the effect of the related parameters on the heat transport system.
2. Mathematical Modeling
A two-dimensional flow of Williamson nanofluid is assumed over a stretching sheet. The fluid is deemed to be incompressible and, due to the supremacy of the viscous forces in the boundary layer flow, the flow is believed to be laminar. As the sheet is extended in the positive x-direction with a non-uniform velocity, the fluid properties are known not to differ with time.
where the value of c denotes an initial stretching rate. The insulated sheet temperature is and for convenience it is presumed to be fixed at , where and show the temperature of the wall and surroundings, respectively. A surface is considered to be slippery and a temperature gradient is applied to the sheet. The uniform magnetic field of intensity is introduced in the normal flow direction.
Model Assumptions and Conditions
The mathematical model is considered under the following assumptions and conditions:
- Two-Dimensional laminar steady flow;
- Boundary layer approximation;
- Tiwari and Das model;
- Non-Newtonian Williamson nanofluids;
- Magnetohydrodynamics (MHD);
- variable Thermal conductivity;
- Thermal radiation;
- Nanoparticles shape factor;
- Porous stretching sheet;
- Convective and slip boundary conditions.
The mathematical form of Williamson fluid stress tensor is given by (see for example, Dapra [45])
where,
where , , , and are the extra stress tensor, limiting viscosity at zero shear rate, limiting viscosity at infinite shear rate, time constant and the first Rivlin–Erickson tensor, respectively, and is defined as:
Here, we assumed and . Hence, Equation (3) can be written as
or by utilizing the binomial expansion we get
Figure 1 is the schematic flow model of the present problem.
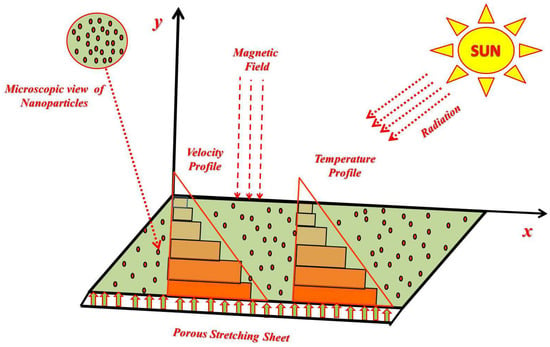
Figure 1.
Physical model of the schematic diagram.
The constitutive equations [46] of flow pertaining to a viscous Williamson nanofluid along with entropy equation aptly modified under usual boundary layer approximations along with thermal radiation and temperature dependent thermal conductivity. The dynamics of fluid flow could be presented in the following equation.
While eliminating in Equations (2) and (8), we find the following (9) and (10) equations,
The following boundary conditions are assumed:
Here the velocity of the flow is of the form . Whereas the time is represented by t, is a temperature of the fluid. While describes the permeability of the stretching surface. The velocity slip factor is represented by . The other parameter represents the heat transfer coefficient. denotes the variable thermal conductivity.
Radiation only moves a short distance in Williamson’s nanofluid due to fluid thickness. Because of this phenomena, the Rosseland [47] radiation approximation is used in Equation (11) and is given as Equation (11) . The non-dimensional entropy generation (NG) can be given as follows: .

Table 1.
Thermophysical properties for Williamson nanofluid.
Hamilton and Crosser model [50] is adopted for the problem under consideration,
The particle shape factor m is defined in Figure 2 (for details, see for example, Xu and Chen [51]).
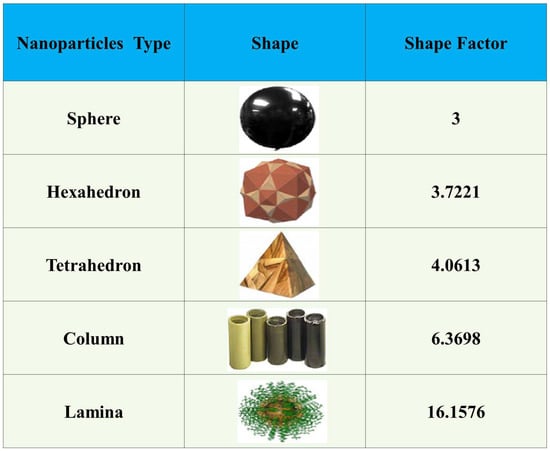
Figure 2.
Nanoparticle types, shapes and factors.
The material properties of the base fluid water and various nanoparticles being used in the current work are given in the Table 2 (for details, [52,53,54]).

Table 2.
Material properties of base fluid and nanoparticles.
3. Solution of the Problem
The (BVP) Equations (9)–(14) are transformed in light of a similarity technique that converts the governing PDEs into ODEs. Introducing stream functions of the form
and similarity variables of the form
into Equations (9)–(14). We get
With
where is in Equations (18)–(20) describes the preceding thermophysical charactersitic for Williamson nanofluid
and all the derivatives are considered with respect to . Non-Newtonian fluid and magnetic parameters are labeled here by and , respectively. Whereas = shows the Prandtl number. The thermal diffusivity parameter, mass transfer parameter and thermal radiation parameter are given by = , and = , respectively. is the velocity slip parameter and represents the Biot number. and in Equation (20) show the Reynolds and Brinkman number, respectively. A dimensionless temperature gradient is given by .
After implementing the non-dimensional transformations (17) on reduced skin friction and Nusselt numbers , the following equations are acquired (see for example, Nadeem and Hussain [46])
The nonlinear system of ordinary differential Equations (18) and (19), arising from mathematical modeling of the physical system of nanofluid flow are difficult to solve analytically. Hence, the Keller box method [55] scheme is implemented to obtain the numerical approximate solutions. The numerical scheme is inherently stable and is second order convergent and also known as the implicit finite difference method. The Keller box method is defined in the form of flow map as depicted in Figure 3.
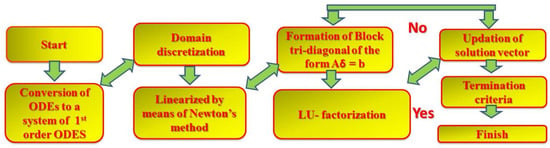
Figure 3.
Flow sheet of the Keller box method (KBM).
4. Verification of Numerical Results
We compare our results to those already available in the literature [56,57,58,59] as the special case for our analysis to validate the accuracy of derived calculations. So the test case is MHD flow along with heat transfer over a permeable stretching sheet with slip conditions. Results are verified for , , , , , , and . The comparisons shown in Table 3 are found to be in excellent accordance, assuring the accuracy of our obtained results.

Table 3.
Numerical results of heat transfer rate (Nusselt Number) for various values of the Prandtl Number.
5. Numerical Results and Discussion
The following discussion is based on the numerically obtained results by the framework detailed in the previous sections. The effect on the velocity and temperature profiles of the physical parameter and the entropy generation on the Williamson nanofluid is conscious. For and water-based nanofluids, the numerical calculations are performed. In Table 4, a few of the values of the drag and heat transfer rate at the surface corresponding to flow governing parameters are collated in a table. These results have been recorded for , , , , , , and . In the subsequent graphs, the behavior of -water nanofluid is embodied in blue color and the behavior of -water is shown by red color.

Table 4.
Values of Skin Friction and Nusselt Number for , .
5.1. Effect of Williamson Parameter
Graphical interpretations in Figure 4, Figure 5 and Figure 6 demonstrate the effects of parameter on the flow and thermal profiles, respectively. Computations are performed for for water based non-Newtonian Williamson nanofluids. The decay in velocity profile can be seen with an increment in as a result of which the momentum boundary layer thickness shrinks. The resistance experienced by the fluid declines its motion. The reason behind this is because the Williamson parameter is the ratio of relaxation and retardation time. Whereas when the increase in the Williamson parameter thermal boundary layer expands, temperature boosts due to an upsurge in elasticity stress parameter. A comparison of the momentum boundary layer of -water and -water nanofluid in Figure 4 reveals that it is more pronounced for the former than the latter. The Nusselt number for -water and -water decreases in this case. The temperature of the nanofluid also decreases as the Williamson parameter increases. The entropy of the system rises (see Figure 6) with increasing values of .
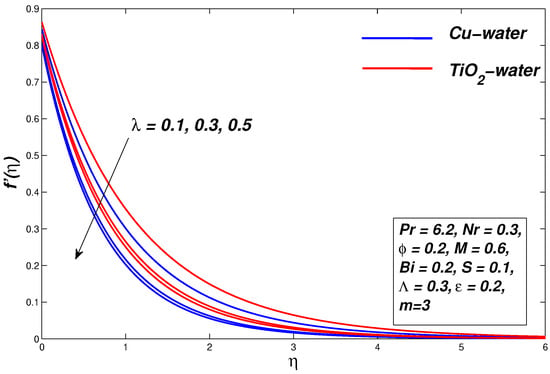
Figure 4.
Velocity graph for various values of .
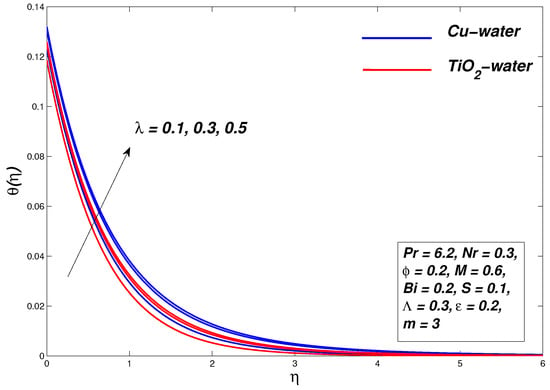
Figure 5.
Temperature graph for various values of .
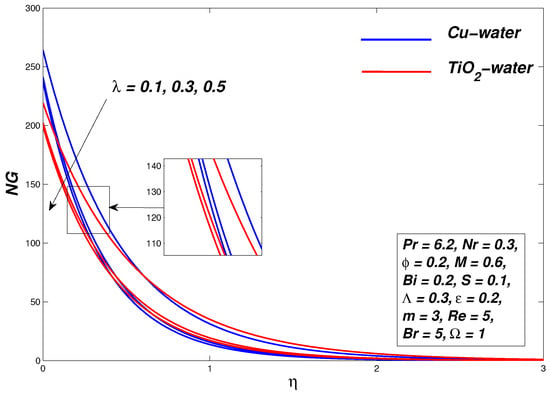
Figure 6.
Entropy generation graph for various values of .
5.2. Effect of Magnetic Parameter M
Figure 7, Figure 8 and Figure 9 illustrate the graphical representation of the influence of the external magnetic field on the flow of the nanofluid as well as on the distribution of its temperature in the boundary layer and the generation of entropy. The declining behavior of the velocity profile strengthens with a strong magnetic M; hence, the thickness of the momentum boundary layer decreases. The physical explanation behind the regression of the boundary layer thickness is that the Lorentz force appears when a normally applied magnetic field interacts with an electrically conducting nanofluid. As the strength of the applied magnetic field increases, the strength of Lorentz force also increases and acts opposite to the fluid motion and thus the resulting resistance in fluid reduces the thickness of the momentum boundary layer. In Figure 8, the temperature of nanofluids rises with an upsurge in the strength of parameter M and thus increases the thickening of the thermal boundary layer. It is also found that the parameter M is inversely proportional to the density of the nanofluid, and therefore the increase in M reduces the density as a result of the increase in the temperature of the fluid. The increase in nanofluid temperature within the boundary layer decreases the heat transfer rate at the boundary, but the drag coefficient increases by variation of M. The entropy of the system increases by increasing magnetic parameter strength.
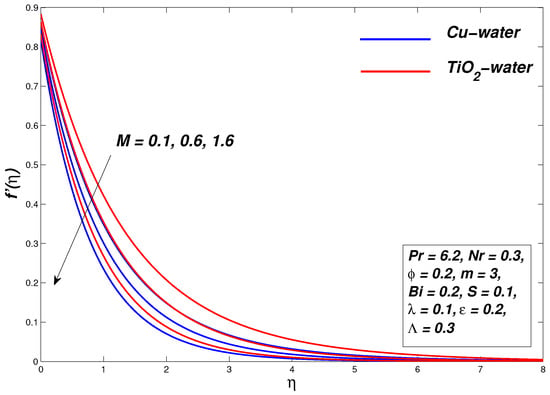
Figure 7.
Velocity graph for various values of M.
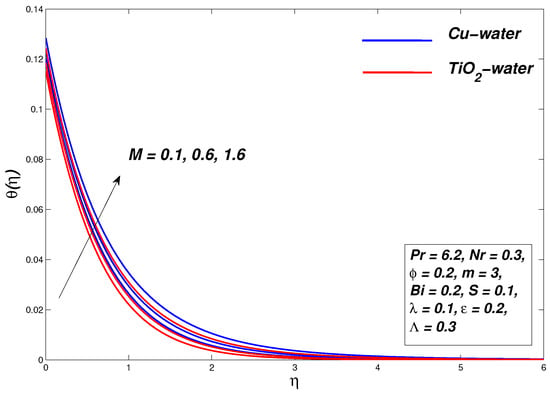
Figure 8.
Temperature graph for various values of M.
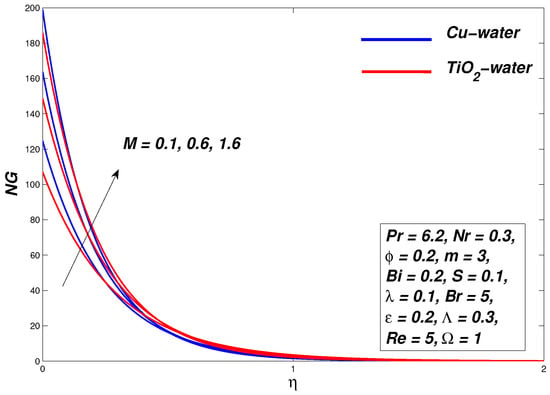
Figure 9.
Entropy generation graph for various values of M.
5.3. Effect of Nanoparticle Concentration
The role of the concentration of nanoparticles to fluid motion and temperature distribution is shown in Figure 10, Figure 11 and Figure 12. The velocity is decreased by increasing the parameter, which decreases the momentum of the boundary layer thickness. Greater nanoparticles make the fluid thick, as a result of which the velocity boundary layer shrinks. The thermal conductivity of nanofluids is enhanced due to a rise in the volume of nanoparticles. As a result, the momentum boundary layer showed a downward trend due to an improvement in thermal conductivity. On the other hand, an increase in the thermal conductivity of nanofluids has a positive effect on the fluid temperature as it increases with an increase in the concentration of nanoparticles. The velocity and temperature gradient are shown at the boundary corresponding to the parameter as depicted in Table 4. Figure 12 shows that the process entropy increases by increasing the parameter. It is also apparent that irreversible activity near the wall has increased its maximum value and decreases when moving away from the surface.
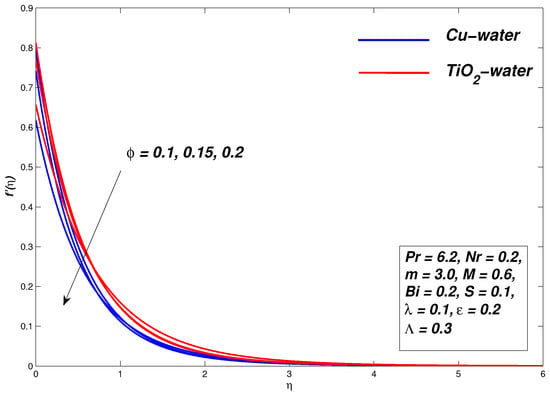
Figure 10.
Velocity graph for various values of .
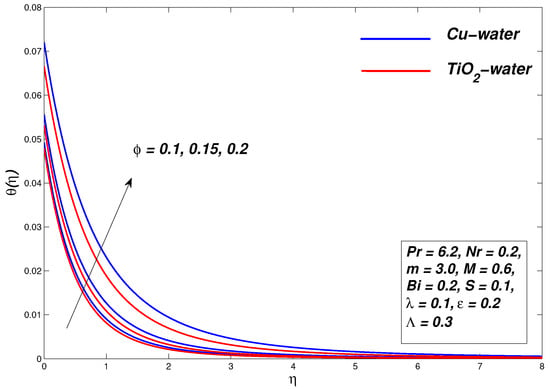
Figure 11.
Temperature graph for various values of .
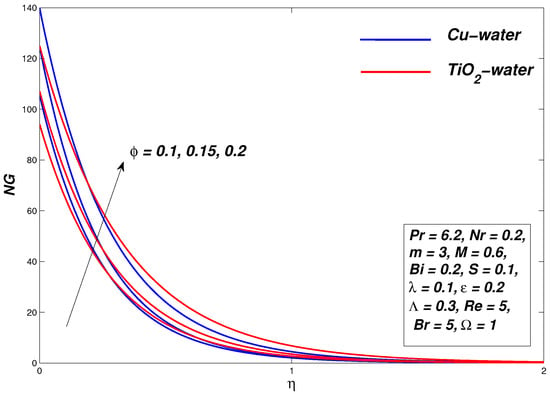
Figure 12.
Entropy generation graph for various values of .
5.4. Effect of Velocity Slip Parameter
Figure 13, Figure 14 and Figure 15 demonstrate the influence of a variation of slip parameters on flow and thermal profiles and entropy generation profiles, respectively, for Williamson nanofluids. Decreasing behavior in the velocity profile is seen for the slip parameter , the reason may be because an increase in slip effect retards the fluid flow, which decelerates the fluid. It affects the thermal energy of fluid oppositely as the temperature of nanofluid rises with an increase in parameter . The skin friction coefficient decreases due to the reason that greater slip minimizes friction between the fluid and the boundary bounding it. Here it is significant to distinguish that by increasing the slip velocity, the entropy of the system decreases, as shown in Figure 15. It is clear that the surface temperature and the volume fraction of nano particles are reduced by increasing the slip parameter. The explanation is the positive value of the gradient of the fluid velocity adjacent to the surface of the sheet and thus the decrease in the thickness of the layer.
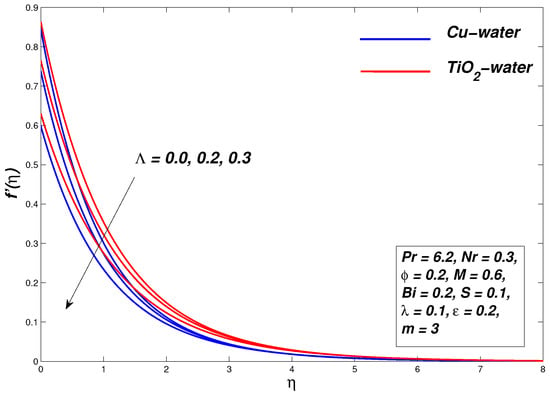
Figure 13.
Velocity graph for various values of .
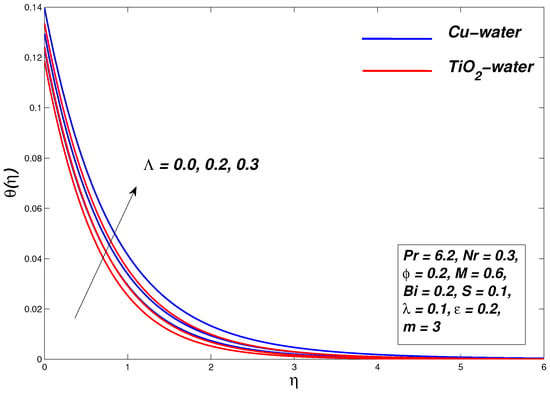
Figure 14.
Temperature graph for various values of .
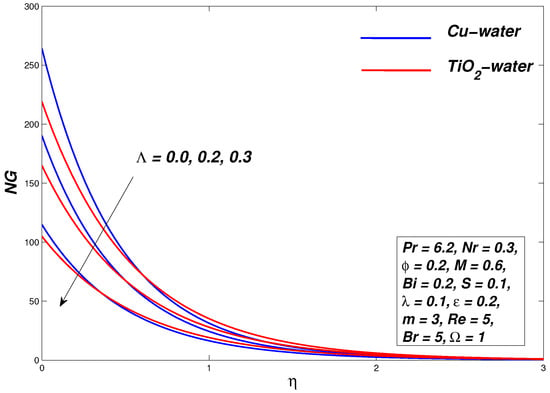
Figure 15.
Entropy generation graph for various values of .
5.5. Effect of Thermal Radiation Parameter
Figure 16 ponders upon the thermal radiation parameter impact on temperature distribution profile of Williamson nanofluids, showing that the temperature of nanofluid decreases for ascending values of . The thickness of the thermal boundary layer reduces with fall in temperature. Figure 17 displays the affect imposed by on the entropy profile for water based nanofluids. There is no change in the velocity profile but the entropy of nanofluids slows down by variating Nr. The results are steady for all the distances into the boundary layer, which validates the benefits of using the thermal radiation in nano scale material exemption processes. Successively, thermal emission enhances the thermal diffusivity of the nanofluid for the rise of the radiation parameter, heat will be added up to the routine and temperature will be increasing. Furthermore, it is evident from Table 4 that at the surface, heat exchange rate rises for both -water and -water; on the other hand, the velocity gradient remains constant.
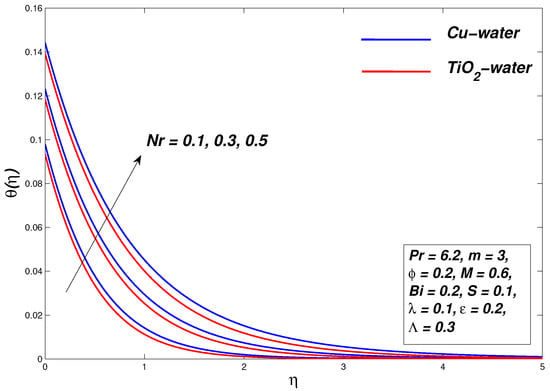
Figure 16.
Temperature graph for various values of .
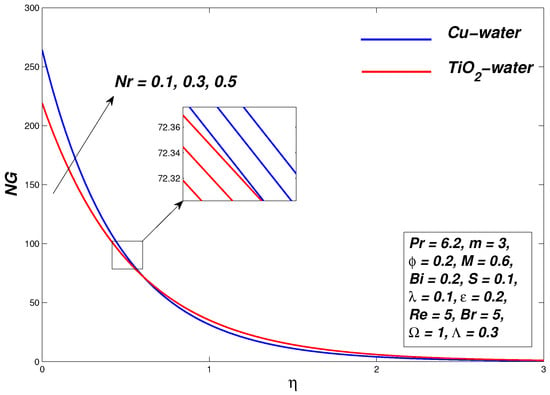
Figure 17.
Entropy generation graph for various values of .
5.6. Effect of Biot Number
Figure 18 and Figure 19 display the plots of the nanofluid temperature and entropy generation, respectively. Figure 18 depicted the temperature of the nanofluids, which rises due to a greater Biot number. The lower value of the Biot number indicates a stronger conduction within the surface and the high Biot number concludes an extreme conduction at the surface level. The temperature continues to expand due to increased thermal energy in nanofluids. An increase in causes the greater heat transfer from the boundary to the fluid, which occurs to increase the conduction of the boundary layer. However, there are marginal effects of the Biot number on the velocity profile of the nanofluid. In this case, entropy increases due to the heat transfer. The internal thermal resistance to the sheet surface is very high and there is no convective heat transfer from the sheet surface to the cold fluid well away from the sheet.
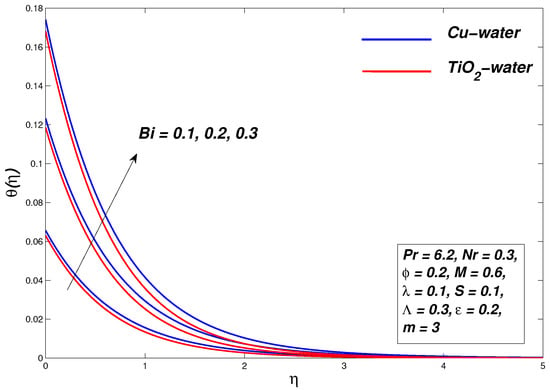
Figure 18.
Temperature graph for various values of .
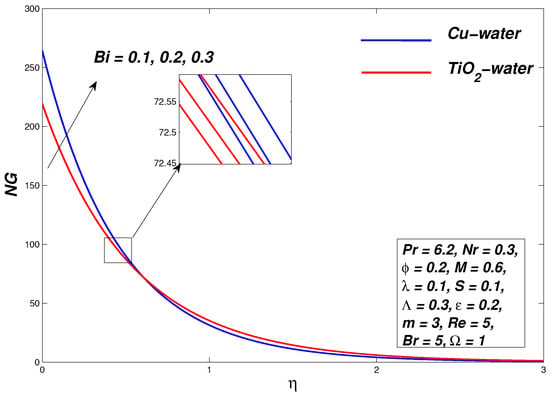
Figure 19.
Entropy generation graph for various values of .
5.7. Effect of the Nanoparticles Shape Factor m
Figure 20 describes the impact of different nanoparticles shapes on the heat transfer abilities of the nanofluid within the boundary layer flow of – and – nanofluids, at a fixed volume fraction . From the graph, it is shown that the non-dimensional temperature of the nanofluid rises as the values of m increases. Temperature is found lowest for spherical shape nanoparticles, followed by hexahedron, tetrahedron, column and lamina. Whereas the spherical shaped particle due to their enhanced surface area tends to draw more heat from the boundary layer while this effect is less obvious for the rest of the shapes. This accounts for the highest rate of heat transfer at the boundary for the spherical shaped nanoparticles, as can be seen in Table 4. Figure 21 shows that the smooth texture of spherical shaped nanoparticles helps minimizing the entropy of the system, as expected.
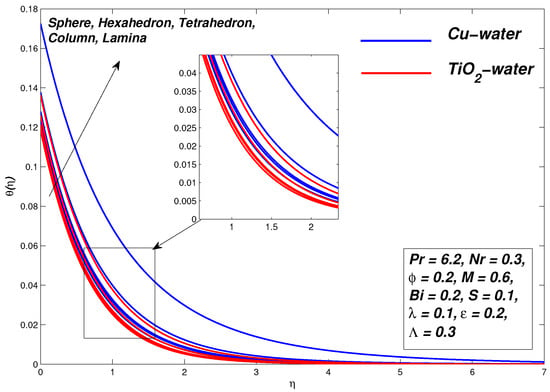
Figure 20.
Temperature generation graph for various values of m.
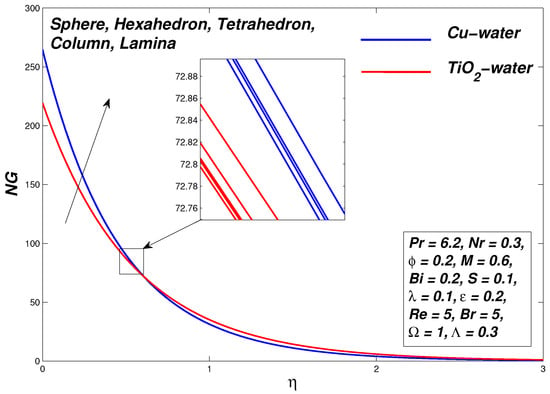
Figure 21.
Entropy generation graph for various values of m.
5.8. Effect of the Ehanced Frictional Forces via Reynolds Number and Brinkman Number on the Entropy
Figure 22 and Figure 23 give an account of the Brinkman number (Br) and Reynolds number (Re) impact on the entropy of the system, respectively. It is clear from the graphs that the entropy of the system rises rapidly when Reynolds number values are increased. Physically this means that at higher Reynolds number the viscous forces dominates by inertial forces thus systems entropy rises. It is found that the overall entropy of system increases with increments in the Brinkman number.
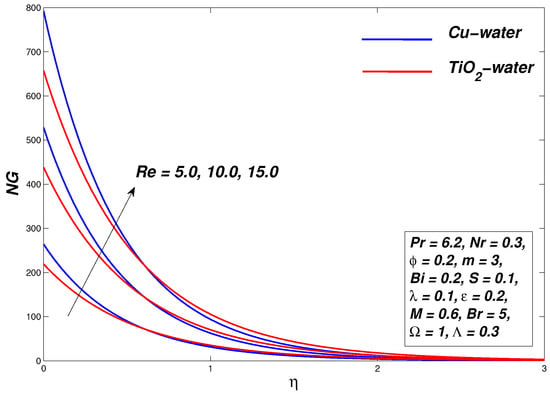
Figure 22.
Entropy generation graph for various values of .
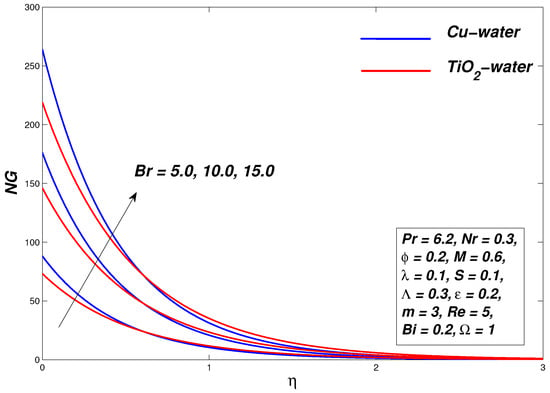
Figure 23.
Entropy generation graph for various values of .
5.9. Effect of Magnetic M and Radiation Parameters on the Physical Quantaties
The effect of magnetic parameter M and radiation parameter on the physical quantities of skin friction coefficient and Nusselt number profiles of -water and -water nanofluids are shown in Figure 24 and Figure 25, respectively. In Figure 24, computations are performed for whereas the parameter takes the values . It is noted when we increase the magnetic parameter M the skin friction coefficient increases. In Figure 25, computations are performed for whereas the Prandtl number is fixed on . It is seen that with the increase in , the rate of convective heat exchange also increases, which means that the boundary temperature goes up as the radiation parameter increases while the thickness of the boundary layer decreases.
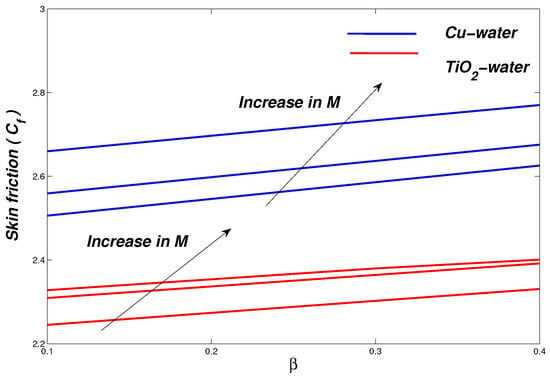
Figure 24.
Skin Friction against the parameter .
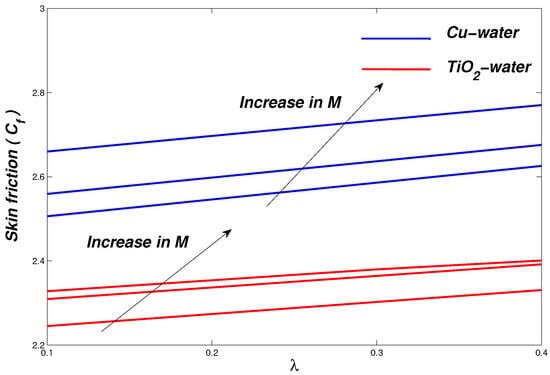
Figure 25.
Nusselt Number against the parameter .
5.10. Effect of Flow Parameters on Skin Friction and Nusselt Number
For fixed values of and , some values of the Skin friction and the Nusselt numbers are listed in the following Table 4. It is notable that the skin fraction coefficient for the Williamson nanofluid decreases with the increase in the Williamson parameter. So the heat transfer rate at the surface goes down because of local Nusselt number representation. Due to this reason, it can be used as a lubricant in cooling systems because of the suspended nano particles, which may remain in the base fluid for a larger time and cause to magnify the flow parameters of the nanofluid. By increasing the thickness parameter of the wall, skin fraction also increases, while the Williamson parameter is decreased. The Skin friction parameter also gets increased by increasing the values of the magnetic field parameter.
6. Conclusions
The two-dimensional magnetohydrodynamic flow of Williamson nanofluid under the impact of thermal conductivity ranging from temperature to thermal radiation along the stretchable surface was analyzed. By using a proper similarity transformation, the governing nonlinear PDEs of momentum and energy are transformed into ODEs. The mathematical model solution was computed using the second order stable Keller box scheme. The importance of the non-dimensional velocity, temperature and entropy profile effects of the various physical parameters under consideration are graphically delineated. The coefficient of skin friction and the Nusselt number are given in tabular form for the different values of the distinctive governing parameters. We have made the following concluding observation after a detailed review.
- A decrease in the velocity profile is observed for an increment in the Williamson and volume fraction parameters.
- Nanoparticles are mainly used in fluids to boost up thermal behavior of fluids. Therefore, an increase in nanoparticle concentration enhances the temperature of the nanofluid and hence the thermal boundary layer thickness.
- The -water based nanofluid is detected as a superior thermal conductor instead of -water-based nanofluid.
- A rise in magnetic parameter decreases the thickness of the momentum boundary layer whereas it increases the temperature and entropy profile.
- Although slipperiness retards the fluid flow and causes to reduce the velocity and temperature profile, it is significant to observe that the entropy of a system decreases by increasing the slip parameter.
Funding
This research was funded by DSR, KFUPM, by grant number SB191007 and the APC was funded by DSR, KFUPM through the above mentioned grant.
Acknowledgments
The author expresses his thanks to DSR, King Fahd University of Petroleum and Minerals for financial support through grant number SB191007.
Conflicts of Interest
The author declares no conflict of interest.
References
- Choi, S. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, San Francisco, CA, USA, 12–17 November 1995; Argonne National Lab.: DuPage County, IL, USA, 1995; Volume 66, pp. 99–105. [Google Scholar]
- Eastman, J.A.; Choi, S.U.S.; Li, S.; Thompson, L.J.; Lee, S. Enhanced thermal conductivity through the development of nanofluids. In Proceedings of the Fall Meeting of the Materials Research Society, MRS, Boston, MA, USA, 2–6 December 1996; Argonne National Lab.: DuPage County, IL, USA, 1996. [Google Scholar]
- Eastman, J.A.; Choi, S.; Li, S.; Yu, W.; Thompson, L.J. Anomalously inceases effective thermal conductvities of ethylene glycol-bases nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar] [CrossRef]
- Lomascolo, M.; Colangelo, G.; Milanese, M.; Risi, A. Review of heat transfer in nanofluids: Conductive, convective and radiative experimental results. Renew. Sustain. Energy Rev. 2015, 43, 1182–1198. [Google Scholar] [CrossRef]
- Sakiadis, B.C. Boundary Layer Equations for Two Dimensional and Axisymmetric Flow, Boundary Layer Behavior on Continuous Solid Surfaces; American Institute of Chemical Engineers: New York, NY, USA, 1961; pp. 26–28. [Google Scholar]
- Hakeem, A.k.A.; Ganesh, N.V.; Ganga, B. Magnetic field effect on second order slip flow of nanofluid over a stretching/shrinking sheet with thermal radiation effect. J. Magn. Magn. Mater. 2015, 381, 243–257. [Google Scholar] [CrossRef]
- Rehman, K.U.; Malik, M.Y.; Bilal, S.; Zehra, I.; Gaffar, S. On Both Magnetohydrodynamics Thermal Stratified and Dual Convection Flow Field Features: A Computational Study. J. Nanofluids 2019, 8, 460–465. [Google Scholar] [CrossRef]
- Ali, U.; Malik, M.Y.; Alderremy, A.A.; Aly, S.; Rehman, K.U. A generalized findings on thermal radiation and heat generation/absorption in nanofluid flow regime. Physica A 2020, 553, 124026. [Google Scholar] [CrossRef]
- Hsiao, K.L. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 2017, 112, 983–990. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Heat transfer analysis of the unsteady flow of a Maxwell fluid over a stretching surface in the presence of a Heat Source/Sink. Chin. Phys. Soc. 2012, 29, 054703. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. J. Appl. Math. Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Ishak, A.; Jafarand, K.; Nazar, R.; Pop, I. MHD stagnation point flow towards a stretching sheet, Statistical Mechanics and its Applications. Stat. Mech. Appl. 2009, 388, 3377–3383. [Google Scholar] [CrossRef]
- Dorrepaal, J.M. Slip flow in converging and diverging channels. J. Eng. Math. 1993, 27, 343–356. [Google Scholar] [CrossRef]
- Noghrehabadi, A.; Pourrajab, R.; Ghalambaz, M. Effect of partial slip boundary condition on the flow and heat transfer of nanofluids past stretching sheet prescribed constant wall temperature. Int. J. Therm. Sci. 2012, 54, 253–261. [Google Scholar] [CrossRef]
- Ahmed, F.; Iqbal, M.; Ioan, P. Numerical simulation of forced convective power law nanofluid through circular annulus sector. J. Therm. Anal. Calorim. 2019, 135, 861–871. [Google Scholar] [CrossRef]
- Ahmed, F.; Iqbal, M. Heat transfer Analysis of MHD Power Law Nano fluid flow through Annular Sector Duct. J. Therm. Sci. 2020, 29, 169–181. [Google Scholar] [CrossRef]
- Sharma, R.; Ishak, A.; Pop, I. Partial slip flow and heat transfer over a stretching sheet in a nanofluid. Math. Probl. Eng. 2013, 2013, 724547. [Google Scholar] [CrossRef]
- Darjani, S.; Koplik, J. Extracting the equation of state of lattice gases from random sequential adsorption simulations by means of the Gibbs adsorption isotherm. Phys. Rev. E 2017, 96, 052803. [Google Scholar] [CrossRef]
- Rahmati, A.R.; Akbari, O.A.; Marzban, A.; Karimi, R.; Pourfattah, F. Simultaneous investigations the effects of non-Newtonian nanofluid flow in different volume fractions of solid nanoparticles with slip and no-slip boundary conditions. Therm. Sci. Eng. Prog. 2018, 5, 263–277. [Google Scholar] [CrossRef]
- Arabpour, A.; Toghraie, D.; Akbari, O.A. Investigation into the effects of slip boundary condition on nanofluid flow in a double-layer microchannel. J. Therm. Anal. Calorim. 2018, 131, 2975–2991. [Google Scholar] [CrossRef]
- Koriko, O.K.; Animasaun, I.L.; Reddy, M.G.; Sandeep, N. Scrutinization of thermal stratification, nonlinear thermal radiation and quartic autocatalytic chemical reaction effects on the flow of three-dimensional Eyring-Powell Alumina-water nanofluid. Multidiscip. Model. Mater. Struct. 2018, 14, 261–283. [Google Scholar] [CrossRef]
- Tlili, I.; Khan, W.A.; Khan, I. Multiple slips effects on MHD SA–Al2O3 and SA–Cu non-Newtonian nanofluid flow over a stretching cylinder in porous medium with radiation and chemical reaction. Results Phys. 2018, 8, 213–222. [Google Scholar] [CrossRef]
- Barnoon, P.; Toghraie, D. Numerical investigation of laminar flow and heat transfer of non-Newtonian nanofluid within a porous medium. J. Mol. Liq. 2018, 325, 78–91. [Google Scholar] [CrossRef]
- Sheikholeslami, M. CuO-water nanofluid flow due to magnetic field inside a porous media considering Brownian motion. J. Mol. Liq. 2018, 249, 921–929. [Google Scholar] [CrossRef]
- Ghasemi, H.; Darjani, S.; Mazloomi, H.; Mozaffari, S. Preparation of stable multiple emulsions using food-grade emulsifiers: Evaluating the effects of emulsifier concentration, W/O phase ratio, and emulsification process. SN Appl. Sci. 2020, 2, 1–9. [Google Scholar] [CrossRef]
- Ghasemi, H.; Aghabarari, B.; Alizadeh, M.; Khanlarkhani, A.; Zahra, N.A. High efficiency decolorization of wastewater by Fenton catalyst: Magnetic iron-copper hybrid oxides. J. Water Process Eng. 2020, 37, 101540. [Google Scholar] [CrossRef]
- Mukhtar, T.; Jamshed, W.; Aziz, A.; Kouz, W.A. Computational investigation of heat transfer in a flow subjected to magnetohydrodynamic of Maxwell nanofluid over a stretched flat sheet with thermal radiation. Numer. Methods Part. Differ. Equ. 2020. [Google Scholar] [CrossRef]
- Hussain, S.; Oztop, H.F.; Qureshi, M.A.; Hamdeh, N.A. Magnetohydrodynamic flow and heat transfer of ferrofluid in a channel with non symmetric cavities. J. Therm. Anal. Calorim. 2020, 140, 811–823. [Google Scholar] [CrossRef]
- Ibrahim, W.; Negera, M. MHD slip flow of upper-convected Maxwell nanofluid over a stretching sheet with chemical reaction. J. Egypt. Math. Soc. 2020, 28, 7. [Google Scholar] [CrossRef]
- Patel, H.R.; Mittal, A.S.; Darji, R.R. MHD flow of micropolar nanofluid over a stretching/shrinking sheet considering radiation. Int. Commun. Heat Mass Transf. 2019, 108, 104322. [Google Scholar] [CrossRef]
- Ghobadi, A.H.; Hassankolaei, M.G. Numerical treatment of magneto Carreau nanofluid over a stretching sheet considering Joule heating impact and nonlinear thermal ray. Heat Transf. Asian Res. 2019, 48, 4133–4151. [Google Scholar] [CrossRef]
- Aziz, A.; Jamshed, W.; Aziz, T. Mathematical model for thermal and entropy analysis of thermal solar collectors by using Maxwell nanofluids with slip conditions, thermal radiation and variable thermal conductivity. Open Phys. 2018, 16, 123–136. [Google Scholar] [CrossRef]
- Khan, M.; Irfan, M.; Khan, W.A.; Alshomrani, A.S. A new modeling for 3D Carreau fluid flow considering nonlinear thermal radiation. Results Phys. 2017, 7, 2692–2704. [Google Scholar] [CrossRef]
- Naseem, F.; Shafiq, A.; Zhao, L.; Naseem, A. MHD biconvective flow of Powell–Eyring nanofluid over stretched surface. AIP Adv. 2017, 7, 065013. [Google Scholar] [CrossRef]
- Reddy, C.S.; Kishan, N.; Madhu, M. Finite Element Analysis of Eyring–Powell Nano Fluid Over an Exponential Stretching Sheet. Int. J. Appl. Comput. Math. 2017, 4, 8. [Google Scholar] [CrossRef]
- Ansari, M.S.; Motsa, S.S.; Trivedi, M. A New Numerical Approach to MHD Maxwellian nanofluid Flow Past an Impulsively Stretching Sheet. J. Nanofluids 2018, 7, 449–459. [Google Scholar] [CrossRef]
- Mahmood, A.; Jamshed, W.; Aziz, A. Entropy and heat transfer analysis using Cattaneo-Christov heat flux model for a boundary layer flow of Casson nanofluid. Result Phys. 2018, 10, 640–649. [Google Scholar] [CrossRef]
- Khan, S.A.; Nie, Y.; Ali, B. Multiple Slip Effects on Magnetohydrodynamic Axisymmetric Buoyant nanofluid Flow above a Stretching Sheet with Radiation and Chemical Reaction. Symmetry 2019, 11, 1171. [Google Scholar] [CrossRef]
- Hussain, S.; Oztop, H.F.; Qureshi, M.A.; Hamdeh, N.A. Double diffusive buoyancy induced convection in stepwise open porous cavities filled nanofluid. Int. Commun. Heat Mass Transf. 2020, 119, 104949. [Google Scholar] [CrossRef]
- Shah, Z.; Alzahrani, E.O.; Dawar, A.; Ullah, A.; Khan, I. Influence of Cattaneo-Christov model on Darcy-Forchheimer flow of Micropolar Ferrofluid over a stretching/shrinking sheet. Int. Commun. Heat Mass Transf. 2020, 220, 104385. [Google Scholar] [CrossRef]
- Abdal, S.; Ali, B.; Younas, S.; Ali, L.; Mariam, A. Thermo-Diffusion and Multislip Effects on MHD Mixed Convection Unsteady Flow of Micropolar nanofluid over a Shrinking/Stretching Sheet with Radiation in the Presence of Heat Source. Symmetry 2020, 12, 49. [Google Scholar] [CrossRef]
- Shafiq, A.; Rasool, G.; Khalique, C.M. Significance of Thermal Slip and Convective Boundary Conditions in Three Dimensional Rotating Darcy-Forchheimer nanofluid Flow. Symmetry 2020, 12, 741. [Google Scholar] [CrossRef]
- Jamshed, W.; Aziz, A. A comparative entropy based analysis of Cu and Fe3O4/methanol Powell-Eyring nanofluid in solar thermal collectors subjected to thermal radiation, variable thermal conductivity and impact of different nanoparticles shape. Result Phys. 2018, 9, 195–205. [Google Scholar] [CrossRef]
- Tiwari, R.J.; Das, M.K. heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Dapra, S.G. Perturbation solution for pulsatile flow of a non-Newtonian Williamson fluid in a rock fracture. Int. J. Rock Mech. Min. Sci. 2007, 44, 271–278. [Google Scholar] [CrossRef]
- Nadeem, S.; Hussain, S.T. Flow and heat transfer analysis of Williamson nanofluid. Appl. Nanosci. 2013, 4, 1005–1012. [Google Scholar] [CrossRef]
- Brewster, M.Q. Thermal Radiative Transfer and Properties; John Wiley and Sons: Hoboken, NJ, USA, 1992. [Google Scholar]
- Bhaskar, N.; Reddy, T.P.; Sreenivasulu, P. Influence of variable thermal conductivity on MHD boundary layar slip flow of ethylene-glycol based CU nanofluids over a stretching sheet with convective boundary condition. Int. J. Eng. Math. 2014, 10, 1–10. [Google Scholar] [CrossRef]
- Asif, M.; Aziz, A.; Jamshed, W.; Hussian, S. Mathematical model for thermal solar collectors by using magnetohydrodynamic Maxwell nanofluids with slip conditions, thermal radiation and variable thermal conductivity. Result Phys. 2017, 7, 3425–3433. [Google Scholar]
- Hamilton, R.L.; Crosser, O.K. Thermal conductivity of heterogeneous two-component systems. Ind. Eng. Chem. Fundam. 1962, 13, 27–40. [Google Scholar] [CrossRef]
- Xu, X.; Chen, S. Cattaneo Christov Heat Flux Model for Heat Transfer of Marangoni Boundary Layer Flow in a Copper Water Nanofluid; Wiley: Hoboken, NJ, USA, 2017; pp. 1–13. [Google Scholar]
- Mutuku, W.N. Ethylene glycol (EG) based nanofluids as a coolant for automotive radiator. Int. J. Comput. Electr. Eng. 2016, 3, 1–15. [Google Scholar] [CrossRef]
- Minea, A.A. A review on the Thermophysical properties of water-based nanofluids and their hybrids. Ann. "Dunarea de Jos" Univ. Galati Fascicle IX Metall. Mater. Sci. 2016, 39, 35–47. [Google Scholar]
- Aziz, A.; Jamshed, W.; Aziz, T.; Bahaidarah, H.M.S.; Rehman, K.U. Entropy analysis of Powell-Eyring hybrid nanofluid including effect of linear thermal radiation and viscous dissipation. J. Therm. Anal. Calorim. 2020, 1–13. [Google Scholar] [CrossRef]
- Keller, H.B. A New Difference Scheme for Parabolic Problems. In Numerical Solutions of Partial Differential Equations; Hubbard, B., Ed.; Academic Press: New York, NY, USA, 1971; Volume 2, pp. 327–350. [Google Scholar]
- Abolbashari, M.H.; Freidoonimehr, N.; Nazari, F.; Rashidi, M.M. Entropy analysis for an unsteady MHD flow past a stretching permeable surface in nano-fluid. Powder Technol. 2014, 267, 256–267. [Google Scholar] [CrossRef]
- Das, S.; Chakraborty, S.; Jana, R.N.; Makinde, O.D. Entropy analysis of unsteady magneto-nanofluid flow past accelerating stretching sheet with convective boundary condition. Appl. Math. Mech. 2015, 36, 1593–1610. [Google Scholar] [CrossRef]
- Jamshed, W.; Aziz, A. Cattaneo-Christov based study of TiO2–CuO/H2O Casson hybrid nanofluid flow over a stretching surface with entropy generationn. Appl. Nanosci. 2018, 8, 1–14. [Google Scholar] [CrossRef]
- Aziz, A.; Jamshed, W.; Ali, Y.; Shams, M. Heat transfer and entropy analysis of Maxwell hybrid nanofluid including effects of inclined magnetic field, Joule heating and thermal radiation. Discret. Contin. Dyn. Syst. S 2019, 13, 2667. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).