Exact Solutions and Continuous Numerical Approximations of Coupled Systems of Diffusion Equations with Delay

Abstract

In this work, we obtain exact solutions and continuous numerical approximations for mixed problems of coupled systems of diffusion equations with delay. Using the method of separation of variables, and based on an explicit expression for the solution of the separated vector initial-value delay problem, we obtain exact infinite series solutions that can be truncated to provide analytical–numerical solutions with prescribed accuracy in bounded domains. Although usually implicit in particular applications, the method of separation of variables is deeply correlated with symmetry ideas.

1. Introduction

In real-world problems, there are time lags between actions and responses. When these time delays are much shorter than the scale of observation, and they do not significantly affect the dynamics of the system, these problems might be satisfactorily modeled using ordinary or partial differential equations (PDEs). However, there are many situations where the presence of delays can not be safely ignored, requiring the use of modeling tools such as delay differential equations (DDEs) and partial delay differential equations (PDDEs) [1,2], including, among others, problems in life sciences [3], population dynamics [4], and control engineering [5].

For transport phenomena, diffusion, and heat conduction problems, it has been long pointed out that classical models, derived from Fourier or Fick laws and resulting in parabolic partial differential equations, implied infinite speed of propagation [6,7,8,9], and alternative models including the presence of delays have been proposed, finding increasing interest and wider areas of applications in recent years (see [10,11] and references therein).

Exact and analytical–numerical solutions for the generalized diffusion equation with delay, where a delay term is added to the classical model, have been previously obtained [12,13]. In the present work, we consider coupled systems of generalized diffusion equations with delay, written in matrix form as

$$u_t(t,x)=A{u}_{xx}(t,x)+B{u}_{xx}(t-\tau ,x),t>0,0\le x\le l,$$

(1)

where $u(t,x)\in {\mathbb{R}}^M$; $\tau >0$ is the delay; and the coefficient matrices A, $B\in {\mathbb{R}}^{M\times M}$ are, in general, not simultaneously diagonalizable. We consider mixed problems for these systems, with initial condition

$$u(t,x)=\phi (t,x),-\tau \le t\le 0,0\le x\le l,$$

(2)

and boundary conditions

$$u(t,0)=u(t,l)=0,t\ge -\tau .$$

(3)

Exact solutions in the form of infinite series for linear constant coefficients PDEs can be obtained using the method of separation of variables (MSV). Application of the MSV to particular problems is usually straightforward, without explicit symmetry ideas, but the MSV itself, and the properties of special functions appearing in the solutions of some problems, are deeply correlated with symmetry concepts (see, e.g., [14]).

Truncating the exact infinite series solutions, obtained by applying the MSV, up to a certain term can provide continuous numerical solutions satisfying a-priori error bounds in bounded domains. The use of these approaches has proven to be useful for more general PDEs, including time-dependent PDEs [15,16], strongly coupled problems [17], and also for different types of PDDEs [12,13,18,19,20,21,22].

In the case of PDDEs, application of the MSV results in initial-value problems for DDEs, and explicit constructive solutions for these problems are required in order to derive computable analytical–numerical solutions satisfying accuracy prescriptions. One key point in the problem considered in this work is being able to obtain closed form constructive solutions of the separated vector delay problem without requiring commutativity of the matrix coefficients. A result of this type will be obtained in the next section, and, as will be indicated in the final section, it could also pave the way to address different related problems.

The structure of this paper is as follows. In the next section, an explicit expression for the initial-value vector delay problem resulting from the application of the MSV to (1)–(3) is obtained. In Section 4, a formal series solution of problems (1)–(3), resulting from the application of the MSV, is proved to be an exact classical solution of this problem under certain regularity conditions on the initial function $\phi (t,x)$. Next, in Section 4, bounds on the approximation errors from truncating the infinite series solution to a finite number of terms are given, allowing the construction of continuous numerical solutions with prescribed accuracy in bounded domains. In the final section, the results are summarized and discussed.

2. Separated Initial-Value Vector Delay Differential Problem

We apply the MSV to problem (1)–(3) by writing $u(t,x)=T\left(t\right)X\left(x\right)$, where $T\left(t\right)\in {\mathbb{R}}^M$ and $X\left(x\right)\in \mathbb{R}$. Thus, we are led to two separated problems, the spatial scalar boundary problem

$$\begin{array}{ccc}& & X^{″}\left(x\right)+{\lambda }^{2}X\left(x\right)=0,0\le x\le l,\hfill \end{array}$$

(4)

$$\begin{array}{ccc}& & X\left(0\right)=X\left(l\right)=0,\hfill \end{array}$$

(5)

with solutions $X_n\left(x\right)=sin\left({\lambda }_{n}x\right)$, corresponding to the sequence of eigenvalues ${\lambda }_n=\frac{n\pi }{l},n=1,2,\dots$; and the corresponding temporal initial-value vector delay differential problems

$$\begin{array}{ccc}& & T_n^{\prime }\left(t\right)+{\lambda }_n^2(A{T}_n\left(t\right)+B{T}_n(t-\tau ))=0,t>0,\hfill \end{array}$$

(6)

$$\begin{array}{ccc}& & T_n\left(t\right)=B_n\left(t\right),-\tau \le t\le 0,\hfill \end{array}$$

(7)

where $B_n\left(t\right)$ are the Fourier coefficients in the expansion of the initial function $\phi (t,x)$ in terms of the eigenfunctions $X_n\left(x\right)$, i.e.,

$$B_n\left(t\right)=\frac{2}{l}{\int }_0^l\phi (t,x)sin\left(\frac{n\pi x}{l}\right)dx,$$

(8)

so that

$$\phi (t,x)=\sum _{n=1}^{\infty }{B}_n\left(t\right)sin\left(\frac{n\pi x}{l}\right),-\tau \le t\le 0,0\le x\le l.$$

(9)

Then, the formal series

$$u(t,x)=\sum _{n=1}^{\infty }{T}_n\left(t\right)sin\left(\frac{n\pi x}{l}\right)$$

(10)

will be a candidate for the exact solution of problem (1)–(3).

Problems (6) and (7) are of the general form

$$\begin{array}{ccc}\hfill F^{\prime }\left(t\right)& =& \mathcal{A}F\left(t\right)+\mathcal{B}F(t-\tau ),t>0,\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill F\left(t\right)& =& \psi \left(t\right),-\tau \le t\le 0,\hfill \end{array}$$

(12)

with $F\left(t\right),\psi \left(t\right)\in {\mathbb{R}}^M$ and $\mathcal{A},\mathcal{B}\in {\mathbb{R}}^{M\times M}$.

We consider first the auxiliary matrix problem

$$\begin{array}{ccc}\hfill G^{\prime }\left(t\right)& =& \mathcal{A}G\left(t\right)+\mathcal{B}G(t-\tau ),t>0,\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill G\left(t\right)& =& I,-\tau \le t\le 0,\hfill \end{array}$$

(14)

where $G\left(t\right)\in {\mathbb{R}}^{M\times M}$ and I is the identity matrix, whose solution is given in the next lemma.

Lemma 1.

Consider problem (13) and (14) with $\mathcal{A}$ invertible. Write $\mathcal{C}={\mathcal{A}}^{-1}\mathcal{B}$ and let

$$Q_1\left(t\right)=\left({\mathrm{e}}^{\mathcal{A}t}-I\right)(I+\mathcal{C}),Q_k\left(t\right)={\int }_0^t{\mathrm{e}}^{\mathcal{A}(t-s)}\mathcal{B}{Q}_{k-1}\left(s\right)ds,k>1.$$

(15)

Then, the solution of (13) and (14) in the interval $\left[\right(m-1)\tau ,m\tau ]$ is given by

$$\begin{array}{ccc}\hfill G\left(t\right)& =& I,m=0,\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill G\left(t\right)& =& I+\sum _{k=1}^m{Q}_k(t-(k-1)\tau ),m\ge 1.\hfill \end{array}$$

(17)

Proof. 

It is clear that $G\left(t\right)$ is a well-defined continuous function, as in each interval $\left[\right(m-1)\tau ,m\tau ]$ it is a sum of continuous functions, and values at the ends of the intervals agree. It is also immediate to check that the matrix functions $Q_k\left(t\right)$ defined in (15) satisfy

$$Q_1^{\prime }\left(t\right)=\mathcal{A}{Q}_1\left(t\right)+\mathcal{A}+\mathcal{B},Q_k^{\prime }\left(t\right)=\mathcal{A}{Q}_k\left(t\right)+\mathcal{B}{Q}_{k-1}\left(t\right),k\ge 2.$$

(18)

Thus, for $t\in [0,\tau ]$, one has

$$G^{\prime }\left(t\right)=Q_1^{\prime }\left(t\right)=\mathcal{A}{Q}_1\left(t\right)+\mathcal{A}+\mathcal{B}=\mathcal{A}G\left(t\right)+\mathcal{B}G(t-\tau ).$$

(19)

Moreover, for $t\in \left[\right(m-1)\tau ,m\tau ]$, with $m>1$, one has

$$\begin{array}{ccc}\hfill G^{\prime }\left(t\right)& =& \sum _{k=1}^m{Q}_k^{\prime }(t-(k-1)\tau )=\mathcal{A}{Q}_1\left(t\right)+\mathcal{A}+\mathcal{B}+\sum _{k=2}^m\mathcal{A}{Q}_k(t-(k-1)\tau )+\sum _{k=2}^m\mathcal{B}{Q}_{k-1}(t-\tau -(k-2)\tau )\hfill \\ & =& \mathcal{A}\left(I+\sum _{k=1}^m{Q}_k(t-(k-1)\tau )\right)+\mathcal{B}\left(I+\sum _{k=1}^{m-1}{Q}_k(t-(k-1)\tau )\right)=\mathcal{A}G\left(t\right)+\mathcal{B}G(t-\tau ).\hfill \end{array}$$

(20)

 □

The next lemma gives an expression for the solution of problem (11) and (12) in terms of the function $G\left(t\right)$ defined in Lemma 1.

Lemma 2.

Consider problem (11) and (12) with $\mathcal{A}$ and $I+\mathcal{C}$ invertible. For a differentiable initial function $\psi \left(t\right)$, its solution is given by $F\left(t\right)=\psi \left(t\right)$, for $-\tau \le t\le 0$, and, for $(m-1)\tau <t\le m\tau$ and $m\ge 1$, by

$$F\left(t\right)=G\left(t\right){(I+\mathcal{C})}^{-1}\left(\mathcal{C}\psi (-\tau )+\psi \left(0\right)\right)+{\int }_{-\tau }^{0}G(t-\tau -s){(I+\mathcal{C})}^{-1}\mathcal{C}{\psi }^{\prime }\left(s\right)ds.$$

(21)

Proof. 

It is clear that $F\left(t\right)$ is continuous, as it is defined in terms of continuous functions. It is also immediate from (20) that $F\left(t\right)$ satisfies (11) for $t\in \left[\right(m-1)\tau ,m\tau ]$ when $m>1$. Thus, we only need to check that (11) is also satisfied for $t\in [0,\tau ]$. In this case, since $G(t-\tau -s)=I$ for $s>t-\tau$, one has

$$\begin{array}{ccc}\hfill F^{\prime }\left(t\right)& =& G^{\prime }\left(t\right){(I+\mathcal{C})}^{-1}\left(\mathcal{C}\psi (-\tau )+\psi \left(0\right)\right)+{\int }_{-\tau }^{t-\tau }{G}^{\prime }(t-\tau -s){(I+\mathcal{C})}^{-1}\mathcal{C}{\psi }^{\prime }\left(s\right)ds\hfill \\ & =& \left(\mathcal{A}G\left(t\right)+\mathcal{B}\right){(I+\mathcal{C})}^{-1}\left(\mathcal{C}\psi (-\tau )+\psi \left(0\right)\right)+{\int }_{-\tau }^{t-\tau }\left(\mathcal{A}G(t-\tau -s)+\mathcal{B}\right){(I+\mathcal{C})}^{-1}\mathcal{C}{\psi }^{\prime }\left(s\right)ds\hfill \\ & =& \mathcal{A}\left(G\left(t\right){(I+\mathcal{C})}^{-1}\left(\mathcal{C}\psi (-\tau )+\psi \left(0\right)\right)+{\int }_{-\tau }^{0}G(t-\tau -s){(I+\mathcal{C})}^{-1}\mathcal{C}{\psi }^{\prime }\left(s\right)ds-{\int }_{t-\tau }^0{(I+\mathcal{C})}^{-1}\mathcal{C}{\psi }^{\prime }\left(s\right)ds\right)\hfill \\ & & +\mathcal{B}{(I+\mathcal{C})}^{-1}\left(\mathcal{C}\psi (-\tau )+\psi \left(0\right)\right)+{\int }_{-\tau }^{t-\tau }\mathcal{B}{(I+\mathcal{C})}^{-1}\mathcal{C}{\psi }^{\prime }\left(s\right)ds\hfill \\ & =& \mathcal{A}F\left(t\right)+\mathcal{B}\psi (t-\tau )=\mathcal{A}F\left(t\right)+\mathcal{B}F(t-\tau ).\hfill \end{array}$$

(22)

 □

A more explicit expression for the solution is presented in the next theorem.

Theorem 1.

The solution of problem (11) and (12), with conditions as in Lemma 2, is given by $F\left(t\right)=\psi \left(t\right)$ for $-\tau \le t\le 0$, and, for $(m-1)\tau <t\le m\tau$ and $m\ge 1$, by

$$\begin{array}{ccc}\hfill F\left(t\right)& =& \psi \left(0\right)+\sum _{k=1}^m{Q}_k(t-(k-1)\tau ){(I+\mathcal{C})}^{-1}\left(\mathcal{C}\psi (-\tau )+\psi \left(0\right)\right)\hfill \\ & +& \sum _{k=1}^{m-1}{\int }_{-\tau }^0{Q}_k(t-(k-1)\tau -s){(I+\mathcal{C})}^{-1}\mathcal{C}{\psi }^{\prime }\left(s\right)ds\hfill \\ & +& {\int }_{-\tau }^{t-m\tau }{Q}_m(t-(m-1)\tau -s){(I+\mathcal{C})}^{-1}\mathcal{C}{\psi }^{\prime }\left(s\right)ds,\hfill \end{array}$$

(23)

where the second summation is assumed to be empty for $m=1$.

Proof. 

It is immediate by substituting in (21) the expression of $G\left(t\right)$ given in (17), taking into account that $t-\tau -s>(m-1)\tau \iff s<t-m\tau$, and cancelling out some terms. □

Remark 1.

Although the matrix functions $Q_k\left(t\right)$ have been defined in (15) recursively, they can be written explicitly as iterated integrals,

$$Q_k\left(t\right)={\int }_0^t{\mathrm{e}}^{\mathcal{A}(t-s_k)}\mathcal{B}d{s}_k{\int }_0^{s_k}{\mathrm{e}}^{\mathcal{A}(s_k-s_{k-1})}\mathcal{B}d{s}_{k-1}\cdots {\int }_0^{s_2}{\mathrm{e}}^{\mathcal{A}(s_2-s_1)}(\mathcal{A}+\mathcal{B})d{s}_1.$$

(24)

When $\mathcal{A}$ and $\mathcal{B}$ commute, it is not difficult to check that they are given by the following compact expression without integrals,

$$Q_k\left(t\right)=\left({\mathrm{e}}^{\mathcal{A}t}\sum _{j=0}^{k-1}\frac{{(-\mathcal{A}t)}^j}{j!}-I\right){(-\mathcal{C})}^{k-1}(I+\mathcal{C}),k\ge 1.$$

(25)

In particular, if $\mathcal{A}$ and $\mathcal{B}$ are diagonal, or with the appropriate change of variables when they are simultaneously diagonalizable, problems (11) and (12) consist of M independent scalar problems, and it can be checked that the expressions given by Theorem 1 for each component of $F\left(t\right)$ agree with those given in [12,13] for the corresponding scalar problems.

Remark 2.

In scalar problems, diffusion coefficients are always positive, so it is common to assume in diffusion vector problems that the corresponding matrix coefficients are positive defined (see, e.g., [23]). In the next sections, where exact and numerical solutions for the coupled diffusion problems (1) and (3) are derived, we will assume the weaker condition of A being positive stable, i.e., having eigenvalues with positive real part, similar to the condition assumed in [16] for diffusion problems without delay. In this section, in Lemma 2 and Theorem 1, we have only required A to be invertible, and similarly for $I+C$, or equivalently $A+B$, which would be the coefficient when $\tau =0$. As will be indicated in the last section, the solution of (11) and (12) given in Theorem 1 might find application in different problems, not necessarily of diffusion type, so that only conditions guaranteeing the obtention of compact, closed form solutions of (11) and (12) have been assumed.

When A is singular, matrices $Q_k\left(t\right)$ can still be defined, by replacing the definition of $Q_1\left(t\right)$ in (15) with the nonintegrated form

$$Q_1\left(t\right)={\int }_0^t{\mathrm{e}}^{\mathcal{A}(t-s)}(\mathcal{A}+\mathcal{B})ds.$$

(26)

However, even in the much simpler case of commuting coefficients, infinite sums seem unavoidable, as the expression corresponding to (25) would be

$$Q_k\left(t\right)={\mathrm{e}}^{\mathcal{A}t}\sum _{r=0}^{\infty }{(-\mathcal{A})}^r\frac{t^{r+k}}{(r+k)!}{\mathcal{B}}^{k-1}(\mathcal{A}+\mathcal{B}),k\ge 1.$$

(27)

3. Exact Infinite Series Solution

The solution of the general initial-value vector DDE problem given in Theorem 1 provides expressions for the functions $T_n\left(t\right)$ in (10), by taking in (11) and (12) $\mathcal{A}=-{\lambda }_n^{2}A$, $\mathcal{B}=-{\lambda }_n^{2}B$, and $\psi \left(t\right)=B_n\left(t\right)$. The corresponding functions $Q_k\left(t\right)$ for each of these problems will be denoted $Q_k^n\left(t\right)$. Writing $p=\pi /l$, the candidate series solution of problem (1)–(3) for $t\in \left[\right(m-1)\tau ,m\tau ]$ can be written as

$$u(t,x)=\phi (0,x)+u_1(t,x)+u_2(t,x)+u_3(t,x),$$

(28)

where

$$\begin{array}{ccc}\hfill u_1(t,x)& =& \sum _{n=1}^{\infty }\sum _{k=1}^m{Q}_k^n(t-(k-1)\tau ){(I+C)}^{-1}\left(C{B}_n(-\tau )+B_n\left(0\right)\right)sin\left(npx\right),\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill u_2(t,x)& =& \sum _{n=1}^{\infty }{\int }_{-\tau }^0\sum _{k=1}^{m-1}{Q}_k^n(t-(k-1)\tau -s){(I+C)}^{-1}C{B}_n^{\prime }\left(s\right)sin\left(npx\right)ds,\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill u_3(t,x)& =& \sum _{n=1}^{\infty }{\int }_{-\tau }^{t-m\tau }{Q}_m^n(t-(m-1)\tau -s){(I+C)}^{-1}C{B}_n^{\prime }\left(s\right)sin\left(npx\right)ds.\hfill \end{array}$$

(31)

In the next theorem, we show that under a condition on the eigenvalues of A and for sufficiently regular initial functions, the three series in (29)–(31) converge uniformly and can be differentiated termwise with respect to t and twice with respect to x, and the candidate series (29) is a classical solution of problem (1)–(3). Specifically, we will assume the following conditions on the initial function $\phi (t,x)$:

$$\begin{array}{ccc}& & \phi (·,x)\mathrm{is}\mathrm{continuously}\mathrm{differentiable}\mathrm{for}\mathrm{each}x,\hfill \\ & & \phi (t,·),{\phi }_t(t,·)\mathrm{are}\mathrm{twice}\mathrm{continuously}\mathrm{differentiable}\mathrm{for}\mathrm{each}t,\hfill \\ & & {\phi }_{xx}(t,x)\mathrm{is}\mathrm{continuous}\mathrm{in}t\mathrm{and}\mathrm{of}\mathrm{bounded}\mathrm{variation}\mathrm{in}x.\hfill \end{array}$$

(32)

Theorem 2.

Consider problem (1)–(3). Assume that every eigenvalue of A has positive real part, and that $(I+C)$ is invertible, where $C=A^{-1}B$ and I is the identity matrix. For any initial function $\phi (t,x)$ satisfying the conditions given in (32), the function $u(t,x)$ defined in (29) is continuous in $[0,\infty )\times [0,l]$, its derivatives $u_t(t,x)$ and $u_{xx}(t,x)$ are continuous in $(0,\infty )\times (0,l)$, and it is an exact solution of problem (1)–(3).

Before proving this theorem, we present in the next lemmas bounds for the norms of matrix exponentials and of the functions $Q_k^n\left(t\right)$. In what follows, $\parallel \parallel$ denotes a vector norm or a compatible norm for matrices, and we will assume that the conditions of Theorem 2 hold.

Lemma 3.

For a matrix $\mathcal{A}$, let $\sigma \left(\mathcal{A}\right)$ be the set of its eigenvalues, and $\alpha \left(\mathcal{A}\right)=max\{\Re (z\left)\right|z\in \sigma \left(\mathcal{A}\right)\}$. Then, for each $\nu >\alpha \left(\mathcal{A}\right)$, we can find a constant $K_{\nu }$ such that

$$\parallel {\mathrm{e}}^{\mathcal{A}t}\parallel \le K_{\nu }{\mathrm{e}}^{\nu t},\forall t\ge 0.$$

(33)

Proof. 

Consider the Jordan decomposition $\mathcal{A}=PJ{P}^{-1}$, so that $J=D+E$, where D is diagonal, with eigenvalues of $\mathcal{A}$, and E is an upper triangular nilpotent matrix. Letting $P\left(t\right)={\sum }_{k=0}^{m-1}{\parallel Et\parallel }^k/k!$, one has ([24], p. 396) that $\parallel {\mathrm{e}}^{\mathcal{A}t}\parallel \le {\mathrm{e}}^{\sigma \left(\mathcal{A}\right)t}P\left(t\right)$. Thus, for any $\nu >\alpha \left(\mathcal{A}\right)$, there is $T>0$ such that ${\mathrm{e}}^{t\alpha \left(\mathcal{A}\right)}P\left(t\right)\le {\mathrm{e}}^{\nu t}$ for $t>T$, and we can take $K_{\nu }=max\{max\left\{P\left(t\right)\right|t\in [0,T]\},1\}$. □

Lemma 4.

Let $\alpha =\parallel A\parallel$ and $\gamma =\parallel C\parallel$. Fix $\nu >0$ such that $-\nu >\alpha (-A)$, and write K for a constant $K_{-\nu }>1$ satisfying the condition of Lemma 3. Then, $Q_k^n\left(t\right)$ can be written in the form

$$Q_k^n\left(t\right)={(-1)}^k{C}^{k-1}(I+C)+S_k^n\left(t\right),$$

(34)

where the matrices $S_k^n\left(t\right)$ admit the bounds

$$\parallel S_k^n\left(t\right)\parallel \le (1+\gamma ){\gamma }^{k-1}{K}^k{\mathrm{e}}^{-\nu n^2{p}^{2}t}\sum _{j=0}^{k-1}\frac{{\left(n^2{p}^2\alpha t\right)}^j}{j!}.$$

(35)

Proof. 

We proceed by induction on k. For $k=1$, one has $Q_1^n\left(t\right)=({\mathrm{e}}^{-n^2{p}^{2}At}-I)(I+C)$, and we can write $Q_1^n\left(t\right)=-(I+C)+S_1^n\left(t\right)$, where $S_1^n\left(t\right)={\mathrm{e}}^{-n^2{p}^{2}At}(I+C)$, so that

$$\parallel S_k^n\left(t\right)\parallel \le \parallel (I+C)\parallel \parallel {\mathrm{e}}^{-n^2{p}^{2}At}\parallel \le (1+\gamma )K{\mathrm{e}}^{-\nu n^2{p}^{2}t},$$

(36)

which is of the form (35).

For $k>1$, from (15) and assuming the induction hypothesis, one has

$$\begin{array}{ccc}\hfill Q_k^n\left(t\right)& =& -{\int }_0^t{\mathrm{e}}^{-n^2{p}^{2}A(t-s)}{n}^2{p}^{2}AC\left({(-1)}^{k-1}{C}^{k-2}(I+C)+S_{k-1}^n\left(s\right)\right)ds\hfill \\ & =& {(-1)}^k{C}^{k-1}(I+C)+S_k^n\left(t\right),\hfill \end{array}$$

(37)

where

$$S_k^n\left(t\right)={\mathrm{e}}^{-n^2{p}^{2}At}{(-1)}^{k-1}{C}^{k-1}(I+C)-{\int }_0^t{\mathrm{e}}^{-n^2{p}^{2}A(t-s)}{n}^2{p}^{2}AC{S}_{k-1}^n\left(s\right)ds.$$

(38)

Thus,

$$\begin{array}{ccc}\hfill \parallel S_k^n\left(t\right)\parallel & \le & K{\mathrm{e}}^{-n^2{p}^2\nu t}{\gamma }^{k-1}(1+\gamma )+{\int }_0^{t}K{\mathrm{e}}^{-n^2{p}^2\nu (t-s)}{n}^2{p}^2\alpha \gamma (1+\gamma ){\gamma }^{k-2}{K}^{k-1}{\mathrm{e}}^{-\nu n^2{p}^{2}s}\sum _{j=0}^{k-2}\frac{{\left(n^2{p}^2\alpha s\right)}^j}{j!}ds\hfill \\ & \le & (1+\gamma ){\gamma }^{k-1}{K}^k{\mathrm{e}}^{-\nu n^2{p}^{2}t}\sum _{j=0}^{k-1}\frac{{\left(n^2{p}^2\alpha t\right)}^j}{j!}.\hfill \end{array}$$

(39)

 □

We can now proceed to the proof of Theorem 2. We note that the conditions (3) assumed for the initial function $\phi (t,x)$ ensure convergence of the Fourier expansions of ${\phi }_t(t,x)$ and ${\phi }_{xx}(t,x)$.

Proof of Theorem 2.

From Lemma 2, since $\nu >0$, it follows that for each k and any finite positive t, the functions $Q_k^n\left(t\right)$ are bounded. In addition, for each t there is N such that $Q_k^n\left(t\right)$ is decreasing for $n>N$.

Consider now the series obtained by termwise differentiating $u(t,x)$, as given in (28) and (29)–(31), with respect to t. We denote this series $u_t(t,x)$, as it will be proved that it converges uniformly in $(0,\infty )\times (0,l)$. For each of the subseries in (29)–(31) and for each k, and letting aside some constant terms, one gets infinite series of the form

$$\sum _{n=1}^{\infty }-n^2{p}^2{Q}_k^n(t-(k-1)\tau ){(I+C)}^{-1}\left(C{B}_n(-\tau )+B_n\left(0\right)\right)sin\left(npx\right)$$

(40)

for $u_1(t,x)$, and of the form

$$\sum _{n=1}^{\infty }-n^2{p}^2{Q}_k^n(t-(k-1)\tau -s){(I+C)}^{-1}C{B}_n^{\prime }\left(s\right)sin\left(npx\right)ds$$

(41)

for $u_2(t,x)$ and $u_3(t,x)$. From the conditions assumed in (3) for the initial function $\phi (t,x)$, it follows the uniform converge and continuity of the series

$$\begin{array}{ccc}& & {(I+C)}^{-1}\left(C\sum _{n=1}^{\infty }-n^2{p}^2{B}_n(-\tau )sin\left(npx\right)+\sum _{n=1}^{\infty }-n^2{p}^2{B}_n\left(0\right)sin\left(npx\right)\right)\hfill \\ & & ={(I+C)}^{-1}\left(C{\phi }_{xx}(-\tau ,x)+{\phi }_{xx}(0,x)\right)\hfill \end{array}$$

(42)

and

$${(I+C)}^{-1}C\sum _{n=1}^{\infty }-n^2{p}^2{B}_n^{\prime }\left(s\right)sin\left(npx\right)ds={(I+C)}^{-1}C{\phi }_{txx}(s,x)$$

(43)

for $x\in (0,l)$. Hence, since $Q_k^n\left(t\right)$ are bounded and decreasing for n large, it follows that $u_t(t,x)$ converges uniformly in $\left[\right(m-1)\tau ,m\tau ]\times (0,l)$. It is immediate to check the continuity at the connecting intervals for $m>1$. For $m=1$, at $t=0$ it is easy to check the continuity of $u(t,x)$, but in general this is not the case for $u_t(t,x)$, unless a special condition is required on the initial function $\phi (t,x)$.

Similar arguments apply for the series resulting from termwise twice differentiating $u(t,x)$ with respect to x, since they have the same form as those previously discussed for $u_t(t,x)$. □

4. Continuous Numerical Solutions

In this section, we will obtain bounds on the errors of continuous numerical solutions of problem (1)–(3), computed by truncating to N terms the exact series solution defined in Theorem 2.

Using the decomposition of $Q_k^n\left(t\right)$ given in (34), it is immediate that the series in (29)–(31) can be written in the form

$$\begin{array}{ccc}\hfill u_1(t,x)& =& \sum _{k=1}^m{(-1)}^k{C}^{k-1}\left(C\phi (-\tau ,x)+\phi (0,x)\right)+S_1(t,x),\hfill \end{array}$$

(44)

$$\begin{array}{ccc}\hfill u_2(t,x)& =& \sum _{k=1}^{m-1}{(-1)}^k{C}^k(\phi (0,x)-\phi (-\tau ,x))+S_2(t,x),\hfill \end{array}$$

(45)

$$\begin{array}{ccc}\hfill u_3(t,x)& =& {(-1)}^m{C}^m(\phi (t-m\tau ,x)-\phi (-\tau ,x))+S_3(t,x),\hfill \end{array}$$

(46)

where $S_i(t,x),i=1,2,3,$ are the respective infinite sums in (29)–(31) corresponding to the terms $S_k^n\left(t\right)$. Hence, the errors resulting from approximating $u(t,x)$ by using the expressions for $u_i(t,x),i=1,2,3,$ given in (44)–(46) but computing only a finite number of terms, N, in the infinite sums $S_i(t,x)i=1,2,3,$ are

$$\begin{array}{ccc}\hfill R_1^N& =& \sum _{n=N+1}^{\infty }\sum _{k=1}^m{S}_k^n(t-(k-1)\tau ){(I+C)}^{-1}\left(C{B}_n(-\tau )+B_n\left(0\right)\right)sin\left(npx\right),\hfill \end{array}$$

(47)

$$\begin{array}{ccc}\hfill R_2^N& =& \sum _{n=N+1}^{\infty }{\int }_{-\tau }^0\sum _{k=1}^{m-1}{S}_k^n(t-(k-1)\tau -s){(I+C)}^{-1}C{B}_n^{\prime }\left(s\right)sin\left(npx\right)ds,\hfill \end{array}$$

(48)

$$\begin{array}{ccc}\hfill R_3^N& =& \sum _{n=N+1}^{\infty }{\int }_{-\tau }^{t-m\tau }{S}_m^n(t-(m-1)\tau -s){(I+C)}^{-1}C{B}_n^{\prime }\left(s\right)sin\left(npx\right)ds.\hfill \end{array}$$

(49)

To bound these errors, we will use bounds for $S_k^n\left(t\right)$ derived from (35), in terms of incomplete gamma functions ([25], p. 174). Letting ${\mu }_k=max\{{(\alpha /\nu )}^j,j=0,\dots ,k-1\}$, from (35) it follows that

$$\parallel S_k^n\left(t\right)\parallel \le (1+\gamma ){\gamma }^{k-1}{K}^k{\mu }_k{\mathrm{e}}^{-\nu n^2{p}^{2}t}\sum _{j=0}^{k-1}\frac{{\left(n^2{p}^2\nu t\right)}^j}{j!}=(1+\gamma ){\gamma }^{k-1}{K}^k{\mu }_k\frac{\Gamma (k,n^2{p}^2\nu t)}{\Gamma \left(k\right)}.$$

(50)

We note that, from the conditions (3) assumed for the initial function $\phi (t,x)$, the Fourier coefficients of $\phi (t,x)$ and ${\phi }_t(t,x)$ decay as $O\left(n^{-2}\right)$, so we can find constants H and $H_1$ such that, for $s\in [-\tau ,0]$,

$$\parallel B_n\left(s\right)\parallel \le \frac{H}{n^2},\parallel B_n^{\prime }\left(s\right)\parallel \le \frac{H_1}{n^2}.$$

(51)

Hence, writing ${\gamma }_1=\parallel {(I+C)}^{-1}\parallel$, one has

$$\begin{array}{ccc}\hfill \parallel R_1^N\parallel & \le & {\gamma }_1{(1+\gamma )}^{2}H\sum _{k=1}^m\frac{{\gamma }^{k-1}{K}^k{\mu }_k}{\Gamma \left(k\right)}\sum _{n=N+1}^{\infty }\frac{\Gamma (k,n^2{p}^2\nu (t-(k-1)\tau )}{n^2},\hfill \\ & \le & {\gamma }_1{(1+\gamma )}^{2}H\sum _{k=1}^m\frac{{\gamma }^{k-1}{K}^k{\mu }_k}{\Gamma \left(k\right)}\frac{\Gamma (k,{(N+1)}^2{p}^2\nu (t-(k-1)\tau )}{N},\hfill \end{array}$$

(52)

since $\Gamma (k,v)$ is decreasing with respect to v and ${\sum }_{n=N+1}^{\infty }1/n^2\le 1/N$.

Similarly, for $R_2^N$, one has

$$\begin{array}{ccc}\hfill \parallel R_2^N\parallel & \le & {\gamma }_1(1+\gamma )H_1\sum _{k=1}^{m-1}\frac{{\gamma }^k{K}^k{\mu }_k}{\Gamma \left(k\right)}\sum _{n=N+1}^{\infty }{\int }_{-\tau }^0\frac{\Gamma (k,n^2{p}^2\nu (t-(k-1)\tau -s)}{n^2}ds,\hfill \\ & \le & {\gamma }_1(1+\gamma )H_1\tau \sum _{k=1}^{m-1}\frac{{\gamma }^k{K}^k{\mu }_k}{\Gamma \left(k\right)}\frac{\Gamma (k,{(N+1)}^2{p}^2\nu (t-k\tau )}{N},\hfill \end{array}$$

(53)

since $\Gamma (k,n^2{p}^2\nu (t-(k-1)\tau -s)\le \Gamma (k,n^2{p}^2\nu (t-k\tau )$ for $s\in [-\tau ,0]$.

Finally, for $R_3^N$, one has

$$\parallel R_3^N\parallel \le {\gamma }_1(1+\gamma )H_1\frac{{\gamma }^m{K}^m{\mu }_m}{\Gamma \left(m\right)}\sum _{n=N+1}^{\infty }{\int }_{-\tau }^{t-m\tau }\frac{\Gamma (k,n^2{p}^2\nu (t-(m-1)\tau -s)}{n^2}ds,$$

(54)

and with the change of variable $v=n^2{p}^2\nu (t-m\tau -s)$, one gets

$$\begin{array}{ccc}\hfill \parallel R_3^N\parallel & \le & {\gamma }_1(1+\gamma )H_1\frac{{\gamma }^m{K}^m{\mu }_m}{\Gamma \left(m\right)}\sum _{n=N+1}^{\infty }\frac{1}{n^4{p}^2\nu }{\int }_0^{n^2{p}^2\nu (t-(m-1)\tau )}\Gamma (m,v+n^2{p}^2\nu \tau )dv,\hfill \\ & \le & {\gamma }_1(1+\gamma )H_1\frac{{\gamma }^m{K}^m{\mu }_m}{\Gamma \left(m\right)}\sum _{n=N+1}^{\infty }\frac{1}{n^4{p}^2\nu }{\int }_0^{\infty }\Gamma (m,v)dv\le {\gamma }_1(1+\gamma )H_1\frac{m{\gamma }^m{K}^m{\mu }_m}{3p^2\nu N^3},\hfill \end{array}$$

(55)

since ${\int }_0^{\infty }\Gamma (m,v)dv=\Gamma (m+1)$ and ${\sum }_{n=N+1}^{\infty }1/n^4\le 1/\left(3N^3\right)$.

Therefore, we have proved the following theorem.

Theorem 3.

Consider problem (1)–(3), let $u(t,x)$ be the exact series solution given in Theorem 2, and let $u_N(t,x)$ be the approximation obtained when the infinite series’ in (44)–(46) are replaced by the corresponding partial sums with N terms. Then, for $(t,x)\in \left[\right(m-1)\tau ,m\tau ]\times [0,l],$

$$\begin{array}{cc}\hfill \parallel u_N(t,x)-u(t,x)\parallel & \le \sum _{k=1}^m\frac{{\gamma }_1{(1+\gamma )}^{2}H{\gamma }^{k-1}{K}^k{\mu }_k}{\Gamma \left(k\right)}\frac{\Gamma (k,{(N+1)}^2{p}^2\nu (t-(k-1)\tau ))}{N}\hfill \\ \hfill & +\sum _{k=1}^{m-1}\frac{{\gamma }_1(1+\gamma )H_1\tau {\gamma }^k{K}^k{\mu }_k}{\Gamma \left(k\right)}\frac{\Gamma (k,{(N+1)}^2{p}^2\nu (t-k\tau ))}{N}+\frac{{\gamma }_1(1+\gamma )H_{1}m{\gamma }^m{K}^m{\mu }_m}{3p^2\nu N^3}.\hfill \end{array}$$

(56)

Consequently, for any $\delta >0$ and given a prescribed a-priori error $ϵ>0,$ there is N such that $\parallel u_N(t,x)-u(t,x)\parallel \le ϵ$ for $(t,x)\in \left[\right(m-1)\tau +\delta ,m\tau ]\times [0,l].$

Next, we present an example showing the practical feasibility of computing the numerical solutions $u_N(t,x)$ and the error bounds given in Theorem 3. In this example, we used the infinity norm; computations were performed using Maple${}^{\circledR }$, and graphics were prepared using Matlab${}^{\circledR }$.

Example 1.

Figure 1 shows the numerical solutions computed with $N=20$ for problem (1)–(3) with parameters $\tau =1$, $l=1$, and

$$A=\left(\begin{array}{cc}2& 1\\ 1& 3\end{array}\right),B=\left(\begin{array}{cc}1& 0\\ 1& -1\end{array}\right),\phi (t,x)=\left(\begin{array}{c}(t+1)x(x^2-1)\\ {\mathrm{e}}^{-(t+1)}x(x^2-1)\end{array}\right).$$

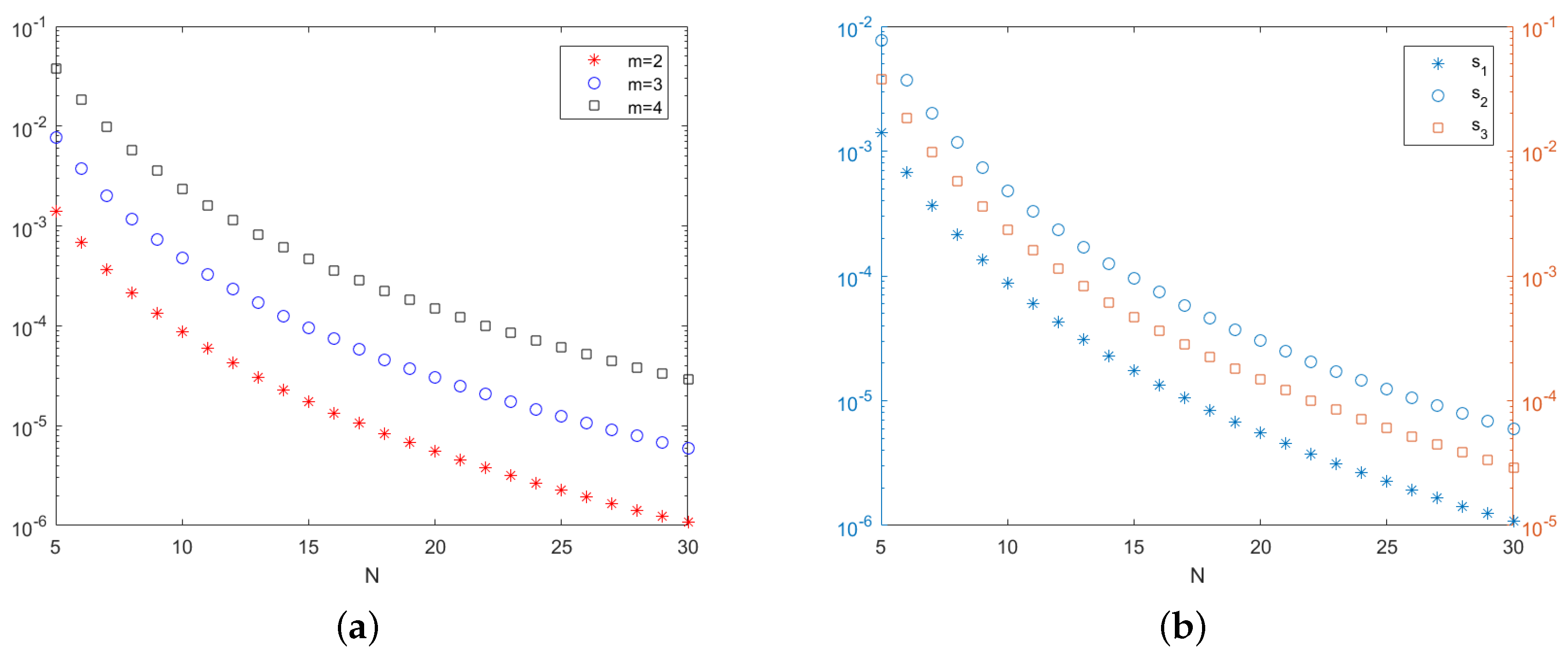
In the next figure (Figure 2), total error bounds and individual contributions to the error bounds by the three terms in (56) are presented.

In this example, the Fourier coefficients of the initial function satisfy more stringent conditions than those assumed in (51), since one has

$$B_n\left(s\right)={\left(\begin{array}{cc}\frac{12{(-1)}^n(s+1)}{n^3{\pi }^3}& \frac{12{(-1)}^n{\mathrm{e}}^{-(s+1)}}{n^3{\pi }^3}\end{array}\right)}^T,B_n^{\prime }\left(s\right)={\left(\begin{array}{cc}\frac{12{(-1)}^n}{n^3{\pi }^3}& \frac{12{(-1)}^{n+1}{\mathrm{e}}^{-(s+1)}}{n^3{\pi }^3}\end{array}\right)}^T.$$

(57)

Thus, taking $H=H_1=12/{\pi }^3$, one has $\parallel B_n\left(s\right)\parallel \le H/n^3$ and $\parallel B_n^{\prime }\left(s\right)\parallel \le H_1/n^3$. Hence, the bounds given in (56) can be refined for this example by substituting N in the denominator of the first two terms by $2N^2$, and $3N^3$ in the denominator of the third term by $4N^4$.

For the rest of the constants in (56), it is straightforward to compute that $\gamma =1$ and ${\gamma }_1=5$. Since $\alpha (-A)=-1$, letting $\nu =0.9$ we can choose $K=1.1$, and also, since $\alpha =3$, one gets ${\mu }_k={(3/0.9)}^{k-1}$, for $k=1\dots m$.

As seen in Figure 2, the order of the global error bound is essentially determined by the third term in (56).

5. Conclusions

In this work, we have presented exact and continuous numerical solutions for coupled systems of diffusion equations with delay, extending previous results for scalar problems [12,13]. These solutions are expressed in terms of the parameters of the problem, and may be used to analyze how the system behavior depends on those parameters.

As shown in Theorem 3, the analytic–numerical solutions proposed in this work may provide numerical approximations with a-priori prescribed errors in bounded domains. The error bounds given in Theorem 3 for the first two terms, $R_1^N$ and $R_2^N$, depending on gamma incomplete functions, are essentially exponentially decaying with N; and the third term, $R_3^N$, is $O\left(N^{-3}\right)$. As was shown in [13], the rate of convergence can also be made exponential for this last term, by using suitable polynomial approximations to the initial function. In any case, the error bounds guaranteed by Theorem 3 are usually far from being sharp, and convergence can be much faster, especially for problems with highly regular initial functions. Additionally, when the initial function consists of a finite combination of the eigenfunctions $sin\left(npx\right)$, the exact solution defined in Theorem 2 reduces to a finite sum.

The expression given in Theorem 1 for the solution of a general initial value vector DDE problem may find applications in a wide variety of problems, beyond its use in this work. For instance, it would provide the basis to deal with related problems for coupled system with delay, as the type of reaction–diffusion equations with delay considered in [13]. More generally, since the matrix coefficients are not required to commute, this expression can be applied to obtain constructive solutions for problems involving scalar higher-order linear DDE, as they can be converted into a first-order system of the type considered in Theorem 1. The exact solution given in Theorem 1 could also provide the basis for extending previous works dealing with random scalar delay problems [26,27] to general vector delay problems, or with the construction of numerical schemes based on exact solutions [28,29,30].