Reconstructed f(R) Gravity and Its Cosmological Consequences in theChameleon Scalar Field with a Scale Factor Describing the Pre-Bounce Ekpyrotic Contraction
Abstract
1. Introduction
2. Brief Overview of Gravity
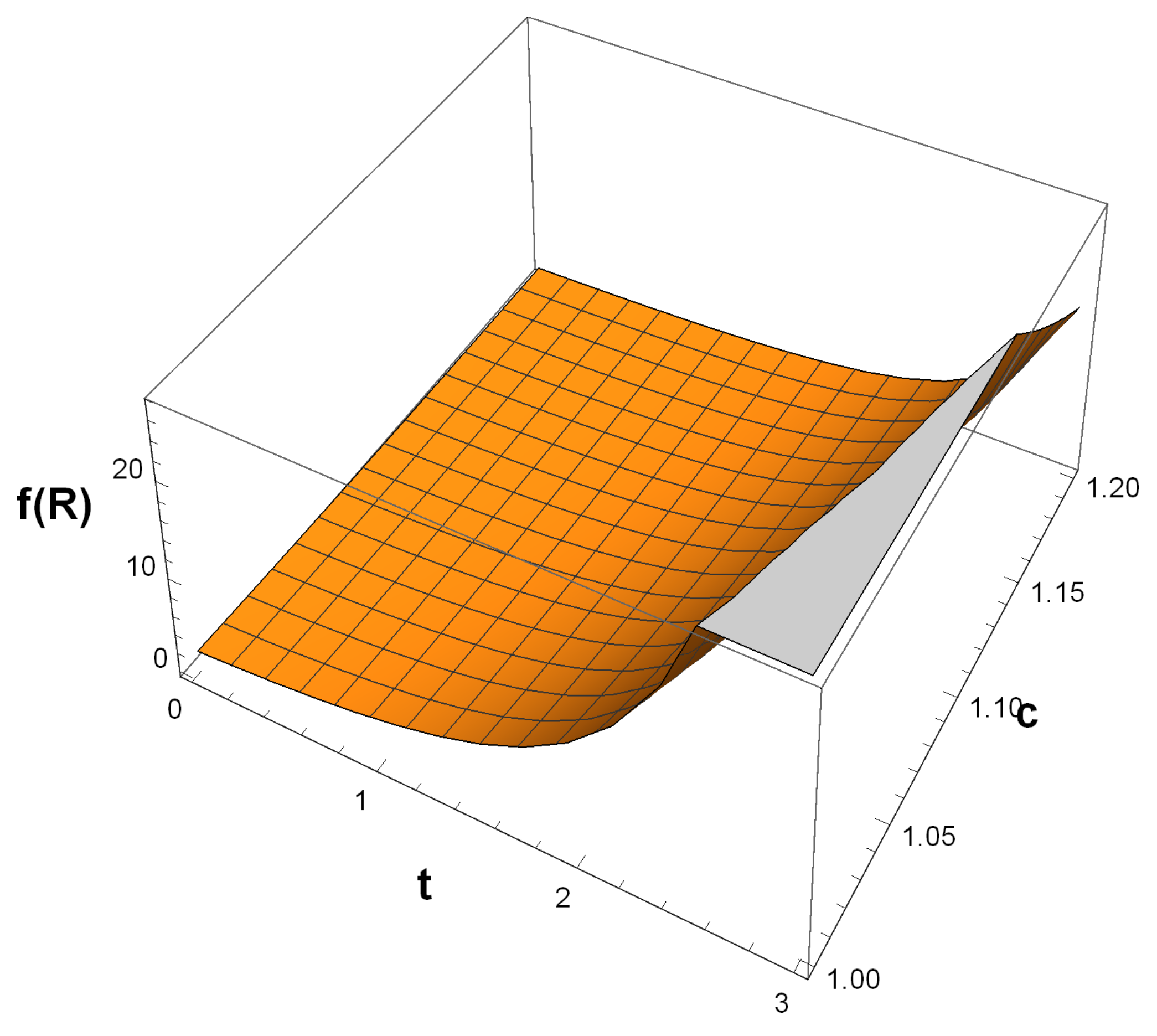
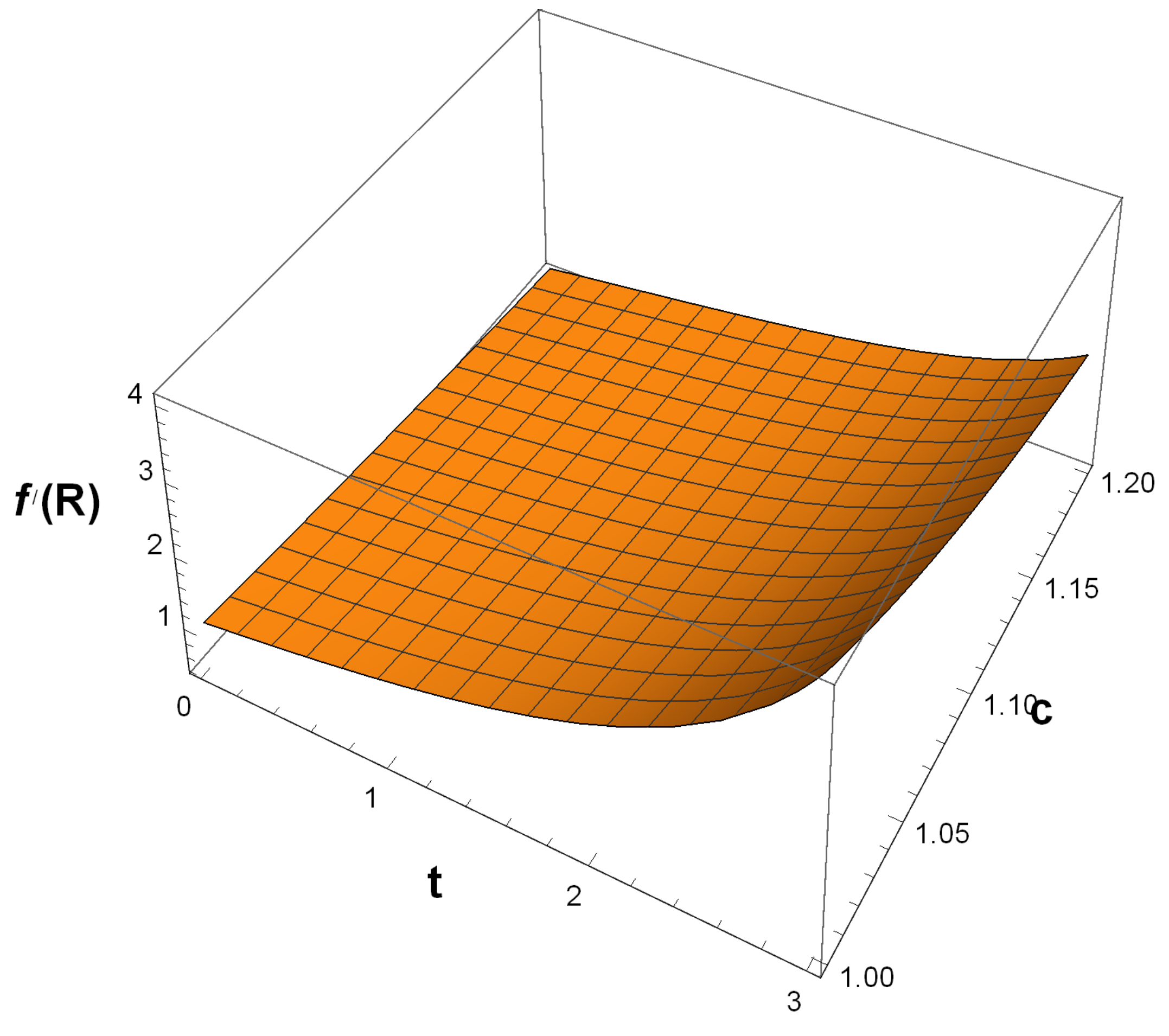
3. A Reconstruction Scheme for Gravity
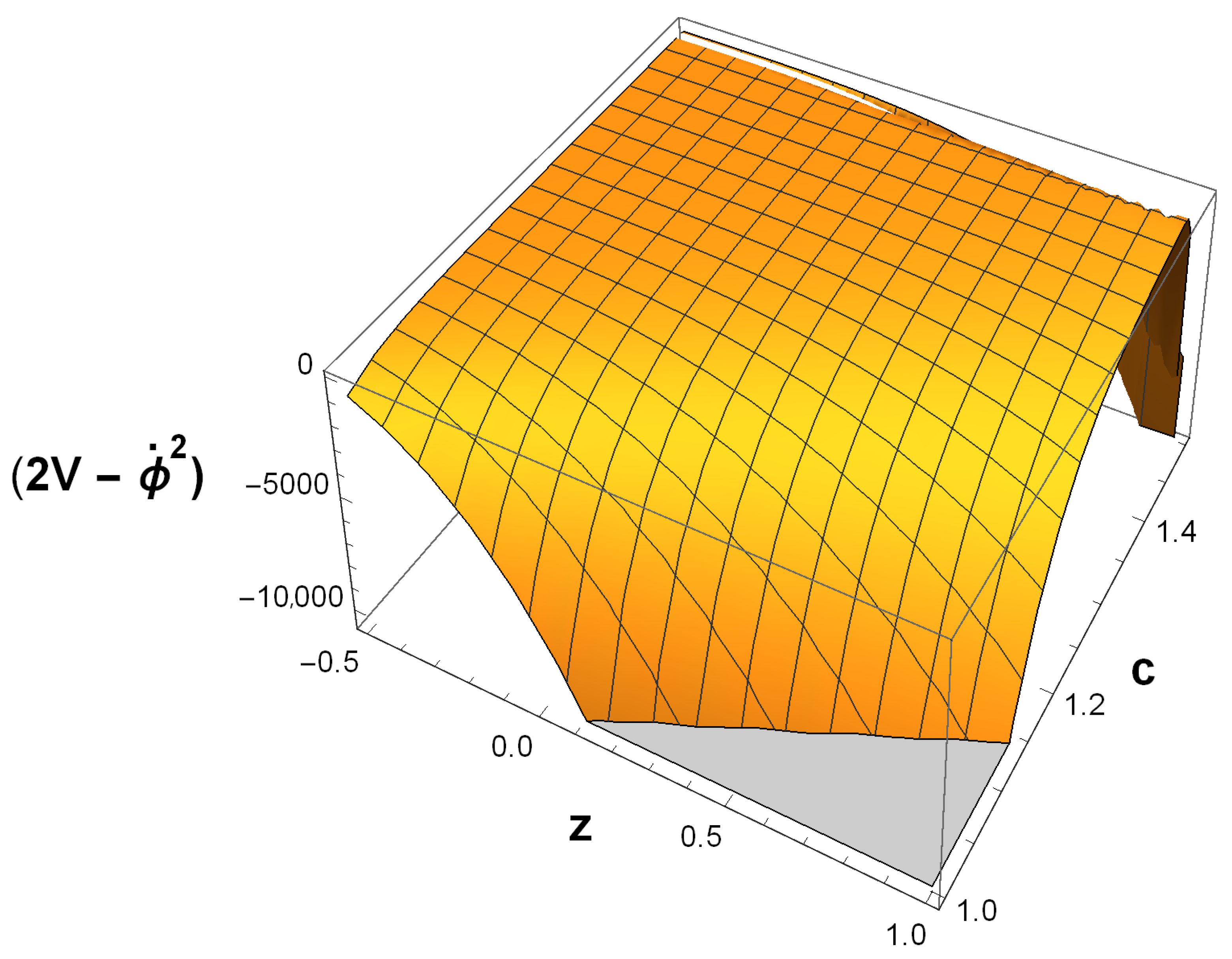
4. Chameleon Scalar Field under Modified Gravity
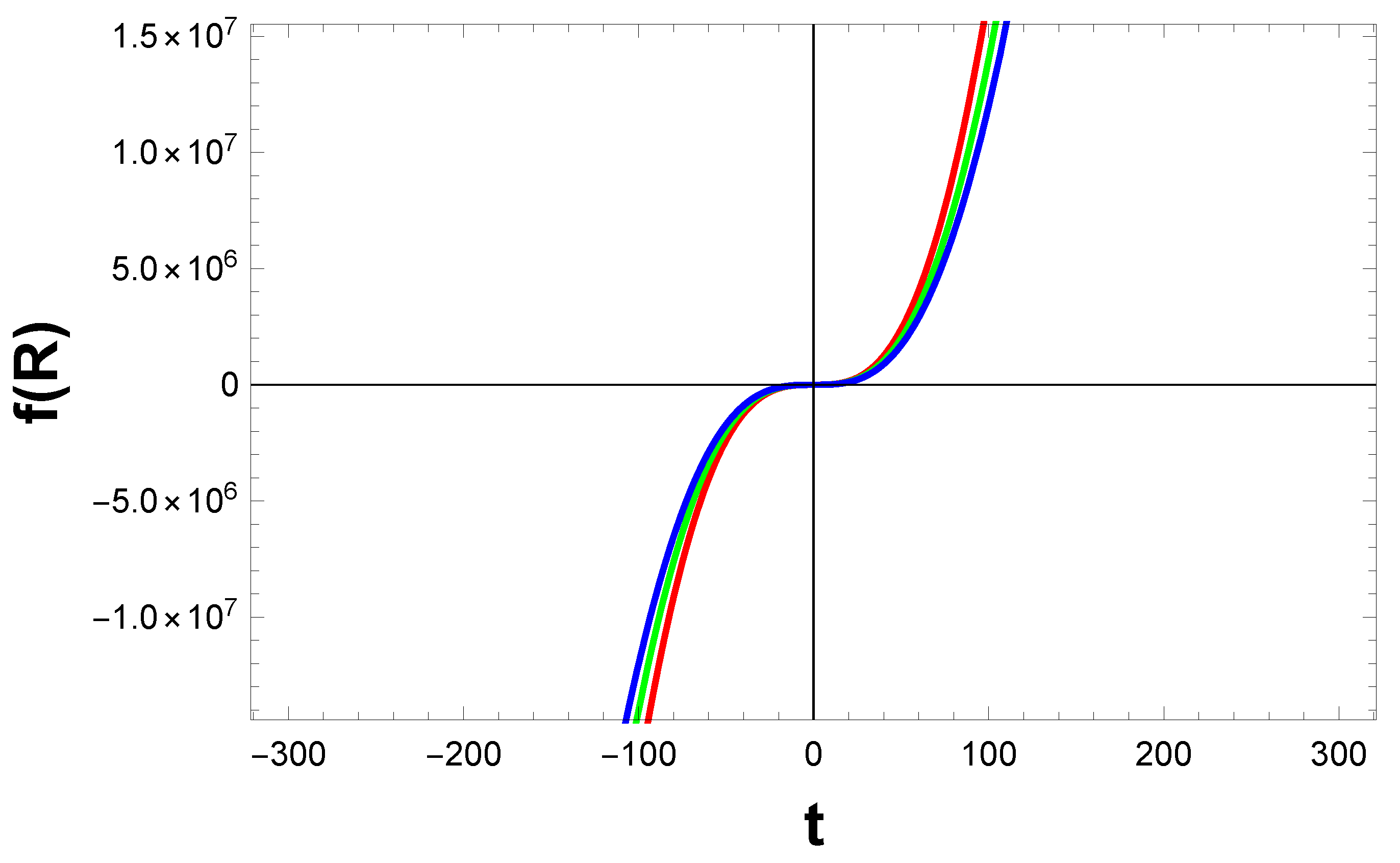
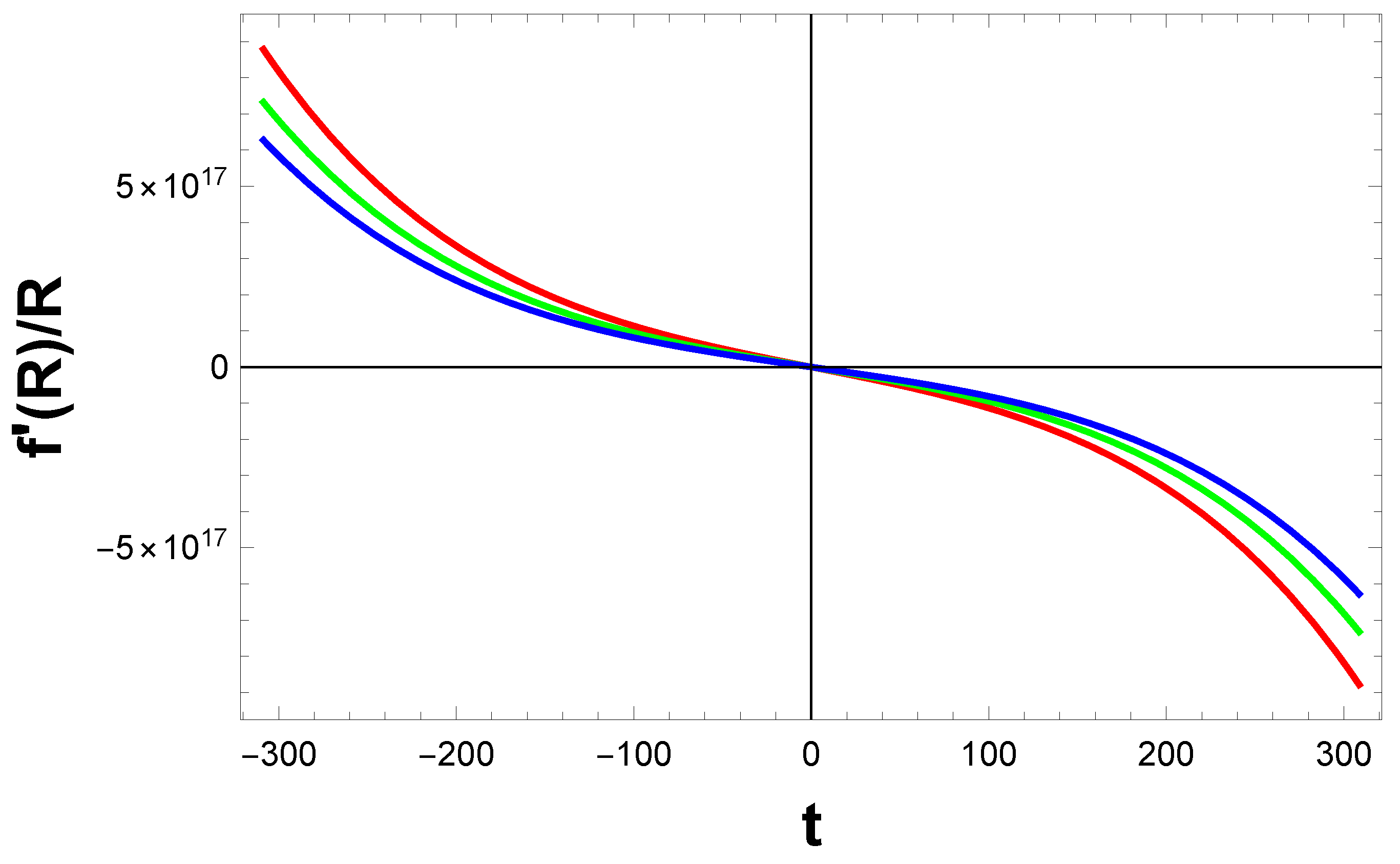
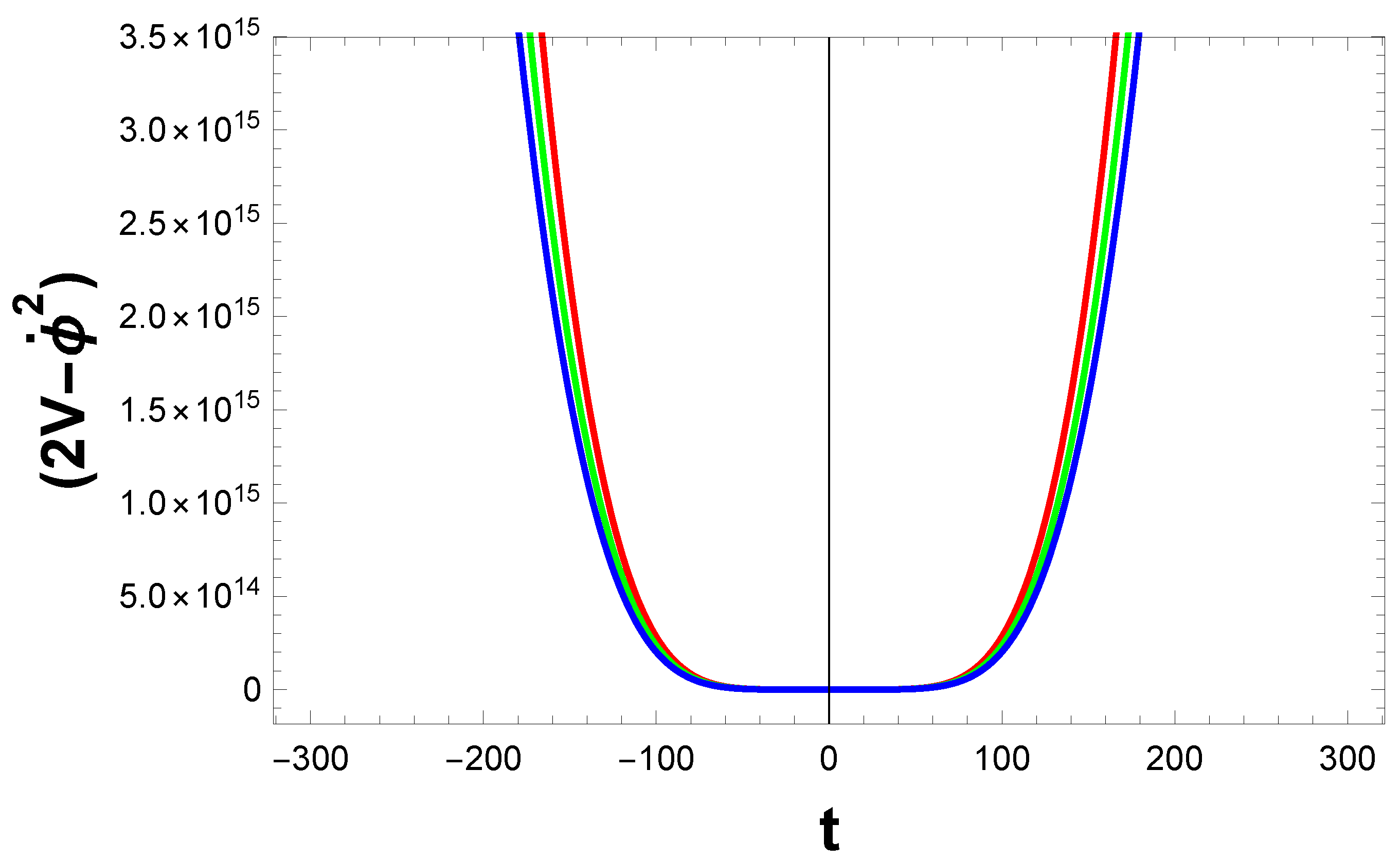
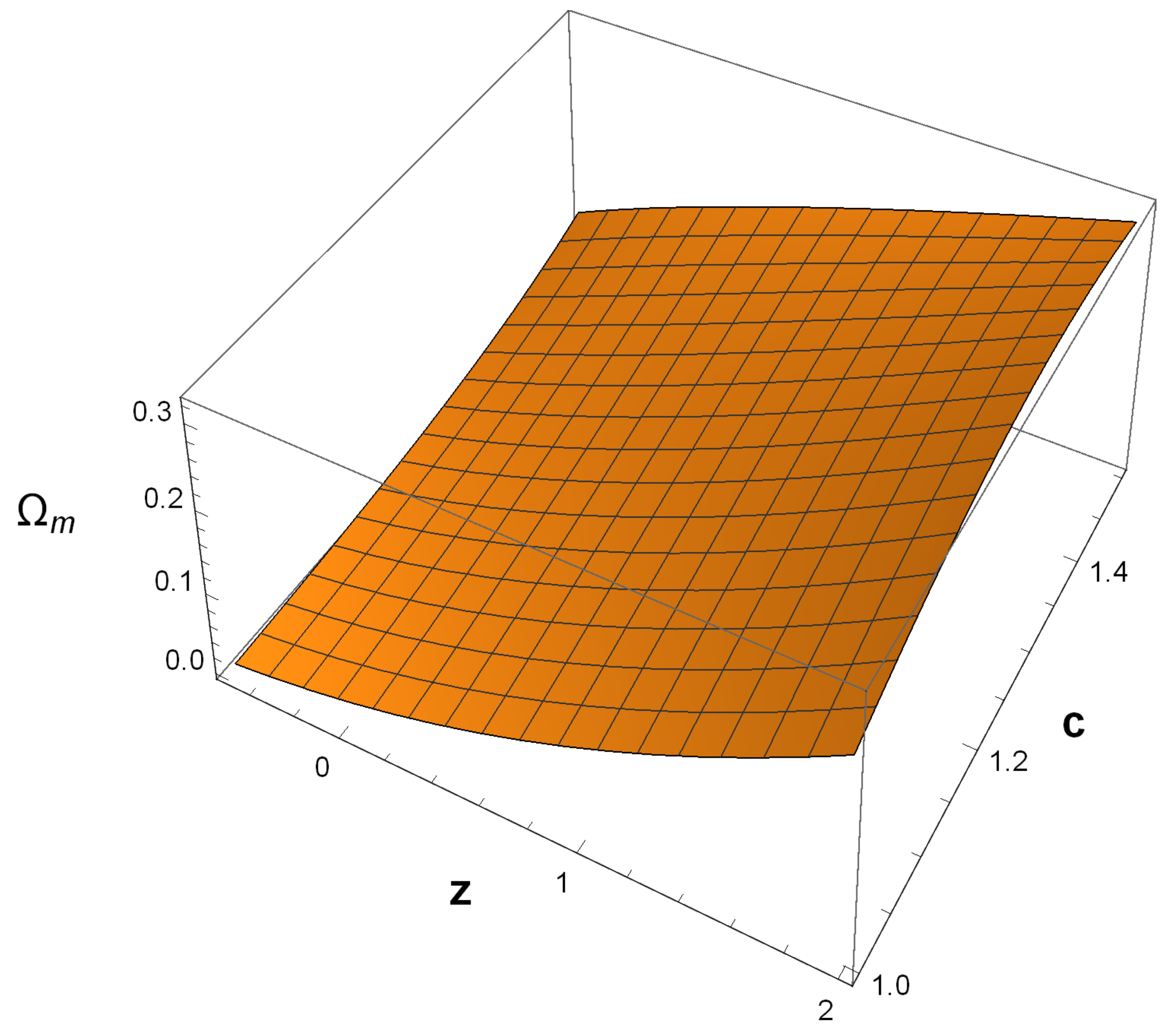
5. Background Solution for Matter Bounce
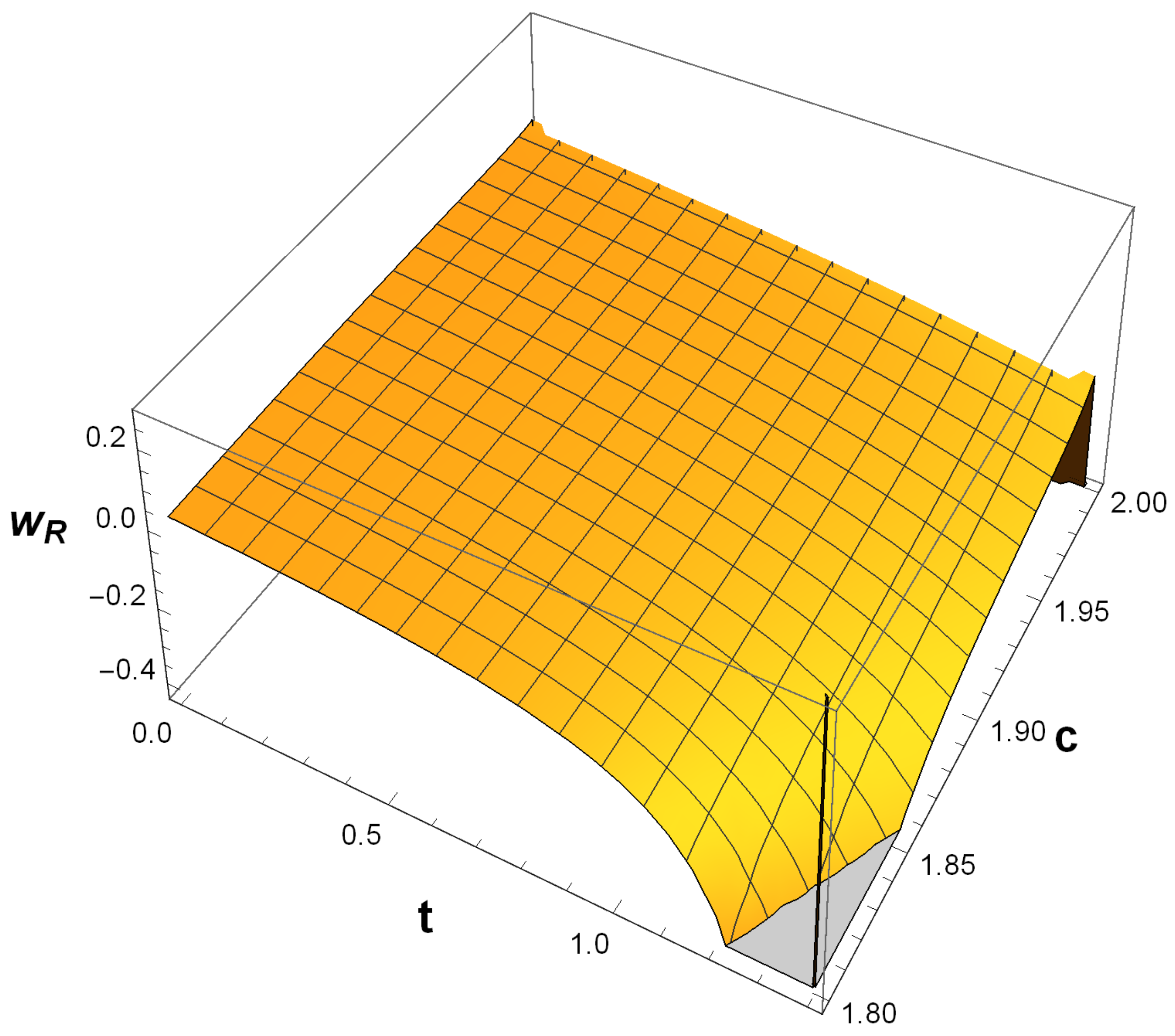
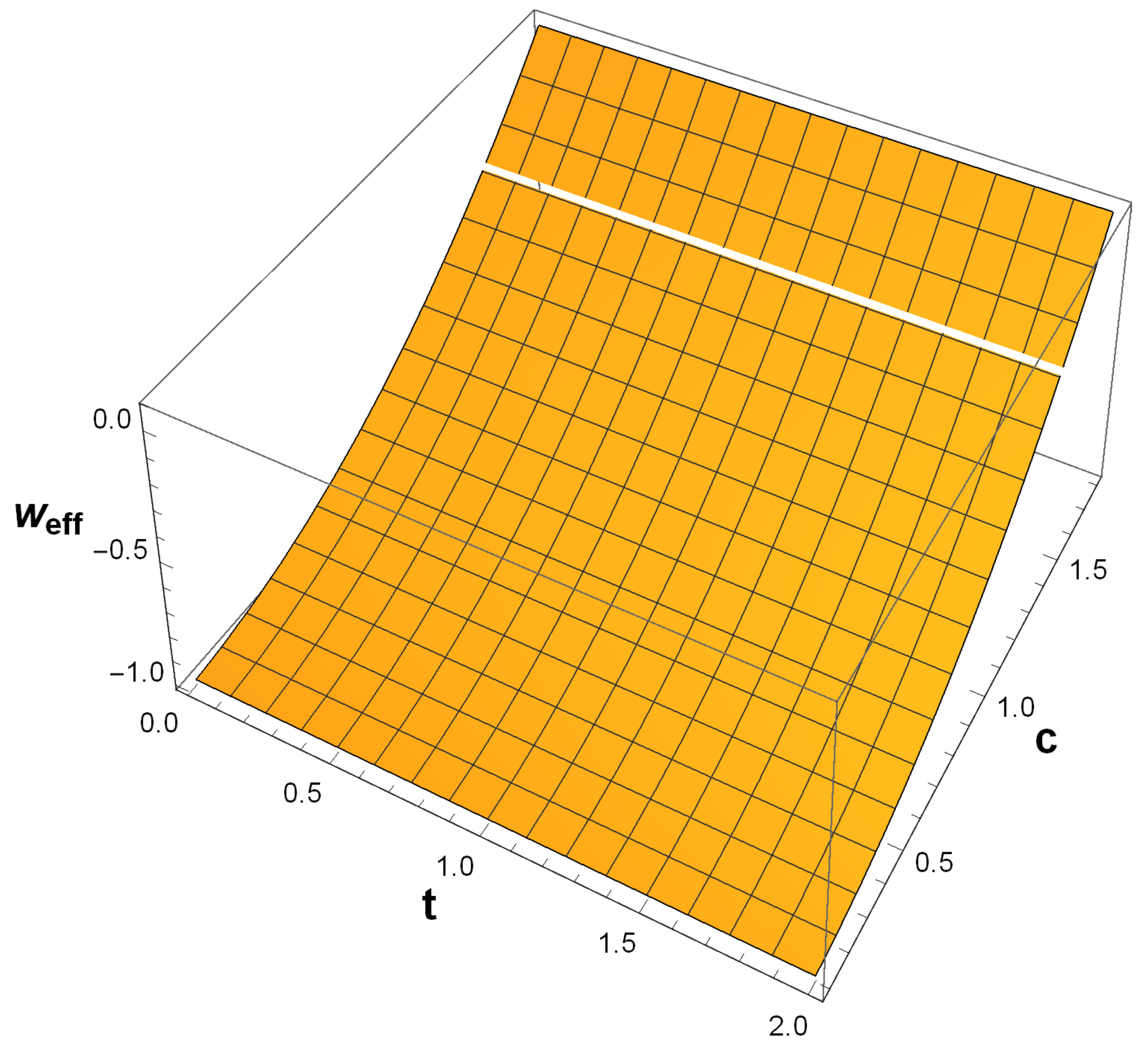
6. Results and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- De Bernardis, P.; Ade, P.A.R.; Bock, J.J.; Bond, J.R.; Borrill, J.; Boscaleri, A.; Coble, K.; Crill, B.P.; De Gasperis, G.; Farese, P.C.; et al. A flat Universe from high-resolution maps of the cosmic microwave background radiation. Nature 2000, 404, 955. [Google Scholar] [CrossRef] [PubMed]
- Knop, R.A.; Aldering, G.; Amanullah, R.; Astier, P.; Blanc, G.; Burns, M.S.; Conley, A.; Deustua, S.E.; Doi, M.; Ellis, R.; et al. New Constraints on ΩM, ΩΛ, and w from an Independent Set of 11 High-Redshift Supernovae Observed with the Hubble Space Telescope. Astrophys. J. 2003, 598, 102. [Google Scholar] [CrossRef]
- Padmanabhan, T. Cosmological constant—The weight of the vacuum. Phys. Rep. 2003, 380, 235. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753. [Google Scholar] [CrossRef]
- Sahni, V. Dark Matter and Dark Energy. Lect. Notes Phys. 2004, 653, 141–180. [Google Scholar]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Methods Mod. Phys. 2007, 4, 115. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) theories of gravity. Rev. Mod. Phys. 2010, 82, 451. [Google Scholar] [CrossRef]
- Tsujikawa, S. Modified gravity models of dark energy. Lect. Notes Phys. 2010, 800, 99. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Accelerating cosmology in modified gravity: From convenient F(R) or string-inspired theory to bimetric F(R) gravity. Int. J. Geom. Methods Mod. Phys. 2014, 11, 1460006. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Extended gravity cosmography. Int. J. Mod. Phys. D 2019, 28, 483. [Google Scholar] [CrossRef]
- Capozziello, S.; Carloni, S.; Troisi, A. Quintessence without scalar fields. Recent Res. Dev. Astron. Astrophys. 2003, 1, 625. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Where new gravitational physics comes from: M-theory? Phys. Lett. B 2003, 576, 5. [Google Scholar] [CrossRef]
- Carroll, S.M.; Duvvuri, V.; Trodden, M.; Turner, M.S. Is cosmic speed-up due to new gravitational physics? Phys. Rev. D 2004, 70, 043528. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified gravity theories on a nutshell: Inflation, bounce and late-time evolution. Phys. Rep. 2017, 692, 1. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified f(R) gravity consistent with realistic cosmology: From a matter dominated epoch to a dark energy universe. Phys. Rev. D 2006, 74, 086005. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Saez-Gomez, D. Cosmological reconstruction of realistic modified F(R) gravities. Phys. Lett. B 2009, 681, 74. [Google Scholar] [CrossRef]
- Carloni, S.; Goswami, R.; Dunsby, P.K.S. A new approach to reconstruction methods in f(R) gravity. Class. Quantum Gravity 2012, 29, 135012. [Google Scholar] [CrossRef]
- Dunsby, P.K.; Elizalde, E.; Goswami, R.; Odintsov, S.; Saez-Gomez, D. ΛCDM universe in f(R) gravity. Phys. Rev. D 2010, 82, 023519. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity and its reconstruction from the universe expansion history. J. Phys. Conf. Ser. 2007, 66, 012005. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of curvature: Unification of inflation and cosmic acceleration. Phys. Rev. D 2003, 68, 123512. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unifying inflation with ΛCDM epoch in modified f(R) gravity consistent with Solar System tests. Phys. Lett. B 2007, 657, 238. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified f(R) gravity unifying Rm inflation with the ΛCDM epoch. Phys. Rev. D 2008, 77, 026007. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Class of viable modified f(R) gravities describing inflation and the onset of accelerated expansion. Phys. Rev. D 2008, 77, 046009. [Google Scholar] [CrossRef]
- Capozziello, S.; Tsujikawa, S. Solar system and equivalence principle constraints on f(R) gravity by the chameleon approach. Phys. Rev. D 2008, 77, 107501. [Google Scholar] [CrossRef]
- Brax, P.; Van de Bruck, C.; Davis, A.; Shaw, D.J. f(R) gravity and chameleon theories. Phys. Rev. D 2008, 78, 104021. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Disappearing cosmological constant in f(R) gravity. JETP Lett. 2007, 86, 157. [Google Scholar] [CrossRef]
- Appleby, S.A.; Battye, R.A. Do consistent F(R) models mimic general relativity plus Λ? Phys. Lett. B 2007, 654, 7. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Newton law corrections and instabilities in f(R) gravity with the effective cosmological constant epoch. Phys. Lett. B 2007, 652, 343. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Odintsov, S.D.; Tretyakov, P.; Zerbini, S. Initial and final de Sitter universes from modified f(R) gravity. Phys. Rev. D 2009, 79, 044001. [Google Scholar] [CrossRef]
- Bamba, K.; Nojiri, S.; Odintsov, S.D. The future of the universe in modified gravitational theories: Approaching a finite-time future singularity. JCAP 2008, 2008, 045. [Google Scholar] [CrossRef]
- Barrow, J.D.; Clifton, T. Exact cosmological solutions of scale-invariant gravity theories. Class. Quantum Gravity 2005, 23, L1. [Google Scholar] [CrossRef]
- Clifton, T.; Barrow, J.D. Further exact cosmological solutions to higher-order gravity theories. Class. Quantum Gravity 2006, 23, 2951. [Google Scholar] [CrossRef]
- Capozziello, S.; De Felice, A. f(R) cosmology from Noether’s symmetry. JCAP 2008, 2008, 016. [Google Scholar] [CrossRef]
- Karami, K.; Khaledian, M.S. Reconstructing f(R) modified gravity from ordinary and entropy-corrected versions of the holographic and new agegraphic dark energy models. J. High Energy Phys. 2011, 2011. [Google Scholar] [CrossRef]
- Granda, L.N. Reconstructing modified gravity with holographic vacuum energy density. Int. J. Mod. Phys. D 2019, 28, 1950052. [Google Scholar] [CrossRef]
- Horava, P.; Minic, D. Probable values of the cosmological constant in a holographic theory. Phys. Rev. Lett. 2000, 85, 1610. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, V.; Horava, P.; Minic, D. Deconstructing de Sitter. Phys. Rev. Lett. 2001, 2001, 043. [Google Scholar] [CrossRef]
- Thomas, S. Holography stabilizes the vacuum energy. Phys. Rev. Lett. 2002, 89, 081301. [Google Scholar] [CrossRef] [PubMed]
- Susskind, L. The world as a hologram. J. Math. Phys. 1995, 36, 6377. [Google Scholar] [CrossRef]
- Salako, I.G.; Jawad, A.; Chattopadhyay, S. Holographic dark energy reconstruction in f(T,τ) gravity. Astrophys. Space Sci. 2015, 358, 13. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Jawad, A.; Rani, S. Holographic Polytropic f(T) Gravity Models. Adv. High Energy Phys. 2015, 2015, 798902. [Google Scholar] [CrossRef]
- Jawad, A.; Pasqua, A.; Chattopadhyay, S. Holographic reconstruction of f(G) gravity for scale factors pertaining to emergent, logamediate and intermediate scenarios. Eur. Phys. J. Plus 2013, 128, 156. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Big bounce with finite-time singularity: The F(R) gravity description. Int. J. Mod. Phys. D 2017, 26, 1750085. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. ΛCDM bounce cosmology without ΛCDM: The case of modified gravity. Phys. Rev. D 2015, 91, 064036. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Matter bounce loop quantum cosmology from F(R) gravity. Phys. Rev. D 2014, 90, 124083. [Google Scholar] [CrossRef]
- Cai, Y.F.; Easson, D.A.; Brandenburgers, R. Towards a nonsingular bouncing cosmology. JCAP 2012, 2012, 020. [Google Scholar] [CrossRef]
- Koehn, M.; Lehners, J.L.; Ovrut, B.A. Cosmological super-bounce. Phys. Rev. D 2014, 90, 025005. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Singular inflationary universe from F(R) gravity. Phys. Rev. D 2015, 92, 124024. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K.; Saridakis, E.N. Superbounce and loop quantum ekpyrotic cosmologies from modified gravity: F(R), F(G) and F(T) theories. Ann. Phys. 2015, 363, 141. [Google Scholar] [CrossRef]
- Song, Y.-S.; Hu, W.; Sawicki, I. Large scale structure of f(R) gravity. Phys. Rev. D 2007, 75, 044004. [Google Scholar] [CrossRef]
- Amendola, L.; Gannouji, R.; Polarski, D.; Tsujikawa, S. Conditions for the cosmological viability of f(R) dark energy models. Phys. Rev. D 2007, 75, 083504. [Google Scholar] [CrossRef]
- Frusciante, N.; Papadomanolakis, G.; Peirone, S.; Silvestri, A. The role of the tachyonic instability in Horndeski gravity. J. Cosmol. Astropart. Phys. 2019, 2019, 029. [Google Scholar] [CrossRef]
- Velasquez, J.; Castaneda, L. Equivalence between Scalar-Tensor theories and f(R)-gravity: From the action to Cosmological Perturbations. J. Phys. Commun. 2020, 4, 055007. [Google Scholar] [CrossRef]
- Chiba, T. 1/R gravity and scalar-tensor gravity. Phys. Lett. B 2003, 575, 1. [Google Scholar] [CrossRef]
- Burrage, C.; Sakstein, J.J. Tests of chameleon gravity. Living Rev. Relativ. 2018, 21, 1. [Google Scholar] [CrossRef] [PubMed]
- Chattopadhyay, S.; Debnath, U. Emergent universe in the chameleon, f(R) and f(T) gravity theories. Int. J. Mod. Phys. D 2011, 20, 1135. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Chen, S.-H.; Dent, J.B.; Dutta, S.; Saridakis, E.N. Matter bounce cosmology with the f(T) gravity. Class. Quantum Gravity 2011, 28, 215011. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Chattopadhyay, S.; Radinschi, I. A study of the bulk viscous pressure in scalar fields and holographic Ricci dark energy considered in the modified gravity framework. Can. J. Phys. 2020, 98, 664. [Google Scholar] [CrossRef]
- Chattopadhyay, S. Reconstruction of f(T) gravity with interacting variable-generalised Chaplygin gas and the thermodynamics with corrected entropies. Z. Naturforsch. 2017, 72, 231. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Pasqua, A.; Radinschi, I.; Beesham, A. Dynamics of single-field inflation in the framework of holographic f(T) gravity. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1850167. [Google Scholar] [CrossRef]
- Bamba, K.; Makarenko, A.N.; Myagky, A.N.; Odintsov, S.D. Bouncing cosmology in modified Gauss–Bonnet gravity. Phys. Lett. B 2014, 732, 349. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K.; Paul, T. Nonsingular bounce cosmology from Lagrange multiplier F(R) gravity. Phys. Rev. D 2019, 100, 084056. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Bounce universe history from unimodular F(R) gravity. Phys. Rev. D 2016, 93, 084050. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Unifying inflation with early and late-time dark energy in F(R) gravity. Phys. Dark Universe 2020, 29, 100602. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karmakar, S.; Myrzakulov, K.; Chattopadhyay, S.; Myrzakulov, R. Reconstructed f(R) Gravity and Its Cosmological Consequences in theChameleon Scalar Field with a Scale Factor Describing the Pre-Bounce Ekpyrotic Contraction. Symmetry 2020, 12, 1559. https://doi.org/10.3390/sym12091559
Karmakar S, Myrzakulov K, Chattopadhyay S, Myrzakulov R. Reconstructed f(R) Gravity and Its Cosmological Consequences in theChameleon Scalar Field with a Scale Factor Describing the Pre-Bounce Ekpyrotic Contraction. Symmetry. 2020; 12(9):1559. https://doi.org/10.3390/sym12091559
Chicago/Turabian StyleKarmakar, Soumyodipta, Kairat Myrzakulov, Surajit Chattopadhyay, and Ratbay Myrzakulov. 2020. "Reconstructed f(R) Gravity and Its Cosmological Consequences in theChameleon Scalar Field with a Scale Factor Describing the Pre-Bounce Ekpyrotic Contraction" Symmetry 12, no. 9: 1559. https://doi.org/10.3390/sym12091559
APA StyleKarmakar, S., Myrzakulov, K., Chattopadhyay, S., & Myrzakulov, R. (2020). Reconstructed f(R) Gravity and Its Cosmological Consequences in theChameleon Scalar Field with a Scale Factor Describing the Pre-Bounce Ekpyrotic Contraction. Symmetry, 12(9), 1559. https://doi.org/10.3390/sym12091559