Bifurcation and Nonlinear Behavior Analysis of Dual-Directional Coupled Aerodynamic Bearing Systems
Abstract
1. Introduction
2. Governing Equations of a DCAB System
2.1. Design and Analysis of a DCAB System
2.2. Equations of Rotor Dynamics
3. Mathematical Formulation of the Numerical Simulation
4. Results
4.1. Comparison of the Results Obtained with Different Numerical Methods
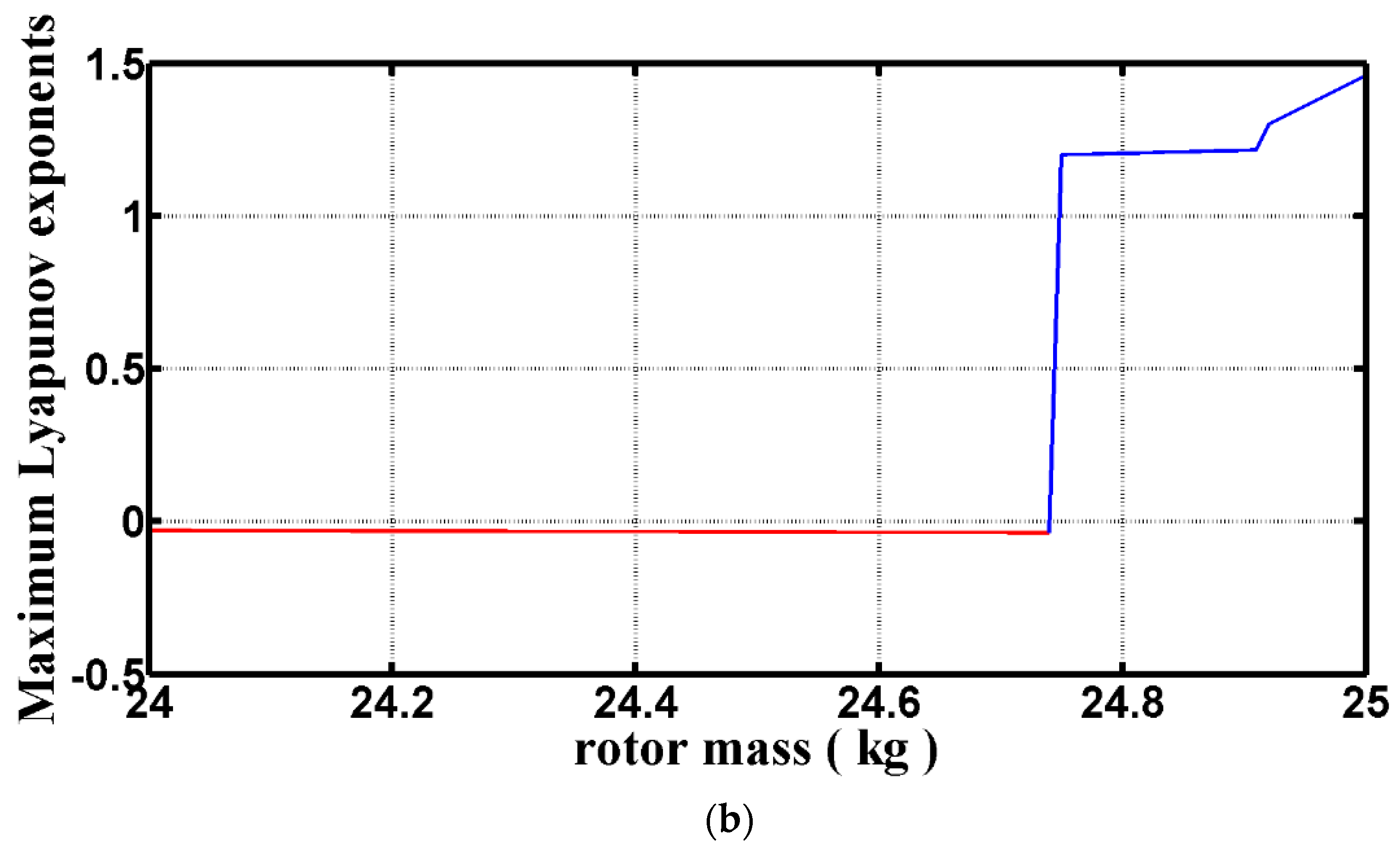
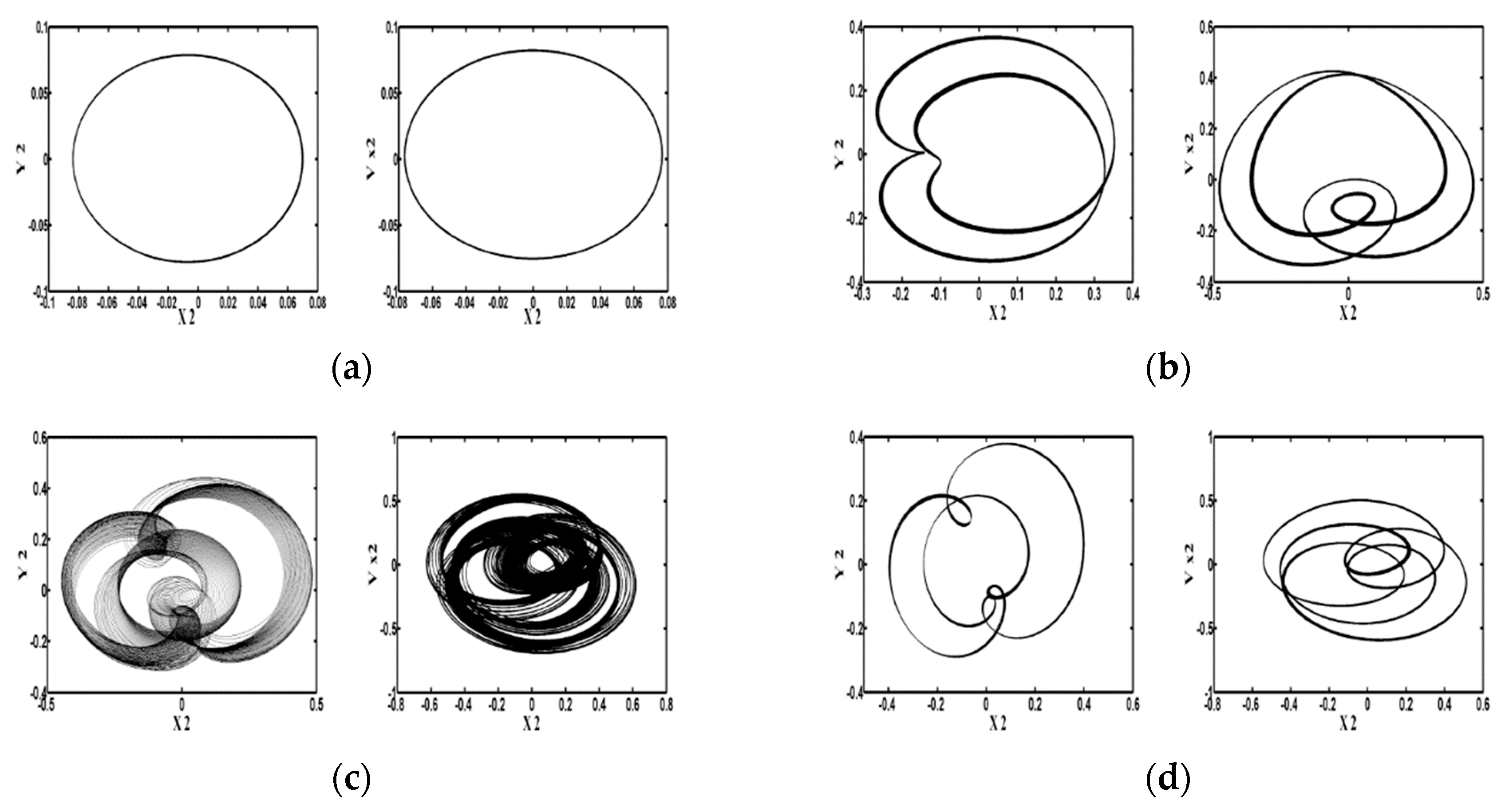
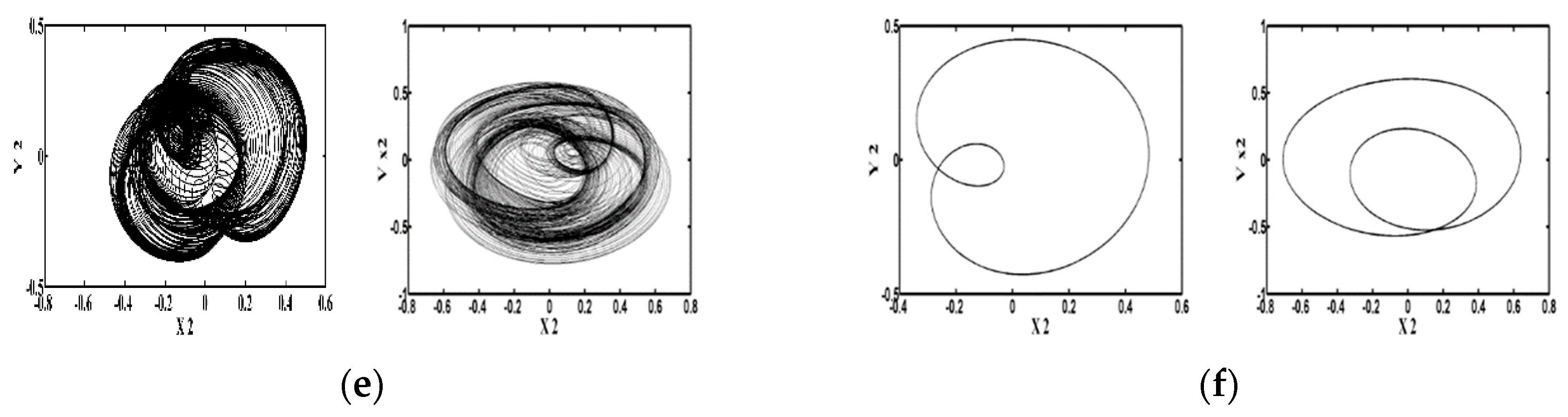
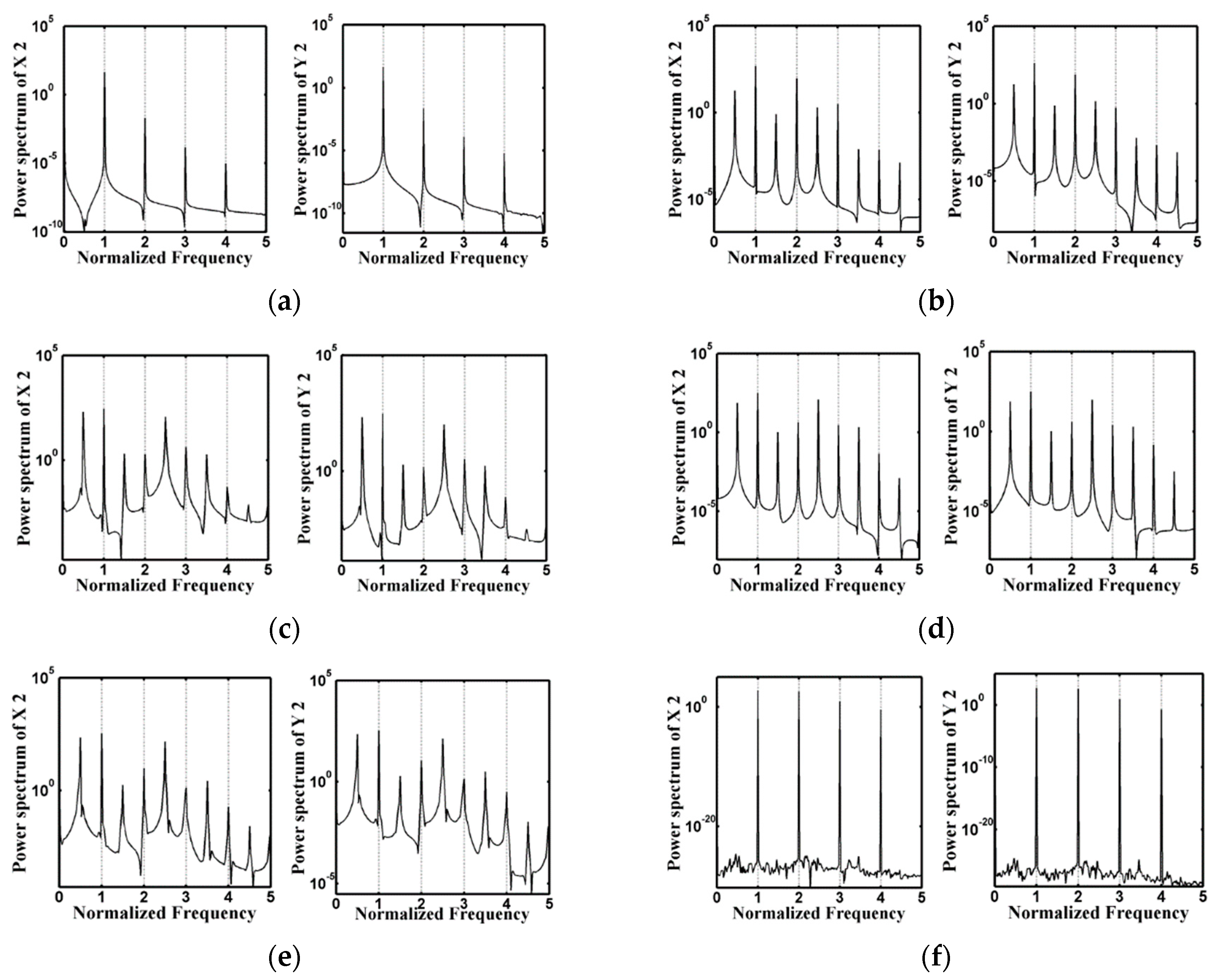
4.2. Dynamic Behavior of a DCAB System: Using the Rotor Mass as the Bifurcation Parameter
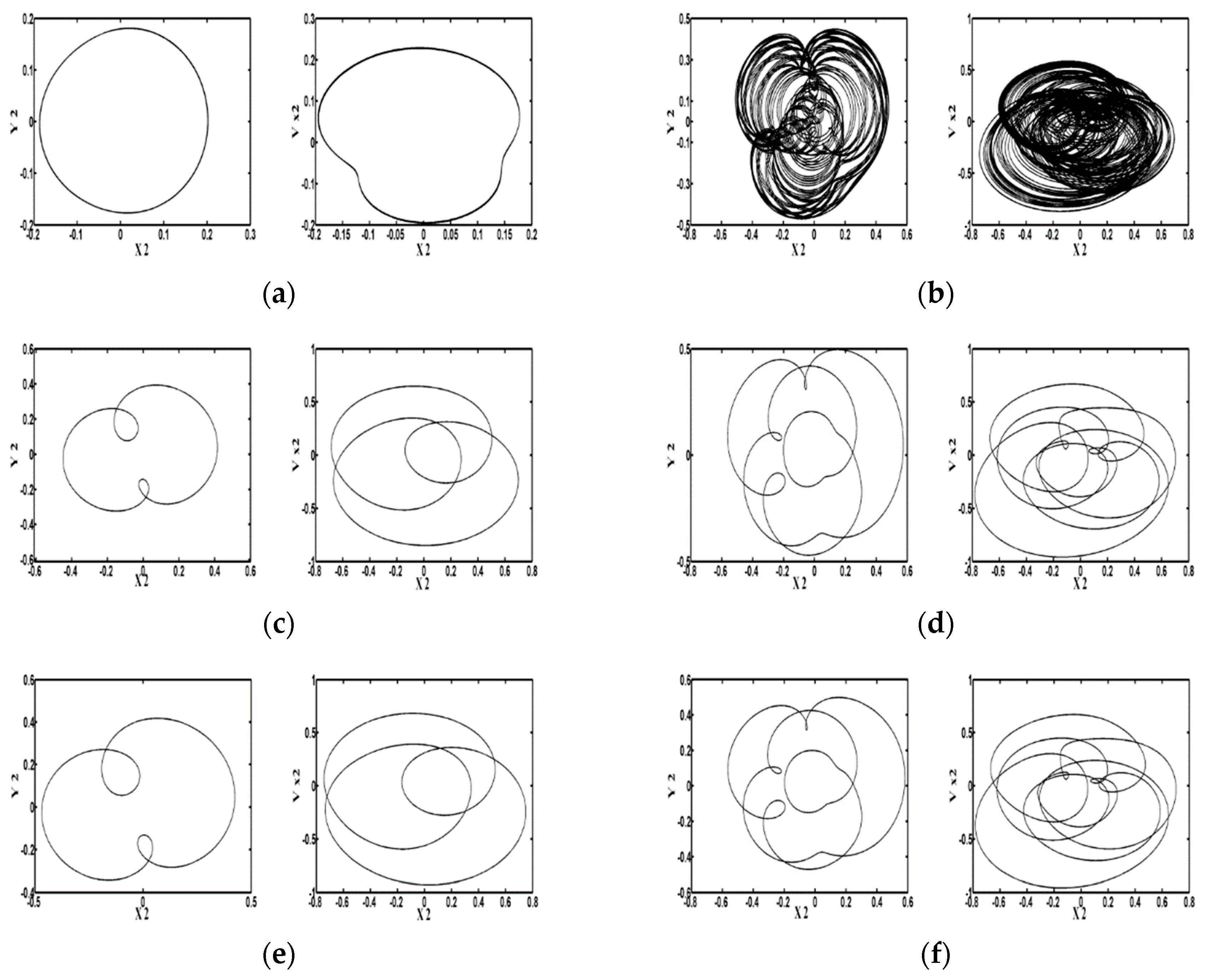
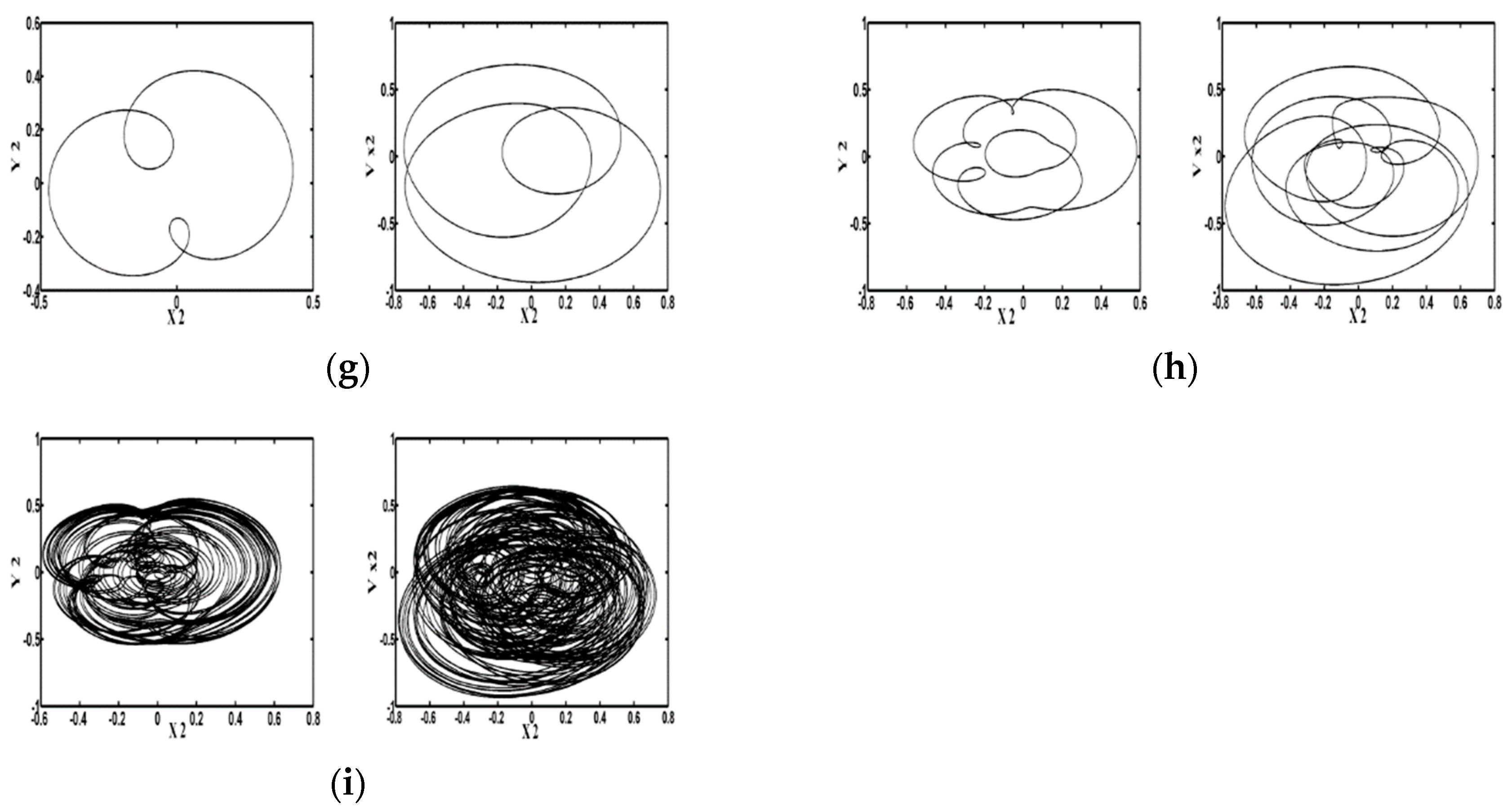
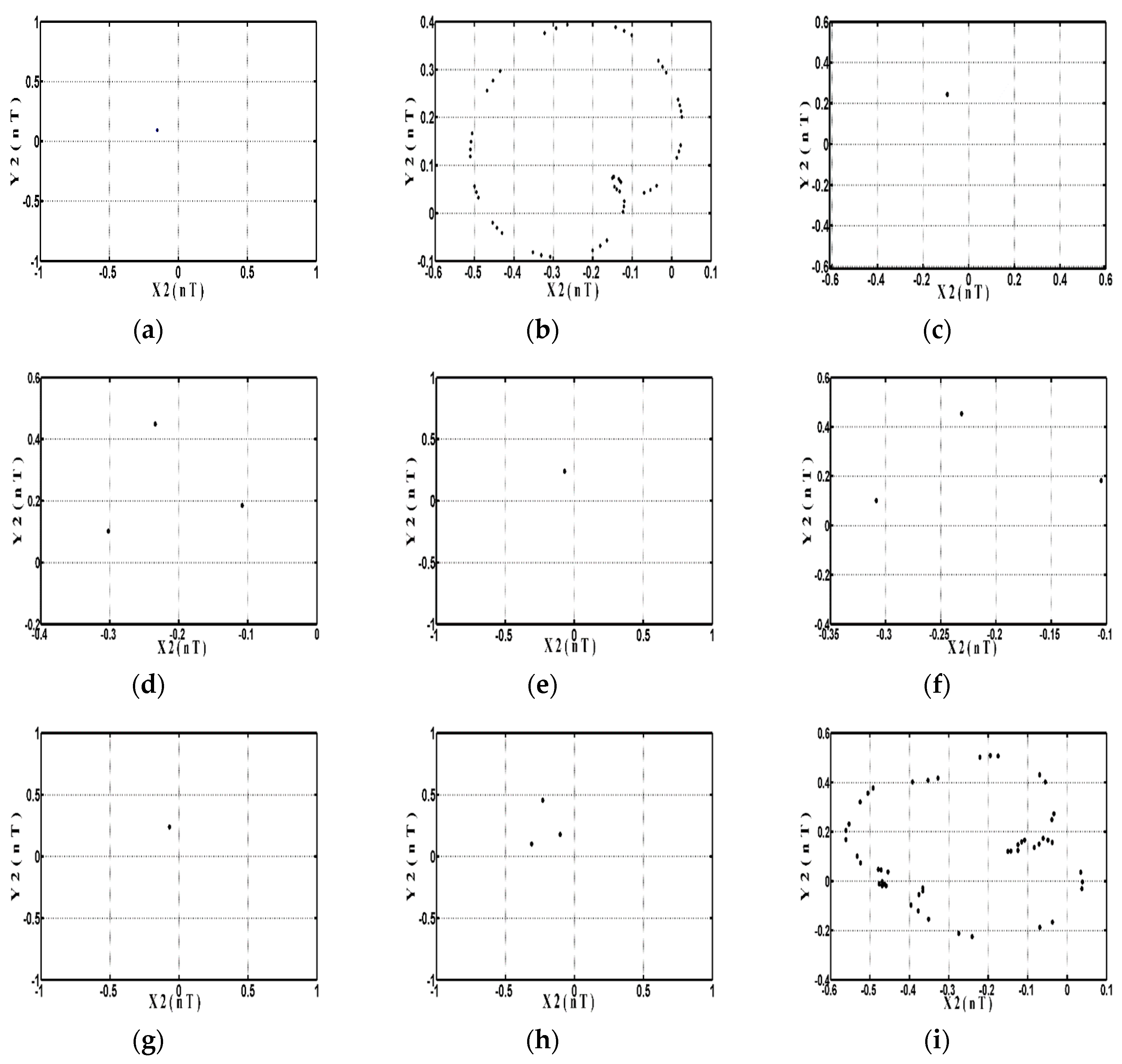
4.2.1. Dynamic Trajectory and Phase Plane Analysis
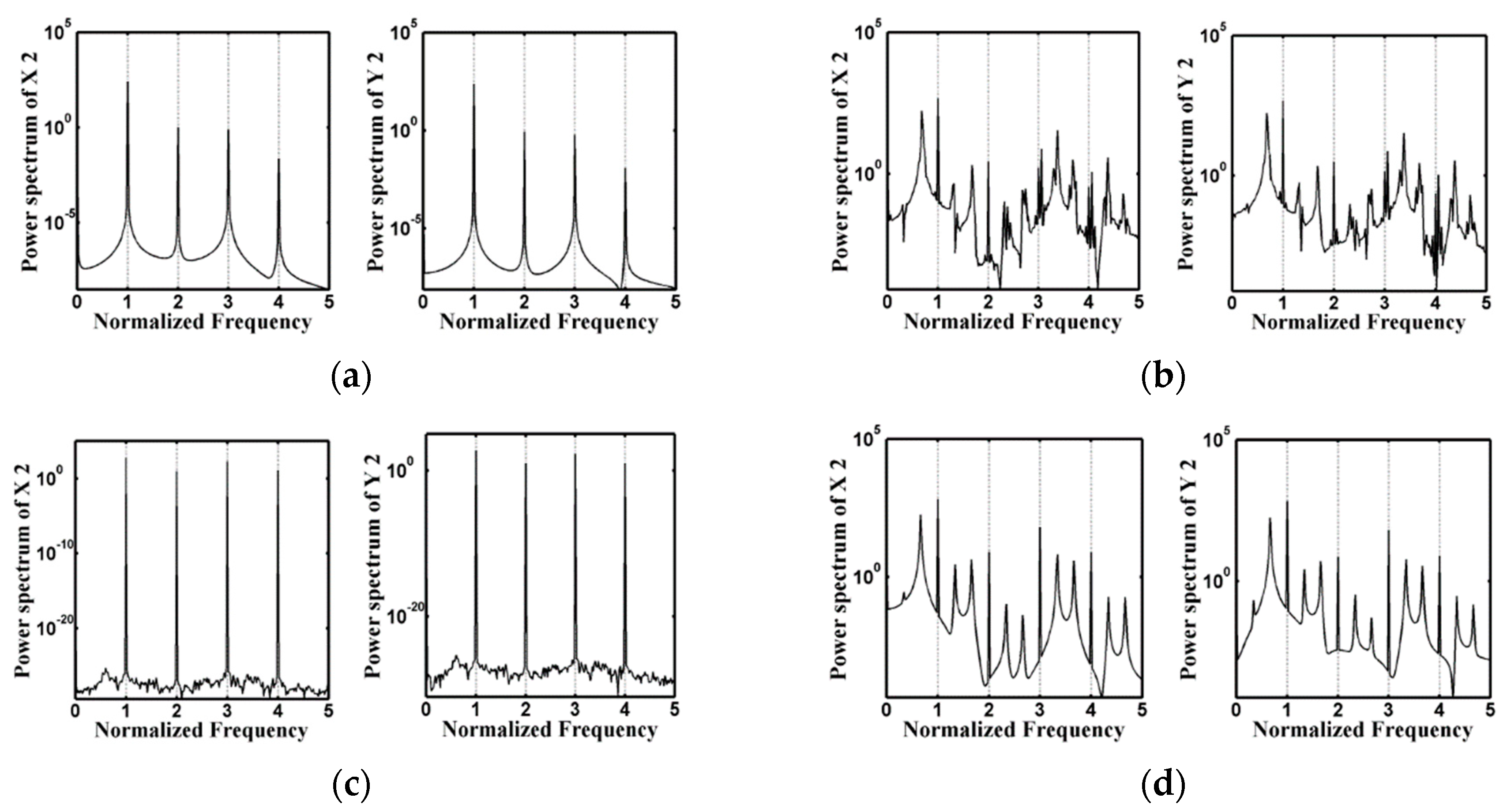
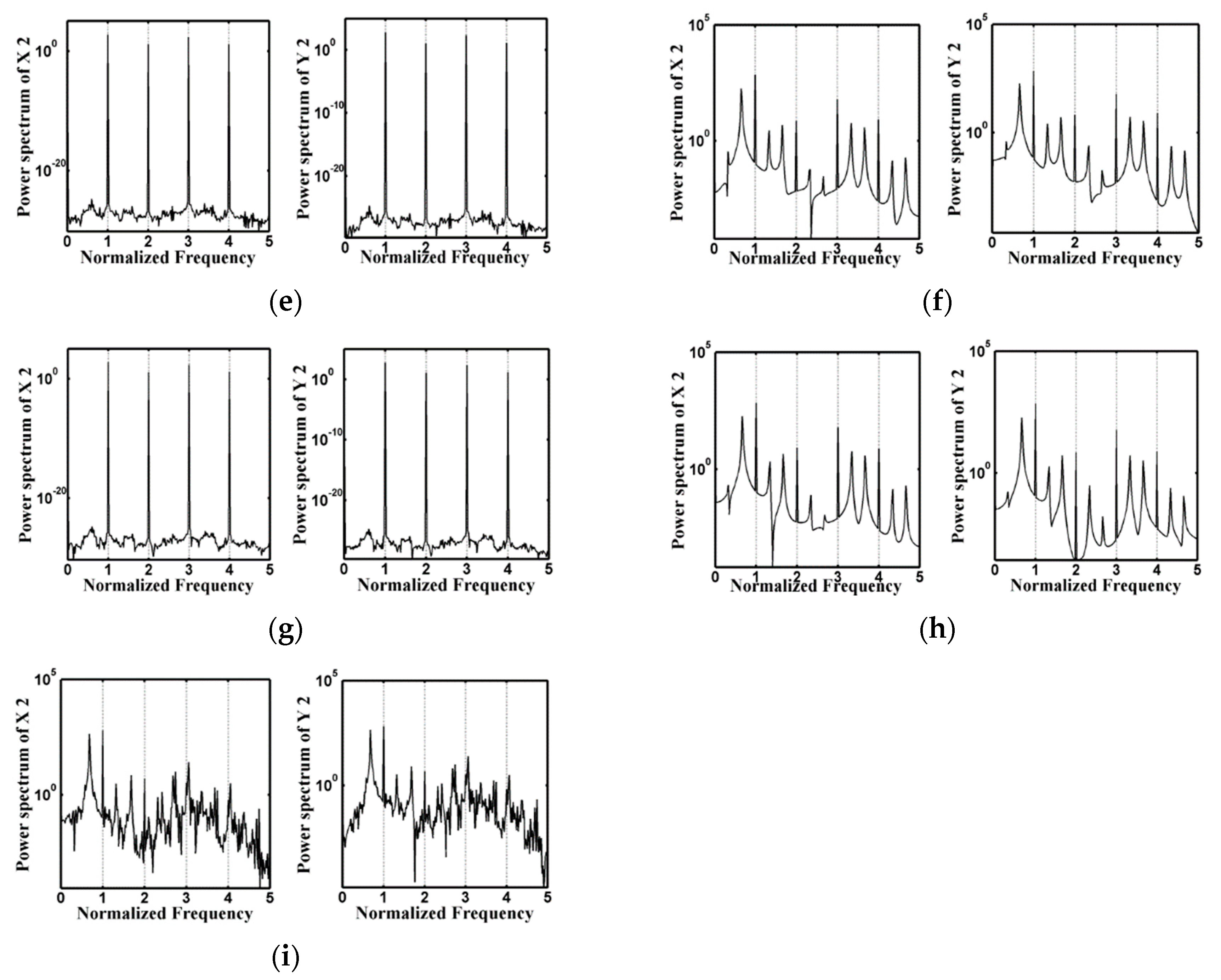
4.2.2. Spectral Analysis
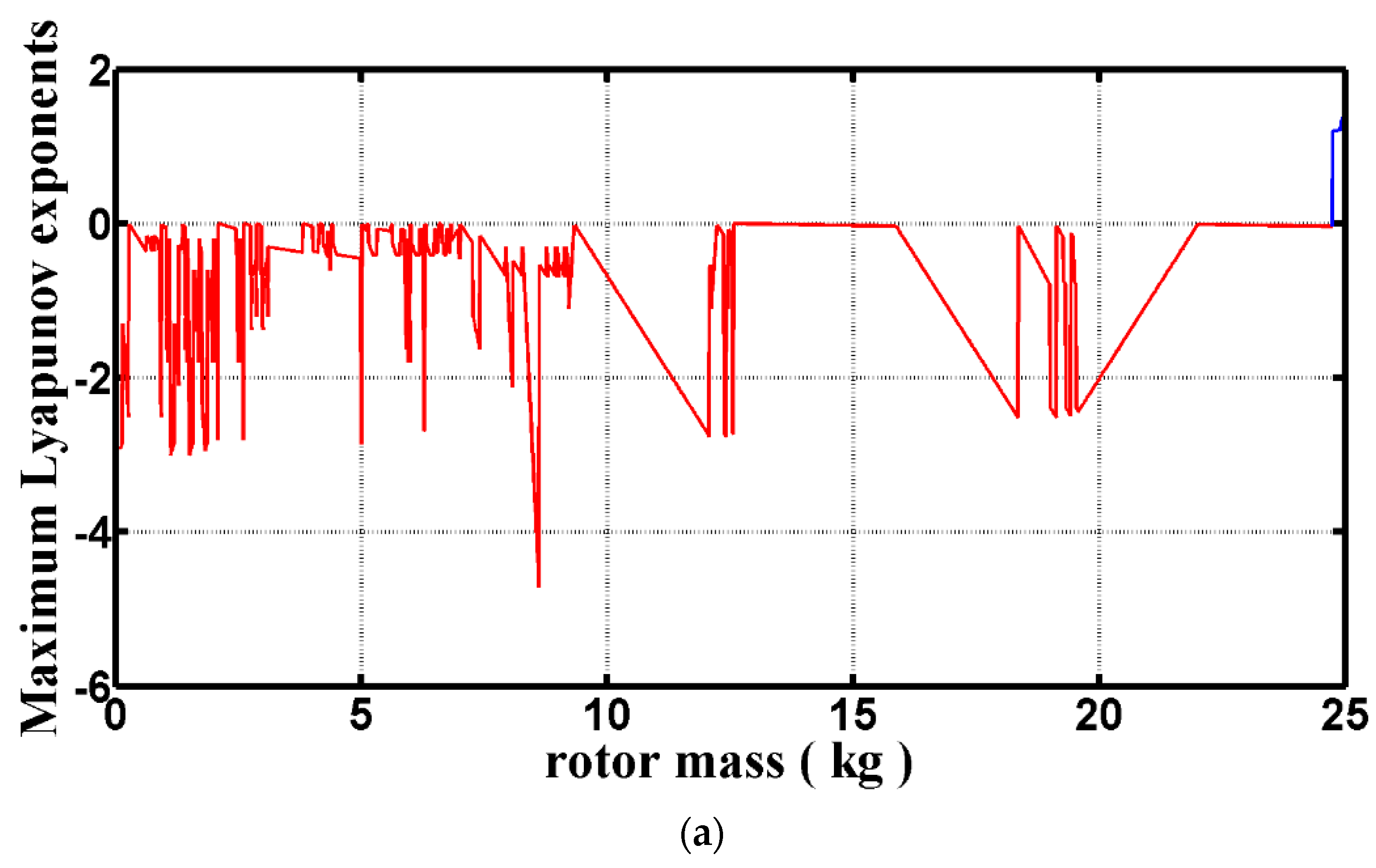
4.2.3. Bifurcation Analysis
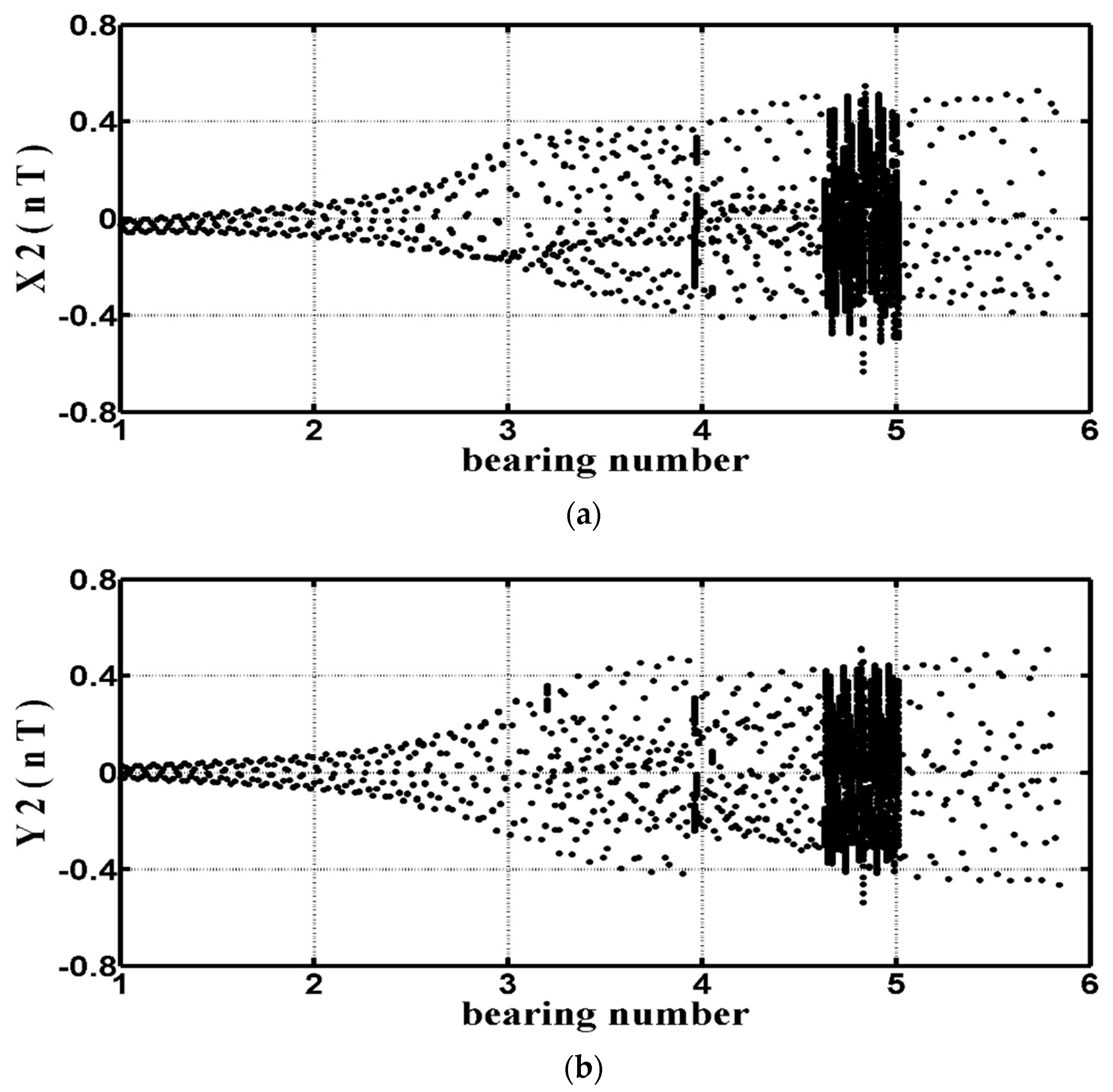
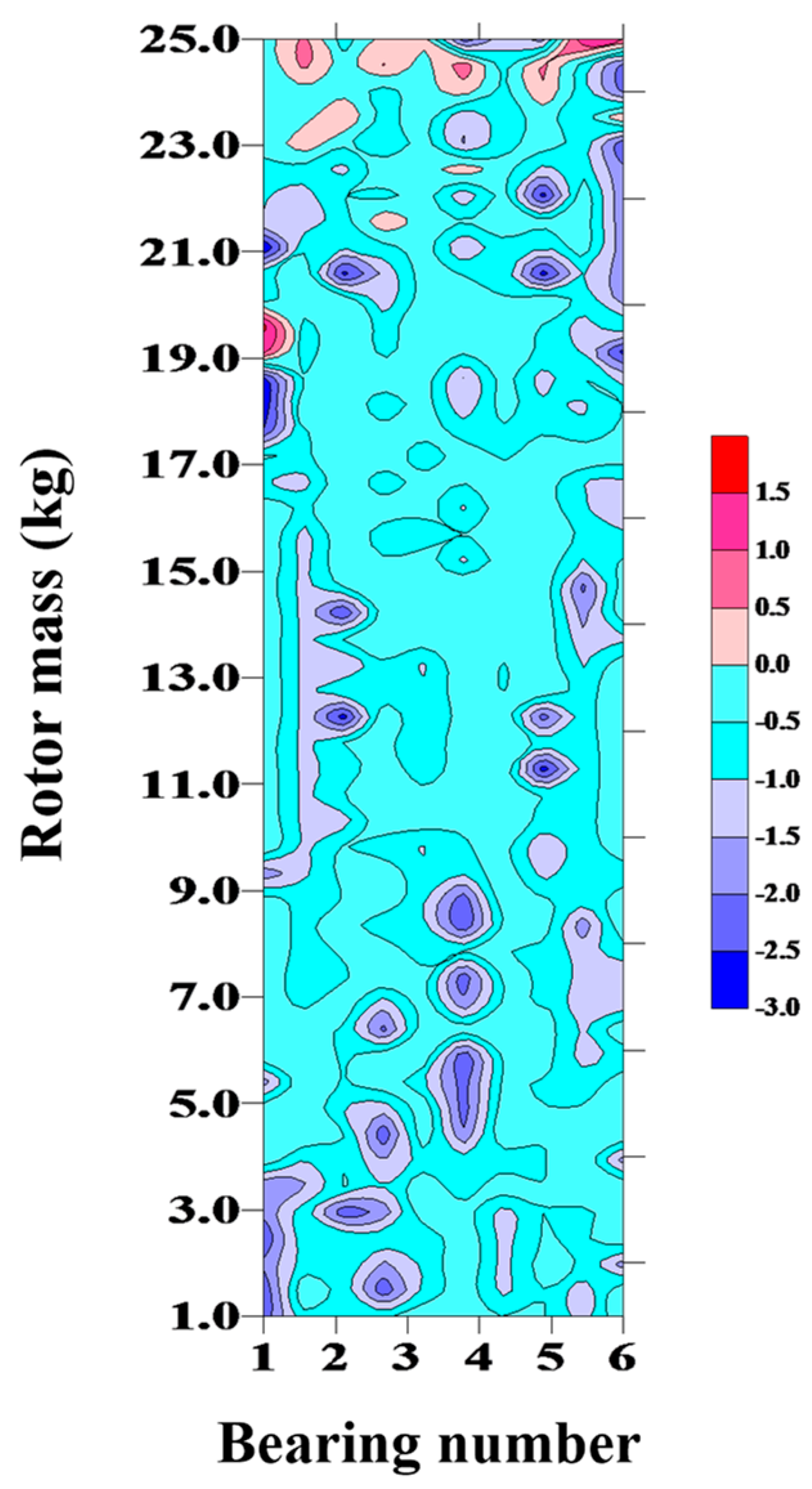
4.3. Dynamic Behavior of a DCAB System: Using the Bearing Number as the Bifurcation Parameter
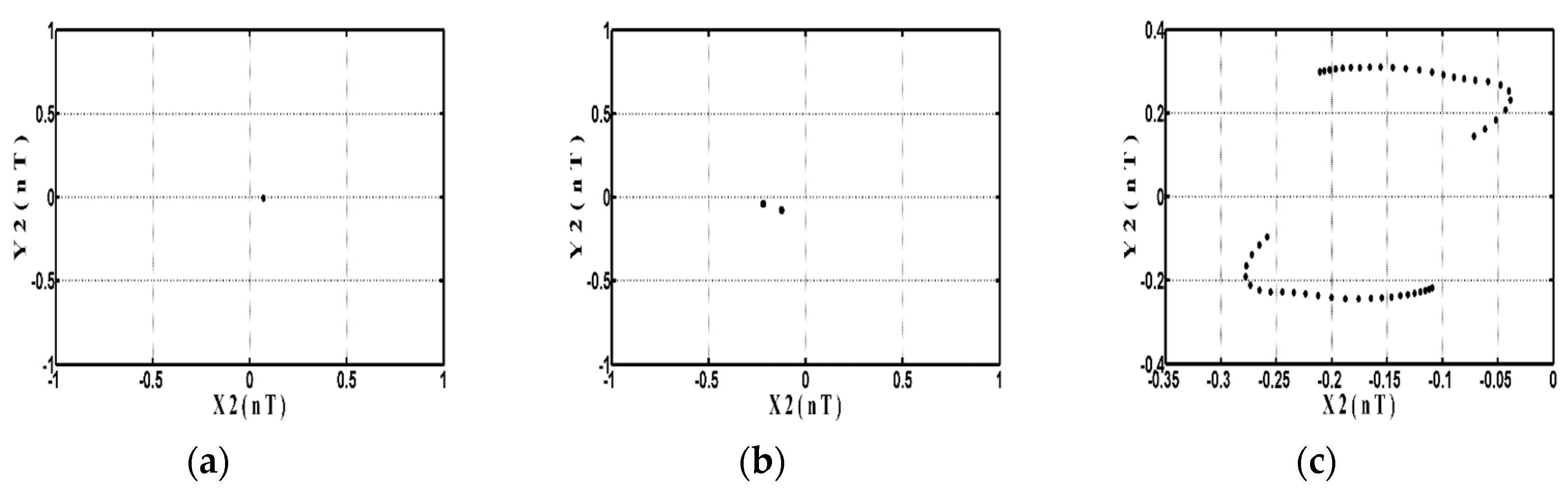
4.3.1. Dynamic Trajectory and Phase Plane Analysis
4.3.2. Spectral Analysis
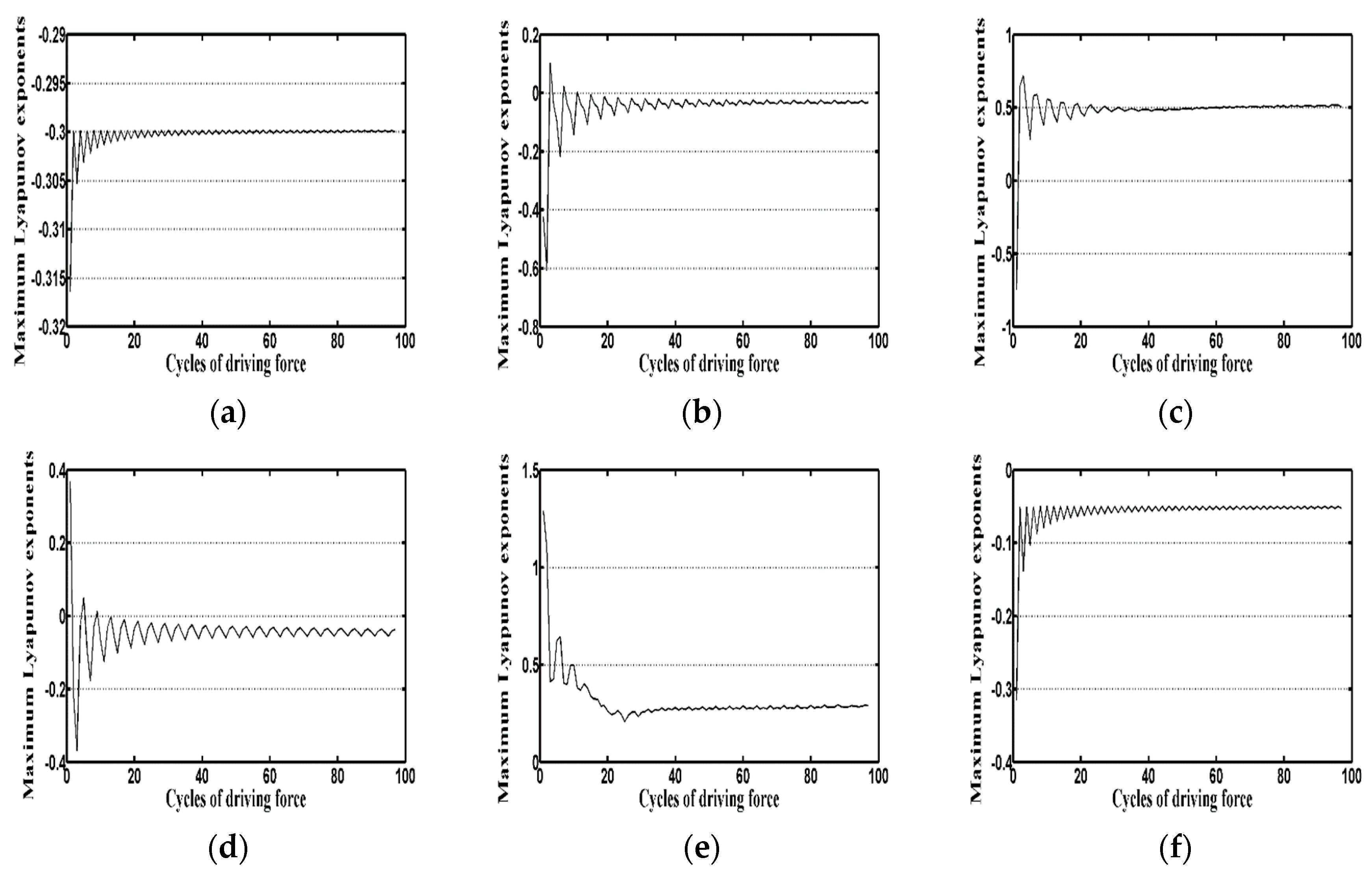
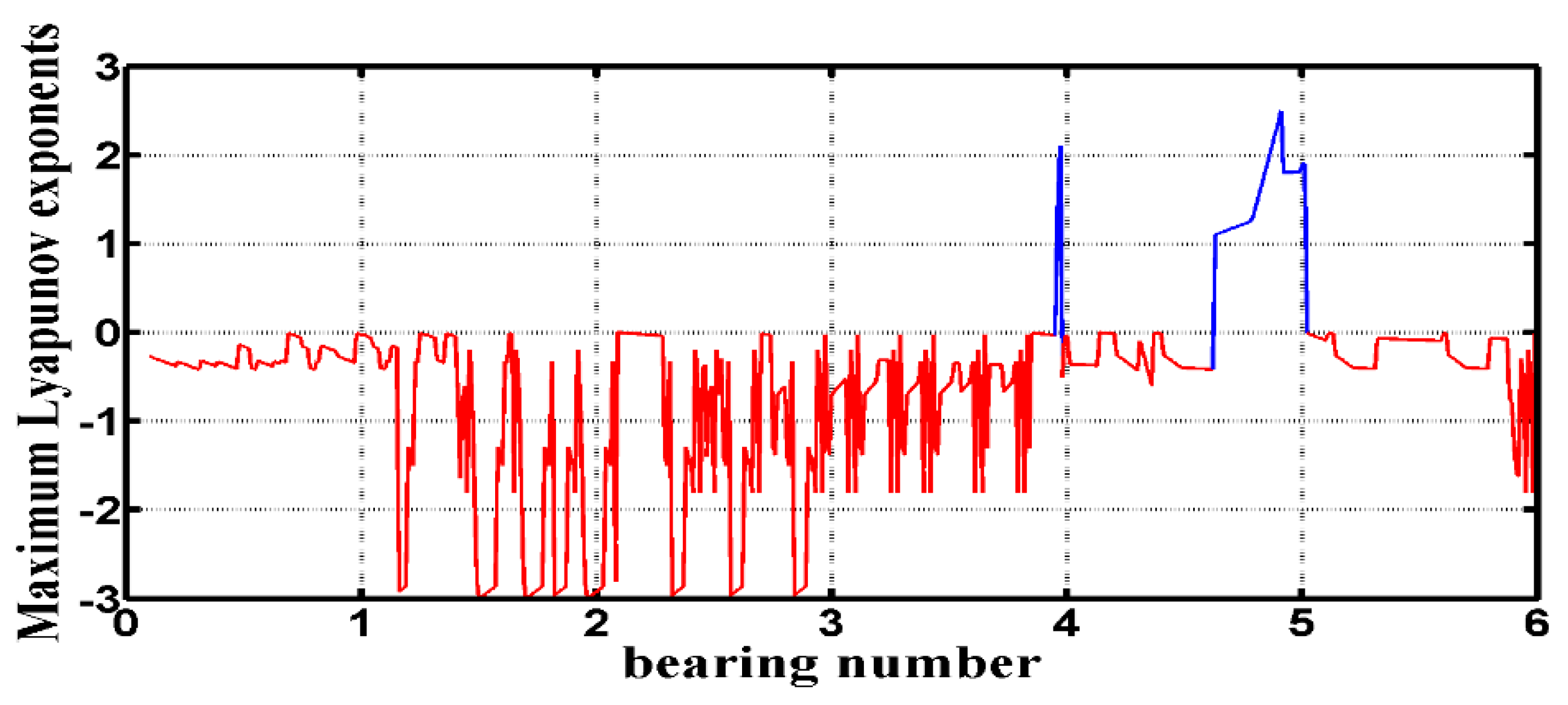
4.3.3. Bifurcation Analysis
4.4. Establishment of the Steady and Nonsteady Operation Regions of the DCAB System
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Reynolds, O. On the theory of lubrication and its application to Mr. Beauchamp tower’s experiments, including an axperimental determination of the viscosity of olive oil. Philos. Trans. R. Soc. Lond. Ser. A 1886, 177, 157–234. [Google Scholar]
- Whipple, R.T. The Inclined Groove Bearing; Atomic Energy Research Establishment: Harwell, UK, 1958. [Google Scholar]
- Whitley, S.; Williams, L.G. United Kingdom Atomic Energy Authority, I G Report 28(RD/CA); Industrial Group Headquarters: Risley, UK, 1959. [Google Scholar]
- Vohr, J.H.; Pan, C.H.T. On the Spiral-Grooved, Self-Acting, Gas Bearing; MTI Technical Report MTI63TR52, Prepared under Office of Naval Research Contract Nonr-3780(00), Task NR061-131; Mechanical Technology Inc.: Latham, NY, USA, 1964. [Google Scholar]
- Absi, J.; Bonneau, D. Caracteristiques statiques et dynamiques desPaliers a chevrons. In Proceedings of the 10 erne Congres Francois de Mecanique, Paris, France, 2–6 September 1991; Volume 1, pp. 253–256. [Google Scholar]
- Coleman, S.M. High capacity aerodynamic air bearing (HCAB) for laser scanning applications. In Optical Scanning: 31 Jul-1 Aug 2005; International Society for Optics and Photonics: San Diego, CA, USA, 2005; Volume 5873, pp. 56–64. [Google Scholar]
- Liu, Z.S.; Zhang, G.H.; Xu, H.J. Performance analysis of rotating externally pressurized air bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2009, 223, 653–663. [Google Scholar] [CrossRef]
- Simek, J.; Lindovsky, P. Development of aerodynamic bearing support for application in air cycle machines. Appl. Comput. Mech. 2014, 8, 101–114. [Google Scholar]
- Bao, X.; Mao, J. Dynamic modeling method for air bearings in ultra-precision positioning stages. Adv. Mech. Eng. 2016, 8, 1–9. [Google Scholar] [CrossRef]
- Guo, P.; Gao, H. An active non-contact journal bearing with bi-directional driving capability utilizing coupled resonant mode. CIRP Ann. 2018, 67, 405–408. [Google Scholar] [CrossRef]
- Bently, D. Forced Subrotative Speed Dynamic Action of Rotating Machinery. In ASME Paper No. 74-PET-16, Proceedings of the Petroleum Mechanical Engineering Conference, Dallas, TX, USA, 15–18 September 1974; ASME: New York, NY, USA, 1974. [Google Scholar]
- Childs, D.W. Fractional-frequency rotor motion due to nonsymmetric clearance effects. ASME J. Eng. Gas Turbines Power 1982, 104, 533–541. [Google Scholar] [CrossRef]
- Wang, C.C. Non-periodic and chaotic response of three-multilobe air bearing system. Appl. Math. Model. 2017, 47, 859–871. [Google Scholar] [CrossRef]
- Wang, C.C.; Lee, T.E. Nonlinear dynamic analysis of bi-directional porous aero-thrust bearing systems. Adv. Mech. Eng. 2017, 9, 1–11. [Google Scholar] [CrossRef]
- Wang, C.C.; Lee, R.M.; Yau, H.T.; Lee, T.E. Nonlinear analysis and simulation of active hybrid aerodynamic and aerostatic bearing system. J. Low Freq. Noise Vib. Act. Control. 2019, 38, 1404–1421. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Machine learning and deep learning algorithms for bearing fault diagnostics—A comprehensive review. arXiv 2019, arXiv:1901.08247. [Google Scholar]
- Imani, M.; Ghoreishi, S.F. Bayesian optimization objective-based experimental design. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 3405–3411. [Google Scholar]
- Ni, G.; Chen, J.; Wang, H. Degradation assessment of rolling bearing towards safety based on random matrix single ring machine learning. Saf. Sci. 2019, 118, 403–408. [Google Scholar] [CrossRef]
- Hashimoto, H.; Ochiai, M. Optimization of groove geometry for thrust air bearing to maximize bearing stiffness. ASME J. Tribol. 2008, 130, 031101. [Google Scholar] [CrossRef]
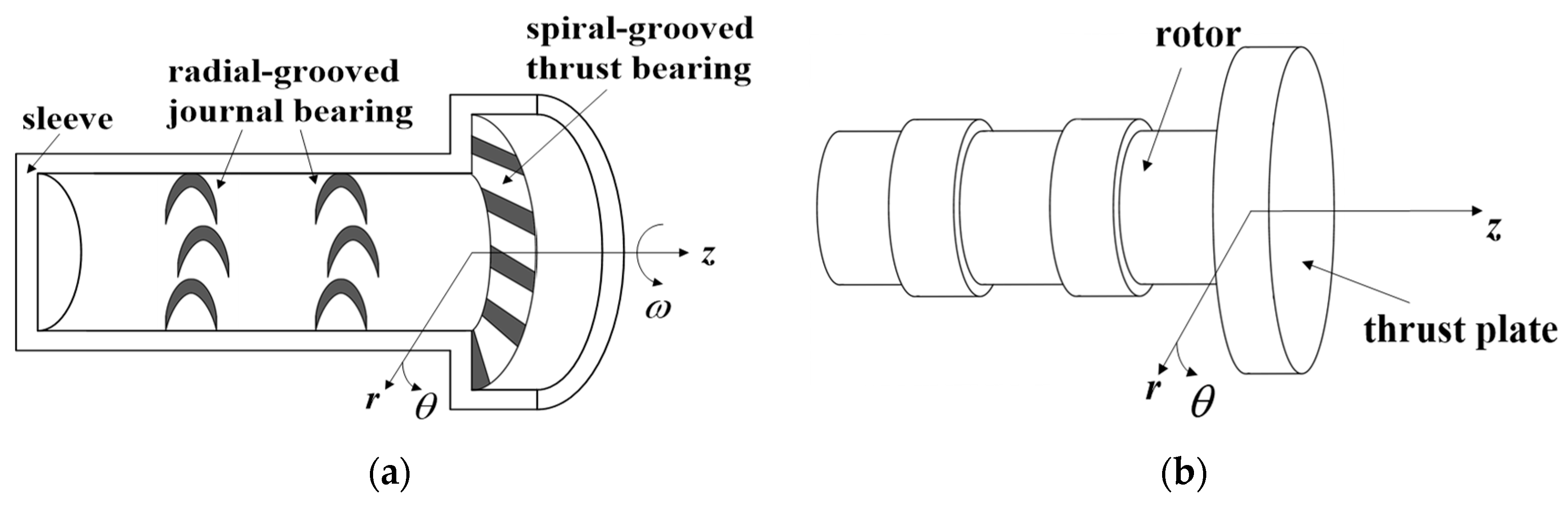



| Variable | Meaning |
|---|---|
| x, y, z, and | degrees of freedom for five directions |
| R | journal radius |
| L | bearing length |
| h | air film thickness |
| P | air film pressure |
| atmospheric pressure | |
| μ | viscosity coefficient |
| r,θ,z | coordinate system |
| t | time |
| physical quantity of perturbation | |
| rigidity of journal bearing and thrust bearing, respectively | |
| damping of journal bearing and thrust bearing, respectively | |
| mr | rotor mass |
| x2, y2 | displacements of rotor center |
| x3, y3 | displacements of journal center |
| rotational speed of rotor | |
| eccentricity of rotor | |
| stiffness coefficient of rotor | |
| equilibrium equation of forces acting to the journal center | |
| , , , ,,, | nondimensional group |
| time step | |
| Λ | dimensionless bearing number |
| Displacement | X2 | Y2 | |||
|---|---|---|---|---|---|
| Methods and Operating Conditions | |||||
| Perturbation method | mr = 11.2 kg Λ = 2.5 | −0.1823706379 | −0.1828876288 | 0.1788323797 | 0.1784390291 |
| Traditional finite-difference method | −0.1827916378 | −0.1826400484 | 0.1785890294 | 0.1788268449 | |
| Hybrid method | −0.1828351986 | −0.1828336582 | 0.1782085821 | 0.1782019995 | |
| Perturbation method | mr = 9.3 kg Λ = 2.5 | −0.1108152973 | −0.1100040131 | 0.0818502819 | 0.0810126263 |
| Traditional finite-difference method | −0.1106937267 | −0.1101360701 | 0.0811265030 | 0.0813032587 | |
| Hybrid method | −0.1105966888 | −0.1105993378 | 0.0812939956 | 0.0812912614 | |
| Perturbation method | mr = 5.7 kg Λ = 2.1 | 0.0743158143 | 0.0745814316 | −0.0022026672 | −0.0020779572 |
| Traditional finite-difference method | 0.0742887199 | 0.0740141869 | −0.0023085543 | −0.0024181594 | |
| Hybrid method | 0.07451222055 | 0.0745196645 | −0.0021489664 | −0.0021435547 | |
| Perturbation method | mr = 5.7 kg Λ = 3.0 | −0.2386678975 | −0.2384812317 | −0.0587582454 | −0.0582706309 |
| Traditional finite-difference method | −0.2389323073 | −0.2387243330 | −0.0585839042 | −0.0587359340 | |
| Hybrid method | −0.2385255159 | −0.2385242494 | −0.0584736366 | −0.0584706615 | |
| τ | X2(n T) | Y2(n T) |
|---|---|---|
| π/300 | −0.089320590874 | 0.052302554355 |
| π/600 | −0.089329265030 | 0.052301040131 |
| Rotor Mass | [0.1, 20.92) | [20.92, 23.13) | [23.13, 24.31) | [24.31, 24.4) | [24.4, 24.52) |
| Dynamic Behavior | T | Quasi | T | 3T | T |
| Rotor Mass | [24.52, 24.58) | [24.58, 24.6) | [24.6, 24.75) | [24.75, 25.0] | |
| Dynamic Behavior | 3T | T | 3T | Chaotic |
| Λ | [1.0, 3.21) | [3.21, 3.96) | [3.96, 3.98) |
| Behavior | T | 2T | Chaos |
| Λ | [3.98, 4.63) | [4.63, 5.02) | [5.02, 6.0] |
| Behavior | 2T | Chaos | T |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.-C.; Lin, C.-J. Bifurcation and Nonlinear Behavior Analysis of Dual-Directional Coupled Aerodynamic Bearing Systems. Symmetry 2020, 12, 1521. https://doi.org/10.3390/sym12091521
Wang C-C, Lin C-J. Bifurcation and Nonlinear Behavior Analysis of Dual-Directional Coupled Aerodynamic Bearing Systems. Symmetry. 2020; 12(9):1521. https://doi.org/10.3390/sym12091521
Chicago/Turabian StyleWang, Cheng-Chi, and Chih-Jer Lin. 2020. "Bifurcation and Nonlinear Behavior Analysis of Dual-Directional Coupled Aerodynamic Bearing Systems" Symmetry 12, no. 9: 1521. https://doi.org/10.3390/sym12091521
APA StyleWang, C.-C., & Lin, C.-J. (2020). Bifurcation and Nonlinear Behavior Analysis of Dual-Directional Coupled Aerodynamic Bearing Systems. Symmetry, 12(9), 1521. https://doi.org/10.3390/sym12091521






