LISA Sensitivity to Gravitational Waves from Sound Waves
Abstract
1. Introduction
2. Signal
3. Noise
4. Sensitivity
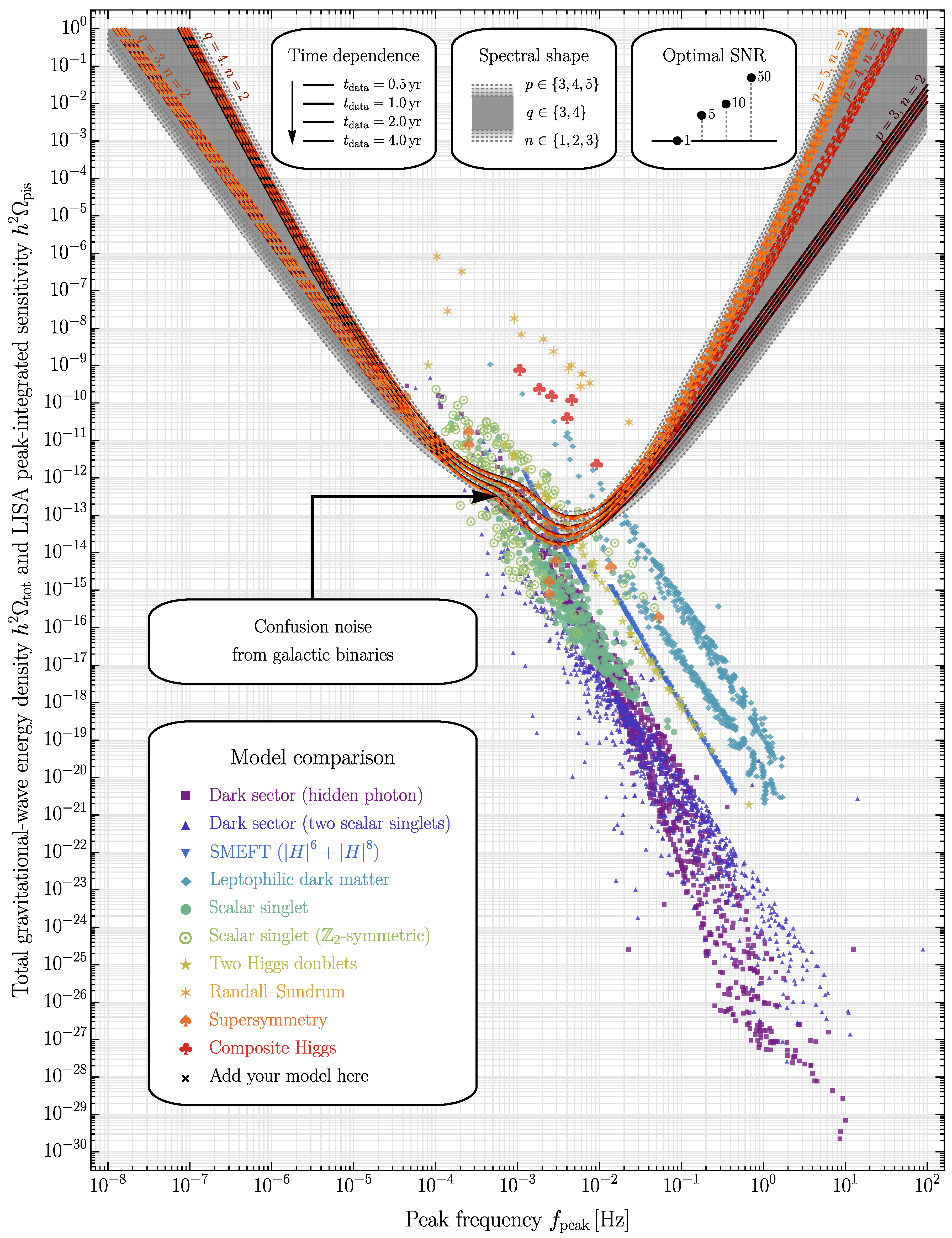
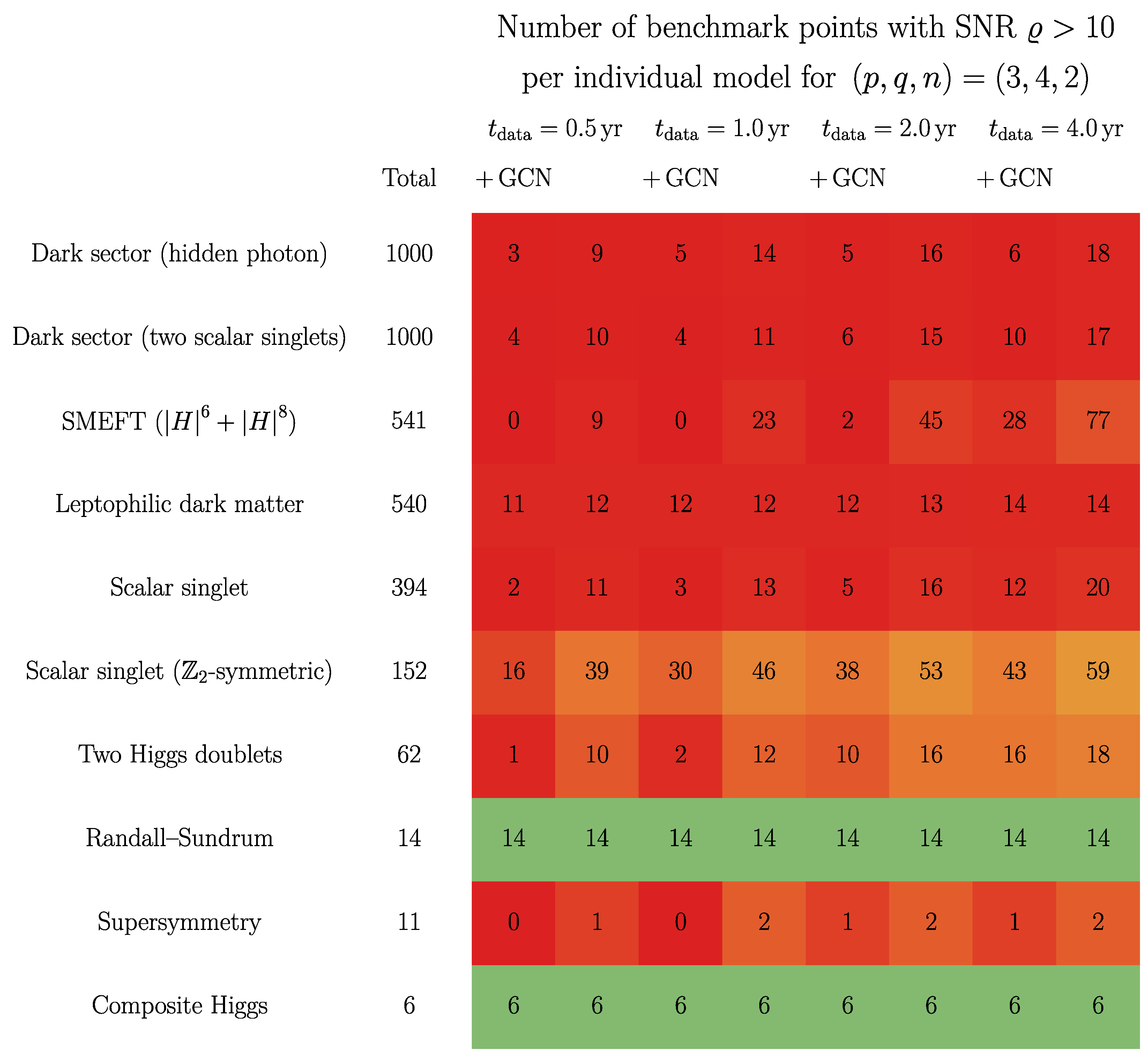
- Dark-sector model featuring a spontaneously broken gauge symmetry [60].
- Dark-sector model featuring two gauge-singlet scalars [60].
- and operators in the standard model effective field theory (SMEFT) [61].
- Dark-matter model based on gauged and spontaneously broken lepton number [62].
- Holographic phase transitions in extra-dimensional Randall–Sundrum models [70].
- Composite-Higgs models featuring different pseudo-Nambu–Goldstone bosons [75].
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser Interferometer Space Antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Baker, J.; Bellovary, J.; Bender, P.L.; Berti, E.; Caldwell, R.; Camp, J.; Conklin, J.W.; Cornish, N.; Cutler, C.; DeRosa, R.; et al. The Laser Interferometer Space Antenna: Unveiling the Millihertz Gravitational Wave Sky. arXiv 2019, arXiv:1907.06482. [Google Scholar]
- Maggiore, M. Gravitational wave experiments and early universe cosmology. Phys. Rept. 2000, 331, 283. [Google Scholar] [CrossRef]
- Romano, J.D.; Cornish, N.J. Detection methods for stochastic gravitational-wave backgrounds: A unified treatment. Living Rev. Rel. 2017, 20, 2. [Google Scholar] [CrossRef] [PubMed]
- Caprini, C.; Figueroa, D.G. Cosmological Backgrounds of Gravitational Waves. Class. Quant. Grav. 2018, 35, 163001. [Google Scholar] [CrossRef]
- Christensen, N. Stochastic Gravitational Wave Backgrounds. Rept. Prog. Phys. 2019, 82, 016903. [Google Scholar] [CrossRef]
- Weir, D.J. Gravitational waves from a first order electroweak phase transition: A brief review. Philos. Trans. R. Soc. Lond. A 2018, 376, 20170126. [Google Scholar] [CrossRef]
- Mazumdar, A.; White, G. Review of cosmic phase transitions: Their significance and experimental signatures. Rept. Prog. Phys. 2019, 82, 076901. [Google Scholar] [CrossRef]
- Caprini, C.; Hindmarsh, M.; Huber, S.; Konst, T.; Kozaczuk, J.; Nardini, G.; No, J.M.; Petiteau, A.; Schwaller, P.; Servant, G.; et al. Science with the space-based interferometer eLISA. II: Gravitational waves from cosmological phase transitions. J. Cosmol. Astropart. Phys. 2016, 4, 1. [Google Scholar] [CrossRef]
- Caprini, C.; Chala, M.; Dorsch, G.C.; Hindmarsh, M.; Huber, S.J.; Konst, T.; Kozaczuk, J.; Nardini, G.; No, J.M.; Rummukainen, K.; et al. Detecting gravitational waves from cosmological phase transitions with LISA: An update. J. Cosmol. Astropart. Phys. 2020, 2003, 24. [Google Scholar] [CrossRef]
- Hindmarsh, M.; Huber, S.J.; Rummukainen, K.; Weir, D.J. Gravitational waves from the sound of a first order phase transition. Phys. Rev. Lett. 2014, 112, 041301. [Google Scholar] [CrossRef] [PubMed]
- Giblin, J.T.; Mertens, J.B. Vacuum Bubbles in the Presence of a Relativistic Fluid. J. High Energy Phys. 2013, 12, 42. [Google Scholar] [CrossRef]
- Giblin, J.T.; Mertens, J.B. Gravitional radiation from first-order phase transitions in the presence of a fluid. Phys. Rev. D 2014, 90, 023532. [Google Scholar] [CrossRef]
- Hindmarsh, M.; Huber, S.J.; Rummukainen, K.; Weir, D.J. Numerical simulations of acoustically generated gravitational waves at a first order phase transition. Phys. Rev. D 2015, 92, 123009. [Google Scholar] [CrossRef]
- Hindmarsh, M. Sound shell model for acoustic gravitational wave production at a first-order phase transition in the early Universe. Phys. Rev. Lett. 2018, 120, 071301. [Google Scholar] [CrossRef]
- Hindmarsh, M.; Huber, S.J.; Rummukainen, K.; Weir, D.J. Shape of the acoustic gravitational wave power spectrum from a first order phase transition. Phys. Rev. 2017, D96, 103520. [Google Scholar] [CrossRef]
- Hindmarsh, M.; Hijazi, M. Gravitational waves from first order cosmological phase transitions in the Sound Shell Model. J. Cosmol. Astropart. Phys. 2019, 1912, 62. [Google Scholar] [CrossRef]
- Kosowsky, A.; Turner, M.S.; Watkins, R. Gravitational radiation from colliding vacuum bubbles. Phys. Rev. D 1992, 45, 4514. [Google Scholar] [CrossRef]
- Kosowsky, A.; Turner, M.S.; Watkins, R. Gravitational waves from first order cosmological phase transitions. Phys. Rev. Lett. 1992, 69, 2026. [Google Scholar] [CrossRef]
- Kosowsky, A.; Turner, M.S. Gravitational radiation from colliding vacuum bubbles: Envelope approximation to many bubble collisions. Phys. Rev. D 1993, 47, 4372. [Google Scholar] [CrossRef]
- Kamionkowski, M.; Kosowsky, A.; Turner, M.S. Gravitational radiation from first order phase transitions. Phys. Rev. D 1994, 49, 2837. [Google Scholar] [CrossRef] [PubMed]
- Caprini, C.; Durrer, R.; Servant, G. Gravitational wave generation from bubble collisions in first-order phase transitions: An analytic approach. Phys. Rev. D 2008, 77, 124015. [Google Scholar] [CrossRef]
- Huber, S.J.; Konstandin, T. Gravitational Wave Production by Collisions: More Bubbles. J. Cosmol. Astropart. Phys. 2008, 9, 22. [Google Scholar] [CrossRef]
- Caprini, C.; Durrer, R. Gravitational waves from stochastic relativistic sources: Primordial turbulence and magnetic fields. Phys. Rev. D 2006, 74, 063521. [Google Scholar] [CrossRef]
- Kahniashvili, T.; Kosowsky, A.; Gogoberidze, G.; Maravin, Y. Detectability of Gravitational Waves from Phase Transitions. Phys. Rev. D 2008, 78, 043003. [Google Scholar] [CrossRef]
- Kahniashvili, T.; Campanelli, L.; Gogoberidze, G.; Maravin, Y.; Ratra, B. Gravitational Radiation from Primordial Helical Inverse Cascade MHD Turbulence. Phys. Rev. D 2008, 78, 123006. [Google Scholar] [CrossRef]
- Kahniashvili, T.; Kisslinger, L.; Stevens, T. Gravitational Radiation Generated by Magnetic Fields in Cosmological Phase Transitions. Phys. Rev. D 2010, 81, 023004. [Google Scholar] [CrossRef]
- Caprini, C.; Durrer, R.; Servant, G. The stochastic gravitational wave background from turbulence and magnetic fields generated by a first-order phase transition. J. Cosmol. Astropart. Phys. 2009, 12, 24. [Google Scholar] [CrossRef]
- Kisslinger, L.; Kahniashvili, T. Polarized Gravitational Waves from Cosmological Phase Transitions. Phys. Rev. D 2015, 92, 043006. [Google Scholar] [CrossRef]
- Thrane, E.; Romano, J.D. Sensitivity curves for searches for gravitational-wave backgrounds. Phys. Rev. 2013, D88, 124032. [Google Scholar] [CrossRef]
- Alanne, T.; Hugle, T.; Platscher, M.; Schmitz, K. A fresh look at the gravitational-wave signal from cosmological phase transitions. J. High Energy Phys. 2020, 3, 1–27. [Google Scholar] [CrossRef]
- Schmitz, K. New Sensitivity Curves for Gravitational-Wave Experiments. arXiv 2020, arXiv:2002.04615. [Google Scholar]
- Nelemans, G.; Tout, C. Reconstructing the evolution of white dwarf binaries: Further evidence for an alternative algorithm for the outcome of the common-envelope phase in close binaries. Mon. Not. Roy. Astron. Soc. 2005, 356, 753. [Google Scholar] [CrossRef]
- Toonen, S.; Nelemans, G.; Zwart, S.P. Supernova Type Ia progenitors from merging double white dwarfs: Using a new population synthesis model. Astron. Astrophys. 2012, 546, A70. [Google Scholar] [CrossRef]
- Korol, V.; Rossi, E.M.; Groot, P.J.; Nelemans, G.; Toonen, S.; Brown, A.G. Prospects for detection of detached double white dwarf binaries with Gaia, LSST and LISA. Mon. Not. R. Astron. Soc. 2017, 470, 1894. [Google Scholar] [CrossRef]
- Cornish, N.; Robson, T. Galactic binary science with the new LISA design. J. Phys. Conf. Ser. 2017, 840, 012024. [Google Scholar] [CrossRef]
- Littenberg, T.; Cornish, N.; Lackeos, K.; Robson, T. Global Analysis of the Gravitational Wave Signal from Galactic Binaries. arXiv 2020, arXiv:2004.08464. [Google Scholar] [CrossRef]
- Espinosa, J.R.; Konstandin, T.; No, J.M.; Servant, G. Energy Budget of Cosmological First-order Phase Transitions. J. Cosmol. Astropart. Phys. 2010, 1006, 028. [Google Scholar] [CrossRef]
- Giese, F.; Konstandin, T.; van de Vis, J. Model-independent energy budget of cosmological first-order phase transitions. arXiv 2020, arXiv:2004.06995. [Google Scholar]
- Ellis, J.; Lewicki, M.; No, J.M. On the Maximal Strength of a First-Order Electroweak Phase Transition and its Gravitational Wave Signal. J. Cosmol. Astropart. Phys. 2019, 1904, 3. [Google Scholar] [CrossRef]
- Ellis, J.; Lewicki, M.; No, J.M.; Vaskonen, V. Gravitational wave energy budget in strongly supercooled phase transitions. J. Cosmol. Astropart. Phys. 2019, 1906, 24. [Google Scholar] [CrossRef]
- Ellis, J.; Lewicki, M.; No, J.M. Gravitational waves from first-order cosmological phase transitions: Lifetime of the sound wave source. arXiv 2020, arXiv:2003.07360. [Google Scholar] [CrossRef]
- Robson, T.; Cornish, N.J.; Liu, C. The construction and use of LISA sensitivity curves. Class. Quant. Grav. 2019, 36, 105011. [Google Scholar] [CrossRef]
- Edwards, M.C.; Maturana-Russel, P.; Meyer, R.; Gair, J.; Korsakova, N.; Christensen, N. Identifying and Addressing Nonstationary LISA Noise. arXiv 2020, arXiv:2004.07515. [Google Scholar]
- Larson, S.L.; Hiscock, W.A.; Hellings, R.W. Sensitivity curves for spaceborne gravitational wave interferometers. Phys. Rev. 2000, D62, 062001. [Google Scholar] [CrossRef]
- Larson, S.L.; Hellings, R.W.; Hiscock, W.A. Unequal arm space borne gravitational wave detectors. Phys. Rev. 2002, D66, 062001. [Google Scholar] [CrossRef]
- Tinto, M.; Alves, M.E.D. LISA Sensitivities to Gravitational Waves from Relativistic Metric Theories of Gravity. Phys. Rev. 2010, D82, 122003. [Google Scholar] [CrossRef]
- Blaut, A. Angular and frequency response of the gravitational wave interferometers in the metric theories of gravity. Phys. Rev. 2012, D85, 043005. [Google Scholar]
- Liang, D.; Gong, Y.; Weinstein, A.J.; Zhang, C.; Zhan, C.G. Frequency response of space-based interferometric gravitational-wave detectors. Phys. Rev. 2019, D99, 104027. [Google Scholar] [CrossRef]
- Zhang, C.; Gao, Q.; Gong, Y.; Liang, D.; Weinstein, A.J.; Zhang, C. Frequency response of time-delay interferometry for space-based gravitational wave antenna. Phys. Rev. 2019, D100, 064033. [Google Scholar] [CrossRef]
- Lu, X.-Y.; Tan, Y.-J.; Shao, C.-G. Sensitivity functions for space-borne gravitational wave detectors. Phys. Rev. 2019, D100, 044042. [Google Scholar] [CrossRef]
- Zhang, C.; Gao, Q.; Gong, Y.; Wang, B.; Weinstein, A.J.; Zhang, C. Full analytical formulas for frequency response of space-based gravitational wave detectors. arXiv 2020, arXiv:2003.01441. [Google Scholar] [CrossRef]
- Wang, G.; Ni, W.-T.; Han, W.-B. Sensitivity investigation for unequal-arm LISA and TAIJI: The first-generation time-delay interferometry optimal channels. arXiv 2020, arXiv:2008.05812. [Google Scholar]
- Vallisneri, M.; Bayle, J.-B.; Babak, S.; Petiteau, A. TDI-infinity: Time-delay interferometry without delays. arXiv 2020, arXiv:2008.12343. [Google Scholar]
- Littenberg, T.B.; Cornish, N.J. Bayesian inference for spectral estimation of gravitational wave detector noise. Phys. Rev. D 2015, 91, 084034. [Google Scholar] [CrossRef]
- Allen, B. The Stochastic gravity wave background: Sources and detection. In Proceedings of the Relativistic Gravitation and Gravitational Radiation, School of Physics, Les Houches, France, 26 September–6 October 1995; pp. 373–417. [Google Scholar]
- Allen, B.; Romano, J.D. Detecting a stochastic background of gravitational radiation: Signal processing strategies and sensitivities. Phys. Rev. 1999, D59, 102001. [Google Scholar] [CrossRef]
- Kuroyanagi, S.; Chiba, T.; Takahashi, T. Probing the Universe through the Stochastic Gravitational Wave Background. J. Cosmol. Astropart. Phys. 2018, 1811, 38. [Google Scholar] [CrossRef]
- Schmitz, K. LISA Sensitivity to Gravitational Waves from Sound Waves. Available online: https://doi.org/10.5281/zenodo.3837876 (accessed on 8 September 2020).
- Breitbach, M.; Kopp, J.; Madge, E.; Opferkuch, T.; Schwaller, P. Dark, Cold, and Noisy: Constraining Secluded Hidden Sectors with Gravitational Waves. J. Cosmol. Astropart. Phys. 2019, 7, 7. [Google Scholar] [CrossRef]
- Chala, M.; Krause, C.; Nardini, G. Signals of the electroweak phase transition at colliders and gravitational wave observatories. J. High Energy Phys. 2018, 7, 62. [Google Scholar] [CrossRef]
- Madge, E.; Schwaller, P. Leptophilic dark matter from gauged lepton number: Phenomenology and gravitational wave signatures. J. High Energy Phys. 2019, 2, 48. [Google Scholar] [CrossRef]
- Chen, C.-Y.; Kozaczuk, J.; Lewis, I.M. Non-resonant Collider Signatures of a Singlet-Driven Electroweak Phase Transition. J. High Energy Phys. 2017, 8, 96. [Google Scholar] [CrossRef]
- Huang, P.; Long, A.J.; Wang, L.-T. Probing the Electroweak Phase Transition with Higgs Factories and Gravitational Waves. Phys. Rev. D 2016, 94, 075008. [Google Scholar] [CrossRef]
- Beniwal, A.; Lewicki, M.; Wells, J.D.; White, M.; Williams, A.G. Gravitational wave, collider and dark matter signals from a scalar singlet electroweak baryogenesis. J. High Energy Phys. 2017, 8, 108. [Google Scholar] [CrossRef]
- Dorsch, G.; Huber, S.; No, J. A strong electroweak phase transition in the 2HDM after LHC8. J. High Energy Phys. 2013, 10, 29. [Google Scholar] [CrossRef]
- Dorsch, G.; Huber, S.; Mimasu, K.; No, J. Echoes of the Electroweak Phase Transition: Discovering a second Higgs doublet through A0→ZH0. Phys. Rev. Lett. 2014, 113, 211802. [Google Scholar] [CrossRef] [PubMed]
- Dorsch, G.; Huber, S.; Konstandin, T.; No, J. A Second Higgs Doublet in the Early Universe: Baryogenesis and Gravitational Waves. J. Cosmol. Astropart. Phys. 2017, 5, 52. [Google Scholar] [CrossRef]
- Dorsch, G.; Huber, S.; Mimasu, K.; No, J. The Higgs Vacuum Uplifted: Revisiting the Electroweak Phase Transition with a Second Higgs Doublet. J. High Energy Phys. 2017, 12, 86. [Google Scholar] [CrossRef]
- Megías, E.; Nardini, G.; Quirós, M. Cosmological Phase Transitions in Warped Space: Gravitational Waves and Collider Signatures. J. High Energy Phys. 2018, 9, 95. [Google Scholar] [CrossRef]
- Huber, S.J.; Konstandin, T.; Nardini, G.; Rues, I. Detectable Gravitational Waves from Very Strong Phase Transitions in the General NMSSM. J. Cosmol. Astropart. Phys. 2016, 3, 36. [Google Scholar] [CrossRef]
- Garcia-Pepin, M.; Quiros, M. Strong electroweak phase transition from Supersymmetric Custodial Triplets. J. High Energy Phys. 2016, 5, 177. [Google Scholar] [CrossRef]
- Bian, L.; Guo, H.-K.; Shu, J. Gravitational Waves, baryon asymmetry of the universe and electric dipole moment in the CP-violating NMSSM. Chin. Phys. C 2018, 42, 093106. [Google Scholar] [CrossRef]
- Demidov, S.; Gorbunov, D.; Kirpichnikov, D. Gravitational waves from phase transition in split NMSSM. Phys. Lett. B 2018, 779, 191. [Google Scholar] [CrossRef]
- Bruggisser, S.; Harling, B.V.; Matsedonskyi, O.; Servant, G. Electroweak Phase Transition and Baryogenesis in Composite Higgs Models. J. High Energy Phys. 2018, 12, 99. [Google Scholar] [CrossRef]
- LIGO Cosmology Working Group; Weir, D. Available online: http://ptplot.org (accessed on 8 September 2020).

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmitz, K. LISA Sensitivity to Gravitational Waves from Sound Waves. Symmetry 2020, 12, 1477. https://doi.org/10.3390/sym12091477
Schmitz K. LISA Sensitivity to Gravitational Waves from Sound Waves. Symmetry. 2020; 12(9):1477. https://doi.org/10.3390/sym12091477
Chicago/Turabian StyleSchmitz, Kai. 2020. "LISA Sensitivity to Gravitational Waves from Sound Waves" Symmetry 12, no. 9: 1477. https://doi.org/10.3390/sym12091477
APA StyleSchmitz, K. (2020). LISA Sensitivity to Gravitational Waves from Sound Waves. Symmetry, 12(9), 1477. https://doi.org/10.3390/sym12091477





