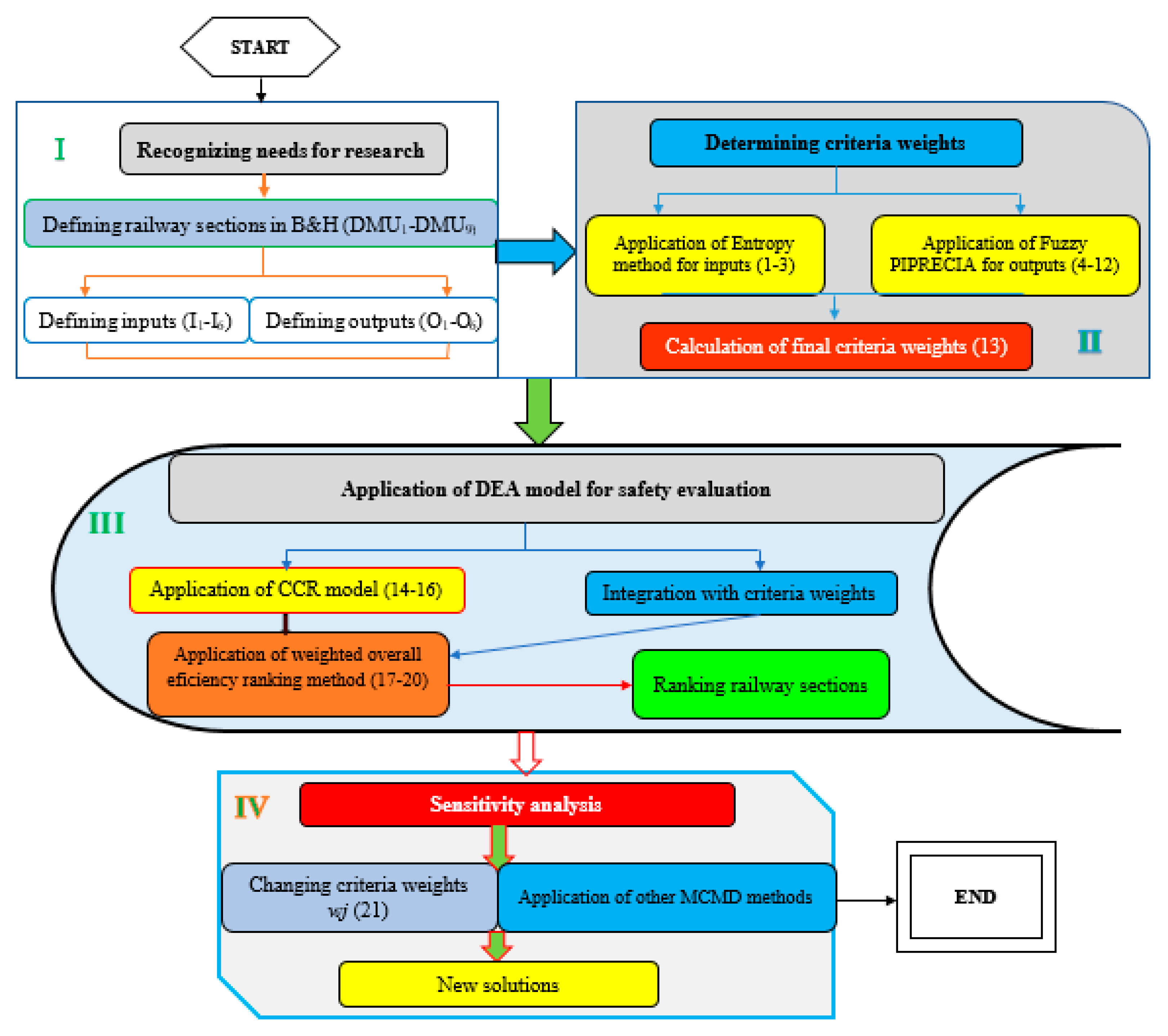
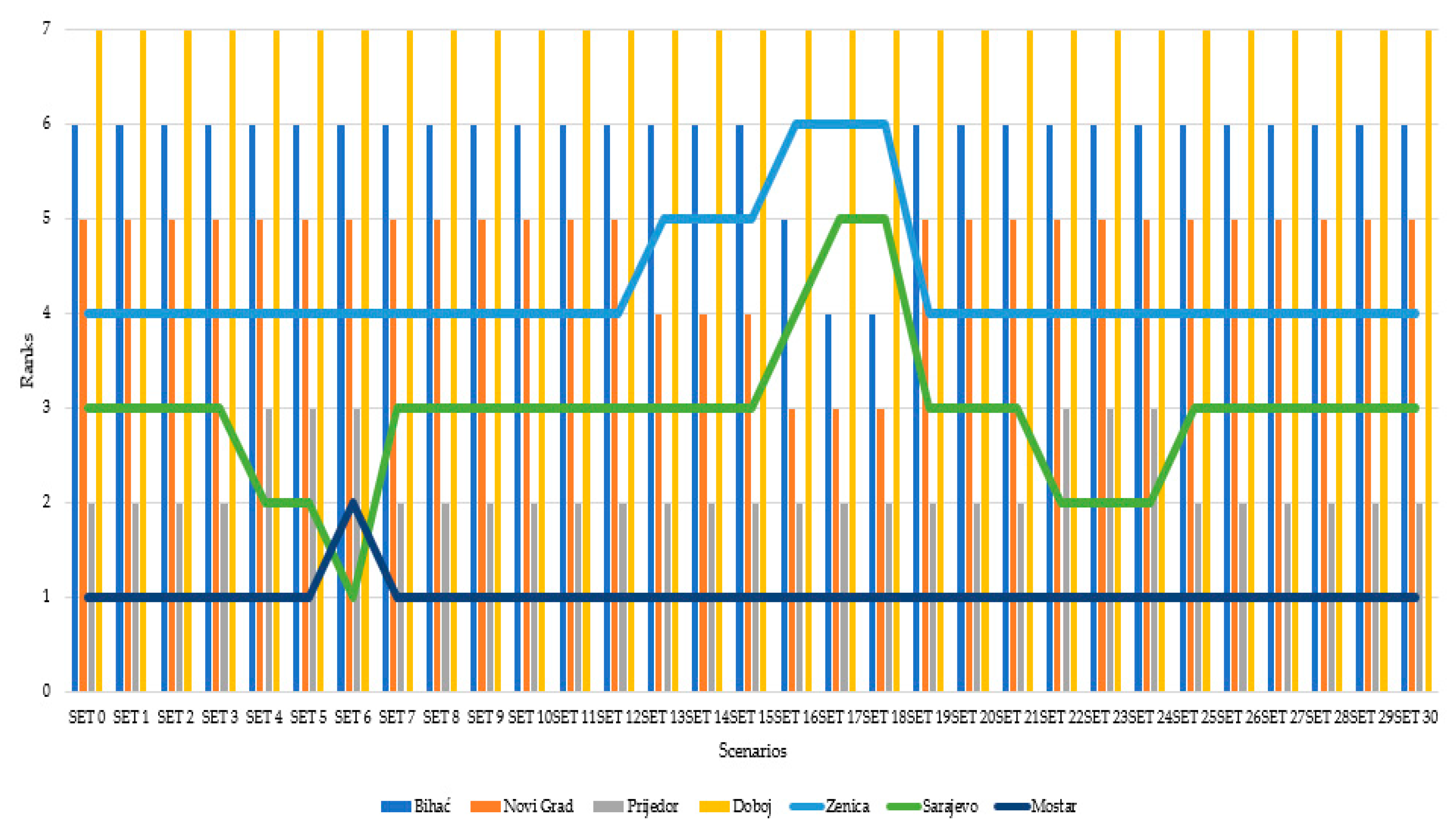
4.2. Defining Input-Output Parameters
The essence, meaning and reasons of each criterion are explained in the further text. Note: The transport of dangerous goods in Bosnia and Herzegovina is small in scale, and it is not possible to take into account the type of goods; for this reason, this criterion has not been considered.
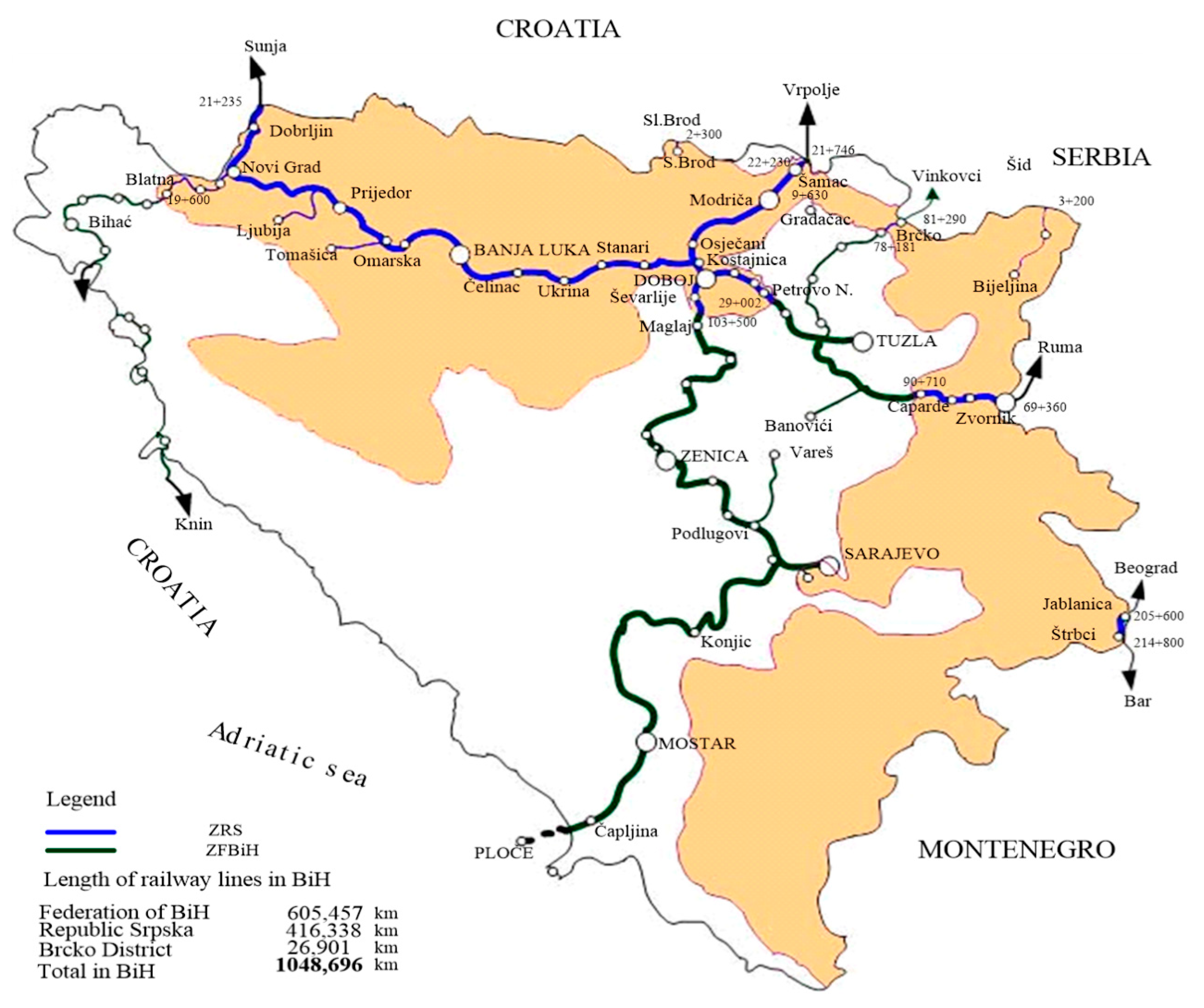
The total length of railway network—I1. This criterion refers to the characteristics of the network and greatly affects railway traffic safety. The safety of transport of goods and passengers is significantly affected by the condition and the degree of wear of the railway network. Even though the technical condition of the network has been improved by reconstruction and modernization, it still does not correspond to the condition of modern and safe transport. The technical equipment of the railway, as a basis of traffic safety, most clearly reflects the ability of railways, signaling and telecommunication devices and rolling stock. Despite efforts to improve the condition of the railway network, it is still not at the required level due to a high percentage of wear and tear of materials, especially the superstructure (tracks, sleepers, track material and ballast) and other facilities. It is estimated that the degree of wear of track superstructure is over 40%. The level of traffic safety is also affected by a large number of slow drives, i.e., reduction of speed caused by the deterioration of materials and weak points on the railway, which cause very frequent speed changes. Thirty to forty permanent slow drives are introduced annually on the B&H railway network. Due to low temperatures and insufficient ballast, the track is deformed 10 to 15 times a year, especially on parts of the track with continuous welded rails. A significant number of railway network sections are exposed to the influence of natural disturbances, which occasionally endanger traffic and cause its interruptions. The most common are torrential rains, floods and landslides, which pose a danger to traffic safety because these phenomena usually occur suddenly. Traffic safety has been reduced due to the condition of tracks, which is determined by the technical parameters of facilities on particular tracks and the manner and policy of track maintenance.
The total number of stations—I2. Railway traffic safety, in addition to the human factor, is most significantly determined by the degree of security of stations with signaling and telecommunication devices. On the B&H railway network, 54% of stations are protected with modern and more extensive security, while 46% of stations are protected with simplified security. The degree of modernization program implementation and installation of modern signaling devices significantly affects the level of railway traffic safety, reducing the number of staff involved in providing and regulating traffic, reducing delays in technological processes, improving working conditions of station staff, better clarity of signal items along tracks, etc. The lack of adequate infrastructure has become a limiting factor for the implementation of new systems for the purpose of safe and regular railway traffic and connecting the railways in B&H with the railways in the region and beyond with the railways of EU countries. Raising the level of train traffic safety largely depends on the installation of modern signaling devices. Some accidents with severe consequences could be avoided if these devices were installed.
The number of level crossings—I3. Many accidents and incidents, especially those with serious consequences, occur at the intersections of railway tracks and roads. The number of traffic accidents and incidents in these places is increasing, and growing with an increase in the number of vehicles in traffic. It is symptomatic that the number of accidents and incidents at level crossings is growing and that the number of human casualties and injured persons is increasing as well as material damage. Accidents at level crossings occur particularly due to the negligence of road vehicle drivers, which is manifested in disrespect of signs at level crossings, careless crossing of vehicles over tracks, etc. Accidents occur due to the fault of railway workers in only 1% of cases. Accidents and incidents occur despite the fact that level crossings are protected by light signals, barriers or half-length barriers. Level crossings on the B&H railway network are locations that generate great risk in terms of railway and road traffic safety. Level crossings should be accepted as a necessary evil, i.e., places where there is a high risk of endangering traffic safety with fatal consequences. To increase traffic safety, it is necessary to take all available measures to reduce negative consequences of accidents at level crossings.
The number of available vehicles—I4. A serious problem in transport execution and timetable realization is poor technical conditions, poor maintenance and a high percentage of immobilization of rolling stock. It was especially manifested in a large number of immobilized locomotives caused by poor maintenance, improper handling of vehicles and their devices, lack of spare parts, prolongation of repairs and damage to locomotives in accidents and incidents. The most common failures in towing vehicles are on drive and auxiliary devices. Special attention should be paid to those defects of rolling stock that directly endanger traffic safety, such as axle fractures or gearbox failures, pantograph fractures on electric locomotives, etc. The number of defects in towing vehicles is very large and is constantly increasing, and that is the reason radical measures should be taken to improve their technical functionality. Immobilization of freight and passenger cars as a consequence of their condition and maintenance adversely affects traffic safety and quality of transport. Due to the unfavorable condition of rolling stock and inadequate maintenance, the number of vehicles removed from traffic because of breakdowns is high. Additionally, the number of accidents and incidents due to vehicle breakdowns is large. According to available data, vehicles in B&H are mostly of old average age, over 41 years, which represents difficulties in maintaining vehicles in good condition. Railway safety largely depends on a level of modernization of rolling stock.
The total number of train-kilometers—I5. Train-kilometers are quantitative indicators that are able to show a certain amount of work or quantity in the transport of passengers and goods. A railway undertaking, providing transport, performs a certain amount of work in train-kilometers, which is considered to be a realized transport service for which a certain price is charged. Train-kilometers characterize the operation of locomotives and cars (electric or diesel engine sets) on one network or on particular lines. The most common criterion for determining the reliability of vehicles is their lifespan, which is expressed in the number of train-kilometers traveled. In essence, the level of railway traffic safety is reduced if the number of train-kilometers traveled is higher. Thus, in B&H, a serious problem is the condition of mobile capacities which are mostly of old age and at the end of their lifespan.
The total number of executive staff—I6. This criterion is the most significant for railway traffic safety because it is dominant in a chain of railway traffic safety components. It can be freely stated that in all accidents and incidents except those caused by “force majeure” (a phenomenon that man cannot predict, manage or control, such as earthquakes, floods, large landslides, large-scale fires, etc.), a man, compared to the resources he has created, is the most susceptible to deviations from standard (standardized, prescribed, expected) behavior and hence becomes a (direct or indirect) cause of most railway accidents and incidents. In some sections, the problem is an insufficient number of executive staff (train drivers, train dispatchers, shunters and switchers), which requires great efforts and responsibilities in order to maintain a high level of safety. The lack of executive staff requires the introduction of extended work, which increases fatigue and creates unfavorable safety conditions. Basically, the cause of some railway accidents and incidents is a man who has failed (directly or indirectly). Thus, he has erred in designing, manufacturing, maintaining, controlling, and handling of technical means which are the cause of some events (serious accidents, accidents and incidents). For these reasons, and in order to increase safety, executive staff must be constantly checked in terms of: health status, professional skills, fatigue, and work and technical discipline.
Table 2 shows the values of all DMUs in relation to input parameters.
To maintain safety at a high level, the European Union in its documents [
27] has prescribed the definitions of accidents and incidents and limitations of common safety objectives.
Serious accident—O1. A serious accident means any train collision or derailment of trains resulting in the death of at least one person, serious injuries to five or more persons or extensive damage to rolling stock (extensive damage means damage that can be immediately assessed by the investigating body to cost at least EUR 2 million), infrastructure or the environment, and any other accident which has an obvious impact on railway safety or safety management.
Accident—O2. An accident is an unwanted or unintended sudden event or a specific chain of such events which have harmful consequences (collisions, derailments, level crossing accidents, accidents to persons involving rolling stock in motion, fires, etc.).
Incident—O3. An incident is any occurrence, other than an accident or serious accident, and which is related to the traffic of trains or shunting rolling stock and affects the safety of railway traffic.
Killed persons—O4. Killed persons are any persons killed immediately or dying within 30 days as a result of an accident, serious accident or incident, except persons who committed suicide.
Injured persons—O5. Injured persons are any persons injured who were hospitalized for more than 24 h as a result of an accident, serious accident or incident, except suicide attempt.
Table 3 shows the values of all DMUs in relation to output parameters.