Abstract
The goal of this investigation is to explore the influence of viscous dissipation and Brownian motion on Jeffrey nanofluid flow over an unsteady moving surface with thermophoresis and mixed convection. Zero mass flux is also addressed at the surface such that the nanoparticles fraction of maintains itself on huge obstruction. An aiding transformation is adopted to renovate the governing equations into a set of partial differential equations which is solved using a new fourth-order finite difference continuation method and various graphical outcomes are discussed in detail with several employed parameters. The spectacular influence of pertinent constraints on velocity and thermal curves are inspected through various plots. Computational data for the heat transfer rate and skin-friction coefficient are also reported graphically. Graphical outcomes indicate that an augmentation in buoyance ratio and thermophoretic parameter leads to diminish the velocity curves and increase the temperature curves. Furthermore, it is inspected that escalating Deborah number exhibits increasing in the skin friction and salient decreasing heat transmission. Increasing magnetic strength leads to a reduction in the skin friction and enhancement in the Nusselt number, whilst a reverse reaction is manifested with mixed convection aspects.
1. Introduction
In modern times, the novel investigations of nanofluid flow through stretchable surfaces have got valuable attention among study scientists and community because of its abundant practical utilization, in several areas of science and biotechnology. Nanofluids play a momentous role in the mechanism of heat transfer. The typical base fluids, e.g., water, alcohol, ethylene glycol, and oil have a weak capacity to promote the heat transfer rate. However, this complex scenario was resolved by asserting the tiny sized solid fragments in the base fluids. It was basically proposed by Choi [1] that the tendency of the base fluids to embellish the thermal properties can be more effective by adding nanoparticles in these fluids. Nanofluids are spawned by dispersion of nanoparticles along with base fluids and these fluids are the amalgamations of suspended nano-sized pieces (1–100 nm) in base fluids. The constituents of nanoparticles may contain metals, carbides, nitrides, and oxides. With enhanced and improved thermal mechanism, nanofluids have huge applications containing microwave tubes, microelectronic chips engines, grinder machines, drag reduction, refrigerators, pharmacology, tumor and cancer therapy, gas recovery of boiler exhaust fuel, supersonic and ultrasonic fields, high power lasers, welding cooling, vehicle engine cooling, nuclear system cooling, and thermal storage capacity [2,3]. In a new era of research, the study community has made tremendous efforts to enrich the experimental work, theoretical models, and numerical simulations of magneto-nanofluids. The characteristics of radiation impact on the stretched magneto-flow of non-Newtonian nanofluid were explored by Kumar et al. [4]. The hybrid linearization differential quadrature method was utilized to scrutinize the magneto-nanofluid flow past a radiative surface with streamwise diversity in wall temperature reported by EL-Zahar et al. [5]. Many investigators [6,7,8,9,10,11,12,13,14] to undertake the nanofluids flow past various configurations and geometries.
Lately, there have been serious developments in studying the non-Newtonian fluid flows. The non-Newtonian fluids are viscoelastic in nature, such as oils, paints, ketchup, and fluid polymers, all of which show some amazing marvels. Improving enthusiasm of numerous researchers has elucidated that these flows are imperative in industry, food and paper production, polymer processing, and technology that these flows are important. The rheological characteristics of fluids are indicated by their purported constitutive equations. The pattern of liquid under examination is Jeffrey liquid. This pattern has a time derivative instead of the convected derivative. Sandeep et al. [15], Dalir et al. [16], Hayat et al. [17], and Shehzad et al. [18] investigated the magneto-Jeffery nanofluid flow with several aspects. Raju et al. [19] communicated the magneto-Jeffrey nanofluid flow over a radiated cone with thermophoresis and Brownian impacts. Hayat et al. [20] examined Jeffrey nanoliquid flow and heat transmission through a stretchable cylinder. Nadeem and Saleem [21] addressed analytically the unsteady rotating Jeffrey nanofluid flow on rotating cone by unsteady mixed convection. Zin et al. [22] explained the magneto-rotating Jeffrey nanoliquid through a vertical disk in a permeable medium. Hsiao [23,24,25,26] examined significant investigations about magneto-mixed convection of non-Newtonian nanofluid flows.
The major goal of the current work is to model the effectiveness of viscous dissipation and Brownian motion together on Jeffrey-nanofluid flow owing to an unsteady moving surface with thermophoresis. To the researcher’s knowledge, there is no discussion of Jeffrey-nanofluid flow across the unsteady stretchable surface with thermophoresis. Furthermore, the roles of nanofluids parameters and Eckert and Deborah numbers have been computationally exhibited.
2. Modeling
Here, the magneto-mixed convection Jeffrey-nanofluid flow is treated cross over an unsteady vertical moving surface. Brownian motion characteristics are addressed through thermophoresis and dissipation effects. Constant magnetic strength, B0, is utilized perpendicular to the surface and zero nanoparticles mass flux is assumed. As proposed, the constant temperature at the surface Tw, whilst the ambient temperature field is T∞, and the concentration distribution is C∞. The flow sketch is exhibited in Figure 1. The flow under these attentions can be evaluated in the ensuing form:
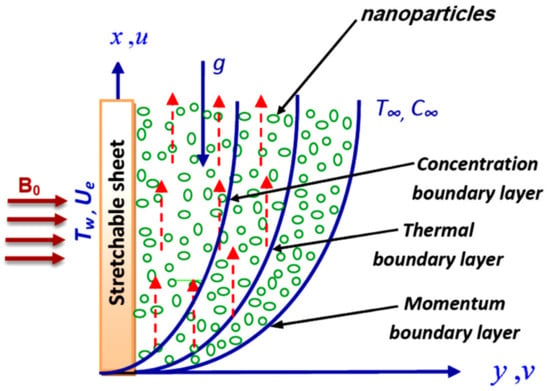
Figure 1.
The flow pattern geometry.
The corresponding initial and boundary conditions are:
Note that u and v characterize the flow velocities in x- and y-trends respectively while υ = μ/ρ, μ, ρ describe kinematic viscosity, dynamic viscosity, and density of base liquid respectively. The symbols g are for gravity g, and λ1 for retardation time; λ2 for the ratio of relaxation to retardation times; σ symbolizes the electrical conductivity; B0 symbolizes the magnetic field; T the temperature; αm = k/(ρC)f, k, (ρC)f, (ρC)p symbolize the thermal diffusivity, thermal conductivity, liquid heat capacity, and nanoparticles effective heat capacity; is the nanofluid heat capacity ratio, DB the Brownian diffusion coefficient, DT for the thermophoretic diffusion coefficient; and T and C for fluid temperature and concentration, respectively.
Launching the dimensionless variables as:
into Equations (1)–(5) gives us the following dimensionless equations:
The transformed initial and boundary conditions become:
where designates differentiation concerning the transformed transverse coordinate, η. The parameters in Equations (7)–(10) are defined as follows:
where Nb symbolizes the Brownian motion parameter, Nt symbolizes the thermophoresis parameter, Nr reflects the buoyancy ratio parameter, Sc reflects the Schmidt number, β relates the Deborah number, Ec symbolizes the Eckert number, λ symbolizes the mixed convection parameter, Grx and Rex define the Grashof and Reynolds numbers, respectively, Ha reflects the Hartmann number, and Pr symbolizes the Prandtl number.
The quantities of engineering interest in dimensionless form skin friction and Nusselt number may be defined as:
3. Fourth-Order Finite Difference Continuation Method (FFDCM)
The partial differential equations (PDE) system (7)–(10) has a multi-scale solution behavior over an infinite interval where the solution varies quickly over the boundary layer and away from this layer the solution varies slowly and behaves regularly and that is according to the time constants of the solution components. Moreover, the PDE system (7)–(10) is very sensitive to the initial conditions due to the singularity associated with the highest derivative-term in the system and hence more accurate and efficient adaptive methods are required for solving this class of PDE systems [5,27,28,29,30,31,32]. System (7)–(10) is converted into a first-order PDE system and discretized using a fourth-order finite difference method in -orientation and a two-point backward finite difference method [28] in -orientation. The solution is obtained through a continuation technique in -orientation. We will denote the suggested method as fourth-order finite difference continuation method (FFDCM).
By defining system (7)–(10) can be rewritten as:
with boundary conditions (BCs)
The mesh grid-points () of the problem are defined by:
where , and are the step-size and the number of subintervals in and - orientations, respectively. Applying FFDCM on PDE system (14) results in the following system of algebraic equations.
where is the fourth-order finite-difference differentiation matrix defined in [27], and are the solution vectors , , respectively, , and is the coordinate vector .
BCs (15) are inserted into the system (17) as follows:
The nonlinear algebraic system (17)–(18) is solved at each line using the nonlinear built-in MATLAB solver ‘fsolve’ with an initial guess satisfying the BCs(10) such as:
The solution of (17)–(18) is obtained through a continuation technique in - orientation taking as our continuation parameter. Starting with an initial estimation of the parameter and the initial guess , an estimate solution is obtained for system (17)–(18) which is taken as a new initial guess to get a new estimate solution for system (17)–(18) after adding an increment in the continuation parameter and the process is repeated as shown in Figure 2. The continuation technique is stopped at:
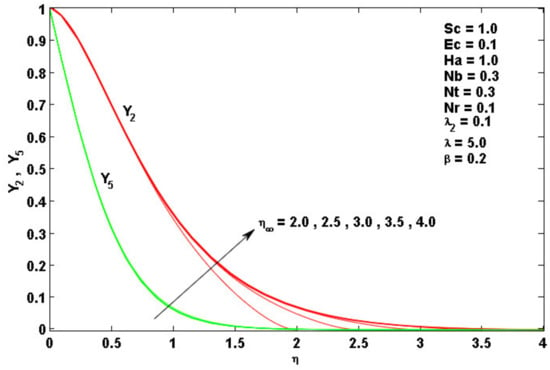
Figure 2.
The continuation process on for solving system (17)–(18) using .
The numerical results are obtained at , using absolute tolerance and relative tolerance for the nonlinear Matlab solver ‘fsolve’.
Table 1 shows the good agreement between the numerical results obtained by FFDCM and Ishak et al. [33] approach for different values of λ and Pr for at τ = 1.0 (steady-state flow).

Table 1.
Comparison of and for different values of λ and Pr for at τ = 1.0 (steady-state flow).
4. Discussion
This precise segment is dispensed to analyze the magneto-mixed convection and heat transport characteristics for convection Jeffrey-nanofluid flow towards an unsteady vertical moving surface. The graphical explanation is deliberated and the variation of velocity, temperature, skin friction and Nusselt number for various thermophysical parameters are characterized in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 and those parameters are fixed at β = 0.2, Nb = 0.5, Nt = 0.3, Nr = 0.1, Sc = 1.0, Ec = 0.1, λ = 5.0, Ha = 1.0, λ2 = 0.1 and Pr = 6.8.
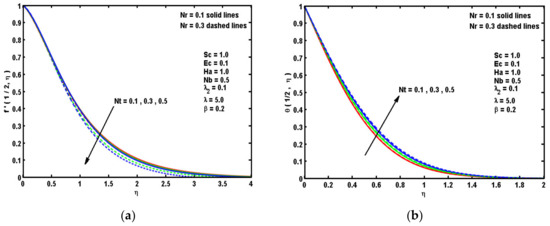
Figure 3.
Impacts of Nr and Nt on (a) and (b) .
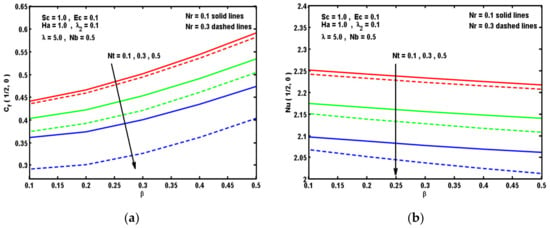
Figure 4.
Impacts of Nr and Nt on (a) Cf(τ,0) and (b) Nu(τ,0).
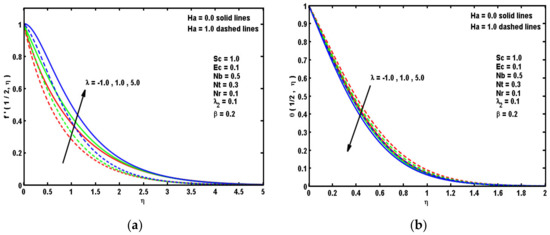
Figure 5.
Impacts of λ and Ha on (a) and (b) .
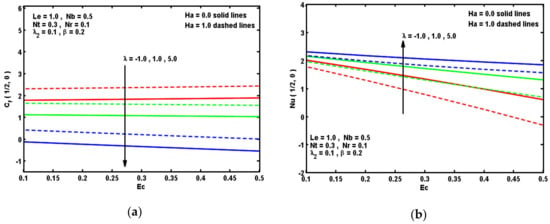
Figure 6.
Impacts of λ and Ha on (a) Cf(τ,0) and (b) Nu(τ,0).
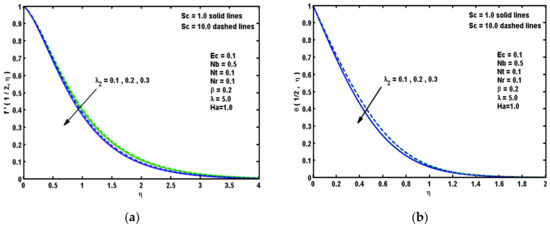
Figure 7.
Impacts of Sc and λ2 on (a) and (b) .
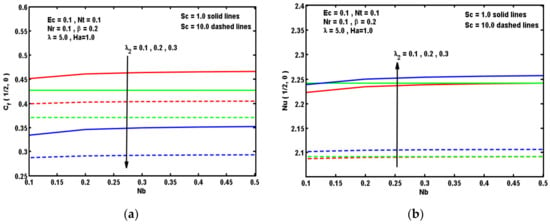
Figure 8.
Impacts of Sc and λ2 on (a) Cf(τ,0) and (b) Nu(τ,0).
The nature of velocity and temperature curves for magnifying the buoyance ratio Nr and thermophoretic Nt is pointed out in Figure 2b and Figure 3a. It is manifested that velocity diminishes with the augmentation of Nr and Nt, and this phenomenon yields an increase in temperature curves ability that boosts the thermal boundary. This is due to the reality that greater values of Nr boost the temperature fluid. Figure 4a,b uncovers the impacts of Nr and Nt on skin friction coefficient Cf(τ,0) and the local Nusselt number Nu(τ,0) with several values of β. It is observed that both of Cf(τ,0) and Nu(τ,0) diminish sufficiently for physical parameters Nr and Nt. This because the thermophoresis strength triggers the nanoparticles to transmit the warm sheet to cold sheet which creates the thermal related boundary layer thickness to magnify. In addition, an enlarge in β corresponds to an enhancement in the Cf(τ,0) and salient reduction in Nu(τ,0). This is because a weaker Deborah number, β, gives a viscous impact compared to the elastic impact, whilst a greater β exhibits in the elastically solid material in nature which leads to a reduction in Nusselt number.
The nature of velocity and temperature curves against mixed convection parameter λ and Hartmann number Ha are sketched in Figure 5a,b. From these curves, it is concluded that intensifying λ improving the flow velocity and decaying the temperature curves. Because when growing λ, the impact of gravity is decreased, and then velocity within a boundary layer decreases. In addition, it is shown that the sway of magnetic strength reduces the fluid movement. This is realistic because magnetic strength is responsible to inspire Lorentz intensity which resists the fluid motion. Figure 6a,b determines the Cf(τ,0) and Nu(τ,0) against the λ and Ha with several values of Ec. It is noticed that Nu(τ,0) enhances but Cf(τ,0) reduces for the improved values of Ha, while an opposite reaction is found with λ. The reason, as mentioned above, is that Ha has a tendency to magnify the Lorentz intensity. This intensity resists the fluid movement and provides heat ability in the flowing. Furthermore, it is clear that an elevation in Ec results in an enhancement in the internal source of energy which boosts the thermal boundary layer, which results in a reduction in the Nusselt number for greater Ec.
Figure 7a,b are plotted to analyze the impacts of the ratio of relaxation to retardation times λ2 and Schmidt number Sc on velocity and temperature curves. It is apparent that both of velocity and temperature curves decline with the enhancement in λ2 parameter while opposite results are obtained for the intensity of Sc. The consequences of Sc and λ2 on Cf(τ,0) and Nu(τ,0) on along with Nb is visualized in Figure 8a,b. It is observed that Cf(τ,0) reduces and Nu(τ,0) enhances by augmenting λ2. Moreover, both Cf(τ,0) and Nu(τ,0) reduce sufficiently by enlarging Sc. This may occur owing to the cause that Schmidt number is reversely symmetrical to the Brownian diffusion coefficient. This Brownian diffusion coefficient becomes lower corresponding to the greater values of Sc and also Brownian movement happens in the system of the nanofluid due to contact of nanoparticles with the regular fluid.
5. Conclusions
The effectiveness of Brownian motion and viscous dissipation on magneto-mixed convection flow of Jeffrey nanofluid through an unsteady moving surface is examined with thermophoresis. An aiding transformation is adopted to renovate the governing equations into a set of PDEs which are sensitive to the initial conditions due to the singularity associated with the highest derivative-term and so the numerical solution is gotten with the aid of a new FFDCM and various graphical outcomes are discussed in detail with several employed parameters.
- A comparative investigation among the current outcomes and the former cited investigation are explored to trust our outcomes and a notable agreement is observed. The following observations are structured for the current investigation:
- Augmentation in buoyance ratio and thermophoretic parameters leads to diminish the velocity curves and increase the temperature curves ability that boosts the thermal boundary.
- A greater Deborah number exhibits increasing skin friction and salient decreasing heat transmission.
- The Nusselt number enhances and skin friction reduces for the improved magnetic strength, while an opposite reaction is found with mixed convection aspects.
- Both velocity and temperature curves decline with the enhancement in the ratio of relaxation to retardation times while opposite results are obtained for the intensity of Schmidt number.
Author Contributions
Conceptualization, A.M.R., E.R.E.-Z. and L.F.S.; software, E.R.E.-Z. and L.F.S.; validation, A.M.R., E.R.E.-Z. and L.F.S.; formal analysis, A.M.R.; investigation, A.M.R. and E.R.E.-Z. resources, E.R.E.-Z. and L.F.S.; data curation, A.M.R.; writing—original draft preparation, A.M.R., E.R.E.-Z. and L.F.S.; writing—review and editing, A.M.R.; E.R.E.-Z. and L.F.S.; supervision, L.F.S and E.R.E.-Z.; project administration, L.F.S. and E.R.E.-Z.; funding acquisition, L.F.S. and E.R.E.-Z. All authors have read and agreed to the published version of the manuscript.
Funding
This project was supported by the Deanship of Scientific Research at Prince Sattam bin Abdulaziz University under the research project No. 2020/01/16595.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab.: Lemont, IL, USA, 1995.
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Kumar, K.G.; Ramesh, G.K.; Gireesha, B.J.; Rashad, A.M. On Stretched Magnetic Flow of Carreau Nanofluid with Slip Effects and Nonlinear Thermal Radiation. Nonlinear Eng. 2019, 8, 340–349. [Google Scholar] [CrossRef]
- EL-Zahar, E.R.; Rashad, A.M.; Seddek, L.F. The Impact of Sinusoidal Surface Temperature on the Natural Convective Flow of a Ferrofluid along a Vertical Plate. Mathematics 2019, 7, 1014. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Rashad, A.M. MHD Forced Convection Flow of a Nanofluid Adjacent to a Non-isothermal Wedge. Comput. Therm. Sci. 2014, 6, 27–39. [Google Scholar] [CrossRef]
- Murthy, P.V.S.N.; RamReddy, C.; Chamkha, A.J.; Rashad, A.M. Significance of Viscous Dissipation and Chemical Reaction on Convective Transport In A Boundary Layer Stagnation Point Flow Past A Stretching/Shrinking Sheet In A Nanofluid. J. Nanofluids 2015, 4, 214–222. [Google Scholar] [CrossRef]
- EL-Zahar, E.R.; Rashad, A.M.; Gelany, A.M. Studying High Suction Effect on Boundary-Layer Flow of a Nanofluid on Permeable Surface via Singular Perturbation Technique. J. Comput. Theor. Nanosci. 2015, 12, 4828–4836. [Google Scholar] [CrossRef]
- Reddy, P.B.A. Magnetohydrodynamic flow of a Casson fluid over an exponentially inclined permeable stretching surface with thermal radiation and chemical reaction. Ain Shams Eng. J. 2016, 7, 593–602. [Google Scholar] [CrossRef]
- Rashad, A.M.; Mallikarjuna, B.; Chamkha, A.J.; Raju, S.H. Thermophoresis Effect on Heat and Mass Transfer from A Rotating Cone In A Porous Medium With Thermal Radiation. Afr. Mat. 2016, 27, 1409–1424. [Google Scholar] [CrossRef]
- Sheikholeslami, L.Z.M.; Chamkha, A.J.; Raizah, Z.A.; Saleem, S. Control volume finite element method for nanofluid MHD natural convective flow inside a sinusoidal annulus under the impact of thermal radiation. Comput. Methods Appl. Mech. Eng. 2018, 338, 618–633. [Google Scholar]
- Nasir, S.; Islam, S.; Gul, T.; Khan, Z.S.; Khan, M.A.; Khan, W.; Khan, S. Three-dimensional rotating flow of MHD single wall carbon nanotubes over a stretching sheet in presence of thermal radiation. Appl. Nanosci. 2018, 8, 1361–1378. [Google Scholar] [CrossRef]
- Alwawi, F.A.; Alkasasbeh, H.T.; Rashad, A.M.; Idris, R. MHD Natural Convection of Sodium Alginate Casson Nanofluid Over A Solid Sphere. Results Phys. 2020, 16, 102818. [Google Scholar] [CrossRef]
- Nabwey, H.A.; Khan, W.A.; Rashad, A.M. Lie Group Analysis of Unsteady Flow of Kerosene/Cobalt Ferrofluid Past A Radiated Stretching Surface with Navier Slip and Convective Heating. Mathematics 2020, 8, 826. [Google Scholar] [CrossRef]
- Sandeep, N.; Sulochana, C.; Isaac Lare, A. Stagnation-point flow of a Jeffrey nanofluid over a stretching surface with induced magnetic field and chemical reaction. Int. J. Eng. Res. Afr. 2015, 20, 93–111. [Google Scholar] [CrossRef]
- Dalir, N.; Dehsara, M.; Salman Nourazar, S. Entropy analysis for magnetohydrodynamic flow and heat transfer of a jeffrey nanofluid over a stretching sheet. Energy 2015, 79, 351–362. [Google Scholar] [CrossRef]
- Hayat, T.; Imtiaz, M.; Alsaedi, A. Magnetohydrodynamic stagnation point flow of a Jeffrey nanofluid with newtonian heating. J. Aerosp. Eng. 2016, 29, 04015063. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Abdullah, Z.; Alsaedi, A.; Abbasi, F.M.; Hayat, T. Thermally radiative three-dimensional flow of jeffrey nanofluid with internal heat generation and magnetic field. J. Magn. Magn. Mater. 2016, 397, 108–114. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Jayachandra Babu, M.; Sandeep, N. Chemically reacting radiative MHD Jeffrey nanofluid flow over a cone in porous medium. Int. J. Eng. Res. Afr. 2015, 19, 75–90. [Google Scholar] [CrossRef]
- Hayat, T.; Asad, S.; Alsaedi, A. Analysis for flow of Jeffrey fluid with nanoparticles. Chin. Phys. B 2015, 24, 044702. [Google Scholar] [CrossRef]
- Nadeem, S.; Saleem, S. An optimized study of mixed convection flow of a rotating Jeffrey nanofluid on a rotating vertical cone. J. Thermophys. Heat Transf. 2015, 12, 3028–3035. [Google Scholar] [CrossRef]
- Zin, N.A.M.; Khan, I.; Shafie, S.; Alshomrani, A.S. Analysis of heat transfer for unsteady MHD free convection flow of rotating Jeffrey nanofluid saturated in a porous medium. Results Phys. 2017, 7, 288–309. [Google Scholar]
- Hsiao, K.L. To promote radiation electrical MHD activation energy thermal extrusion manufacturing system efficiency by using Carreau-Nanofluid with parameters control method. Energy 2017, 130, 486–499. [Google Scholar] [CrossRef]
- Hsiao, K.L. Combined electrical MHD heat transfer thermal extrusion system using Maxwell fluid with radiative and viscous dissipation effects. Appl. Therm. Eng. 2017, 112, 1281–1288. [Google Scholar] [CrossRef]
- Hsiao, K.L. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 2017, 112, 983–990. [Google Scholar] [CrossRef]
- Hsiao, K.L. Stagnation electrical MHD nanofluid mixed convection with slip boundary on a stretching sheet. Appl. Therm. Eng. 2016, 98, 850–861. [Google Scholar] [CrossRef]
- Habib, H.M.; El-Zahar, E.R. An algorithm for solving singular perturbation problems with mechanization. Appl. Math. Comput. 2007, 188, 286–302. [Google Scholar] [CrossRef]
- Burden, L.R.; Faires, J.D.; Reynolds, A.C. Numerical Analysis: Teachers Manual to Accompany; Prindle Weber Schmidt: Boston, MA, USA, 1981. [Google Scholar]
- Roberts, S.M.; Shipman, J.S. Continuation in shooting methods for two-point boundary value problems. J. Math. Anal. Appl. 1967, 18, 45–58. [Google Scholar] [CrossRef]
- Kotamraju, G.R.; Akella, M.R. Stabilized continuation methods for boundary value problems. Appl. Math. Comput. 2000, 112, 317–332. [Google Scholar] [CrossRef]
- EL-Zahar, E.R.; AL-Gelany, A.M.; Rashad, A.M. Sinusoidal Natural Convective Flow of Non-Newtonian Nanoliquid over a Radiative Vertical Plate in a Saturated Porous Medium. IEEE Access 2020, 8, 136131–136140. [Google Scholar]
- EL-Zahar, E.R.; Rashad, A.M.; Saad, W.; Seddek, L.F. Magneto-Hybrid Nanofluids Flow via Mixed Convection past a Radiative Circular Cylinder. Sci. Rep. 2020, 10, 10494. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Unsteady Mixed Convection Boundary Layer Flow Due To A Stretching Vertical Surface. Arab. J. Sci. Eng. (Springer Sci. Bus. Media BV) 2006, 31, 2B. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).