1. Introduction
The occurrence of extreme events such as extreme temperatures, excess flood peaks, and rapid increases in pollutant concentrations has steadily increased over the past decade. However, the volume of data generated by such events is relatively small compared to big data generated by normal events occurring daily. In this case, providing accurate predictions for extreme events might be a challenging task due to the insufficient number of past records. Bayesian methods may be more suitable for modeling data to small sample sizes with skewness or lack of symmetry as in the case of record values, provided that the Bayesian method involves a reasonable choice for the prior distribution because the Bayesian methods do not rely on asymptotic theory in the same way that frequentist methods do.
The concept of record values was introduced by Chandler [
1] and it can be described as follows. Let
be a sequence of independent and identically distributed random variables. Then, for every
,
is called the upper (lower) record value if
, which indicates that
is higher (lower) than all previous observations. That is, the upper (lower) record values include the members of a series that are larger (smaller) than all preceding members. The indices for which upper record values occur are informed by the record times
, where
,
, with
. The record times for the lower record values are
, where
, with
. Therefore, the sequences of the upper and lower record values are denoted as
and
, respectively, from the original sequence
.
Since such record values arise in many real-world situations related to climate, economics, sports, and life test, relevant studies have been conducted in various fields. Coles and Tawn [
2] analyzed a daily rainfall series for modeling the extremes of the rainfall process in the context of record values. Madi and Raqab [
3] analyzed average temperatures in Neuenburg, Switzerland, using a Bayesian predictive method for record values from the Pareto distribution. Wergen et al. [
4] analyzed both the probability of occurrence and PDF of record-breaking values for temperatures in Europe and the United States. Seo and Kim [
5] proposed an objective Bayesian inference method for record values from the Gumbel distribution, which was applied to the concentration analysis of sulfur dioxide. Seo and Kang [
6] proposed a estimation method using record values from an exponentiated half-logistic distribution in Bayesian and non-Bayesian perspectives. The authors demonstrated the efficiency of their method by comparing it to the existing estimation methods through rainfall data analysis.
This paper proposes a predictive method based on an objective Bayesian approach that can save the effort of finding an exact prior distribution when there is no sufficient information in the context of record statistics values from the exponentiated Gumbel distribution (EGD) with cumulative distribution function (CDF)
where
and
denote the scale and shape parameters, respectively. The EGD is a generalized version of the GD, which is the most widely applied statistical distribution in the extreme value analysis of extreme events such as global warming, floods, heavy rainfall, and high wind speeds. The EGD can be considered as being simply the
th power of the CDF of the GD with the scale parameter
. Therefore, the EGD can lead to an improved performance and applicability of models built over a variety of complex datasets compared to the GD. Note that it is possible to apply time-series techniques if no data are lost during acquiring record values since the lower record time
is the serial number of record values in an infinite time series. For comparison with the proposed objective Bayesian predictive method, two types of time-series models are considered in this study: the autoregressive integrated moving average (ARIMA) model introduced by Box et al. [
7] and the dynamic linear model (DLM) developed by West and Harrison [
8].
The rest of the paper is organized as follows.
Section 2 presents objective priors for unknown parameters of the EGD in the context of record statistics values, along with the corresponding posterior analysis and predictive method.
Section 3 provides a brief description of the ARIMA and DLM that are employed in this study as benchmarks to validate the proposed objective Bayesian method.
Section 4 presents the results of applying both the time-series and objective Bayesian models to real data.
Section 5 concludes this paper.
2. Bayesian Prediction
The aim of this study is to predict future lower record values based on an objective Bayesian approach. To accomplish this, an objective Bayesian approach that does not require determining hyperparameters is presented first. The following subsection introduces objective priors based on the Fisher information (FI) matrix for unknown parameters of the EGD with the CDF (
1).
2.1. Objective Prior
Let
be the lower record values from the CDF (
1). Then, the corresponding likelihood function and its natural logarithm can be expressed as
and
respectively. For computational convenience, let
=
. Then, based on the log-likelihood (
2), the FI matrix for
can be defined as follows.
Proposition 1. The FI matrix for is of the formwhereand and are the digamma and trigamma functions, respectively. Proof. In the FI matrix
the element
can be easily computed, while the other elements can be expressed as
and
Then, the proof is completed given the marginal density function of
defined in Ahsanullah [
9] as
and assuming
. □
The objective priors such as the Jeffreys and reference priors based on the FI matrix (
3) are defined according to the following theorem.
Theorem 1. The Jeffreys prior for is Proof. According to the definition of the Jeffreys prior (Jeffreys [
10]), it follows that
where
denotes the determinant of the FI matrix (
3). This completes the proof. □
In the following, the reference priors for each parameter of interest are derived from the algorithm provided in Berger and Bernardo [
11].
Theorem 2. If λ is the parameter of interest, the reference prior for isand, if θ is the parameter of interest, the reference prior for is Proof. When
is the parameter of interest, the conditional prior distribution of
given
can be defined based on the FI matrix (
3) as
Then, by choosing a sequence of compact sets
for
such that
,
,
as
, it follows that
and
In addition, the marginal reference prior for
can be defined based on the FI matrix (
3) and (
4) as
which leads to the following reference prior:
for any fixed point
. When
is the parameter of interest, the same argument is applied.
In addition, the marginal reference prior for
can be expressed as
from which the reference prior can be expressed as
for any fixed point
. This completes the proof. □
Note that, since all the derived objective priors are improper, the corresponding posterior distribution should be proved to be proper. Since the Jeffreys prior and reference prior have the same form, the notation is used from now on.
2.2. Posterior Analysis
Let
be the observed lower record values. Then, the objective prior
results in the following marginal posterior density functions of
and
:
and
respectively. Note that the marginal posterior distribution of
has a gamma distribution with the parameters
k and
. Then, the Bayes estimators under the squared error loss function from the marginal posterior density functions (
5) and (
6) can be expressed as
and
respectively.
In terms of
, the corresponding marginal posterior density function can be expressed as
Since it is the PDF of an inverse gamma distribution with the parameters
k and
, the Bayes estimator of
under the squared error loss function can be expressed as
Theorem 3. From the Frequentist perspective, the estimator is an unbiased estimator of σ.
Proof. According to Lemma 2 provided in Wang and Ye [
12], independent and identically distributed random variables from the uniform distribution on
are defined as
where
are independent random variables having
distributions with
degrees of freedom. Then, the estimator
has a gamma distribution with the parameters
and
for any
because
has a gamma distribution with the parameters
and 1. This completes the proof. □
The highest posterior density (HPD) credible intervals (CrIs) for
and
can be constructed by generating the MCMC samples from the marginal posterior density functions (
5) and (
6), respectively. However, since the marginal posterior density function (
5) is not a well-known probability distribution, sampling from it is a difficult task. Instead, sampling can be indirectly performed from the relationship
because the conditional posterior distribution
has a gamma distribution with the parameters
k and
. To achieve this,
should be generated from its marginal posterior distribution first, and then
should be generated from its conditional posterior distribution given the generated value of
. Finally,
can be computed. Then, the
equal-tails (ETs) and HPD CrIs can be constructed for
using the method proposed in Chen and Shao [
13].
Under the prior , the resulting posterior is proper because . However, since it is not possible to express it in a closed form as we know it, MCMC samples for and can be generated using the Metropolis–Hastings algorithm. For efficient mixing, the proposal variance-covariance structure is updated adaptively. For the corresponding Bayes estimators under the squared error loss function, the notations and are used.
2.3. Prediction
Let
be the future lower record values. Since the sequence
,
is a Markov chain, the conditional density function of
given
is the same as that of
given
. That is, it follows that
by Ahsanullah [
9]. Then, for the EGD with the CDF (
1), (
7) becomes
and the corresponding Bayesian predictive density function can be expressed as
where
is a general joint posterior distribution for
.
Note that it requires very complex and tedious computations. In fact, there is no guarantee that it can be expressed in a closed form. Instead, a much simpler approach is to use the pivotal quantity that can be obtained by the transformation of a random variable.
Let
in the conditional density function (
8). Then, it has a gamma distribution with the parameters
and 1 with a PDF of
because
maps onto
and the Jacobian of the transformation is
which leads to the following algorithm for generating the MCMC samples
.
- Step 1a.
Generate from the gamma distribution with the parameters and 1.
- Step 1b.
Generate and from the joint posterior distribution .
- Step 2.
- Step 3.
Repeat steps 1 and 2, N times.
Then, the corresponding
predictive interval (PI) for
can be constructed using the method proposed in [
13] as in the case of
and
. For the purpose of clarity,
and
are used to denote future lower record values under the priors
and
, respectively.
3. Time Series Approach
Providing that record values are observed from time series of uncorrelated random variables sampled from continuous probability distributions, the proposed Bayesian method presented in the previous section is compared to the ARIMA and DLM time-series techniques as described below.
The ARIMA model is the most widely used approach to time-series forecasting. Conventionally, it is defined using three components (p, d, q), where
p denotes the order of the autoregressive (AR) term
d denotes the number of differencing required to make the time series stationary
q denotes the order of the moving average (MA) term.
Here, the autoregressive (AR) process assumes that the current value of the series
can be expressed as a function of
p past values
in a form of
for
, where
,
is the mean of this process,
are constants
, and
is a weak white noise series with a mean of zero and a variance of
. The MA process uses past forecast errors expressed as
that is, a weighted average of the past values of the white noise process
. Then, the time series
is an ARIMA
process if
is ARMA
obtained by combing the AR and MA terms, where
is the
dth-order differencing operator. For non-stationary data, one usually fits an ARMA model after taking differences for the data until stationarity is achieved.
The second time-series approach considered in this study for comparison with the proposed method is the DLM. Let
be an
m-dimensional vector observed at time
t, while
be a generally unobservable
p-dimensional state vector of the system at time
t. Then, the DLM can be defined as
for each time
together with a prior distribution for the
p-dimensional state vector at time
,
, where
and
are known matrices of
and
, respectively, and
and
are variance matrices. Furthermore, it is assumed that the error sequences
and
are independent, and independent of
.
Note that the lower record value from a univariate time series has a strong trend of decreasing through time. Therefore, a DLM with
is considered, namely, the linear growth model (LGM)
where
and
denote the local level and local growth rate at time
t, respectively, and
,
, and
denote uncorrelated errors.
4. Sulfur Dioxide Data
This section demonstrates the superiority of the proposed Bayesian method by comparing it to the ARIMA and DLM methods.
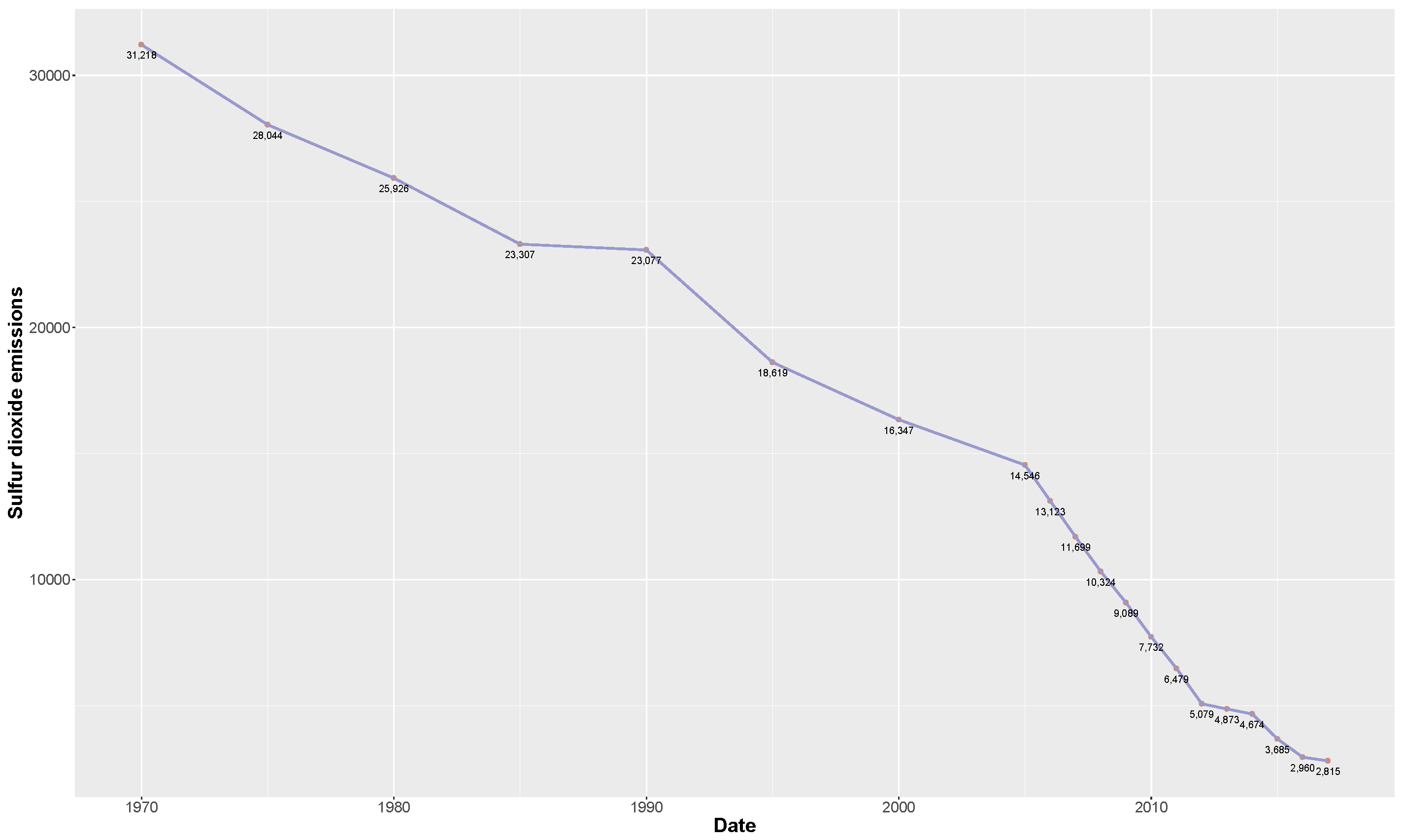
The three methods are applied to the time-series data representing sulfur dioxide emissions in the United States (U.S.) from 1970 to 2017 (in 1000 tons) measured by the U.S. Environmental Protection Agency. Due to the implementation of the Acid Rain Program created under Title IV of the 1990 Clean Air Act, sulfur dioxide emissions have decreased significantly over the last decades through a cap and trade program for fossil-fuel powered plants. The observed volume of sulfur dioxide emissions and its descriptive statistics are presented in
Figure 1 and
Table 1, respectively. Note that each data point was divided by 1000 for computational convenience; given that the data continued to decrease during the observation period as shown in
Figure 1, they were all used without losing data during acquiring the lower record values.
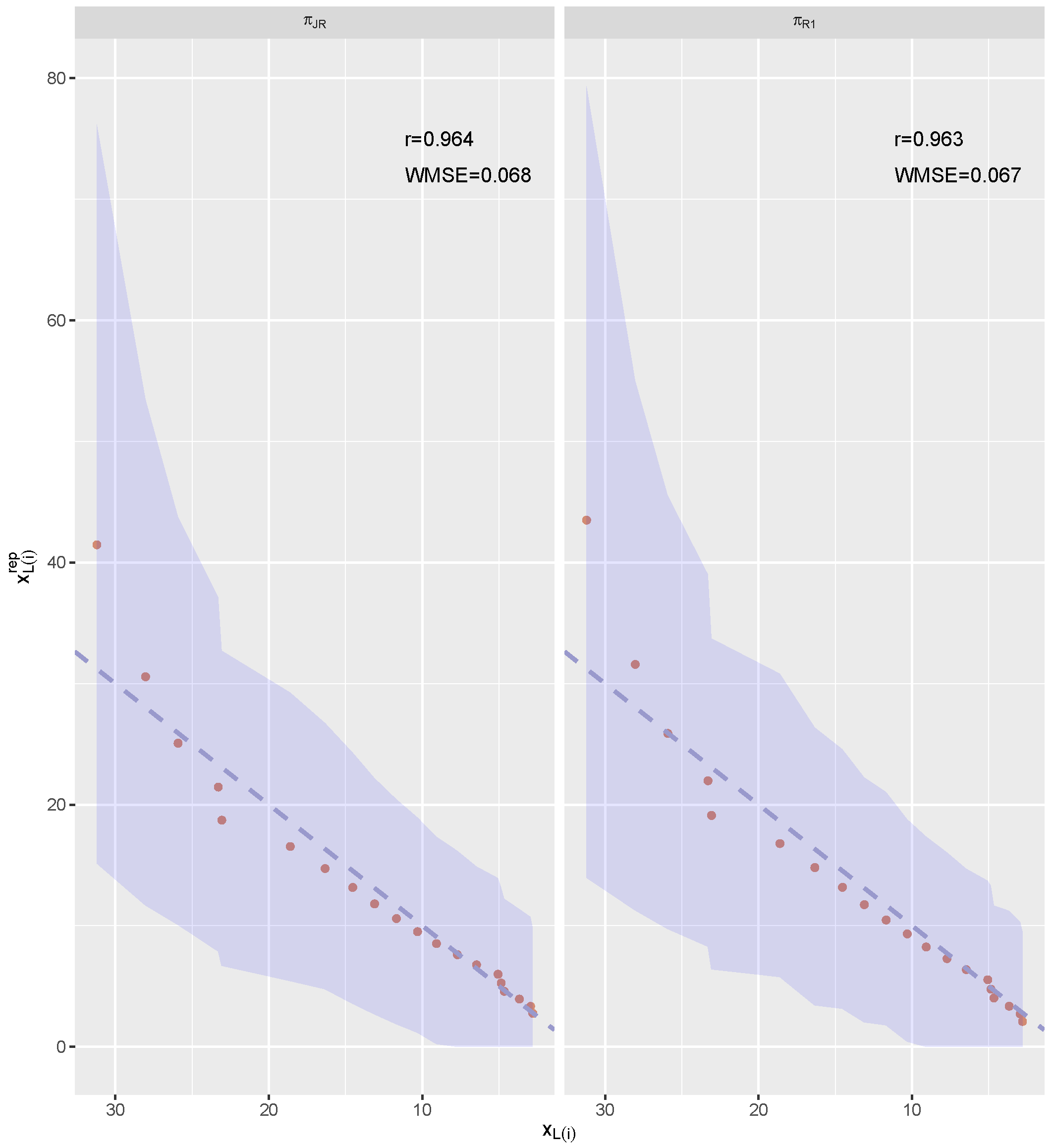
To conduct the goodness-of-fit test for the observed sulfur dioxide data, the replicated data are first considered. If the estimated model is adequate, then it should look similar to the observed data. The replicated data are generated from the Bayesian predictive function
and denoted as
for
. Under each prior distribution, the correlation coefficient of the mean
and observed lower record values
r can then be computed. For further examination, the weighted mean squared error (WMSE)
is also computed. These results are reported in
Figure 2.
It can be noticed from
Figure 2 that the estimated models fit the observed sulfur dioxide lower record values very well, and the estimated models under the priors
and
provide almost the same results for the considered statistical criteria.
Table 2 reports the estimation results for the derived priors for comparison and corresponding maximum likelihood counterparts. For the maximum likelihood procedure, the maximum likelihood estimators (MLEs)
and
are obtained by maximizing the log-likelihood function (
2), while the approximate
confidence intervals (CIs) are calculated based on the MLEs as
where
denotes the upper
percentile point of the standard normal distribution, and
and
are the diagonal elements of the asymptotic variance-covariance matrix of the MLE obtained by inverting the Fisher information matrix (
3). For the shape parameter
, the Bayes estimate
has a slightly lower value than the other estimates
and
that have almost the same values. However, the
HPD CrI under the prior
has the shortest length. For the scale parameter
, all estimates vary slightly, while the approximate
CI based on the
has a shorter length than the other CrIs have.
For prediction, the last lower record value is assumed to be known. As mentioned earlier, since no data are lost during acquiring the observed lower record values, the time-series analysis outlined in
Section 3 can be conducted at the same time.
Table 3 reports the prediction results for the next lower record value
. The R package
dlm (Petris [
14]) was used to estimate the parameters and state vector in the LGM (
9) with
In addition, for the ARIMA model, ARIMA
was chosen as the best model in terms of the corrected Akaike Information Criterion (AICc), indicating that it has the smallest AICc value when
with
after differencing the data twice. The forecast accuracy are evaluated in terms of the mean absolute deviation (MAD), the mean square error (MSE), and the mean absolute percentage error (MAPE), defined respectively as
where
and
is a point forcast of
. In this example,
and
. These results are reported in
Table 4, which indicates that there is little difference in the predictive performance of the two models.
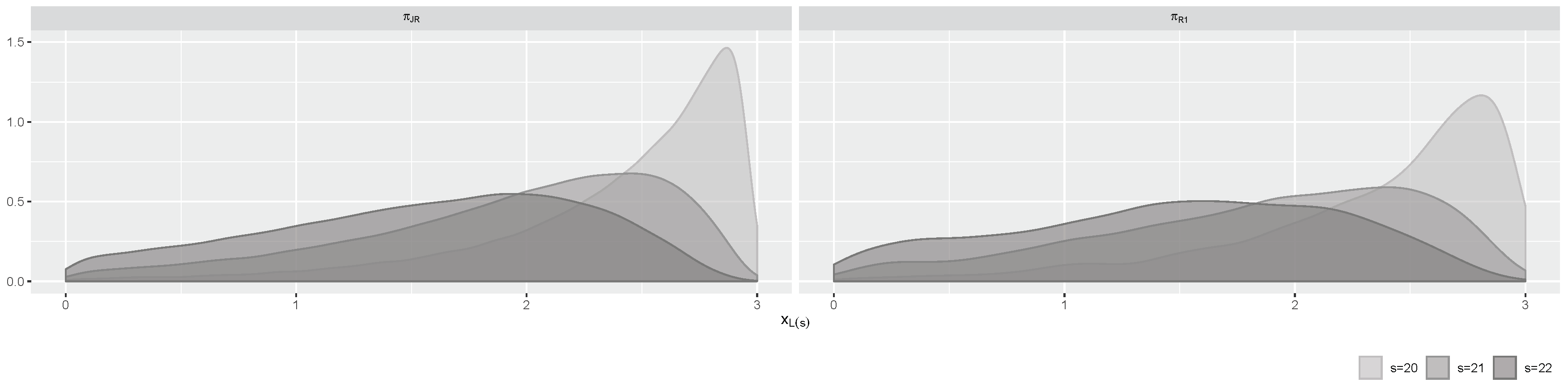
Table 3 shows that the proposed Bayesian PI has a shorter length than those obtained for the considered time-series ARIMA model and DLM, especially under the prior
. That is, the predictive result under the prior
shows the best performance in terms of uncertainty. Using the best performing Bayesian predictive model in terms of uncertainty, the Bayesian predictive density functions for the three future record values are estimated as the kernel density functions based on their MCMC samples. The results are plotted in
Figure 3, which shows that both estimated Bayesian predictive models under the priors
and
have a greater variance as the future record time
increases.
5. Conclusions
This paper defined the Jeffreys and reference priors for unknown parameters of the EGD based on record values and proposed a Bayesian method for predicting future record values. The method makes it very easy to generate MCMC samples for prediction. To validate the proposed method, it was compared to two time-series approaches, namely, the ARIMA model and DLM, using a sulfur dioxide emissions dataset. The results of the comparison demonstrated that the proposed method outperforms the time-series approaches in terms of uncertainty.
While there was no clear difference in the results of the goodness-of-fit tests among the proposed objective prior distributions when analyzing the observed data, the results of forecasting under the prior distribution were better than those under the prior distribution ; both derived prior distributions were proved to be valid.