Abstract
In this article, we propose a new modified extragradient-like method to solve pseudomonotone equilibrium problems in real Hilbert space with a Lipschitz-type condition on a bifunction. This method uses a variable stepsize formula that is updated at each iteration based on the previous iterations. The advantage of the method is that it operates without prior knowledge of Lipschitz-type constants and any line search method. The weak convergence of the method is established by taking mild conditions on a bifunction. In the context of an application, fixed-point theorems involving strict pseudo-contraction and results for pseudomonotone variational inequalities are considered. Many numerical results have been reported to explain the numerical behavior of the proposed method.
1. Introduction
Let be a nonempty, closed and convex subset of a real Hilbert space and be the sets of real numbers and natural numbers, respectively. Assume that f is a bifunction and denotes the solution set of an equilibrium problem over the set Now, consider the following definitions of a bifunction monotonicity (see [1,2] for more details). A function on for is said to be:
- (1)
- γ-strongly monotone if
- (2)
- monotone if
- (3)
- γ-strongly pseudomonotone if
- (4)
- pseudomonotone if
It is clear from the definitions mentioned above that they have the following consequences:
In general, the converses are not true. A bifunction is said to be Lipschitz-type continuous on if there exist two positive constants such that
Let be a nonempty closed convex subset of and be a bifunction with for all An equilibrium problem [1,3] for f on the set is to
An equilibrium problem (1) had many mathematical problems as a particular case, i.e., the variational inequality problems (VIP), optimization problems, fixed point problems, complementarity problems, the Nash equilibrium of non-cooperative games, saddle point problems and the vector optimization problem (for details see [1,4,5]). The equilibrium problem is also known as the famous Ky Fan inequality [3]. However, the particular format of an equilibrium problem (1) was initiated by Muu and Oettli [6] in 1992 and further investigation on its theoretical properties were provided by Blum and Oettli [1]. The construction of new iterative schemes and the modification of existing methods, as well as the study their convergence analysis, constitute an important research direction in equilibrium problem theory. Several methods have been developed in the past few years to approximate the solution of an equilibrium problem in finite and infinite dimensional real Hilbert spaces, i.e., extragradient methods [7,8,9,10,11,12,13,14,15,16], subgradient methods [17,18,19,20,21,22], inertial methods [23,24,25] and methods for particular classes of equilibrium problems [26,27,28,29,30,31,32,33,34,35].
In particular, a proximal method [36] was used to solve equilibrium problems based on solving minimization problems. This approach was also known as the two-step extragradient-like method in [7] due to the early contribution of the Korpelevich [37] extragradient method to solve the saddle point problems. More precisely, Tran et al. introduced a method in [7], and an iterative sequence was generated as follows:
where . The iterative sequence generated from the above-mentioned method provides a weak convergent iterative sequence and in order to operate it, prior information regarding the Lipschitz-type constants is required. These Lipschitz-type constants are mostly unknown or hard to compute. To overcome this situation, Hieu et al. [14] introduced an extension of the method in [38] for solving the equilibrium problem as follows: Let and choose with such that
where the stepsize sequence is updated in the following way:
Recently, Vinh and Muu proposed an inertial iterative algorithm in [39] to solve a pseudomonotone equilibrium problem. Their main contribution is the availability of an inertial effect in the algorithm that is used to improve the convergence rate of the iterative sequence. The iterative sequence has been generated in the following manner:
- (i)
- Choose while a sequence is satisfying the following condition:
- (ii)
- Choose such that where
- (iii)
- Determine
This article focuses on projection methods that are well-known and easy to execute due to their efficient and straightforward mathematical computation. Motivated by the works of [14,40], we formulate an inertial explicit subgradient extragradient algorithm to solve the pseudomonotone equilibrium problem. The proposed algorithm can be seen as the modification of the methods that appear in [7,14,39]. Under certain mild conditions, a weak convergence result has been proven to correspond to the iterative sequence of the algorithm. Moreover, experimental studies have shown that the proposed method tends to be more efficient compared to the existing method [39].
The remainder of this paper is arranged as follows: Section 2 contains some definitions and basic results used in the paper. Section 3 contains our main algorithm and proves its convergence. Section 4 and Section 5 incorporate the implementation of our results. Section 6 carries out the numerical results that demonstrates the computational effectiveness of our proposed algorithm.
2. Background
Let be a convex function on a nonempty, closed and convex subset of a real Hilbert space , and the subdifferential of a function h at is defined as:
Let be a nonempty, closed and convex subset of a real Hilbert space and a normal cone of at is defined by:
The metric projection for onto a closed and convex subset of is defined by:
Lemma 1
([41]). Let be a nonempty, closed and convex subset of a real Hilbert space and be a metric projection from onto .
- (i)
- Let and we have
- (ii)
- if and only if
- (iii)
- For and
Lemma 2
([42]). Let be a convex, subdifferentiable and lower semicontinuous function on where is a nonempty, convex and closed subset of a real Hilbert space Then, an element is a minimizer of a function h if and only if where and represent the subdifferential of h at and normal cone of at , respectively.
Lemma 3
([43]). Let be a sequence in and such that the following conditions hold:
- (i)
- For each the exists;
- (ii)
- Each sequentially weak cluster limit point of the sequence belongs to .
Then, the sequence weakly converges to some element in
Lemma 4.
[44] Let and be sequences of non-negative real numbers satisfying for each If then exists.
Assume that a bifunction f satisfies the following conditions:
- (f1)
- for all and f is pseudomonotone on
- (f2)
- f satisfies the Lipschitz-type condition on through and
- (f3)
- for every and satisfying ;
- (f4)
- needs to be convex and subdifferentiable on for each
3. Convergence Analysis for an Algorithm
We provide a method consisting of two strongly convex minimization problems through an inertial factor and an explicit stepsize formula, which are being used to improve the convergence rate of the iterative sequence and to make the method independent of the Lipschitz constants. The detailed method is provided below Algorithm 1:
| Algorithm 1 (Inertial methods for pseudomonotone equilibrium problems) |
|
Lemma 5.
The sequence is decreasing monotonically with a lower bound and converges to
Proof.
From the definition of we see that this sequence is monotone and non-increasing. It is given that f satisfies the Lipschitz-type condition with constants and . Let such that
The above implies that the sequence has a lower bound Moreover, there exists a real number such that □
Remark 1.
Due to the summability of , Expression (5) implies that:
which implies that:
Lemma 6.
Assume that a bifunction satisfies the conditions (f1)–(f4). For each we have
Proof.
From the value of we have
For some there exists such that
The above equality implies that
Since it follows that for all Thus, we have
Further, and due to the definition of subdifferential, we have
From the definition of we can write
Due to , we have
By substituting in the above expression, we have
By substituting in Expression (11), we have
Since , we have From the pseudomonotonicity of bifunction f, we obtain Hence, it follows from Expression (15) that
From the definition of we obtain
We have the following formulas:
Theorem 1.
Assume that a bifunction satisfies the conditions (f1)–(f4) and belongs to solution set Then, the sequences and generated by Algorithm 1 converge weakly to the solution of the problem (1). In addition,
Proof.
Since there exists a fixed number such that
Thus, there is a finite number such that
By Lemma 6, we obtain
From the definition of in Algorithm 1, we have
Expression (23) can be written as
From the definition of the , we also have
Combining relations (23) and (27), we obtain
By using Lemma 4 with (7) and (28), we have
From Equality (8), we have
By letting in Expression (24), we obtain
From Lemma 6 and Expression (25), we have
which further implies that (for )
By letting in (33), we obtain
By using the Cauchy inequality and Expression (34), we obtain
From Expressions (31) and (34), we also obtain
It follows from Expressions (29), (31), and (36) that the sequences , and are bounded. Next, we need to use Lemma 3, for it is compulsory to prove that all sequential weak cluster limit points of the sequence belong to the solution set Assume that z is any weak cluster limit point of the sequence , i.e., there exists a subsequence of such that Since it follows that also weakly converges to z and so Now, it remains to prove that By Expression (11), the definition of , and (14), we have
where It follows from (30), (34), (35), and the boundedness of that the right hand side tends to zero. Due to condition (f3), and we have
Since it follows that This implies that Finally, from Lemma 3, the sequences , and converge weakly to as
Moreover, the renaming part consists of proving that Let For any we have
The above expression implies that the sequence is bounded. Next, we prove that is a Cauchy sequence. By Lemma 1(iii) and (27), we have
Lemma 4 provides the existence of From Expression (27) for all we have
Suppose that for By using Lemma 1(i) and Expression (40), we have
The existence of and the summability of the series imply that for all As a result, is a Cauchy sequence and due to the closeness of a solution set the sequence strongly converges to Next, we show that Due to Lemma 1(ii) and we can write
Due to and we obtain
which gives that □
4. Applications to Solve Fixed Point Problems
Now, consider the applications of our results from Section 3 to solve fixed-point problems involving -strict pseudo-contraction. A mapping is said to be
- (i)
- -strict pseudo-contraction [45] on ifwhich is equivalent to
- (ii)
- sequentially weakly continuous on if
The fixed point problem for a mapping is formulated in the following way:
Note: If we define bifunction Then, the equilibrium problem (1) converts into the fixed point problem with From the value of in Algorithm 1, we have
Since , it follows from the definition of the subdifferential that we have
and consequently This implies that
Similarly to Expression (45), we obtain
As a consequence of the results in Section 3, we have the following fixed point theorem:
Corollary 1.
Let be a subset of a Hilbert space and be a κ-strict pseudocontraction and weakly continuous with The sequences , and are generated in the following way:
- (i)
- Fix and with a sequence such that
- (ii)
- Choose such that and
- (iii)
- Evaluatewhere
- (iv)
- Set and revise the stepsize in the following way:
Then, sequences , and weakly converge to
5. Application to Solve Variational Inequality Problems
Now, consider the applications of our results from in Section 3 to solve variational inequality problems involving a pseudomonotone and Lipschitz-type continuous operator. An operator is said to be
- (i)
- L-Lipschitz continuous on if
- (ii)
- pseudomonotone on if
The variational inequality problem for a operator is formulated in the following way:
Note: If we define a bifunction Thus, the equilibrium problem (1) translates into a variational inequality problem with From the value of we have
Since it follows from the subdifferential definition that we have
and consequently This implies that
In similar way to Expression (52), we have
Suppose that K satisfies the following conditions:
- (K1)
- K is pseudomonotone on with ;
- (K2)
- K is L-Lipschitz continuous on with ;
- (K3)
- and satisfying
Corollary 2.
Assume that a operator satisfies the conditions (K1)–(K3) and that the sequences , and are generated in the following way:
- (i)
- Choose and with such that
- (ii)
- Choose satisfying such that
- (iii)
- Set and computewhere
- (iv)
- Set and stepsize is revised in the following way:
Then, the sequences , and weakly converge to
6. Numerical Experiments
The computational results are presented in this section to illustrate the effectiveness of our proposed Algorithm 1 (EiEGM) compared to Algorithm 1 (iEGM) in [39]. The MATLAB program was operated on a PC (with Intel(R) Core(TM)i3-4010U CPU @ 1.70GHz 1.70GHz, RAM 4.00 GB) in MATLAB version 9.5 (R2018b). We used the built-in MATLAB fmincon function to solve the minimization problems.
Example 1.


Let be defined by
where The bifunction f is Lipschitz-type continuous operator with constants , and it satisfies conditions (f1)–(f4). To evaluate the best possible value of the control parameters, two tests were performed taking into consideration the variation of the control parameters and inertial factor The numerical results are shown in the Table 1 and Table 2 by choosing and

Table 1.
Example 1: Algorithm 1 numerical comparison with Algorithm 1 in [39].

Table 2.
Example 1: Algorithm 1 numerical comparison with Algorithm 1 in [39].
Example 2.
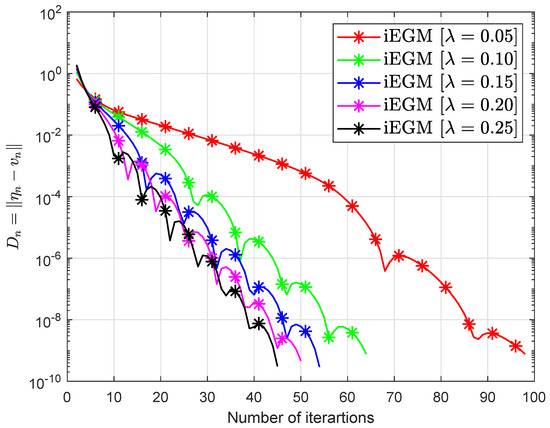
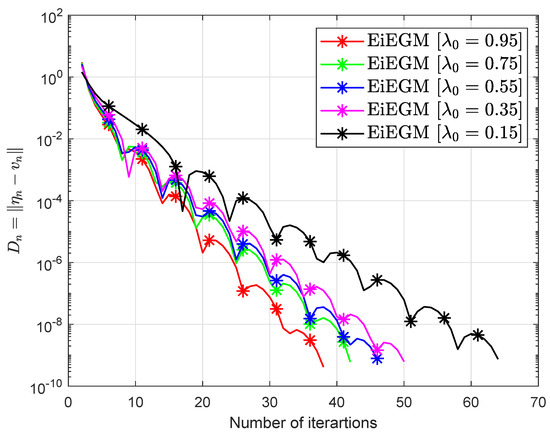
Consider the Nash–Cournot equilibrium model that appeared in the paper [7]. The bifunction f has been defined in the following way:
where and matrices A, B are
while Lipschitz constants (see for more details [7,46,47]). The set is Figure 1 and Figure 2 and Table 3 report the numerical results by choosing and

Figure 1.
Example 2: numerical behavior of Algorithm 3.1 in [39] by choosing different values of .

Figure 2.
Example 2: numerical behavior of Algorithm 1 by choosing different values of
Example 3.
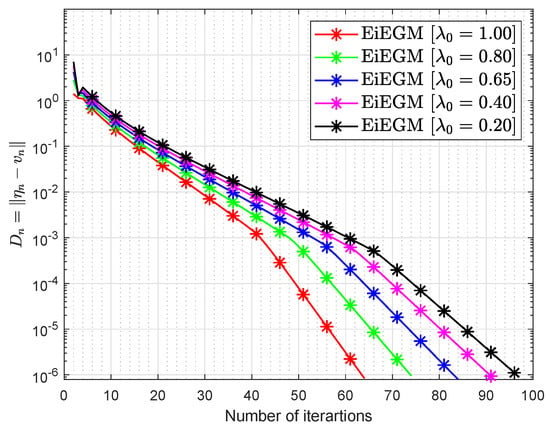
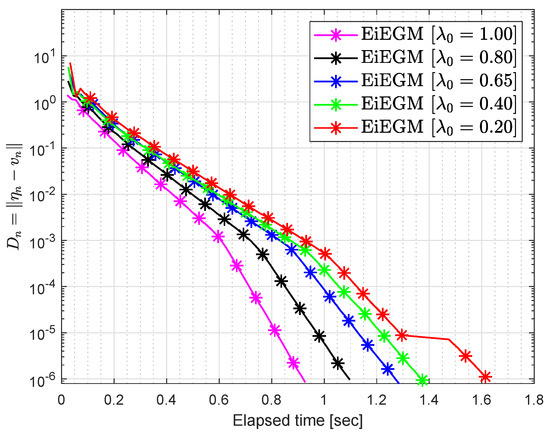
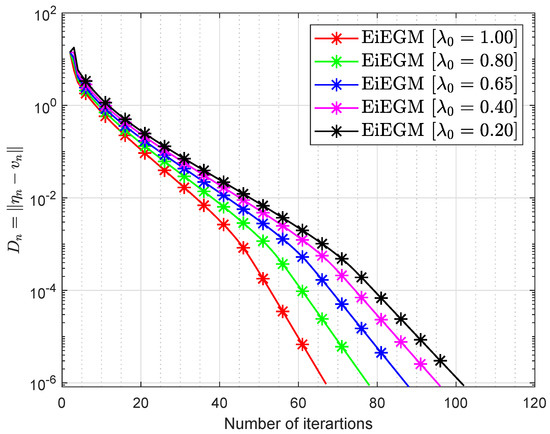
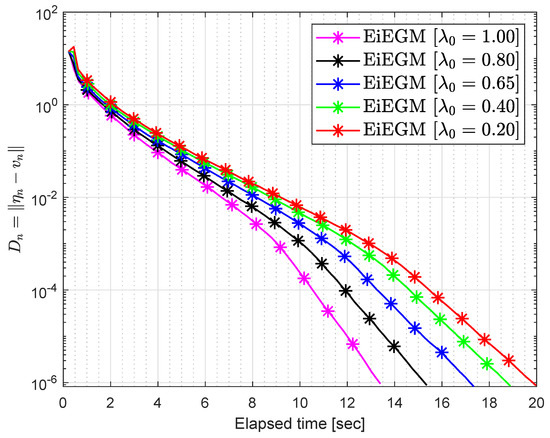
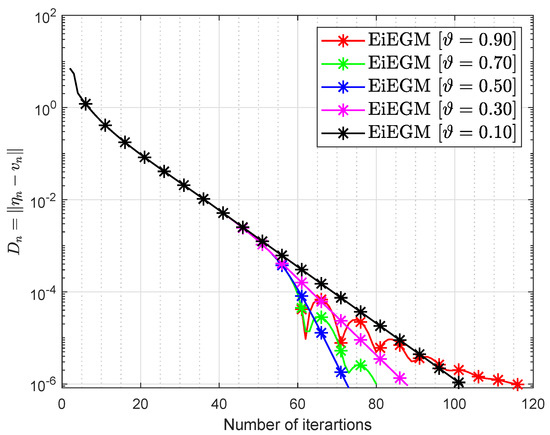
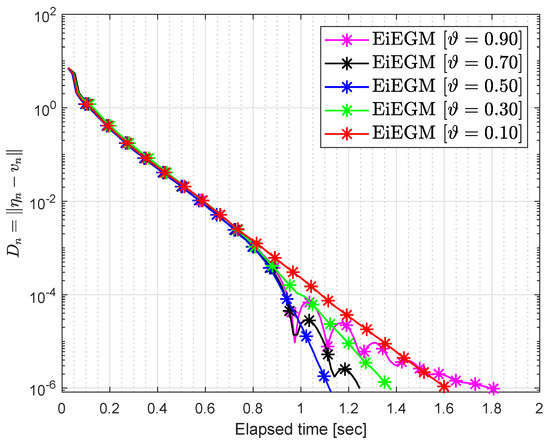


Let and where
and
The entries of a square matrix E are taken in the following way:
where To see the optimum values of the control parameters, some experiments were carried out taking into account the variation of the control parameters and the inertial factor ϑ. Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 and Table 4 and Table 5 report the numerical results by choosing and

Figure 3.
Numerical conduct of Algorithm 1 in by choosing different values of

Figure 4.
Numerical conduct of Algorithm 1 in by choosing different values of

Figure 5.
Numerical conduct of Algorithm 1 in by choosing different values of

Figure 6.
Numerical conduct of Algorithm 1 in by choosing different values of

Figure 7.
Numerical conduct of Algorithm 1 in by choosing different values of

Figure 8.
Numerical conduct of Algorithm 1 in by choosing different values of

Table 4.
Numerical results for Algorithm 1 in by choosing different values of and

Table 5.
Numerical results for Algorithm 1 in by choosing different values of and
Example 4.
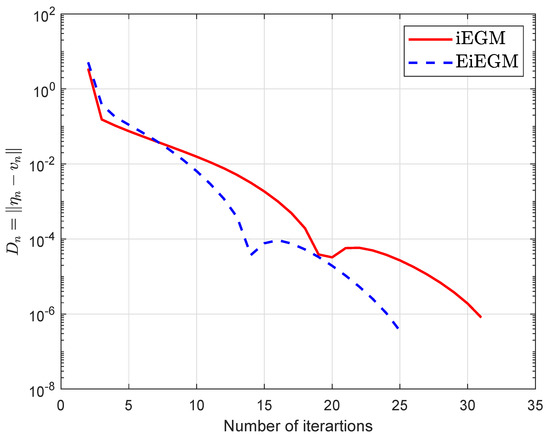
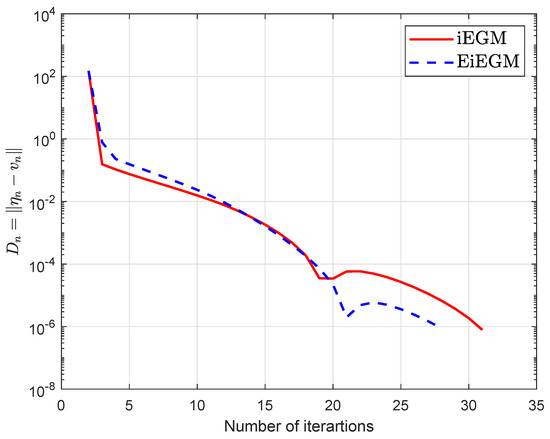

Suppose that is a Hilbert space with an inner product and the induced norm
Assume that is the unit ball. Let be
where
We can see in [48] that K is monotone and Lipschitz-continuous with a Lipschitz constant of . Figure 9 and Figure 10 and Table 6 show the numerical results by choosing different values of and

Figure 9.
Algorithm 1 comparison with Algorithm 1 in [39] by choosing values of

Figure 10.
Algorithm 1 comparison with Algorithm 1 in [39] by choosing values of

Table 6.
Example 4: numerical comparison of Algorithm 1 with Algorithm 1 in [39].
Discussion on the Numerical Experiments: We have the following findings about the above-mentioned experiments:
- (1)
- The proposed Algorithm 1 does not depend on the Lipschitz constants, unlike Algorithm 1 in [39]. Algorithm 1 uses a variable stepsize that is updated for each iteration and depends on some of the previous iterations. The key advantage of Algorithm 1 is that it works without prior knowledge of the Lipschitz-type constants and unlike Algorithm 1 in [39].
- (2)
- Four examples were discussed to compare our proposed method with Algorithm 1 in [39]. In particular, information on Lipschitz constants is missing in Example 3. Due to the missing information of the Lipschitz constants we cannot run Algorithm 1 in [39] because the stepsize is dependent on Lipschitz constants, i.e., However, we can use the proposed Algorithm 1 to solve Example 3.
- (3)
- It is noted that the selection of the value is always important, and precisely the value is better than most other values.
- (4)
- Choosing of the value is critical and the proposed algorithm performs better when is closer to
- (5)
- It can also be acknowledged that the efficiency of an algorithms significantly depends on the nature of the problem and tolerance. More time and a considerable number of iterations are needed for large-scale problems. In this case, we could see that a certain stepsize value improves the efficiency of the algorithm and improves the convergence rate.
- (6)
Author Contributions
Conceptualization, T.B., P.K. and H.u.R.; Writing-Original Draft Preparation, T.B., N.P. and H.u.R.; Writing-Review & Editing, T.B., N.P., H.u.R., P.K. and W.K.; Methodology, N.P. and H.u.R.; Visualization, T.B. and N.P.; Software, H.u.R.; Funding Acquisition, P.K. and W.K.; Supervision, P.K. and W.K.; Project Administration; P.K. and W.K.; Resources; P.K. and W.K. All authors have read and agreed to the published version of this manuscript.
Funding
This research work was financially supported by King Mongkut’s University of Technology Thonburi through the "KMUTT 55th Anniversary Commemorative Fund". Moreover, this project was supported by the Theoretical and Computational Science (TaCS) Center under the Computational and Applied Science for Smart research Innovation research Cluster (CLASSIC), Faculty of Science, KMUTT. In particular, Nuttapol Pakkaranang was supported by the Thailand Research Fund (TRF) through the Royal Golden Jubilee Ph.D. (RGJ-PHD) Program [Grant No. PHD/0205/2561]. Habib ur Rehman was supported by the Petchra Pra Jom Doctoral Academic Scholarship for a Ph.D. Program at KMUTT [grant number 39/2560]. Wiyada Kumam was financially supported by the Rajamangala University of Technology Thanyaburi (RMUTTT) [grant No. NSF62D0604].
Acknowledgments
We are very grateful to the editor and the anonymous referees for their valuable and useful comments, which helped in improving the quality of this work. The second author would like to thank the “Thailand Research Fund (TRF) through the Royal Golden Jubilee Ph.D. (RGJ-PHD) Program (Grant No. PHD/0205/2561)”. The third author would like to thank the “Petchra Pra Jom Klao PhD Research Scholarship from the King Mongkut’s University of Technology Thonburi”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Blum, E. From optimization and variational inequalities to equilibrium problems. Math. Stud. 1994, 63, 123–145. [Google Scholar]
- Bianchi, M.; Schaible, S. Generalized monotone bifunctions and equilibrium problems. J. Optim. Theory Appl. 1996, 90, 31–43. [Google Scholar] [CrossRef]
- Fan, K. A Minimax Inequality and Applications, Inequalities III; Shisha, O., Ed.; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Facchinei, F.; Pang, J.S. Finite-Dimensional Variational Inequalities and Complementarity Problems; Springer Science & Business Media: Berlin, Germany, 2007. [Google Scholar]
- Konnov, I. Equilibrium Models and Variational Inequalities; Elsevier: Amsterdam, The Netherlands, 2007; Volume 210. [Google Scholar]
- Muu, L.D.; Oettli, W. Convergence of an adaptive penalty scheme for finding constrained equilibria. Nonlinear Anal. Theory Methods Appl. 1992, 18, 1159–1166. [Google Scholar] [CrossRef]
- Quoc Tran, D.; Le Dung, M.N.V.H. Extragradient algorithms extended to equilibrium problems. Optimization 2008, 57, 749–776. [Google Scholar] [CrossRef]
- Ur Rehman, H.; Kumam, P.; Cho, Y.J.; Yordsorn, P. Weak convergence of explicit extragradient algorithms for solving equilibirum problems. J. Inequalities Appl. 2019, 2019. [Google Scholar] [CrossRef]
- Quoc, T.D.; Anh, P.N.; Muu, L.D. Dual extragradient algorithms extended to equilibrium problems. J. Glob. Optim. 2011, 52, 139–159. [Google Scholar] [CrossRef]
- Lyashko, S.I.; Semenov, V.V. A new two-step proximal algorithm of solving the problem of equilibrium programming. In Optimization and Its Applications in Control and Data Sciences; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 315–325. [Google Scholar] [CrossRef]
- Takahashi, S.; Takahashi, W. Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. J. Math. Anal. Appl. 2007, 331, 506–515. [Google Scholar] [CrossRef]
- Ur Rehman, H.; Kumam, P.; Je Cho, Y.; Suleiman, Y.I.; Kumam, W. Modified Popov’s explicit iterative algorithms for solving pseudomonotone equilibrium problems. Optim. Methods Softw. 2020, 1–32. [Google Scholar] [CrossRef]
- Anh, P.N.; Hai, T.N.; Tuan, P.M. On ergodic algorithms for equilibrium problems. J. Glob. Optim. 2015, 64, 179–195. [Google Scholar] [CrossRef]
- Hieu, D.V.; Quy, P.K.; Vy, L.V. Explicit iterative algorithms for solving equilibrium problems. Calcolo 2019, 56. [Google Scholar] [CrossRef]
- Hieu, D.V. New extragradient method for a class of equilibrium problems in Hilbert spaces. Appl. Anal. 2017, 97, 811–824. [Google Scholar] [CrossRef]
- Ur Rehman, H.; Kumam, P.; Abubakar, A.B.; Cho, Y.J. The extragradient algorithm with inertial effects extended to equilibrium problems. Comput. Appl. Math. 2020, 39. [Google Scholar] [CrossRef]
- Santos, P.; Scheimberg, S. An inexact subgradient algorithm for equilibrium problems. Comput. Appl. Math. 2011, 30, 91–107. [Google Scholar]
- Ur Rehman, H.; Kumam, P.; Kumam, W.; Shutaywi, M.; Jirakitpuwapat, W. The inertial sub-gradient extra-gradient method for a class of pseudo-monotone equilibrium problems. Symmetry 2020, 12, 463. [Google Scholar] [CrossRef]
- Hieu, D.V. Halpern subgradient extragradient method extended to equilibrium problems. Rev. Real Acad. Cienc. Exactas Físicas y Nat. Ser. A Matemáticas 2016, 111, 823–840. [Google Scholar] [CrossRef]
- Anh, P.N.; An, L.T.H. The subgradient extragradient method extended to equilibrium problems. Optimization 2012, 64, 225–248. [Google Scholar] [CrossRef]
- Ur Rehman, H.; Kumam, P.; Argyros, I.K.; Deebani, W.; Kumam, W. Inertial extra-gradient method for solving a family of strongly pseudomonotone equilibrium problems in real Hilbert spaces with application in variational inequality problem. Symmetry 2020, 12, 503. [Google Scholar] [CrossRef]
- Muu, L.D.; Quoc, T.D. Regularization algorithms for solving monotone Ky Fan inequalities with application to a Nash-Cournot equilibrium model. J. Optim. Theory Appl. 2009, 142, 185–204. [Google Scholar] [CrossRef]
- Ur Rehman, H.; Kumam, P.; Argyros, I.K.; Alreshidi, N.A.; Kumam, W.; Jirakitpuwapat, W. A self-adaptive extra-gradient methods for a family of pseudomonotone equilibrium programming with application in different classes of variational inequality problems. Symmetry 2020, 12, 523. [Google Scholar] [CrossRef]
- Ur Rehman, H.; Kumam, P.; Argyros, I.K.; Shutaywi, M.; Shah, Z. Optimization based methods for solving the equilibrium problems with applications in variational inequality problems and solution of Nash equilibrium models. Mathematics 2020, 8, 822. [Google Scholar] [CrossRef]
- Ur Rehman, H.; Kumam, P.; Shutaywi, M.; Alreshidi, N.A.; Kumam, W. Inertial optimization based two-step methods for solving equilibrium problems with applications in variational inequality problems and growth control equilibrium models. Energies 2020, 13, 3292. [Google Scholar] [CrossRef]
- Gibali, A.; Hieu, D.V. A new inertial double-projection method for solving variational inequalities. J. Fixed Point Theory Appl. 2019, 21. [Google Scholar] [CrossRef]
- Thong, D.V.; Hieu, D.V. Modified subgradient extragradient method for variational inequality problems. Numer. Algorithms 2017, 79, 597–610. [Google Scholar] [CrossRef]
- Thong, D.V.; Hieu, D.V. Inertial extragradient algorithms for strongly pseudomonotone variational inequalities. J. Comput. Appl. Math. 2018, 341, 80–98. [Google Scholar] [CrossRef]
- Censor, Y.; Gibali, A.; Reich, S. Extensions of Korpelevich’s extragradient method for the variational inequality problem in Euclidean space. Optimization 2012, 61, 1119–1132. [Google Scholar] [CrossRef]
- Yordsorn, P.; Kumam, P.; Rehman, H.U. Modified two-step extragradient method for solving the pseudomonotone equilibrium programming in a real Hilbert space. Carpathian J. Math. 2020, 36, 313–330. [Google Scholar]
- Hammad, H.A.; ur Rehman, H.; la Sen, M.D. Advanced algorithms and common solutions to variational inequalities. Symmetry 2020, 12, 1198. [Google Scholar] [CrossRef]
- Gibali, A. A new non-Lipschitzian projection method for solving variational inequalities in Euclidean spaces. J. Nonlinear Anal. Optim. Theory Appl. 2015, 6, 41–51. [Google Scholar]
- Dong, Q.L.; Jiang, D.; Gibali, A. A modified subgradient extragradient method for solving the variational inequality problem. Numer. Algorithms 2018, 79, 927–940. [Google Scholar] [CrossRef]
- Abubakar, J.; Kumam, P.; ur Rehman, H.; Ibrahim, A.H. Inertial iterative schemes with variable step sizes for variational inequality problem involving pseudomonotone operator. Mathematics 2020, 8, 609. [Google Scholar] [CrossRef]
- Abubakar, J.; Sombut, K.; ur Rehman, H.; Ibrahim, A.H. An accelerated subgradient extragradient algorithm for strongly pseudomonotone variational inequality problems. Thai J. Math. 2019, 18. [Google Scholar]
- Flåm, S.D.; Antipin, A.S. Equilibrium programming using proximal-like algorithms. Math. Program. 1996, 78, 29–41. [Google Scholar] [CrossRef]
- Korpelevich, G. The extragradient method for finding saddle points and other problems. Matecon 1976, 12, 747–756. [Google Scholar]
- Yang, J.; Liu, H.; Liu, Z. Modified subgradient extragradient algorithms for solving monotone variational inequalities. Optimization 2018, 67, 2247–2258. [Google Scholar] [CrossRef]
- Vinh, N.T.; Muu, L.D. Inertial extragradient algorithms for solving equilibrium problems. Acta Math. Vietnam. 2019, 44, 639–663. [Google Scholar] [CrossRef]
- Censor, Y.; Gibali, A.; Reich, S. The subgradient extragradient method for solving variational inequalities in Hilbert space. J. Optim. Theory Appl. 2010, 148, 318–335. [Google Scholar] [CrossRef] [PubMed]
- Kreyszig, E. Introductory Functional Analysis with Applications, 1st ed.; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Tiel, J.V. Convex Analysis: An Introductory Text, 1st ed.; Wiley: New York, NY, USA, 1984. [Google Scholar]
- Opial, Z. Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull. Am. Math. Soc. 1967, 73, 591–598. [Google Scholar] [CrossRef]
- Tan, K.; Xu, H. Approximating Fixed Points of Nonexpansive Mappings by the Ishikawa Iteration Process. J. Math. Anal. Appl. 1993, 178, 301–308. [Google Scholar] [CrossRef]
- Browder, F.; Petryshyn, W. Construction of fixed points of nonlinear mappings in Hilbert space. J. Math. Anal. Appl. 1967, 20, 197–228. [Google Scholar] [CrossRef]
- Ur Rehman, H.; Pakkaranang, N.; Hussain, A.; Wairojjana, N. A modified extra-gradient method for a family of strongly pseudomonotone equilibrium problems in real Hilbert spaces. J. Math. Comput. Sci. 2020, 22, 38–48. [Google Scholar] [CrossRef]
- Yordsorn, P.; Kumam, P.; ur Rehman, H.; Ibrahim, A.H. A weak convergence self-adaptive method for solving pseudomonotone equilibrium problems in a real Hilbert space. Mathematics 2020, 8, 1165. [Google Scholar] [CrossRef]
- Van Hieu, D.; Anh, P.K.; Muu, L.D. Modified hybrid projection methods for finding common solutions to variational inequality problems. Comput. Optim. Appl. 2017, 66, 75–96. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).