1. Introduction
Recently, several techniques have been proposed to increase the speed of physics-based dynamic simulation by approximating rigid and deformable bodies with ellipsoids for interactive applications such as computer games [
1,
2,
3]. Computing the closest approach distance between two ellipsoids in their inter-center direction is a key technique for collision handling among ellipsoids.
Given the positions and orientations of two ellipsoids, their overlap can be determined in a relatively easy manner by examining the signs of the solutions of their quartic characteristic equation without obtaining the actual solutions [
4,
5,
6,
7]. However, it is not easy to separate two overlapping ellipsoids. Position-based dynamics with ellipsoids [
1] takes an approach that translates two ellipsoids outward along their inter-center direction by the closest approach distance to make them contact each other externally. To find the closest approach distance, a set of equations is formulated intuitively in terms of the inter-center distance, contact point, and contact normal vector. However, there is an error in the derivation of this solution; consequently, the solution is correct only for two spheres. In this paper, we rectify this error to find the closest approach distance correctly and intuitively. In [
2,
3], the method to compute the closest approach distance is not described.
The closest approach distance between two ellipsoids also plays important roles in the simulation of liquid crystals and colloidal systems [
8,
9,
10,
11,
12]. In [
10], an indirect formulation was introduced with the optimization of the elliptic contact function proposed in [
8,
9]. However, the derivation was complicated, and the numerical solution method was not addressed. In the method proposed in [
12], the golden section search is employed with an analytic method [
11] that computes the closest approach distance between two ellipses formed by the cross-section of two ellipsoids with a plane rotating about the line joining their centers. However, this method is considerably slow.
This paper presents two robust and efficient methods for computing the closest approach distance between two ellipsoids within a user-specified tolerance. The proposed methods are based on the intuitive approach introduced in position-based dynamics with ellipsoids [
1]. We formulate the problem with a set of conditions in terms of the inter-center distance, contact point, and contact normal vector of two externally-contacting ellipsoids. The resulting equations are solved robustly and efficiently using a hybrid of the fixed-point iteration method and bisection method with root bracketing, and a hybrid of Newton’s method and the bisection method. In addition to a stopping criterion expressed with the change of the solution in a single solver iteration, we introduce a novel criterion expressed in terms of the actual error in distance. This can be effectively employed to increase the efficiency of the proposed methods in real-time applications such as computer games by allowing unnoticeable interferences between ellipsoids.
3. Experimental Results
We propose two methods to compute the closest approach distance of two ellipsoids. One method employs a hybrid of the bisection method with Newton’s method, and the other with fixed-point iteration. We call the former hybrid Newton’s method and the latter the hybrid fixed-point iteration method. In this section, we describe a performance comparison of four methods: (1) hybrid Newton’s method, (2) hybrid fixed-point iteration method, (3) Brent’s method with the elliptic contact potential [
9], and (4) cross-section search [
12] in various examples. The proposed methods were implemented using C++ and the Eigen library (eigen.tuxfamily.org) to perform the vector and matrix operations. All of the experiments were performed using a workstation equipped with a 2.3 GHz 18-core Intel Xeon W processor and 128 GB 2666 MHz DDR4 RAM.
The first experiment was conducted to test the number of solver iterations and the computation times for 10 million pairs of randomly generated ellipsoids. The ratio between the maximum and minimum radii of each ellipsoid was restricted to less than
, and the ratio between the maximum radii in a pair of ellipsoids was restricted to less than
. The orientation of an ellipsoid and the inter-center direction between a pair of ellipsoids were generated randomly without any restriction. For robustness of physics-based simulation,
was used in [
1] and
in [
2,
3].
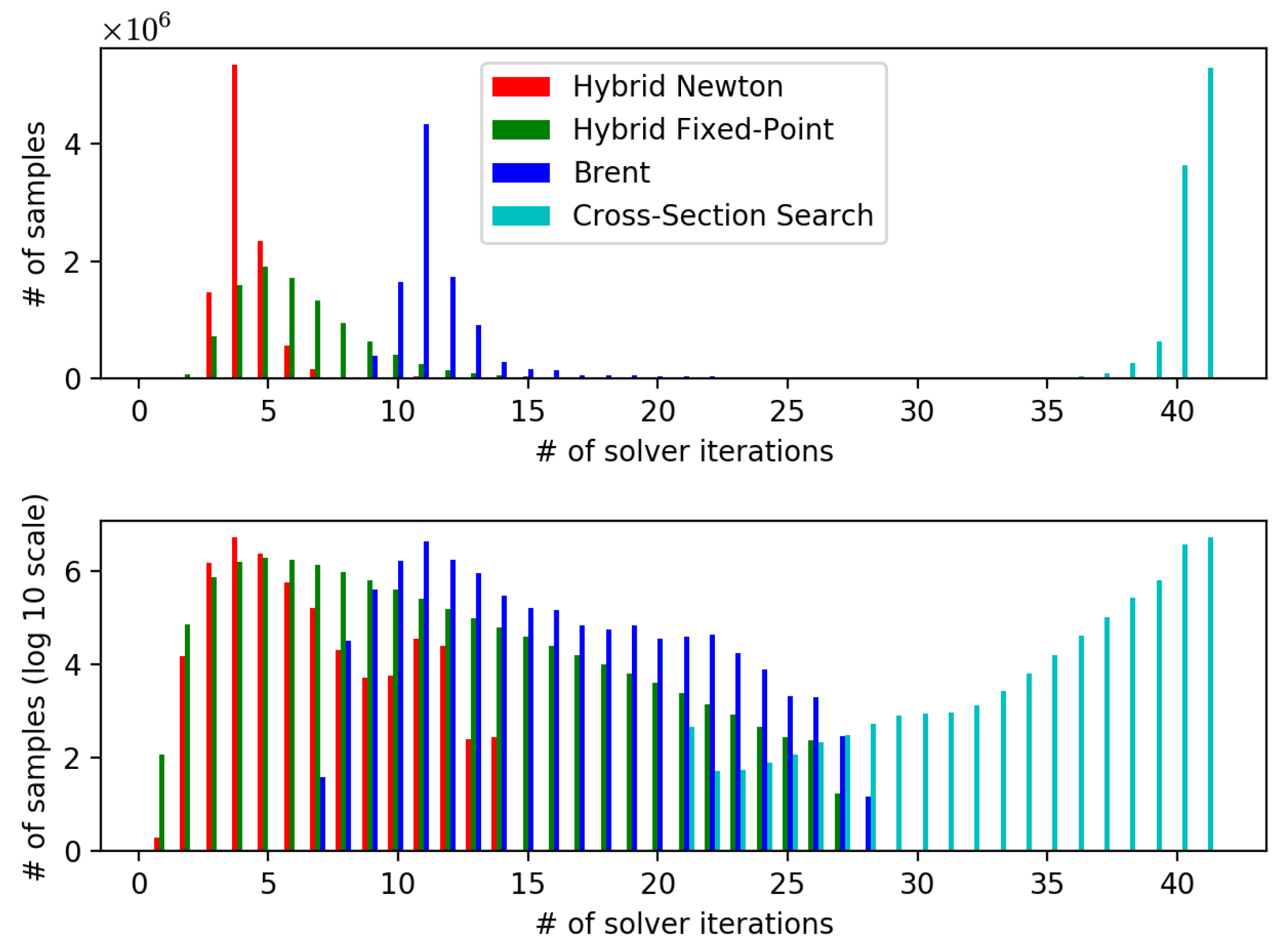
Figure 2 shows the distributions of the numbers of solver iterations required for
for the four methods with
and
. The average and maximum number of solver iterations and the average computation time are listed in
Table 1. The computation time was measured using a single core in this experiment. The hybrid Newton’s method performed better than the others in all aspects.
The error in the analytic method for the closest approach distance of two ellipses increased as
increased [
11]. Correspondingly, the error in the cross-section search [
12] also increased, regardless of the number of solver iterations in the golden section search that found the angle of the cross section resulting in the closest approach distance of two ellipsoids. In contrast, the other methods computed the closest approach distance within a user-specified tolerance even with a large
. However, the number of solver iterations increased as
increased. This result was verified with the second experiment, in which the closest approach distances were computed for each of the 1 million pairs of ellipsoids generated randomly with
increasing from 1 to 200 and
fixed at 3. For the stopping criterion, we employed Equation (
13) with
and the maximum number of solver iterations set to 100.
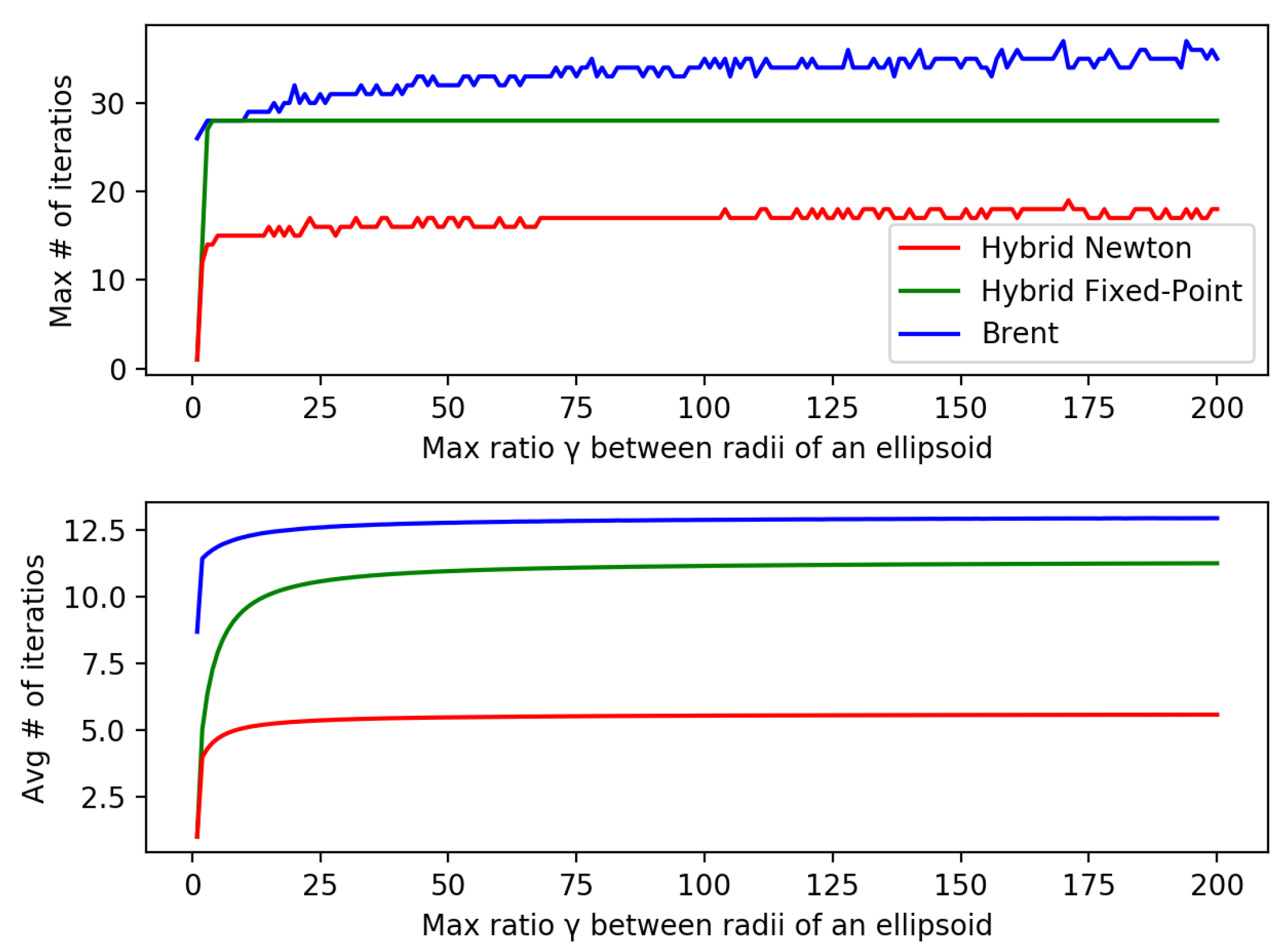
Figure 3 shows the maximum and average number of solver iterations. In the traditional fixed-point iteration method, the number of solver iterations exceeded 100 when
became larger than 7. However, the hybrid fixed-point iteration method was robust, even when
reached 200, with an average of 11.3 solver iterations. The hybrid Newton’s and Brent’s methods were also robust and reached
with an average of 5.6 and 13.0 solver iterations, respectively.
implied the maximum radius could be 200 times larger than the minimum in a single ellipsoid, and thus it was sufficient for physics-based simulation with ellipsoids.
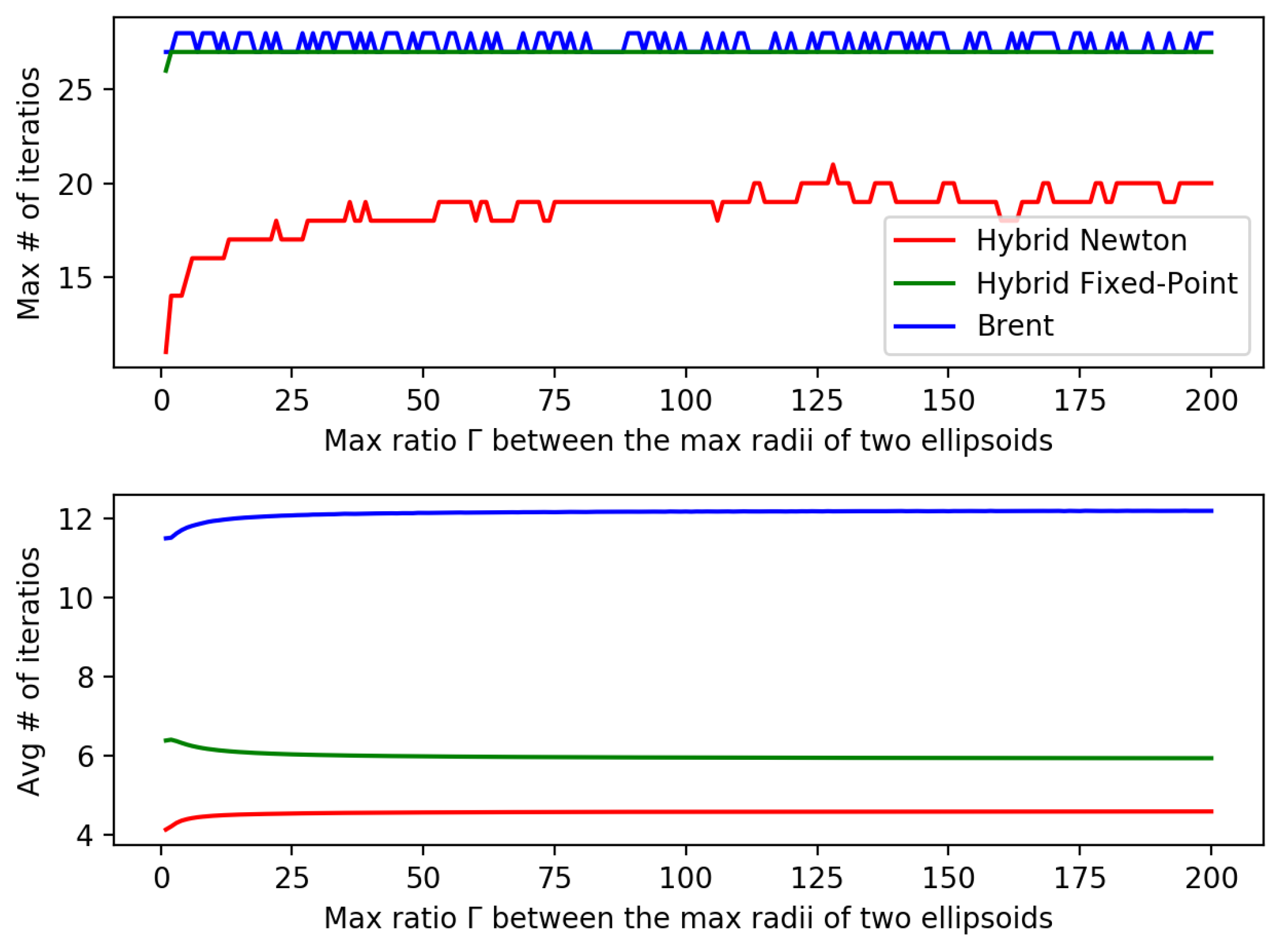
The number of solver iterations was almost insensitive to
in contrast to
.
Figure 4 shows the maximum and average number of solver iterations required to compute the closest approach distances for each of the 1 million pairs of ellipsoids generated randomly, with
increasing from 1 to 200 and
fixed at 3. We can observe that the computation time was almost insensitive to
, the proportion between the gross sizes of the ellipsoids. Consequently, the proposed methods could be effectively used for simulating ellipsoids with various sizes.
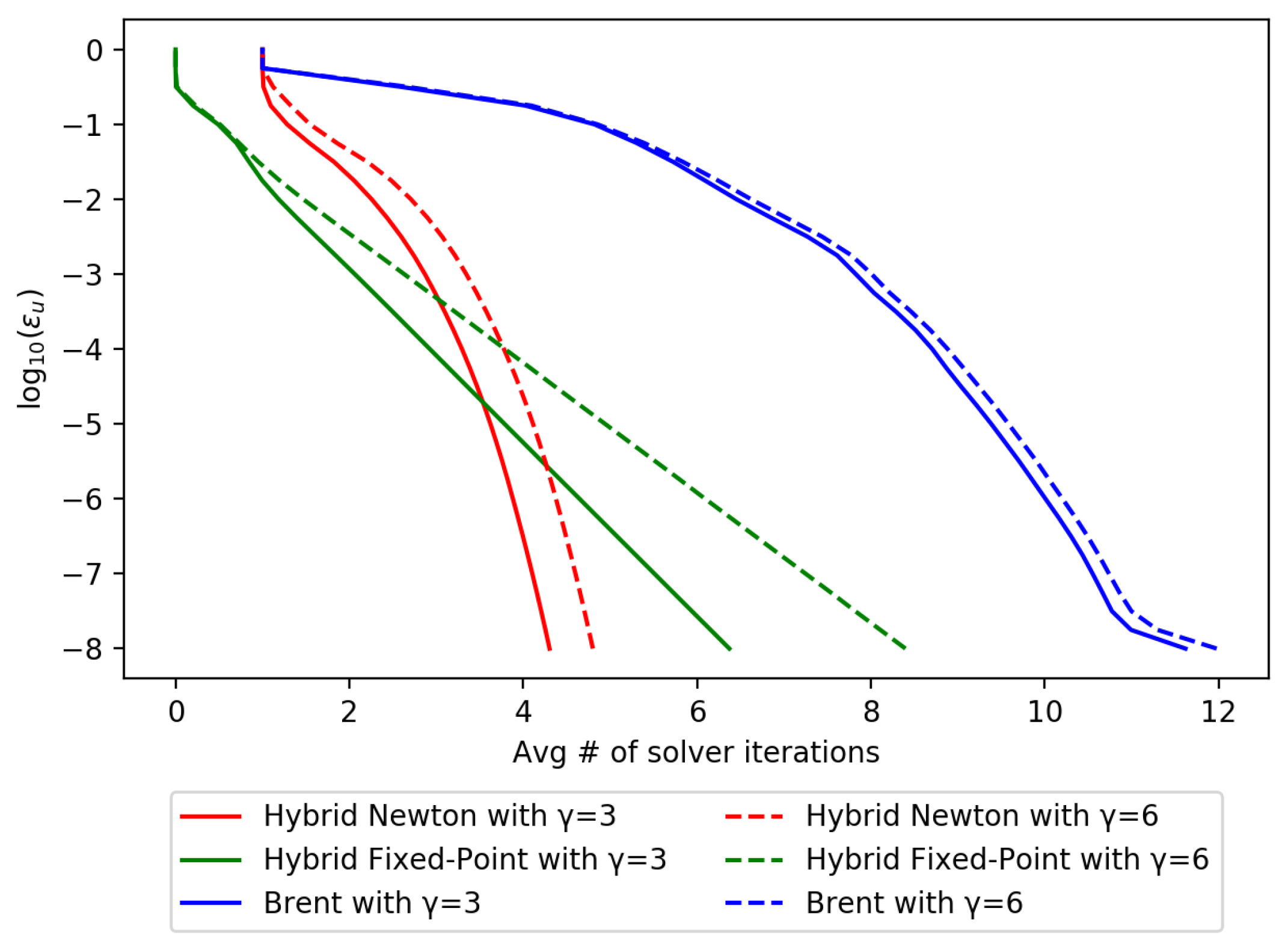
The next experiment was conducted to test the number of solver iterations with respect to the error tolerance.
Figure 5 shows the average number of solver iterations required to compute the closest approach distances for 1 million pairs of random ellipsoids with
(solid lines) and
(dashed lines) when
decreases from 1 to
.
was fixed at 3. The hybrid Newton’s and Brent’s methods exhibited quadratic convergence, whereas the hybrid fixed-point iteration method exhibited linear convergence. However, when
was small and the error tolerance was large, the hybrid fixed-point iteration method performed better than the others. This observation can be effectively exploited with the actual error tolerance given in Equation (
14) as illustrated in the final experiment.
The final experiment demonstrated the effectiveness of the proposed methods in real-time as-rigid-as-possible dynamic simulation of deformable bodies approximated with ellipsoids [
3].
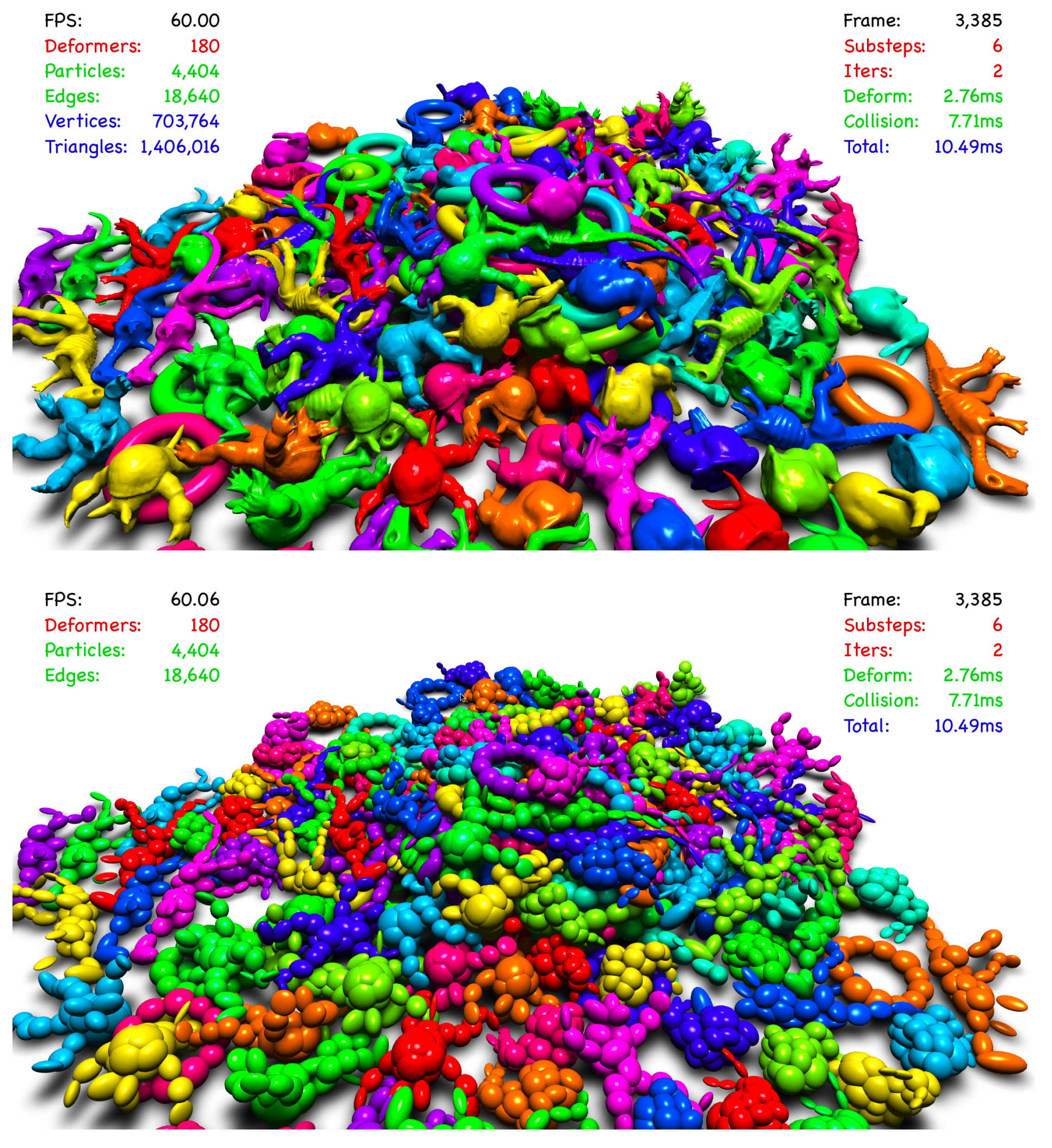
Figure 6 shows the simulation result of 180 deformable bodies approximated with 4404 ellipsoids. A spatial subdivision technique [
15] was employed to reduce the number of collision tests between a pair of ellipsoids, and 49,716,944 collision tests were performed during 60 s of simulation. The ratios
and
between radii were 4.86 and 2.55, respectively.
Table 1 lists the average and maximum number of solver iterations and the average computation time required to satisfy the stopping criterion given in Equation (
13) with
. The computation time was measured in two different manners that exploited (1) a single core and (2) all 18 cores with a simple parallelization using OpenMP. In both cases, the hybrid Newton’s method was the most efficient.
In real-time applications such as computer games, computational efficiency has higher priority over simulation accuracy. Moreover, the interference between ellipsoids was scarcely noticeable even when the interference was
of the minimum radius. Thus, the actual error tolerance given in Equation (
14) was adequate as a stopping criterion.
Table 1 lists the average and maximum number of solver iterations and the average computation time when
. With the actual error tolerance, the hybrid fixed-point iteration method was shown to be the most efficient. From this experiment, we can conclude that the hybrid Newton’s method is a good choice when the accuracy is important, and the hybrid fixed-point iteration method is a good choice in real-time applications.