Next Article in Journal
Generalized Bessel Polynomial for Multi-Order Fractional Differential Equations
Next Article in Special Issue
A Bibliometric Analysis of Symmetry (2009–2019)
Previous Article in Journal
Chiral Perturbation Theory at NNNLO
Previous Article in Special Issue
Similarity Measures of Quadripartitioned Single Valued Bipolar Neutrosophic Sets and Its Application in Multi-Criteria Decision Making Problems
 
Search for Articles:
Title / Keyword
Author / Affiliation
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
Journals
Symmetry
Volume 12
Issue 8
10.3390/sym12081263
symmetry-logo
Submit to this Journal Review for this Journal Edit a Special Issue
► Article Menu

Article Menu

Printed Edition

A printed edition of this Special Issue is available at MDPI Books....
share announcement question_answer thumb_up
...
textsms
...
Article

A Novel Extension of the TOPSIS Method Adapted for the Use of Single-Valued Neutrosophic Sets and Hamming Distance for E-Commerce Development Strategies Selection

by
Darjan Karabašević
1,*,
Dragiša Stanujkić
2,
Edmundas Kazimieras Zavadskas
3,
Predrag Stanimirović
4,
Gabrijela Popović
1,
Bratislav Predić
5 and
Alptekin Ulutaş
6
1
Faculty of Applied Management, Economics and Finance, University Business Academy in Novi Sad, Belgrade, Serbia, Jevrejska 24, 11000 Belgrade, Serbia
2
Technical Faculty in Bor, University of Belgrade, Vojske Jugoslavije 12, 19210 Bor, Serbia
3
Institute of Sustainable Construction, Vilnius Gediminas Technical University, LT 10223 Vilnius, Lithuania
4
Faculty of Sciences and Mathematics, University of Niš, Višegradska 33, 18000 Niš, Serbia
5
Faculty of Electronic Engineering, University of Niš, Aleksandra Medvedeva 14, 18000 Niš, Serbia
6
Department of International Trade and Logistics, Faculty of Economics and Administrative Sciences, Sivas Cumhuriyet University, Sivas 58140, Turkey
*
Author to whom correspondence should be addressed.
Symmetry 2020, 12(8), 1263; https://doi.org/10.3390/sym12081263
Received: 23 June 2020 / Revised: 3 July 2020 / Accepted: 3 July 2020 / Published: 30 July 2020
(This article belongs to the Special Issue Symmetric and Asymmetric Data in Solution Models)
View Full-Text Download PDF
Browse Figures

Abstract

Neutrosophic sets have been recognized as an effective approach in solving complex decision-making (DM) problems, mainly when such problems are related to uncertainties, as published in numerous articles thus far. The use of the three membership functions that can be used to express accuracy, inaccuracy, and indeterminacy during the evaluation of alternatives in multiple-criteria DM can be said to be a significant advantage of these sets. By utilizing these membership functions, neutrosophic sets provide an efficient and flexible approach to the evaluation of alternatives, even if DM problems are related to uncertainty and predictions. On the other hand, the TOPSIS method is a prominent multiple-criteria decision-making method used so far to solve numerous decision-making problems, and many extensions of the TOPSIS method are proposed to enable the use of different types of fuzzy as well as neutrosophic sets. Therefore, a novel extension of the TOPSIS method adapted for the use of single-valued neutrosophic sets was considered in this paper. View Full-Text
Keywords: multiple-criteria decision-making; neutrosophic; single-valued neutrosophic sets; TOPSIS; Hamming distance; Euclidean distance; e-commerce development strategies multiple-criteria decision-making; neutrosophic; single-valued neutrosophic sets; TOPSIS; Hamming distance; Euclidean distance; e-commerce development strategies
►▼ Show Figures

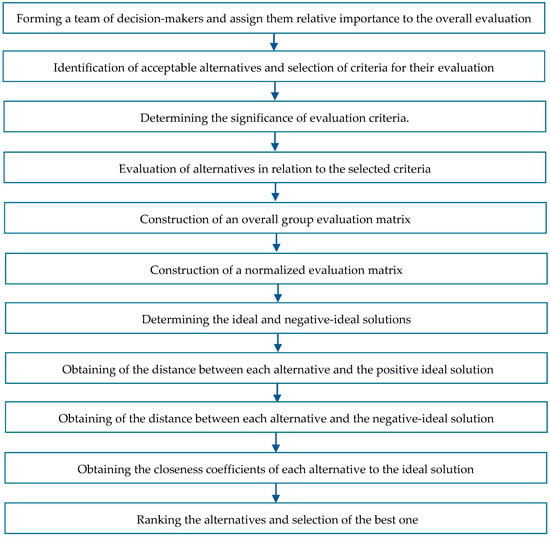
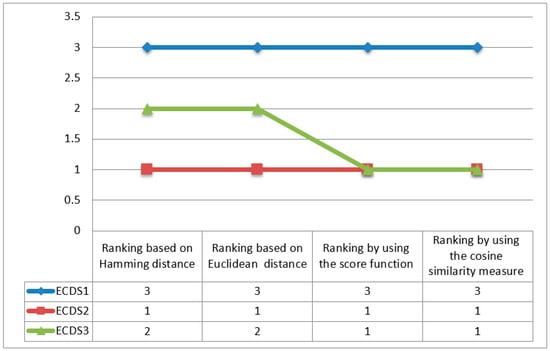
Figure 1

This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited
SciFeed

Share and Cite

MDPI and ACS Style

Karabašević, D.; Stanujkić, D.; Zavadskas, E.K.; Stanimirović, P.; Popović, G.; Predić, B.; Ulutaş, A. A Novel Extension of the TOPSIS Method Adapted for the Use of Single-Valued Neutrosophic Sets and Hamming Distance for E-Commerce Development Strategies Selection. Symmetry 2020, 12, 1263. https://doi.org/10.3390/sym12081263

AMA Style

Karabašević D, Stanujkić D, Zavadskas EK, Stanimirović P, Popović G, Predić B, Ulutaş A. A Novel Extension of the TOPSIS Method Adapted for the Use of Single-Valued Neutrosophic Sets and Hamming Distance for E-Commerce Development Strategies Selection. Symmetry. 2020; 12(8):1263. https://doi.org/10.3390/sym12081263

Chicago/Turabian Style

Karabašević, Darjan, Dragiša Stanujkić, Edmundas K. Zavadskas, Predrag Stanimirović, Gabrijela Popović, Bratislav Predić, and Alptekin Ulutaş. 2020. "A Novel Extension of the TOPSIS Method Adapted for the Use of Single-Valued Neutrosophic Sets and Hamming Distance for E-Commerce Development Strategies Selection" Symmetry 12, no. 8: 1263. https://doi.org/10.3390/sym12081263

Find Other Styles
Note that from the first issue of 2016, MDPI journals use article numbers instead of page numbers. See further details here.

Article Metrics

Article Access Map by Country/Region

1
Back to TopTop