Abstract
In this paper, we introduce q-cosine and q-sine Euler polynomials and determine identities for these polynomials. From these polynomials, we obtain some special properties using a power series of q-trigonometric functions, properties of q-exponential functions, and q-analogues of the binomial theorem. We investigate the approximate roots of q-cosine Euler polynomials that help us understand these polynomials. Moreover, we display the approximate roots movements of q-cosine Euler polynomials in a complex plane using the Newton method.
Keywords:
q-cosine Euler polynomials; q-sine Euler polynomials; q-trigonometric function; q-exponential function MSC:
11B68; 11B75; 33A10
1. Introduction
In 1990, Jackson who published influential papers on the subject introduced the q-number and its notation stems, see [1]. Floreanini and Vinet found that some properties of q-orthogonal polynomials are connected to the q-oscillator algebra in [1,2,3,4]. We begin by introducing several definitions related to q-numbers used in this paper, see [3,5,6,7,8].
Throughout this paper, the symbols, and denotes the set of natural numbers, the set of integers, the set of real numbers and the set of complex numbers, respectively.
For , and , the q-shifted factorial is defined by
It is well known that
Let with . The number
is called q-number. We note that . In particular, for , is a q-integer.
After the appearance of q-numbers, many mathematicians have studied topics such as q-differential equations, q-series, and q-trigonometric functions. Of course, mathematicians also constructed and researched q-Gaussian binomial coefficients, see [2,3,4,7,8,9,10,11].
Definition 1.
For and , the q-Gaussian binomial coefficients are defined by
For , we note that with , and also, we note that and !=1.
Definition 2.
Let and . Then, the q-exponential function is defined by
For and , the other form of q-exponential function can be defined as
We note that . Exponential function is expanded to the power series expressions of the two q-exponential functions by combining with q-numbers. Also, q-derivatives and q-integrals were extensively studied by many mathematicians, see [1,5,12]. Following the determination of the limit formulas for q-exponential functions taken from Rawlings [10], several other interesting q-series expansions were presented in the classical book by Andrews [5].
Theorem 1.
From Definition 2, we note that
The proof of Theorem 1 and more properties of q-exponential functions can be found in [2,13].
Definition 3.
For real variable function f where , the q-derivative operator is defined as
We note that . It is possible to prove that f is differentiable at 0 and it is clear that .
In 2002, Kac and Pokman published a book about quantum calculus including q-derivatives and q-analogue of and q-trigonometric functions, see [14].
Definition 4.
Let n be a nonnegative integer. The q-analogues of subtraction and addition are defined by
Definition 5.
Let and . Then, the q-trigonometric functions are defined by
where .
Theorem 2.
Using Theorem 1 and applying the chain rule, we have
Moreover, we note Theorem 2 is the q-analogue of the identity , see [3,4,7].
In 2004, Gasper and Rahman introduced a comprehensive account of the basic q-hypergeometric series, see [4]. During the last three decades, one of the bridges between science and applied mathematics has been q-calculus, see [10]. Based on the above concepts, many mathematicians explored various fields of mathematics including q-differential equations, q-series, q-hypergeometric functions, and q-gamma and q-beta functions. Moreover, various discrete distributions combining q-numbers can be found in [2]. Therefore, q-calculus plays an important role in many different areas of mathematics.
Many researchers who studied the Bernoulli, Euler, and Genocchi polynomials in various fields realized the important role of q-calculus in mathematics. For a long time, the topics of Bernoulli, Euler, and Genocchi polynomials have been extensively researched in many mathematical applications including analytical number theory, combinatorial analysis, p-adic analytic number theory, and other fields. Therefore, many mathematicians have started researching Bernoulli, Euler, and Genocchi polynomials combining q-numbers, see [9,13,15,16,17,18,19,20,21].
The following diagram briefly explains the relation between the various types of degenerate Euler polynomials, Euler polynomials, and q-Euler polynomials. The polynomials in the first row are researched by Calitz [21], Kim and Ryoo [16], respectively. The study of the second row of the diagram has brought about beneficial results in combinatorics and number theory. In particular, the cosine and sine Euler polynomials in the second row of the diagram contain a motive in this paper. This is because we hold several questions regarding what is a definition form of q-cosine and q-sine Euler polynomials and what is different properties between the q-cosine, q-sine Euler polynomials and the cosine, sine Euler polynomials.
The main subject of this paper is to construct q-cosine and q-sine Euler polynomials using Definitions 4 and 5. Also, we derive identities and properties for these polynomials in the third row of the diagram.
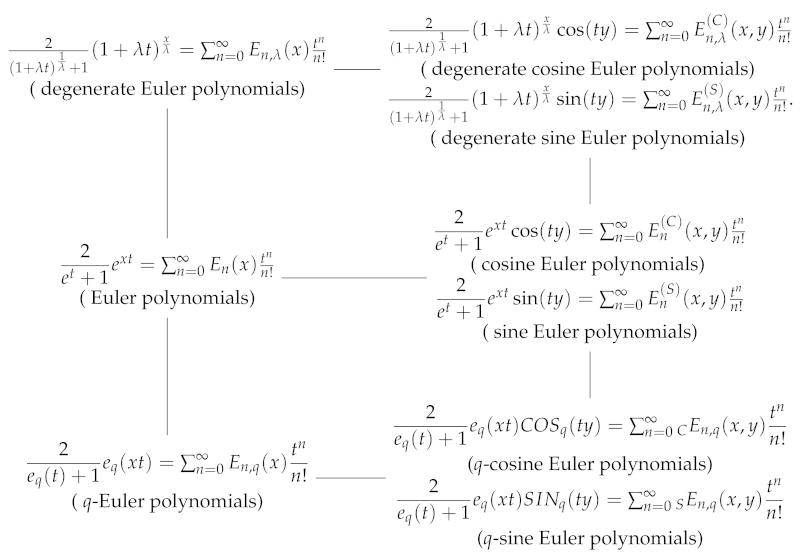

The definition of q-Euler polynomials of the third row are as follows.
Definition 6.
The q-Euler numbers and polynomials are defined respectively as see [19]
.
Recently, Kim and Ryoo introduced the basic concepts of cosine and sine Euler polynomials. In [16], the definitions and representative properties of cosine and sine Euler polynomials are as follows.
Definition 7.
The cosine Euler polynomials and the sine Euler polynomials are defined by means of the generating functions
In this paper, we denote that and .
Theorem 3.
For , we have
Based on [16], which contains Definition 7 and Theorem 3, many researchers found various expanded numbers and polynomials and their identities, see [15,20].
The main goal of this paper is to find various properties of q-cosine and q-sine Euler polynomials such as addition theorem, partial q-derivative, basic symmetric properties so on. In Section 2, we construct q-cosine and q-sine Euler polynomials. Then, using q-calculus, we identify basic properties of these polynomials. Section 3 presents an investigation of the special properties of q-cosine and q-sine Euler polynomials such as the identity of q-sine Euler polynomials using q-analogues of subtraction and addition. This is based on the properties of q-trigonometric and q-exponential functions. Moreover, we derive relationships between q-cosine and q-sine Euler polynomials and q-cosine and q-sine Bernoulli polynomials. In Section 4, we display the structure of approximate roots for q-cosine and q-sine Euler polynomials and find properties of these polynomials. We present some figures of the approximate roots of these polynomials in a complex plane using Newton’s method.
2. Some Basic Properties of q-cosine and q-sine Euler Polynomials
In this section, we construct the q-cosine and q-sine Euler polynomials by using Theorem 4. From the generating functions of these polynomials, we obtain some basic properties and identities. Moreover, we derive symmetric properties and partial q-derivatives for q-cosine and q-sine Euler polynomials.
Definition 8.
The generating functions of q-cosine Euler polynomials and q-sine Euler polynomials are correspondingly defined by
From Definition 8, q-sine Euler polynomials can be confirmed as the following:
We will introduce the certain form of q-cosine Euler polynomials in Section 4. The motivation to derive the definition of q-cosine Euler polynomials and q-sine Euler polynomials can be found in Theorem 4.
Theorem 4.
For and , we have
Proof.
We defined the generating function of q-Euler polynomials in Definition 6. Let us substitute instead of z in the q-Euler polynomials. By using a property of q-analogues of the sine and cosine functions and by using Definition 1, we can find
By using a similar method as when finding Equation (17), we can also obtain
We can prove Theorem 4 through Equations (17) and (18). ☐
Remark 1.
From the Theorem 4 and Definition 8, the following holds
In [15], and are defined as follows:
Theorem 5.
For any real numbers , we have
where is the q-Euler numbers.
Proof.
From the generating function of q-cosine Euler polynomials, we can find a relation between the q-Euler numbers and as follows.
and we obtain the required result of Theorem 5 .
We also find a relation between the q-Euler numbers and in a similar way as in the proof of and we have the required result. ☐
Theorem 6.
For a nonnegative integer k and , we derive
where is the greatest integer not exceeding x and is the q-Euler polynomials.
Proof.
From the generating function of q-Euler polynomials, we can change the q-cosine Euler polynomials as follows
By using the power series of , the right-hand side of Equation (24) is transformed as
and we complete the proof of Theorem 6 .
By applying the power series of in the generating function of q-sine Euler polynomials, we have
and we finish the proof of Theorem 6 . ☐
Corollary 1.
Let in Theorem 6. Then, the following holds
where is the greatest integer not exceeding x and is the q-Euler polynomials.
Theorem 7.
Let , , and . Then, we have
Proof.
When , we can consider the generating function of the q-cosine Euler polynomials to be
The left-hand side of Equation (29) is changed as follows.
The right-hand side of (29) is transformed as
By using Equations (30) and (31), we find the required result.
In a similar method as in the proof of , we have
Then, we obtain
Therefore, we finish the proof of Theorem 7 . ☐
Corollary 2.
If in Theorem 7, we have
where is the cosine Euler polynomials and is the sine Euler polynomials.
Theorem 8.
For any real number and , we have
Proof.
For any real number x, we can find the partial q-derivative for q-cosine Euler polynomials as
Using the q-derivative of the q-cosine function, we find
From Equation (37), we get
and we obtain the required results.
We also consider the partial q-derivative of q-sine Euler polynomials as
and note that . Then, we obtain the results of Theorem 8. ☐
In [18], Liu and Wang studied some symmetric properties of the Bernoulli and Euler polynomials. Based on the above paper, we observe some symmetric properties of the q-cosine and q-sine Euler polynomials. Moreover, symmetric properties can be found in the cosine and sine Euler polynomials.
Theorem 9.
For any integers , we have
Proof.
To find a symmetric property, we assume form A such that
By considering the generating function of q-cosine Euler polynomials in Equation (41), we can find the following equation:
and
From Equations (42) and (43), we can find the required result.
In a similar way as with form A, we can make form such that
and we can find Theorem 9 in a same manner as . ☐
Corollary 3.
Assume in Theorem 9. Then, the following holds
Corollary 4.
Assume in Theorem 9. Then, the following holds
where is the cosine Euler polynomials and is the sine Euler polynomials.
Theorem 10.
For any integers , and . Then, we obtain
Proof.
To derive a symmetric relation mixing the q-cosine Euler polynomials and the q-sine Euler polynomials, we take form B as the following.
From form B, we can find the following equations:
and
From (49) and (50), we can immediately complete the proof of Theorem 10. ☐
Corollary 5.
Suppose in Theorem 10. Then the following holds
3. Some Special Properties of q-cosine Euler Polynomials and q-sine Euler Polynomials
In this section, we obtain some special properties of q-cosine and q-sine Euler polynomials using the properties of q-trigonometric functions, , and so on. Moreover, we find various types of relationships between q-cosine, sine Euler polynomials and other polynomials.
Theorem 11.
For , we obtain
Proof.
When in the generating function of q-cosine Euler polynomials, , we have
Using and , the left-hand side of Equation (53) can be written as the following:
Comparing the both sides of Equation (54), we obtain the required result.
By using the same method as in the proof of , we have the proof of Theorem 11 . ☐
Corollary 6.
When in Theorem 11, the following holds
where is the cosine Euler polynomials and is the sine Euler polynomials.
Lemma 1.
For and a real number r, we have
Proof.
By substituting instead of x in the generating function of q-cosine Euler polynomials and using q-exponential functions, we derive
Thus, we find the required result immediately.
Putting into x in the generating function of q-cosine Euler polynomials and using q-exponential functions, we have
We find the required result in a similar way as in the proof of .
We consider that
Then, we have the following result.
If we set in x in the generating function of q-sine Euler polynomials, then we have
From Equation (60), we obtain the desired result. ☐
Theorem 12.
Let and . From the Lemma 1, we have
Proof.
By using Lemma 1 and , we obtain
If n is an odd or even number, then we derive the required result.
We omit the proof of Theorem 12 because we obtain the desired result in the same manner. ☐
Corollary 7.
Let in Theorem 12. Then, we have
Corollary 8.
Let in Theorem 12. Then, we have
Corollary 9.
From Lemma 1, one holds
Theorem 13.
For , we have the following relation:
where is the q-Euler polynomials and is the greatest integer not exceeding x.
Proof.
We consider a multiplication between the generating function of q-cosine Euler polynomials and the q-cosine function such as
From Equations (67) and (68), we have
In a similar way, we find the multiplication between the q-sin Euler polynomials and the q-sin function as follows.
We can find (72) by using , which is a property of q-trigonometric functions.
From Equation (72), we can find the required result of Theorem 13. ☐
Corollary 10.
If in Theorem 13, then we have
Corollary 11.
Setting in Theorem 13, one holds
Corollary 12.
From the Theorem 13 and Corollary 11, we have
To find a relationship between the q-cosine Euler polynomials and the q-cosine Bernoulli polynomials, we recall the definitions of q-cosine and q-sine Bernoulli polynomials, see [15]. The q-cosine Bernoulli polynomials and q-cosine Bernoulli polynomials are defined by means of the generating functions
Theorem 14.
Let and . Then we derive
where is the q-cosine Bernoulli polynomials and is the q-sine Bernoulli polynomials.
Proof.
We substitute the generating function of q-cosine Euler polynomials with an expression that is related to the q-cosine Bernoulli polynomials as
From Equation (78), we have
We replace the left-hand side of (79) with the following equation.
Then, the right-hand side of (79) is transformed as
By comparing Equations (80) and (81), we investigate a relation between the q-cosine Euler polynomials and q-cosine Bernoulli polynomials and complete the proof of Theorem 14.
By using a similar method as in , we derive the required result. ☐
Corollary 13.
When in Theorem 14, the following holds
where is the cosine Bernoulli polynomials, and is the sine Bernoulli polynomials.
4. Symmetric Structures of Approximate Roots for q-cosine Euler Polynomials and Their Application
In this section, we show the actual forms for q-cosine and q-sine Euler polynomials using the theorems from Section 2 and the Mathematica program. We observe the structure of the approximate roots of these polynomials and find some properties. We also show examples of q-cosine Euler polynomials using Newton’s method.
First, we discuss q-cosine Euler polynomials. A few forms of q-cosine Euler polynomials are as follows:
Next, we show the approximate roots table of q-cosine Euler polynomials. Based on Equation (83), we construct Table 1 for the approximate roots of q-cosine Euler polynomials. In Table 1, we vary the values of p and n when . Then, we obtain only real roots with in and .

Table 1.
Approximate zeros of .
From Table 1, we can consider two previews:
- (1)
- When n increases, the absolute values of the real roots approach to approximately and 1 for .
- (2)
- When q approaches 1, the approximate root distribution of q-cosine Euler polynomials are spread and most of them appear as real roots.
Figure 1 shows the structure of the approximate roots for q-cosine Euler polynomials. Let and . The left graph in Figure 1 is q=0.99, the middle graph is , and the right graph is . The blue color denotes that n is small, and the red color denotes that n is 30. In Figure 1, we show that the approximate roots of q-cosine Euler polynomials include all real numbers in when . In addition, we conject that the approximate roots of q-cosine Euler polynomials show a circle structure near 0 when q approaches 0 and n continues to increase.
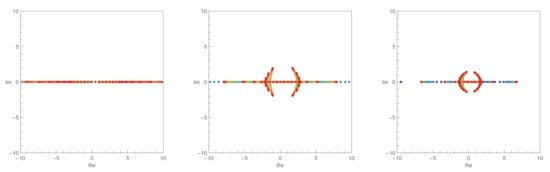
Figure 1.
Stacking structure of approximation roots in q-cosine Euler polynomials when and and .
Figure 2 shows the 3D structure of Figure 1 under the same conditions. The left shape is the approximate roots of q-cosine Euler polynomials when , , and . This shape indicates that all the approximate roots are located on an imaginary axis. The middle shape in Figure 2 shows the approximate roots of q-cosine Euler polynomials when , , and . Here, we can observe the movement of the approximate roots. When and , we can see the right shape of Figure 2. The shape variation in Figure 2 implies that the approximate roots change to imaginary numbers from real numbers and that the root structure for q-cosine Euler polynomials vary according to q.
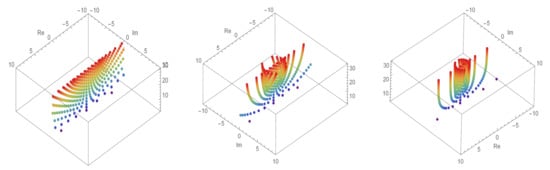
Figure 2.
Stacking structure of the approximation roots in q-cosine Euler polynomials when and and in 3D.
Conjecture 1.
If n increases and , then the approximate roots of q-cosine Euler polynomials display a circle shape near the origin except for some zeros.
In Figure 3, and when . Under these conditions, we observe that the approximate roots of q-cosine Euler polynomials have a symmetric property and include all real numbers. By observing the right graphs in Figure 1 and Figure 3, we can consider Conjecture 2.
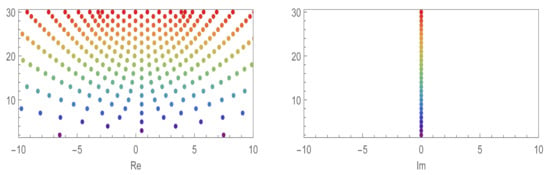
Figure 3.
Stacking structure of the approximate roots in q-cosine Euler polynomials when and .
Conjecture 2.
Prove that is reflection symmetry analytic complex functions which has in addition to the usual , when y is a fixed point in real numbers.
By using the Newton’s method(see [22]), we see the following Example 1. The equation of the left figure in Example 3 is , that is . In Table 1, we note that the approximate roots are and , where and . When we choose and , we obtain the left figure in a complex plane. The complex numbers in the red, violet, yellow, and sky-blue ranges move to , , , and , respectively. The right figure in Example 3 illustrates the 4-th q-cosine Euler polynomials when and . Numbers of the red, violet, yellow, and sky-blue ranges in the complex plane become , , , and , respectively (Figure 4).
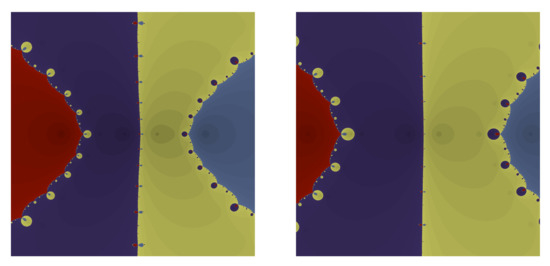
Figure 4.
The 4-th q-cosine Euler polynomials for and .
Example 3.
The 4-th q-cosine Euler polynomials display the following figures in a complex plane:
5. Conclusions
In this paper, we have identified several properties of q-cosine Euler polynomials and q-sine Euler polynomials. In addition, the relationship between polynomials was confirmed according to the various conditions of the variables. We were able to assume the structure of the approximate roots of the q-cosine Euler polynomials and the q-sine Euler polynomials and finally, produce some speculations. The structure of the approximate roots will come out in various ways depending on the condition of the variables, and new methods and theorems related to approaching this needs to be created and proved.
Author Contributions
Conceptualization, J.Y.K.; Data curation, C.S.R.; Formal analysis, C.S.R.; Methodology, J.Y.K.; Software, J.Y.K.; Writing—Original draft, J.Y.K. These authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT and Future Planning (No. 2017R1E1A1A03070483).
Acknowledgments
The authors would like to thank the referees for their valuable comments, which improved the original manuscript in its present form.
Conflicts of Interest
The authors declare that there is no conflict of interests regarding the publication of this paper.
References
- Jackson, H.F. q-Difference equations. Am. J. Math. 1910, 32, 305–314. [Google Scholar] [CrossRef]
- Charalambides, C.A. Discrete q-distributions; Wiley: New York, NY, USA, 2016; ISBN 9781119119050. [Google Scholar]
- Ernst, T. A Comprehensive Treatment of q-calculus; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Gasper, G.; Rahman, M. Basic Hypergeometric Series, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; ISBN 9780511526251. [Google Scholar]
- Andrews, G.E.; Crippa, D.; Simon, K. q-Series arising from the study of random graphs. SIAM J. Discrete Math. 1997, 10, 41–56. [Google Scholar] [CrossRef]
- Charalambides, C.A. On the q-differences of the generalized q-factorials. J. Statist. Plann. Inference 1996, 54, 31–43. [Google Scholar] [CrossRef]
- Exton, H. q-Hypergeometric Functions and Applications; Halstead Press: New York, NY, USA; Ellis Horwood: Chichester, UK, 1983; ISBN 0853124914. [Google Scholar]
- Kemp, A. Certain q-analogues of the binomial distribution. Sankhya A 2002, 64, 293–305. [Google Scholar]
- Ostrovska, S. q-Bernstein polynomials and their iterates. J. Approx. Theory 2003, 123, 232–255. [Google Scholar] [CrossRef]
- Rawlings, D. Limit formulas for q-exponential functions. Discrete Math. 1994, 126, 379–383. [Google Scholar] [CrossRef]
- Sparavigna, A.C. Graphs of q-exponentials and q-trigonometric functions. 2016. Available online: https://hal.archives-ouvertes.fr/hal-01377262 (accessed on 15 June 2020).
- Jackson, H.F. On q-functions and a certain difference operator. Trans. R. Soc. Edinb. 2013, 46, 253–281. [Google Scholar] [CrossRef]
- Phillips, G.M. Bernstein polynomials based on q-integers. Ann. Numer. Anal. 1997, 4, 511–518. [Google Scholar]
- Kac, V.; Pokman, C. Quantum Calculus Universitext; Springer: New York, NY, USA, 2002; ISBN 9781461300717. [Google Scholar]
- Kang, J.Y.; Ryoo, C.S. Various structures of the roots and explicit properties of q-cosine Bernoulli polynomials and q-sine Bernoulli polynomials. Mathematics 2020, 8, 463. [Google Scholar] [CrossRef]
- Kim, T.; Ryoo, C.S. Some identities for Euler and Bernoulli polynomials and their zeros. Axioms 2018, 7, 56. [Google Scholar] [CrossRef]
- Kim, T.; Ryoo, C.S. Sheffer Type Degenerate Euler and Bernoulli Polynomials. Filomat 2019, 33, 6173–6185. [Google Scholar] [CrossRef]
- Liu, H.; Wang, W. Some identities on the Bernoulli, Euler and Genocchi polynomials via power sums and alternate power sums. Discrete Math. 2009, 309, 3346–3363. [Google Scholar] [CrossRef]
- Mahmudov, N.I.; Momenzadeh, M. On a class of q-Bernoulli, q-Euler, and q-Genocchi polynomials. Abstr. Appl. Anal. 2014, 2014, 696454. [Google Scholar] [CrossRef]
- Park, M.J.; Kang, J.Y. A study on the cosine tangent polynomials and sine tangent polynomials. J. Appl. Pure Math. 2020, 2, 47–56. [Google Scholar]
- Carlitz, L. Degenerate Stiling, Bernoulli and Eulerian numbers. Utilitas Math. 1979, 15, 51–88. [Google Scholar]
- Kharab, A.; Guenther, R.B. An Introduction to Numerical Methods: A Matlab Approach, 3rd ed.; Chapman and Hall/crc: Boca Raton, FL, USA, 2018; ISBN-13 978-1439868997. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).