Durrmeyer-Type Generalization of Parametric Bernstein Operators

Abstract

In this paper, we present a Durrmeyer type generalization of parametric Bernstein operators. Firstly, we study the approximation behaviour of these operators including a local and global approximation results and the rate of approximation for the Lipschitz type space. The Voronovskaja type asymptotic formula and the rate of convergence of functions with derivatives of bounded variation are established. Finally, the theoretical results are demonstrated by using MAPLE software.

1. Introduction

A first fundamental result in approximation theory was Weierstrass approximation theorem [1] which forms the solid foundation of Approximation Theory. The proof of the theorem was quite long and difficult. So there were several proofs given by different famous mathematicians. One of them was given by Bernstein [2] which was easy and elegant, which also motivated the researchers to construct operators to deal with the approximation problems in different settings. Here, we give a Durrmeyer type generalization of parametric Bernstein operators. Let $C\left(𝚥\right)$ be the space of all real valued continuous functions $\mathcal{S}$ on the interval $𝚥=[0,1].$ For $\mathcal{S}\in C\left(𝚥\right)$, Chen et al. [3] introduced a new family of generalized Bernstein operators depending upon a non-negative real parameter $0\le \theta \le 1,$ which is given as follows:

$$\begin{array}{c}\hfill T_m^{\left(\theta \right)}(\mathcal{S};x)=\sum _{s=0}^m{p}_{m,s}^{\left(\theta \right)}\left(x\right)\mathcal{S}\left(\frac{s}{m}\right),x\in 𝚥,\end{array}$$

(1)

where

${\displaystyle p_{m,s}^{\left(\theta \right)}\left(x\right)=\left[\left(\genfrac{}{}{0pt}{}{m-2}{s}\right)(1-\theta )x+\left(\genfrac{}{}{0pt}{}{m-2}{s-2}\right)(1-\theta )(1-x)+\left(\genfrac{}{}{0pt}{}{m}{s}\right)\theta x(1-x)\right]x^{s-1}{(1-x)}^{m-s-1}}$,

$m\ge 2$, $p_{1,0}^{\left(\theta \right)}\left(x\right)=1-x$, $p_{1,1}^{\left(\theta \right)}\left(x\right)=x$. For $\theta =1,$ it reduces to original Bernstein operators.

Several types of such operators have been studied so far, for example, Kajla and Acar [4] gave the integral variant of the operators (1) and studied the approximation properties of these operators. Genuine Bernstein–Durrmeyer type operators were defined and studied in [5]. Abel and Heilmann [6] studied the complete asymptotic expansion of the Bernstein–Durrmeyer operators. Cárdenas–Morales and Gupta [7] considered a two-parameter family of summation-integral type operators involving Pólya–Eggenberger distribution. In 2015, Abel et al. [8] presented the Durrmeyer type modification of the Stancu operators and obtained some approximation theorems. Agrawal et al. [9] defined Stancu type Kantorovich modification of q-Bernstein-Schurer operators and studied some approximation theorems on uniform convergence as well as A-statistical convergence. Ansari et al. in [10] proposed Jakimovski–Leviatan–Durrmeyer type operators based on Appell polynomials and obtained some approximation results, e.g.,Voronovskaja type asymptotic formula, rate of convergence and weighted approximation of these operators. Acar et al. [11] presented a general class of linear positive operators and established Voronovskaya type theorems. In 2019, Mursaleen et al. [12] considered Stancu–Jakimovski–Leviatan–Durrmeyer type operators and studied simultaneous approximation and A-statistical approximation properties of these operators.

Acu and Kajla [13] established $\theta$-Bernstein operators depend on parameters ${\rho }_1,{\rho }_2\in \mathbb{N}\cup \left\{0\right\}$ as follows:

$$\begin{array}{c}\hfill {\mathcal{B}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)=\sum _{\mu =0}^{m-{\rho }_1{\rho }_2}{p}_{m-{\rho }_1{\rho }_2,\mu }^{\left(\theta \right)}\left(x\right)\sum _{s=0}^{{\rho }_2}{p}_{{\rho }_2,s}^{\left(\theta \right)}\left(x\right)\mathcal{S}\left(\frac{\mu +s{\rho }_1}{m}\right).\end{array}$$

(2)

If ${\rho }_1={\rho }_2=0,$ these operators reduces to the operators $T_m^{\left(\theta \right)}.$

For $\mathcal{S}\in C\left(𝚥\right),$ we introduce a Durrmeyer type modification of the operators (2) as follows:

$$\begin{array}{c}\hfill U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)=(m+1)\sum _{\mu =0}^{m-{\rho }_1{\rho }_2}{p}_{m-{\rho }_1{\rho }_2,\mu }^{\left(\theta \right)}\left(x\right)\sum _{s=0}^{{\rho }_2}{p}_{{\rho }_2,s}^{\left(\theta \right)}\left(x\right){\int }_0^1{p}_{m,\mu +s{\rho }_1}\left(t\right)\mathcal{S}\left(t\right)dt.\end{array}$$

(3)

The aim of this paper is to derive approximation properties for the operators (3) by working on Korovkin’s results [14]. We also compute the rate of convergence involving modulus of smoothness and Lipschitz type function.

2. Auxiliary Results

In this section, we derive some auxiliary results which will be used in proving our main results of subsequent sections. First, we determine moments and central moments for the operators (3).

Lemma 1.

Let $e_i\left(t\right)=t^i,i=0,1,2\cdots$. For the operators $U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)},$ we have

(i)

$U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(e_0;x)=1;$

(ii)

$U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(e_1;x)={\displaystyle \frac{mx+1}{(m+2)}};$

(iii)

$\begin{array}{l}{U}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(e_2;x)={\displaystyle \frac{x^2\left(m^2-m-2+{\rho }_1{\rho }_2-{\rho }_1^2({\rho }_2-2\theta +2)+2\theta \right)}{(m+3)(m+2)}}\\ +{\displaystyle \frac{x\left(2+4m-{\rho }_1{\rho }_2+{\rho }_1^2({\rho }_2-2\theta +2)-2\theta \right)}{(m+3)(m+2)}}+{\displaystyle \frac{2}{(m+3)(m+2)}};\end{array}$

(iv)

$\begin{array}{l}{U}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(e_3;x)={\displaystyle \frac{x^3}{(m+4)(m+3)(m+2)}}[m^3-3m^2-4m+{\rho }_1{\rho }_2(3m-2)+2{\rho }_1^3({\rho }_2-6\theta +6)\\ -3m{\rho }_1^2(2+{\rho }_2-2\theta )-12(\theta -1)+6m\theta ]\\ +{\displaystyle \frac{x^2}{(m+4)(m+3)(m+2)}}[9m^2+9{\rho }_1{\rho }_2-3m-3m{\rho }_1{\rho }_2-3{\rho }_1^3(6+{\rho }_2-6\theta )-6{\rho }_1^2(2+{\rho }_2-2\theta )\\ +3m{\rho }_1^2(2+{\rho }_2-2\theta )+30(\theta -1)-6m\theta ]\\ +{\displaystyle \frac{x\left(18m-7{\rho }_1{\rho }_2+{\rho }_1^3({\rho }_2-6\theta +6)+6{\rho }_1^2(2+{\rho }_2-2\theta )-18(\theta -1)\right)}{(m+4)(m+3)(m+2)}}+{\displaystyle \frac{6}{(m+4)(m+3)(m+2)}};\end{array}$

(v)

$U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(e_4;x)={\displaystyle \frac{x^4}{(m+5)(m+4)(m+3)(m+2)}}\left[54m-m^2-6m^3+m^4-6{\rho }_1{\rho }_2-14m{\rho }_1{\rho }_2+3{\rho }_1^2{\rho }_2^2-6{\rho }_1^3{\rho }_2^2+3{\rho }_1^4{\rho }_2^2-6m^2{\rho }_1(-{\rho }_2+{\rho }_1(2+{\rho }_2))+8m{\rho }_1^3(6+{\rho }_2-6\theta )+6{\rho }_1^4{\rho }_2(1-2\theta )+6m{\rho }_1^2(2+{\rho }_2-2\theta )+72(-1+\theta )+72{\rho }_1^4(-1+\theta )-12{\rho }_1^2{\rho }_2(-1+\theta )+12{\rho }_1^3{\rho }_2(-1+\theta )+24{\rho }_1^2{(-1+\theta )}^2-60m\theta +12m^2\left(1+{\rho }_1^2\right)\theta +12{\rho }_1{\rho }_2\theta \right]+{\displaystyle \frac{x^3}{(m+5)(m+4)(m+3)(m+2)}}\left[16m^3-124m-36m^2-8{\rho }_1{\rho }_2+54m{\rho }_1{\rho }_2+32{\rho }_1^3{\rho }_2-6{\rho }_1^2{\rho }_2^2+12{\rho }_1^3{\rho }_2^2-6{\rho }_1^4{\rho }_2^2+6m^2{\rho }_1(-{\rho }_2+{\rho }_1(2+{\rho }_2))-12m{\rho }_1^3(6+{\rho }_2-6\theta )-12{\rho }_1^4{\rho }_2(1-2\theta )-42m{\rho }_1^2(2+{\rho }_2-2\theta )-264(-1+\theta )-120{\rho }_1^3(-1+\theta )-144{\rho }_1^4(-1+\theta )+24{\rho }_1^2{\rho }_2(-1+\theta )-12{\rho }_1^3{\rho }_2(-1+\theta )-48{\rho }_1^2{(-1+\theta )}^2+156m\theta -12m^2\left(1+{\rho }_1^2\right)\theta -24{\rho }_1{\rho }_2\theta -12{\rho }_1^3{\rho }_2\theta \right]+{\displaystyle \frac{x^2}{(m+5)(m+4)(m+3)(m+2)}}\left[24m+72m^2+60{\rho }_1{\rho }_2-40m{\rho }_1{\rho }_2-35{\rho }_1^2{\rho }_2-42{\rho }_1^3{\rho }_2-{\rho }_1^4{\rho }_2+3{\rho }_1^2{\rho }_2^2-6{\rho }_1^3{\rho }_2^2+3{\rho }_1^4{\rho }_2^2+4m{\rho }_1^3(6+{\rho }_2-6\theta )+6{\rho }_1^4{\rho }_2(1-2\theta )+36m{\rho }_1^2(2+{\rho }_2-2\theta )+336(-1+\theta )+70{\rho }_1^2(-1+\theta )+180{\rho }_1^3(-1+\theta )+86{\rho }_1^4(-1+\theta )-12{\rho }_1^2{\rho }_2(-1+\theta )+24{\rho }_1^2{(-1+\theta )}^2-96m\theta +12{\rho }_1{\rho }_2\theta +12{\rho }_1^3{\rho }_2\theta \right]+{\displaystyle \frac{x\left(96m-46{\rho }_1{\rho }_2+35{\rho }_1^2{\rho }_2+10{\rho }_1^3{\rho }_2+{\rho }_1^4{\rho }_2-144(-1+\theta )-70{\rho }_1^2(-1+\theta )-60{\rho }_1^3(-1+\theta )-14{\rho }_1^4(-1+\theta )\right)}{(m+5)(m+4)(m+3)(m+2)}}+{\displaystyle \frac{24}{(2+m)(3+m)(4+m)(5+m)}}$.

Let ${\Theta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),m}:=U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}({(t-x)}^m;x),m=1,2,4$ be the central moments of $U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}$.

Lemma 2.

For the operators $U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)},$ we get

(i)

${\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),1}\left(x\right)=\left({\displaystyle \frac{1-2x}{2+m}}\right);$

(ii)

$\begin{array}{l}{\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),2}\left(x\right)={\displaystyle \frac{2}{(2+m)(3+m)}}+{\displaystyle \frac{x(2m-{\rho }_1({\rho }_2-{\rho }_1(2+{\rho }_2-2\theta ))-2(2+\theta ))}{(2+m)(3+m)}}\\ +{\displaystyle \frac{x^2(-2m+{\rho }_1({\rho }_2-{\rho }_1(2+{\rho }_2-2\theta ))+2(2+\theta ))}{(2+m)(3+m)}}.\end{array}$

Lemma 3.

For $m\in \mathbb{N}$, we have

$$U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}({(t-x)}^2;x)\le \frac{{\mathcal{W}}_{{\rho }_1,{\rho }_2}^{\left(\theta \right)}x(1-x)}{(m+2)}={\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(x\right),\forall x\in 𝚥,$$

where ${\mathcal{W}}_{{\rho }_1,{\rho }_2}^{\left(\theta \right)}$ is a positive constant depending on ${\rho }_1,{\rho }_2$ and $\theta .$

Proof. 

This lemma is established by direct computation and the details are missing. □

Remark 1.

For the operators $U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)},$ we get

$$\begin{array}{cc}\hfill & {\displaystyle \underset{m\to \infty }{lim}m{\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),1}\left(x\right)=(1-2x),}\hfill \\ \hfill & {\displaystyle \underset{m\to \infty }{lim}m{\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),2}\left(x\right)=2x(1-x),}\hfill \\ \hfill & {\displaystyle \underset{m\to \infty }{lim}{m}^2{\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),4}\left(x\right)=12x^2{(1-x)}^2.}\hfill \end{array}$$

Lemma 4.

For $\mathcal{S}\in C\left(𝚥\right),$ we have

$$\parallel U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)\parallel \le \parallel \mathcal{S}\parallel .$$

Proof. 

From Lemma 1 and Equation (3), we obtain

$$\begin{array}{cc}\hfill \parallel U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\parallel & \le (m+1)\sum _{\mu =0}^{m-{\rho }_1{\rho }_2}{p}_{m-{\rho }_1{\rho }_2,\mu }^{\left(\theta \right)}\left(x\right)\sum _{s=0}^{{\rho }_2}{p}_{{\rho }_2,s}^{\left(\theta \right)}\left(x\right){\int }_0^1{p}_{m,\mu +s{\rho }_1}\left(t\right)\left|\mathcal{S}\left(t\right)\right|dt\hfill \\ \hfill & \le \parallel \mathcal{S}\parallel U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(e_0;x)=\parallel \mathcal{S}\parallel .\hfill \end{array}$$

 □

Theorem 1.

Suppose that $\mathcal{S}\in C\left(𝚥\right).$ Show that ${\displaystyle \underset{m\to \infty }{lim}{U}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)=\mathcal{S}\left(x\right),}$ uniformly in 𝚥.

Proof. 

Since $U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(1;x)=1,$ $U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(t;x)\to x,$ $U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(t^2;x)\to x^2$ as $m\to \infty ,$ uniformly in 𝚥. By Korovkin’s results, it follows that $U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)$ converges to $\mathcal{S}\left(x\right)$ uniformly on 𝚥. □

3. Voronovskaja Type Theorems

Here, we establish the Voronovskaja, Grüss-Voronovskaja type theorems and related results.

Theorem 2.

Suppose that $\mathcal{S}\in C\left(𝚥\right).$ If ${\mathcal{S}}^{\prime },{\mathcal{S}}^{\prime \prime }$ exists at a point $x\in 𝚥$ then

$$\begin{array}{c}\hfill {\displaystyle \underset{m\to \infty }{lim}m\left(U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)-\mathcal{S}\left(x\right)\right)=(1-2x){\mathcal{S}}^{\prime }\left(x\right)+x(1-x){\mathcal{S}}^{\prime \prime }\left(x\right),}\end{array}$$

(4)

Further, if ${\mathcal{S}}^{\prime \prime }\in C\left(𝚥\right)$ then (4) holds uniformly in 𝚥.

Proof. 

Applying the application of Taylor’s theorem, we have

$$\begin{array}{c}\hfill \mathcal{S}\left(t\right)=\mathcal{S}\left(x\right)+(t-x){\mathcal{S}}^{\prime }\left(x\right)+\frac{1}{2}{(t-x)}^2{\mathcal{S}}^{\prime \prime }\left(x\right)+{\rho }_1(t,x){(t-x)}^2,\end{array}$$

(5)

where ${\rho }_1(t,x)\to 0$ as $t\to x$ and is a continuous function on 𝚥. Applying $U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}$ to (5), we get

$$\begin{array}{c}\hfill U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)-\mathcal{S}\left(x\right)={\mathcal{S}}^{\prime }\left(x\right)U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}((t-x);x)+\frac{1}{2}{\mathcal{S}}^{\prime \prime }\left(x\right)U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}({(t-x)}^2;x)+U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}({\rho }_1(t,x){(t-x)}^2;x),\\ \hfill {\displaystyle \underset{m\to \infty }{lim}m\left(U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)-\mathcal{S}\left(x\right)\right)=(1-2x){\mathcal{S}}^{\prime }\left(x\right)+x(1-x){\mathcal{S}}^{\prime \prime }\left(x\right)+\underset{m\to \infty }{lim}m{U}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}({\rho }_1(t,x){(t-x)}^2;x).}\end{array}$$

Since ${\rho }_1(t,x)\to 0$ as $t\to x,$ for a given $ϵ>0,$ there exists $\delta >0$ such that $|{\rho }_1(t,x)|<ϵ$ whenever $|t-x|<\delta .$ For $|t-x|\ge \delta ,$ we have $|{\rho }_1(t,x)|\le M\frac{{(t-x)}^2}{{\delta }^2},$ for some $M>0.$ Let ${\chi }_{\delta }\left(t\right)$ denote the characteristic function of the interval $(x-\delta ,x+\delta ).$ In view of Remark 1, we have

$$\begin{array}{ccc}\hfill |U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}({\rho }_1(t,x){(t-x)}^2;x)|& \le & U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(\right|{\rho }_1{(t,x)|(t-x)}^2{\chi }_{\delta }\left(t\right);x)+U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(\right|{\rho }_1(t,x)|{(t-x)}^2(1-{\chi }_{\delta }\left(t\right));x)\hfill \\ & <& ϵU_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}({(t-x)}^2;x)+\frac{M}{{\delta }^2}{U}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}({(t-x)}^4;x)\hfill \\ & =& ϵO\left(\frac{1}{m}\right)+O\left(\frac{1}{m^2}\right).\hfill \end{array}$$

which implies that ${\displaystyle \underset{m\to \infty }{lim}m{U}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}({\rho }_1(t,x){(t-x)}^2;x)=0,}$ due to the arbitrariness of $ϵ>0.$ This complete the first half of the theorem.

To show the uniformity postulation, by the definition of uniformly continuity of $\mathcal{S}$ in 𝚥, the $\delta$ must be independent of x and all the other estimates hold uniformly in $x\in 𝚥.$ □

In [15], Acar et al. obtained a Grüss type approximation result and a Grüss-Voronovskaja-type result for linear and positive operators. Many authors have established in this direction so that we refer the authors to [16,17,18] and references therein.

The next result is the Grüss–Voronovskaja type theorem for $U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}$.

Theorem 3.

Let $\mathcal{S},\hslash \in C^2\left(𝚥\right)$. Then, for each $x\in 𝚥$,

$$\begin{array}{c}\hfill \underset{m\to \infty }{lim}m\left\{U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\left(\mathcal{S}\hslash \right);x)-U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\hslash ;x)\right\}={\mathcal{S}}^{\prime }\left(x\right){\hslash }^{\prime }\left(x\right)2x(1-x).\end{array}$$

Proof. 

The following relation holds

$$\begin{array}{cc}\hfill & {\displaystyle U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S}\hslash ;x)-U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\hslash ;x)=U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S}\hslash ;x)-\mathcal{S}\left(x\right)\hslash \left(x\right)-{\left(\mathcal{S}\hslash \right)}^{\prime }\left(x\right){\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),1}\left(x\right)-\frac{1}{2}{\left(\mathcal{S}\hslash \right)}^{\prime \prime }\left(x\right){\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),2}\left(x\right)}\hfill \\ \hfill & -\hslash \left(x\right)\left\{{\displaystyle U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)-\mathcal{S}\left(x\right)-{\mathcal{S}}^{\prime }\left(x\right){\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),1}\left(x\right)-\frac{1}{2}{\mathcal{S}}^{\prime \prime }\left(x\right){\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),2}\left(x\right)}\right\}\hfill \\ \hfill & -U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)\left\{{\displaystyle U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\hslash ;x)-\hslash \left(x\right)-{\hslash }^{\prime }\left(x\right){\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),1}\left(x\right)-\frac{1}{2}{\hslash }^{\prime \prime }\left(x\right){\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),2}\left(x\right)}\right\}\hfill \\ \hfill & {\displaystyle +\frac{1}{2}{\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),2}\left(x\right)\left\{\mathcal{S}\left(x\right){\hslash }^{\prime \prime }\left(x\right)+2{\mathcal{S}}^{\prime }\left(x\right){\hslash }^{\prime }\left(x\right)-{\hslash }^{\prime \prime }\left(x\right)U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)\right\}+{\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),1}\left(x\right)\left\{\mathcal{S}\left(x\right){\hslash }^{\prime }\left(x\right)-{\hslash }^{\prime }\left(x\right)U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)\right\}.}\hfill \end{array}$$

Now, by using Theorem 1, Theorem 2 and Remark 1, we get

$$\begin{array}{c}\underset{m\to \infty }{lim}m\left\{U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S}\hslash ;x)-U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\hslash ;x)\right\}\hfill \\ {\displaystyle =\underset{m\to \infty }{lim}m{\mathcal{S}}^{\prime }\left(x\right){\hslash }^{\prime }\left(x\right){\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),2}\left(x\right)+\underset{m\to \infty }{lim}\frac{1}{2}m{\hslash }^{\prime \prime }\left(x\right)\left\{\mathcal{S}\left(x\right)-U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)\right\}{\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),2}\left(x\right)}\hfill \\ +\underset{m\to \infty }{lim}m{\hslash }^{\prime }\left(x\right)\left\{\mathcal{S}\left(x\right)-U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)\right\}{\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),1}\left(x\right)={\mathcal{S}}^{\prime }\left(x\right){\hslash }^{\prime }\left(x\right)2x(1-x).\hfill \end{array}$$

 □

Lipschitz-type space with two parameters ${\alpha }_1\ge 0,{\alpha }_2>0$ is defined in [19] as below:

$$\begin{array}{c}\hfill Li{p}_M^{({\alpha }_1,{\alpha }_2)}\left(\sigma \right):=\left\{\mathcal{S}\in C\left(𝚥\right):|\mathcal{S}\left(t\right)-\mathcal{S}\left(x\right)|\le M\frac{{|t-x|}^{\sigma }}{{(t+{\alpha }_1{x}^2+{\alpha }_{2}x)}^{\frac{\sigma }{2}}};t\in 𝚥,x\in (0,1]\right\},\end{array}$$

where $0<\sigma \le 1.$

Theorem 4.

Suppose that $\mathcal{S}\in Li{p}_M^{({\alpha }_1,{\alpha }_2)}\left(\sigma \right)$. Prove that

$$\begin{array}{c}\hfill \left|U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)-\mathcal{S}\left(x\right)\right|\le M{\left(\frac{{\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),2}\left(x\right)}{{\alpha }_1{x}^2+{\alpha }_{2}x}\right)}^{\sigma /2},\forall x\in (0,1].\end{array}$$

Proof. 

Using the application of Holder’s inequality and Lemma 2, we may write

$$\begin{array}{ccc}\hfill \left|U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)-\mathcal{S}\left(x\right)\right|& \le & {\displaystyle (m+1)\sum _{\mu =0}^{m-{\rho }_1{\rho }_2}{p}_{m-{\rho }_1{\rho }_2,\mu }^{\left(\theta \right)}\left(x\right)\sum _{s=0}^{{\rho }_2}{p}_{{\rho }_2,s}^{\left(\theta \right)}\left(x\right){\int }_0^1\left|\mathcal{S}\left(t\right)-\mathcal{S}\left(x\right)\right|p_{m,\mu +s{\rho }_1}\left(t\right)dt}\hfill \\ & \le & {\displaystyle (m+1)\sum _{\mu =0}^{m-{\rho }_1{\rho }_2}{p}_{m-{\rho }_1{\rho }_2,\mu }^{\left(\theta \right)}\left(x\right)\sum _{s=0}^{{\rho }_2}{p}_{{\rho }_2,s}^{\left(\theta \right)}\left(x\right){\left({\displaystyle {\int }_0^1{\left|\mathcal{S}\left(t\right)-\mathcal{S}\left(x\right)\right|}^{\frac{2}{\sigma }}{p}_{m,\mu +s{\rho }_1}\left(t\right)dt}\right)}^{\frac{\sigma }{2}}}\hfill \\ & \le & {\left\{{\displaystyle (m+1)\sum _{\mu =0}^{m-{\rho }_1{\rho }_2}{p}_{m-{\rho }_1{\rho }_2,\mu }^{\left(\theta \right)}\left(x\right)\sum _{s=0}^{{\rho }_2}{p}_{{\rho }_2,s}^{\left(\theta \right)}\left(x\right){\int }_0^1{\left|\mathcal{S}\left(t\right)-\mathcal{S}\left(x\right)\right|}^{\frac{2}{\sigma }}{p}_{m,\mu +s{\rho }_1}\left(t\right)dt}\right\}}^{\frac{\sigma }{2}}\hfill \\ & & \times {\left((m+1)\sum _{\mu =0}^{m-{\rho }_1{\rho }_2}{p}_{m-{\rho }_1{\rho }_2,\mu }^{\left(\theta \right)}\left(x\right)\sum _{s=0}^{{\rho }_2}{p}_{{\rho }_2,s}^{\left(\theta \right)}\left(x\right){\int }_0^1{p}_{m,\mu +s{\rho }_1}\left(t\right)dt\right)}^{\frac{2-\sigma }{2}}\hfill \\ & =& {\left({\displaystyle (m+1)\sum _{\mu =0}^{m-{\rho }_1{\rho }_2}{p}_{m-{\rho }_1{\rho }_2,\mu }^{\left(\theta \right)}\left(x\right)\sum _{s=0}^{{\rho }_2}{p}_{{\rho }_2,s}^{\left(\theta \right)}\left(x\right){\int }_0^1{\left|\mathcal{S}\left(t\right)-\mathcal{S}\left(x\right)\right|}^{\frac{2}{\sigma }}{p}_{m,\mu +s{\rho }_1}\left(t\right)dt}\right)}^{\frac{\sigma }{2}}\hfill \\ & \le & M{\left({\displaystyle (m+1)\sum _{\mu =0}^{m-{\rho }_1{\rho }_2}{p}_{m-{\rho }_1{\rho }_2,\mu }^{\left(\theta \right)}\left(x\right)\sum _{s=0}^{{\rho }_2}{p}_{{\rho }_2,s}^{\left(\theta \right)}\left(x\right){\int }_0^1\frac{{(t-x)}^2}{(t+{\alpha }_1{x}^2+{\alpha }_{2}x)}{p}_{m,\mu +s{\rho }_1}\left(t\right)dt}\right)}^{\frac{\sigma }{2}}\hfill \\ & \le & \frac{M}{{\left({\alpha }_1{x}^2+{\alpha }_{2}x\right)}^{\frac{\sigma }{2}}}{\left({\displaystyle (m+1)\sum _{\mu =0}^{m-{\rho }_1{\rho }_2}{p}_{m-{\rho }_1{\rho }_2,\mu }^{\left(\theta \right)}\left(x\right)\sum _{s=0}^{{\rho }_2}{p}_{{\rho }_2,s}^{\left(\theta \right)}\left(x\right){\int }_0^1{(t-x)}^2{p}_{m,\mu +s{\rho }_1}\left(t\right)dt}\right)}^{\frac{\sigma }{2}}\hfill \\ & =& \frac{M}{{\left({\alpha }_1{x}^2+{\alpha }_{2}x\right)}^{\frac{\sigma }{2}}}{U}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}{({(t-x)}^2;x)}^{\frac{\sigma }{2}}\hfill \\ & =& \frac{M}{{\left({\alpha }_1{x}^2+{\alpha }_{2}x\right)}^{\frac{\sigma }{2}}}{\left({\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),2}\left(x\right)\right)}^{\frac{\sigma }{2}}.\hfill \end{array}$$

 □

Theorem 5.

For $\mathcal{S}\in C^1\left(𝚥\right)$ and $x\in 𝚥,$ we have

$$\begin{array}{c}\hfill \left|U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)-\mathcal{S}\left(x\right)\right|\le \left|{\displaystyle \frac{1-2x}{(m+2)}}\right|\left|{\mathcal{S}}^{\prime }\left(x\right)\right|+2\sqrt{{\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),2}\left(x\right)}\omega \left({\mathcal{S}}^{\prime },\sqrt{{\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),2}\left(x\right)}\right).\end{array}$$

(6)

Proof. 

Let $\mathcal{S}\in C^1\left(𝚥\right)$. For any $t,x\in 𝚥,$ we have

$$\mathcal{S}\left(t\right)-\mathcal{S}\left(x\right)={\mathcal{S}}^{\prime }\left(x\right)(t-x)+{\int }_x^t\left({\mathcal{S}}^{\prime }\left(u\right)-{\mathcal{S}}^{\prime }\left(x\right)\right)du.$$

Using $U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(·;x)$ on both sides of the above relation, we have

$$U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S}\left(t\right)-\mathcal{S}\left(x\right);q_m,x)={\mathcal{S}}^{\prime }\left(x\right)U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(t-x;x)+U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left({\int }_x^t\left({\mathcal{S}}^{\prime }\left(u\right)-{\mathcal{S}}^{\prime }\left(x\right)\right)du;x\right)$$

Applying $|\mathcal{S}\left(t\right)-\mathcal{S}\left(x\right)|\le \omega (\mathcal{S},\delta )\left(\frac{|t-x|}{\delta }+1\right),\delta >0,$ we have

$$\left|{\int }_x^t\left({\mathcal{S}}^{\prime }\left(u\right)-{\mathcal{S}}^{\prime }\left(x\right)\right)du\right|\le \omega ({\mathcal{S}}^{\prime },\delta )\left(\frac{{(t-x)}^2}{\delta }+|t-x|\right),$$

it follows that

$$\left|U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)-\mathcal{S}\left(x\right)\right|\le |{\mathcal{S}}^{\prime }\left(x\right)\left|\right|U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(t-x;x)|+\omega ({\mathcal{S}}^{\prime },\delta )\left\{\frac{1}{\delta }{U}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}({(t-x)}^2;x)+U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(\right|t-x|;x)\right\}.$$

Applying Cauchy–Schwarz inequality, we get

$$\begin{array}{ccc}\hfill \left|U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)-\mathcal{S}\left(x\right)\right|& \le & |{\mathcal{S}}^{\prime }\left(x\right)\left|\right|U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(t-x;x)|\hfill \\ & & +\omega ({\mathcal{S}}^{\prime },\delta )\left\{{\displaystyle \frac{1}{\delta }}\sqrt{U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}({(t-x)}^2;x)}+1\right\}\sqrt{U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}({(t-x)}^2;x)}.\hfill \end{array}$$

Now, taking $\delta =\sqrt{{\mathsf{\Theta }}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right),2}\left(x\right)},$ we get (6). □

4. Local Approximation

In this section, we study the local approximation property for our operators with the help of K-functional.

The K-functional is given by:

$$K_2(\mathcal{S},\delta )=inf\left\{\right||\mathcal{S}-\hslash \left|\right|+\delta \left|\right|{\hslash }^{\prime \prime }\left|\right|:\hslash \in W^2\}(\delta >0),$$

where $W^2=\{\hslash :{\hslash }^{\prime \prime }\in C\left(𝚥\right)\}$ and uniform norm on $C\left(𝚥\right)$ is denoted by $\left|\right|.\left|\right|$. By [20] there will be a positive constant $M>0$ such that

$$\begin{array}{c}\hfill K_2(\mathcal{S},\delta )\le M{\omega }_2(\mathcal{S},\sqrt{\delta }),\end{array}$$

(7)

where the second order modulus of continuity for $\mathcal{S}\in C\left(𝚥\right)$ is defined as

$${\displaystyle {\omega }_2(\mathcal{S},\sqrt{\delta })=\underset{0<h\le \sqrt{\delta }}{sup}\underset{x,x+2h\in 𝚥}{sup}|\mathcal{S}(x+2h)-2\mathcal{S}(x+h)+\mathcal{S}\left(x\right)|.}$$

We define the usual modulus of continuity for $\mathcal{S}\in C\left(𝚥\right)$ as

$${\displaystyle \omega (\mathcal{S},\delta )=\underset{0<h\le \delta }{sup}\underset{x,x+h\in 𝚥}{sup}|\mathcal{S}(x+h)-\mathcal{S}\left(x\right)|.}$$

Theorem 6.

For the operators $U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)},$ there exists a constant $M>0$ such that

$$\mid U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)-\mathcal{S}\left(x\right)\mid \le M{\omega }_2\left(\mathcal{S},{(m+2)}^{-1/2}\sqrt{{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}}\left(x\right)\right)+\omega \left(\mathcal{S},\left|\frac{1-2x}{m+2}\right|\right),$$

where $\mathcal{S}\in C\left(𝚥\right)$, $\theta \in 𝚥,$ ${\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(x\right)={\phi }^2\left(x\right)+\frac{1}{(m+2)}$ and $x\in 𝚥.$

Proof. 

We define the auxiliary operators as follows:

$${\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)=U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)+\mathcal{S}\left(x\right)-\mathcal{S}\left(\frac{mx+1}{m+2}\right).$$

Then, we can easily check that

$${\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(1;x)=1and{\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(t;x)=x.$$

By the application of Taylor’s theorem and taking $t\in 𝚥$ and $\hslash \in W^2,$ we get

$$\hslash \left(t\right)=\hslash \left(x\right)+(t-x){\hslash }^{\prime }\left(x\right)+{\int }_x^t(t-u){\hslash }^{\prime \prime }\left(u\right)du.$$

The operator ${\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}$ is applied in the above equation on both sides, we obtain

$$\begin{array}{cc}\hfill {\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\hslash ;x)& =\hslash \left(x\right)+{\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left({\int }_x^t(t-u){\hslash }^{\prime \prime }\left(u\right)du\right)\hfill \\ \hfill & =\hslash \left(x\right)+U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left({\int }_x^t(t-u){\hslash }^{\prime \prime }\left(u\right)du,x\right)-{\int }_x^{\frac{mx+1}{(m+2)}}\left(\frac{mx+1}{m+2}-u\right){\hslash }^{\prime \prime }\left(u\right)du.\hfill \end{array}$$

Hence

$$\begin{array}{cc}\hfill \mid {\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\hslash ;x)-\hslash \left(x\right)\mid & \le U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(|{\int }_x^t|t-u||{\hslash }^{\prime \prime }\left(u\right)\left|du\right|,x\right)+\left|{\int }_x^{\frac{mx+1}{(m+2)}}\right|\frac{mx+1}{m+2}-u\left|\left|{\hslash }^{\prime \prime }\left(u\right)\right|du\right|\hfill \\ \hfill & \le \left\{U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}({(t-x)}^2;x)+{\left(\frac{mx+1}{m+2}-x\right)}^2\right\}\left|\right|{\hslash }^{\prime \prime }\left|\right|\hfill \\ \hfill & =\left\{U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}({(t-x)}^2;x)+{\left(\frac{1-2x}{m+2}\right)}^2\right\}\left|\right|{\hslash }^{\prime \prime }\left|\right|.\hfill \end{array}$$

(8)

From Lemma 3, we have

$$\begin{array}{cc}\hfill U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}({(t-x)}^2;x)+{\left(\frac{1-2x}{m+2}\right)}^2& \le \frac{2}{(m+2)}{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(x\right)+{\left(\frac{1-2x}{m+2}\right)}^2\hfill \\ & \le \frac{2}{(m+2)}{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(x\right)+\frac{1}{{(m+2)}^2}\hfill \\ & \le \frac{3}{(m+2)}{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(x\right).\hfill \end{array}$$

(9)

Thus, by (8) we have

$$\begin{array}{c}\hfill \mid {\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\hslash ;x)-\hslash \left(x\right)\mid \le \frac{3}{(m+2)}{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(x\right)\left|\right|{\hslash }^{\prime \prime }\left|\right|,\end{array}$$

(10)

where $x\in 𝚥.$ Furthermore, by Lemma 4, we have

$$\begin{array}{cc}\hfill \mid {\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)\mid & \le 3\left|\right|\mathcal{S}\left|\right|,\hfill \end{array}$$

(11)

for all $\mathcal{S}\in C\left(𝚥\right)$ and $x\in 𝚥$.

Now, for $\mathcal{S}\in C\left(𝚥\right)$ and $\hslash \in W^2$, using (10) and (11) we obtain that

$$\begin{array}{cc}\hfill \mid U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)-\mathcal{S}\left(x\right)\mid & \le \left|{\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)-\mathcal{S}\left(x\right)+\mathcal{S}\left(\frac{mx+1}{m+2}\right)-\mathcal{S}\left(x\right)\right|\hfill \\ & \le |{\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S}-\hslash ;x)|+|{\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\hslash ;x)-\hslash \left(x\right)|+|\hslash \left(x\right)-\mathcal{S}\left(x\right)|\hfill \\ & +\left|\mathcal{S}\left(\frac{mx+1}{m+2}\right)-\mathcal{S}\left(x\right)\right|\hfill \\ & \le 4\left|\right|\mathcal{S}-\hslash \left|\right|+\frac{3}{(m+2)}{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(x\right)\left|\right|{\hslash }^{\prime \prime }\left|\right|+\omega \left(\mathcal{S},\left|\frac{1-2x}{m+2}\right|\right).\hfill \end{array}$$

Using the property of infimum on the right hand side over all $\hslash \in W^2,$ we have

$$\begin{array}{c}\hfill \mid U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)-\mathcal{S}\left(x\right)\mid \le 4K_2\left(\mathcal{S},\frac{1}{(m+2)}{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(x\right)\right)+\omega \left(\mathcal{S},\left|\frac{1-2x}{m+2}\right|\right).\end{array}$$

Now by examining the relation (7), we get

$$\mid U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)-\mathcal{S}\left(x\right)\mid \le M{\omega }_2\left(\mathcal{S},{(m+2)}^{-1/2}\sqrt{{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}}\left(x\right)\right)+\omega \left(\mathcal{S},\left|\frac{1-2x}{m+2}\right|\right).$$

 □

5. Global Approximation

The following result provides the global approximation using the modulus of continuity of Ditzian–Totik and the related K-functional.

Suppose that $\mathcal{S}\in C\left(𝚥\right)$ and $\phi \left(x\right)$ is defined as $\sqrt{x(1-x)},x\in 𝚥.$ The second order modulus of continuity which is given by Ditzian-Totik

$$\begin{array}{c}\hfill {\displaystyle {\omega }_2^{\phi }(\mathcal{S},\sqrt{\delta })=\underset{0<h\le \sqrt{\delta }}{sup}\underset{x\pm h\phi \left(x\right)\in 𝚥}{sup}\mid \mathcal{S}(x+h\phi \left(x\right))-2\mathcal{S}\left(x\right)+\mathcal{S}(x-h\phi \left(x\right))\mid ,}\end{array}$$

and related K-functional is defined as,

$$\begin{array}{c}\hfill {\tilde{K}}_{2,\phi \left(x\right)}(\mathcal{S},\delta )=inf\left\{\right||\mathcal{S}-\hslash \left|\right|+\delta \left|\right|{\phi }^2{\hslash }^{\prime \prime }\left|\right|+{\delta }^2\left|\right|{\hslash }^{\prime \prime }\left|\right|:\hslash \in W^2\left(\phi \right)\},(\delta >0),\end{array}$$

where $W^2\left(\phi \right)=\{\hslash \in C\left(𝚥\right):{\hslash }^{\prime }\in A{C}_{loc}𝚥,{\phi }^2{\hslash }^{\prime \prime }\in C\left(𝚥\right)\}$ and ${\hslash }^{\prime }\in A{C}_{loc}𝚥$ means that ℏ is derivable and ${\hslash }^{\prime }$ is absolutely continuous on every closed interval $[a,b]\subset (0,1).$ By ([21], Theorem 1.3.1) we can say that ∃$M>0,$ such that

$$\begin{array}{c}\hfill {\tilde{K}}_{2,\phi \left(x\right)}(\mathcal{S},\delta )\le M{\omega }_2^{\phi }(\mathcal{S},\sqrt{\delta }).\end{array}$$

(12)

The first order Ditzian–Totik modulus is defined as

$${\displaystyle \overrightarrow{{\omega }_{\psi }}(\mathcal{S},\delta )=\underset{0<h\le \delta }{sup}\underset{x\pm \frac{h}{2}\psi \left(x\right)\in 𝚥}{sup}\left|\mathcal{S}\left(x+\frac{h}{2}\psi \left(x\right)\right)-\mathcal{S}\left(x-\frac{h}{2}\psi \left(x\right)\right)\right|,}$$

where $\psi :𝚥\to \mathbb{R}$ is an admissible step-weight function.

Now we state our next main theorem.

Theorem 7.

Let $\mathcal{S}\in C\left(𝚥\right)$ and $0\le \theta \le 1.$ Then, for $x\in 𝚥,$

$$\left|\right|U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\mathcal{S}-\mathcal{S}\left|\right|\le M{\omega }_2^{\phi }(\mathcal{S},{(m+2)}^{-1/2})+\overrightarrow{{\omega }_{\psi }}\left(\mathcal{S},{(m+2)}^{-1}\right)+\omega \left(\mathcal{S};{(m+2)}^{-1}\right),$$

where ${\phi }^2\left(x\right)=x(1-x)$ and $\psi \left(x\right)=\left\{\begin{array}{cc}1-2x& x\in \left[0,1/2\right]\\ 2x-1& x\in \left[1/2,1\right]\end{array}\right..$

Proof. 

The auxiliary operators is considered as

$${\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)=U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)+\mathcal{S}\left(x\right)-\mathcal{S}\left(\frac{mx+1}{m+2}\right).$$

Let $\hslash \in W^2\left(\phi \right)$ then by expanding ℏ using Taylor’s theorem and as given in the proof of Theorem 6, we get

$$\begin{array}{c}\hfill \mid {\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\hslash ;x)-\hslash \left(x\right)\mid \le U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(|{\int }_x^t|t-u||{\hslash }^{\prime \prime }\left(u\right)\left|du\right|,x\right)+{\int }_x^{\frac{mx+1}{(m+2)}}|\frac{mx+1}{m+2}-u|\left|{\hslash }^{\prime \prime }\left(u\right)\right|du.\end{array}$$

(13)

Setting $u=\beta x+(1-\beta )t,\beta \in 𝚥,$ and also applying the concavity of ${\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}$, we have

$$\begin{array}{c}\hfill \frac{\mid t-u\mid }{{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(u\right)}=\frac{\beta \mid t-x\mid }{{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\beta x+(1-\beta )t)}\le \frac{\beta \mid t-x\mid }{{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(x\right)\beta +{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(t\right)(1-\beta )}\le \frac{\mid t-x\mid }{{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(x\right)}.\end{array}$$

(14)

Thus, using (14) in the inequality (13)

$$\begin{array}{cc}\hfill \mid {\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\hslash ;x)-\hslash \left(x\right)\mid & \le U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(\left|{\int }_x^t\frac{|t-u|}{{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(u\right)}du\right|,x\right)\left|\right|{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}{\hslash }^{\prime \prime }\left|\right|+\left({\int }_x^{\frac{mx+1}{(m+2)}}\frac{|\frac{mx+1}{m+2}-u|}{{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(u\right)}du\right)\left|\right|{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}{\hslash }^{\prime \prime }\left|\right|.\hfill \\ \hfill & \le \frac{1}{{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}\left(x\right)}\left|\right|{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}{\hslash }^{\prime \prime }\left|\right|\left[U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}({(t-x)}^2;x)+{\left(\frac{1-2x}{m+2}\right)}^2\right].\hfill \end{array}$$

(15)

Now, using the inequality (9), we get

$$\begin{array}{cc}\hfill \mid {\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\hslash ;x)-\hslash \left(x\right)\mid & \le \frac{3}{(m+2)}\left|\right|{\delta }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}{\hslash }^{\prime \prime }\left|\right|\hfill \\ \hfill & \le \frac{3}{(m+2)}\left(\left|\right|{\phi }^2{\hslash }^{\prime \prime }\left|\right|+\frac{1}{(m+2)}\left|\right|{\hslash }^{\prime \prime }\left|\right|\right).\hfill \end{array}$$

Applying (11) and (15), we have for $\mathcal{S}\in C\left(𝚥\right),$

$$\begin{array}{cc}\hfill \mid U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)-\mathcal{S}\left(x\right)\mid & \le \mid {\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S}-\hslash ,x)\mid +\mid {\overline{U}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\hslash ;x)-\hslash \left(x\right)\mid +\mid \hslash \left(x\right)-\mathcal{S}\left(x\right)\mid \hfill \\ & +|\mathcal{S}\left(\frac{mx+1}{m+2}\right)-\mathcal{S}\left(x\right)|\hfill \\ & \le 4\left|\right|\mathcal{S}-\hslash \left|\right|+\frac{3}{(m+2)}\left|\right|{\phi }^2{\hslash }^{\prime \prime }\left|\right|+\frac{3}{{(m+2)}^2}\left|\right|{\hslash }^{\prime \prime }\left|\right|+|\mathcal{S}\left(\frac{mx+1}{m+2}\right)-\mathcal{S}\left(x\right)|\hfill \end{array}$$

For all $\hslash \in W^2\left(\phi \right)$ using the property of infimum on the right hand side, we have

$$\begin{array}{c}\hfill \mid U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)-\mathcal{S}\left(x\right)\mid \le 4{\tilde{K}}_{2,\phi }\left(\mathcal{S},\frac{1}{m+2}\right)+|\mathcal{S}\left(\frac{mx+1}{m+2}\right)-\mathcal{S}\left(x\right)|.\end{array}$$

(16)

Also,

$$\begin{array}{cc}\hfill |\mathcal{S}\left(\frac{mx+1}{m+2}\right)-\mathcal{S}\left(x\right)|& =|\mathcal{S}\left(x+\frac{1-2x}{m+2}\right)-\mathcal{S}\left(x\right)|\hfill \\ \hfill & \le |\mathcal{S}\left(x+\frac{(1-2x)}{m+2}\right)-\mathcal{S}\left(x-\frac{(1-2x)}{m+2}\right)|+|\mathcal{S}\left(x-\frac{(1-2x)}{m+2}\right)-\mathcal{S}\left(x\right)|\hfill \\ \hfill & \le \overrightarrow{{\omega }_{\psi }}\left(\mathcal{S},{(m+2)}^{-1}\right)+\omega \left(\mathcal{S};{(m+2)}^{-1}\right).\hfill \end{array}$$

(17)

Hence, combining (12), (16) and (17), the desired relation is immediate. □

6. Rate of Approximation

In this section, we study the rate of convergence of functions with derivatives of bounded variation.

The class of all absolutely continuous functions $\mathcal{S}$ is denoted by $DB{V}_{\left(𝚥\right)}$, defined and having a derivative ${\mathcal{S}}^{\prime }$ on 𝚥, analogous to a bounded variation function on 𝚥.

The representation of functions $\mathcal{S}$ $\in DB{V}_{\left(𝚥\right)}$ is

$$\begin{array}{c}\hfill \mathcal{S}\left(x\right)={\int }_0^x\hslash \left(t\right)dt+\mathcal{S}\left(0\right)\end{array}$$

where ℏ is a bounded variation function on 𝚥.

The operators $U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)$ also admit the integral representation

$$\begin{array}{c}\hfill U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)={\int }_0^1{\mathcal{N}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(x,t)\mathcal{S}\left(t\right)dt,\end{array}$$

(18)

where the kernel ${\mathcal{N}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(x,t)$ is given by

$${\mathcal{N}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(x,t)=(m+1)\sum _{\mu =0}^{m-{\rho }_1{\rho }_2}{p}_{m-{\rho }_1{\rho }_2,\mu }^{\left(\theta \right)}\left(x\right)\sum _{s=0}^{{\rho }_2}{p}_{{\rho }_2,s}^{\left(\theta \right)}\left(x\right)p_{m,\mu +s{\rho }_1}\left(t\right).$$

Lemma 5.

For a fixed $x\in (0,1)$ and sufficiently large m, we have

(i)

${\displaystyle {\lambda }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(x,y)={\int }_0^y{\mathcal{N}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(x,t)dt\le {\displaystyle \frac{{\mathcal{W}}_{{\rho }_1,{\rho }_2}^{\left(\theta \right)}}{(m+2)}}\frac{x(1-x)}{{(x-y)}^2},0\le y<x,}$

(ii)

${\displaystyle 1-{\lambda }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(x,z)={\int }_z^1{\mathcal{N}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(x,t)dt\le }$${\displaystyle \frac{{\mathcal{W}}_{{\rho }_1,{\rho }_2}^{\left(\theta \right)}}{(m+2)}}{\displaystyle \frac{x(1-x)}{{(z-x)}^2}},$$x<z<1,$

where ${\mathcal{W}}_{{\rho }_1,{\rho }_2}^{\left(\theta \right)}$ is given in Lemma 3.

Proof. 

$\left(i\right)$ From Lemma 3, we get

$$\begin{array}{ccc}\hfill {\lambda }_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(x,y)& =& \underset{0}{\overset{y}{\int }}{\mathcal{N}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(x,t)dt\le {\int }_0^y{\left(\frac{x-t}{x-y}\right)}^2{\mathcal{N}}_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(x,t)dt\hfill \\ & =& U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}({(t-x)}^2;x){(x-y)}^{-2}\le {\displaystyle \frac{{\mathcal{W}}_{{\rho }_1,{\rho }_2}^{\left(\theta \right)}}{(m+2)}}{\displaystyle \frac{x(1-x)}{{(x-y)}^2}}.\hfill \end{array}$$

The $\left(ii\right)$ can be proved in the same way hence the details are skipped. □

Theorem 8.

Suppose that $\mathcal{S}$ $\in DBV\left(𝚥\right).$ Then for every $x\in (0,1)$ and sufficiently large m, we have

$$\begin{array}{ccc}\hfill |U_{m,{\rho }_1,{\rho }_2}^{\left(\theta \right)}(\mathcal{S};x)-\mathcal{S}\left(x\right)|& \le & \frac{(1-2x)}{(m+2)}\frac{|{\mathcal{S}}^{\prime }(x+)+{\mathcal{S}}^{\prime }(x-)|}{2}+\sqrt{\frac{{\mathcal{W}}_{{\rho }_1,{\rho }_2}^{\left(\theta \right)}x(1-x)}{(m+2)}}\frac{|{\mathcal{S}}^{\prime }(x+)-{\mathcal{S}}^{\prime }(x-)|}{2}\hfill \\ & & +\frac{{\mathcal{W}}_{{\rho }_1,{\rho }_2}^{\left(\theta \right)}(1-x)}{(m+2)}\sum _{s=1}^{\left[\sqrt{m}\right]}\underset{x-(x/s)}{\overset{x}{\bigvee }}\left({\mathcal{S}}_x^{\prime }\right)+\frac{x}{\sqrt{m}}\underset{x-(x/\sqrt{m})}{\overset{x}{\bigvee }}\left({\mathcal{S}}_x^{\prime }\right)\hfill \\ & & +\frac{{\mathcal{W}}_{{\rho }_1,{\rho }_2}^{\left(\theta \right)}x}{(m+2)}\sum _{s=1}^{\left[\sqrt{m}\right]}\underset{x}{\overset{x+\left(\right(1-x)/s)}{\bigvee }}\left({\mathcal{S}}_x^{\prime }\right)+\frac{(1-x)}{\sqrt{m}}\underset{x}{\overset{x+((1-x)/\sqrt{m})}{\bigvee }}\left({\mathcal{S}}_x^{\prime }\right),\hfill \end{array}$$

where ${\bigvee }_c^d\left({\mathcal{S}}_x^{\prime }\right)$ denotes the total variation of ${\mathcal{S}}_x^{\prime }$ on $[c,d]$ and ${\mathcal{S}}_x^{\prime }$ is defined by

$$\begin{array}{c}\hfill {\mathcal{S}}_x^{\prime }\left(t\right)=\left\{\begin{array}{cc}{\mathcal{S}}^{\prime }\left(t\right)-{\mathcal{S}}^{\prime }(x-),& 0\le t<x\\ 0,& t=x\\ {\mathcal{S}}^{\prime }\left(t\right)-{\mathcal{S}}^{\prime }(x+)& x<t<1.\end{array}\right.\end{array}$$

(19)

Proof. 

This theorem can be proved in the same way as in ([4], Theorem 7). Hence, the proof of this theorem is skipped. □

7. Numerical Examples

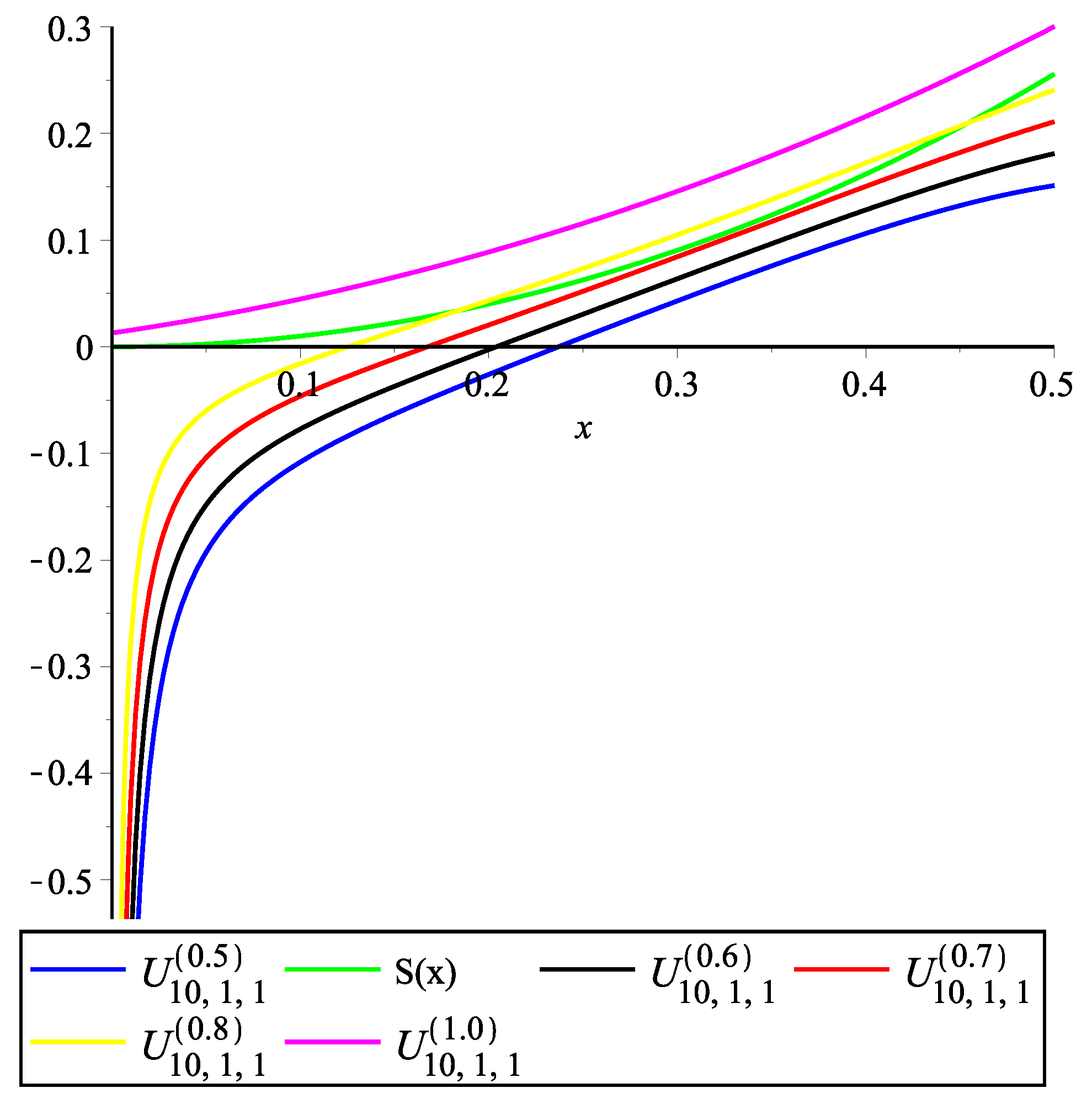
In the following examples, we demonstrate the theoretical results by graphs.

Example 1.

Let $m=10,{\rho }_1={\rho }_2=1$ and $\theta =0.5,0.6,0.7,0.8,1.0.$ The convergence of the operators $U_{10,1,1}^{\left(0.5\right)}(\mathcal{S};x)$, $U_{10,1,1}^{\left(0.6\right)}(\mathcal{S};x)$, $U_{10,1,1}^{\left(0.7\right)}(\mathcal{S};x)$, $U_{10,1,1}^{\left(0.8\right)}(\mathcal{S};x)$ and $U_{10,1,1}^{\left(1.0\right)}(\mathcal{S};x)$ to the function $\mathcal{S}\left(x\right)=x^2{e}^{\frac{x^3}{x+5}}$ is illustrated in Figure 1.

Example 2.

Let $m=50,{\rho }_1={\rho }_2=1$ and $\theta =0.5,0.6,0.7,0.8,1.0.$ The convergence of the operators $U_{50,1,1}^{\left(0.5\right)}(\mathcal{S};x)$, $U_{50,1,1}^{\left(0.6\right)}(\mathcal{S};x)$, $U_{50,1,1}^{\left(0.7\right)}(\mathcal{S};x)$, $U_{50,1,1}^{\left(0.8\right)}(\mathcal{S};x)$ and $U_{50,1,1}^{\left(1.0\right)}(\mathcal{S};x)$ to the function $\mathcal{S}\left(x\right)=x^3{e}^{\frac{x^2}{x+10}}$ is illustrated in Figure 2.

8. Conclusions

We have introduced generalized Bernstein–Durrmeyer type operators depending on non-negative integers. We developed many approximation properties such as local and global approximation, the rate of approximation for the Lipschitz type space, Voronovskaja type asymptotic formula and the rate of convergence of functions with derivatives of bounded variation. The constructed operators have better flexibility and rate of convergence which are depending on the selection of the ${\rho }_1,{\rho }_2$ and $\theta .$ Graphical representations of our operators for different selections of ${\rho }_1,{\rho }_2$ and $\theta$ are also given.