Abstract
In the current study, the characteristics of heat transfer of a steady, two-dimensional, stagnation point, and magnetohydrodynamic (MHD) flow of shear thickening Casson fluid on an exponentially vertical shrinking/stretching surface are examined in attendance of convective boundary conditions. The impact of the suction parameter is also considered. The system of governing partial differential equations (PDEs) and boundary conditions is converted into ordinary differential equations (ODEs) with the suitable exponential similarity variables of transformations and then solved using the shooting method with the fourth order Runge–Kutta method. Similarity transformation is an important class of phenomena in which scale symmetry allows one to reduce the number of independent variables of the problem. It should be noted that solutions of the ODEs show the symmetrical behavior of the PDES for the profiles of velocity and temperature. Similarity solutions are obtained for the case of stretching/shrinking and suction parameters. It is revealed that there exist two ranges of the solutions in the specific ranges of the physical parameters, three solutions depend on the opposing flow case where stagnation point (A) should be equal to 0.1, two solutions exist when λ1 = 0 where λ1 is a mixed convection parameter and A > 0.1, and a single solution exists when λ1 > 0. Moreover, the effects of numerous applied parameters on velocity, temperature distributions, skin friction, and local Nusselt number are examined and given through tables and graphs for both shrinking and stretching surfaces.
1. Introduction
The topic of boundary layer fluid flow on the stretching surfaces is widely investigated for single solution cases. Stretching surface has many applications in many processes of manufacturing, such as the extrusion of molten polymers due to the slit die in the production of plastic sheets, paper production, wires as well as in the fiber coating process of foodstuffs. The qualities of final products in such processes largely depend upon the cooling rate in the process of heat exchange. A magnetohydrodynamic parameter is an important parameter to use, such that the rate of the cooling might be controlled so that the desired products with quality can be obtained. Crane [1] gave the method of solution for the incompressible steady-state 2D boundary layer flow in the case of viscous fluid on the stretching surface. Furthermore, the problem examined by Crane has been studied more by extending it into many diverse aspects–some of its recent important directions over the stretching flows were considered by Mabood et al., [2], Rana et al., [3], Hamad [4], Hassan et al. [5] and Haq et al., [6]. Hamad and Ferdows [7] examined metallic nanofluid over a stretching surface. Vajravelu [8] and Cortell [9] considered viscous fluid on the non-linear stretching sheet. In this paper, we also considered the stretching surface because of its extensive usages in different areas.
During the past few decades, the stagnation-point flow has engrossed the intention of many scholars because of its growing industrial and scientific utilization—for example, electronic devices cooled by fans, cooling of nuclear reactors during an emergency shutdown, solar central receivers exposed to wind currents, hydrodynamic processes, etc. In fluid mechanics problems, the point in the flow field where the fluid local velocity becomes zero is known as a stagnation point. This point occurs at an object facade where the fluid is at rest because of a force exerted by the object. Hayat et al. [10] considered the stagnation point of Casson fluid flow on the vertical linear surface by including the viscous dissipation effect. The governing equations were resolved by homotopic analysis and the velocity field and fluid temperature were calculated to decrease Prandtl count functions. Casson fluid can be defined as a shear thinning fluid which is presumed to include an unlimited viscosity at zero shear rate, a yield stress at which no flow exists, and zero viscosity at an infinite shear rate. Abbas et al. [11] inspected Casson fluid on the stretching/shrinking surface where a fluid is the stagnation point flow. It was concluded during the examination that the velocity field rises by increasing the Casson parameter, but the thickness of the momentum boundary layer declines. In an analysis of stagnation point flow, Bhattacharyya et al. [12] obtained a dual solution. Recently, Nadeem et al. [13] investigated the three-dimensional stagnation point flow of nanofluids and obtained dual solutions. They concluded that a stable solution is a primary solution. The significant research is listed on such a phenomenon can be seen in the papers of Bhattacharyya [14]; Hayat et al. [15]; Ramesh et al. [16]; Haldar et al. [17]; Shafiq et al. [18]; and Jafarimoghaddam [19].
In the last couple of years, the non-uniqueness of solutions of fluid flow problems has been considered on the moving, shrinking and stretching sheets in the presence and absence of a bouncy effect by many researchers [20,21]. These multiple solutions exist due to several physical parameters’ impacts, such as the suction parameter, mixed convection parameter, and so forth. Most past investigations demonstrated that the probabilities of occurrence of numerous solutions of fluid flow on a shrinking surface are higher, as a contrast with stretching surfaces [12]. The possibilities of non-uniqueness solutions of the flow field on a stretching surface are probable when a flow is opposing or when there is stagnation point flow. Similarly, multiple solutions for Newtonian fluids can be obtained easily as compared to non-Newtonian fluids. Several researchers have proposed that because of non-linearity in the fluid model, numerous solutions exist [20,22]. However, the models of non-Newtonian fluids contain many non-linear terms and because of these terms, multiple solutions are not going to exist. The value of several solutions for fluid boundary layers has significantly increased due to the occurrence of these fluids in many industrial applications [23]. Numerous solutions in actual situations of fluid flow problems cannot be visualized, because in reality many researchers have failed to notice multiple solutions [24]. The multiple solutions of magnetohydrodynamic (MHD) fluid flow problems have been examined experimentally as well as numerically by several scholars. Ishak et al. [25] considered the mixed convective MHD flow next to incompressible viscous fluid flow and obtained dual solutions. Subhashini et al. [26] considered the MHD convection mixed flow over a vertical surface and found the dual solution using the shooting technique. Ridha and Curie [27] were possibly the first to indicate that there are dual solutions in the opposing flow system and that the flow regime persists. The goal of this research is to examine the stagnation point flow of Casson fluid on a permeable exponentially vertical stretching and shrinking surfaces unanimously with the effect of convective boundary condition numerically.
The governing PDEs are first transformed into ODEs. The obtained system of equations is converted from boundary value problems (BVPs) to initial value problems (IVPs) with the help of the shooting method. Finally, the system of equations of IVPs is solved by the Runge Kutta (RK) method with the aid of maple software in the shootlib function. Furthermore, the three-stage Labatto three-A method is applied to performed stability analysis with the help of a bvp4c solver in MATLAB.
2. Mathematical Description of the Problem
We considered an incompressible, steady, 2-D stagnation point flow of Casson electrically conducting fluid on an exponentially vertical shrinking/stretching sheet with the convective boundary condition effect, as revealed in Figure 1. It is also supposed that the state of the isotropic rheological equation and the incompressible flow of the Casson fluid is defined as (see Lund et al. [28]):
where is the plastic dynamic viscosity, denotes the yield stress of the fluid, and the product of deformation rate component is denoted by where π = is the (i, j)-th deformation rate component and the critical value of is . The uniform magnetic field of the strength is B, which was applied perpendicularly to the stretching/shrinking surface (refer to Figure 1). It is supposed that a constant convective sheet temperature is , while is the ambient fluid temperature where . Due to the very low value of the magnetic Reynolds number, the induced magnetic field vanished.
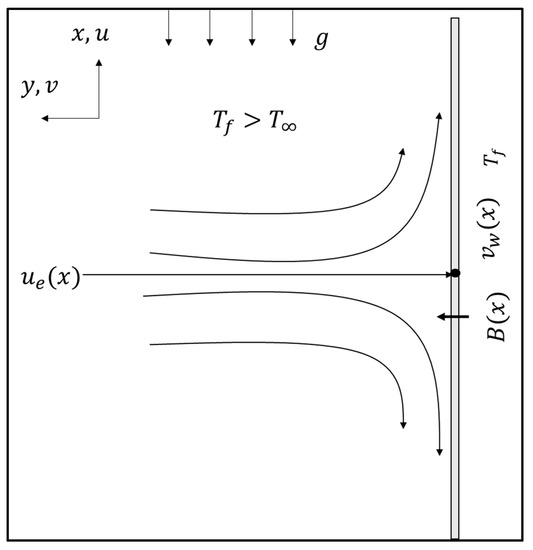
Figure 1.
The geometry of the problem.
The equations of steady Casson fluid flow over the vertical surface with all assumptions can be expressed as follows:
Along with boundary conditions
In these equations, u and v are the velocity components along the direction of x- and y-axis, respectively. Moreover, is the fluid density, is the Casson fluid parameter, is the kinematic viscosity, is the electrical conductivity of fluid, B = is the magnetic field where is the magnetic constant, T is the fluid temperature, and is the thermal diffusivity. Furthermore, is the temperature of wall, and is the ambient temperature. In addition, the thermal conductivity of Casson fluid is and the convective heat transfer coefficient is , where S is the suction/injunction parameter, and is the velocity of surface.
We look for the similarity solutions of Equations (2)–(4) by introducing the following transformations
and the stream function can be expressed in velocity components as,
By applying Equations (6) and (7) in Equations (2)–(5), we have
Along with these conditions
where is the magnetic parameter, is the stretching/shrinking parameter, denotes the Prandtl number, is Biot number or convective parameter where ( is a constant), which implies that , is the mixed convection parameter where Gr is the heat Grashof number. It should be noted that the flow in opposite (assisting) flow is indicated by
The physical quantities of interest are the skin friction coefficient and the local Nusselt number, which are written in the following terms:
where is the local Reynolds number.
3. Stability Analysis
In the current study, we found triple solutions of Equations (8) and (9) along with boundary conditions (10) for both surfaces. Thus, it is needed to perform stability analysis to notice a stable solution which can be physically reliable after the time passes. In order to accomplish the solutions’ temporal stability, the unsteady form of Equations (3) and (4) must be considered by proposing the new dimensionless time variable where is related to the initial solutions of Equations (8) and (9) (without perturbation functions). Equations (3) and (4) can be expressed for the unsteady state flow as follows
The new dimensionless time-dependent variable is where is time. Therefore, Equation (6) can be written as follows:
By putting Equation (15) in Equations (13) and (14), it is obtained
With corresponding boundary conditions
According to Lund et al. [29,30], Hamid et al. [31], and Mustafa et al. [32], the stability analysis of the dual solutions is verified by perturbing the steady solution by using following functions
where corresponding small relatives of and are and and the unknown eigenvalue is γ. It is worth mentioning that perturbated function is considered in the form of an exponential as compared to power function, as these functions increase and decrease more rapidly as compared to the power functions. By putting Equation (19) into Equations (16) and (17), we get the linearized eigenvalue problem as follows:
with boundary conditions
System of linearized eigenvalue problem Equations (20) and (21) along with boundary conditions (22) is solved and obtained the infinite set of eigenvalues . The solution is said to be a stable flow if and only if the sign of the is positive, which shows the initial decay, as time passes. On the other hand, if the sign of the is negative, at that point the flow solution shows the initial growth of development, and the solution is said to be an unstable solution, as time passes.
4. Three-Stage Lobatto IIIA Formula
The three-stage Lobatto IIIa formula is a well-known numerical method. This method can easily solve all kinds of non-linear and linear ODEs. It is developed with the support of finite difference code in bvp4c. After that, the study of stability is conducted by employing of the bvp4c solver function. According to Rehman et al. [33], “this collocation formula and the collocation polynomial provides a continuous solution that is fourth-order accurate uniformly in . Mesh selection and error control are based on the residual of the continuous solution”. Furthermore, the tolerance of relative error is fixed at . The suitable mesh determination is created and returned in the field sol.x. The bvp4c returns solution, named sol.y., as a construction. In any case, values of the solution are gotten from the array named sol.y, relating to the field sol.x. The general procedure of this technique, along with the stability analysis, is shown in Figure 2.
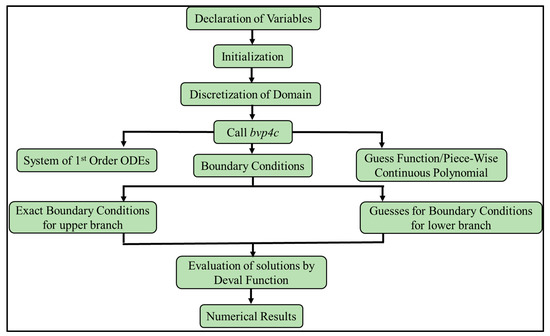
Figure 2.
Procedure of three-stage Lobatto IIIa formula along with stability analysis.
5. Discussion
In the following section, we discuss the numerical results of Equations (8) and (9) with their boundary conditions (10). These equations are highly non-linear third order ODEs, therefore, there is the possibility of the presence of multiple solutions. In this regard, we solved these equations numerically by using of shooting method with the fourth order RK technique in Maple software with the help of the shootlib function. It is noticed that there exist triple solutions in the ranges of the different physical parameters. It is worth indicating that triple solutions depend on the opposing flow case where should be equal to 0.1, dual solutions exist when and , and a single solution exists when . In this investigation, we tried to obtain all possible solutions of the considered problem over the stretching and shrinking surfaces; therefore, we kept and . It should be noted that demonstrates that surface velocity is more(less) than the free stream velocity, while implies that the surface and free stream velocities are equivalent.
We compared findings with those of Hussain et al. [34] in order to verify the numerical coding of the analysis for various values of and in Table 1. It can be concluded from the comparison that our numerical method and coding are working properly and can be used effectively.

Table 1.
Values of for different and values where and .
Table 2 is given for the smallest eigenvalue values of the solutions. The three-stage Labatto III-A method is adopted to get the smallest eigenvalues by solving Equations (20) and (21) with a relaxed boundary ( as is converted to ) condition (22). It is observed that only the first solution is stable, since the values of are in the sign of plus, which shows the initial decay of the disturbance, while two remaining solutions are the unstable solutions as the values of are in the sign of minus, which indicate the initial growth of the disturbance.

Table 2.
The values of the smallest eigenvalue for numerous and values where .
The effect of on the field of velocity is presented in Figure 3. Figure 3 shows that velocity is a decreasing (growing) function of for the shrinking (stretching) case in the first solution. It is detected for the second solution that initially velocity field rises and then declines as rises in the case of the shrinking surface, while opposing behavior is noticed in the case of the stretching surface. The third solution exits only when —the dual nature of the velocity field on both surfaces can easily be noticed.
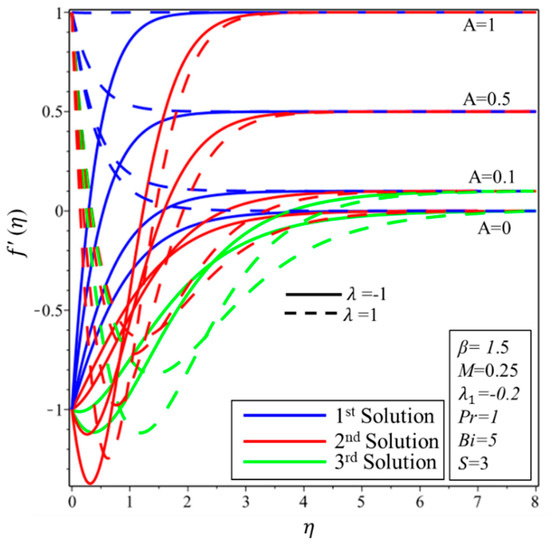
Figure 3.
Effect of on .
Figure 4 and Figure 5 are presented to notice an effect of the Casson parameter () on the velocity field and temperature field, respectively. From Figure 5, it is noted that the increments in decrease the velocity field and the corresponding thickness of the boundary layer on both surfaces in the first solution. Moreover, the velocity filed increases at first and then begins to decrease in the second and the third solutions when , while decreasing behavior is noticed when . For the third solution. It seems that there is no big variation in the temperature field for higher values of for first solution for both surfaces (see Figure 5). The temperature of the fluid increases (decreases) over the shrinking (stretching) surface in the second solution when increases. This might happen since the rise in upsurges (decreases) the forces of viscous, and forces produce (impede) some heat energy in the flow. Hence, the temperature distribution with the corresponding thickness of the thermal boundary layer enhances (reduces) with advance values of . For the third solution, the temperature reduces (initially decreases and then increases) over the shrinking (stretching) surface.
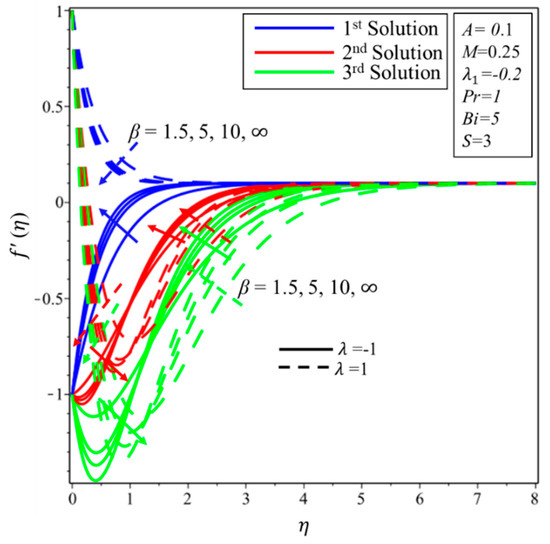
Figure 4.
Effect of on .
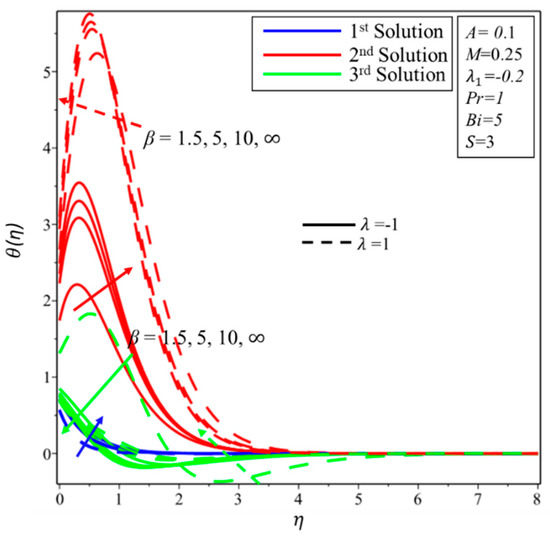
Figure 5.
Effect of on
The impact of a magnetic parameter () on the fields of velocity and temperature is revealed in Figure 6 and Figure 7. It is perceived that when the effect of increases, as a result a decrement in velocity profile over both surfaces in the first solution occur. An increase in yields a resistive kind of force known as Lorentz force, which is created in the flow—as an effect, velocity field curves decrease. The same behaviors of declination of the momentum boundary layer thickness are noticed in the second and third solutions for the case of stretching surface. When , the velocity field increases in unstable solutions. From Figure 7, it can be seen that expansion in raises the temperature distribution over both surfaces in all solutions. Physically, it can be justified as “some extra heat is produced in the flow due to the Lorentz force”. Henceforth, an increment in the field of the magnetic parameter amplifies the thickness of the thermal boundary layer.
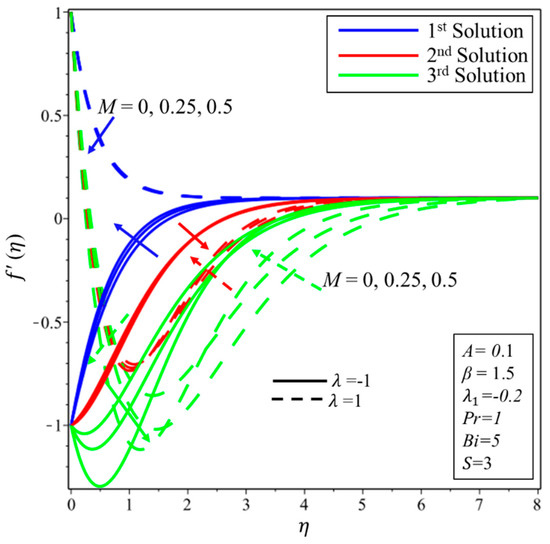
Figure 6.
Effect of on .
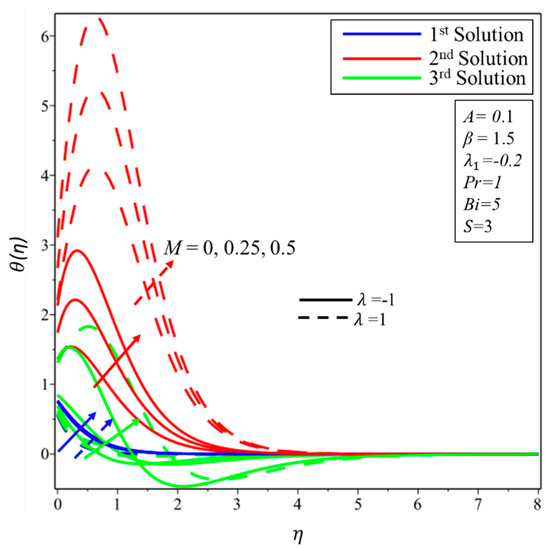
Figure 7.
Effect of on
Figure 8 and Figure 9 are demonstrated to check the impact of Prandtl () on profiles of velocity and temperature field, respectively. In general, the Prandtl number does not affect the velocity field, except when the flow is flowing over the vertical surface. For the shrinking (stretching) surface, it is found that the velocity field decreases in the first (second) solution for the higher magnitudes of . Moreover, it is determined that the field of velocity is the rising function of in the second and third solutions for the case of a shrinking surface and the third solution for the case of a stretching surface. From Figure 9, the temperature of the fluid drops concerning the higher effect of in all solutions and both surfaces, as is expected. Physically, this happens since the Prandtl number () is the ratio of the momentum diffusion to thermal, which implies a lower thermal effect for a higher effect of .
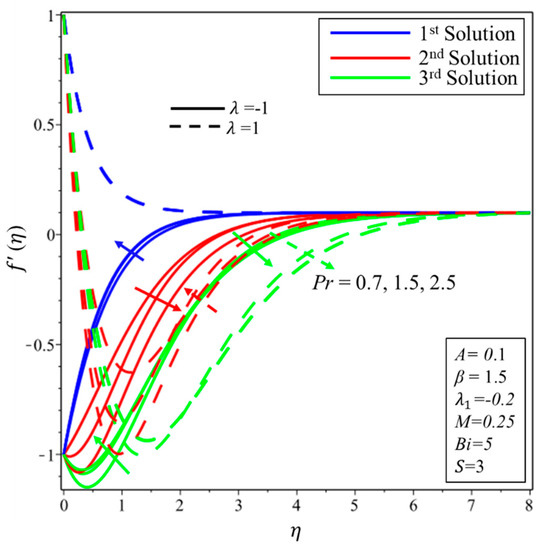
Figure 8.
Effect of on .
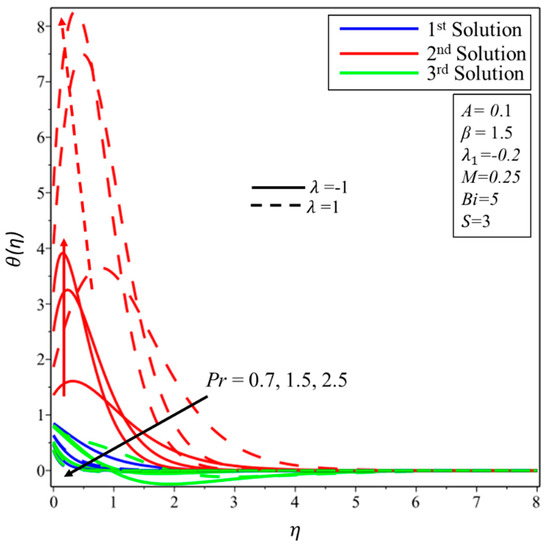
Figure 9.
Effect of on .
Figure 10 and Figure 11 display the variation of the coefficient of skin-friction () and coefficient of heat transfer () for several values of suction parameter with fixed values of the Casson parameter (), respectively. From Figure 10, it can be stated that there are two series of solutions, specifically one solution and multiple solutions. These solutions depend on the effect of the suction parameter. There exist triple solutions and a single solution when and , respectively, where and is the critical value where solutions also exist. It has been perceived that the increases (declines) with increasing suction and Casson parameters in the first (second and third) solution. It is worth mentioning that the shear stress is negative (positive) in the third (first and second) solution. A negative sign suggests that the sheet applies a dragging strength on fluid, and a positive sign suggests the opposite. Moreover, the rise in leads to an increase in for the third and first solutions, while it decreases in the second solution (see Figure 11).
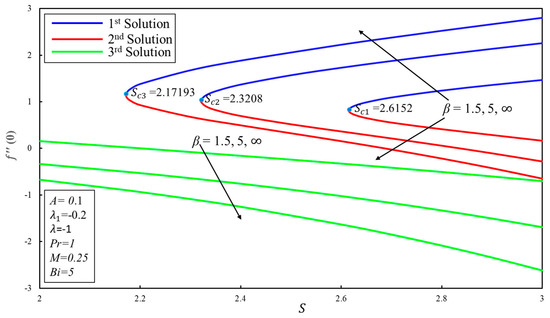
Figure 10.
Effect of on .
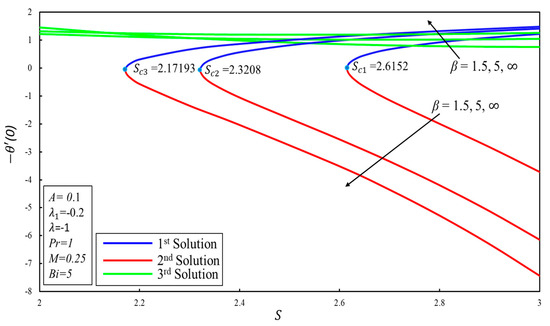
Figure 11.
Effect of on .
Figure 12 demonstrates the variation of the coefficient of skin-friction () for the various values of the stretching/shrinking parameter with fixed values of mixed convection () parameter. From this figure, we can state that multiple solutions depend on the values of the mixed convection parameter. Triple solutions exist in both surface when or (opposing flow case), two solutions exist when and a single solution exists when (assisting flow case).
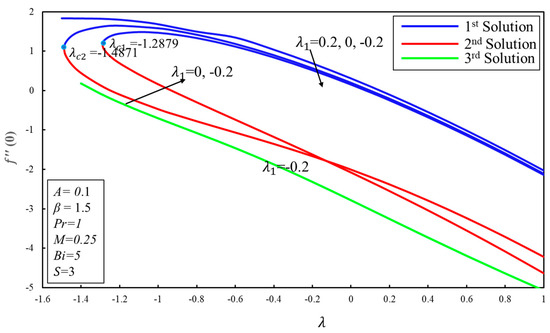
Figure 12.
Effect of on .
Figure 13 and Figure 14 display the variation of the coefficient of skin-friction () and coefficient of heat transfer () for the several magnitudes of suction parameter with certain values of the Biot number or surface convection parameter (), respectively. From Figure 13, it can be stated that there are two ranges of solutions—multiple solutions exist when and one solution exists when , where and is the critical value where solutions also exist. Furthermore, increases (diminishes) for strong mass suction effect (Biot number) in the first solution, while the third and second solutions are decreasing functions of the suction parameter and Biot number. Moreover, the rise in the Biot number leads to the increase in in the first and third solutions.
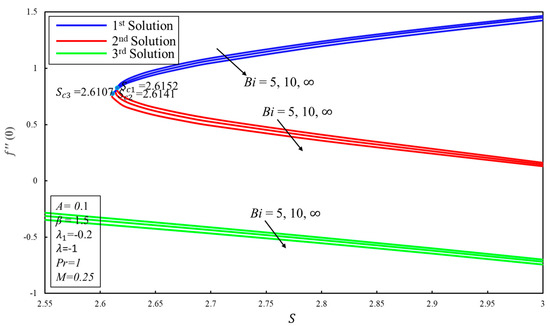
Figure 13.
Effect of on .
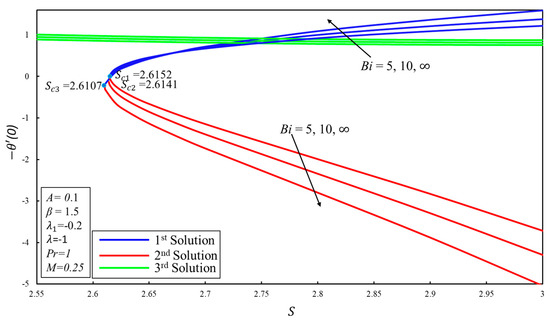
Figure 14.
Effect of on .
Meanwhile, it decreases in the second solution (see Figure 14). Physically, this is due to the fact that Equation (10) contains a negative sign in front of ; therefore, a higher value of Biot number causes opposite convective heat to be advanced in the thermal equilibrium. Biot number can be explained as “it is a measure of the ratio of surface internal and external thermal resistances”. It should be noted that when , the sheet’s lower side contains hot fluid which is entirely isolated, and therefore the inner thermal resistance of the sheet is tremendously high and no convective heat transfer to the cold fluid over the surface happens.
6. Conclusions
The flow of steady, stagnation point, MHD of a Casson fluid on a vertical exponentially stretching/shrinking sheet is examined. The effect of the Biot number is also taken into account. The triple solutions are noticed. The significant outcomes of the current study are briefed as follows:
- Triple solutions for the coefficient of skin friction, the gradient of temperature, velocity, and temperature profiles occur for specific values of the applied quantity examined in the current examination.
- The critical value and the range of the first and second solutions for the coefficient of skin friction rise with a higher magnitude of the Casson parameter.
- For the stable solution, the velocity of the Casson fluid reduces (as expected) over both surfaces for the strong field of the Lorentz force.
- For the shrinking surface, additional mass suction is required for the occurrence of single and multiple solutions for non-Newtonian Casson fluid ( corresponding to ) compared to Newtonian fluid ( when ).
- The magnitude of increases (corresponding critical points of for Biot number are and ) for the advanced values of convective parameter.
- Fluid temperature reduces in all solutions and both surfaces when the effect of increases.
- The only first solution is stable from triple solutions.
Author Contributions
L.A.L. derived the equations and generated the results and wrote the paper. Z.O. formulated the model and proofread the manuscript. I.K. checked the whole manuscript and generated the stability values. D.B., and K.S.N. paid the APC of the journal, helped to revise the manuscript and read the revised version. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank the anonymous reviewers for their insightful comments and suggestions. The first author (L.A.L) would also like to thank his beloved family for continued support during the conducting of this research, particularly his sweet little son (Balach Hussain) and daughter (Zunera Fatima) for their unconditional love.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Crane, L.J. Flow past a stretching plate. J. Appl. Math. Phys. (ZAMP) 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Mabood, F.; Khan, W.A.; Ismail, A.M. MHD boundary layer flow and heat transfer of nanofluids over a nonlinear stretching sheet: A numerical study. J. Magn. Magn. Mater. 2015, 374, 569–576. [Google Scholar] [CrossRef]
- Rana, P.; Bhargava, R. Flow and heat transfer of a nanofluid over a nonlinearly stretching sheet: A numerical study. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 212–226. [Google Scholar] [CrossRef]
- Hamad, M.A.A. Analytical solution of natural convection flow of a nanofluid over a linearly stretching sheet in the presence of magnetic field. Int. Commun. Heat Mass Transf. 2011, 38, 487–492. [Google Scholar] [CrossRef]
- Hassan, M.; Fetecau, C.; Majeed, A.; Zeeshan, A. Effects of iron nanoparticles’ shape on convective flow of ferrofluid under highly oscillating magnetic field over stretchable rotating disk. J. Magn. Magn. Mater. 2018, 465, 531–539. [Google Scholar] [CrossRef]
- Haq, R.U.; Nadeem, S.; Khan, Z.H.; Akbar, N.S. Thermal radiation and slip effects on MHD stagnation point flow of nanofluid over a stretching sheet. Phys. E Low-Dimens. Syst. Nanostruct. 2015, 65, 17–23. [Google Scholar] [CrossRef]
- Hamad, M.A.A.; Ferdows, M. Similarity solutions to viscous flow and heat transfer of nanofluid over nonlinearly stretching sheet. Appl. Math. Mech. 2012, 33, 923–930. [Google Scholar] [CrossRef]
- Vajravelu, K. Viscous flow over a nonlinearly stretching sheet. Appl. Math. Comput. 2001, 124, 281–288. [Google Scholar] [CrossRef]
- Cortell, R. Viscous flow and heat transfer over a nonlinearly stretching sheet. Appl. Math. Comput. 2007, 184, 864–873. [Google Scholar] [CrossRef]
- Hayat, T.; Shehzad, S.A.; Alsaedi, A.; Alhothuali, M.S. Mixed convection stagnation point flow of Casson fluid with convective boundary conditions. Chin. Phys. Lett. 2012, 29, 114704. [Google Scholar] [CrossRef]
- Abbas, Z.; Sheikh, M.; Motsa, S.S. Numerical solution of binary chemical reaction on stagnation point flow of Casson fluid over a stretching/shrinking sheet with thermal radiation. Energy 2016, 95, 12–20. [Google Scholar] [CrossRef]
- Bhattacharyya, K. Dual solutions in boundary layer stagnation-point flow and mass transfer with chemical reaction past a stretching/shrinking sheet. Int. Commun. Heat Mass Transf. 2011, 38, 917–922. [Google Scholar] [CrossRef]
- Nadeem, S.; Israr-ur-Rehman, M.; Saleem, S.; Bonyah, E. Dual solutions in MHD stagnation point flow of nanofluid induced by porous stretching/shrinking sheet with anisotropic slip. AIP Adv. 2020, 10, 065207. [Google Scholar] [CrossRef]
- Bhattacharyya, K. Boundary layer stagnation-point flow of casson fluid and heat transfer towards a shrinking/stretching sheet. Front. Heat Mass Transf. (FHMT) 2013, 4. [Google Scholar] [CrossRef]
- Hayat, T.; Farooq, M.; Alsaedi, A. Thermally stratified stagnation point flow of Casson fluid with slip conditions. Int. J. Numer. Methods Heat Fluid Flow 2015. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Prasannakumara, B.C.; Gireesha, B.J.; Rashidi, M.M. Casson Fluid Flow near the Stagnation Point over a Stretching Sheet with Variable Thickness and Radiation. J. Appl. Fluid Mech. 2016, 9, 1115–1122. [Google Scholar] [CrossRef]
- Haldar, S.; Mukhopadhyay, S.; Layek, G.C. Flow and heat transfer of Casson fluid over an exponentially shrinking permeable sheet in presence of exponentially moving free stream with convective boundary condition. Mech. Adv. Mater. Struct. 2019, 26, 1498–1504. [Google Scholar] [CrossRef]
- Shafiq, A.; Khan, I.; Rasool, G.; Seikh, A.H.; Sherif, E.S.M. Significance of double stratification in stagnation point flow of third-grade fluid towards a radiative stretching cylinder. Mathematics 2019, 7, 1103. [Google Scholar] [CrossRef]
- Jafarimoghaddam, A. Numerical analysis of the nanofluids flow near the stagnation point over a permeable stretching/shrinking wall: A new modeling. Arab. J. Sci. Eng. 2020, 45, 1001–1015. [Google Scholar] [CrossRef]
- Barletta, A.; Magyari, E.; Keller, B. Dual mixed convection flows in a vertical channel. Int. J. Heat Mass Transf. 2005, 48, 4835–4845. [Google Scholar] [CrossRef]
- Makinde, O.D.; Khan, W.A.; Khan, Z.H. Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet. Int. J. Heat Mass Transf. 2013, 62, 526–533. [Google Scholar] [CrossRef]
- Cliffe, K.A.; Spence, A.; Tavener, S.J. The numerical analysis of bifurcation problems with application to fluid mechanics. Acta Numer. 2000, 9, 39–131. [Google Scholar] [CrossRef]
- Gelfgat, A.Y.; Bar-Yoseph, P.Z. Multiple solutions and stability of confined convective and swirling flows–a continuing challenge. Int. J. Numer. Methods Heat Fluid Flow 2004, 14, 213–241. [Google Scholar] [CrossRef]
- Raza, J. Similarity Solutions of Boundary Layer Flows in a Channel Filled by Non-Newtonian Fluids. Ph.D. Thesis, Universiti Utara Malaysia, Sintok, Kedah, Malaysia, 2018. Available online: http://etd.uum.edu.my/id/eprint/6928 (accessed on 25 January 2019).
- Ishak, A.; Nazar, R.; Bachok, N.; Pop, I. MHD mixed convection flow adjacent to a vertical plate with prescribed surface temperature. Int. J. Heat Mass Transf. 2010, 53, 4506–4510. [Google Scholar] [CrossRef]
- Subhashini, S.V.; Sumathi, R.; Pop, I. Dual solutions in a double-diffusive MHD mixed convection flow adjacent to a vertical plate with prescribed surface temperature. Int. J. Heat Mass Transf. 2013, 56, 724–731. [Google Scholar] [CrossRef]
- Ridha, A.; Curie, M. Aiding flows non-unique similarity solutions of mixed-convection boundary-layer equations. Z. Angew. Math. Phys. ZAMP 1996, 47, 341–352. [Google Scholar] [CrossRef]
- Ali Lund, L.; Omar, Z.; Raza, J.; Khan, I.; Sherif, E.S.M. Effects of Stefan Blowing and Slip Conditions on Unsteady MHD Casson Nanofluid Flow Over an Unsteady Shrinking Sheet: Dual Solutions. Symmetry 2020, 12, 487. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Baleanu, D.; Sooppy Nisar, K. Triple Solutions and Stability Analysis of Micropolar Fluid Flow on an Exponentially Shrinking Surface. Crystals 2020, 10, 283. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Raza, J.; Khan, I. Triple solutions of micropolar nanofluid in the presence of radiation over an exponentially preamble shrinking surface: Convective boundary condition. Heat Transf. 2020. [Google Scholar] [CrossRef]
- Hamid, M.; Usman, M.; Khan, Z.H.; Ahmad, R.; Wang, W. Dual solutions and stability analysis of flow and heat transfer of Casson fluid over a stretching sheet. Phys. Lett. A 2019, 383, 2400–2408. [Google Scholar] [CrossRef]
- Mustafa, I.; Abbas, Z.; Arif, A.; Javed, T.; Ghaffari, A. Stability analysis for multiple solutions of boundary layer flow towards a shrinking sheet: Analytical solution by using least square method. Phys. A Stat. Mech. Its Appl. 2020, 540, 123028. [Google Scholar] [CrossRef]
- Rahman, M.M.; Rosca, A.V.; Pop, I. Boundary layer flow of a nanofluid past a permeable exponentially shrinking surface with convective boundary condition using Buongiorno’s model. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 299–319. [Google Scholar] [CrossRef]
- Hussain, T.; Shehzad, S.A.; Alsaedi, A.; Hayat, T.; Ramzan, M. Flow of Casson nanofluid with viscous dissipation and convective conditions: A mathematical model. J. Cent. South. Univ. 2015, 22, 1132–1140. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).