An Explicit Hybrid Method for the Nonlocal Allen–Cahn Equation
Abstract
1. Introduction
2. Numerical Algorithm
3. Numerical Results
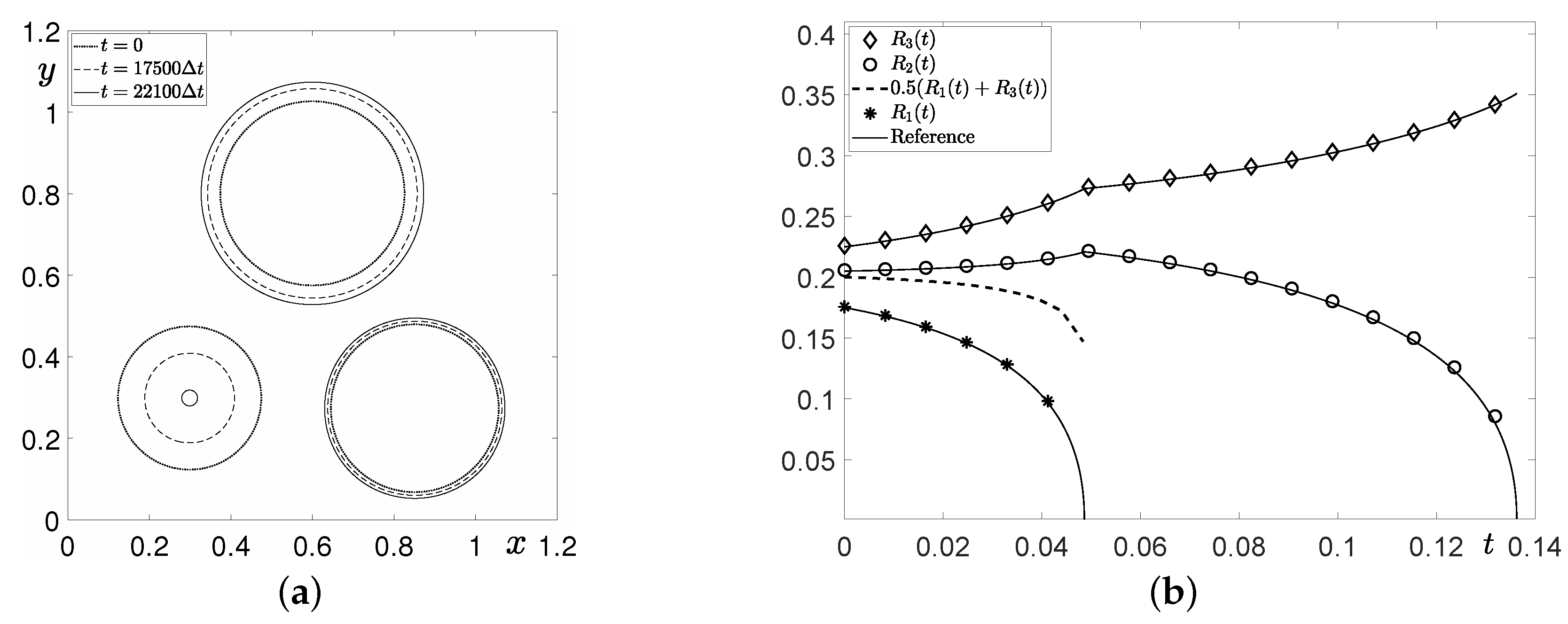
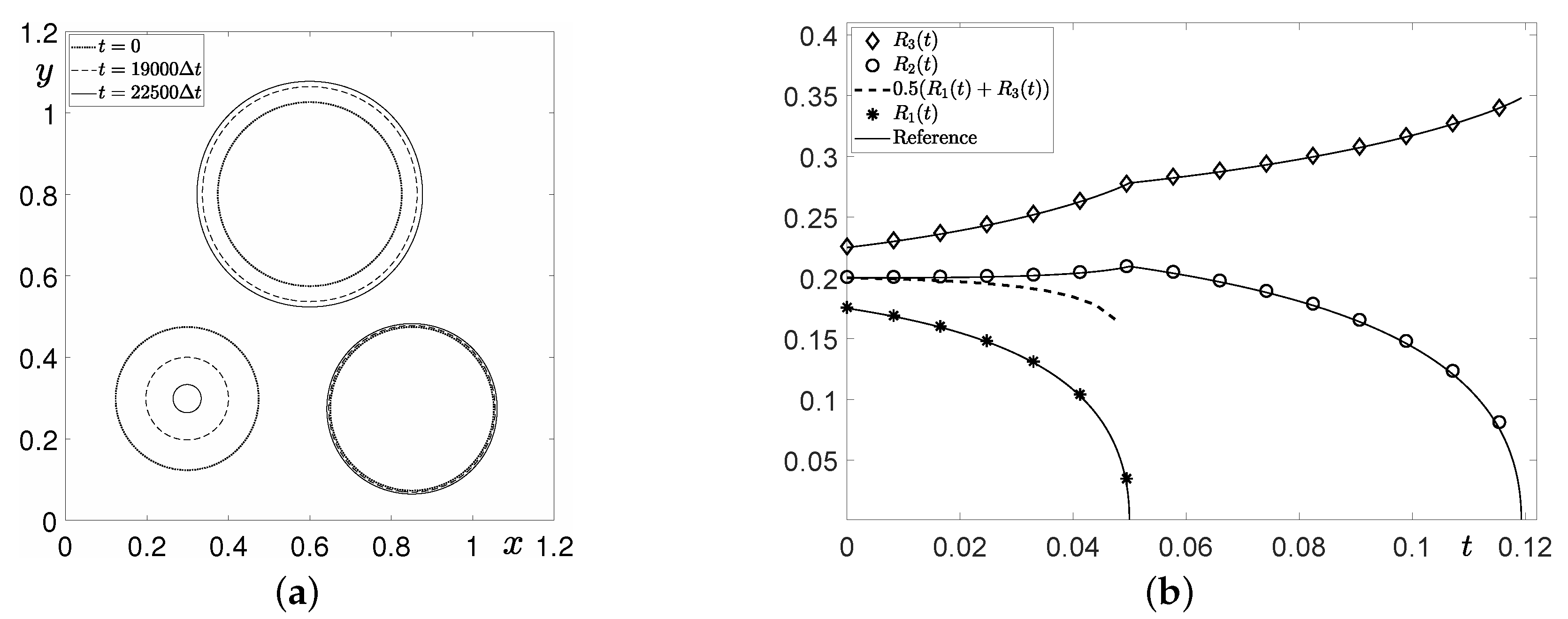
3.1. Evolution of Disks
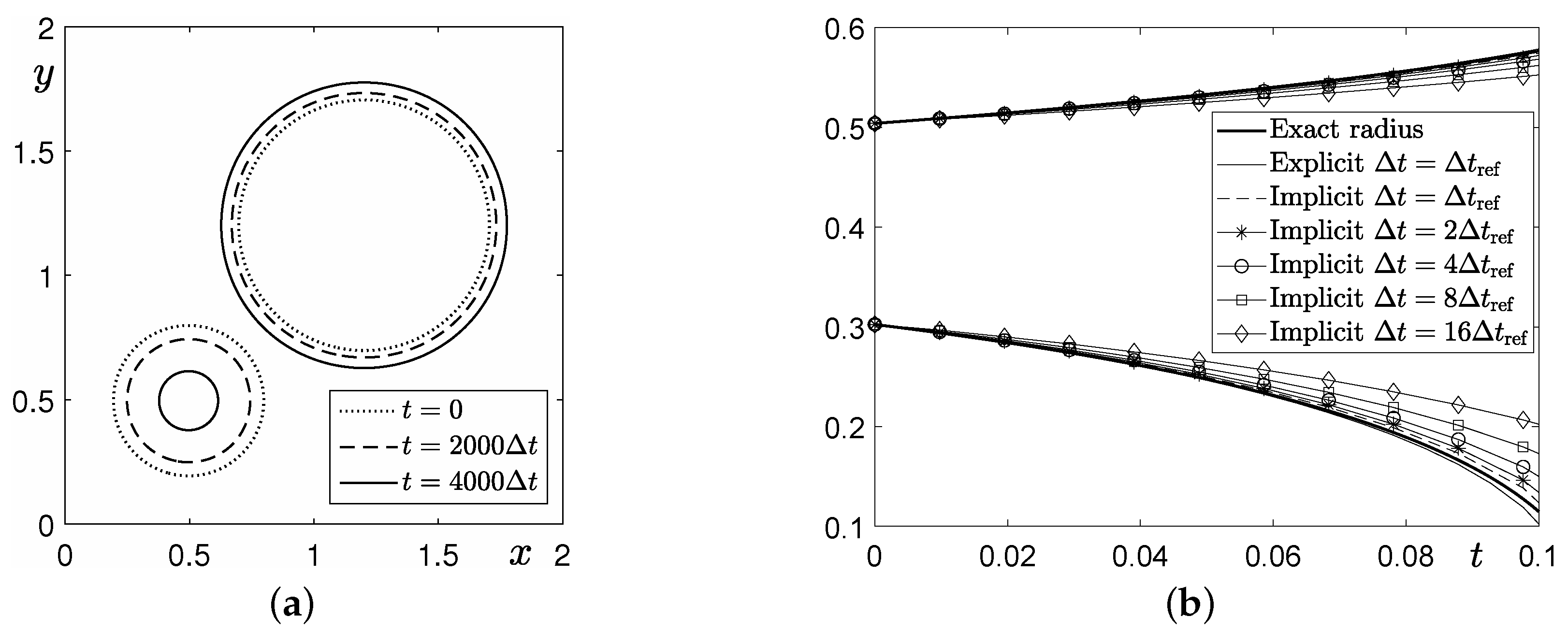
3.2. Comparison Test with a Conventional Method
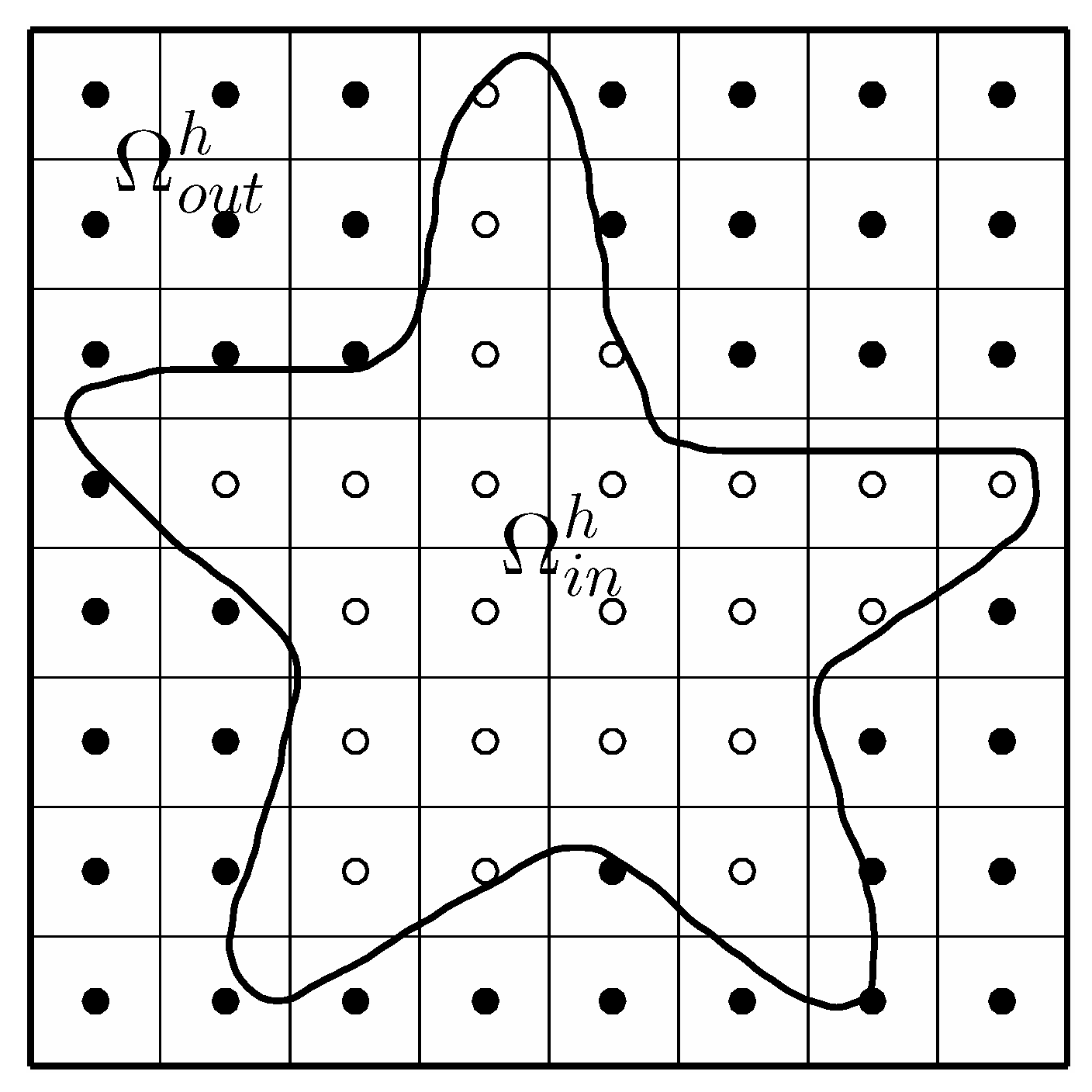
3.3. Cell Growth in a Complex Domain
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Stenger, F.; Voigt, A. Towards infinite tilings with symmetric boundaries. Symmetry 2019, 11, 444. [Google Scholar] [CrossRef]
- Allen, S.M.; Cahn, J.W. A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 1979, 27, 1085–1095. [Google Scholar] [CrossRef]
- Broadbridge, P.; Triadis, D.; Gallage, D.; Cesana, P. Nonclassical symmetry solutions for fourth-order phase field reaction-diffusion. Symmtery 2018, 10, 72. [Google Scholar] [CrossRef]
- Jeong, D.; Kim, J. An explicit hybrid finite difference scheme for the Allen–Cahn equation. J. Comput. Appl. Math. 2018, 340, 247–255. [Google Scholar] [CrossRef]
- Lee, S.; Lee, D. The fractional Allen–Cahn equation with the sextic potential. Appl. Math. Comput. 2019, 351, 176–192. [Google Scholar] [CrossRef]
- Li, C.; Huang, Y.; Yi, N. An unconditionally energy stable second order finite element method for solving the Allen–Cahn equation. J. Comput. Appl. Math. 2019, 353, 38–48. [Google Scholar] [CrossRef]
- Lee, H.G.; Park, J.; Yoon, S.; Lee, C.; Kim, J. Mathematical model and numerical simulation for tissue growth on bioscaffolds. Appl. Sci. 2019, 9, 4058. [Google Scholar] [CrossRef]
- Hu, X.; Li, Y.; Ji, H. A nodal finite element approximation of a phase field model for shape and topology optimization. Appl. Math. Comput. 2018, 339, 675–684. [Google Scholar] [CrossRef]
- Sire, Y.; Valdinoci, E. Fractional Laplacian phase transitions and boundary reactions: A geometric inequality and a symmetry result. J. Funct. Anal. 2009, 256, 1842–1864. [Google Scholar] [CrossRef]
- Brassel, M.; Bretin, E. A modified phase field approximation for mean curvature flow with conservation of the volume. Math. Methods Appl. Sci. 2011, 34, 1157–1180. [Google Scholar] [CrossRef]
- Rubinstein, J.; Sternberg, P. Nonlocal reaction-diffusion equations and nucleation. IMA J. Appl. Math. 1992, 48, 249–264. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.; Choi, Y. A conservative Allen–Cahn equation with a space-time dependent Lagrange multiplier. Int. J. Eng. Sci. 2014, 84, 11–17. [Google Scholar] [CrossRef]
- Chai, Z.; Sun, D.; Wang, H.; Shi, B. A comparative study of local and nonlocal Allen–Cahn equations with mass conservation. Int. J. Heat Mass Transf. 2018, 122, 631–642. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, C.; Yang, X.; Chu, Y.; Xia, Z. Efficient, non-iterative, and second-order accurate numerical algorithms for the anisotropic Allen–Cahn Equation with precise nonlocal mass conservation. J. Comput. Appl. Math. 2020, 363, 444–463. [Google Scholar] [CrossRef]
- Guan, Z.; Lowengrub, J.; Wang, C. Convergence analysis for second-order accurate schemes for the periodic nonlocal Allen–Cahn and Cahn–Hilliard equations. Math. Methods Appl. Sci. 2017, 40, 6836–6863. [Google Scholar] [CrossRef]
- Du, Q.; Yang, J. Fast and accurate implementation of Fourier spectral approximations of nonlocal diffusion operators and its applications. J. Comput. Phys. 2017, 332, 118–134. [Google Scholar] [CrossRef]
- Lee, H.G. High-order and mass conservative methods for the conservative Allen–Cahn equation. Comput. Math. Appl. 2016, 72, 620–631. [Google Scholar] [CrossRef]
- Weng, Z.; Zhuang, Q. Numerical approximation of the conservative Allen–Cahn equation by operator splitting method. Math. Methods Appl. Sci. 2017, 40, 4462–4480. [Google Scholar] [CrossRef]
- Zhai, S.; Weng, Z.; Feng, X. Fast explicit operator splitting method and time-step adaptivity for fractional non-local Allen–Cahn model. Appl. Math. Model. 2016, 40, 1315–1324. [Google Scholar] [CrossRef]
- Ren, F.; Song, B.; Sukop, M.C.; Hu, H. Improved lattice Boltzmann modeling of binary flow based on the conservative Allen–Cahn equation. Phys. Rev. E 2016, 94, 023311. [Google Scholar] [CrossRef]
- Aihara, S.; Takaki, T.; Takada, N. Multi-phase-field modeling using a conservative Allen–Cahn equation for multiphase flow. Comput. Fluids 2019, 178, 141–151. [Google Scholar] [CrossRef]
- Joshi, V.; Jaiman, R.K. An adaptive variational procedure for the conservative and positivity preserving Allen–Cahn phase-field model. J. Comput. Phys. 2018, 366, 478–504. [Google Scholar] [CrossRef]
- Li, Y.; Lee, H.G.; Jeong, D.; Kim, J. An unconditionally stable hybrid numerical method for solving the Allen–Cahn equation. Comput. Math. Appl. 2010, 60, 1591–1606. [Google Scholar] [CrossRef]
- Kim, J. Phase-field models for multi-component fluid flows. Commun. Comput. Phys. 2012, 12, 613–661. [Google Scholar] [CrossRef]
- Bronsard, L.; Stoth, B. Volume-preserving mean curvature flow as a limit of a nonlocal Ginzburg–Landau equation. SIAM J. Math. Anal. 1997, 28, 769–807. [Google Scholar] [CrossRef]
- Kanagarajan, K.; Suresh, R. Runge–Kutta method for solving fuzzy differential equations under generalized differentiability. Comput. Appl. Math. 2018, 37, 1294–1305. [Google Scholar] [CrossRef]
- Jeong, D.; Kim, J. Conservative Allen–Cahn–Navier–Stokes system for incompressible two-phase fluid flows. Comput. Fluids 2017, 156, 239–246. [Google Scholar] [CrossRef]
- Minc, N.; Burgess, D.; Chang, F. Influence of cell geometry on division-plane positioning. Cell 2011, 144, 414–426. [Google Scholar] [CrossRef]
- Li, Y.; Jeong, D.; Shin, J.; Kim, J. A conservative numerical method for the Cahn—Hilliard equation with Dirichlet boundary conditions in complex domains. Comput. Math. Appl. 2013, 65, 102–115. [Google Scholar] [CrossRef]
- Yang, J.; Li, Y.; Lee, C.; Kim, J. Conservative Allen–Cahn equation with a nonstandard variable mobility. Acta Mech. 2020, 231, 561–576. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Choi, Y.; Lee, C.; Kim, J. Fast and accurate smoothing method using a modified Allen—Cahn equation. Comput. Aided Des. 2020, 120, 102804. [Google Scholar] [CrossRef]
- Kim, J.; Jeong, D.; Yang, S.D.; Choi, Y. A finite difference method for a conservative Allen–Cahn equation on non-flat surfaces. J. Comput. Phys. 2017, 334, 170–181. [Google Scholar] [CrossRef]



| CPU time (sec) | 198.452 | 94.984 | 48.499 | 29.000 | 17.124 |
| Ratio | 4.40 | 2.16 | 1.10 | 0.66 | 0.39 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.; Yoon, S.; Park, J.; Kim, J. An Explicit Hybrid Method for the Nonlocal Allen–Cahn Equation. Symmetry 2020, 12, 1218. https://doi.org/10.3390/sym12081218
Lee C, Yoon S, Park J, Kim J. An Explicit Hybrid Method for the Nonlocal Allen–Cahn Equation. Symmetry. 2020; 12(8):1218. https://doi.org/10.3390/sym12081218
Chicago/Turabian StyleLee, Chaeyoung, Sungha Yoon, Jintae Park, and Junseok Kim. 2020. "An Explicit Hybrid Method for the Nonlocal Allen–Cahn Equation" Symmetry 12, no. 8: 1218. https://doi.org/10.3390/sym12081218
APA StyleLee, C., Yoon, S., Park, J., & Kim, J. (2020). An Explicit Hybrid Method for the Nonlocal Allen–Cahn Equation. Symmetry, 12(8), 1218. https://doi.org/10.3390/sym12081218






