Linear Diophantine Fuzzy Soft Rough Sets for the Selection of Sustainable Material Handling Equipment
Abstract
1. Introduction
1.1. Literature Review
1.2. Motivation and Objectives
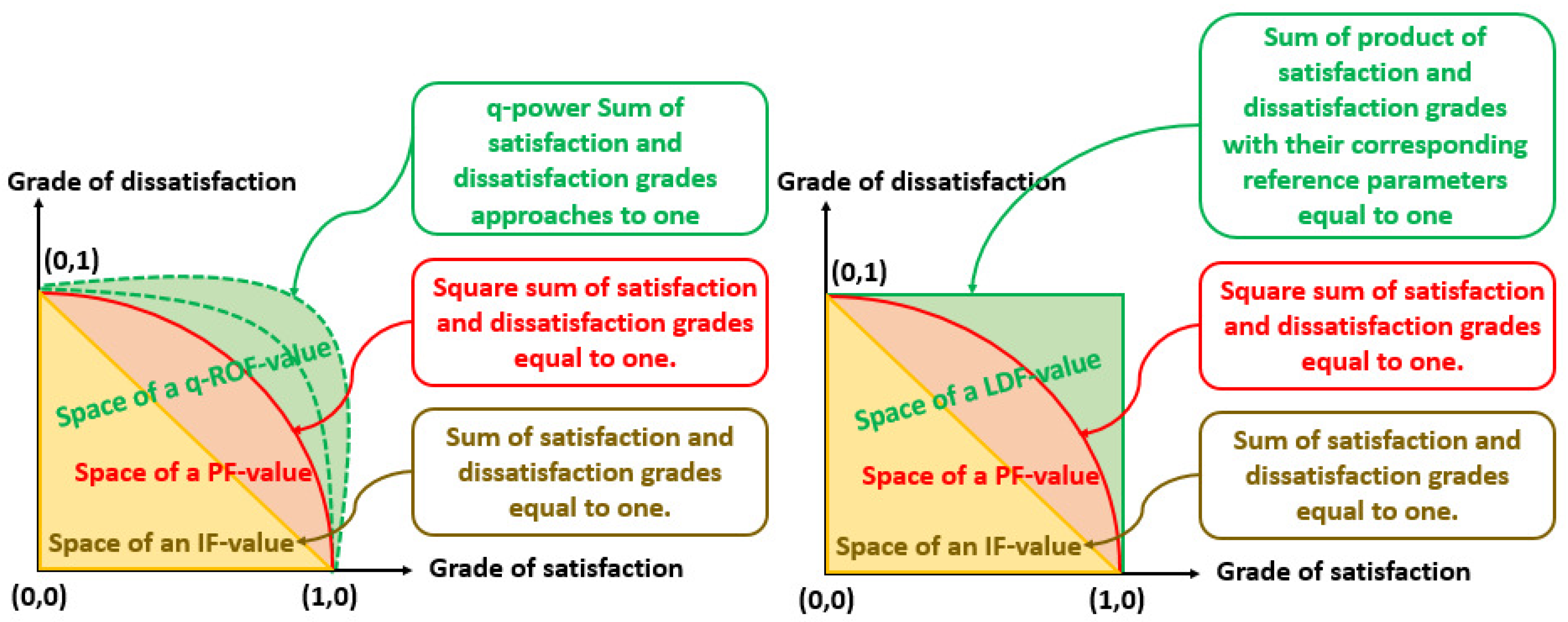
2. Some Basic Concepts
- ;
- ;
- .
- ;
- ;
- ;
- .
- ;
- .
- (1)
- implies that certainly contains the elements of .
- (2)
- implies that does not contains the elements of .
- (3)
- implies that may or may not contain the elements of .
3. Construction of SRLDFSs and LDFSRSs
3.1. Soft Rough Linear Diophantine Fuzzy Sets
- (1)
- ,
- (2)
- ,
- (3)
- ,
- (4)
- ,
- (5)
- ,
- (6)
- ,
- (7)
- ,
- (8)
- .
- (1)
- ,
- (2)
- ,
- (3)
- ,
- (4)
- ,
- (5)
- ,
- (6)
- ,
- (7)
- ,
- (8)
- .
3.2. Linear Diophantine Fuzzy Soft Rough Sets
- (1)
- ,
- (2)
- ,
- (3)
- ,
- (4)
- ,
- (5)
- ,
- (6)
- ,
- (7)
- ,
- (8)
- .
- (1)
- ,
- (2)
- ,
- (3)
- ,
- (4)
- ,
- (5)
- ,
- (6)
- ,
- (7)
- ,
- (8)
- .
- (1)
- ,
- (2)
- .
- 1.
- ,
- 2.
- ,
- 3.
- ,
- 4.
- ,
- 5.
- 6.
- If and , then, and .
- 1.
- 2.
- and for arbitrary , we have:
- 3.
- .
- 4.
- .
- 1.
- 2.
- and for arbitrary , we have:
- 3.
- .
- 4.
- .
4. MCDM for Sustainable Material Handling Equipment
4.1. Selection of a Sustainable Material Handling Equipment by Using LDFSRSs
- “Technical: convenience, maintainability, safety required” means that the alternative is “highly technical” or may be “low”.
- “Monetary: setting up and operational cost, maintenance cost, purchasing cost” means that the alternative may be “expansive” or “inexpensive”.
- “Operational: fuel consumption, moving speed, capacity” means that the alternative is “highly operational” or may be “low”.
- “Strategic: flexibility, level of training required, guarantee” means that the alternative is “highly strategic” or may be “low”.
| Algorithm 1: Selection of a best material handling equipment by using LDFSRSs. |
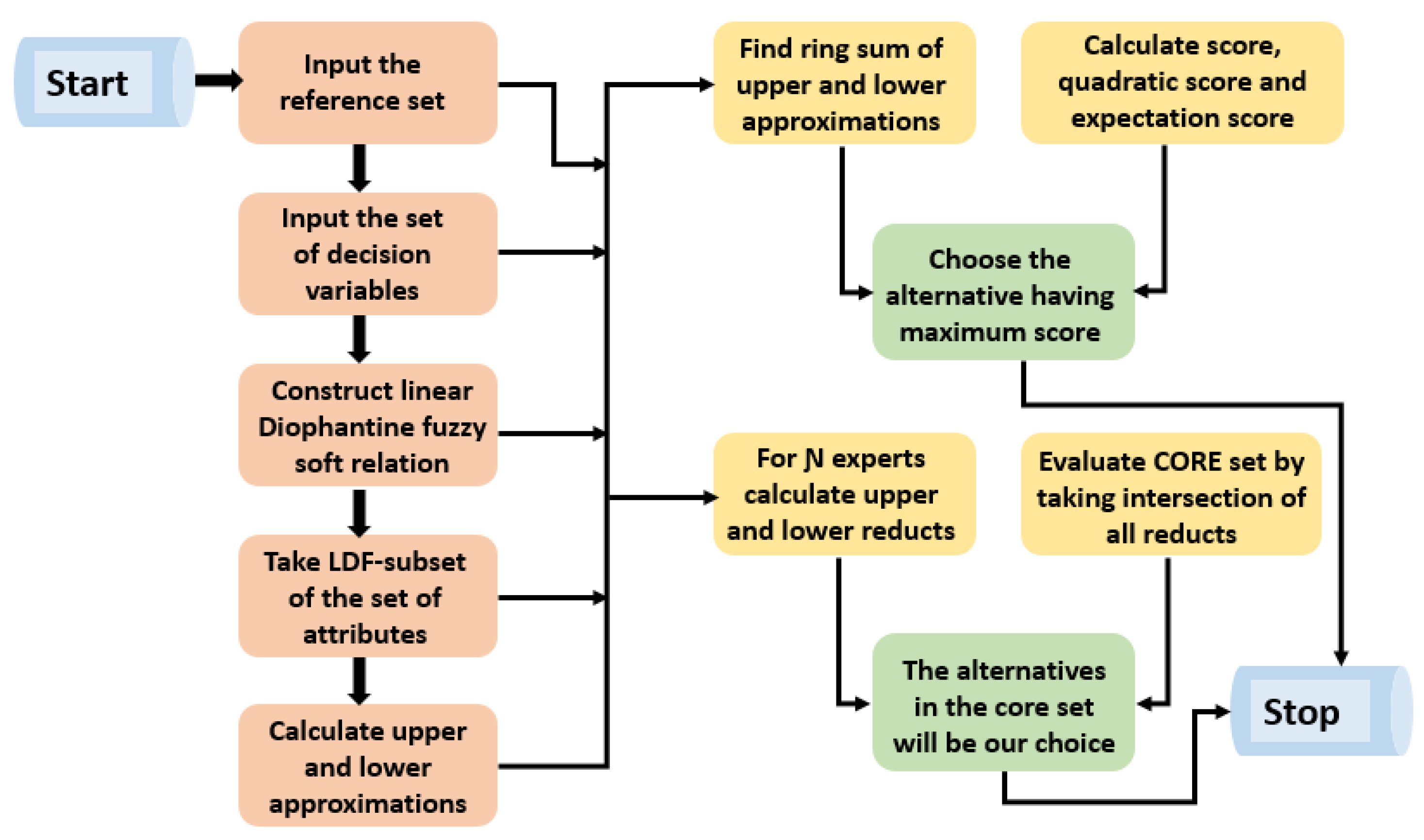
| Input: 1. Input the reference set . 2. Input the assembling of attributes . Construction: 3. According to the necessity of the DM, build an LDFSR . 4. Based on the needs of the decision maker, construct LDF-subset of as an optimal normal decision set. Calculation: 5. Calculate the “LDFSR approximation operators” and as lower and upper using Definition 12. 6. By using Definition 13 of the ring sum operation, find the choice of LDFS . Output: 7. We use the definitions of score, quadratic score, and expectation score functions for LDFNs given in [54] and written respectively as: 8. Rank the alternatives by using calculated score values. Final decision: 9. Choose the alternative having the maximum score value. |
| Algorithm 2: Selection of the best material handling equipment by using LDFSRSs. |
| Input: 1. Input the reference set . 2. Input the assembling of attributes . Construction: 3. According to the necessity of the DM, build an LDFSR . 4. Based on the needs of the decision maker, construct LDF-subset of as an optimal normal decision set. Calculation: 5. Calculate the “LDFSR approximation operators” and as lower and upper using Definition 12. 6. For “” number of experts, calculate upper and lower reducts from the calculated “upper and lower approximation operators”, respectively. Output: 7. From the calculated “” reducts, we get “” crisp subsets of the reference set . The subsets can be constructed by using the “YES” and “NO” logic. The only alternatives in the reduct having final decision “YES” will become the object of the crisp subset. 8. Calculate the core set by taking the intersection of all crisp subsets obtained from the calculated reducts. Final decision: 9. The alternatives in the core will be our choice for the final decision. |
4.1.1. Calculations by Using Algorithm 1
4.1.2. Calculations by Using Algorithm 2
4.2. Selection of the Most Appropriate Material Handling Equipment by Using SRLDFSs
| Algorithm 3: Selection of the best material handling equipment by using SRLDFSs. |
| Input: 1. Input the reference set . 2. Input the assembling of attributes . Construction: 3. According to the necessity of the DM, build a crisp soft relation over . 4. Based on the needs of the decision maker, construct LDF-subset of as an optimal normal decision set. Calculation: 5. Calculate the “SRLDF approximation operators” and as “lower and upper approximations” by using Definition 9. 6. By using Definition 13 of the ring sum operation, find the choice of LDFS . Output: 7. We use the definitions of the score, quadratic score, and expectation score functions for LDFNs given in [54] and written respectively as: 8. Rank the alternatives by using calculated score values. Final decision: 9. Select the object having the highest score value. |
| Algorithm 4: Selection of the best material handling equipment by using SRLDFSs. |
| Input: 1. Input the reference set . 2. Input the assembling of attributes . Construction: 3. According to the necessity of the DM, build a crisp soft relation over . 4. Based on the needs of the decision maker, construct LDF-subset of as an optimal normal decision set. Calculation: 5. Calculate the “SRLDF approximation operators” and as “lower and upper approximations” by using Definition 9. 6. For “” number of experts, calculate upper and lower reducts from the calculated “upper and lower approximation operators”, respectively. Output: 7. From calculated “” reducts, we get “” crisp subsets of the reference set . The subsets can be constructed by using the “YES” and “NO” logic. The only alternatives in the reduct having final decision “YES” will become the object of the crisp subset. 8. Calculate the core set by taking the intersection of all crisp subsets obtained from the calculated reducts. Final decision: 9. The alternatives in the core will be our choice for the final decision. |
4.2.1. Calculations by Using Algorithm 3
4.2.2. Calculations by Using Algorithm 4
4.3. Discussion, Comparison, and Symmetrical Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FSs | Fuzzy sets |
| IFSs | Intuitionistic fuzzy sets |
| PFSs | Pythagorean fuzzy sets |
| q-ROFSs | q-rung orthopair fuzzy sets |
| LDFSs | Linear Diophantine fuzzy sets |
| LDFNs | Linear Diophantine fuzzy numbers |
| LDFSSs | Linear Diophantine fuzzy soft sets |
| LDFSRSs | Linear Diophantine fuzzy soft rough sets |
| SRLDFSs | Soft rough linear Diophantine fuzzy sets |
| MCDM | Multi-criteria decision making |
Appendix A
- (1)
- From Definition 9, we can write that:
- (2)
- It can be easily proven from Definition 9.
- (3)
- We consider that:
- (4)
- From Definition 9, we can write that:
References
- Bellman, R.E.; Zadeh, L.A. Decision-making in a fuzzy environment. Manag. Sci. 1970, 4, 141–164. [Google Scholar] [CrossRef]
- Akram, M.; Ali, G.; Alshehri, N.O. A new multi-attribute decision making method based on m-polar fuzzy soft rough sets. Symmetry 2017, 9, 271. [Google Scholar] [CrossRef]
- Ali, M.I. A note on soft sets, rough soft sets and fuzzy soft sets. Appl. Soft Comput. 2011, 11, 3329–3332. [Google Scholar]
- Chen, S.M.; Tan, J.M. Handling multi-criteria fuzzy decision-makling problems based on vague set theory. Fuzzy Sets Syst. 1994, 67, 163–172. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Advances in prospect theory: Cumulative representation of uncertainity. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef]
- Feng, F.; Jun, Y.B.; Liu, X.; Li, L. An adjustable approach to fuzzy soft set based decision making. J. Comput. Appl. Math. 2010, 234, 10–20. [Google Scholar] [CrossRef]
- Feng, F.; Li, C.; Davvaz, B.; Ali, M.I. Soft sets combined with fuzzy sets and rough sets; A tentative approach. Soft Comput. 2010, 14, 899–911. [Google Scholar] [CrossRef]
- Feng, F.; Liu, X.Y.; Leoreanu-Fotea, V.; Jun, Y.B. Soft sets and soft rough sets. Inf. Sci. 2011, 181, 1125–1137. [Google Scholar] [CrossRef]
- Feng, F.; Fujita, H.; Ali, M.I.; Yager, R.R.; Liu, X. Another view on generalized intuitionistic fuzzy soft sets and related multiattribute decision making methods. IEEE Trans. Fuzzy Syst. 2019, 27, 474–488. [Google Scholar] [CrossRef]
- Garg, H. A new generalized Pythagorean fuzzy information aggregation using Einstein operations and its application to decision making. Int. J. Intell. Syst. 2016, 31, 886–920. [Google Scholar] [CrossRef]
- Hashmi, M.R.; Riaz, M.; Smarandache, F. m-polar Neutrosophic Topology with Applications to Multi-Criteria Decision-Making in Medical Diagnosis and Clustering Analysis. Int. J. Fuzzy Syst. 2020, 22, 273–292. [Google Scholar] [CrossRef]
- Hashmi, M.R.; Riaz, M. A Novel Approach to Censuses Process by using Pythagorean m-polar Fuzzy Dombi’s Aggregation Operators. J. Intell. Fuzzy Syst. 2020, 38, 1977–1995. [Google Scholar] [CrossRef]
- Jose, S.; Kuriaskose, S. Aggregation operators, score function and accuracy function for multi criteria decision making in intuitionistic fuzzy context. Notes Intuitionistic Fuzzy Sets 2014, 20, 40–44. [Google Scholar]
- Naeem, K.; Riaz, M.; Peng, X.; Afzal, D. Pythagorean fuzzy soft MCGDM methods based on TOPSIS, VIKOR and aggregation operators. J. Intell. Fuzzy Syst. 2019, 37, 6937–6957. [Google Scholar] [CrossRef]
- Pawlak, Z.; Skowron, A. Rough sets: Some extensions. Inf. Sci. 2007, 177, 28–40. [Google Scholar] [CrossRef]
- Riaz, M.; Hashmi, M.R. MAGDM for agribusiness in the environment of various cubic m-polar fuzzy averaging aggregation operators. J. Intell. Fuzzy Syst. 2019, 37, 3671–3691. [Google Scholar] [CrossRef]
- Riaz, M.; Hashmi, M.R. Soft Rough Pythagorean m-Polar Fuzzy Sets and Pythagorean m-Polar Fuzzy Soft Rough Sets with Application to Decision-Making. Comput. Appl. Math. 2020, 39, 16. [Google Scholar] [CrossRef]
- Riaz, M.; Davvaz, B.; Firdous, A.; Fakhar, A. Novel Concepts of Soft Rough Set Topology with Applications. J. Intell. Fuzzy Syst. 2019, 36, 3579–3590. [Google Scholar] [CrossRef]
- Riaz, M.; Samrandache, F.; Firdous, A.; Fakhar, A. On Soft Rough Topology with Multi-Attribute Group Decision Making. Mathematics 2019, 7, 67. [Google Scholar] [CrossRef]
- Riaz, M.; Tehrim, S.T. Certain properties of bipolar fuzzy soft topology via Q-neighborhood. Punjab Univ. J. Math. 2019, 51, 113–131. [Google Scholar]
- Riaz, M.; Tehrim, S.T. Cubic bipolar fuzzy ordered weighted geometric aggregation operators and their application using internal and external cubic bipolar fuzzy data. Comput. Appl. Math. 2019, 38, 87. [Google Scholar] [CrossRef]
- Riaz, M.; Tehrim, S.T. Multi-attribute group decision making based cubic bipolar fuzzy information using averaging aggregation operators. J. Intell. Fuzzy Syst. 2019, 37, 2473–2494. [Google Scholar] [CrossRef]
- Roy, J.; Adhikary, K.; Kar, S.; Pamucar, D. A rough strength relational DEMATEL model for analysing the key success factors ofhospital service quality. Decis. Mak. Appl. Manag. Eng. 2018, 1, 121–142. [Google Scholar] [CrossRef]
- Sharma, H.K.; Kumari, K.; Kar, S. A rough set theory application in forecasting models. Decis. Mak. Appl. Manag. Eng. 2020, 3, 1–21. [Google Scholar] [CrossRef]
- Wei, G.; Wang, H.; Zhao, X.; Lin, R. Hesitant triangular fuzzy information aggregation in multiple attribute decision making. J. Intell. Fuzzy Syst. 2014, 26, 1201–1209. [Google Scholar] [CrossRef]
- Zhang, H.; Shu, L.; Liao, S. Intuitionistic fuzzy soft rough set and its applications in decision making. Abstr. Appl. Anal. 2014, 1–13. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, Z.S.; Ni, M.F.; Lui, S.S. Generalized aggregation operators for intuitionistic fuzzy sets. Int. J. Intell. Syst. 2010, 25, 1–30. [Google Scholar] [CrossRef]
- Xu, Z.S.; Chen, J. An overview on distance and similarity measures on intuitionistic fuzzy sets. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2008, 16, 529–555. [Google Scholar] [CrossRef]
- Kulak, O.; Satoglu, S.I.; Durmusoglu, M.B. Multi-attribute material handling equipment selection using information axiom. In Proceedings of the ICAD2004, The third international conferenec on Axiomatic Design, Seoul, Korea, 21–24 June 2004; pp. 1–9. [Google Scholar]
- Karande, P.; Chakraborty, S. Material handling equipment selection using weighted utility additive theory. J. Ind. Eng. 2013. [Google Scholar] [CrossRef]
- Zubair, M.; Mahmood, S.; Omair, M.; Noor, I. Optimization of material handling system through material handling equipment selection. Int. J. Progress. Sci. Technol. 2019, 15, 235–243. [Google Scholar]
- Vashist, R. An algorithm for finding the reduct and core of the consistent dataset. Int. Conf. Comput. Intell. Commun. Netw. 2015. [Google Scholar] [CrossRef]
- Zhang, L.; Zhan, J. Fuzzy soft β-covering based fuzzy rough sets and corresponding decision making applications. Int. J. Mach. Learn. Cybern. 2018. [Google Scholar] [CrossRef]
- Zhang, L.; Zhan, J. Novel classes of fuzzy soft;-coverings-based fuzzy rough sets with applications to multi-criteria fuzzy group decision making. Soft Comput. 2018. [Google Scholar] [CrossRef]
- Zhang, L.; Zhan, J.; Xu, Z.X. Covering-based generalized IF rough sets with applications to multi-attribute decision making. Inf. Sci. 2019, 478, 275–302. [Google Scholar] [CrossRef]
- Wang, X.; Triantaphyllou, E. Ranking irregularities when evaluating alternatives by using some ELECTRE methods. Omega Int. J. Manag. Sci. 2008, 36, 45–63. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Çifçi, G. A novel hybrid MCDM approach based on fuzzy DEMATEL, fuzzy ANP and fuzzy TOPSIS to evaluate green suppliers. Expert Syst. Appl. 2012, 39, 3000–3011. [Google Scholar] [CrossRef]
- Govindan, K.; Khodaverdi, R.; Vafadarnikjoo, A. Intuitionistic fuzzy based DEMATEL method for developing green practices and performances in a green supply chain. Expert Syst. Appl. 2015, 42, 7207–7720. [Google Scholar] [CrossRef]
- Jeong, J.S.; González-Gómez, D. Adapting to PSTs Pedagogical Changes in Sustainable Mathematics Education through Flipped E-Learning: Ranking Its Criteria with MCDA/F-DEMATEL. Mathematics 2020, 8, 858. [Google Scholar] [CrossRef]
- Wang, R.; Li, Y. A Novel Approach for Green Supplier Selection under a q-Rung Orthopair Fuzzy Environment. Symmetry 2018, 10, 687. [Google Scholar] [CrossRef]
- Xu, Y.; Shang, X.; Wang, J.; Wu, W.; Huang, H. Some q-Rung Dual Hesitant Fuzzy Heronian Mean Operators with Their Application to Multiple Attribute Group Decision-Making. Symmetry 2018, 10, 472. [Google Scholar] [CrossRef]
- Sun, B.; Ma, W. Soft fuzzy rough sets and its application in decision making. Artif. Intell. Rev. 2014, 41, 67–80. [Google Scholar]
- Meng, D.; Zhang, X.; Qin, K. Soft rough fuzzy sets and soft fuzzy rough sets. Comput. Math. Appl. 2011, 62, 4635–4645. [Google Scholar] [CrossRef]
- Hussain, A.; Ali, M.I.; Mahmood, T. Pythagorean fuzzy soft rough sets and their applications in decision making. J. Taibah Univ. Sci. 2020, 14, 101–113. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Ans Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.T. Geometrical interpretation of the elements of the intuitionistic fuzzy objects. Int. J. Bioautom. 2016, 20, S27–S42. [Google Scholar]
- Yager, R.R. Pythagorean membership grades in multi-criteria decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean fuzzy subsets. In Proceedings of the 2013 joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS), Edmonton, AB, Canada, 24–28 June 2013; pp. 57–61. [Google Scholar]
- Yager, R.R.; Abbasov, A.M. Pythagorean membership grades, complex numbers, and decision making. Int. J. Intell. Syst. 2013, 28, 436–452. [Google Scholar] [CrossRef]
- Ali, M.I. Another view on q-rung orthopair fuzzy sets. Int. J. Intell. Syst. 2018, 33, 2139–2153. [Google Scholar] [CrossRef]
- Yager, R.R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 2017, 25, 1222–1230. [Google Scholar] [CrossRef]
- Riaz, M.; Hashmi, M.R. Linear Diophantine fuzzy set and its applications towards multi-attribute decision making problems. J. Intell. Fuzzy Syst. 2019, 37, 5417–5439. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 2, 145–172. [Google Scholar] [CrossRef]
- Molodtsov, D. Soft set theory-first results. Comput. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef]

| Set Theories | Advantages | Semantic Disadvantages |
|---|---|---|
| Fuzzy sets [46] | Contribute knowledge about | Dose not give information about the |
| specific property | falsity and roughness of information system | |
| Intuitionistic fuzzy sets [47,48] | Detect vagueness with | Restricted valuation space and |
| agree and disagree criteria | does not deal with roughness | |
| Pythagorean fuzzy sets [49,50,51] | Detect vagueness with larger | Cannot handle the roughness of the |
| valuation space than IFSs | data and dependency between the grades | |
| q-rung orthopair fuzzy sets [52,53] | Increase the valuation space of grades | For smaller values of q, creates dependency |
| to deal with real-life situations | in grades and cannot handle roughness | |
| Create independency between the degrees | Does not give information about the | |
| Linear Diophantine fuzzy sets [54] | and increase their valuation space under | roughness of information data and cannot |
| the effect of control parameterizations | deal with multi-valued parameterizations | |
| Rough sets [55] | Contain upper and lower approximations of | Does not characterize the agree and |
| information dataset to handle roughness | disagree degrees with parameterizations | |
| Soft sets [56] | Produce multi-valued mapping based | Does not contain fuzziness and |
| parameterizations under different criteria | roughness in optimization | |
| Linear Diophantine fuzzy | Produce multi-valued mapping based | Does not characterize the roughness |
| soft sets (proposed) | on the LDF value information system | of real-life dataset |
| Contain upper and lower approximations | Due to the use of LDFS approximation | |
| Linear Diophantine fuzzy soft | with LDF degrees under double | space for evaluations, it contains |
| rough sets (proposed) | parameterizations (soft and reference) and | heavy calculations, but easy to handle |
| collect data without any loss of information | ||
| Use crisp soft approximation space | Easy calculations as compared to | |
| Soft rough linear Diophantine | to evaluate upper and lower approximations | LDFSRS, but heavy as compared to |
| fuzzy sets (proposed) | with LDF degrees and collect data | others (easy to handle) |
| without any loss of information |
| Alternatives | LDFNs |
|---|---|
| Notation | Explanation |
|---|---|
| Universal set | |
| Set of decision variables | |
| Elements of set | |
| Elements of set | |
| Lower approximation operator for SRLDFSs | |
| Upper approximation operator for SRLDFSs | |
| Lower approximation operator for LDFSRSs | |
| Upper approximation operator for LDFSRSs | |
| Satisfaction grade | |
| Dissatisfaction grade | |
| Collection of all LDFSs over | |
| Collection of all LDFSs over |
| Notation | Formulation | Notation | Formulation |
|---|---|---|---|
| Approximation Space | Set Theories | Family of Sets | Degeneration of SRLDF | After Degeneration of the |
|---|---|---|---|---|
| Approximation Operators | Constructed Model | |||
| Crisp soft | =crisp set | collection of all | Yes | Soft rough |
| crisp subsets of | sets [26] | |||
| Crisp soft | collection of all | Yes | Soft rough | |
| fuzzy subsets of | fuzzy sets [42,43] | |||
| Crisp soft | collection of all | Yes | Soft rough intuitionistic | |
| IF-subsets of | fuzzy sets [26] | |||
| Crisp soft | collection of all | Yes | Soft rough Pythagorean | |
| PF-subsets of | fuzzy sets [44] | |||
| Crisp soft | collection of all | Yes | Soft rough q-rung | |
| PF-subsets of | orthopair fuzzy sets |
| ... | |||
|---|---|---|---|
| ... | |||
| ... | |||
| ... | ... | ... | ... |
| ... |
| Notation | Formulation | Notation | Formulation |
|---|---|---|---|
| Numeric Values of LDFNs | |
|---|---|
| : | |
| : | |
| : | |
| : | |
| : | |
| : |
| Approximation Space | Set Theories | Family of Sets | Degeneration of LDFSR | After Degeneration of the |
|---|---|---|---|---|
| Approximation Operators | Constructed Model | |||
| LDFS | collection of all | Yes | Soft fuzzy | |
| fuzzy subsets of | rough sets [42,43] | |||
| LDFS | collection of all | Yes | Intuitionistic fuzzy | |
| IF-subsets of | soft rough sets [26] | |||
| LDFS | collection of all | Yes | Pythagorean fuzzy | |
| PF-subsets of | soft rough sets [44] | |||
| LDFS | collection of all | Yes | q-rung orthopair | |
| PF-subsets of | fuzzy soft rough sets | |||
| Crisp soft | collection of all | Yes | Soft rough linear | |
| LDF-subsets of | Diophantine fuzzy sets |
| Attributes | Characteristics for LDFSR |
|---|---|
| “Technical: convenience, maintainability, safety required” | |
| “Monetary: operational cost, maintenance cost, purchasing cost” | |
| “Operational: fuel consumption, moving speed, capacity” | |
| “Strategic: flexibility, level of training required, guarantee” |
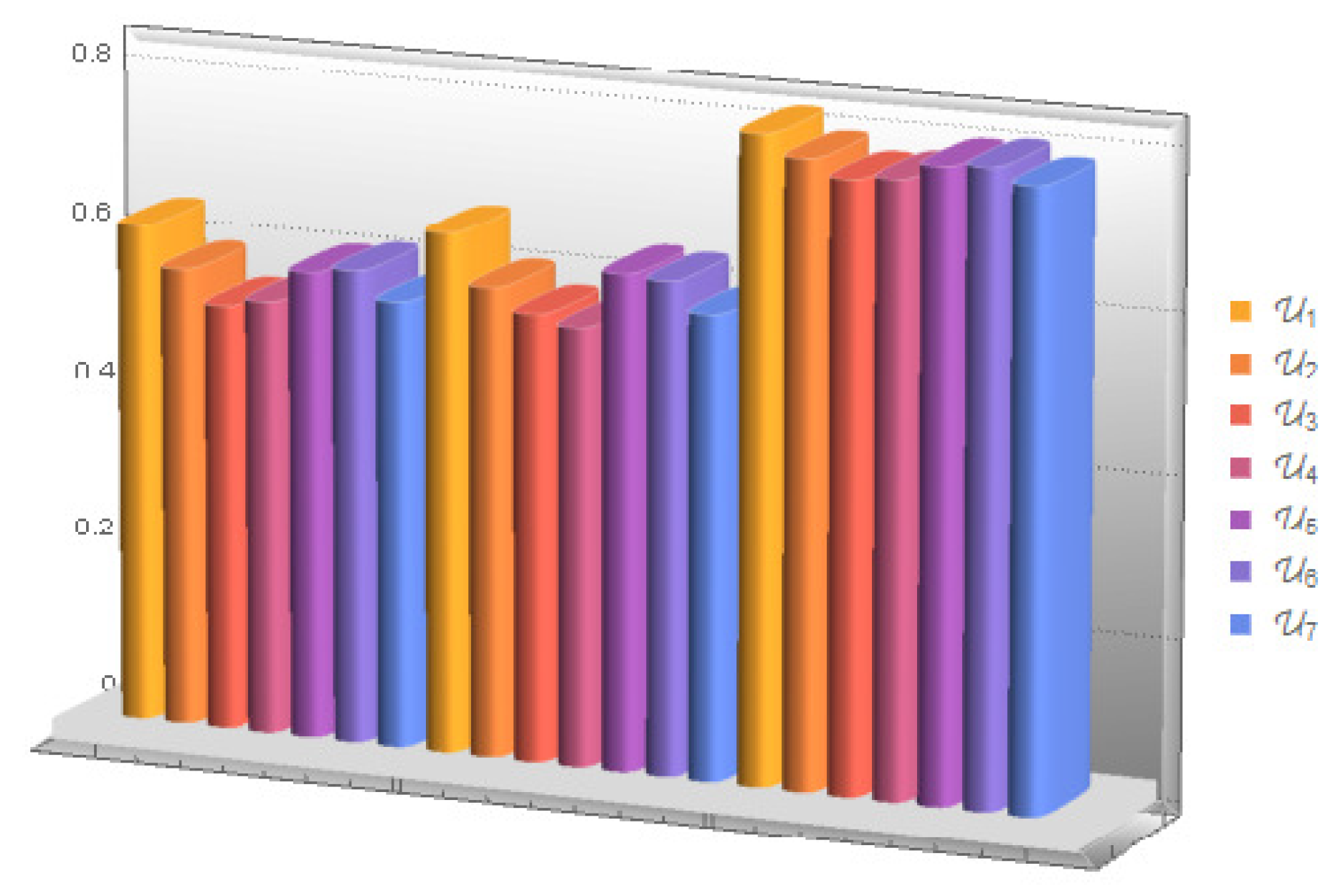
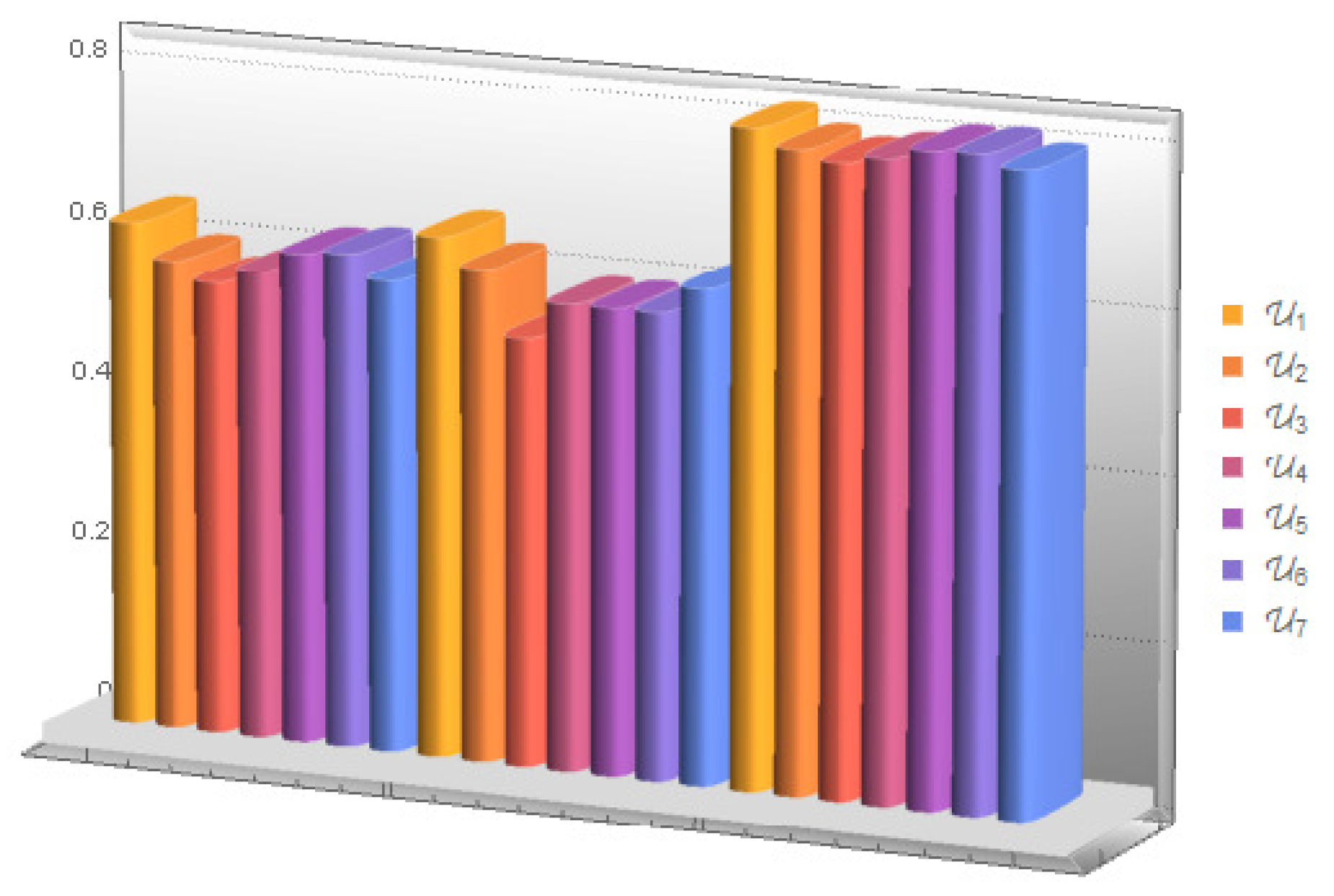
| LDFS | Ranking | Final Decision | |||||||
|---|---|---|---|---|---|---|---|---|---|
| (SF) | |||||||||
| (QSF) | |||||||||
| (ESF) |
| F.D | ||
|---|---|---|
| 0 | NO | NO |
| 1 | YES | YES |
| 0 | YES | NO |
| 1 | NO | NO |
| F.D | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | NO | NO | ||||||
| 0 | NO | NO | ||||||
| 1 | NO | NO | ||||||
| 0 | YES | NO | ||||||
| 1 | YES | YES | ||||||
| 1 | YES | YES | ||||||
| 1 | YES | YES |
| F.D | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | YES | YES | ||||||
| 0 | YES | NO | ||||||
| 1 | NO | NO | ||||||
| 0 | NO | NO | ||||||
| 1 | YES | YES | ||||||
| 1 | YES | YES | ||||||
| 1 | NO | NO |
| F.D | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | NO | NO | ||||||
| 1 | NO | NO | ||||||
| 0 | NO | NO | ||||||
| 1 | YES | YES | ||||||
| 1 | YES | YES | ||||||
| 1 | YES | YES | ||||||
| 0 | YES | NO |
| F.D | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | YES | NO | ||||||
| 1 | YES | YES | ||||||
| 0 | NO | NO | ||||||
| 1 | NO | NO | ||||||
| 1 | YES | YES | ||||||
| 1 | YES | YES | ||||||
| 0 | NO | NO |
| F.D | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | NO | NO | ||||||
| 1 | NO | NO | ||||||
| 0 | NO | NO | ||||||
| 0 | YES | NO | ||||||
| 1 | YES | YES | ||||||
| 0 | YES | NO | ||||||
| 1 | YES | YES |
| F.D | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | YES | YES | ||||||
| 1 | YES | YES | ||||||
| 0 | NO | NO | ||||||
| 0 | NO | NO | ||||||
| 1 | YES | YES | ||||||
| 0 | YES | NO | ||||||
| 1 | NO | NO |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 1 | |
| 1 | 0 | 0 | 1 | |
| 0 | 1 | 1 | 0 |
| LDFS | Ranking | Final Decision | |||||||
|---|---|---|---|---|---|---|---|---|---|
| (SF) | |||||||||
| (QSF) | |||||||||
| (ESF) |
| F.D | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | YES | NO | ||||||
| 1 | NO | NO | ||||||
| 0 | NO | NO | ||||||
| 0 | YES | NO | ||||||
| 1 | YES | YES | ||||||
| 1 | YES | YES | ||||||
| 0 | NO | NO |
| F.D | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | YES | YES | ||||||
| 1 | YES | YES | ||||||
| 1 | NO | NO | ||||||
| 0 | NO | NO | ||||||
| 1 | NO | NO | ||||||
| 1 | YES | YES | ||||||
| 0 | YES | NO |
| F.D | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | YES | YES | ||||||
| 0 | NO | NO | ||||||
| 0 | NO | NO | ||||||
| 1 | YES | YES | ||||||
| 1 | YES | YES | ||||||
| 0 | YES | NO | ||||||
| 1 | NO | NO |
| F.D | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | YES | YES | ||||||
| 0 | YES | NO | ||||||
| 0 | NO | NO | ||||||
| 1 | NO | NO | ||||||
| 1 | NO | NO | ||||||
| 0 | YES | NO | ||||||
| 1 | YES | YES |
| F.D | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | YES | YES | ||||||
| 1 | NO | NO | ||||||
| 0 | NO | NO | ||||||
| 1 | YES | YES | ||||||
| 0 | YES | NO | ||||||
| 1 | YES | YES | ||||||
| 1 | NO | NO |
| F.D | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | YES | YES | ||||||
| 1 | YES | YES | ||||||
| 0 | NO | NO | ||||||
| 1 | NO | NO | ||||||
| 0 | NO | NO | ||||||
| 1 | YES | YES | ||||||
| 1 | YES | YES |
| Concepts | Satisfaction | Dissatisfaction | Reference |
|---|---|---|---|
| Degree | Degree | Parameterizations | |
| Fuzzy set [46] | ✓ | × | × |
| Rough set [55] | × | × | × |
| Soft set [56] | × | × | × |
| Intuitionistic fuzzy set [47,48] | ✓ | ✓ | × |
| Pythagorean fuzzy set [49,50,51] | ✓ | ✓ | × |
| q-rung orthopair fuzzy set [52,53] | ✓ | ✓ | × |
| LDFS [54] | ✓ | ✓ | ✓ |
| LDFSS (proposed) | ✓ | ✓ | ✓ |
| LDFSRS (proposed) | ✓ | ✓ | ✓ |
| SRLDFS (proposed) | ✓ | ✓ | ✓ |
| Concepts | Upper and lower | Boundary | multi-valued |
| approximations | region | parameterizations | |
| Fuzzy set [46] | × | × | × |
| Rough set [55] | ✓ | ✓ | × |
| Soft set [56] | × | × | ✓ |
| Intuitionistic fuzzy set [47,48] | × | × | × |
| Pythagorean fuzzy set [49,50,51] | × | × | × |
| q-rung orthopair fuzzy set [52,53] | × | × | × |
| LDFS [54] | × | × | × |
| LDFSS (proposed) | × | × | ✓ |
| LDFSRS (proposed) | ✓ | ✓ | ✓ |
| SRLDFS (proposed) | ✓ | ✓ | ✓ |
| Concepts | Remarks |
|---|---|
| Fuzzy set [46] | It only deals with the truth values of objects. |
| Rough set [55] | It only deal with the vagueness of input data. |
| Soft set [56] | It only deal with the uncertainties under parameterizations. |
| Intuitionistic fuzzy set [47] | It cannot be applied if for some . |
| Pythagorean fuzzy set [49,50,51] | It cannot be applied if for some . |
| q-rung orthopair fuzzy set [52,53] | It cannot be applied for smaller values of “q” with |
| or if for some . | |
| LDFS [54] | (1) It can deal with all the cases in which FS, IFS, PFS, and q-ROFS |
| cannot be applied; (2) it involves a parameterization perspective | |
| and works under the influence of reference or control parameters; (3) satisfaction | |
| and dissatisfaction degrees can be chosen freely from . | |
| LDFSS (proposed) | It contains all the properties of LDFS with the addition of multi-valued |
| parameterizations to deal with the uncertainties in a parametric manner. | |
| LDFSRS (proposed) | It contains all the properties of LDFSS with the addition of upper |
| and lower approximations to deal with the roughness of input data | |
| under the effect of “LDFS approximation space”. | |
| SRLDFS (proposed) | It contains all the properties of LDFSS with the addition of upper |
| and lower approximations to deal with the roughness of input data | |
| under the effect of “crisp soft approximation space”. |
| Proposed | Score | Core | Final |
|---|---|---|---|
| Algorithm | Function | Set | Decision |
| Algorithm 1 | × | ||
| Algorithm 1 | × | ||
| Algorithm 1 | × | ||
| Algorithm 2 | × | ✓ | |
| Algorithm 3 | × | ||
| Algorithm 3 | × | ||
| Algorithm 3 | × | ||
| Algorithm 4 | × | ✓ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riaz, M.; Hashmi, M.R.; Kalsoom, H.; Pamucar, D.; Chu, Y.-M. Linear Diophantine Fuzzy Soft Rough Sets for the Selection of Sustainable Material Handling Equipment. Symmetry 2020, 12, 1215. https://doi.org/10.3390/sym12081215
Riaz M, Hashmi MR, Kalsoom H, Pamucar D, Chu Y-M. Linear Diophantine Fuzzy Soft Rough Sets for the Selection of Sustainable Material Handling Equipment. Symmetry. 2020; 12(8):1215. https://doi.org/10.3390/sym12081215
Chicago/Turabian StyleRiaz, Muhammad, Masooma Raza Hashmi, Humaira Kalsoom, Dragan Pamucar, and Yu-Ming Chu. 2020. "Linear Diophantine Fuzzy Soft Rough Sets for the Selection of Sustainable Material Handling Equipment" Symmetry 12, no. 8: 1215. https://doi.org/10.3390/sym12081215
APA StyleRiaz, M., Hashmi, M. R., Kalsoom, H., Pamucar, D., & Chu, Y.-M. (2020). Linear Diophantine Fuzzy Soft Rough Sets for the Selection of Sustainable Material Handling Equipment. Symmetry, 12(8), 1215. https://doi.org/10.3390/sym12081215







