Solution of Multi-Term Time-Fractional PDE Models Arising in Mathematical Biology and Physics by Local Meshless Method

Abstract

Fractional differential equations depict nature sufficiently in light of the symmetry properties which describe biological and physical processes. This article is concerned with the numerical treatment of three-term time fractional-order multi-dimensional diffusion equations by using an efficient local meshless method. The space derivative of the models is discretized by the proposed meshless procedure based on the multiquadric radial basis function though the time-fractional part is discretized by Liouville–Caputo fractional derivative. The numerical results are obtained for one-, two- and three-dimensional cases on rectangular and non-rectangular computational domains which verify the validity, efficiency and accuracy of the method.

1. Introduction

Over the most recent couple of decades, fractional-order differential equations have been effectively utilized for modeling a wide range of processes and systems in the applied sciences and engineering. The basic information on fractional calculus can be found in [1,2,3]. The extensive applications in science and engineering are portrayed by fractional partial differential equation (PDEs) [4,5,6,7,8]. It is observed that the multi-term time-fractional PDEs are suggested to improve the modelling accuracy in depicting the anomalous diffusion process, modeling different sorts of viscoelastic damping, precisely catching power-law frequency dependence and simulating flow of a fractional Maxwell fluid [9].

In the present time, the researchers worked developing methods for the approximate and exact solutions for fractional PDEs. In this regard, numerous methods have been employed for the solution like finite difference method [10], homotopy analysis method [11,12], meshless method [13,14,15,16], Riccati transformation approach [17], Adomian decomposition method [18], expansion methods [19,20] and variational iteration algorithms [21,22].

Meshless methods have been got more attention for handling different sort of PDE models arise in various fields of science and technology. Particularly the meshless method based on radial basis functions (RBFs) are one of the most well-known sorts among these techniques. Unlike the traditional methods of finite difference and finite element, the meshless techniques do not need mesh in computational domains and can be applied efficiently to multi-dimensional PDE models with complex domains [23]. As per these realities, meshless strategies are known to be truly adaptable and valuable and are broadly utilized to numerous useful problems [24]. Despite the fact that the standard global meshless collocation strategy depends on the globally supported RBFs is known to be a proficient computational procedure. In this procedure the RBFs are used to obtain the coefficients, so that the derivatives of a function $f\left(x\right)$ can be written as a linear combination of the functional values at the predetermined nodes, but the technique leads to an ill-conditioned and dense system of algebraic equations due to shape parameters sensitivity and a large number of collocation points. Tragically, the computational cost of execution and ill-conditioning of the procedure will increment drastically by increasing the number of collocation points. To avoid these limitations, the researchers recommended local meshless techniques [25,26]. The beauty of the local meshless technique is utilizing just neighbouring collocation points which results in a sparse matrix system and ward off the main deficiency of ill-conditioning. This sparse system of equations can effectively be solved [27,28,29].

According to [30], Symmetry is a fundamental property of nature and its phenomena. Therefore, the fractional-order diffusion equations are able to adequately describe physical and biological processes and have symmetry properties, which follow from some fundamental laws. The current work is dedicated to utilize the local meshless method (LMM) for the numerical investigation of three-term time fractional-order diffusion model equations up to three space dimensions. The space derivatives of the model equations are calculated by the proposed local meshless algorithm utilizing multiquadric (MQ) radial basis functions (RBFs) while time-fractional part is approximated by using Liouville–Caputo definition. The suggested algorithm is tested on non-rectangular domains as well in two- and three-dimensional case in numerical examinations. Consider the unsteady three-term time-fractional diffusion PDE

$$\begin{array}{cc}\hfill a_1\frac{{\partial }^{\alpha }U(\overline{\mathbf{y}},t)}{\partial t^{\alpha }}+a_2\frac{{\partial }^{\beta }U(\overline{\mathbf{y}},t)}{\partial t^{\beta }}+a_3\frac{{\partial }^{\gamma }U(\overline{\mathbf{y}},t)}{\partial t^{\gamma }}=& a_4\nabla U(\overline{\mathbf{y}},t)+F(\overline{\mathbf{y}},t)\equiv \mathcal{L}U(\overline{\mathbf{y}},t),\hfill \\ \hfill & \overline{\mathbf{y}}\in \mathrm{\Omega },0<\gamma \le \beta \le \alpha \le 1,t>0,\hfill \end{array}$$

(1)

where the initial and boundary conditions are as follows

$$U(\overline{\mathbf{y}},0)=U_0,\mathcal{C}(\overline{\mathbf{y}},t)=g(\overline{\mathbf{y}},t),\overline{\mathbf{y}}\in \partial \mathrm{\Omega },$$

(2)

where $a_4$ is the diffusion coefficient and for one-dimensional (1D) case $\overline{\mathbf{y}}=x$, for two-dimensional (2D) case $\overline{\mathbf{y}}=(x,y)$ and for three-dimensional (3D) case $\overline{\mathbf{y}}=(x,y,z)$.

2. Proposed Methodology

The LMM [26,31] is utilized for the solution of time-fractional convection-diffusion models. The derivatives of $U(\overline{\mathbf{y}},t)$ at the centers ${\overline{\mathbf{y}}}_h$ are approximated by the neighborhood of ${\overline{\mathbf{y}}}_h$, $\{{\overline{\mathbf{y}}}_{h1},{\overline{\mathbf{y}}}_{h2},{\overline{\mathbf{y}}}_{h3},\dots ,{\overline{\mathbf{y}}}_{h{n}_h}\}\subset \{{\overline{\mathbf{y}}}_1,{\overline{\mathbf{y}}}_2,\dots ,{\overline{\mathbf{y}}}_{N^n}\},n_h\ll N^n$, where $h=1,2,\dots ,N^n$. The local meshless procedure for 1D case is as follows

$$U^{\left(m\right)}\left(x_h\right)\approx \sum _{k=1}^{n_h}{\lambda }_k^{\left(m\right)}U\left(x_{hk}\right),h=1,2,\dots ,N.$$

(3)

Substituting RBF $\psi (\parallel x-x_p\parallel )$ in Equation (3)

$${\psi }^{\left(m\right)}(\parallel x_h-x_p\parallel )=\sum _{k=1}^{n_h}{\lambda }_{hk}^{\left(m\right)}\psi (\parallel x_{hk}-x_p\parallel ),p=h1,h2,\dots ,h{n}_h,$$

(4)

where $\psi (\parallel x_{hk}-x_p\parallel )=\sqrt{1+(c\parallel x_{hk}-x_p{\parallel )}^2}$ in case of MQ RBF.

Matrix form of Equation (4) can be written as

$${\mathit{\psi }}_{n_h}^{\left(m\right)}={\mathbf{A}}_{n_h}{\mathit{\lambda }}_{n_h}^{\left(m\right)},$$

(5)

From Equation (5), we obtain

$${\mathit{\lambda }}_{n_h}^{\left(m\right)}={\mathbf{A}}_{n_h}^{-1}{\mathit{\psi }}_{n_h}^{\left(m\right)}.$$

(6)

Equations (3) and (6) implies

$$U^{\left(m\right)}\left(x_h\right)={\left({\mathit{\lambda }}_{n_h}^{\left(m\right)}\right)}^T{\mathbf{U}}_{n_h},$$

where

$${\mathbf{U}}_{n_h}={\left[U\left(x_{h1}\right),U\left(x_{h2}\right),\dots ,U\left(x_{h{n}_h}\right)\right]}^T.$$

The derivatives of $U(x,y,t)$ in term of x and y are calculated for 2D case by utilizing the above procedure as follows

$$U_x^{\left(m\right)}(x_h,y_h)\approx \sum _{k=1}^{n_h}{\gamma }_k^{\left(m\right)}U(x_{hk},y_{hk}),h=1,2,\dots ,N^2,$$

(7)

$$U_y^{\left(m\right)}(x_h,y_h)\approx \sum _{k=1}^{n_h}{\eta }_k^{\left(m\right)}U(x_{hk},y_{hk}),h=1,2,\dots ,N^2.$$

(8)

To find coefficients ${\gamma }_k^{\left(m\right)}$ and ${\eta }_k^{\left(m\right)}$ ($k=1,2,\dots ,n_h$ ), we continue as

$${\mathit{\gamma }}_{n_h}^{\left(m\right)}={\mathbf{A}}_{n_h}^{-1}{\mathbf{\Phi }}_{n_h}^{\left(m\right)},$$

(9)

$${\mathit{\eta }}_{n_h}^{\left(m\right)}={\mathbf{A}}_{n_h}^{-1}{\mathbf{\Phi }}_{n_h}^{\left(m\right)}.$$

(10)

The above technique can be rehashed for the three-dimensional case.

2.1. Time Discretization

The derivative in time direction $\frac{{\partial }^{\alpha }U(\overline{\mathbf{y}},t)}{\partial t^{\alpha }}$ for $\alpha \in (0,1)$ is calculated by by means of the Liouville–Caputo derivative definition [32]

$$\frac{{\partial }^{\alpha }U(\overline{\mathbf{y}},t)}{\partial t^{\alpha }}=\left\{\begin{array}{cc}\frac{1}{\mathrm{\Gamma }\left(1-\alpha \right)}\underset{0}{\overset{t}{\int }}\frac{\partial U(\overline{\mathbf{y}},\vartheta )}{\partial \vartheta }{\left(t-\vartheta \right)}^{-\alpha }d\vartheta ,\hfill & 0<\alpha <1\hfill \\ \hfill \\ \frac{\partial U(\overline{\mathbf{y}},t)}{\partial t},\hfill & \alpha =1.\hfill \end{array}\right.$$

Consider $Q+1$ equally spaced time intervals $t_0,t_1,\dots ,t_Q$, in $[0,t]$, such that $t_q=q\tau$, $q=0,1,2,\dots ,Q$, where time step size is denoted by $\tau$ to calculate the time-fractional derivative $(q+1)$th time level is

$$\begin{array}{cc}\hfill \frac{{\partial }^{\alpha }U(\overline{\mathbf{y}},t_{q+1})}{\partial t^{\alpha }}& =\frac{1}{\mathrm{\Gamma }(1-\alpha )}\underset{0}{\overset{t_{q+1}}{\int }}\frac{\partial U(\overline{\mathbf{y}},\vartheta )}{\partial \vartheta }{\left(t_{q+1}-\vartheta \right)}^{-\alpha }d\vartheta ,\hfill \\ \hfill & =\frac{1}{\mathrm{\Gamma }(1-\alpha )}\sum _{s=0}^q\underset{s\tau }{\overset{(s+1)\tau }{\int }}\frac{\partial U(\overline{\mathbf{y}},\vartheta )}{\partial \vartheta }{\left(t_{s+1}-\vartheta \right)}^{-\alpha }d\vartheta ,\hfill \\ \hfill & \approx \frac{1}{\mathrm{\Gamma }(1-\alpha )}\sum _{s=0}^q\underset{s\tau }{\overset{(s+1)\tau }{\int }}\frac{\partial U(\overline{\mathbf{y}},{\vartheta }_s)}{\partial \vartheta }{\left(t_{s+1}-\vartheta \right)}^{-\alpha }d\vartheta .\hfill \end{array}$$

(11)

The term $\frac{\partial U(\overline{\mathbf{y}},{\vartheta }_s)}{\partial \vartheta }$ is approximated as follows

$$\frac{\partial U(\overline{\mathbf{y}},{\vartheta }_s)}{\partial \vartheta }=\frac{U(\overline{\mathbf{y}},{\vartheta }_{s+1})-U(\overline{\mathbf{y}},{\vartheta }_s)}{\vartheta }+R^{s+1}\left(\overline{\mathbf{y}}\right).$$

(12)

with truncation error (see [33])

$$|R^{s+1}\left(\overline{\mathbf{y}}\right)|\le \mathcal{C}{\tau }^{2-\alpha }$$

(13)

$$\begin{array}{cc}\hfill \frac{{\partial }^{\alpha }U(\overline{\mathbf{y}},t_{q+1})}{\partial t^{\alpha }}& \approx \frac{1}{\mathrm{\Gamma }(1-\alpha )}\sum _{s=0}^q\frac{U(\overline{\mathbf{y}},t_{s+1})-U(\overline{\mathbf{y}},t_s)}{\tau }\underset{s\tau }{\overset{(s+1)\tau }{\int }}{\left(t_{s+1}-\vartheta \right)}^{-\alpha }d\vartheta +R^{s+1}\left(\overline{\mathbf{y}}\right),\hfill \\ \hfill & =\frac{1}{\mathrm{\Gamma }(1-\alpha )}\sum _{s=0}^q\frac{U(\overline{\mathbf{y}},t_{q+1-s})-U(\overline{\mathbf{y}},t_{q-s})}{\tau }\underset{s\tau }{\overset{(s+1)\tau }{\int }}{\left(t_{s+1}-\vartheta \right)}^{-\alpha }d\vartheta +R^{s+1}\left(\overline{\mathbf{y}}\right),\hfill \\ \hfill & =\left\{\begin{array}{c}\frac{{\tau }^{-\alpha }}{\mathrm{\Gamma }(2-\alpha )}(U^{q+1}-U^q)+\frac{{\tau }^{-\alpha }}{\mathrm{\Gamma }(2-\alpha )}\sum _{s=1}^q(U^{q+1-s}-U^{q-s})[{(s+1)}^{1-\alpha }-s^{1-\alpha }]+R^{s+1}\left(\overline{\mathbf{y}}\right),q\ge 1\hfill \\ \frac{{\tau }^{-\alpha }}{\mathrm{\Gamma }(2-\alpha )}(U^1-U^0).q=0,\hfill \end{array}\right.\hfill \end{array}$$

(14)

Letting $a_0^{\alpha }=\frac{{\tau }^{-\alpha }}{\mathrm{\Gamma }(2-\alpha )}$ and $b_s^{\alpha }={(s+1)}^{1-\alpha }-s^{1-\alpha }$, $s=0,1,\dots ,q$, the above equation can be written as follows

$$\begin{array}{c}\hfill \frac{{\partial }^{\alpha }U(\overline{\mathbf{y}},t_{q+1})}{\partial t^{\alpha }}\approx \left\{\begin{array}{c}{a}_0^{\alpha }(U^{q+1}-U^q)+a_0^{\alpha }{\displaystyle \sum _{s=1}^q}{b}_s^{\alpha }(U^{q+1-s}-U^{q-s})+R^{s+1}\left(\overline{\mathbf{y}}\right),q\ge 1\hfill \\ a_0^{\alpha }(U^1-U^0),q=0.\hfill \end{array}\right.\end{array}$$

(15)

A similar methodology is employed for fractional derivative of order $\beta$ and $\gamma$.

2.2. A $\theta$-Weighted Technique

A $\theta$-weighted technique is adopted to approximate the model equation in the form (1) with $a_1=a_2=a_3=1$ in time utilizing Equation (15)

$$\begin{array}{c}\hfill \frac{{\partial }^{\alpha }U}{\partial t^{\alpha }}+\frac{{\partial }^{\beta }U}{\partial t^{\beta }}+\frac{{\partial }^{\gamma }U}{\partial t^{\gamma }}\equiv \mathcal{L}U,\end{array}$$

(16)

now using Equation (15) for $q\ge 1$

$$\begin{array}{cc}\hfill & a_0^{\alpha }{U}^{(q+1)}-a_0^{\alpha }{U}^{\left(q\right)}+a_0^{\alpha }\sum _{s=1}^q{b}_s^{\alpha }(U^{q+1-s}-U^{q-s})+a_0^{\beta }{U}^{(q+1)}-a_0^{\beta }{U}^{\left(q\right)}+a_0^{\beta }\sum _{s=1}^q{b}_s^{\beta }(U^{q+1-s}-U^{q-s})\hfill \\ \hfill & +a_0^{\gamma }{U}^{(q+1)}-a_0^{\gamma }{U}^{\left(q\right)}+a_0^{\gamma }\sum _{s=1}^q{b}_s^{\gamma }(U^{q+1-s}-U^{q-s})=\theta \mathcal{L}{U}^{(q+1)}+(1-\theta )\mathcal{L}{U}^{\left(q\right)},\hfill \end{array}$$

(17)

we get

$$\begin{array}{cc}\hfill U^{(q+1)}=& {\left(a_0^{\alpha }I+a_0^{\beta }I+a_0^{\gamma }I-\theta \mathcal{L}\right)}^{-1}\{(a_0^{\alpha }I+a_0^{\beta }I+a_0^{\gamma }I+(1-\theta )\mathcal{L})U^{\left(q\right)}\hfill \\ \hfill & -\left(a_0^{\alpha }\sum _{s=1}^q{b}_s(U^{q+1-s}-U^{q-s})+a_0^{\beta }\sum _{s=1}^q{b}_s(U^{q+1-s}-U^{q-s})+a_0^{\gamma }\sum _{s=1}^q{b}_s(U^{q+1-s}-U^{q-s})\right)\},\hfill \end{array}$$

(18)

similarly for $q=0$

$$U^{\left(1\right)}=({\left(a_0^{\alpha }I+a_0^{\beta }I+a_0^{\gamma }I-\theta \mathcal{L}\right)}^{-1}\left\{(a_0^{\alpha }I+a_0^{\beta }I+a_0^{\gamma }I+(1-\theta )\mathcal{L})U^{\left(0\right)}\right\},$$

(19)

After applying the LMM (discussed in Section 2), Equations (18) and (19) lead to

$$\begin{array}{cc}\hfill U^{(q+1)}=& {\left(a_0^{\alpha }I+a_0^{\beta }I+a_0^{\gamma }I-\theta L\right)}^{-1}\{(a_0^{\alpha }I+a_0^{\beta }I+a_0^{\gamma }I+(1-\theta )L)U^{\left(q\right)}\hfill \\ \hfill & -\left(a_0^{\alpha }\sum _{s=1}^q{b}_s(U^{q+1-s}-U^{q-s})+a_0^{\beta }\sum _{s=1}^q{b}_s(U^{q+1-s}-U^{q-s})+a_0^{\gamma }\sum _{s=1}^q{b}_s(U^{q+1-s}-U^{q-s})\right)\},\hfill \end{array}$$

(20)

$$\begin{array}{c}\hfill U^{\left(1\right)}=({\left(a_0^{\alpha }I+a_0^{\beta }I+a_0^{\gamma }I-\theta L\right)}^{-1}\left\{(a_0^{\alpha }I+a_0^{\beta }I+a_0^{\gamma }I+(1-\theta )L)U^{\left(0\right)}\right\},\end{array}$$

(21)

where $\mathcal{L}$ is known to be differential operator and L is the corresponding weights matrix, additionally I is an identity matrix. For $\theta =1$, Equations (20) and (21) reduce to an implicit method.

3. Numerical Results and Discussions

This section is concerned with the numerical results of the one-, two- and three-dimensional three-term time-fraction diffusion model equations utilizing the suggested efficient local meshless method (LMM). The implicit time discretization scheme is coupled with the LMM based on multiquadric radial basis function with shape parameter $c=1$ in all numerical simulation. Every single numerical trial are performed utilizing local supported domain $n_i=3$, $n_i=5$ and $n_i=7$ in one-, two- and three-dimensional case respectively, additionally the source functions in each case can be computed easily in the accordance of the corresponding exact solution. The accuracy is measure through different error norms which are defined as follows

$$\begin{array}{cc}\hfill & L_{absolute}=|\widehat{\mathbb{U}}-U|,L_2=\sqrt{\Delta h\sum _{h=1}^{N^n}{\left({\widehat{\mathbb{U}}}_h-U_h\right)}^2},\hfill \\ \hfill & Max\left(\epsilon \right)=\max \left(L_{absolute}\right),RMS=\sqrt{\frac{\sum _{h=1}^{N^n}{\left({\widehat{\mathbb{U}}}_h-U_h\right)}^2}{N}},\hfill \end{array}$$

(22)

where $\widehat{\mathbb{U}}$, U and $\Delta h$ denote the exact solutions, approximate solution and space step size respectively.

3.1. Test Problem

Consider Equation (1) as 1D three-term diffusion equation with $a_1=a_2=a_3=a_4=1$, having exact solution [34,35]

$$U(\overline{\mathbf{y}},t)=(1+t^2)(x-x^2),t\ge 0,x\in [0,1],$$

(23)

Initial and boundary conditions can found in accordance to the exact solution.

The simulation results for Test Problem in Section 3.1 are calculated utilizing the suggested LMM and Tabulated in Table 1 using various values of time-step size $\tau$ and nodal points N. It can be revealed from Table 1 that the accuracy increments to some extent with the increase in N and decrease in $\tau$. Figure 1 (left) shows the results of different time t versus $Max\left(\epsilon \right)$ for $\alpha =0.75,0.85,0.95$ whereas Figure 1 (right) shows the results at different nodal points N versus $RMS$ for $\alpha =0.75,0.85,0.95$. This figure is the evidence of good accuracy of the suggested LMM. The visual representation in form of absolute error for $\alpha =0.75,0.95$ up to $t=1$ is given in Figure 2. Figure 3 represents the comparison of the proposed LMM and the method given in [35], and we can see for this figure that the LMM method produced better results.

Table 1. Numerical results using $\alpha =0.75$, $\beta =0.3$, $\gamma =0.2$ and $t=0.5$ for Test Problem Section 3.1.

	$\mathit{N}=10$		$\mathit{N}=20$		$\mathit{N}=30$
$\mathbf{\tau }$	$\mathbf{Max}\left(\mathbf{\epsilon }\right)$	${\mathbf{L}}_{\mathbf{2}}$	$\mathbf{Max}\left(\mathbf{\epsilon }\right)$	${\mathbf{L}}_{\mathbf{2}}$	$\mathbf{Max}\left(\mathbf{\epsilon }\right)$	${\mathbf{L}}_{\mathbf{2}}$
1.0000 × 10${}^{-3}$	1.9384 × 10${}^{-4}$	1.2747 × 10${}^{-4}$	1.6001 × 10${}^{-4}$	7.7998 × 10${}^{-5}$	1.1545 × 10${}^{-4}$	6.2711 × 10${}^{-5}$
5.0000 × 10${}^{-4}$	2.6002 × 10${}^{-4}$	1.6562 × 10${}^{-4}$	8.7511 × 10${}^{-5}$	4.0421 × 10${}^{-5}$	6.6581 × 10${}^{-5}$	3.0006 × 10${}^{-5}$
2.5000 × 10${}^{-4}$	3.1467 × 10${}^{-4}$	2.1193 × 10${}^{-4}$	6.2482 × 10${}^{-5}$	4.1427 × 10${}^{-5}$	3.7293 × 10${}^{-5}$	1.7774 × 10${}^{-5}$
Condition No.	4.6506 × 10${}^4$		7.2601 × 10${}^5$		3.6585 × 10${}^6$

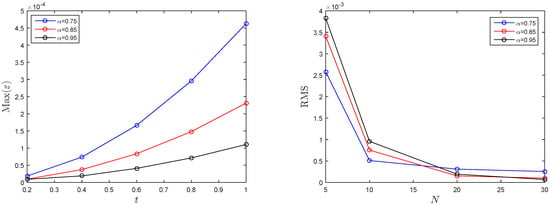
Figure 1. Simulation results using $N=30$ (left), $t=1$ (right) and $\tau =0.001$, $\beta =0.3$, $\gamma =0.2$ for Test Problem in Section 3.1.

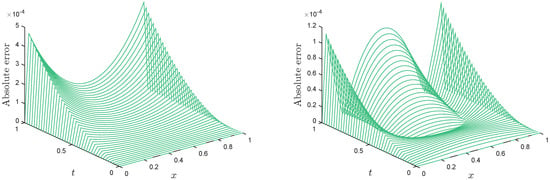
Figure 2. Simulation results using $N=30$, $\tau =0.001$, $\beta =0.3$, $\gamma =0.2$ and $\alpha =0.75$ (left), $\alpha =0.95$ (right) for Test Problem in Section 3.1.

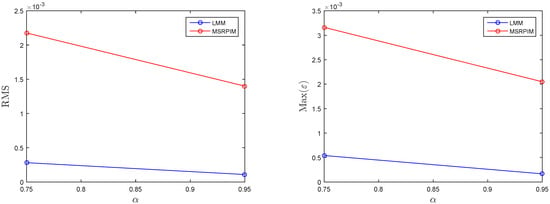
Figure 3. Simulation results of the LMM and the MSRPIM [35] using $N=25$, $\tau =0.001$, $t=1$, $\beta =0.3$ and $\gamma =0.2$ for Test Problem in Section 3.1.

3.2. Test Problem

Consider the Equation (1) as 2D three-term diffusion equation with $a_1=a_2=a_3=a_4=1$, having exact solution [35] is given as

$$U(\overline{\mathbf{y}},t)=sin\left(\pi x\right)sin\left(\pi y\right)exp(-t),t\ge 0.$$

(24)

The simulation results for Test Problem in Section 3.2 are calculated in terms of absolute error, $Max\left(\epsilon \right)$ and $RMS$ norms, are visualized in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 using the suggested LMM. In Figure 4 and Figure 5, we have compared the numerical results, in term of $Max\left(\epsilon \right)$ and $RMS$ error norms, of the suggested LMM and the method given in [35]. It can be seen that in this test problem the LMM gives accurate results when contrasted with the technique in [35]. Figure 6 shows the exact, numerical and absolute error for Test Problem in Section 3.2 which is the evidence of the proposed method for better accuracy. The LMM is tested on non-rectangular domains as shown in Figure 7 and Figure 8. It is obvious from these figures that the LMM gives great numerical results irrespective of the domains.

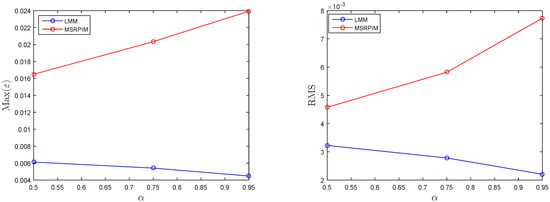
Figure 4. Simulation results of the LMM and the MSRPIM [35] using $[0,1]$, $N^2=20$, $\tau =0.001$, $t=0.1$, $\beta =0.3$ and $\gamma =0.2$ for Test Problem in Section 3.2.

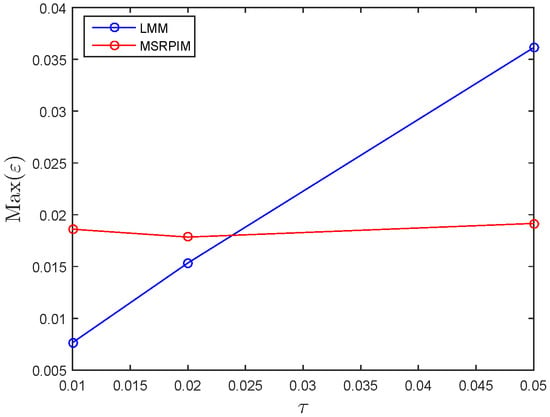
Figure 5. Simulation results of the LMM and the MSRPIM [35] using $[0,1]$, $N^2=20$, $t=0.1$, $\alpha =0.7$, $\beta =0.3$ and $\gamma =0.2$ for Test Problem in Section 3.2.

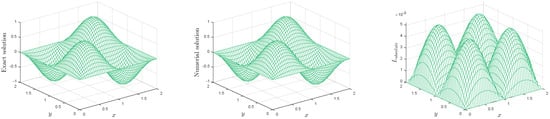
Figure 6. Simulation results using $N^2=20$, $\tau =0.001$, $t=0.1$, $\alpha =0.75$, $\beta =0.3$ and $\gamma =0.2$ for Test Problem in Section 3.2.

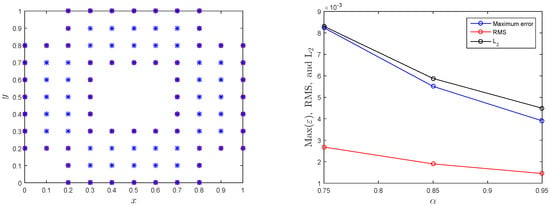
Figure 7. Computational domain (left) and numerical results in term of different errors norms (right) using $N^2=11$, $\tau =0.001$, $t=0.5$, $\beta =0.3$ and $\gamma =0.2$ for Test Problem in Section 3.2.

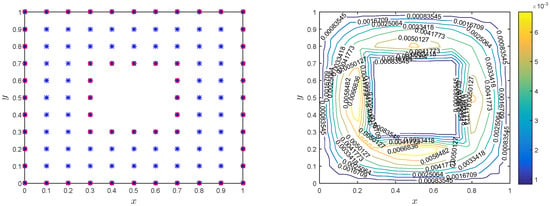
Figure 8. Computational domain (left) and $L_{absolute}$ (right) using $N=112$, $\tau =0.001$, $t=1$, $\alpha =0.75$, $\beta =0.3$ and $\gamma =0.2$ for Test Problem in Section 3.2.

3.3. Test Problem

Consider the 3D three-term fractional-order diffusion Equation (1). For $a_1=a_2=a_3=a_4=1$ the exact solutions is

$$U(\overline{\mathbf{y}},t)=sin\left(\pi x\right)sin\left(\pi y\right)sin\left(\pi z\right)exp(-t),t\ge 0(x,y,z)\in {[0,1]}^3.$$

(25)

The simulation results for Test Problem in Section 3.3 are appeared in Figure 9 for various fractional-order $\alpha$ and N. It tends to be see from the figure that the accuracy increments with increment in nodal points N to some extent. To testify the performance of the LMM on non-rectangular domains in three-dimensional case, the results are shown in Figure 10 and Figure 11.

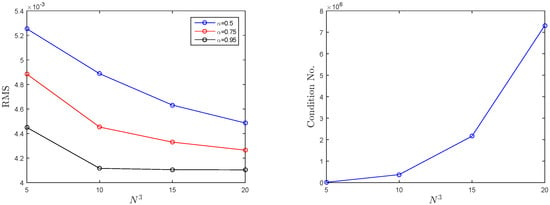
Figure 9. Simulation results using $\tau =0.01$, $t=1$, $\beta =0.3$ and $\gamma =0.2$ (left) and condition number (right) for Test Problem in Section 3.3.

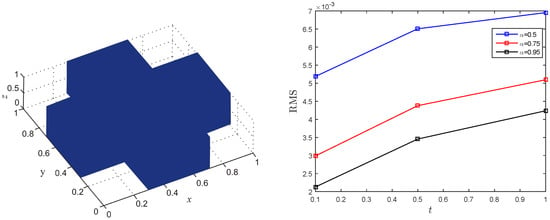
Figure 10. Computational domain (left) and absolute error (right) using $N^3=11$, $\tau =0.001$, $\beta =0.3$ and $\gamma =0.2$ for Test Problem in Section 3.3.

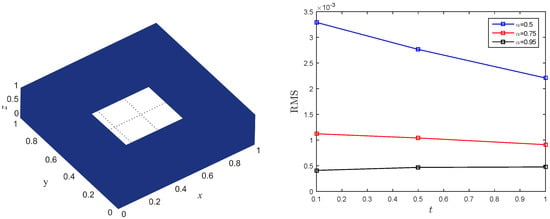
Figure 11. Computational domain (left) and absolute error (right) using $N^3=11$, $\tau =0.001$, $\beta =0.3$ and $\gamma =0.2$ for Test Problem in Section 3.3.

4. Conclusions

The current research is concerned with an efficient computational algorithm, named local meshless method, utilizing radial basis functions to approximate three-term time fractional-order diffusion PDE models in one-, two- and three-dimensions. The Liouville–Caputo definition is utilized in order to compute the time derivative the algorithm is constructed for $0<\gamma \le \beta \le \alpha <1$. To test the accuracy of the suggested LMM both rectangular and non-rectangular domains are considered in the test problems. The simulation results are evidence that the suggested LMM is a flexible interpolation method. In light of the current work, we can say that the proposed technique is powerful and effective to approximate the solution of multi-term time-fractional PDEs, so it can be also applied to a wide range of complex problems that occur in natural sciences and engineering.