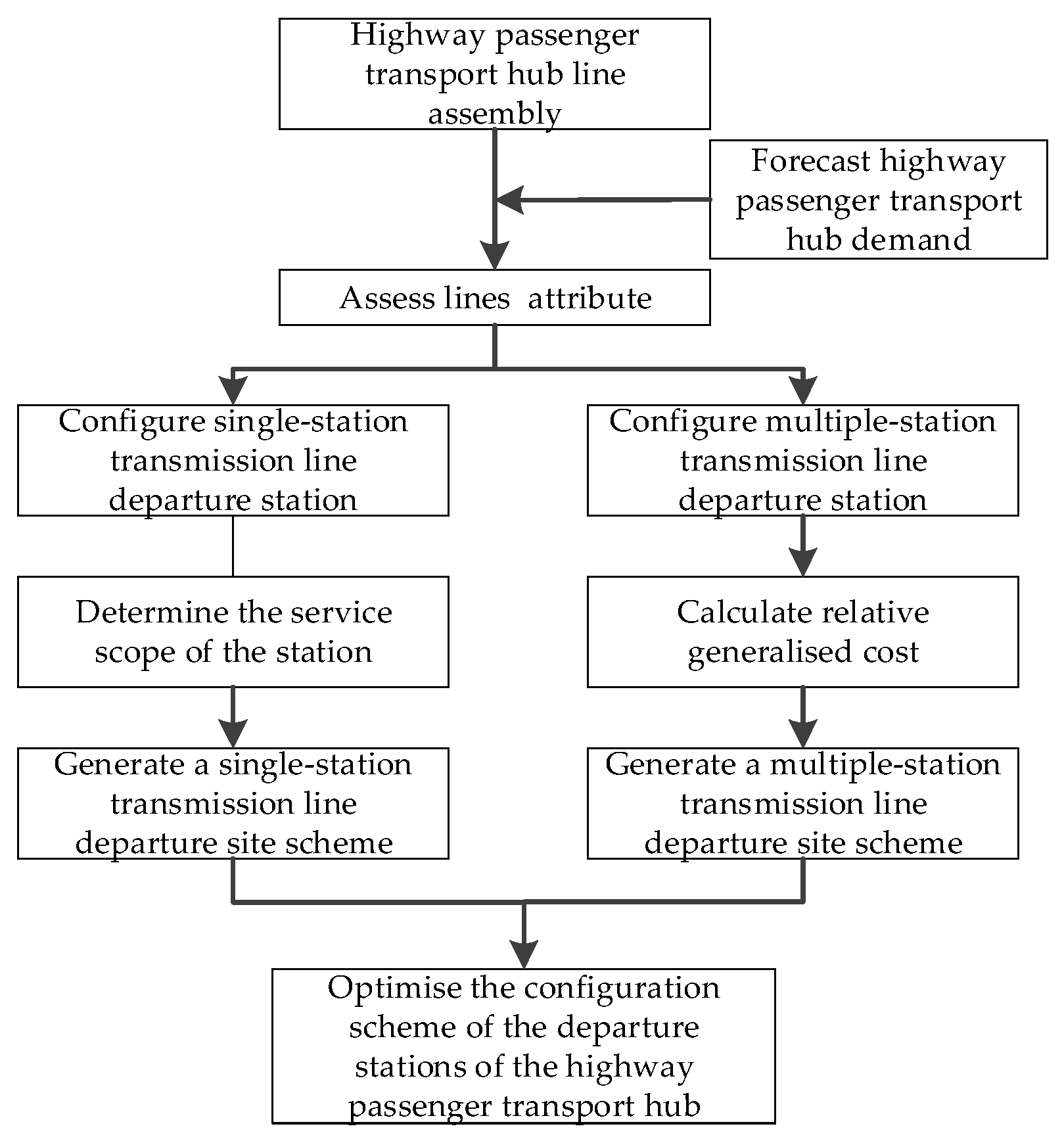
3.2.1. Relative Generalised Travel Cost
The generalised travel cost refers to the sum of the passenger’s economic and time costs during travel. For its calculation, the long-distance travel time on the highway and the coach ticket price are taken as the main costs of highway travel. The relative generalised travel cost is determined as the ratio of the generalised travel cost to the main cost of highway travel. The lower this ratio, the shorter the time passengers spend in the transfer system, the shorter the travel within the city. The relative generalised travel cost is defined as a measure of the departure station configuration.
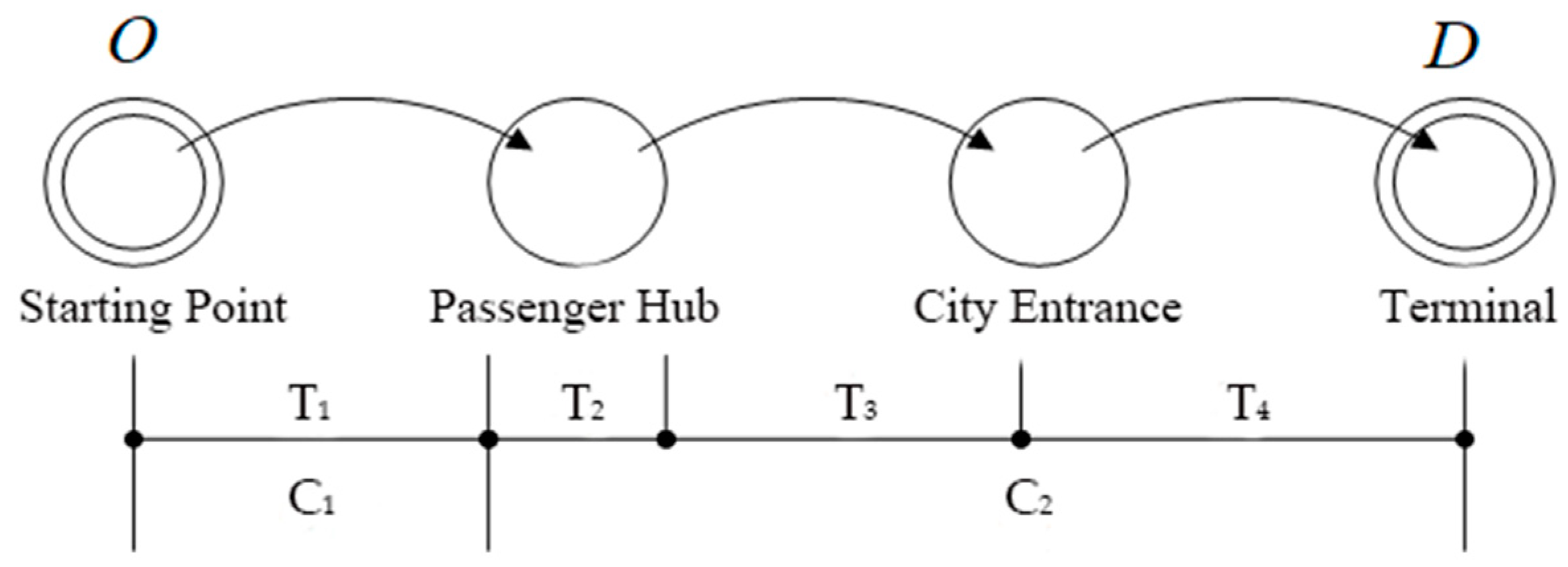
As shown in
Figure 2, the expenses of passengers are segmented according to the travel itinerary, which includes four stages: travelling from the starting point to the passenger station, from the passenger station to the entrance of the city, from the entrance to the exit of the city through the urban road network, and from the exit of the city to the target city through the highway network. The respective travel times are
,
,
and
. The economic cost mainly includes the transportation cost from the starting point to the station (
) and the coach ticket cost (
). The calculation formula for the generalised travel cost is:
where
is the generalised travel cost (min),
is the travel time within the city (min),
is the time spent in the station (min),
is the travel time from the station to the exit of the city (min),
is the travel time on the highway (min),
is the cost of urban travel (CYN),
is the cost of the coach ticket (CYN), and
is a scale parameter which represents the attitude to one minute increased in travel time equal to the one cost in travel expense. The scale parameter reflects the traveller’s attitude towards risk, where a higher value of “δ” means the decision-maker takes more cost consideration than time consideration when choosing the route.
The average value of
in a specific traffic zone to a specific passenger terminal can be calculated according to the weighted calculation of the proportion of the different travel modes that passengers choose to arrive at the passenger terminal of each traffic area.
refers to the time passengers spend entering the station, buying tickets, and waiting for the train. The value of
is related to the scale, streamline organisation, and flow of the passenger terminal, as well as to the individual attributes of the passengers. In the model proposed herein, the average time spent by passengers in each stage could be obtained by investigation and is shown in Equation (5).
where
is the time employed buying tickets (min),
is the waiting time (min), and
is the boarding time (min).
refers to the travel time from the passenger hub to the city entrance, which is mainly related to the location of the hub, the size of the city, and the urban traffic conditions. The formula of
is shown in Equation (6).
where
is the distance travelled in the urban road network (km) and
is the average travel speed of the coach in the city (km/h).
refers to the time the passenger spends travelling on the highway before reaching the terminal, after leaving the city. Since the travel speed depends on the highway grade, the actual travel speed is substituted by the average travel speed, and the actual mileage is substituted by the line mileage. The formula to calculate
is shown in Equation (7).
where
is the line mileage (km) and
is the average travel speed of the coach (km/h).
refers to the cost incurred by the passengers arriving at the hub from the starting point; its value is calculated according to the prices set by the different transport companies operating in the traffic area. The calculation formula for
is shown in Equation (8).
is the passengers’ purchase tickets cost, and the value of
is proportional to the value of
.
where
is the proportion to the distance travelled with travel chain
,
, and
is the price set by travel chain
(CYN).
Based on the city’s per capita income, the time devoted to generate income by each individual can be calculated using the eight-hour working system. Then, the relative generalised travel cost (
) is calculated according to Equation (9). The smaller the
R-value, the higher the social and economic benefits of the line and the less resources are wasted.
3.2.2. Distribution Model of Passenger Flow in Multi-Station Hub Lines
For multi-station hub lines, the objective is to estimate the minimum relative generalised travel cost. The line traffic volume of each hub can be calculated from the passenger demand of the road passenger transport hub corresponding to each traffic area. The problem could be defined as: calculating the demand for road passenger transportation
in traffic area
, calculating the relative generalised travel cost
from traffic zone
to hub station
(where
⊆ {alternative station set}), and estimating passenger traffic
with the restriction of minimum generalised travel cost (
Table 2).
The objective function and the constraints are as shown in Equation (10).
where
is the total passenger volume of the line at highway passenger terminal
,
is the designed maximum passenger volume for highway passenger station
,
is the total number of traffic zones, and
is the number of stations in {alternative station set}. The values of
and
are known, and
is the value obtained after determining the passenger flow distribution and
(
). Then, the model is solved by equivalent transformation.
The total passenger volume of traffic zone
is
, and the demand from zone
to passenger hub
is
.
(
) is the relative generalised travel cost from zone
to passenger hub
. Thus, the distribution problem of the line is equivalent to the model presented in Equation (11). The on-table method is used to solve the model; the flow of the algorithm is shown in
Figure 3.