An Accelerated Symmetric Nonnegative Matrix Factorization Algorithm Using Extrapolation
Abstract
1. Introduction
2. Accelerated SNMF Algorithm
2.1. Multiplicative Update Algorithm for SNMF
| Algorithm 1: = MU-SNMF(, r). |
| Step 1: Initialization Initialize . Set . Step 2: Update stage repeat until the stopping criterion is satisfied Step 3: Output . ⊗ and denote elementwise product and division, respectively. |
2.2. Nesterov’s Accelerated Gradient
2.3. Accelerated MU-SNMF Algorithm
| Algorithm 2: = AMU-SNMF(, r). |
| Step 1: Initialization Initialize . Set , , , . Step 2: Update stage repeat if then else end if if then end if until the stopping criterion is satisfied Step 3: Output . ⊗ and denote elementwise product and division, respectively. |
2.4. Symmetric Nonnegative Tensor Factorization (SNTF)
3. Experiments and Results
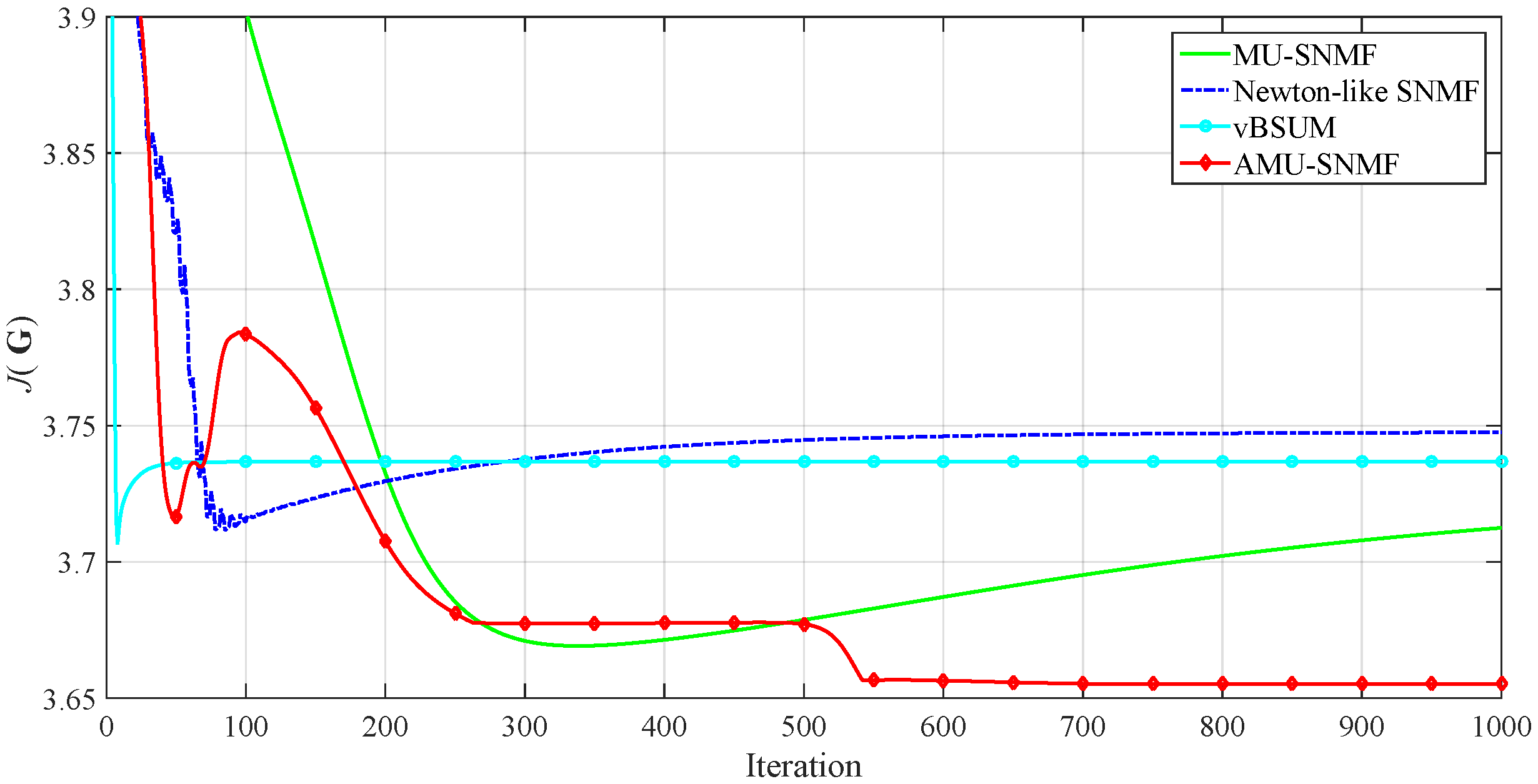
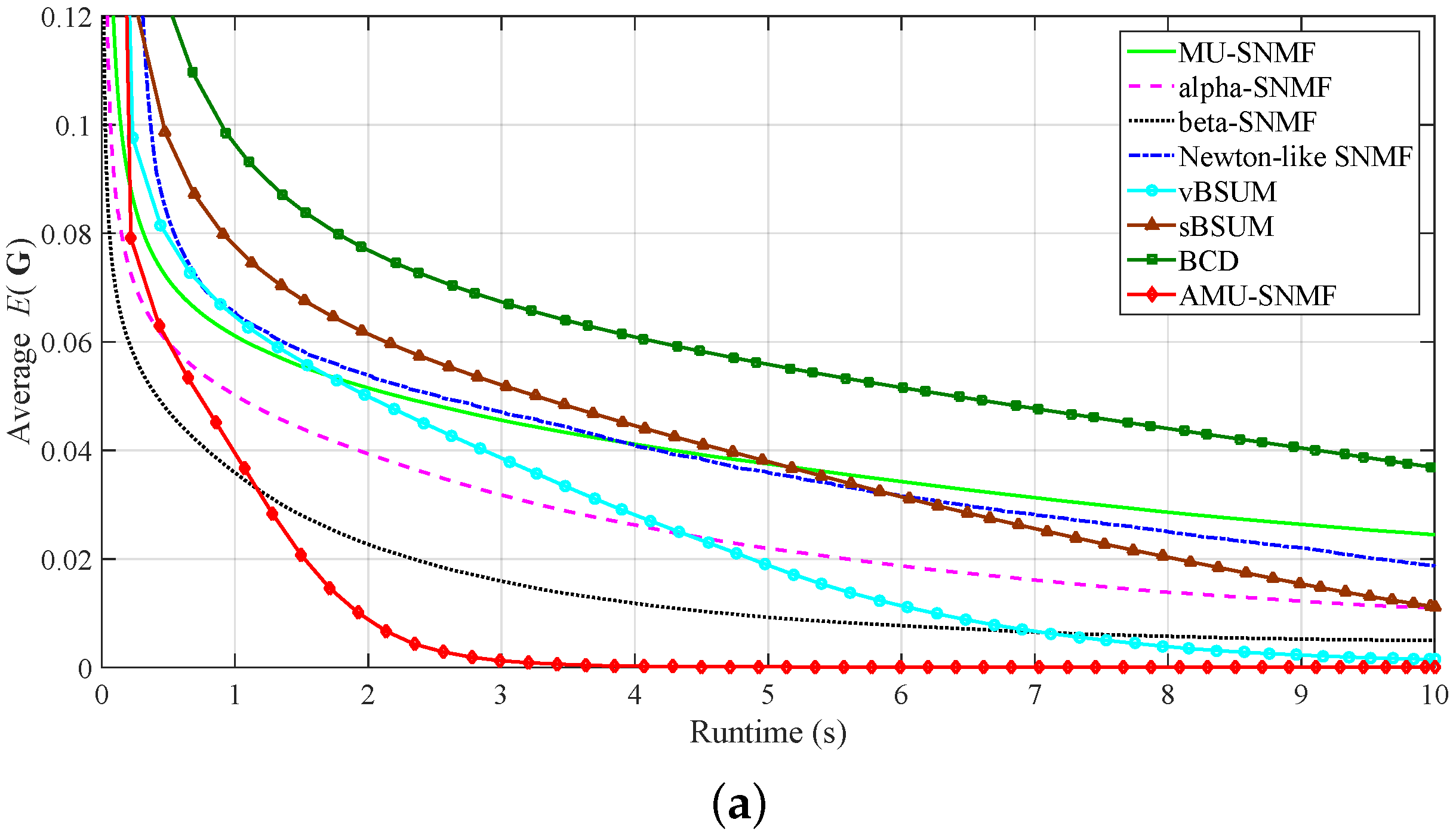
3.1. Synthetic Data
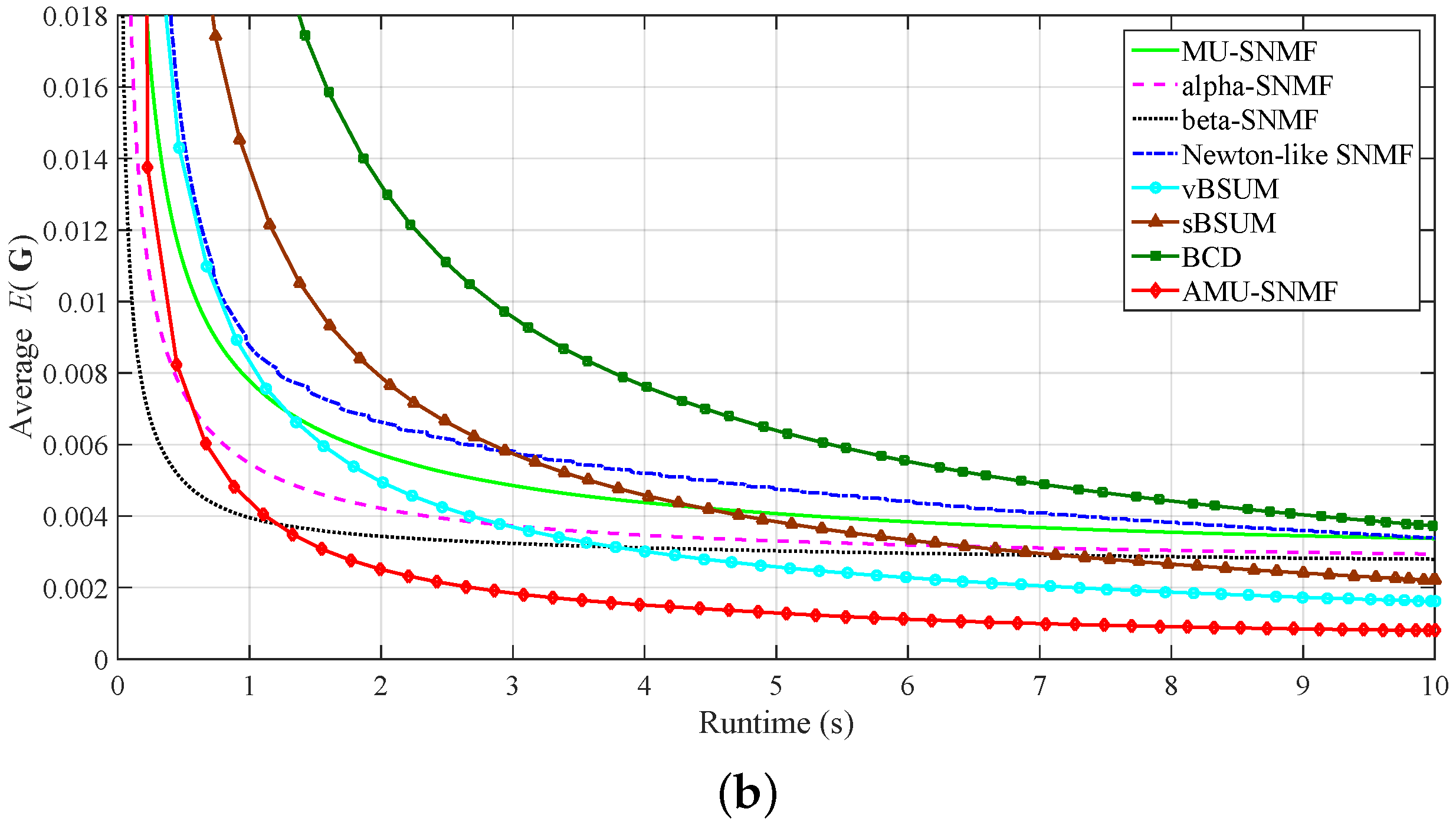
3.2. Document Clustering
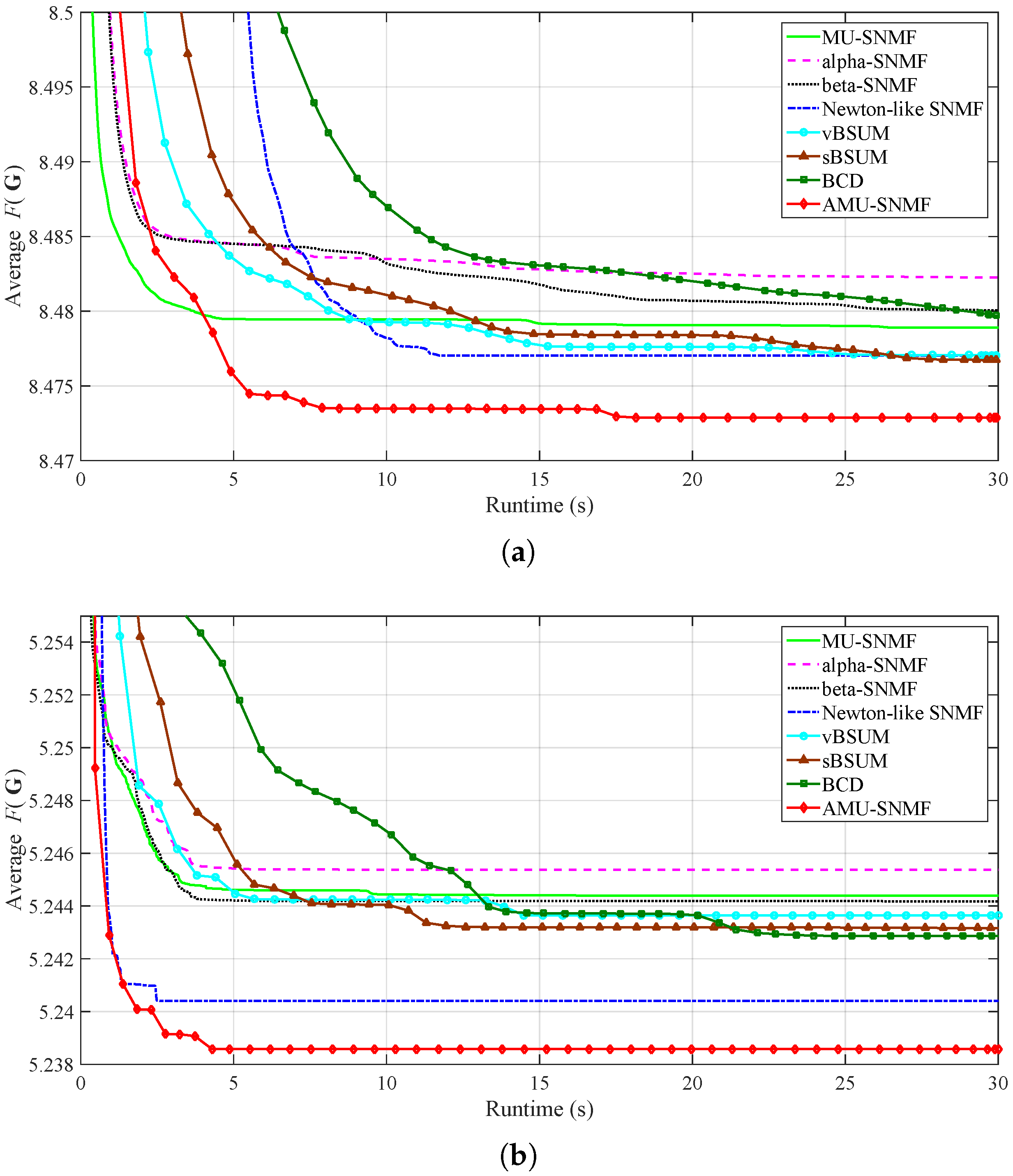
3.3. Object Clustering
3.4. SNTF
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cichocki, A.; Jankovic, M.; Zdunek, R.; Amari, S.I. Sparse super symmetric tensor factorization. In Proceedings of the 2007 International Conference on Neural Information Processing (ICONIP), Kitakyushu, Japan, 13–16 November 2007; pp. 781–790. [Google Scholar]
- Lu, S.; Hong, M.; Wang, Z. A nonconvex splitting method for symmetric nonnegative matrix factorization: Convergence analysis and optimality. IEEE Trans. Signal Process. 2017, 65, 3120–3135. [Google Scholar] [CrossRef]
- Gao, T.; Olofsson, S.; Lu, S. Minimum-volume-regularized weighted symmetric nonnegative matrix factorization for clustering. In Proceedings of the 2016 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Washington, DC, USA, 7–9 December 2016; pp. 247–251. [Google Scholar]
- Marin, M.; Vlase, S.; Paun, M. Considerations on double porosity structure for micropolar bodies. Aip Adv. 2015, 5, 037113. [Google Scholar] [CrossRef]
- Ma, Y.; Hu, X.; He, T.; Jiang, X. Hessian regularization based symmetric nonnegative matrix factorization for clustering gene expression and microbiome data. Methods 2016, 111, 80–84. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Xie, S.; Zdunek, R.; Zhou, G.; Cichocki, A. Symmetric Nonnegative Matrix Factorization: Algorithms and Applications to Probabilistic Clustering. IEEE Trans. Neural Netw. 2011, 22, 2117–2131. [Google Scholar]
- Vandaele, A.; Gillis, N.; Lei, Q.; Zhong, K.; Dhillon, I. Efficient and Non-Convex Coordinate Descent for Symmetric Nonnegative Matrix Factorization. IEEE Trans. Signal Process. 2016, 64, 5571–5584. [Google Scholar] [CrossRef]
- Shi, Q.; Sun, H.; Lu, S.; Hong, M.; Razaviyayn, M. Inexact Block Coordinate Descent Methods for Symmetric Nonnegative Matrix Factorization. IEEE Trans. Signal Process. 2017, 65, 5995–6008. [Google Scholar] [CrossRef]
- Zass, R.; Shashua, A. A unifying approach to hard and probabilistic clustering. In Proceedings of the 2005 International Conference on Computer Vision (ICCV), Beijing, China, 17–20 October 2005; pp. 294–301. [Google Scholar]
- Kuang, D.; Ding, C.; Park, H. Symmetric Nonnegative Matrix Factorization for Graph Clustering. In Proceedings of the 2012 SIAM International Conference on Data Mining (SDM), Anaheim, CA, USA, 26–28 April 2012; pp. 106–117. [Google Scholar]
- Kuang, D.; Yun, S.; Park, H. SymNMF: Nonnegative Low-Rank Approximation of a Similarity Matrix for Graph Clustering. J. Glob. Optim. 2015, 62, 545–574. [Google Scholar] [CrossRef]
- Lu, S.; Wang, Z. Accelerated algorithms for eigen-value decomposition with application to spectral clustering. In Proceedings of the 2015 Asilomar Conference on Signals, Systems and Computers (ACSSC), Pacific Grove, CA, USA, 8–11 November 2015; pp. 355–359. [Google Scholar]
- Bo, L.; Zhang, Z.; Wu, X.; Yu, P.S. Relational clustering by symmetric convex coding. In Proceedings of the 2007 International Conference on Machine Learning (ICML), Corvallis, OR, USA, 20–24 June 2007; pp. 569–576. [Google Scholar]
- Long, B.; Zhang, Z.; Yu, P. Co-clustering by block value decomposition. In Proceedings of the 2005 SIGKDD Conference on Knowledge Discovery and Data Mining (SIGKDD), Chicago, IL, USA, 21–24 August 2005; pp. 635–640. [Google Scholar]
- Nesterov, Y. A method of solving a convex programming problem with convergence rate O(1/k2). Sov. Math. Dokl. 1983, 27, 372–376. [Google Scholar]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the importance of initialization and momentum in deep learning. In Proceedings of the 2013 International Conference on Machine Learning (ICML), Atlanta Marriott Marquis, Atlanta, GA, USA, 16–21 June 2013; pp. 1139–1147. [Google Scholar]
- Botev, A.; Lever, G.; Barber, D. Nesterov’s accelerated gradient and momentum as approximations to regularised update descent. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1899–1903. [Google Scholar]
- Yudin, D.; Nemirovskii, A.S. Informational complexity and efficient methods for the solution of convex extremal problems. Matekon 1976, 13, 3–25. [Google Scholar]
- Wu, W.; Jia, Y.; Kwong, S.; Hou, J. Pairwise Constraint Propagation-Induced Symmetric Nonnegative Matrix Factorization. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 6348–6361. [Google Scholar] [CrossRef]
- Ang, A.M.S.; Gillis, N. Accelerating nonnegative matrix factorization algorithms using extrapolation. Neural Comput. 2019, 31, 417–439. [Google Scholar] [CrossRef] [PubMed]
- Cai, D.; He, X.; Han, J. Document clustering using locality preserving indexing. IEEE Trans. Knowl. Data Eng. 2005, 17, 1624–1637. [Google Scholar] [CrossRef]
- Zelnik-Manor, L.; Perona, P. Self-Tuning Spectral Clustering. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 13–18 December 2004; pp. 1601–1608. [Google Scholar]

| TDT2 | Category | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| Number of documents | 167 | 160 | 145 | 141 | 140 | 131 | 123 | 123 | 120 | 104 | |
| Reuters-21578 | Category | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| Number of documents | 63 | 60 | 53 | 45 | 45 | 44 | 42 | 38 | 38 | 37 |
| MU-SNMF [6] | -SNMF [6] | -SNMF [6] | Newton-Like SNMF [10] | vBSUM [8] | sBSUM [8] | BCD [7] | AMU-SNMF | ||
|---|---|---|---|---|---|---|---|---|---|
| TDT2 | CA | 0.9266 | 0.9035 | 0.9187 | 0.9348 | 0.9299 | 0.9312 | 0.9133 | 0.9631 |
| NMI | 0.9363 | 0.9197 | 0.9292 | 0.9477 | 0.9450 | 0.9464 | 0.9354 | 0.9625 | |
| Reuters-21578 | CA | 0.6711 | 0.6803 | 0.6786 | 0.6778 | 0.6671 | 0.6630 | 0.6749 | 0.6877 |
| NMI | 0.6329 | 0.6380 | 0.6383 | 0.6408 | 0.6365 | 0.6345 | 0.6389 | 0.6449 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; He, Z.; Lu, J.; Tan, B.; Bai, Y.; Tan, J.; Liu, T.; Lin, Z. An Accelerated Symmetric Nonnegative Matrix Factorization Algorithm Using Extrapolation. Symmetry 2020, 12, 1187. https://doi.org/10.3390/sym12071187
Wang P, He Z, Lu J, Tan B, Bai Y, Tan J, Liu T, Lin Z. An Accelerated Symmetric Nonnegative Matrix Factorization Algorithm Using Extrapolation. Symmetry. 2020; 12(7):1187. https://doi.org/10.3390/sym12071187
Chicago/Turabian StyleWang, Peitao, Zhaoshui He, Jun Lu, Beihai Tan, YuLei Bai, Ji Tan, Taiheng Liu, and Zhijie Lin. 2020. "An Accelerated Symmetric Nonnegative Matrix Factorization Algorithm Using Extrapolation" Symmetry 12, no. 7: 1187. https://doi.org/10.3390/sym12071187
APA StyleWang, P., He, Z., Lu, J., Tan, B., Bai, Y., Tan, J., Liu, T., & Lin, Z. (2020). An Accelerated Symmetric Nonnegative Matrix Factorization Algorithm Using Extrapolation. Symmetry, 12(7), 1187. https://doi.org/10.3390/sym12071187




