Model and Solution of Complex Emergency Dispatch by Multiple Rescue Centers with Limited Capacity to Different Disaster Areas
Abstract
1. Introduction
2. Task Allocation Model for Emergency Dispatch
2.1. Proposed Model
2.2. Model Construction
2.3. Model Unfolding
3. Model Solving Based on Genetic Algorithm
3.1. Coding Scheme and Individual Representation
3.2. Fitness Function
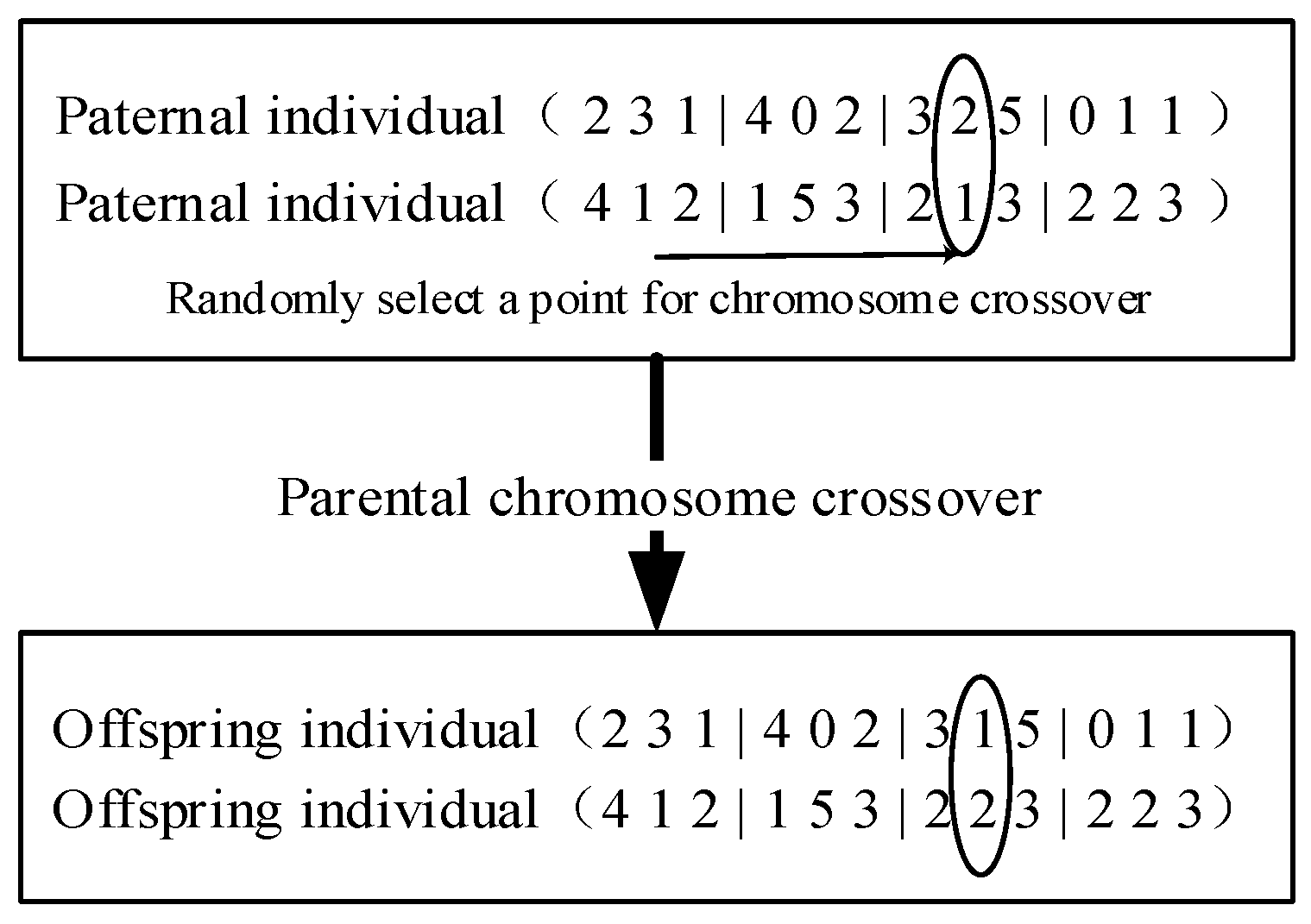
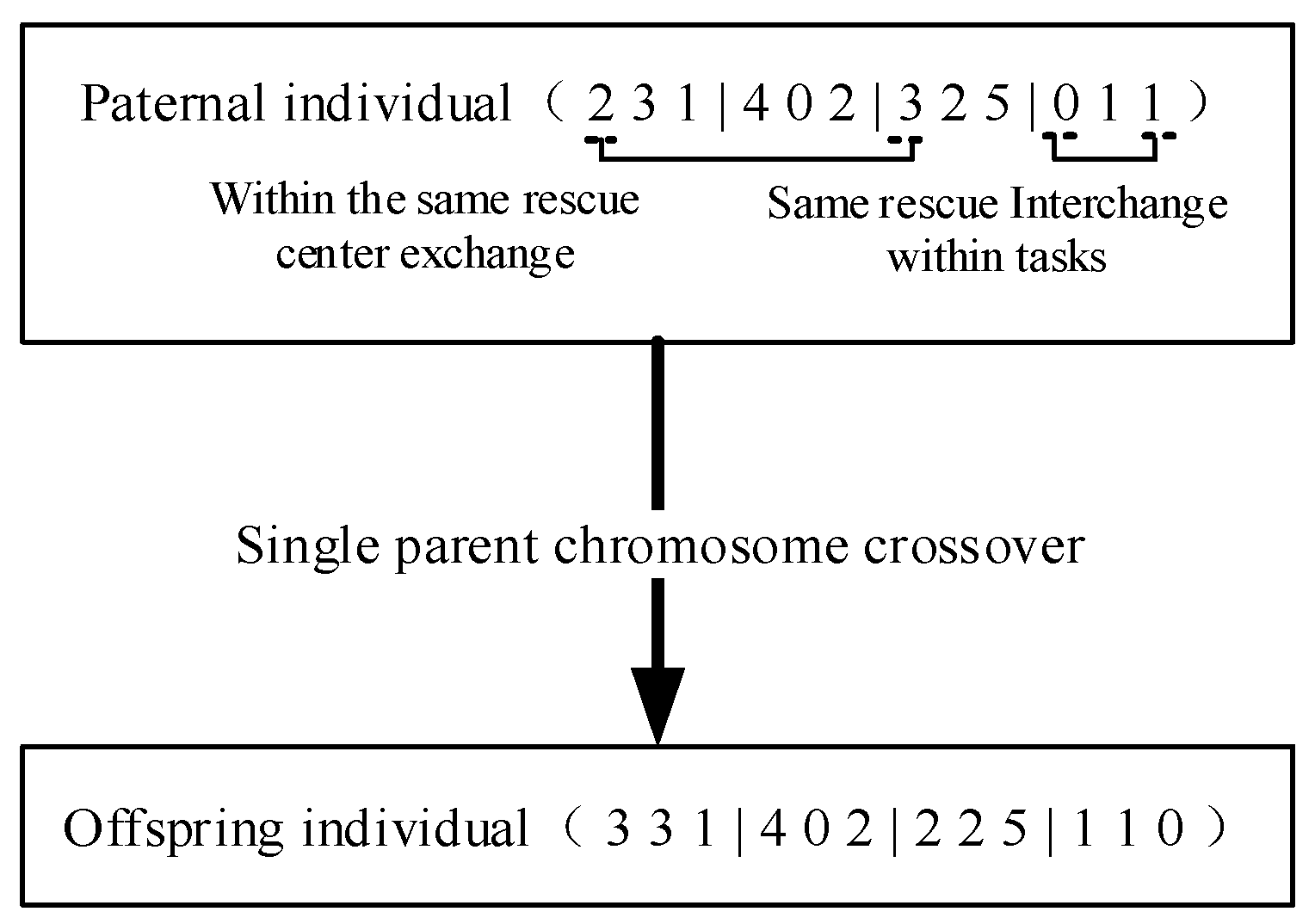
3.3. Crossover Operator
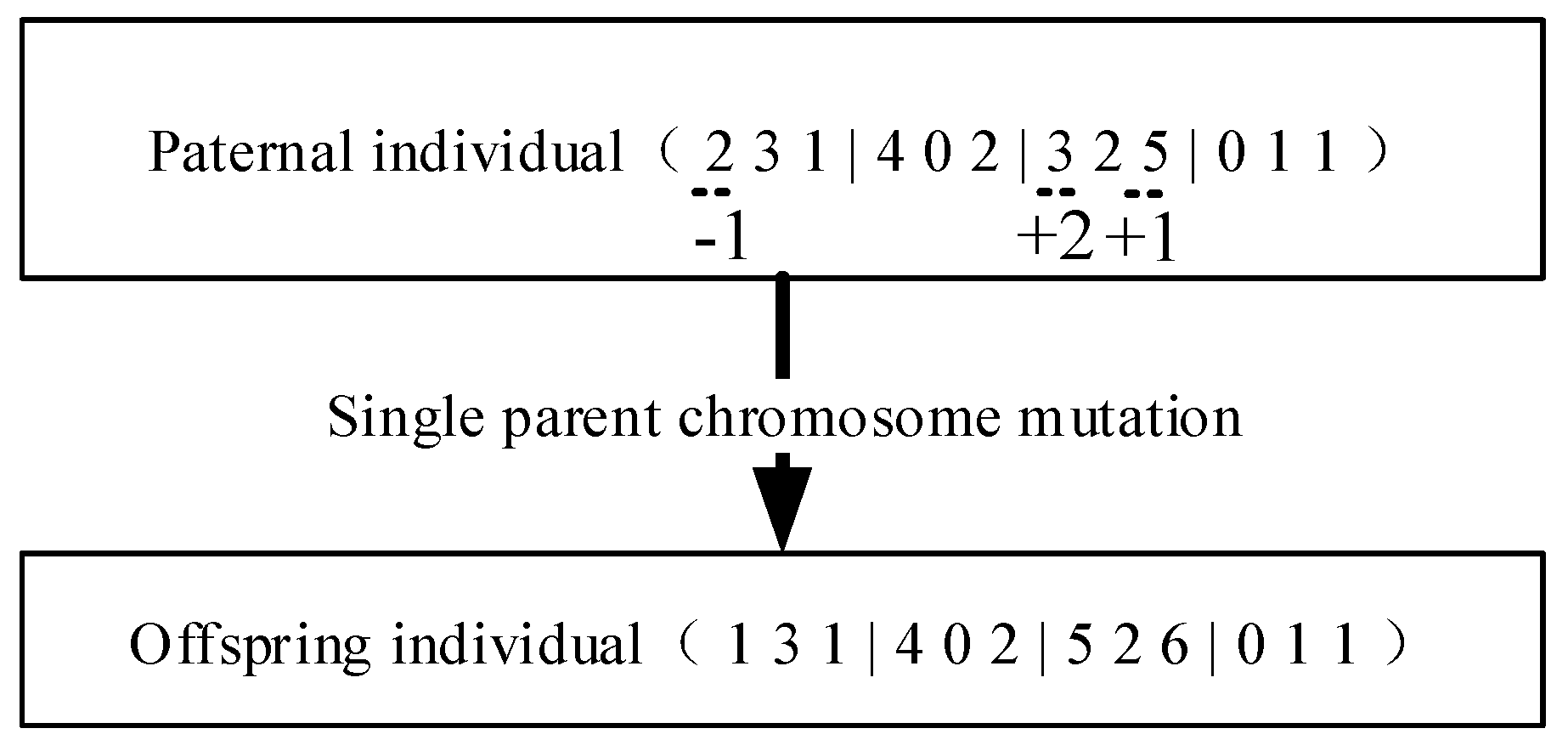
3.4. Mutation
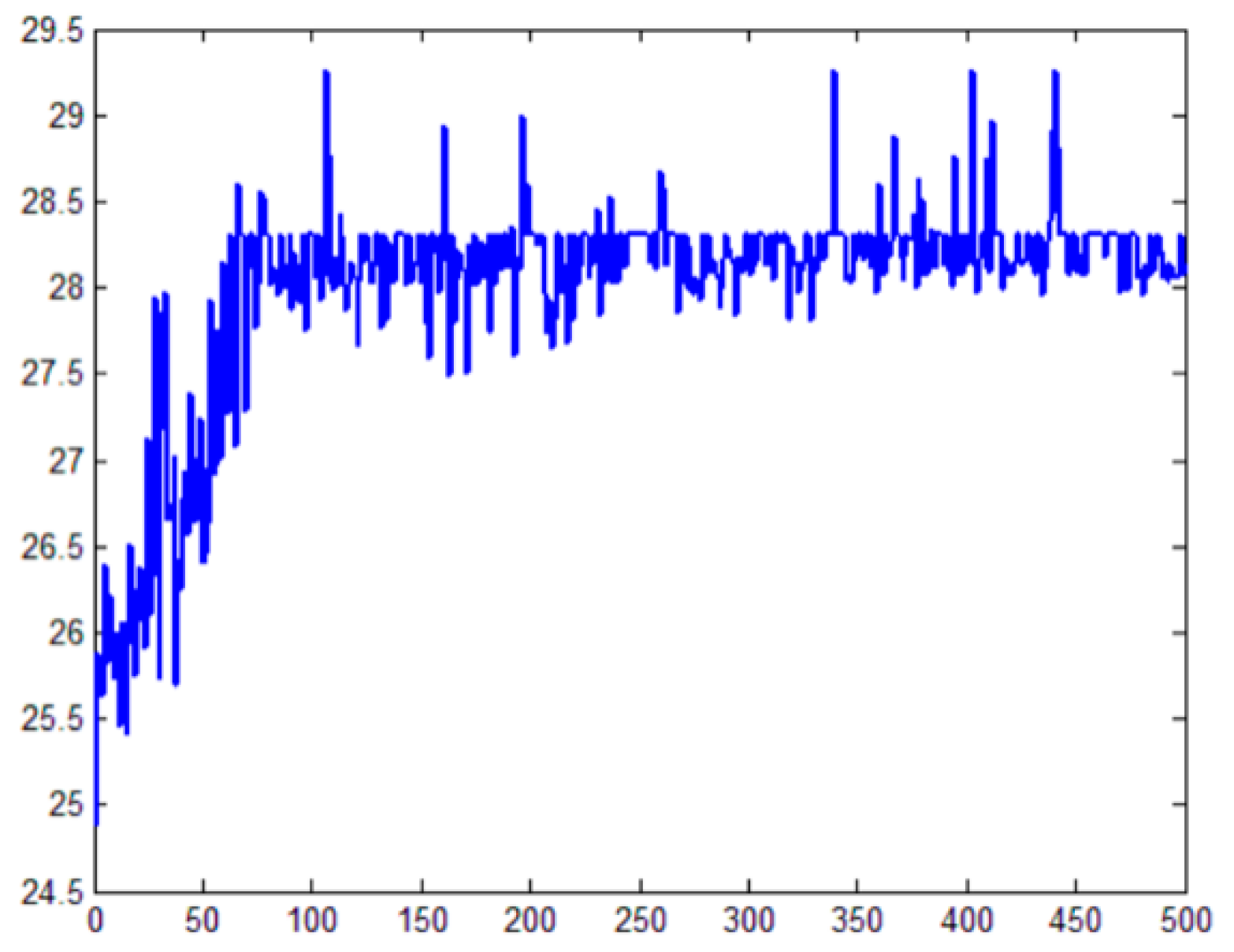
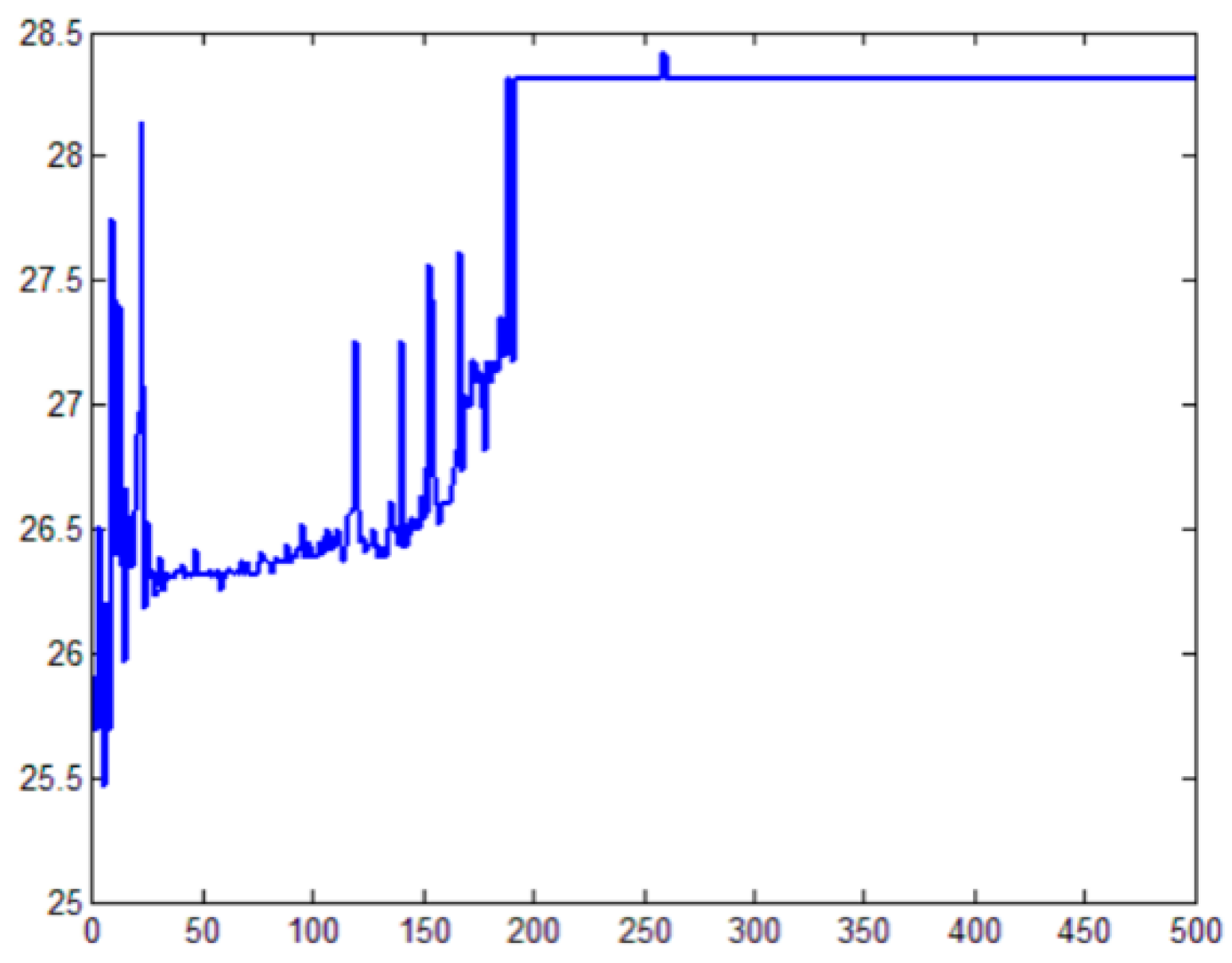
4. Case Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, G.; Song, J.; Shao, X.; Han, Y.; Yang, X. Analysis of recent large-scale geological hazard prediction and risk prevention in China. J. Nat. Disasters 2015, 24, 20–27. [Google Scholar]
- Xu, S.; Xiao, L.; Li, C.; Wang, M. Review on the Development of two typical geological hazard regionalization techniques in China. J. Nat. Disasters 2017, 2, 22–31. [Google Scholar]
- Duan, Z. Chemical Park for Distribution Engineering Risk Analysis and Accident Rescue Research; Beijing Institute of Technology: Beijing, China, 2015. [Google Scholar]
- Niu, X.; Tang, H.; Wu, L. Satellite scheduling of large areal tasks for rapid response to natural disaster using a multi-objective genetic algorithm. Int. J. Disaster Risk Reduct. 2018, 28, 813–825. [Google Scholar] [CrossRef]
- Li, Q.; Tu, W.; Zhuo, L. Reliable Rescue Routing Optimization for Urban Emergency Logistics under Travel Time Uncertainty. Isprs Int. J. Geo-Inf. 2018, 7, 77. [Google Scholar] [CrossRef]
- Zhao, M.; Song, X.; Dong, J.; Wang, S. Using genetic algorithm to solve the optimal problem of emergency material scheduling. J. Shenyang Jianzhu Univ. (Nat. Sci.) 2012, 28, 944–948. [Google Scholar]
- Hu, F.; Tian, Z.; Zhao, M.; Han, X. Study on hierarchical linkage dispatch of emergency material based on genetic algorithm. Appl. Res. Comput. 2016, 33, 439–443. [Google Scholar]
- Wang, Q. An Emergency Logistics vehicle scheduling algorithm based on discrete bee colony. J. Inner Mongolia Normal Univ. (Nat. Sci. Ed.) 2018, 47, 39–43+54. [Google Scholar]
- Wang, Y.; He, Z.; Liu, R. Integrated Optimization of proactive and reactive scheduling for emergency rescue. Syst. Eng.-Theory Pract. 2015, 35, 945–954. [Google Scholar]
- Zhang, P. Study on Optimization of Earthquake Emergency Traffic Scheduling Based on The Lifting of Cyberspace. China Commun. 2015, 12, 138–143. [Google Scholar]
- Wang, Q.; Liu, S.; Liu, W.; Zoran, K.; Dragan, S. Decision Support System for emergency scheduling of raw water supply systems with multiple sources. Front. Environ. Sci. Eng. 2013, 7, 777–786. [Google Scholar] [CrossRef]
- Feng, J.; Gai, W.; Li, J. Multi-objective optimization of rescue station selection for emergency logistics management. Saf. Sci. 2019, 120, 276–282. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, H.; Yu, G.; Ruan, J.; Felix, T.S.; Chan, F.T. A three-stage and multi-objective stochastic programming model to improve the sustainable rescue ability by considering secondary disasters in emergency logistics. Comput. Ind. Eng. 2019, 135, 1145–1154. [Google Scholar] [CrossRef]
- Bi, C.; Fu, B.; Chen, J.; Zhao, Y.; Yang, L.; Duan, Y.; Shi, Y. Machine learning based fast multi-layer liquefaction disaster assessment. World Wide Web 2019, 22, 1935–1950. [Google Scholar] [CrossRef]
- Shen, L.; Tao, F.; Shi, Y.; Qin, R. Optimization of Location-Routing Problem in Emergency Logistics Considering Carbon Emissions. Int. J. Environ. Res. Public Health 2019, 16, 2982. [Google Scholar] [CrossRef]
- Li, M.; Zhao, X.; Fan, Z.; Cao, P.P.; Qu, X.N. A model for assignment of rescuers considering multiple disaster areas. Int. J. Disaster Risk Reduct. 2019, 38, 101201. [Google Scholar] [CrossRef]
- Sotoudeh-Anvari, A.; Sadjadi, S.J.; Hadji Molana, S.M.; Sadi-Nezhad, S. A stochastic multi-objective model based on the classical optimal search model for searching for the people who are lost in response stage of earthquake. Sci. Iran. 2019, 26, 1842–1864. [Google Scholar] [CrossRef]
- Chen, P.; Zhang, J.; Sun, Y. Research on Emergency Rescue of Urban Flood Disaster Based on Wargame Simulation. J. Indian Soc. Remote Sens. 2018, 46, 1677–1687. [Google Scholar] [CrossRef]
- Özdamar, L.; Ekinci, E.; Küçükyazici, B. Emergency logistics planning in natural disasters. Ann. Oper. Res. 2004, 129, 217–245. [Google Scholar] [CrossRef]
- Swamy, R.; Kang, J.E.; Batta, R.; Chung, Y. Hurricane evacuation planning using public transportation. Socio-Econ. Plan. Sci. 2016, 59, 43–55. [Google Scholar] [CrossRef]
- Pérez-Galarce, F.; Canales, L.J.; Vergara, C.; Candia-Véjar, A. An optimization model for the location of disaster refuges. Socio-Econ. Plan. Sci. 2016, 59, 59–66. [Google Scholar] [CrossRef]
- Ren, Y.; Tian, G. Emergency scheduling for forest fires subject to limited rescue team resources and priority disaster areas. Ieej Trans. Electr. Electron. Eng. 2016, 11, 753–759. [Google Scholar] [CrossRef]
- Han, B.; Yao, P.; Sun, Y. UAVS Cooperative Task allocation based on Multi-Objective MSQPSO algorithm. Acta Electron. Sin. 2017, 45, 1856–1863. [Google Scholar]
- Wu, J.; Shi, Z. Distribution Center location problem based on genetic algorithm. J. South China Univ. Technol. (Nat. Sci. Ed.) 2004, 32, 71–74. [Google Scholar]
- Akin, L.; Dusunceli, F. A new approach for weighted hardy’s operator in VELS. Appl. Math. Nonlinear Sci. 2019, 4, 417–432. [Google Scholar] [CrossRef]
- Bunimovich, L.; Smith, D.; Webb, B. Finding hidden structures, hierarchies, and cores in networks via isospectral reduction. Appl. Math. Nonlinear Sci. 2019, 4, 231–254. [Google Scholar] [CrossRef]
- Cai, J.; Zhou, P.; Sheng, B.; He, J. Feedback fuzzy test method based on improved roulette strategy. J. Sichuan Univ. (Eng. Sci. Ed.) 2016, 48, 132–138. [Google Scholar]
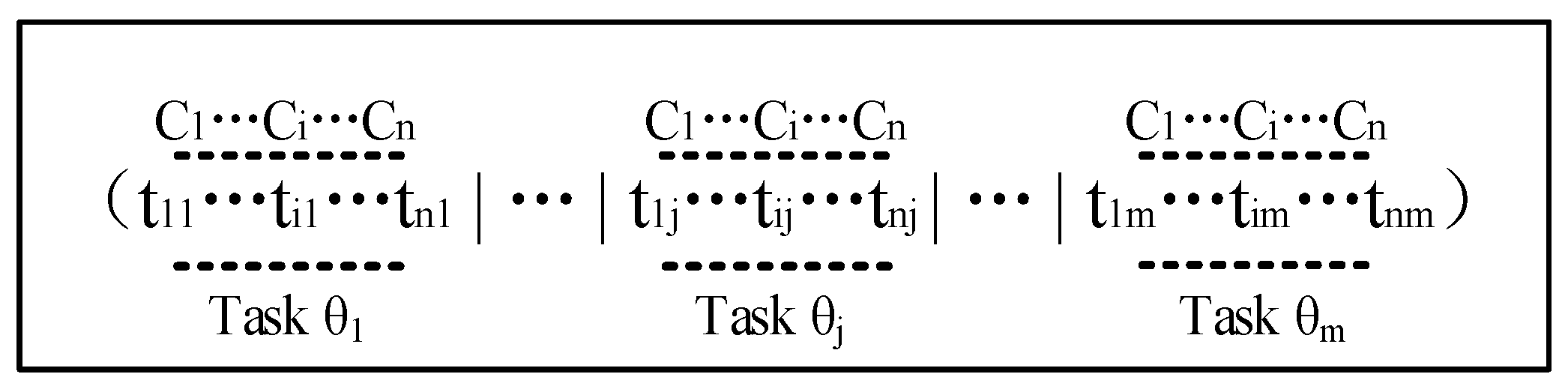


| Rescue Teams Needed in the Disaster Area | … | … | |||||
|---|---|---|---|---|---|---|---|
| Rescue team capacity | … | … | Number of rescue teams to be dispatched by each rescue center | ||||
| … | … | ||||||
| … | … | … | … | … | … | ||
| … | … | ||||||
| … | … | … | … | … | … | ||
| … | … | ||||||
| Number of rescue teams dispatched by each mission | … | … |
| Rescue Team Rescue Capability/Rescue Distance | Rescue Team t θj Required in the Disaster Area | 7 | 8 | 5 | 6 |
|---|---|---|---|---|---|
| Rescue Team Capacity t ci | θ1 | θ2 | θ3 | θ4 | |
| 10 | C1 | 2/9 | 4/14 | 3/7 | 1/12 |
| 10 | C2 | 3/13 | 1/13 | 2/7 | 4/8 |
| 10 | C3 | 1/12 | 2/6 | 4/14 | 3/7 |
| θ1 | θ2 | θ3 | θ4 | |
| C1 | 3 | 3 | 3 | 0 |
| C2 | 3 | 1 | 1 | 3 |
| C3 | 1 | 4 | 1 | 3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, Z.; Huang, Y.; Huang, P.; Guo, J.; Yang, F.; Fu, L. Model and Solution of Complex Emergency Dispatch by Multiple Rescue Centers with Limited Capacity to Different Disaster Areas. Symmetry 2020, 12, 1138. https://doi.org/10.3390/sym12071138
Duan Z, Huang Y, Huang P, Guo J, Yang F, Fu L. Model and Solution of Complex Emergency Dispatch by Multiple Rescue Centers with Limited Capacity to Different Disaster Areas. Symmetry. 2020; 12(7):1138. https://doi.org/10.3390/sym12071138
Chicago/Turabian StyleDuan, Zaipeng, Yueling Huang, Ping Huang, Jin Guo, Fuqiang Yang, and Libi Fu. 2020. "Model and Solution of Complex Emergency Dispatch by Multiple Rescue Centers with Limited Capacity to Different Disaster Areas" Symmetry 12, no. 7: 1138. https://doi.org/10.3390/sym12071138
APA StyleDuan, Z., Huang, Y., Huang, P., Guo, J., Yang, F., & Fu, L. (2020). Model and Solution of Complex Emergency Dispatch by Multiple Rescue Centers with Limited Capacity to Different Disaster Areas. Symmetry, 12(7), 1138. https://doi.org/10.3390/sym12071138




