Solution and Interpretation of Neutrosophic Homogeneous Difference Equation
Abstract
1. Introduction
1.1. Uncertainty Theory and Neutrosophic Sets
1.2. Difference Equation in an Uncertain Environment
1.3. Novelties of the Work
- (1)
- The homogeneous difference equation, solved and analyzed with a neutrosophic initial condition, neutrosophic coefficient, and neutrosophic coefficient and initial together as a different section, which was not done earlier.
- (2)
- Establishment of the corresponding characterization theorem for the neutrosophic set with a difference equation.
- (3)
- Different theorems, lemmas, and corollary drawn for the purpose of the study.
- (4)
- Numerical examples of the difference equation with a neutrosophic number, solved and illustrated for better understanding of our observations.
- (5)
- An application in actuarial science, illustrated in a neutrosophic environment for better understanding of the practical application of the proposed theoretical results.
1.4. Structure of the Paper
2. PreliminaryIdea
- (1)
- is the upper semi continuous.
- (2)
- is the fuzzy convex, i.e., for all and .
- (3)
- is normal, i.e., a such that
- (4)
- Closure of is compact, where .
3. Difference Equation with a Neutrosophic Variable
- (i)
- The initial condition or conditions are the neutrosophic number (Type I);
- (ii)
- The coefficient or coefficients are the neutrosophic number (Type II);
- (iii)
- The initial conditions and coefficient or the coefficients are both neutrosophic numbers (Type III).
- (1)
- The parametric form of the function is:
- (2)
- The functions,,,,andare taken as continuous functions, i.e., for anya, such that:for allwithand for anyan, such that:with, whereand.
- (1)
- A strong solution ifandfor every.
- (2)
- A weak solution ifandfor every.
4. Solution of Neutrosophic Homogeneous Difference Equation
4.1. Solution of Homogeneous Difference Equation of Type I
4.1.1. The Solution When Is a Crisp Number and Is a Neutrosophic Number
4.1.2. The Solution When and the Initial Value Is a Neutrosophic Number
4.1.3. The Solution When and the Initial Value Is a Neutrosophic Number
4.1.4. The Solution When Is Aneutrosophic Number and the Initial Value Is a Crisp Number
4.1.5. The Solution When Is a Neutrosophic Number and the Initial Value Is a Crisp Number
4.1.6. The Solution When and Are Bothneutrosophic Numbers
4.1.7. The Solution When and Are Both Neutrosophic Numbers
4.2. Solution of Homogeneous Difference Equation of Type II
4.2.1. The Solution When and the Initial Condition Is a Neutrosophic Number
4.2.2. The Solution When , a Real Valued Number, and the Initial Condition Is a Neutrosophic Number
4.2.3. The Solution When and when the Initial Condition Is a Neutrosophic Number
4.2.4. The Solution When Is a Positive Neutrosophic Number and the Initial Condition is nota Neutrosophic Number
4.2.5. The Solution When Is a Neutrosophic Number and When the Initial Condition Is a Crisp Number
4.2.6. The Solution When the Initial Condition and Are Both Neutrosophic Numbers
4.2.7. The Solution When the Initial Condition and Are Both Neutrosophic Numbers
5. Numerical Example
6. Application of the Method in Actuarial Science
- For the truth part: low as 3%, medium as 4%, high as 5%;
- For the falsity portion: very low as 2%, medium as 4%, very high as 6%;
- For the indeterminacy part: between low and very low 2.5%, medium 4%, between high and very high 5.5%,
7. Conclusions and Future Research Scope
- (1)
- The difference type of the homogeneous difference equation is solved in a neutrosophic environment and the symmetric behavior between them is discussed.
- (2)
- The characterization theorem for the neutrosophic difference equations are established.
- (3)
- The strong and weak solution concept is applied for the neutrosophic difference equation.
- (4)
- Different examples and real-life applications in actuarial science are illustrated for better understanding of neutrosophic difference equations.
- (1)
- The solution of difference equation can be found with different types of uncertainty, such as Type 2 fuzzy, interval valued fuzzy, hesitant fuzzy, rough fuzzy environment.
- (2)
- Finding several methods (analytical and numerical) for solving non-linear first and higher order difference equations or system of difference equations with uncertainty.
- (3)
- Solving the real-life model associated with the discrete system modeling with uncertain data.
Author Contributions
Funding
Conflicts of Interest
References
- Zadeh, L. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Li, J.; Niu, Q.; Dong, X.-C. Similarity Measure and Fuzzy Entropy of Fuzzy Number Intuitionistic Fuzzy Sets. Adv. Intell. Soft Comput. 2009, 54, 373–379. [Google Scholar] [CrossRef]
- Ye, J. Prioritized aggregation operators of trapezoidal intuitionistic fuzzy sets and their application to multicriteria decision-making. Neural Comput. Appl. 2014, 25, 1447–1454. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics Neutrosophy: Neutrosophic Probability, Set and Logic; American Research Press: Rehoboth, DE, USA, 1998. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.; Sunderraman, R. Single Valued Neutrosophic Sets. Multisspace Multistructure 2010, 4, 410–413. [Google Scholar]
- Ye, J. Single-Valued Neutrosophic Minimum Spanning Tree and Its Clustering Method. J. Intell. Syst. 2014, 23, 311–324. [Google Scholar] [CrossRef]
- Peng, J.-J.; Wang, J.-Q.; Wang, J.; Zhang, H.-Y.; Chen, X.-H. Simplified neutrosophic sets and their applications in multi-criteria group decision-making problems. Int. J. Syst. Sci. 2015, 47, 1–17. [Google Scholar] [CrossRef]
- Peng, X.; Smarandache, F. New multiparametric similarity measure for neutrosophic set with big data industry evaluation. Artif. Intell. Rev. 2019, 53, 3089–3125. [Google Scholar] [CrossRef]
- Chakraborty, A.; Mondal, S.P.; Ahmadian, A.; Senu, N.; Salahshour, S.; Alam, S. Different Forms of Triangular Neutrosophic Numbers, De-Neutrosophication Techniques, and their Applications. Symmetry 2018, 10, 327. [Google Scholar] [CrossRef]
- Chakraborty, A.; Mondal, S.P.; Alam, S.; Ahmadian, A.; Senu, N.; De, D.; Salahshour, S. Disjunctive Representation of Triangular Bipolar Neutrosophic Numbers, De-Bipolarization Technique and Application in Multi-Criteria Decision-Making Problems. Symmetry 2019, 11, 932. [Google Scholar] [CrossRef]
- Deli, I.; Ali, M.; Smarandache, F. Bipolar Neutrosophic Sets and their Application Based on Multi-Criteria Decision Making Problems. In Proceedings of the 2015 International Conference on Advanced Mechatronic Systems (ICAMechS), Beijing, China, 22–24 August 2015; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2015; pp. 249–254. [Google Scholar]
- Lee, K.M. Bipolar-Valued Fuzzy Sets and their Operations. In Proceedings of the International Conference on Intelligent Technologies, Bangkok, Thailand, 12–14 December 2000; pp. 307–312. [Google Scholar]
- Kang, M.K.; Kang, J.G. Bipolar fuzzy set theory applied to sub-semigroups with operators in semi groups. J. Korean Soc. Math. Educ. Ser. B Pure Appl. Math. 2012, 19, 23–35. [Google Scholar]
- Smarandache, F. Neutrosophic Perspectives: Triplets, Duplets, Multisets, Hybrid Operators, Modal Logic, Hedge Algebras and Applications; Degree of Dependence and Independence of the (Sub) Components of Fuzzy Set and Neutrosophic Set. Neutrosophic Sets and Systems; Pons Publishing House: Stuttgart, Germany, 2016; Volume 11, pp. 95–97. [Google Scholar]
- Deeba, E.Y.; De Korvin, A.; Koh, E.L. A fuzzy difference equation with an application. J. Differ. Equ. Appl. 1996, 2, 365–374. [Google Scholar] [CrossRef]
- Deeba, E.; De Korvin, A. Analysis by fuzzy difference equations of a model of CO2 level in the blood. Appl. Math. Lett. 1999, 12, 33–40. [Google Scholar] [CrossRef]
- Lakshmikantham, V.; Vatsala, A. Basic Theory of Fuzzy Difference Equations. J. Differ. Equ. Appl. 2002, 8, 957–968. [Google Scholar] [CrossRef]
- Papaschinopoulos, G.; Papadopoulos, B.K. On the fuzzy difference equation x_(n+1)=A+B⁄x_n. Soft Comput. 2002, 6, 456–461. [Google Scholar] [CrossRef]
- Papaschinopoulos, G.; Papadopoulos, B.K. On the fuzzy difference equation x_(n+1)=A+x_n⁄x_(n-m). Fuzzy Sets Syst. 2002, 129, 73–81. [Google Scholar] [CrossRef]
- Papaschinopoulos, G.; Schinas, C.J. On the fuzzy difference equation . J. Differ. Equ. Appl. 2000, 6, 85–89. [Google Scholar] [CrossRef]
- Papaschinopoulos, G.; Stefanidou, G. Boundedness and asymptotic behavior of the solutions of a fuzzy difference equation. Fuzzy Sets Syst. 2003, 140, 523–539. [Google Scholar] [CrossRef]
- Umekkan, S.A.; Can, E.; Bayrak, M.A. Fuzzy difference equation in finance. IJSIMR 2014, 2, 729–735. [Google Scholar]
- Stefanidou, G.; Papaschinopoulosand, G.; Schinas, C.J. On an exponential–Type fuzzy Difference equation. Advanced in difference equations. Adv. Differ. Equ. 2010, 2010, 1–19. [Google Scholar] [CrossRef][Green Version]
- Din, Q. Asymptotic Behavior of a Second-Order Fuzzy Rational Difference Equation. J. Discret. Math. 2015, 2015, 1–7. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Yang, L.H.; Liao, D.X. Behaviour of solutions of to a fuzzy nonlinear difference equation. Iran. J. Fuzzy Syst. 2012, 9, 1–12. [Google Scholar]
- Memarbashi, R.; Ghasemabadi, A. Fuzzy difference equations of volterra type. Int. J. Nonlinear Anal. Appl. 2013, 4, 74–78. [Google Scholar]
- Stefanidou, G.; Papaschinopoulos, G. A fuzzy difference equation of a rational form. J. Nonlinear Math. Phys. 2005, 12, 300–315. [Google Scholar] [CrossRef]
- Chrysafis, K.A.; Papadopoulos, B.K.; Papaschinopoulos, G. On the fuzzy difference equations of finance. Fuzzy Sets Syst. 2008, 159, 3259–3270. [Google Scholar] [CrossRef]
- Mondal, S.P.; Vishwakarma, D.K.; Saha, A.K. Solution of second order linear fuzzy difference equation by Lagrange’s multiplier method. J. Soft Comput. Appl. 2016, 2016, 11–27. [Google Scholar] [CrossRef][Green Version]
- Mondal, S.P.; Mandal, M.; Bhattacharya, D. Non-linear interval-valued fuzzy numbers and their application in difference equations. Granul. Comput. 2017, 3, 177–189. [Google Scholar] [CrossRef]
- Sarkar, B.; Mondal, S.P.; Hur, S.; Ahmadian, A.; Salahshour, S.; Guchhait, R.; Iqbal, M.W. An optimization technique for national income determination model with stability analysis of differential equation in discrete and continuous process under the uncertain environment. Rairo Oper. Res. 2019, 53, 1649–1674. [Google Scholar] [CrossRef]
- Zhang, Q.; Lin, F. On Dynamical Behavior of Discrete Time Fuzzy Logistic Equation. Discret. Dyn. Nat. Soc. 2018, 2018, 1–8. [Google Scholar] [CrossRef]
- Zhang, Q.; Lin, F.; Zhong, X. Asymptotic Behavior of Discrete Time Fuzzy Single Species Model. Discret. Dyn. Nat. Soc. 2019, 2019, 1–9. [Google Scholar] [CrossRef]
- Zhang, Q.; Lin, F.B.; Zhong, X.Y. On discrete time Beverton-Holt population model with fuzzy environment. Math. Biosci. Eng. 2019, 16, 1471–1488. [Google Scholar] [CrossRef] [PubMed]
- Khastan, A. Fuzzy logistic difference equation. Iran. J. Fuzzy Syst. 2018, 15, 55–66. [Google Scholar]
- Mondal, S.P.; Alam Khan, N.; Vishwakarma, D.; Saha, A.K. Existence and Stability of Difference Equation in Imprecise Environment. Nonlinear Eng. 2018, 7, 263–271. [Google Scholar] [CrossRef]
- Khastan, A.; Alijani, Z. On the new solutions to the fuzzy difference equation xn+1=A+Bxn. Fuzzy Sets Syst. 2019, 358, 64–83. [Google Scholar] [CrossRef]
- Khastan, A. New solutions for first order linear fuzzy difference equations. J. Comput. Appl. Math. 2017, 312, 156–166. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, M.; Hussien, A.N.; Sangaiah, A.K. A novel group decision-making model based on triangular neutrosophic numbers. Soft Comput. 2018, 22, 6629–6643. [Google Scholar] [CrossRef]
- Jensen, A. Lecture Notes on Difference Equation; Department of mathematical Science, Aalborg University: Aalborg, Denmark, 18 July 2011; (It is lecture notes of the courses “Introduction to Mathematical Methods” and “Introduction to Mathematical Methods in Economics”). [Google Scholar]
- Elaydi, S.N. An Introduction to Difference Equations; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
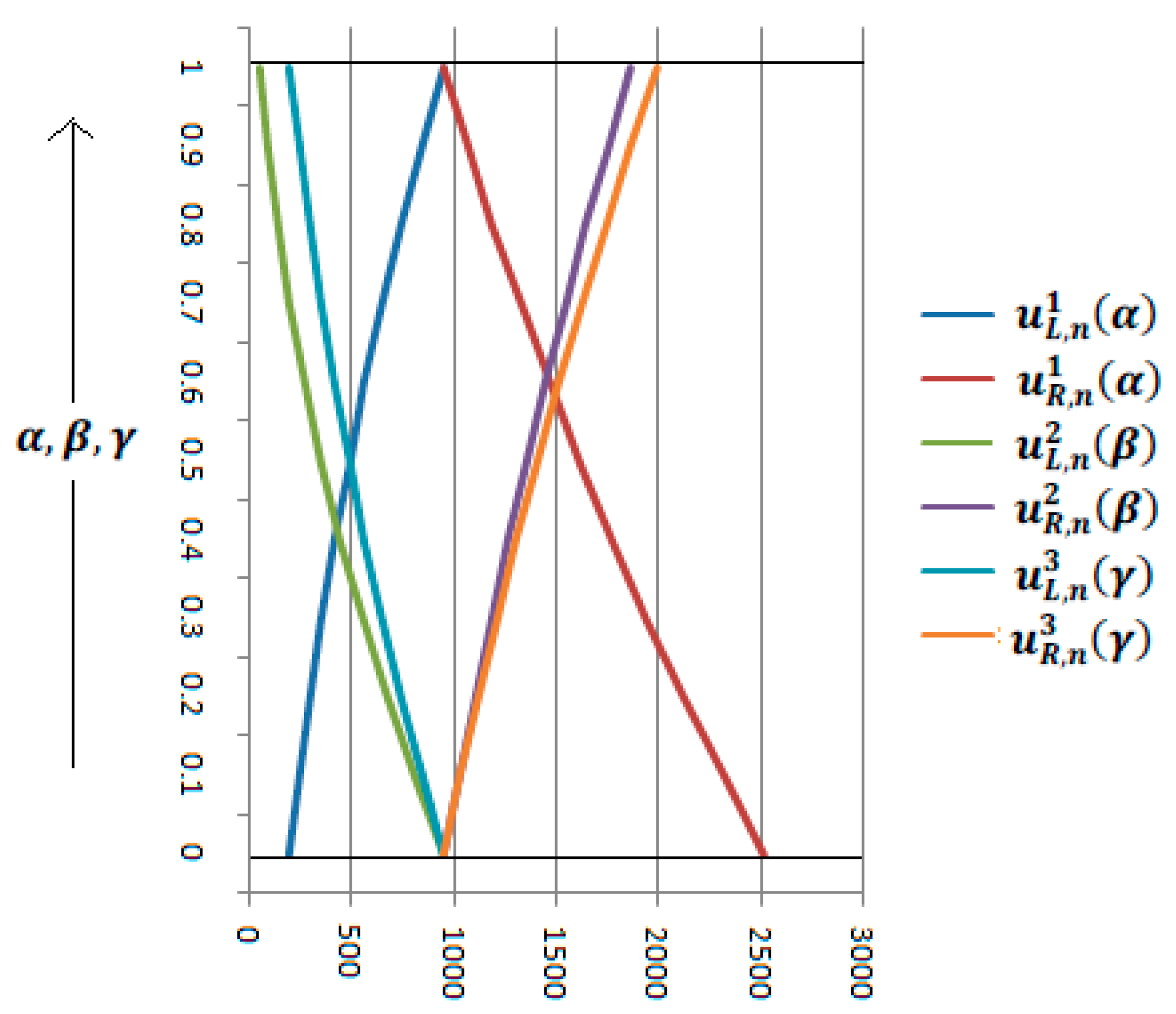
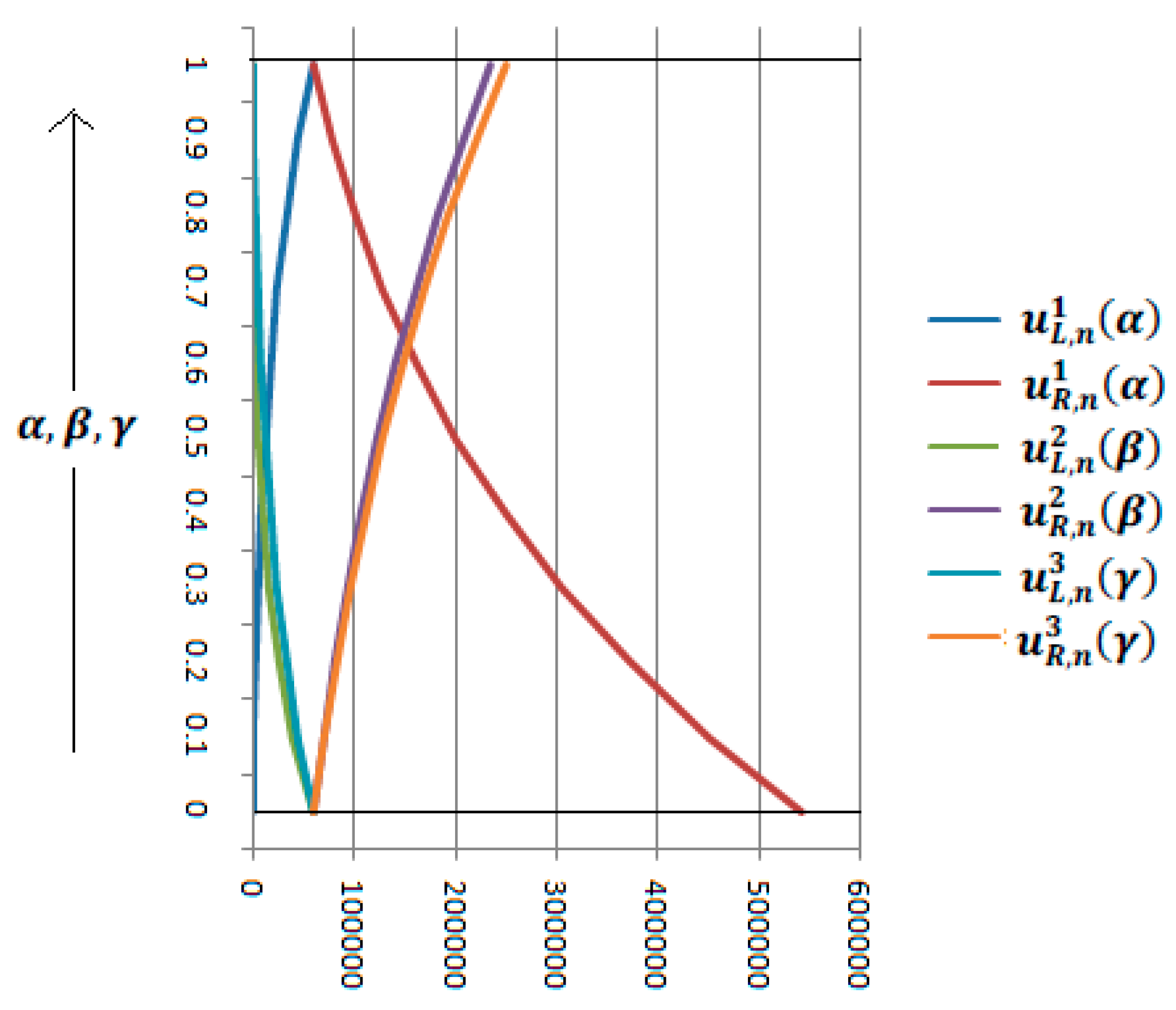


| Type of Uncertain Parameter | Verbal Phrase | Used Functionsand Their Roles |
|---|---|---|
| Triangular Fuzzy Number | [Low, Medium, High] | Membership function for measuring degree of belongingness |
| Triangular Intuitionistic Fuzzy Number | [Low, Medium, High; Very Low, Medium, Very High] | Membership and non-membership function for measuring degree of belongingness and non-belongingness |
| Triangular NeutrosophicNumber | [Low, Medium, High; Very Low, Medium, Very High; Between low and very low; Medium; Between high and very high] | Truthiness, falsity, and indeterminacy function for measuring the degree of truth belongingness, strictly non-belongingness and indeterminacy |
| 0 | 200.00 | 2520.00 | 960.00 | 960.00 | 960.00 | 960.00 |
| 0.1 | 246.84 | 2321.16 | 814.55 | 1033.81 | 851.96 | 1042.22 |
| 0.2 | 299.52 | 2132.48 | 682.04 | 1111.32 | 751.68 | 1128.96 |
| 0.3 | 358.28 | 1953.72 | 562.18 | 1192.60 | 658.92 | 1220.34 |
| 0.4 | 423.36 | 1784.64 | 454.72 | 1277.76 | 573.44 | 1316.48 |
| 0.5 | 495.00 | 1625.00 | 359.37 | 1366.87 | 495.00 | 1417.50 |
| 0.6 | 573.44 | 1474.56 | 275.88 | 1460.04 | 423.36 | 1523.52 |
| 0.7 | 658.92 | 1333.08 | 203.96 | 1557.34 | 358.28 | 1634.66 |
| 0.8 | 751.68 | 1200.32 | 143.36 | 1658.88 | 299.52 | 1751.04 |
| 0.9 | 851.96 | 1076.04 | 93.79 | 1764.73 | 246.84 | 1872.78 |
| 1 | 960.00 | 960.00 | 55.00 | 1875.00 | 200.00 | 2000.00 |
| 0 | 1600.00 | 544,320.00 | 61,440.00 | 61,440.00 | 61,440.00 | 61,440.00 |
| 0.1 | 2628.35 | 452,886.16 | 41,259.65 | 71,251.56 | 46,748.74 | 71,830.84 |
| 0.2 | 4140.56 | 374,497.60 | 26,806.90 | 82,335.47 | 35,070.38 | 83,642.38 |
| 0.3 | 6297.12 | 307,640.56 | 16,748.05 | 94,820.44 | 25,898.19 | 97,025.57 |
| 0.4 | 9293.59 | 250,934.66 | 9982.01 | 108,844.70 | 18,790.48 | 112,143.03 |
| 0.5 | 13,365.00 | 203,125.00 | 5615.23 | 124,556.48 | 13,365.00 | 129,169.68 |
| 0.6 | 18,790.48 | 163,074.53 | 2937.57 | 142,114.45 | 9293.59 | 148,293.34 |
| 0.7 | 25,898.19 | 129,756.67 | 1398.99 | 161,688.22 | 6297.12 | 169,715.30 |
| 0.8 | 35,070.38 | 102,248.05 | 587.20 | 183,458.85 | 4140.56 | 193,651.01 |
| 0.9 | 46,748.74 | 79,721.65 | 206.06 | 207,619.30 | 2628.35 | 220,330.69 |
| 1 | 61,440.00 | 61,440.00 | 55.00 | 234,375.00 | 1600.00 | 250,000.00 |
| 1 | 151.20 | 343.20 | 162.40 | 290.40 | 179.20 | 299.20 |
| 2 | 381.93 | 1513.38 | 410.23 | 1101.80 | 510.47 | 1135.19 |
| 3 | 964.79 | 6673.49 | 1036.26 | 4180.33 | 1454.14 | 4307.01 |
| 4 | 2437.12 | 29,427.69 | 2617.65 | 15,860.57 | 4142.31 | 16,341.19 |
| 5 | 6156.31 | 129,765.52 | 6612.33 | 60,176.40 | 11,799.88 | 61,999.93 |
| 6 | 15,551.16 | 572,219.06 | 16,703.10 | 228,314.58 | 33,613.43 | 235,233.20 |
| 7 | 39,283.04 | 2,523,279.35 | 42,192.90 | 866,245.64 | 95,752.00 | 892,495.51 |
| 8 | 99,231.00 | 11,126,750.35 | 106,581.44 | 3,286,612.28 | 272,761.37 | 3,386,206.59 |
| 9 | 250,662.64 | 49,064,949.17 | 269,230.24 | 12,469,696.48 | 776,994.32 | 12,847,566.07 |
| 10 | 633,186.78 | 216,358,699.65 | 680,089.51 | 47,311,126.78 | 2,213,363.93 | 48,744,797.29 |
| 0 | 13,439.1638 | 16,288.9463 | 14,802.4428 | 14,802.4428 | 14,802.4428 | 14,802.4428 |
| 0.1 | 13,570.2126 | 16,134.4766 | 14,520.2313 | 15,089.5813 | 14,590.3264 | 15,017.3306 |
| 0.2 | 13,702.4105 | 15,981.3266 | 14,242.8714 | 15,381.7230 | 14,380.9496 | 15,235.0219 |
| 0.3 | 13,835.7662 | 15,829.4861 | 13,970.2889 | 15,678.9453 | 14,174.2808 | 15,455.5492 |
| 0.4 | 13,970.2889 | 15,678.9453 | 13,702.4105 | 15,981.3266 | 13,970.2889 | 15,678.9453 |
| 0.5 | 14,105.9876 | 15,529.6942 | 13,439.1638 | 16,288.9463 | 13,768.9430 | 15,905.2433 |
| 0.6 | 14,242.8714 | 15,381.7230 | 13,180.4776 | 16,601.8849 | 13,570.2126 | 16,134.4766 |
| 0.7 | 14,380.9496 | 15,235.0219 | 12,926.2814 | 16,920.2240 | 13,374.0675 | 16,366.6791 |
| 0.8 | 14,520.2313 | 15,089.5813 | 12,676.5060 | 17,244.0464 | 13,180.4776 | 16,601.8849 |
| 0.9 | 14,660.7259 | 14,945.3915 | 12,431.0828 | 17,573.4357 | 12,989.4133 | 16,840.1284 |
| 1 | 14,802.4428 | 14,802.4428 | 12,189.9442 | 17,908.4770 | 12,800.8454 | 17,081.4446 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alamin, A.; Mondal, S.P.; Alam, S.; Ahmadian, A.; Salahshour, S.; Salimi, M. Solution and Interpretation of Neutrosophic Homogeneous Difference Equation. Symmetry 2020, 12, 1091. https://doi.org/10.3390/sym12071091
Alamin A, Mondal SP, Alam S, Ahmadian A, Salahshour S, Salimi M. Solution and Interpretation of Neutrosophic Homogeneous Difference Equation. Symmetry. 2020; 12(7):1091. https://doi.org/10.3390/sym12071091
Chicago/Turabian StyleAlamin, Abdul, Sankar Prasad Mondal, Shariful Alam, Ali Ahmadian, Soheil Salahshour, and Mehdi Salimi. 2020. "Solution and Interpretation of Neutrosophic Homogeneous Difference Equation" Symmetry 12, no. 7: 1091. https://doi.org/10.3390/sym12071091
APA StyleAlamin, A., Mondal, S. P., Alam, S., Ahmadian, A., Salahshour, S., & Salimi, M. (2020). Solution and Interpretation of Neutrosophic Homogeneous Difference Equation. Symmetry, 12(7), 1091. https://doi.org/10.3390/sym12071091








