Abstract
The grand theory of action of Parsons has an important place in social theories. Furthermore, there are many uncertainties in the theory of Parsons. Classical math logic is often insufficient to explain these uncertainties. In this study, we explain the grand theory of action of Parsons in neutrosociology for the first time. Thus, we achieve a more effective way of dealing with the uncertainties in the theory of Parsons as in all social theories. We obtain a similarity measure for single-valued neutrosophic numbers. In addition, we show that this measure of similarity satisfies the similarity measure conditions. By making use of this similarity measure, we obtain applications that allow finding the ideal society in the theory of Parsons within the theory of neutrosociology. In addition, we compare the results we obtained with the data in this study with the results of the similarity measures previously defined. Thus, we have checked the appropriateness of the decision-making application that we obtained.
1. Introduction
There are many uncertainties in the world. Classical math logic is usually insufficient to explain uncertainties. Thus, we are not always able to say for a situation or an event whether it is true or wrong in an absolute manner. For example, we cannot always say the weather is hot or cold. While the weather is hot according to some, it may be cold for others. Therefore, Smarandache obtained the neutrosophic logic and neutrosophic set to deal with uncertainties more objectively in 1998 [1]. ‘T’ is the membership degree, ‘I’ is the uncertainty degree and ‘F’ is the non-membership degree in the neutrosophic logic and neutrosophic sets. “T, I, F” are defined independently. In addition, a neutrosophic number has the form (T, I, F). Furthermore, neutrosophic logic is a generalization of fuzzy logic [2] and intuitionistic fuzzy logic [3] since fuzzy and intuitionistic fuzzy logic’s membership, non–membership degrees are defined dependently. Thus, many researchers have obtained new structures and new applications on neutrosophic logic and sets [4,5,6,7,8,9,10,11,12,13,14,15].
In Section 2 of this study, we provide a literature review. In Section 3, we give related works. In Section 4, we include the definitions of neutrosophic sets [1], single-valued sets [6], similarity measures in [7] and [16], the theory of social action of Parsons [17], Hausdorff measure [18] and Hamming measure [18]. In Section 5, we re-model the social action theory of Parsons which is modeled in neutrosociology. In Section 6, we obtain a similarity measure for single-valued neutrosophic sets and prove that this measure meets the requirements of the similarity measure. In Section 7, we create the decision-making algorithm that we can choose the ideal society among the societies for the social action theory of Parsons in neutrosociology with the help of similarity measure in Section 6. In Section 8, we give sensitivity analysis for numeric example in Section 7; in Section 9, we give comparison methods. We compare the results we obtained with the data in this study with the results of the similarity measures previously defined. Thus, we have checked the appropriateness of the decision-making application we obtained; in Section 10, we discuss what we obtained in this study and make suggestions for studies that can be obtained by making use of this study; in Section 11, we give conclusions.
2. Literature Review
Similarity measure and decision-making practices emerge as an important application theory, especially after the definition of the fuzzy sets and neutrosophic sets. Many researchers have tried to deal with uncertainties by making new applications on neutrosophic sets, using similarity measures, TOPSIS method, VIKOR method, multicriteria method, Maximizing deviation method, decision tree methods, gray relational analysis method, etc. Recently, Şahin et al. studied combined classic neutrosophic sets and double neutrosophic sets [19]; Şahin et al. obtained decision-making applications for professional proficiencies in neutrosophic theory [16]; Uluçay et al. introduced decision-making applications for neutrosophic soft expert graphs [20]; Olgun et al. studied neutrosophic logic on the decision tree [21]; Wang et al. studied an extended VIKOR method with triangular fuzzy neutrosophic numbers [22]; Biswas et al. introduced TOPSIS method for decision–making applications [23]; Şahin et al. obtained a maximizing deviation method in neutrosophic theory [24]; Biswas et al. studied gray relational analysis method for decision-making applications [25].
3. Related Works
Smarandache claims that sociopolitical events can be studied mathematically [4]. In addition, he claims that it is possible to design a tool to describe an equation, an operator, a mathematical structure or a social phoneme. Studying the past gives us an idea about the future, at least partially. For this reason, we need to construct neutrosophic theories that may describe the new possible types of social structures with a neutrosophic number form. Since the social word contains a high degree of subjectivity that causes a low level of unanimity, these theories necessarily address uncertainty. Most of the data we come across in the field of sociology may be vague, incomplete, contradictory, biased, hybrid, ignorant, redundant, etc. Therefore, they are neutrosophic in nature and neutrosophic sciences dealing with indeterminacy should be involved in the study of sociology [4].
For the very same reasons, Smarandache proposed a model to be used in neutrosophic studies. He states that a neutrosophic extension of an element x with a neutrosophic number form.
Parsons, who built his theory on methodological and meta-theoretical debates in the field of social science, also paid special attention to hermeneutic to explain the extent of the individual’s voluntary involvement in action [26]. He made structural and functional explanations to maintain social balance and harmony [21]. While Parsons saw culture as values and norms that guide the actions of individuals in social life, he conceptualized the structure as a system of intertwined and independent parts [27]. According to Parsons, cultural objects are autonomous. He did this by distinguishing between the cultural and social systems. He also viewed society as a general system of action. In addition, many researchers have studied Parsons’s social action theory [26,27,28,29,30,31,32,33,34,35,36].
In this study, Parsons’s social action theory was aimed to re-model neutrosociology. As in all social theories, the social action theory of Parsons could not escape uncertainty [21]. Hence, the handling of it in neutrosociology theory would make this theory more useful. Therefore, we have obtained a similarity measure with single-valued neutrosophic numbers and included applications where this measure can be used as the neutrosophic equivalent of the ideal society in this theory.
4. Preliminaries
This section includes the definitions of neutrosophic sets [1], single-valued neutrosophic sets [6], similarity measures [7,16] and theory of social action of Parsons [17], Hausdorff measure [18] and Hamming measure [18].
Definition 1
([17]). Parsons, who built his theory on methodological and meta-theoretical debates in the field of social science, also paid special attention to hermeneutic to explain the extent of the individual’s voluntary involvement in action (so, which is neutrosophic). He made structural and functional explanations to maintain social balance and harmony. While Parsons saw culture as values and norms that guide the actions of individuals in social life, he conceptualized the structure as a system of intertwined and independent parts. According to Parsons, cultural objects are autonomous. He did this by distinguishing between the cultural and social systems. He also viewed society as a general system of action.
Definition 2
([1]). Let X be a universal set. Neutrosophic set S; is identified as S = {(x:, , >, x X}. Where; on the condition that 0− + + 3+; the functions T:U ]0−,1+[ is truth function, I:U ]0−,1+[ is uncertain function and F:U ]0−,1+[ is falsity function.
Definition 3
([6]). Let X be a universal set. Single-valued neutrosophic number set S; is identified as S = {(x:, , >, x X}. Where; on condition that 0 + + 3; the functions T:X [0,1] is truth function, I:X [0,1] is uncertainly function and F:X [0,1] is falsity function.
Definition 4
([6]). Let A = {(x:<, , >} and B = {(x:<, , >} are single-valued neutrosophic numbers. If A = B; then = , = and = .
Definition 5
([6]). Let A = {(x:<, , >} and B = {(x:<, , >} are single-valued neutrosophic sets for x U. If A < B; then for ∀ x U; < , < and < .
Properties 1
([7]). Let and are three single-valued neutrosophic numbers and S be a similarity measure. S provides the following conditions.
- =
- .
- Ifthen,.
Definition 6
([16]). Let = < > and = < > be two single-valued neutrosophic numbers.
is a similarity measure.
Definition 7
([18]). Let = < > and = < > be two single-valued neutrosophic numbers.
is a Hausdorff similarity measure.
Definition 8
([18]). Let = < > and = < > be two single-valued neutrosophic numbers.
is a Hamming similarity measure.
5. Neutrosophic Modeling of Parson’s Theory of Action
According to the perfection of action categories of Parsons, it is inevitable to have deep doubts in every society and between layers of a particular society. However, “there is no ideal society in the sense that Marx defines, within each society the definition of ideal changes according to the place of a person within the society. By those who are at the top layer, the society is defined as ideal, by those at the lowest layer, it is far from being ideal, and by those in the mid-layer, who can sometimes be completely ignorant of what is an ideal society, it can be described as a fluctuating phenomenon depending on circumstances. Therefore, we always have a neutrosophic ideal society with an opposite and neutral triad. Naturally, this is valid for all societies since there are always people with more privileges than the others. Even in any a democratic society, some people have more privileges although they may form a small minority” [4].
Parsons developed a theory of action to explain how the macro and micro aspects of a particular social order show structural integrity together with the participation of its members. He took into account the voluntary participation of the individual in the social life on one hand, and structural continuity on the other. Here, it is assumed that the individual acts under the motivation of the social structure while taking action. According to him, social sciences should consider a trio considering the purposes, ends and ideals when examining actions.
Grand Theory of Action
The basic paradigm of Parson viewed society as a general system of action is based on the understanding of ‘rational social action’ of Weber [28]. However, according to Weber, sociology is a science that tries its interpretive understanding of social action to achieve a causal explanation of its course and its effects [36].
This interpretation is enriched from the perspective of the sociologist. Thus, social actions become neutrosophic. Others may agree, partially agree or disagree (1, 0, 0). Likewise, in the theory of Parson, the possibility of all members of society to participate in social values and norms that regulate, and guide human relations rather than individual activities is questionable, uncertain. Here we must see neutrosophic triplets.
According to Parson’s theory, all social actions are based on five pattern variables. These:
- Affectivity versus affective neutrality;
- Self-orientation versus collective orientation;
- Universalism versus particularism;
- Quality versus performance;
- Specificity versus diffuseness.
Parsons believes that these variables classify expectations and the structure of relationships, making the intangible action theory more understandable. However, according to Parsons, pattern variables are twofold, and each pattern variable indicates a problem or riddle that must be solved by the actor before the action can be performed. At the same time, there is a wide variety between the traditional society and the modern society. However, these can be seen as binary for neutrosophic sociological analysis (1, 0), it is very difficult to determine which of the individual’s behaviors are modern or traditional. Therefore, each of them should be considered as triple neutrosophic (1, 0, 0). The feminists’ response to Parsons’ family view can be given as an example. According to Parsons, the instrumental leadership role in the family structure in modern societies should be given to the spouse–father, on which the family’s reputation and income are based [32]. However, according to feminists, this statement by Parsons is nothing more than the continuation of the status quo [35]. In addition, these pattern variables (stereotypes) do not say how people will behave when faced with role conflict, and we will once again encounter uncertainty. This uncertainty can only be answered by neutrosociology.
The society model that Parsons has compared to the biologic model of an organism is based on the understanding of “living systems” that continues in a balanced way. According to him, a change in any part of the social system leads to adaptive changes in other parts [33]. There are four main problems an all-action system must solve. These are adaptation, goal-attainment, integration and latent pattern maintenance (AGIL). In short, these are referred to as AGIL in Table 1.

Table 1.
Pure adaptation, goal-attainment, integration and latent pattern maintenance (AGIL) model for all living systems [33].
“Adaptation” (A) is concerned with meeting the needs of the system from its environment and how resources are distributed within the system. Here, the system should provide sufficient resources from the environment and distribute it within itself. Social institutions are related to interrelated social rules and roles system that will meet social needs or functions and help solve social system problems. For example, economy, political order, law, religion, education and family are basic institutions for these. If a social system will continue to live, it needs structures and organizations that will function to adapt to its environment. The most dominant of these institutions is the economy. In “achieving the goal” (G), it is determined that the system reaches the specific target and which of these targets has priority. In other words, it should mobilize the resources and energies of the system and determine the priorities among them. “Integration” (I) refers to the coordination and harmony of parts of the system so that the system functions as a whole. To keep the system running, it must coordinate, correct, and regulate the relationships between the various actors or units in the system. “Latent pattern maintenance” (L) shows how to ensure the continuity of the action within the system according to a certain order or norm. The system should protect its values from deterioration and ensure the transfer of social values. Thus, it ensures the compliance of the members of the system. Especially family, religion, media and education have basic functions. Thanks to these, individuals gain a moral commitment to values shared socially [30].
The General Action Level is as follows in Table 2:

Table 2.
General Action Level [30].
Ultimately we get this series: The social the system, the fiduciary the cognitive.
Let us rebuild this series neutrosociology: (1, 0, 0) (1, 0, 0) (1, 0, 0).
If we go back to the beginning, “Behavioral organic, Personality system, Cultural system and Social system” must work continuously to ensure social balance. This will be through “socialization” and “social control”. If socialization “works”, all members of the society will adhere to shared values, make appropriate choices between pattern variables, and do what is expected of them in harmony, integration and other issues. For example, people will marry and socialize their children (L), and the father in the family will gain bread as it should be (A) [35].
6. A New Measurement of Similarity for Single-Valued Neutrosophic Numbers
Definition 9.
Let= <>,= <> be two single-valued neutrosophic numbers. We define measure of similarity betweenandas follows
We show that the measure of similarity in Definition 9 meets the requirements in Properties 1.
Theorem 1.
Letbe the measure of similarity in Definition 9.provides the following features.
- if and only if.
- If, then.
Proof:
(i) Since and are single-valued neutrosophic numbers, we have
Therefore,
Hence, 01.
(ii)
(iii) We assume that
Therefore,
So,
Therefore,
Now, we write all the cases that can make these statements 0 one-by-one.
(a) We assume that
Therefore, it is
Here, it is obtained that = 0, = 0 and = 0. Hence, we get and . By Definition 4, = .
(b) Let
By (2) and (3), we obtain = 0 and = 0.
Therefore, we obtain = 0, = 0 and = 0. Hence, we obtain and . By Definition 4, = .
(c) We assume that
By , we have
Hence, we obtain that = 0 by (5) and (6).
Hence, and . By Definition 4, we get = .
(d) We assume that
By (7) and (8), we obtain
Hence, = 0 by (9) and (10).
Hence, . By Definition 4, = .
We assume that = . Therefore, by Definition 4, it is = , = , = . Because of this, we have
(iv) We assume that ≤ ≤ . By Definition 5, it is ≤ ≤ , ≥ ≥ , ≥ ≥ . Hence, we obtain that
Therefore, we have
Hence,
In addition,
Therefore, we obtain that
Hence,
In addition,
Hence, we have
Hence,
By (11), (12) and (13), we have
Hence, we get ≤ as desired. □
7. Decision-Making Applications for Neutrosophic Modeling of Talcott Parsons’s Action
In this section, we give an algorithm for applications that allow us to find the ideal society in the grand theory of action of Parsons by taking advantage of the similarity measure in Definition 9. In addition, we give a numeric example to this algorithm.
7.1. Algorithm
1. Step: To find out which societies are closer to the ideal society, the criteria to be considered are determined. The criteria of the ideal society in the grand theory of action of Parsons [17] are taken as below:
- c1 = affectivity versus affective neutrality
- c2 = self-orientation versus collective orientation
- c3 = universalism versus particularism
- c4 = quality versus performance
- c5 = specificity versus diffuseness
Let the set of these criteria be C = {, , …, }.
2. Step: Let the set of weighted values of the criteria be W = {w1, w2, …, wm} and let the weighted values be taken as below:
- the weighted value of the criterion c1 is w1,
- the weighted value of the criterion c2 is w2,
- the weighted value of the criterion c3 is w3,
- the weighted value of the criterion c4 is w4 and
- the weighted value of the criterion c5 is w5.
In addition, it must be = 1 and , , …, [0,1].
In this study, we will take the weighted value of each criterion as equal. If necessary, different weighted values can be selected for each criterion.
3. Step: Each society that will be taken into ideal society assessment should be evaluated by sociologists determined as a single-valued neutrosophic number. Let T = {, , …, } be set of societies. Symbolic representation of societies as single-valued neutrosophic sets are denoted as:
Here, , , …, are the criteria in Step 1. Thus, each society will be obtained as a single-valued neutrosophic number according to the given criteria.
4. Step: To compare how close the societies are to ideal society in the theory of Parsons, an imaginary perfect society is determined. Perfect society under the similarity measure we have obtained should be as
Hence, we will accept the existence of an imaginary society that includes 100% truth, 0% uncertainty and 0% falsity according to each criterion.
5. Step: We express the societies given as a single-valued neutrosophic set in step 3 in a table according to criteria. Thus, we will obtain Table 3.

Table 3.
Criteria table of societies.
6. Step: We will process each criterion values given for each society separately and each criterion values of the perfect society I in Step 4 separately with similarity measure. Hence, we will obtain Table 4.

Table 4.
Similarity table for each social criteria to perfect society criteria.
7. Step: In this step, we will obtain a weighted similarity table (Table 5).

Table 5.
Weighted similarity table for each social criteria to perfect society criteria.
In this study, this step is not needed since we take the same weighted value of each criterion. More precisely, Table 5 and Table 4 will be the same since the weighted values are equal. This step can be used if necessary.
8. Step:
In this last step, we will obtain a similarity value table (Table 6) by applying (, I) = .

Table 6.
Similarity value table of societies to the perfect society.
See Figure 1.
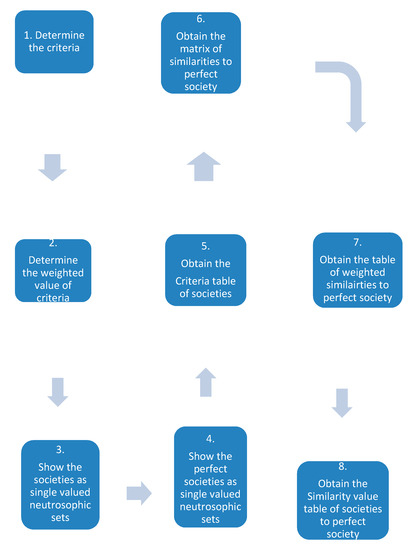
Figure 1.
Diagram of the algorithm.
7.2. Numeric Example
Using the steps in Section 7.1, we show how close the 4 societies are to the ideal society.
1. Step: Let the criteria of an ideal society in the theory of Parsons be as it is in Step 1 of Section 7.1;
- c1 = affectivity versus affective neutrality
- c2 = self-orientation versus collective orientation
- c3 = universalism versus particularism
- c4 = quality versus performance
- c5 = specificity versus diffuseness
Let C = {c1, c2, …, c5} be the set of criteria.
2. Step: In this example, we will take the weight values of each criterion equal so that w1 = w2 = … = w5 = 0.2.
3. Step: Let the set of societies be T = {t1, t2, t3, t4}. We assume that the single-valued neutrosophic set with evaluation of societies by sociologists according to the criteria in Step 1 will be as below:
4. Step: Let the dream perfect society that we compare societies be
5. Step: Let us express the societies as a single-valued neutrosophic set in Step 3 in Table 7.

Table 7.
The criteria table of societies.
6. Step: Using the similarity measure, we obtain the similarity table (Table 8) which is the similarity of the criteria of societies to the criteria of the perfect society.

Table 8.
The similarity table of the criteria of societies to the criteria of the perfect society.
7. Step: In this example, there is no need to make any changes in Table 8 since we take the weighted value of each criterion as equal.
8. Step: In this step, we obtain similarity values of the societies in Table 8 to the perfect society.
Now, we obtain the similarity values of the societies in Table 9 and we obtain Table 10 by dividing the values in Table 9 by 5, taking the weighted values as equal for each society on 5 criteria and, hence, getting the results in the range [0,1].

Table 9.
The similarity value table of the societies to the perfect society.

Table 10.
The similarity rate of the societies to the perfect society.
In addition, the similarity value of each society to the perfect society in Table 10 is obtained. The result of the evaluation is given. Thus, societies closest to the perfect society are obtained as t3, t4, t2 and t1 respectively.
8. Sensitivity Analysis
In 7.1 Numeric example, we take the weighted values of criteria W = {w1, w2, …, wm} equal such that
- the weighted value of c1 criteria w1 = 0.2
- the weighted value of c2 criteria w2 = 0.2
- the weighted value of c3 criteria w3 = 0.2
- the weighted value of c4 criteria w4 = 0.2
- the weighted value of c5 criteria w5 = 0.2
Thus, societies closest to the perfect society are obtained as t3, t4, t2, t1 respectively.
(a) If we take the W = {w1 = 0.1, w2 = 0.3, w3 = 0.2, w4 = 0.2, w5 = 0.2}, then we obtain that societies closest to the perfect society are obtained as t3, t4, t2 and t1 respectively (Table 11).

Table 11.
The similarity rate of the societies to the perfect society for W = {w1 = 0.1, w2 = 0.3, w3 = 0.2, w4 = 0.2, w5 = 0.2}.
Thus, we obtain the same result with the Numeric Example 7.1.
(b) If we take the W = {w1 = 0.2, w2 = 0.2, w3 = 0.3, w4 = 0.1, w5 = 0.2}, then we obtain that societies closest to the perfect society are obtained as t3, t4, t2 and t1 respectively respectively (Table 12).

Table 12.
The similarity rate of the societies to the perfect society for W = {w1 = 0.2, w2 = 0.2, w3 = 0.3, w4 = 0.1, w5 = 0.2}.
Thus, we obtain same result with Numeric Example 7.1.
(c) If we take the W = {w1 = 0.3, w2 = 0.1, w3 = 0.2, w4 = 0.2, w5 = 0.2}, then we obtain that societies closest to the perfect society are obtained as t4, t3, t2 and t1 respectively respectively (Table 13).

Table 13.
The similarity rate of the societies to the perfect society for W = {w1 = 0.3, w2 = 0.1, w3 = 0.2, w4 = 0.2, w5 = 0.2}.
Thus, we obtain a different result from Numeric Example 7.1.
(d) If we take the W = {w1 = 0.2, w2 = 0.2, w3 = 0.1, w4 = 0.3, w5 = 0.2}, then we obtain that societies closest to the perfect society are obtained as t4, t1, t2 and t3 respectively respectively (Table 14).

Table 14.
The similarity rate of the societies to the perfect society for W = {w1 = 0.2, w2 = 0.2, w3 = 0.1, w4 = 0.3, w5 = 0.2}.
Thus, we obtain a different result with Numeric Example 7.1.
(e) If we take the W = {w1 = 0.2, w2 = 0.2, w3 = 0.2, w4 = 0.3, w5 = 0.1}, then we obtain that societies closest to the perfect society are obtained as t3, t4, t1, and t2 respectively respectively (Table 15).

Table 15.
The similarity rate of the societies to the perfect society for W = {w1 = 0.2, w2 = 0.2, w3 = 0.2, w4 = 0.3, w5 = 0.1}.
Thus, we obtain a different result from Numeric Example 7.1.
(f) If we take the W = {w1 = 0.2, w2 = 0.2, w3 = 0.2, w4 = 0.1, w5 = 0.3}, then we obtain that societies closest to the perfect society are obtained as t4, t2, t3, and t1 respectively respectively (Table 16).

Table 16.
The similarity rate of the societies to the perfect society for W = {w1 = 0.2, w2 = 0.2, w3 = 0.2, w4 = 0.1, w5 = 0.3}.
Thus, we obtain a different result from Numeric Example 7.1.
Now, we give results in (a), (b), (c), (d), (e) and (f) in Table 17.

Table 17.
Ideal societies according to weighted values.
As seen in Table 17, if we take W = {w1 = 0.2, w2 = 0.2, w3 = 0.2, w4 = 0.1, w5 = 0.3} or W = {w1 = 0.1, w2 = 0.3, w3 = 0.2, w4 = 0.2, w5 = 0.2}, then we obtain same result with Numeric Example 7.1. In other cases, we obtain different results from Numeric Example 7.1.
9. Study Comparison Methods
In this section, we have compared the obtained results of the data in our Example 1 with the results of the similarity measures, Hausdorff measure [18], Hamming measure [18] and the previously defined similarity measure [16].
1. If we use the similarity measure in Definition 6 [16] for Example 1, we obtain Table 18 as a result.

Table 18.
The similarity rate according to similarity measure, in Definition 6 [16], of the societies to the perfect society.
Thus, societies closest to the perfect society are obtained as t3, t4, t1 and t2 respectively according to similarity measure in Definition 6 [16].
2. If we use the Hausdorff measure [18] for Example 1, we obtain Table 19 as a result.

Table 19.
The similarity rate according to Hausdorff measure, in Definition 7 [18], of the societies to the perfect society.
Thus, societies closest to the perfect society are obtained as t3 = t4, t2 and t1 respectively according to Hausdorff similarity measure in Definition 7 [18].
3. If we use the Hamming measure [18] for Example 1, we obtain Table 20 as a result.

Table 20.
The similarity rate according to Hamming similarity measure, in Definition 8 [18], of the societies to the perfect society.
Thus, societies closest to the perfect society are obtained as t3, t4, t1 and t2 respectively according to Hamming similarity measure, in Definition 8 [18].
As a result,
- according to our similarity measure, the perfect society is obtained as t3, t4, t2, t1 respectively;
- according to similarity measure [16], the perfect society is obtained as t3, t4, t1, t2 respectively;
- according to Hausdorff measure [18], the perfect society is obtained as t3 = t4, t2, t1 respectively;
- according to Hamming measure [18], the perfect society is obtained as t3, t4, t1, t2 respectively.
10. Discussions
In this study, we explained the grand theory of action of Parsons, which has an important place in social theories, for the first time in neutrosociology. Thus, like all social theories, we have achieved a more effective way of dealing with uncertainties in the theory of Parsons. In addition, we have obtained a similarity measure for single-valued neutrosophic numbers. By making use of this similarity measure, we have obtained applications that allow finding the ideal society in the theory of Parsons within the theory of neutrosociology. Hence, we have added a new structure to neutrosophic theory, neutrosociology theory. In addition, by utilizing this study, other social theories can be explained in neutrosociology. Thus, the uncertainties encountered can be dealt with more easily. In addition, by using neutrosophic numbers and sets related to other social theories, new similarity measures can be obtained, and the consistency of these measures can be checked.
11. Conclusions
In Section 9, we obtained different results for the similarity measure [16]; Hausdorff measure [18]; and Hamming measure [18]. In addition, we give a comparison in Table 21.

Table 21.
Comparison methods.
Author Contributions
In this article, each author contributed equally. C.A. obtained Neutrosophic Modeling of Grand Theory of Action of Talcott Parsons; A.K. introduced similarity measure and algorithm; M.Ş. obtained examples and organized the study. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Smarandache, F. A Unifying Field in Logics. Neutrosophy: Neutrosophic Probability, Set and Logic; American Research Press: Rehoboth, DE, USA, 1999. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, T.K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Smarandache, F. Introduction to Neutrosophic Sociology (Neutrosociology); Pons Publishing House/Pons asblQuai du Batelage: Bruxelles, Belgium, 2019. [Google Scholar]
- Broumi, S.; Topal, S.; Bakali, A.; Talea, M.; Smarandache, F. A novel python toolbox for single and ınterval-valued neutrosophic matrices. In Neutrosophic Sets in Decision Analysis and Operations Research; IGI Global: Hershey, PA, USA, 2020; pp. 281–330. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.; Sunderraman, R. Single valued neutrosophic sets. Multispace Multistruct. 2010, 4, 410–413. [Google Scholar]
- Ye, J. Similarity measures between interval neutrosophic sets and their applications in multicriteria decision-making. J. Intell. Fuzzy Syst. 2014, 26, 165–172. [Google Scholar] [CrossRef]
- Broumi, S.; Bakali, A.; Talea, M.; Smarandache, F.; Singh, P.K.; Uluçay, V.; Khan, M. Bipolar complex neutrosophic sets and its application in decision making problem. In Fuzzy Multi-Criteria Decision-Making Using Neutrosophic Sets; Springer: Cham, Switzerland, 2019; pp. 677–710. [Google Scholar]
- Şahin, M.; Olgun, N.; Uluçay, V.; Kargın, A.; Smarandache, F. A new similarity measure on falsity value between single valued neutrosophic sets based on the centroid points of transformed single valued neutrosophic numbers with applications to pattern recognition. Neutrosophic Sets Syst. 2017, 15, 31–48. [Google Scholar] [CrossRef]
- Şahin, M.; Ecemiş, O.; Uluçay, V.; Kargın, A. Some new generalized aggregation operators based on centroid single valued triangular neutrosophic numbers and their applications in multi-attribute decision making. Asian J. Math. Comput. Res. 2017, 16, 63–84. [Google Scholar]
- Şahin, M.; Kargın, A. Neutrosophic triplet groups based on set valued neutrosophic quadruple numbers. Neutrosophic Set Syst. 2019, 30, 122–131. [Google Scholar]
- Uluçay, V.; Şahin, M. Neutrosophic multigroups and applications. Mathematics 2019, 7, 95. [Google Scholar] [CrossRef]
- Dey, A.; Broumi, S.; Bakali, A.; Talea, M.; Smarandache, F. A new algorithm for finding minimum spanning trees with undirected neutrosophic graphs. Granul. Comput. 2019, 4, 63–69. [Google Scholar] [CrossRef]
- Khalid, H.E. Neutrosophic Geometric Programming (NGP) with (max-product) operator, an innovative model. Neutrosophic Sets Syst. 2020, 32, 16. [Google Scholar]
- Bakbak, D.; Uluçay, V.; Şahin, M. Neutrosophic soft expert multiset and their application to multiple criteria decision making. Mathematics 2019, 7, 50. [Google Scholar] [CrossRef]
- Şahin, M.; Kargın, A. New similarity measure between single-valued neutrosophic sets and decision-making applications in professional proficiencies. In Neutrosophic Sets in Decision Analysis and Operations Research; IGI Global: Hershey, PA, USA, 2020; pp. 129–149. [Google Scholar]
- Parsons, T. Social Systems and The Evolution of Action Theory; The Free Press: New York, NY, USA, 1975. [Google Scholar]
- Mukherjee, A.; Sarkar, S. Several Similarity Measures of Neutrosophic Soft Sets and its Application in Real Life Problems. Ann. Pure Appl. Math. 2014, 7, 1–6. [Google Scholar]
- Şahin, M.; Kargın, A.; Smarandache, F. Combined classical-neutrosophic sets and numbers, Double Neutrosophic sets and numbers. In Quadruple Neutrosophic Theory and Applications; Pons Editions: Brussels, Belgium, 2020; Volume 18, pp. 254–265. [Google Scholar]
- Uluçay, V.; Şahin, M. Decision-making method based on neutrosophic soft expert graphs. In Neutrosophic Graph Theory and Algorithms; IGI Global: Hershey, PA, USA, 2020; pp. 33–76. [Google Scholar]
- Olgun, N.; Hatip, A. The effect of the neutrosophic logic on the decision tree. In Quadruple Neutrosophic Theory and Applications; Pons Editions: Brussels, Belgium, 2020; Volume 7, pp. 238–253. [Google Scholar]
- Wang, J.; Wei, G.; Lu, M. An extended VIKOR method for multiple criteria group decision making with triangular fuzzy neutrosophic numbers. Symmetry 2018, 10, 497. [Google Scholar] [CrossRef]
- Biswas, P.; Pramanik, S.; Giri, B.C. TOPSIS Method for Multi-Attribute Group Decision-Making Under Single-Valued Neutrosophic Environment. Neural Comput. Appl. 2016, 27, 727–737. [Google Scholar] [CrossRef]
- Şahin, R.; Liu, P. Maximizing deviation method for neutrosophic multiple attribute decision making with incomplete weight information. Neural Comput. Appl. 2016, 27, 2017–2029. [Google Scholar] [CrossRef]
- Biswas, P.; Pramanik, S.; Giri, B.C. Entropy based grey relational analysis method for multi-attribute decision making under single valued neutrosophic assessments. Neutrosophic Sets Syst. 2014, 2, 102–110. [Google Scholar]
- Bourricaud, F. The Sociology of Talcott Parsons; University of Chicago Press: Chicago, IL, USA, 1981. [Google Scholar]
- Polama, M.M. Contemporary Sociological Theory; Macmillan: New York, NY, USA, 1979. [Google Scholar]
- Dillon, M. Talcott Parsons and Robert Merton, Functionalism and Modernization. In Introduction to Sociological Theory: Theorists, Concepts, and their Applicability to the Twenty-First Century; Wiley: Hoboken, NJ, USA, 2013; pp. 156–157. [Google Scholar]
- Parsons, T. Action Theory and the Human Condition; Free Press: New York, NY, USA, 1978. [Google Scholar]
- Parsons, T. The System of Modern Societies; Prentice-Hall: Englewood Cliffs, NJ, USA, 1971. [Google Scholar]
- Parsons, T. Societies: Evolutionary and Comparative Perspectives; Prentice-Hall: Englewood Cliffs, NJ, USA, 1966. [Google Scholar]
- Parsons, T. Essays in Sociological Theory, Revised Edition; The Free Press: New York, NY, USA, 1954. [Google Scholar]
- Parsons, T.; Shils, E. Toward a General Theory of Action; Harvard University Press: Cambridge, MA, USA, 1951. [Google Scholar]
- Parsons, T. The Structure of Social Action: A Study in Social Theory with Special Reference to a Group of Recent European Writers; Free Press: New York, NY, USA, 1968. [Google Scholar]
- Wallace, R.A.; Wolf, A. Contemporary Sociological Theory: Expanding the Classical Tradition, Subsequent ed.; Prentice Hall, Pearson Education: New York, NY, USA, 1995. [Google Scholar]
- Weber, M. The Theory of Social and Economic Organization; The Free Press: New York, NY, USA, 1947. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).