Overshoot Elimination for Control Systems with Parametric Uncertainty via a PID Controller
Abstract
:1. Introduction
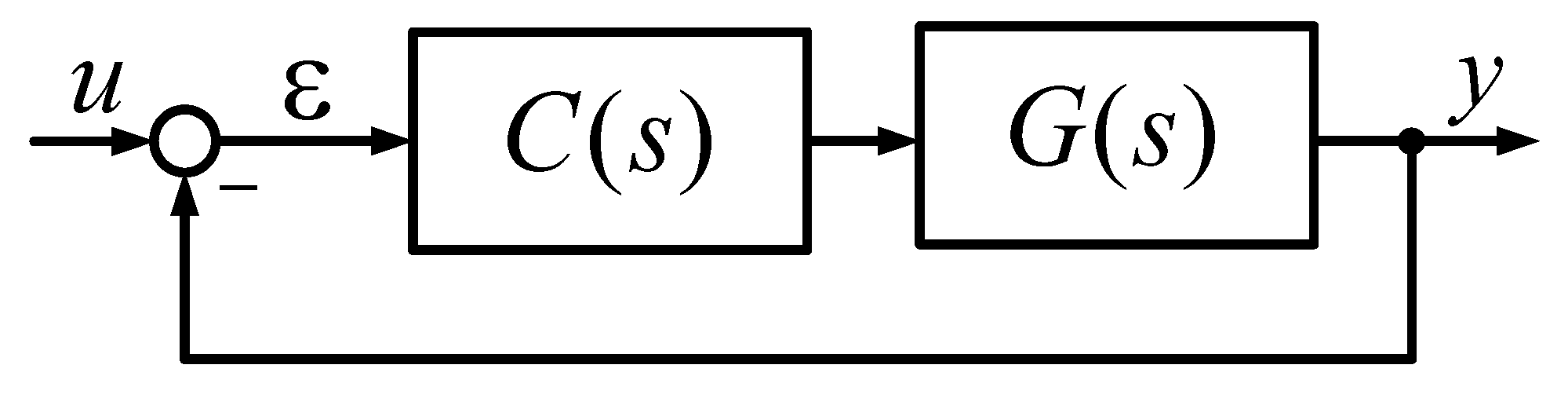
2. Materials and Methods
2.1. Providing Real Closed-Loop Pole Configuration
2.2. Non-Overshoot Step Response Condition
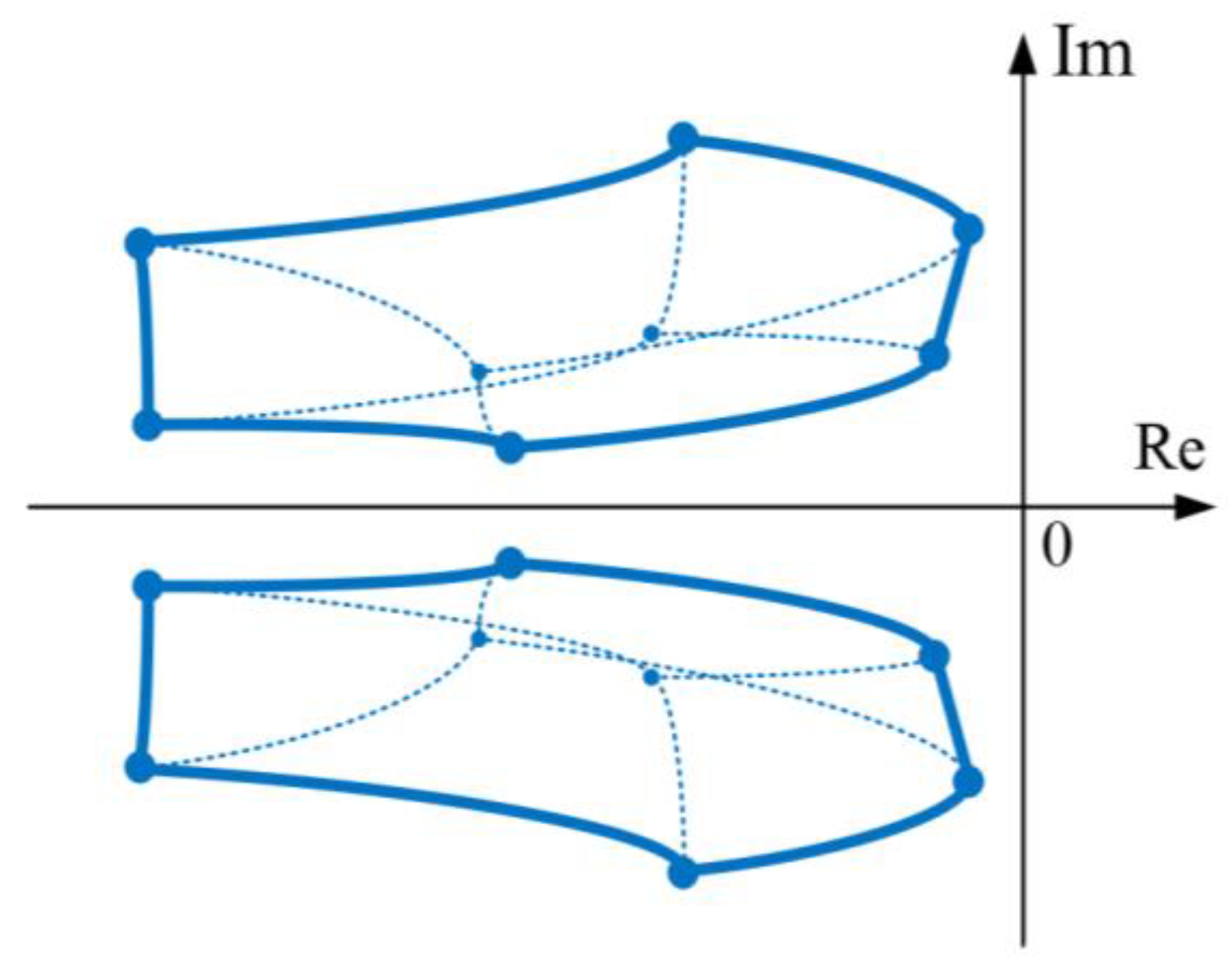
2.3. Plant with Interval-Given Parameters
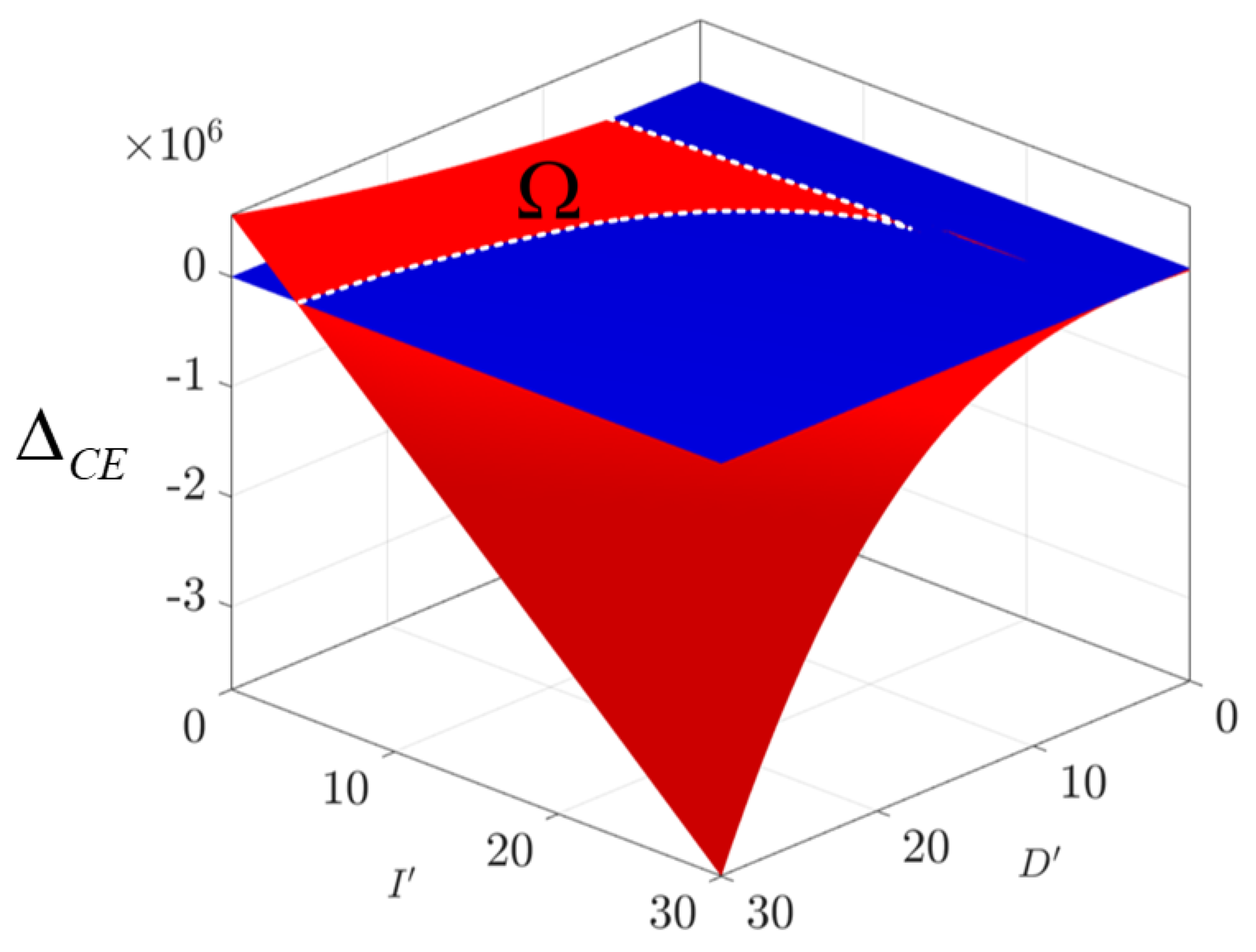
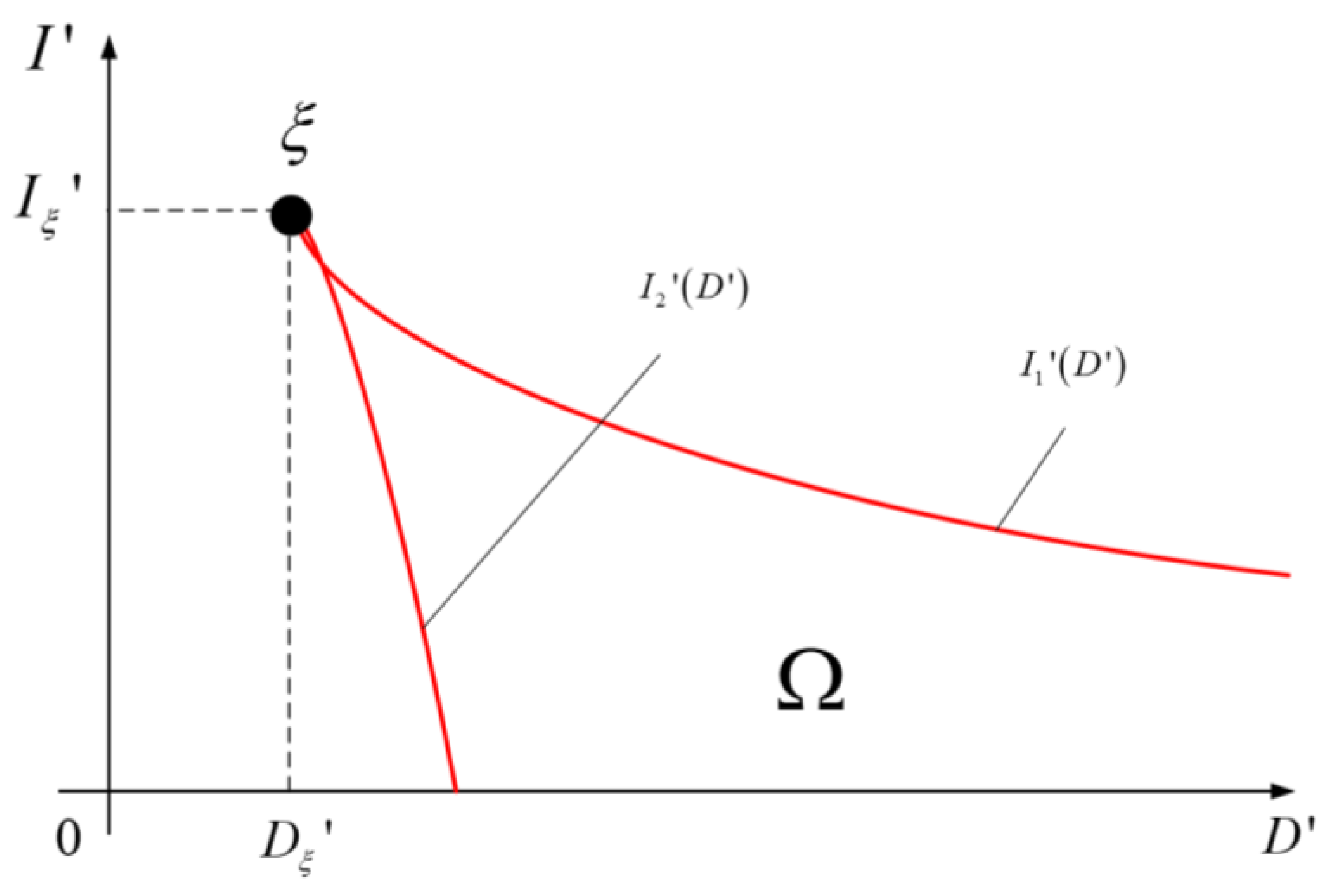
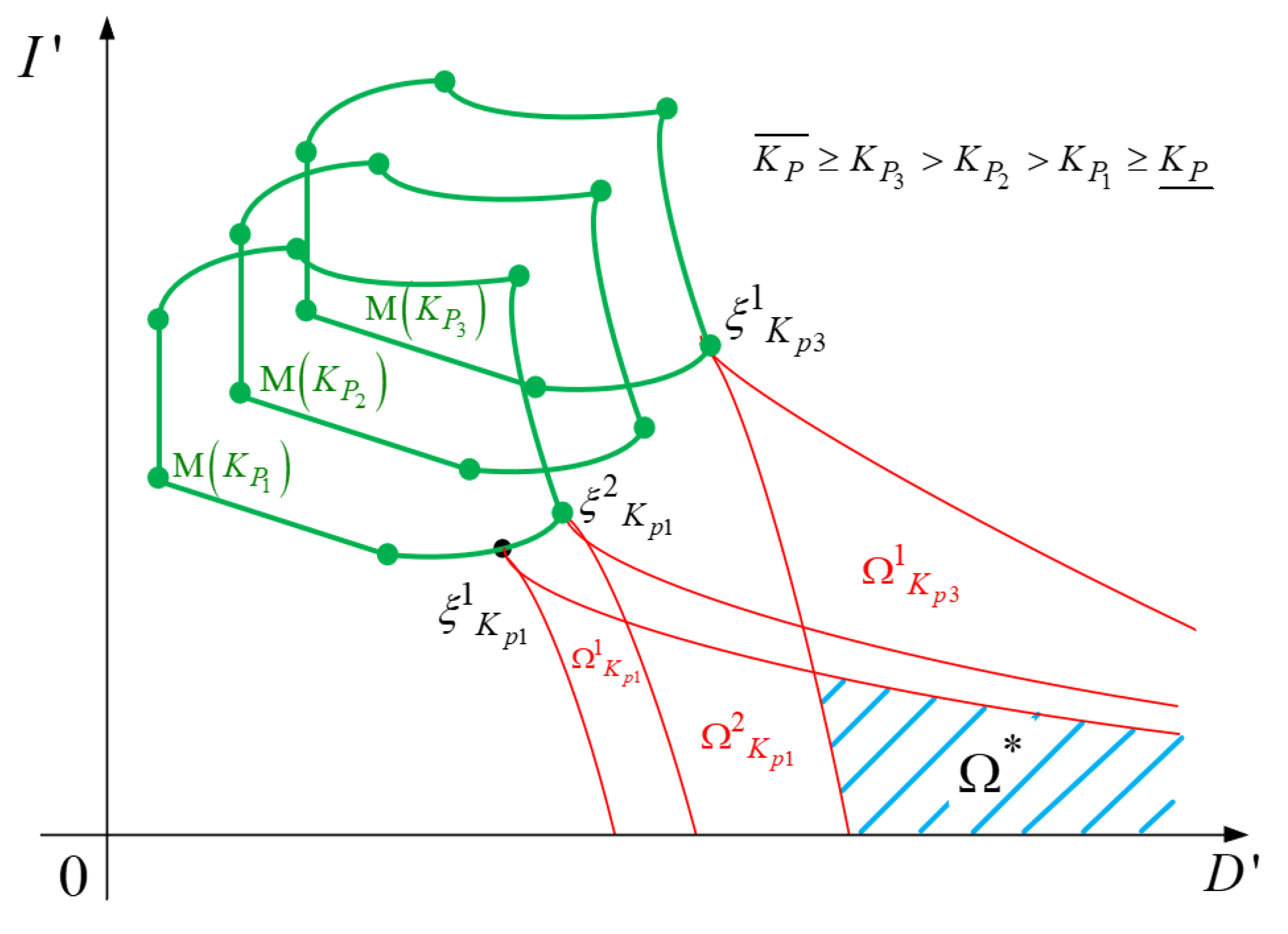
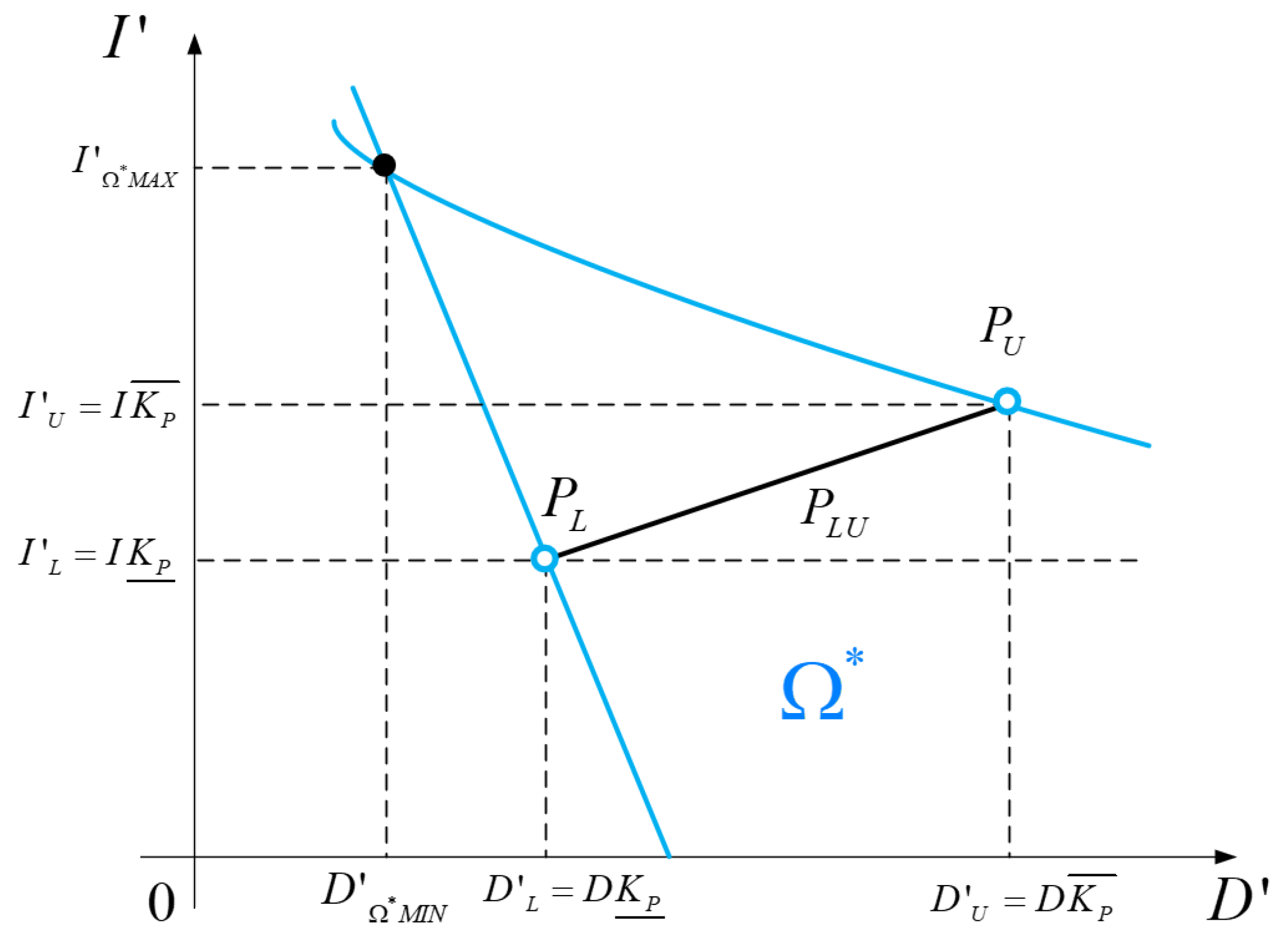
2.4. Constraints Clarification for
2.5. PID-Controller Coefficient Choice
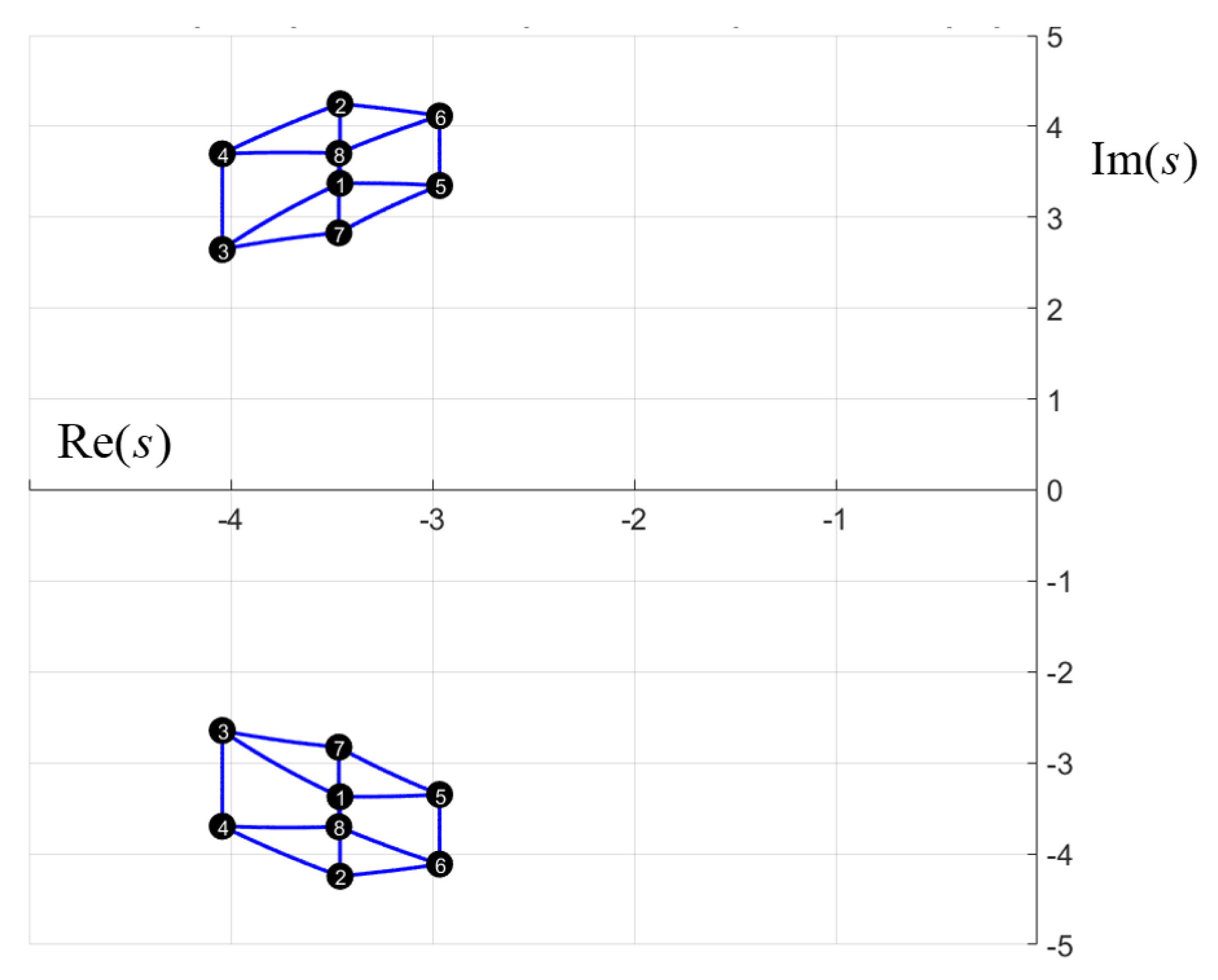
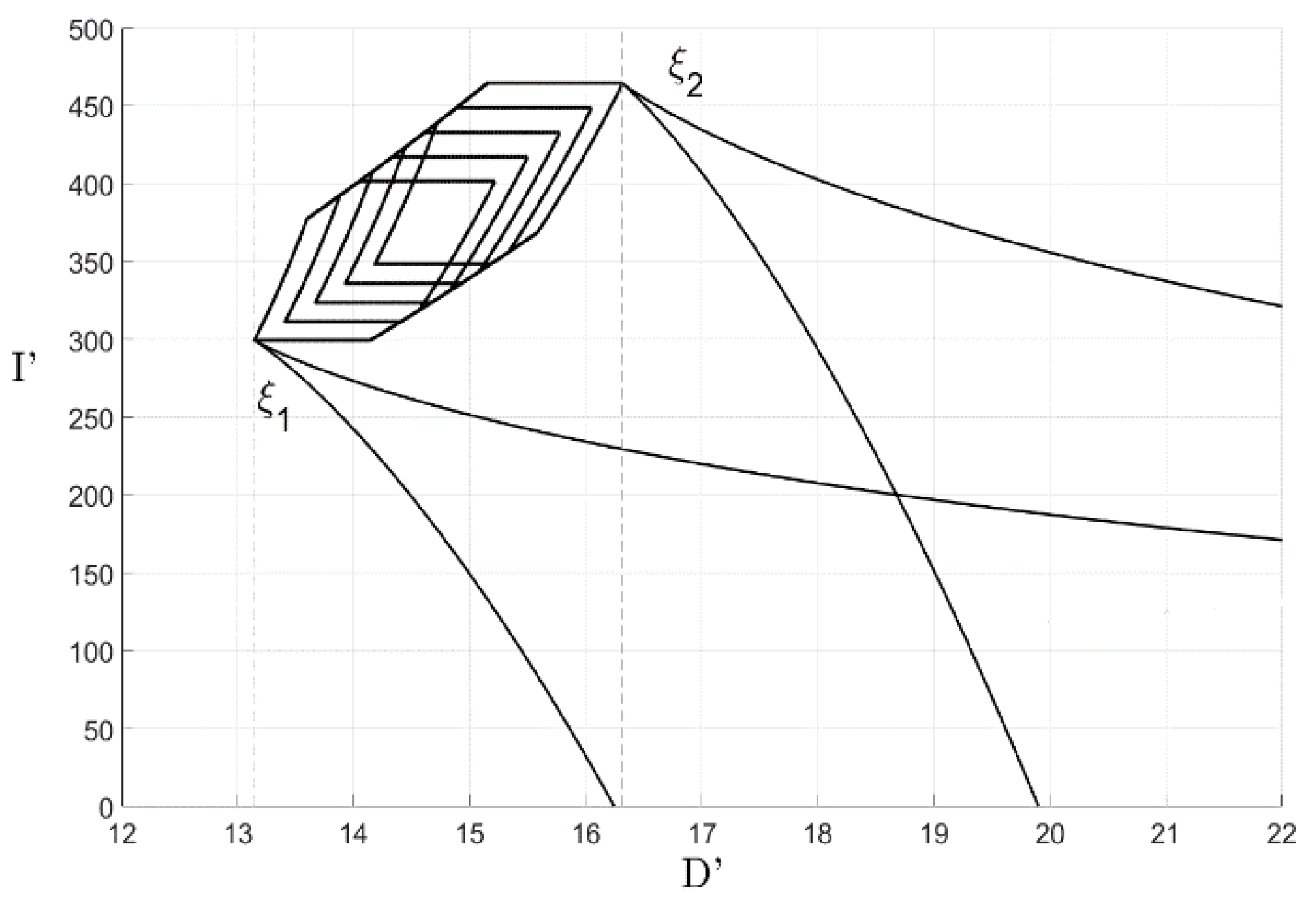
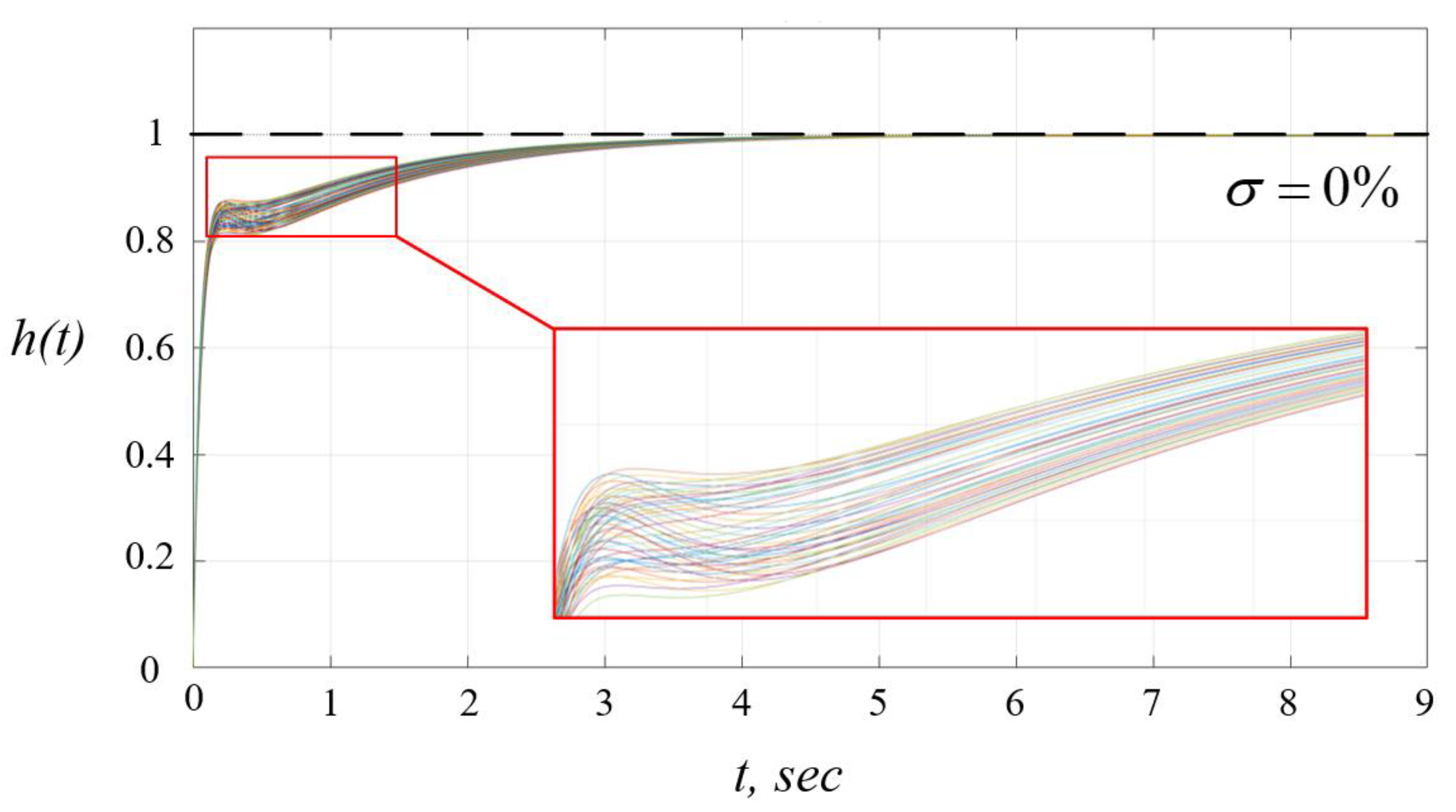
3. Example
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moore, K.L.; Bhattacharyya, S.P. A technique for choosing zero locations for minimal overshoot. IEEE Trans. Autom. Control 1990, 35, 577–580. [Google Scholar] [CrossRef]
- Efimov, S.V.; Kurgankin, V.V.; Zamyatin, S.V. Designing transfer function with the required direct performance measures based on the Laplace transform. Optoelectron. Instrum. Data Process. 2014, 50, 348–353. [Google Scholar] [CrossRef]
- Hauksdottir, A.S. A sufficient and necessary condition for extrema-free step responses of single-zero continuous-time systems with real poles. In Proceedings of the 38 Conference on Decision & Control, Phoenix, AZ, USA, 7–10 December 1999; pp. 499–500. [Google Scholar]
- Hauksdottir, A.S. Analytic Expression of Transfer Function Reponses and Choice Numerator Coefficients (Zeros). IEEE Trans. Autom. Control 1996, 41, 1482–1488. [Google Scholar] [CrossRef]
- Hauksdottir, A.S.; Hjaltadottir, H. Closed-form expressions of transfer function responses. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 3234–3239. [Google Scholar]
- Herjolfsson, G.; Hauksdottir, A.S. Direct computation of optimal PID controllers. In Proceedings of the 42nd IEEE Conference on Decision and Control, Maui, HI, USA, 9–12 December 2003; pp. 1120–1225. [Google Scholar]
- Jayasuriya, S.; Dharne, A.G. Necessary and sufficient conditions for non-overshooting step responses for LTI systems. In Proceedings of the 2002 American Control Conference, Anchorage, AK, USA, 8–10 May 2002; pp. 500–510. [Google Scholar]
- Nguyen, N.H.; Nguyen, P.D. Overshoot and settling time assignment with PID for first-order and second-order systems. IET Control Theory Appl. 2018, 12, 2407–2416. [Google Scholar] [CrossRef]
- Prakash, R.; Anburaja, S.A.; Rishivanth, S.; Govinda Kumar, E. Non-overshoot time response of third order system using cascade PID-Lead compensator controller. In Proceedings of the 2017 Second International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, Tamil Nadu, India, 22–24 February 2017; pp. 1–6. [Google Scholar]
- Visioli, A. Practical PID Control, 1st ed.; Springer: London, UK, 2006; p. 314. [Google Scholar]
- Anbarasan, M.; Suji Prasad, S.J.; Meenakumari, R.; Balakrishnan, P.A. Modified PID controller for avoiding overshoot in temperature of barrel heating system. In Proceedings of the 2013 International Conference on Emerging Trends in VLSI, Embedded System, Nano Electronics and Telecommunication System (ICEVENT), Tiruvannamalai, Tamil Nadu, India, 7–9 January 2013; pp. 1–6. [Google Scholar]
- Souza, M.R.S.B.; Murofushi, R.H.; Tavares, J.J.P.Z.; Ribeiro, J.F. PID Tuning for the Pitch Angle of a Two-Wheeled Vehicle. In Proceedings of the 2015 12th Latin American Robotics Symposium and 2015 3rd Brazilian Symposium on Robotics (LARS-SBR), Uberlândia, Brazil, 28 October–1 November 2015; pp. 371–375. [Google Scholar]
- Wu, H.; Su, W.; Liu, Z. PID controllers: Design and tuning methods. In Proceedings of the 2014 9th IEEE Conference on Industrial Electronics and Applications (ICIEA), Hangzhou, China, 9–11 June 2014; pp. 808–813. [Google Scholar]
- Kobayashi, H. Output overshoot and pole-zero configuration. In Proceedings of the 12th IFAC World Congress Automat. Contr., IFAC, Sydney, Australia, 18–23 July 1993; pp. 529–532. [Google Scholar]
- Lin, S.K.; Fang, C.J. Nonovershooting and monotone nondecreasing step responses of a third-order SISO linear system. IEEE Trans. Autom. Control 1997, 42, 1299–1303. [Google Scholar]
- Zhmud, V.; Yadrishnikov, O.; Poloshchuk, A.; Zavorin, A.A. Modern key technologies in automatics: Structures and numerical optimization of regulators. In Proceedings of the 2012 7th International Forum on Strategic Technology (IFOST), Tomsk, Russia, 18–21 September 2012. [Google Scholar]
- Prokopiev, A.P.; Ivanchura, V.I.; Emelyanov, R.T. Synthesis PID Controller for Objects Second Order with Regard to the Location Poles. J. Sib. Fed. Univ. Eng. Technol. 2016, 1, 50–60. [Google Scholar] [CrossRef]
- Nesenchuk, A.A. A method for synthesis of robust interval polynomials using the extended root locus. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 1715–1720. [Google Scholar]
- Sukhodoev, M.S.; Gayvoronskiy, S.A.; Zamyatin, S.V. Parametric synthesis of linear regulator in interval system with guaranteed root quality indices. Bull. Tomsk Polytech. Univ. 2007, 311, 9–12. [Google Scholar]
- Ouyang, H.; Yue, J.; Su, Y. Design and Application of PID Controllers Based on Interval Computing Theory. In Proceedings of the 2011 International Conference on Electrical and Control Engineering, Yichang, China, 16–18 September 2011; pp. 1505–1510. [Google Scholar]
- Chapellat, H.; Bhattacharyya, S.P. A generalization of Kharitonov’s theorem; Robust stability of interval plants. IEEE Trans. Autom. Control 1989, 34, 306–311. [Google Scholar] [CrossRef]
- Zhmud, V.; Zavorin, A. The design of the control system for object with delay and interval-given parameters. In Proceedings of the 2015 International Siberian Conference on Control and Communications (SIBCON), Omsk, Russia, 21–23 May 2015. [Google Scholar]
- Marcillo, K.E.L.; Guingla, D.A.P.; Barra, W.; De Medeiros, R.L.P.; Rocha, E.M.; Benavides, D.A.V.; Nogueira, F.G. Interval robust controller to minimize oscillations effects caused by constant power load in a DC multi-converter buck-buck system. IEEE Access 2019, 7, 26324–26342. [Google Scholar] [CrossRef]
- Marcillo, K.E.L.; Rocha, E.M.; Junior, W.B.; Benavides, D.A.V.; de Medeiros, R.L.P.; Alves, M.S.; Leão, M.P.V. Robust control for DC–DC buck converter under parametric uncertainties. In Proceedings of the 22nd Congresso Brasileiro de Automatica (CBA), Paraiba, Brazil, 9–12 September 2018; pp. 1–8. [Google Scholar]
- Tsavnin, A.V.; Efimov, S.V.; Zamyatin, S.V. Providing real closed-loop transfer functions poles for plant with interval-given parameters for overshoot elimination. In Proceedings of the 11th International Congress on Ultra Modern Telecommunications and Control Systems and Workshops (ICUMT), Dublin, Ireland, 28–30 October 2019; pp. 1–7. [Google Scholar]
- Andrakhanov, A.; Belyaev, A. Navigation learning system for mobile robot in heterogeneous environment: Inductive modeling approach. In Proceedings of the 12th International Scientific and Technical Conference on Computer Sciences and Information Technologies (CSIT 2017), Lviv, Ukraine, 5–8 September 2017; pp. 543–548. [Google Scholar]
- Andrakhanov, A.; Belyaev, A. GMDH-Based Learning System for Mobile Robot Navigation in Heterogeneous Environment. In Advances in Intelligent Systems and Computing; Shakhovska, N., Stepashko, V., Eds.; Springer: Cham, Switzerland, 2018; Volume 689, pp. 1–20. [Google Scholar]
- Fadeev, A.S.; Zarnitsyn, A.Y.; Tsavnin, A.V.; Belyaev, A.S. Cyber-physical system prototype development for control of mobile robots group for general mission accomplishment. In Proceedings of the Second International Conference on Material Science, Smart Structures and Applications: ICMSS-2019, Erode, India, 21–22 November 2019. [Google Scholar]
- Pushkarev, M.I.; Gaivoronsky, S.A.; Efimov, S.V.; Zamyatin, S.V. Parametric synthesis of maximum stability degree and specified accuracy linear automatic control system PI-controller. In Proceedings of the 18th International Conference on Soft Computing, MENDEL 2012, Brno, Czech Republic, 27–29 June 2012; pp. 344–349. [Google Scholar]
- Pushkarev, M.I.; Efimov, S.V.; Gayvoronsky, S.A.; Chenkova, O.A. A single-loop DC motor control system design with a desired aperiodic degree of stability. In Proceedings of the International Conference on Mechanical Engineering, Automation and Control Systems 2015 MEACS 2015, Tomsk Polytechnic University, Tomsk, Russian, 1–4 December 2015. [Google Scholar]
- Astrom, K.J.; Hagllund, T. PID Controllers Theory, Design and Tuning, 2nd ed.; Instrument Society of America: Pittsburgh, PA, USA, 1994. [Google Scholar]
- Barmish, B.R. New Tool for Robustness of Linear Systems; Macmillan Publishing Company: New York, NY, USA, 1994. [Google Scholar]
- Xiang, W.; Xiao, J. Stabilization of switched continuous-time systems with all modes unstable via dwell time switching. Automatica 2014, 3, 940–945. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsavnin, A.; Efimov, S.; Zamyatin, S. Overshoot Elimination for Control Systems with Parametric Uncertainty via a PID Controller. Symmetry 2020, 12, 1092. https://doi.org/10.3390/sym12071092
Tsavnin A, Efimov S, Zamyatin S. Overshoot Elimination for Control Systems with Parametric Uncertainty via a PID Controller. Symmetry. 2020; 12(7):1092. https://doi.org/10.3390/sym12071092
Chicago/Turabian StyleTsavnin, Alexey, Semen Efimov, and Sergey Zamyatin. 2020. "Overshoot Elimination for Control Systems with Parametric Uncertainty via a PID Controller" Symmetry 12, no. 7: 1092. https://doi.org/10.3390/sym12071092
APA StyleTsavnin, A., Efimov, S., & Zamyatin, S. (2020). Overshoot Elimination for Control Systems with Parametric Uncertainty via a PID Controller. Symmetry, 12(7), 1092. https://doi.org/10.3390/sym12071092




