Heat Transfer Improvement in a Double Backward-Facing Expanding Channel Using Different Working Fluids
Abstract
1. Introduction
2. Numerical Approach
2.1. Physical Model
2.2. Governing Equations
3. Grid Independence Study and Data Validation
4. Results and Discussion
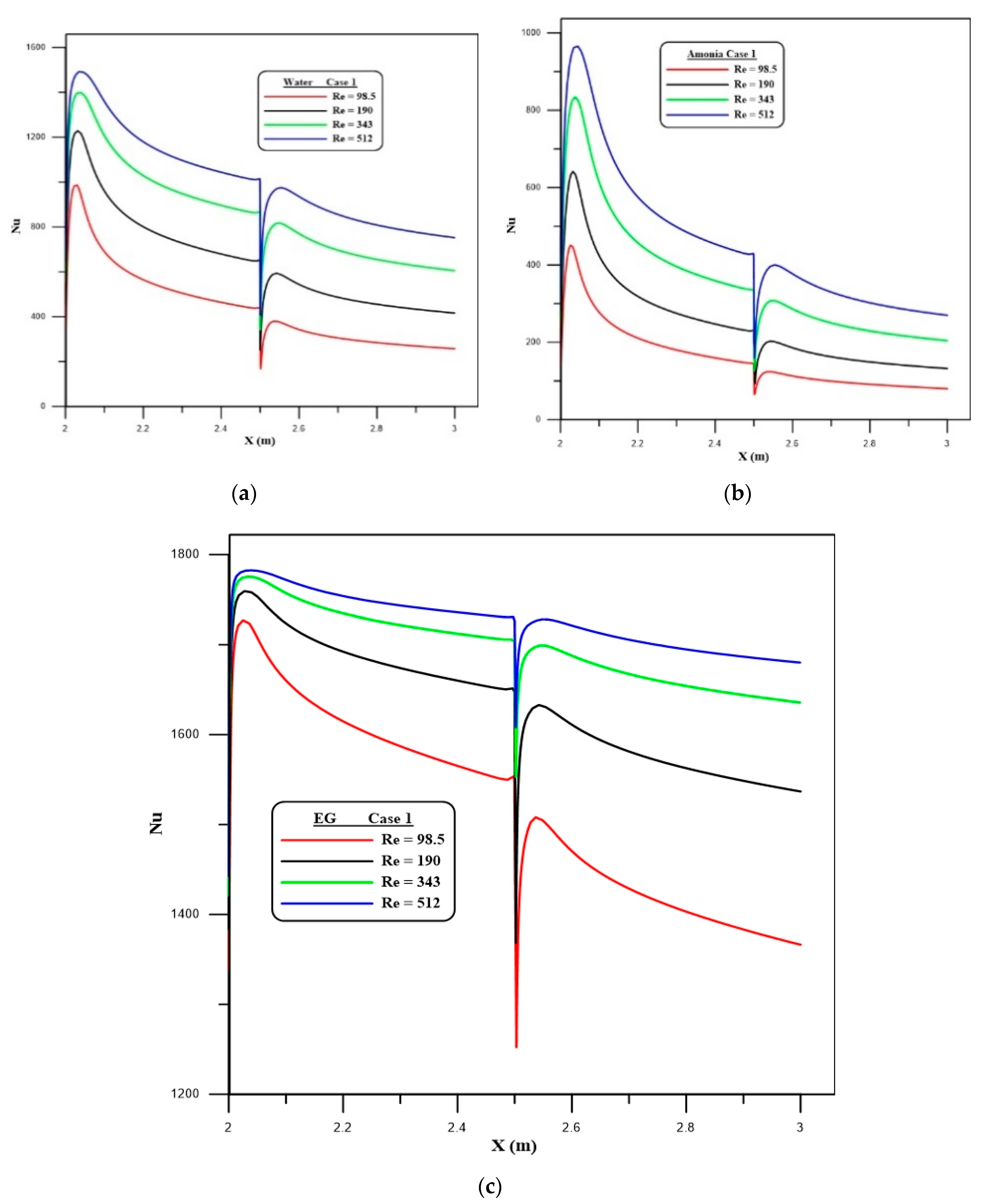
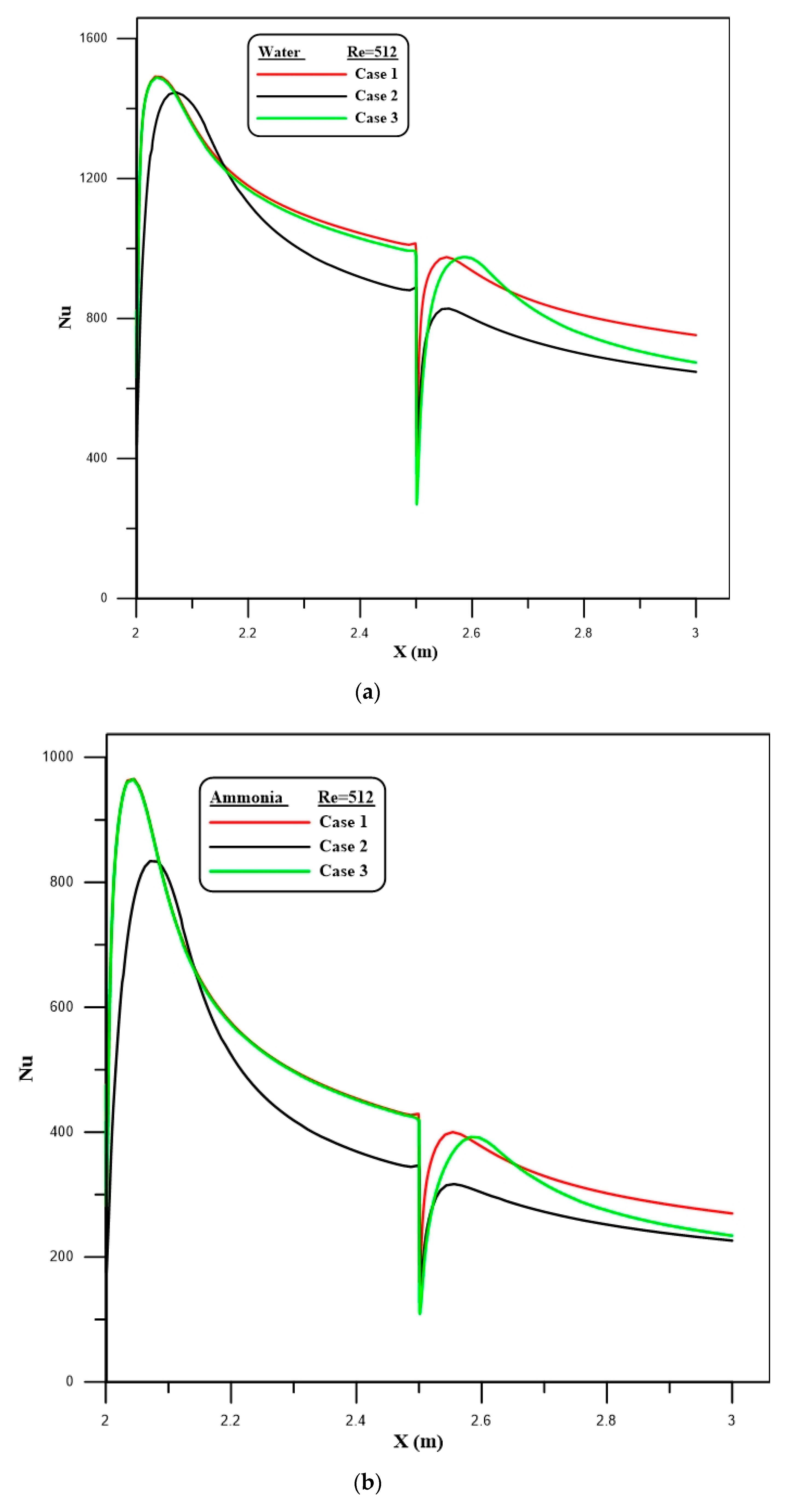
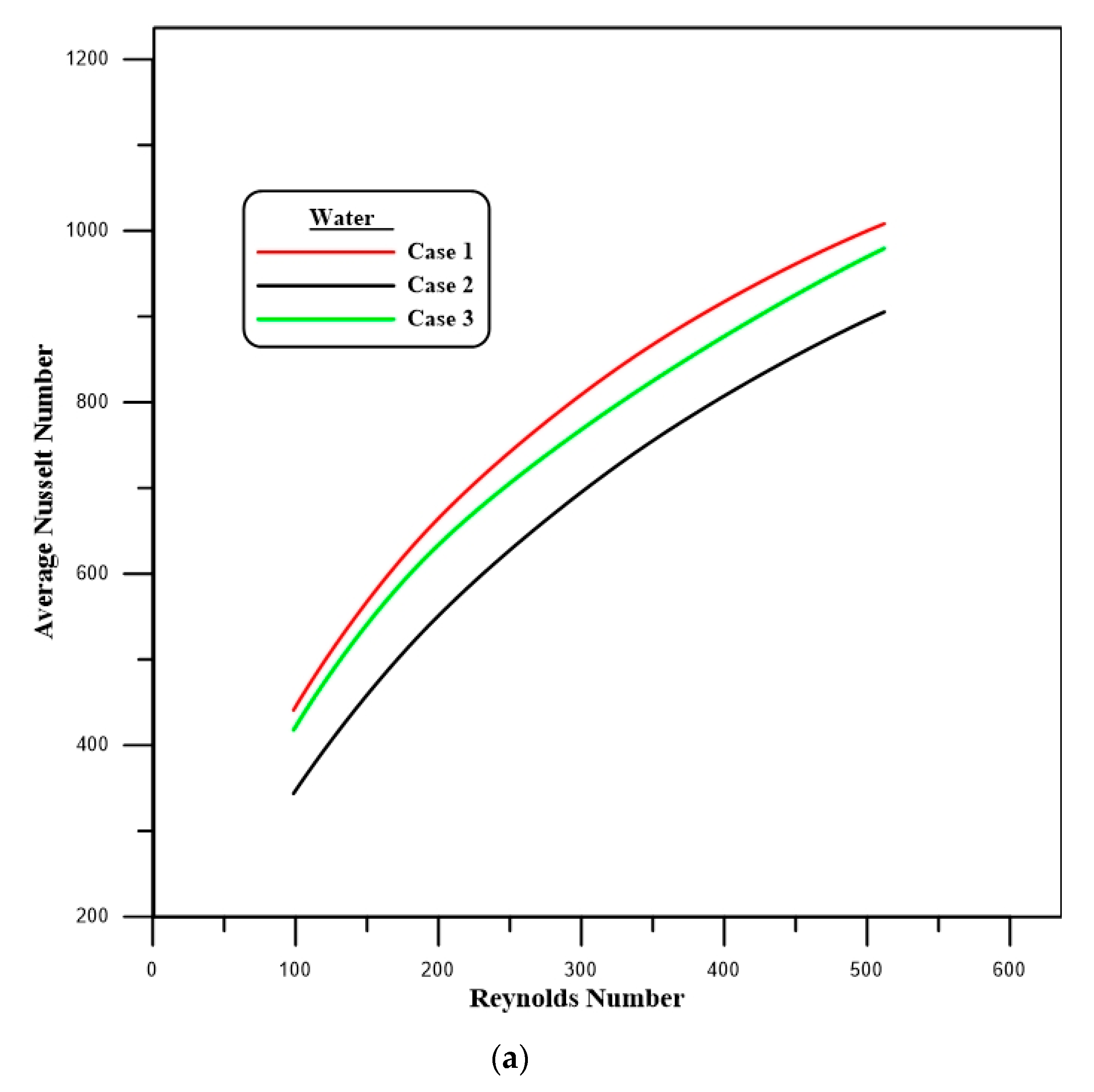
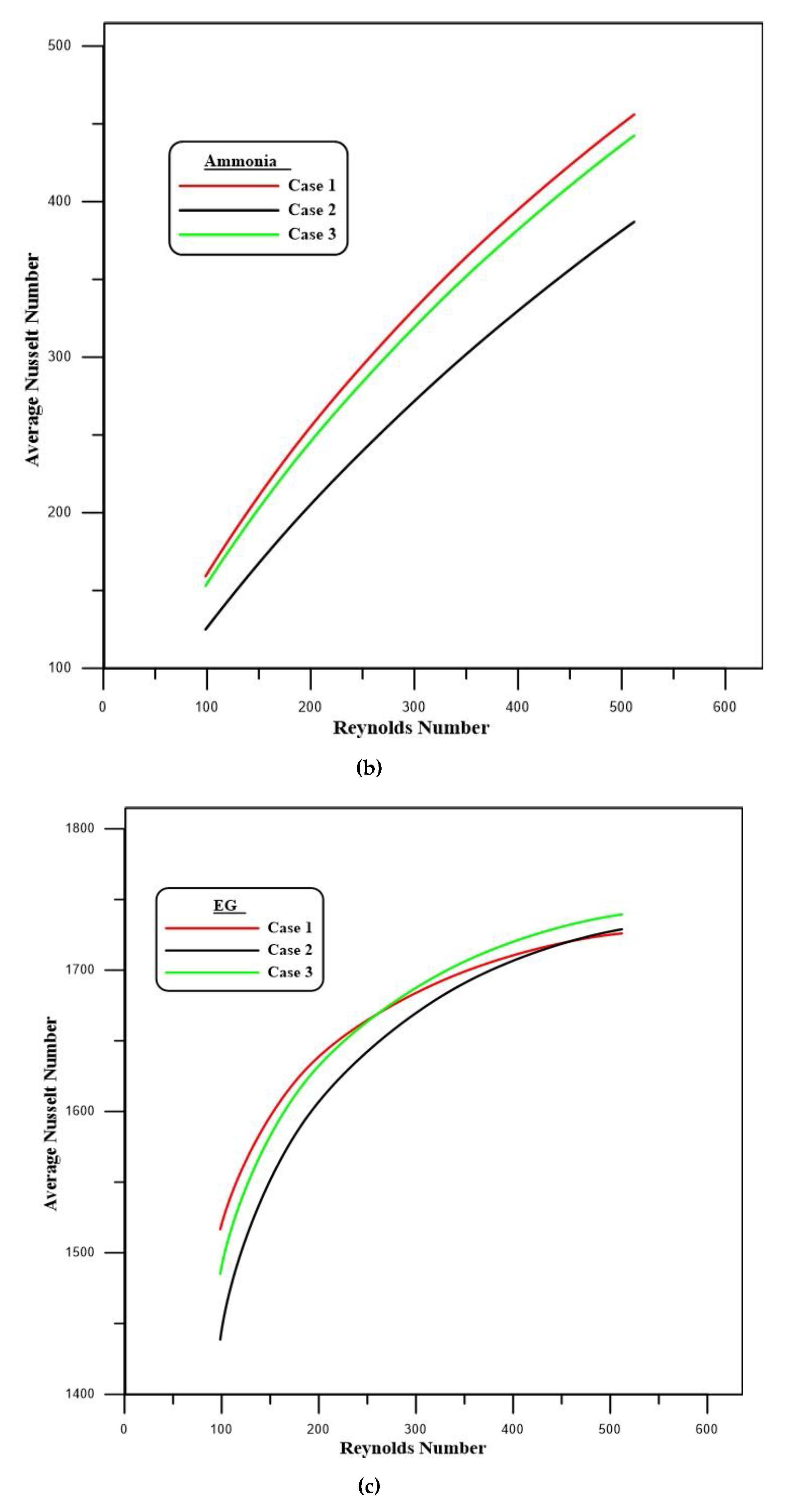
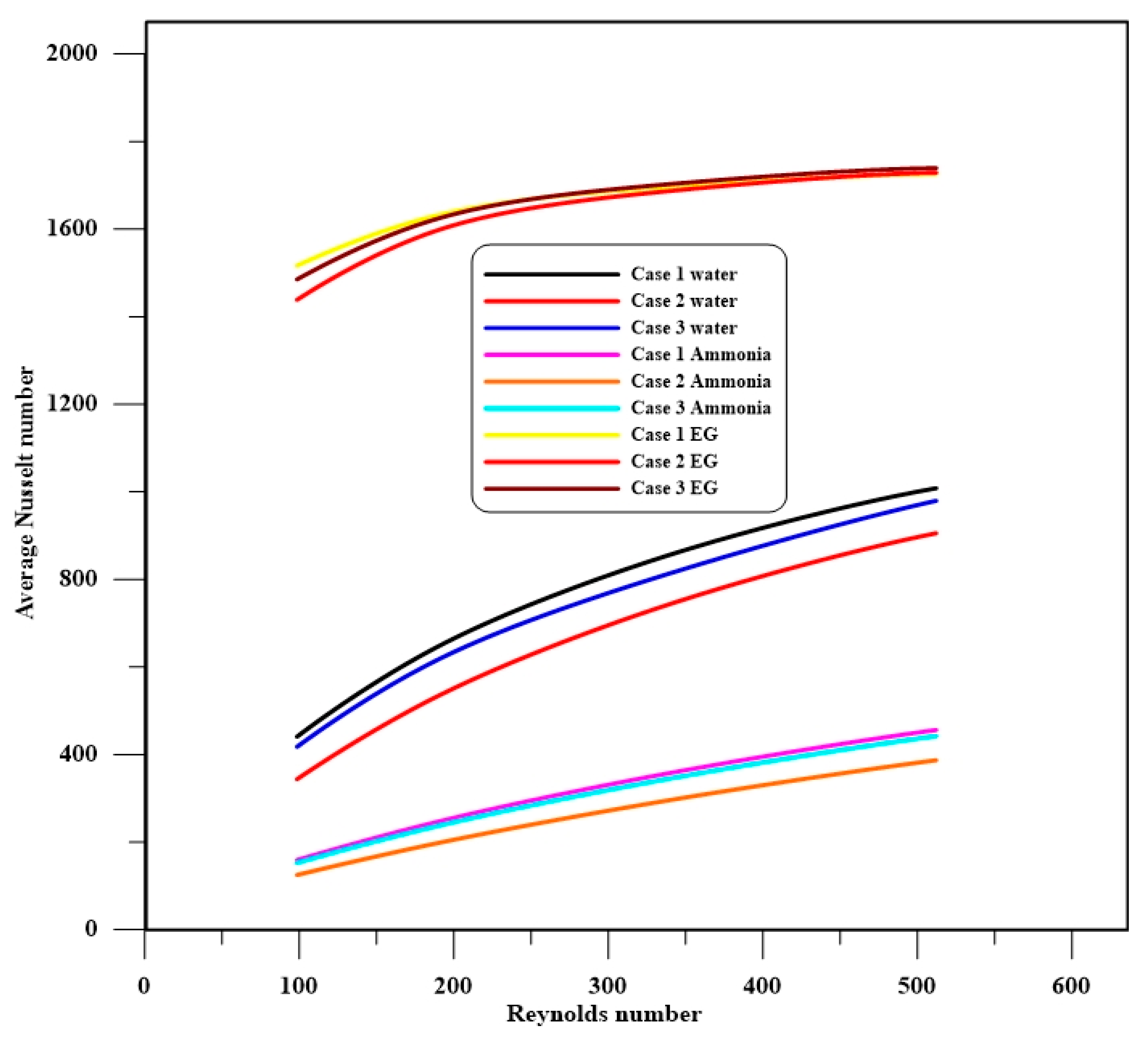
4.1. Nusselt Number
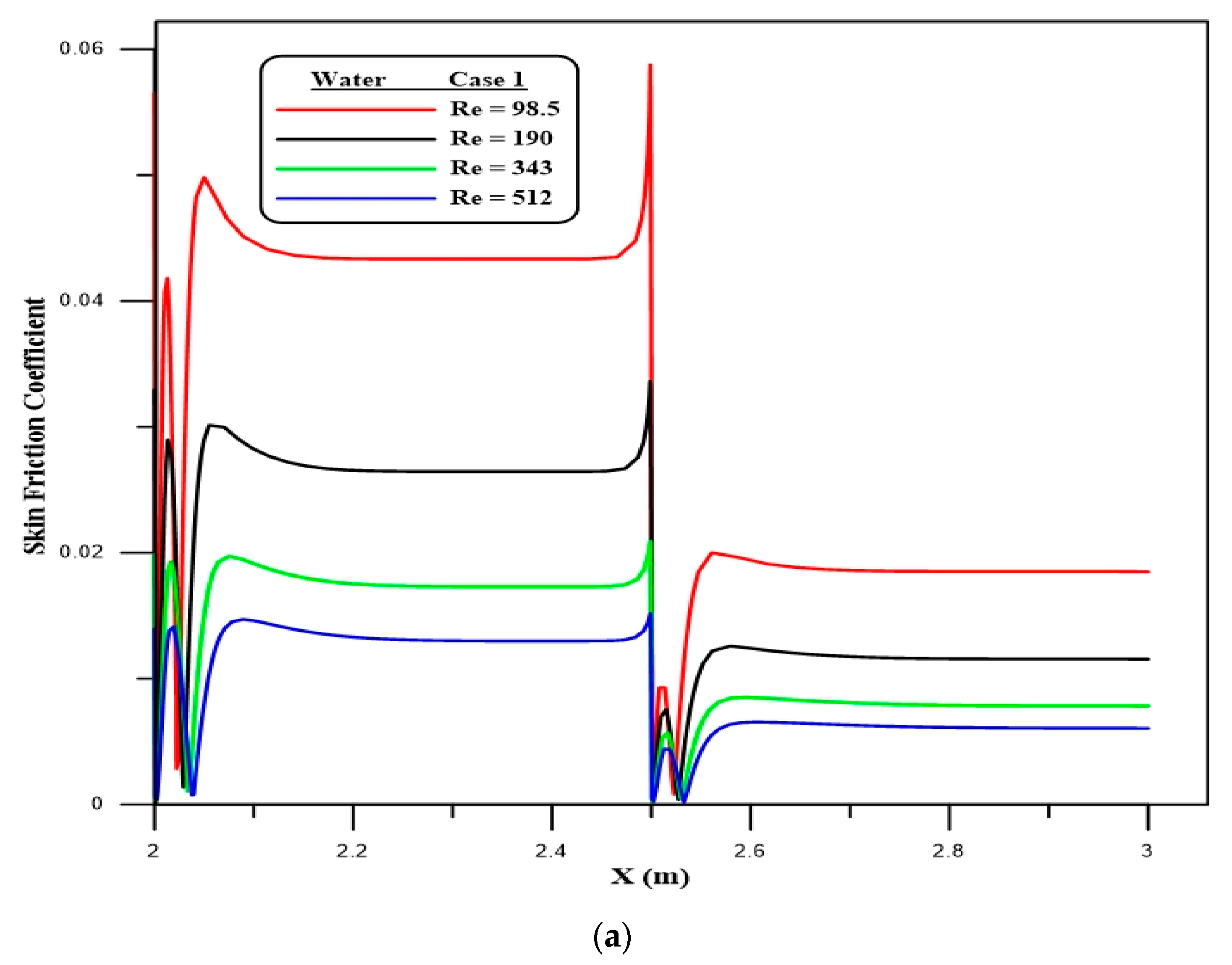
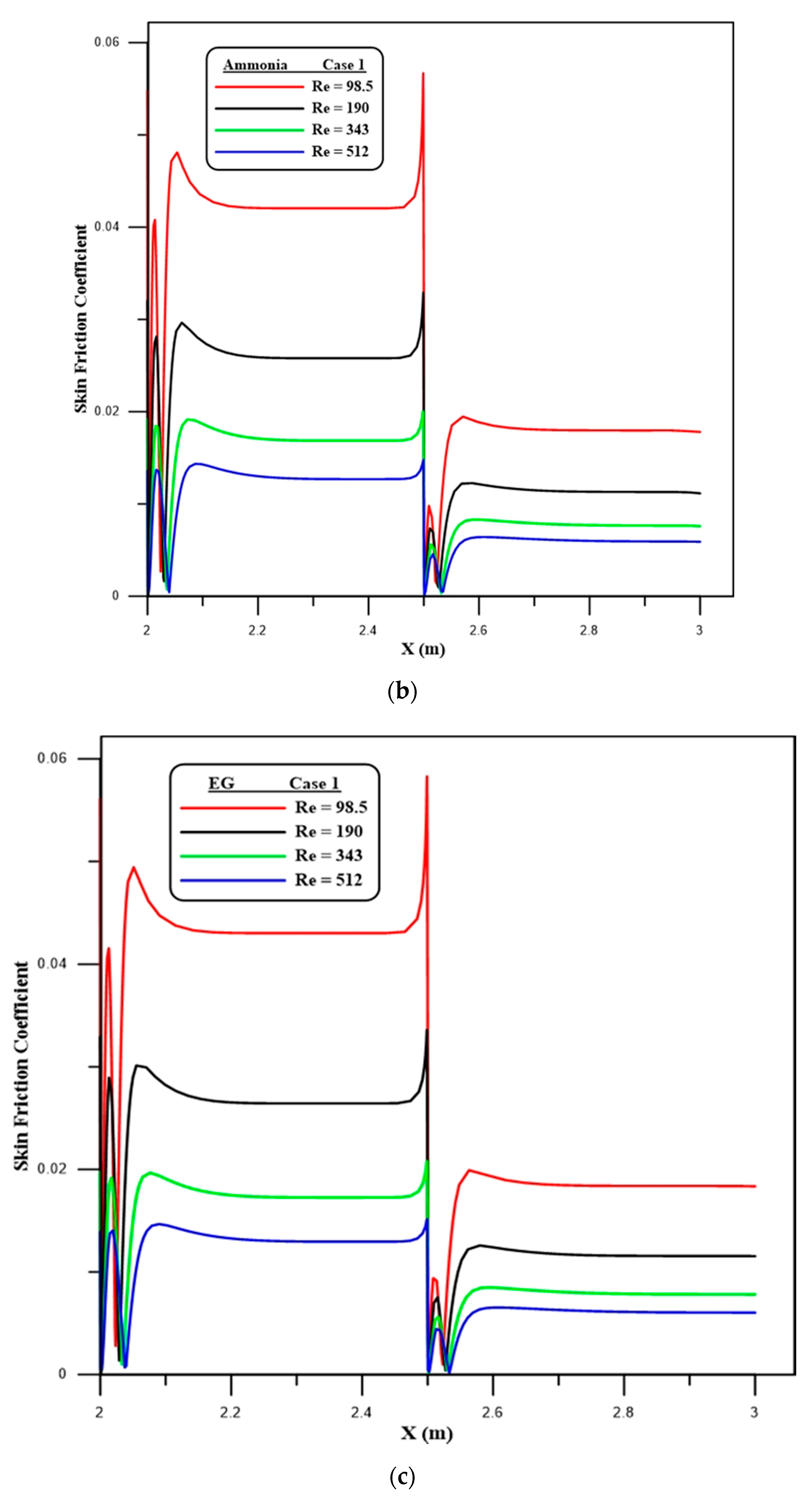
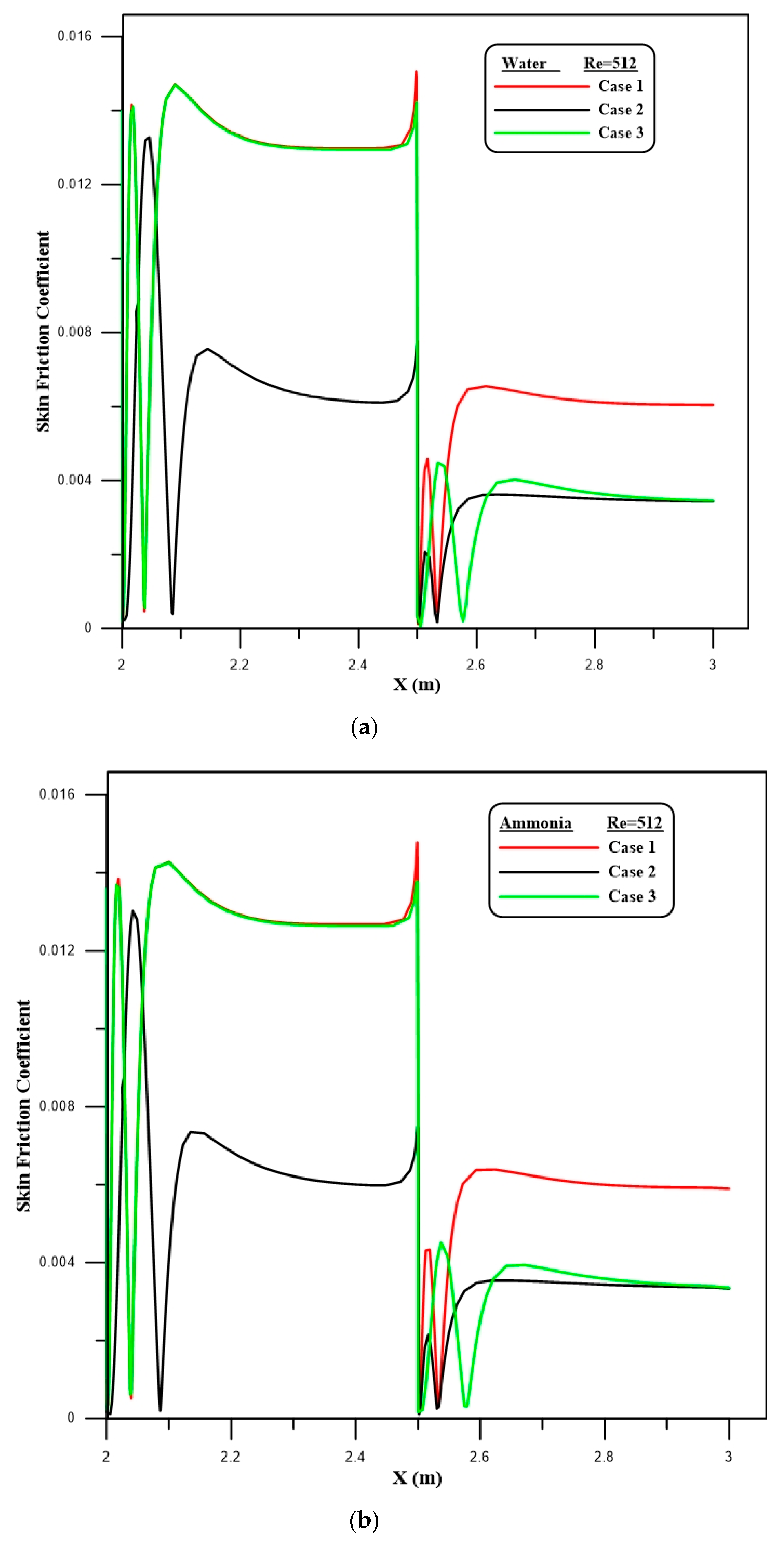
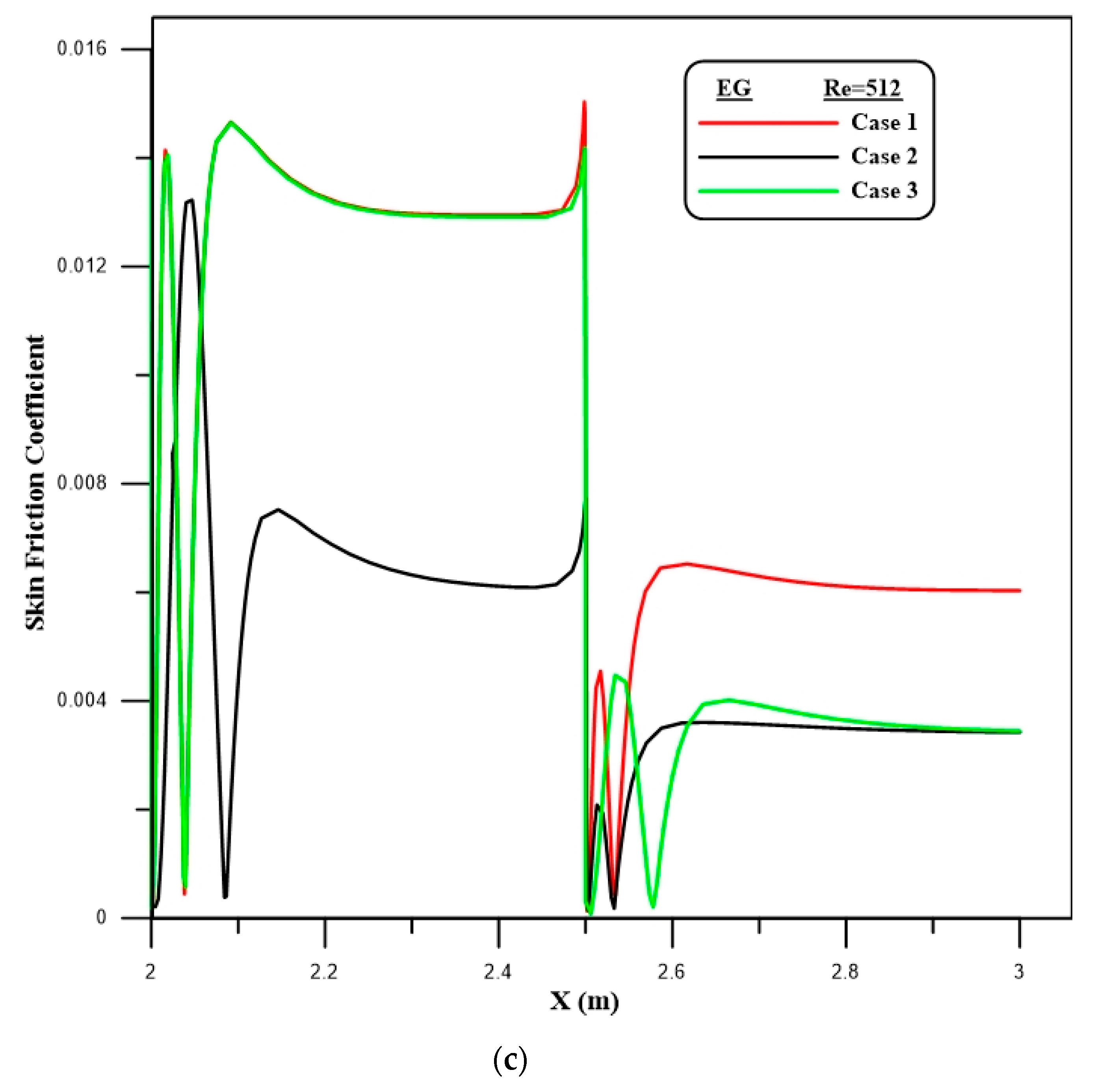
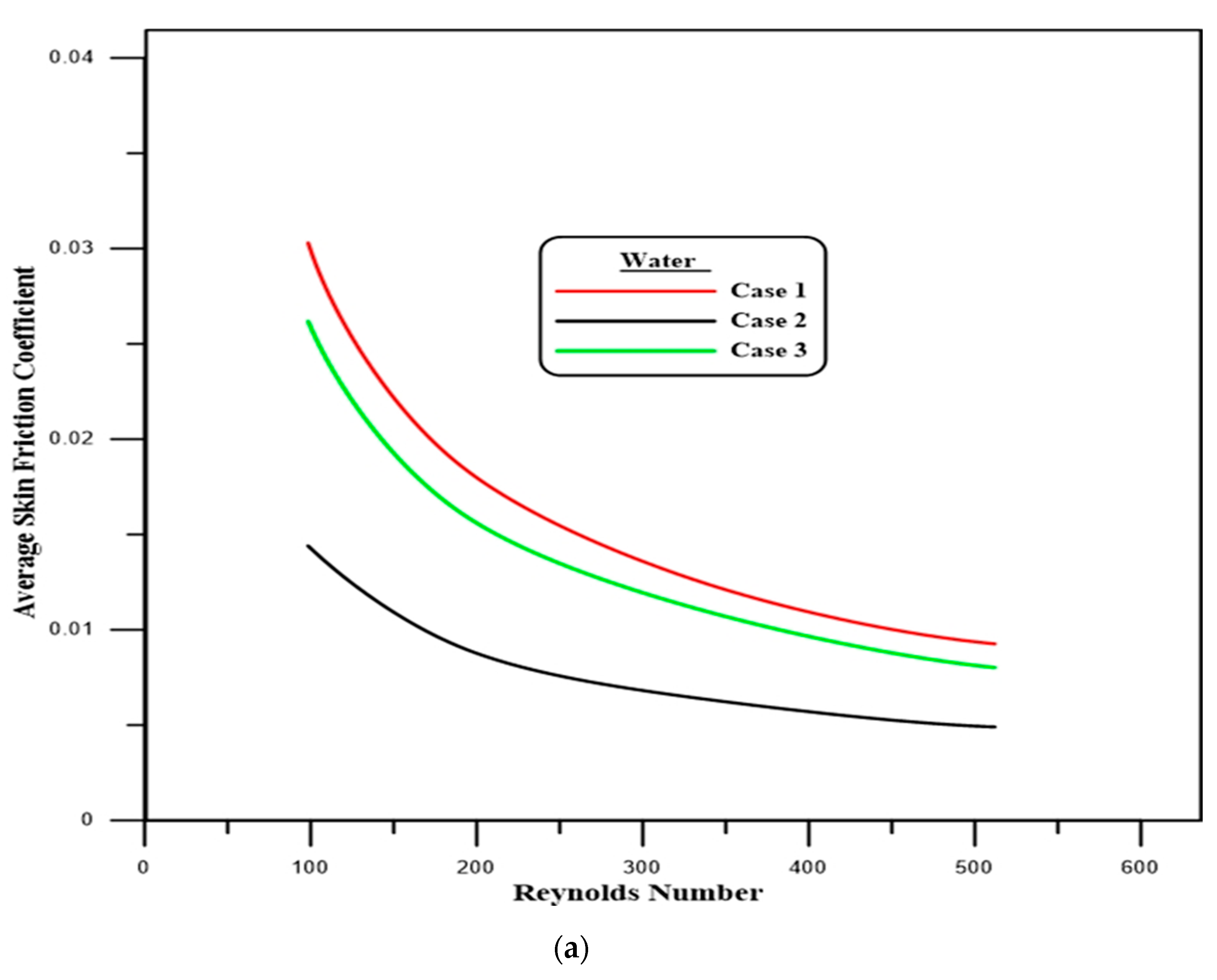
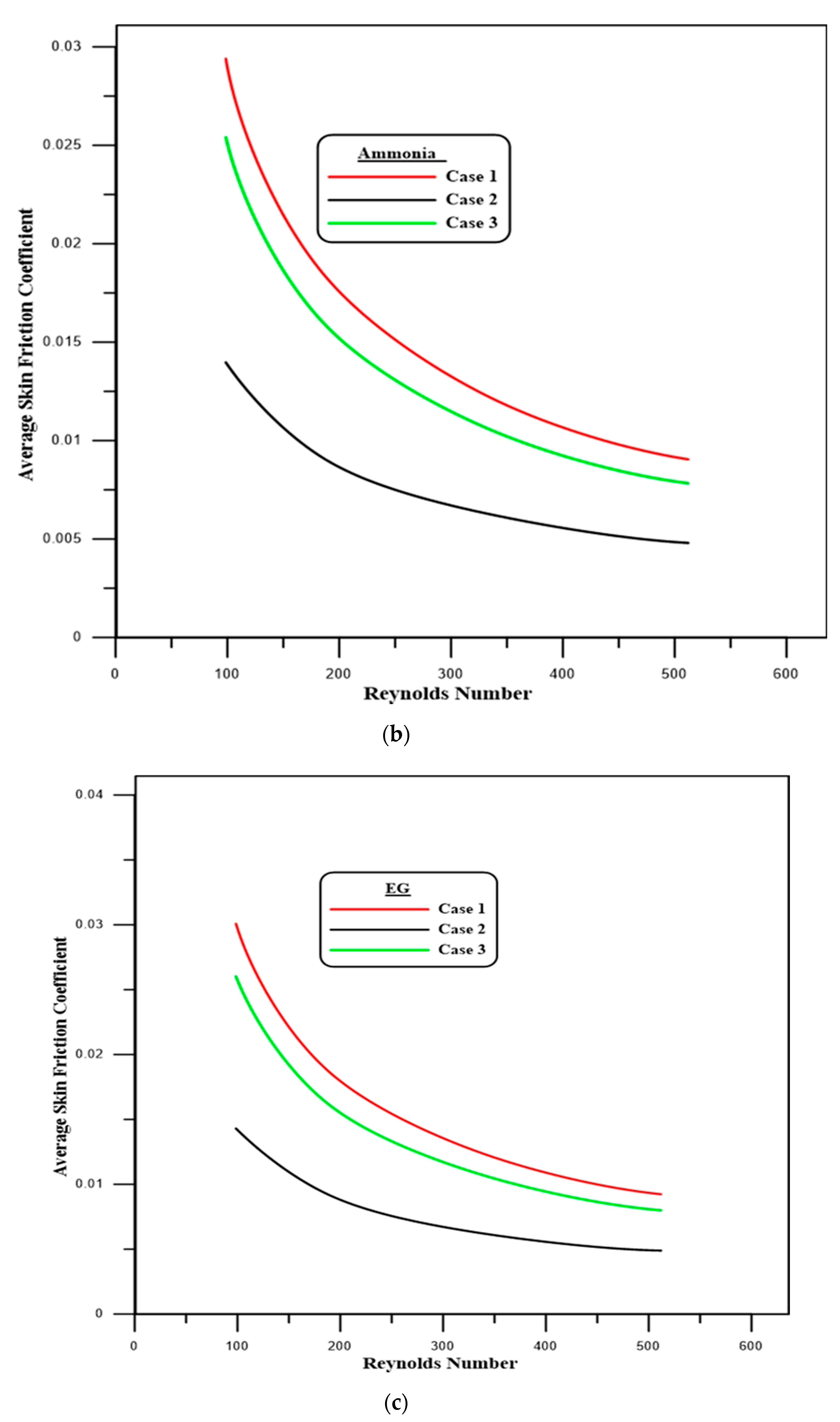
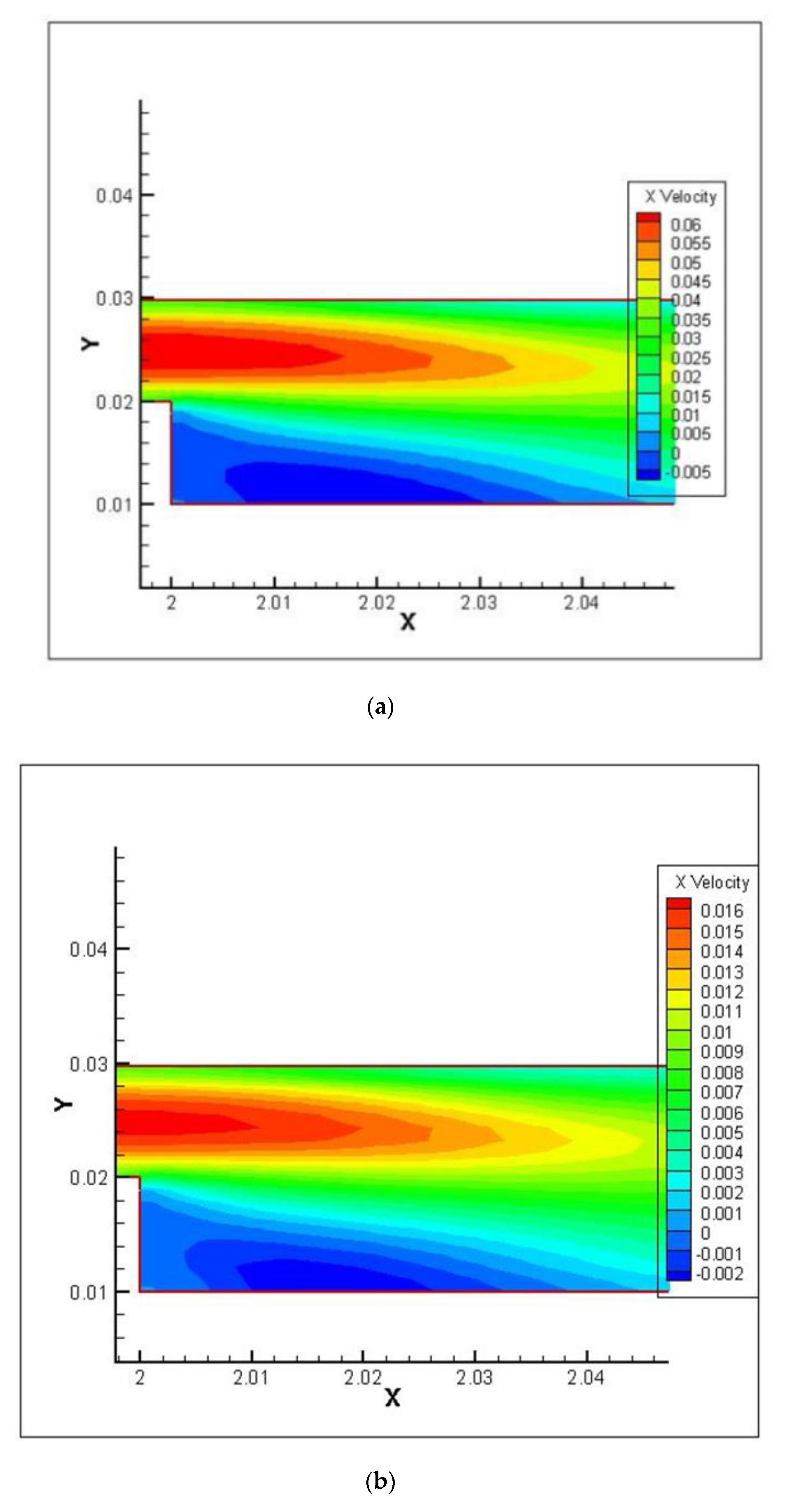
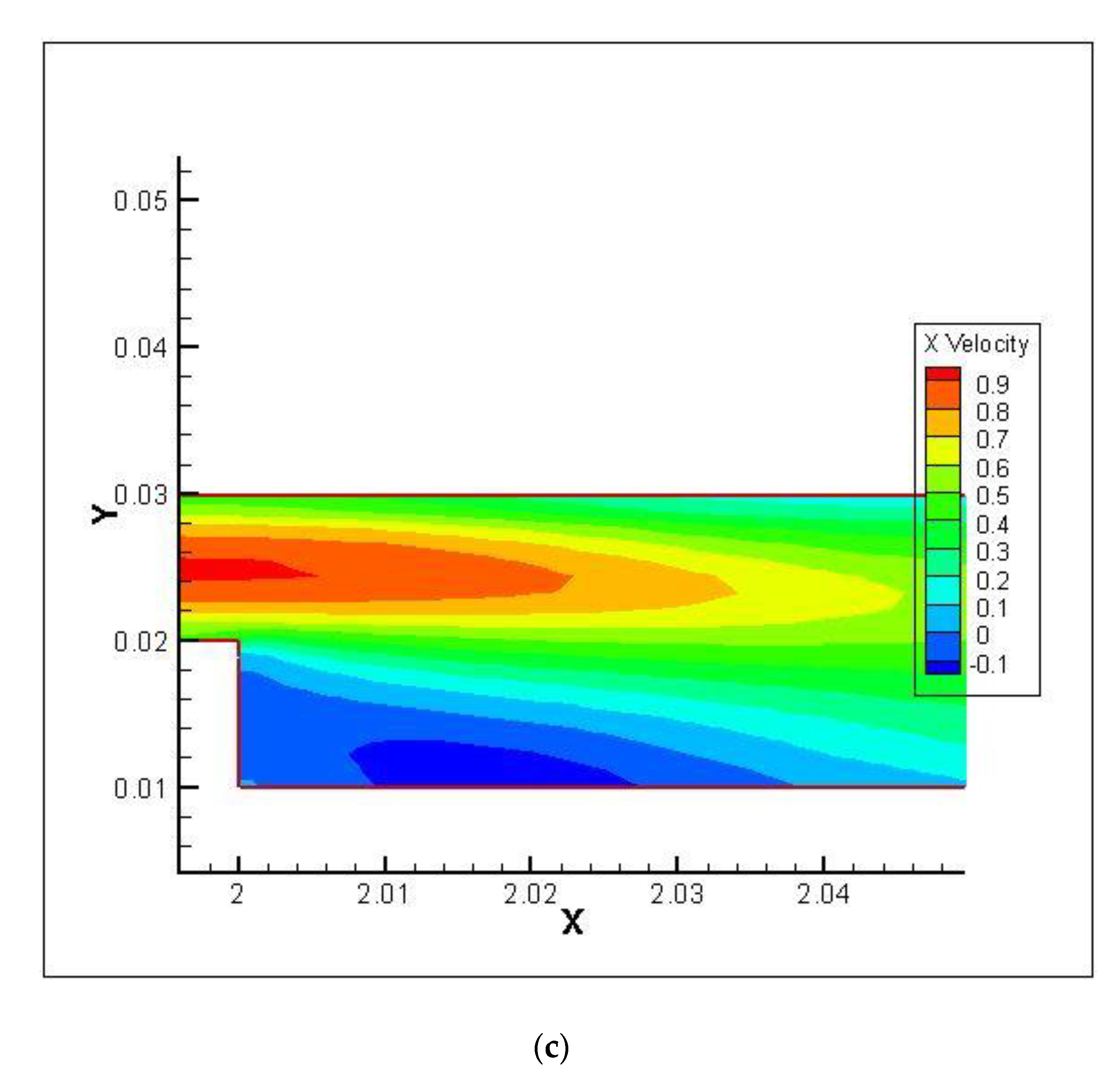
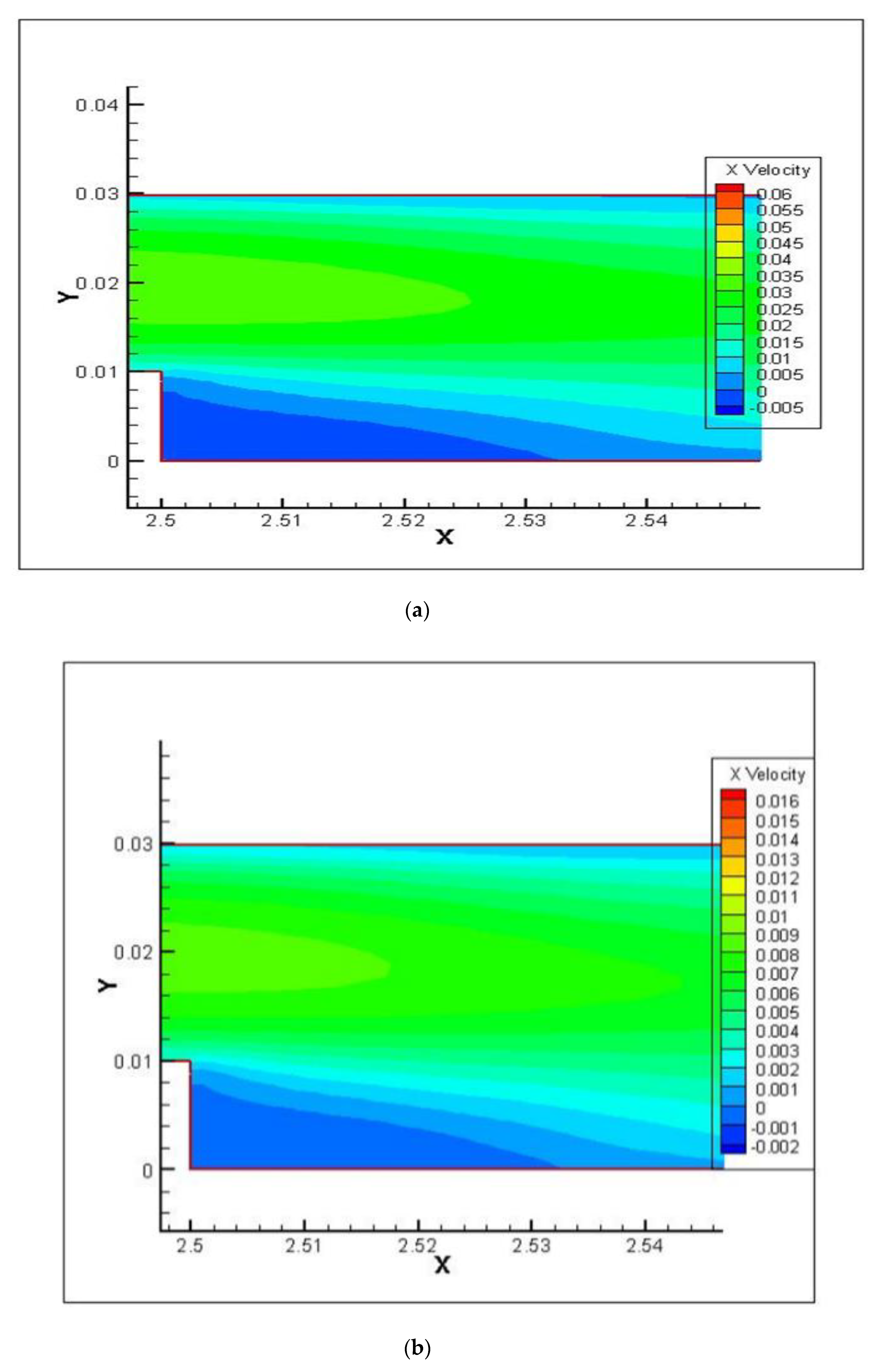
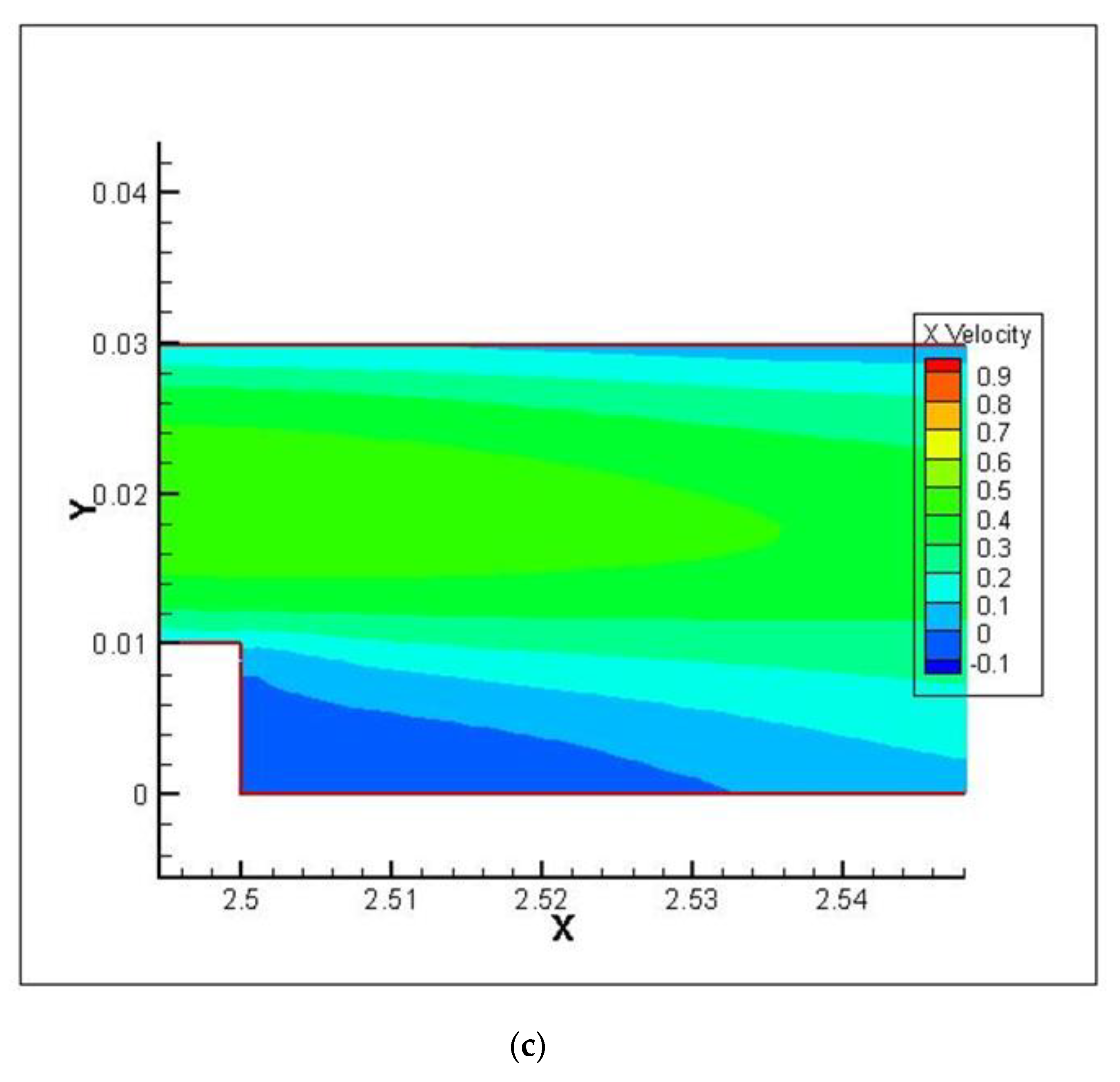
4.2. Flow Characteristics
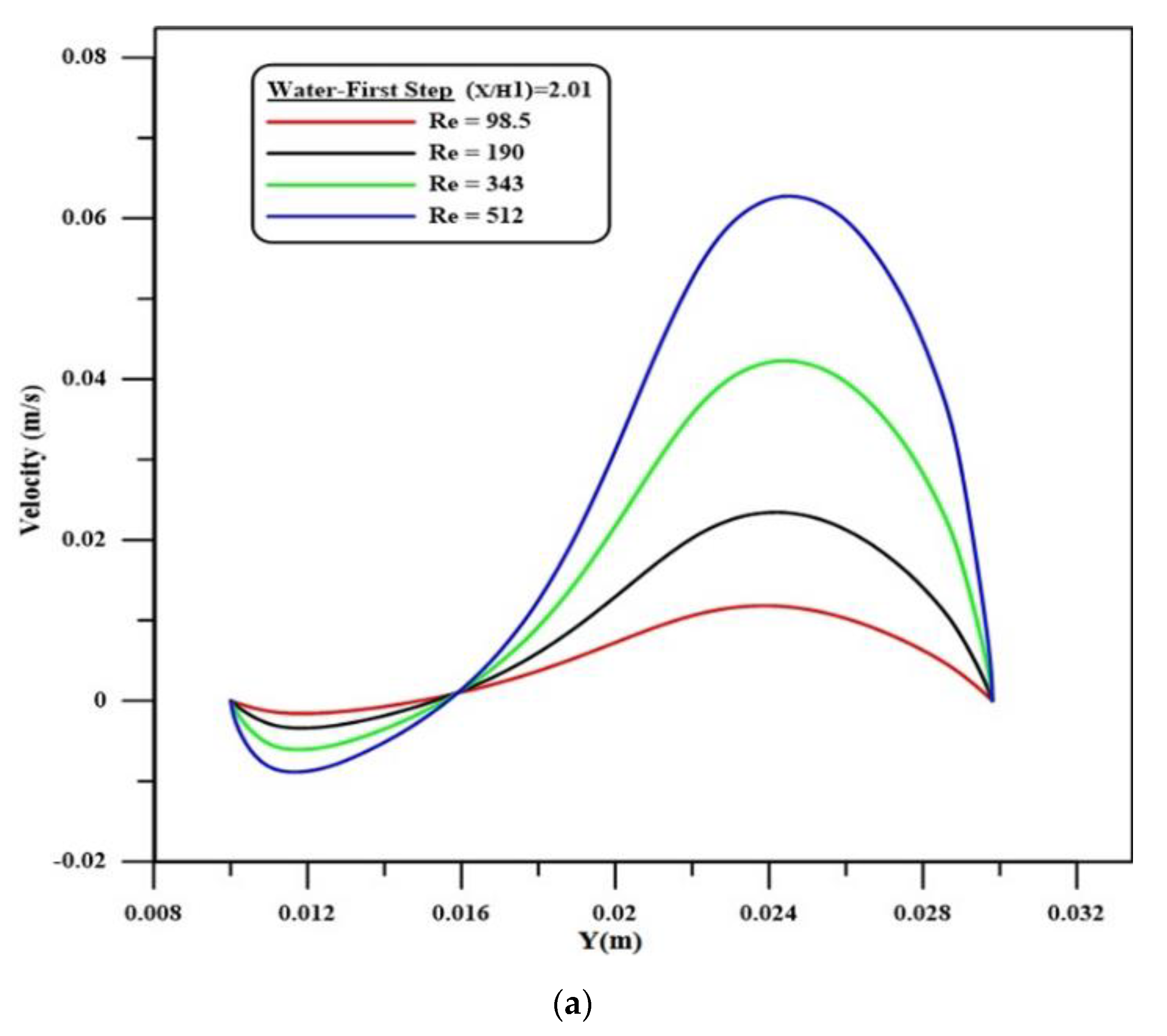
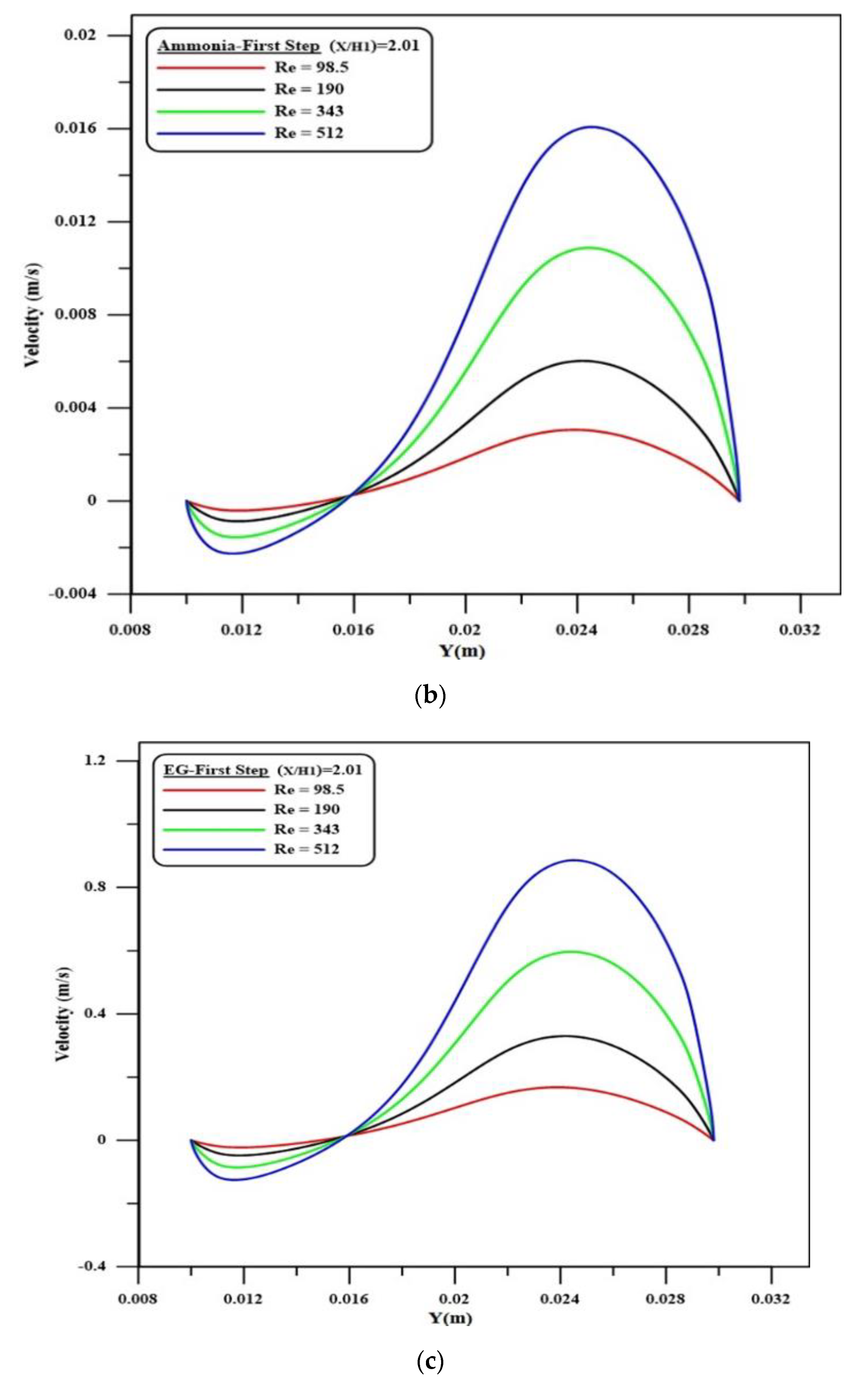
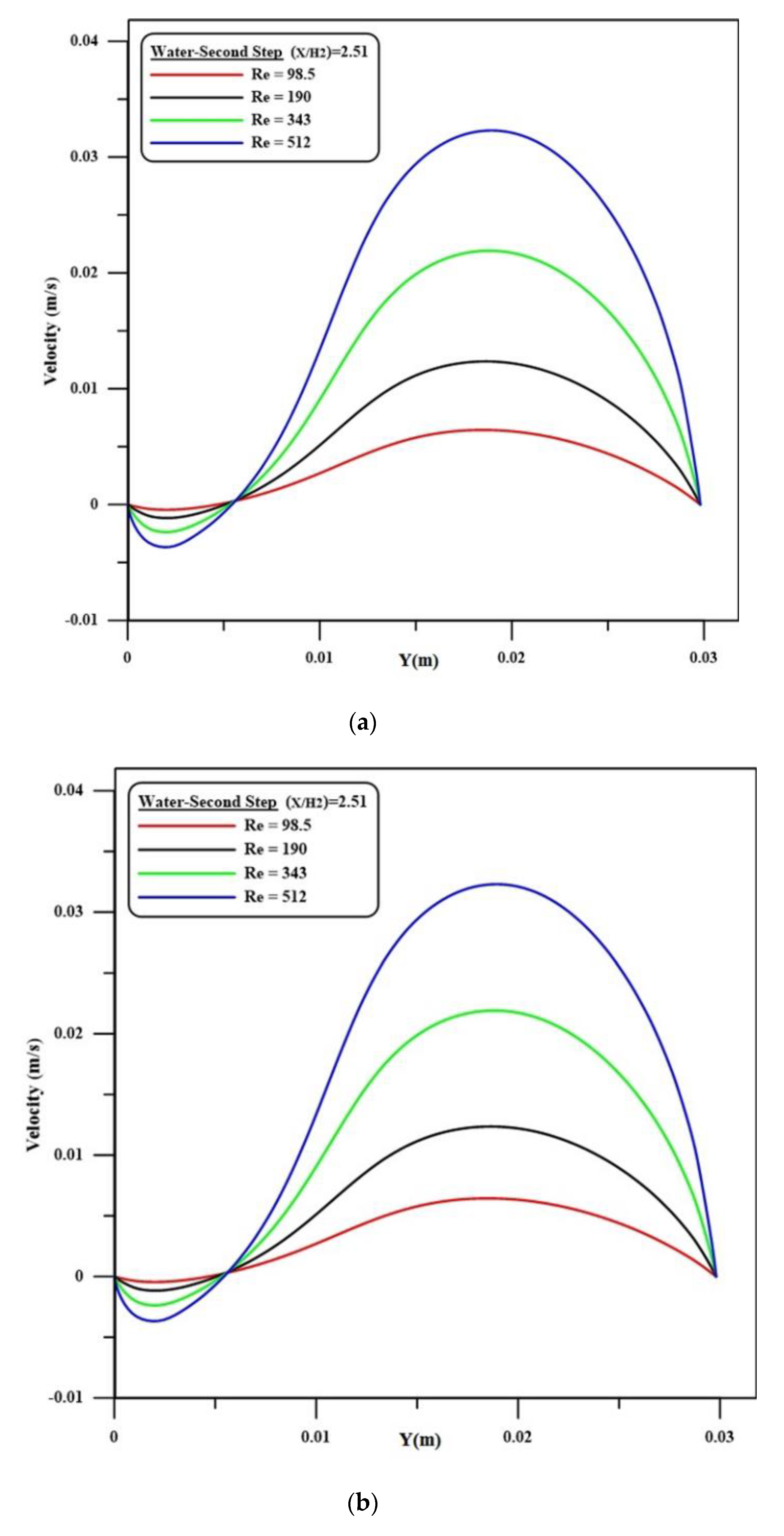
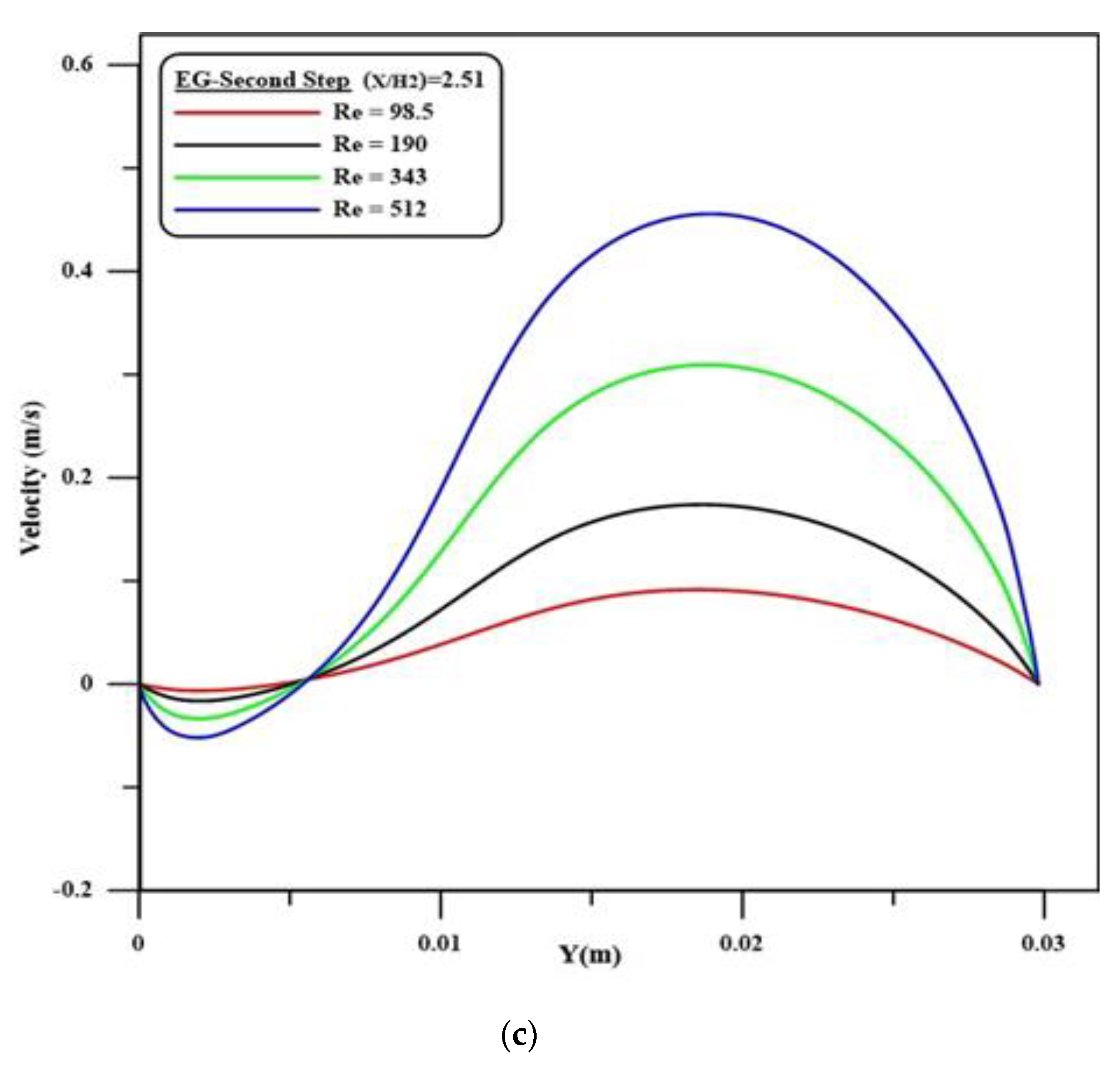
4.3. Velocity Profile
5. Conclusions
- An increase in the local Nusselt number is detected with rises in the Reynolds number, while the critical effects are seen at the start region of the first and second steps.
- The results show that higher local Nusselt numbers occur in cases 1 and 3, compared to case 2, for all types of fluids.
- The maximum average Nusselt number, which represents the thermal performance, can clearly be seen in case 1 for EG, in comparison to water and ammonia.
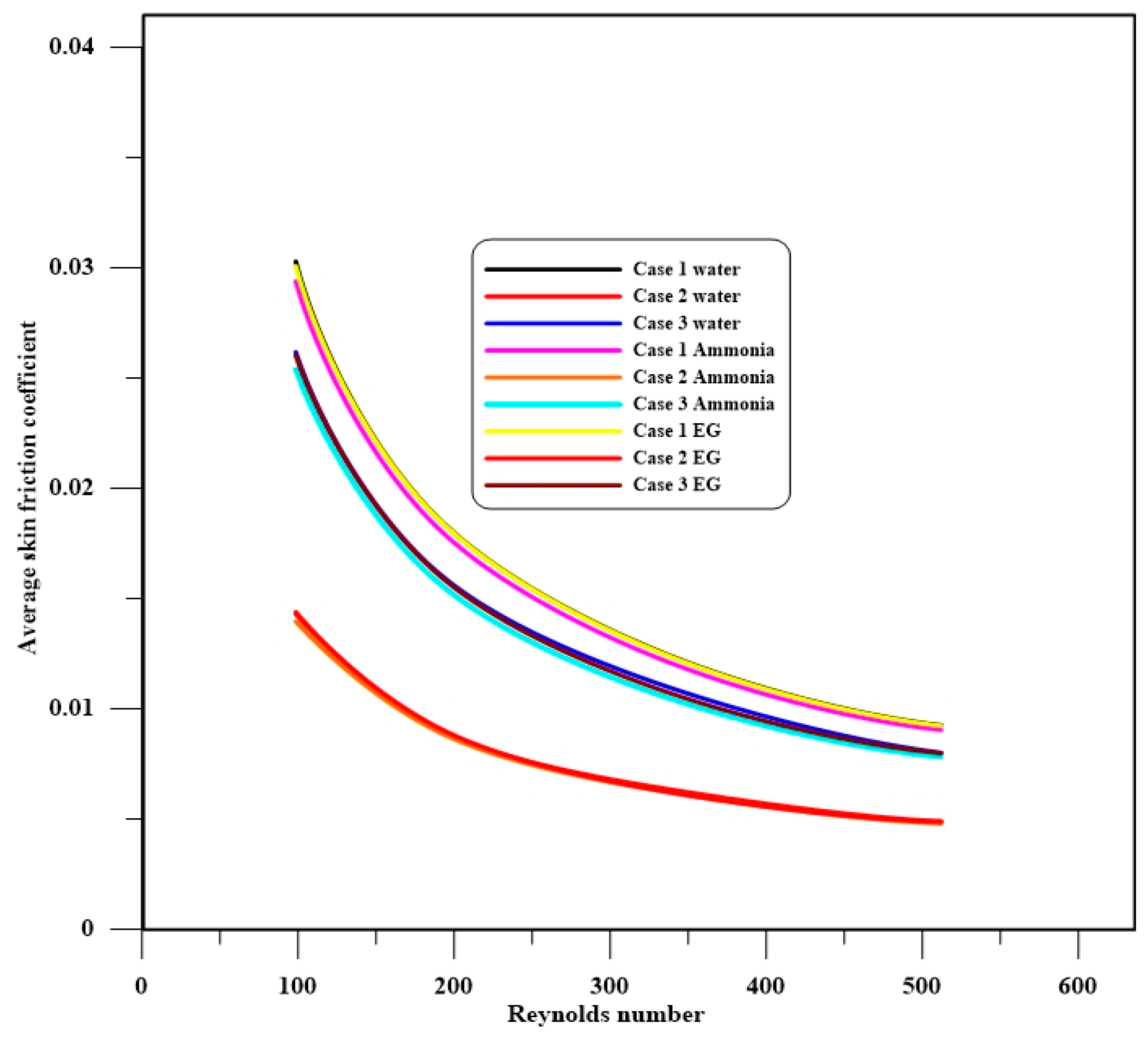
- A rise in the local skin friction coefficient is apparent at the first and second steps of the downstream section due to the expansion of the passage, which produces the separation flow.
- The velocity decreases rapidly at the first and second steps and then increases. This is due to the recirculation flow, which is generated at the zones after the first and second steps.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | Length of the bottom wall before the first step |
| B | Length of the bottom wall after the first step |
| C | Length of the bottom wall after the second step |
| Cp | Specific heat |
| H | Width of the channel at the entrance |
| H1 | The step height of the first step |
| H2 | The step height of the second step |
| L | The total length of the channel |
| Nu | Nusselt number |
| P | Pressure |
| Pr | Prandtl number |
| Re | Reynolds number |
| T | Temperature |
| u, v | Axial velocity |
| X, y | Cartesian coordinates |
| Greek symbols | |
| Ρ | Water density |
| µ | Dynamic viscosity |
References
- Abbott, D.E.; Kline, S.J. Experimental Investigation of Subsonic Turbulent Flow Over Single and Double Backward Facing Steps. J. Basic Eng. 1962, 84, 317–325. [Google Scholar] [CrossRef]
- Goldstein, R.J.; Eriksen, V.L.; Olson, R.M.; Eckert, E.R.G. Laminar Separation, Reattachment, and Transition of the Flow Over a Downstream-Facing Step. J. Basic Eng. 1970, 92, 732–739. [Google Scholar] [CrossRef]
- Armaly, B.F.; Durst, F.; Pereira, J.C.; Schönung, B. Experimental and theoretical investigation of backward-facing step flow. J. Fluid Mech. 1983, 127, 473. [Google Scholar] [CrossRef]
- Aung, W. An Experimental Study of Laminar Heat Transfer Downstream of Backsteps. J. Heat Transf. 1983, 105, 823–829. [Google Scholar] [CrossRef]
- Abu-Nada, E. Entropy generation due to heat and fluid flow in backward facing step flow with various expansion ratios. Int. J. Exergy 2006, 3, 419. [Google Scholar] [CrossRef]
- Abu-Mulaweh, H. A review of research on laminar mixed convection flow over backward- and forward-facing steps. Int. J. Therm. Sci. 2003, 42, 897–909. [Google Scholar] [CrossRef]
- Sano, M.; Suzuki, I.; Sakuraba, K. Control of Turbulent Channel Flow over a Backward-Facing Step by Suction. J. Fluid Sci. Technol. 2009, 4, 188–199. [Google Scholar] [CrossRef]
- Terhaar, S.; Velazquez, A.; Arias, J.R.; Sánchez-Sanz, M. Experimental study on the unsteady laminar heat transfer downstream of a backwards facing step. Int. Commun. Heat Mass Transf. 2010, 37, 457–462. [Google Scholar] [CrossRef]
- Barkley, D.; Gomes, M.G.M.; Henderson, R.D. Three-dimensional instability in flow over a backward-facing step. J. Fluid Mech. 2002, 473, 167–190. [Google Scholar] [CrossRef]
- Abe, K.; Kondoh, T.; Nagano, Y. A new turbulence model for predicting fluid flow and heat transfer in separating and reattaching flows—I. Flow field calculations. Int. J. Heat Mass Transf. 1994, 37, 139–151. [Google Scholar] [CrossRef]
- Abe, K.; Kondoh, T.; Nagano, Y. A new turbulence model for predicting fluid flow and heat transfer in separating and reattaching flows—II. Thermal field calculations. Int. J. Heat Mass Transf. 1995, 38, 1467–1481. [Google Scholar] [CrossRef]
- Vogel, J.C. Heat Transfer and Fluid Mechanics Measurements in the Turbulent Reattaching Flow behind a Backward-facing Step; Stanford University: Stanford, CA, USA, 1984. [Google Scholar]
- Chiang, T.P.; Sheu, T.W.H. A numerical revisit of backward-facing step flow problem. Phys. Fluids 1999, 11, 862–874. [Google Scholar] [CrossRef]
- Tylli, N.; Ineichen, B.; Kaiktsis, L. Sidewall effects in flow over a backward-facing step: Experiments and numerical simulations. Phys. Fluids 2002, 14, 3835–3845. [Google Scholar] [CrossRef]
- Durst, F.; Pereira, J.C. Time-Dependent Laminar Backward-Facing Step Flow in a Two-Dimensional Duct. J. Fluids Eng. 1988, 110, 289–296. [Google Scholar] [CrossRef]
- Biswas, G.; Breuer, M.; Durst, F. Backward-Facing Step Flows for Various Expansion Ratios at Low and Moderate Reynolds Numbers. J. Fluids Eng. 2004, 126, 362–374. [Google Scholar] [CrossRef]
- Öztop, H.F.; Mushatet, K.S.; Yılmaz, I.; Yilmaz, I. Analysis of turbulent flow and heat transfer over a double forward facing step with obstacles. Int. Commun. Heat Mass Transf. 2012, 39, 1395–1403. [Google Scholar] [CrossRef]
- Hussein, T.; Abu-Mulaweh, H.I.; Kazi, S.N. A Badarudin. Numerical simulation of heat transfer and separation Al2O3/nanofluid flow in concentric annular pipe. Int. Commun. Heat Mass Transf. 2016, 71, 108–117. [Google Scholar]
- Mehrez, Z.; El Cafsi, A. Forced convection magnetohydrodynamic Al2O3–Cu/water hybrid nanofluid flow over a backward-facing step. J. Therm. Anal. Calorim. 2018, 135, 1417–1427. [Google Scholar] [CrossRef]
- Togun, H.; Abdulrazzaq, T.; Kazi, S.; Badarudin, A. Augmented of turbulent heat transfer in an annular pipe with abrupt expansion. Therm. Sci. 2016, 20, 1621–1632. [Google Scholar] [CrossRef]
- Alrashed, A.A.; Akbari, O.A.; Heydari, A.; Toghraie, D.; Zarringhalam, M.; Shabani, G.A.S.; Seifi, A.R.; Goodarzi, M. The numerical modeling of water/FMWCNT nanofluid flow and heat transfer in a backward-facing contracting channel. Phys. B Condens. Matter. 2018, 537, 176–183. [Google Scholar] [CrossRef]
- Togun, H.; Tuqa, A.; Kazi, S.N.; Badarudin, A.; Ariffin, M.K.A. Heat transfer to laminar flow over a double backward-facing step. Int. J. Mech. Aerosp. Manuf. Ind. Sci. Eng. World Acad. Sci. Eng. Technol. 2013, 10, 1742–1747. [Google Scholar]
- Abdulrazzaq, T.; Togun, H.; Goodarzi, M.; Kazi, S.N.; Ariffin, M.K.A.; Adam, N.M.; Hooman, K. Turbulent heat transfer and nanofluid flow in an annular cylinder with sudden reduction. J. Therm. Anal. Calorim. 2020, 141, 373–385. [Google Scholar] [CrossRef]
- Abdulrazzaq, T.; Hussein, T.; Ariffin, M.K.A.; Kazi, S.N.; Badarudin, A.; Adam, N.M.; Masuri, S. Heat Transfer and Turbulent Fluid Flow over Vertical Double Forward-Facing Step. World Acad. Sci. Eng. Technol. 2014, 8, 722–726. [Google Scholar]
- Rao, A.N.; Zhang, J.; Minelli, G.; Basara, B.; Krajnović, S. Qualitative assessment of the bi-stable states in the wake of a finite-width double backward facing step. J. Wind. Eng. Ind. Aerodyn. 2019, 186, 241–249. [Google Scholar] [CrossRef]
- Hussein, H. Laminar CuO–water nanofluid flow and heat transfer in a backward-facing step with and without obstacle. Appl. Nanosci. 2016, 6, 371–378. [Google Scholar]
- Salman, S.; Abu Talib, A.; Saadon, S.; Sultan, M.H. Hybrid nanofluid flow and heat transfer over backward and forward steps: A review. Powder Technol. 2020, 363, 448–472. [Google Scholar] [CrossRef]
- Hussein, T.; Safaei, M.R.; Sadri, R.; Kazi, S.N.; Homoon, K.; Sadeghinezhad, E. Heat transfer to turbulent and laminar Cu/water flow over a backward-facing step. Appl. Math. Comput. 2014, 239, 153–170. [Google Scholar]
- Ehsan, K.A.; Mohammad, B.A.; Javad Abolfazli, E. Simulation of rarefied gas flow in a microchannel with backward facing step by two relaxation times using Lattice Boltzmann method—Slip and transient flow regime. Int. J. Mech. Sci. 2019, 157, 802–815. [Google Scholar]
- Togun, H.; Kazi, S.; Badarudin, A. Turbulent heat transfer to separation nanofluid flow in annular concentric pipe. Int. J. Therm. Sci. 2017, 117, 14–25. [Google Scholar] [CrossRef]
- Sadeq, S.; Abd Rahim, A.T.; Ali, H.; Sadeq, R.N.; Mohamed, T.H.S.; Syamimi, S. Numerical study on the turbulent mixed convection heat transfer over 2D Microsclae backward facing step. CFD Lett. 2019, 11, 31–45. [Google Scholar]
- Abdulrazzaq, T.; Togun, H.; Reza, S.M.; Kazi, S.N.; Ariffin, M.; Adam, N.M.; Safaei, M.R. Effect of flow separation of TiO2 nanofluid on heat transfer in the annular space of two concentric cylinders. Therm. Sci. 2020, 24, 1007–1018. [Google Scholar] [CrossRef]
- Bala, S.K.; Saha, L.K.; Hossain, M.A. Simulation of Forced Convection in a Channel Containing Three Obstacles over Backward and Forward Facing Steps by LBM. Int. J. Appl. Comput. Math. 2019, 5, 35. [Google Scholar] [CrossRef]
- Yuan, M.; Rasul, M.; Mohammad, M.R.; Zhigang, Y.; Yuhao, F. Baffle and geometry effects on nanofluid forced convection over forward- and backward-facing steps channel by means of lattice Boltzmann method. Phys. A Stat. Mech. Appl. 2020, 554, 124696. [Google Scholar]
- Fetta, D.; Ahlem, B.; Omar, M.; Seif-Eddine, O.; Nabila, L.; Youb Khaled, B. Effect of backward facing step shape on 3D mixed convection of Bingham fluid. Int. J. Therm. Sci. 2020, 147, 106116. [Google Scholar]
- Jure, O.; Iztok, T.; Wadim, J.; Thomas, S.; Wolfgang, H.; Ivan, O.; Afaque, S. Thermal fluctuations in low-Prandtl number fluid flows over a backward facing step. Nucl. Eng. Des. 2020, 359, 110460. [Google Scholar]
- Safaei, M.R.; Togun, H.; Vafai, K.; Kazi, S.N.; Badarudin, A. Investigation of Heat Transfer Enhancement in a Forward-Facing Contracting Channel Using FMWCNT Nanofluids. Numer. Heat Transf. Part A Appl. 2014, 66, 1321–1340. [Google Scholar] [CrossRef]
- Karimipour, A.; Esfe, M.H.; Safaei, M.R.; Semiromi, D.T.; Jafari, S.; Kazi, S. Mixed convection of copper–water nanofluid in a shallow inclined lid driven cavity using the lattice Boltzmann method. Phys. A Stat. Mech. Appl. 2014, 402, 150–168. [Google Scholar] [CrossRef]
- Armaly, B.; Li, A.; Nie, J. Measurements in three-dimensional laminar separated flow. Int. J. Heat Mass Transf. 2003, 46, 3573–3582. [Google Scholar] [CrossRef]
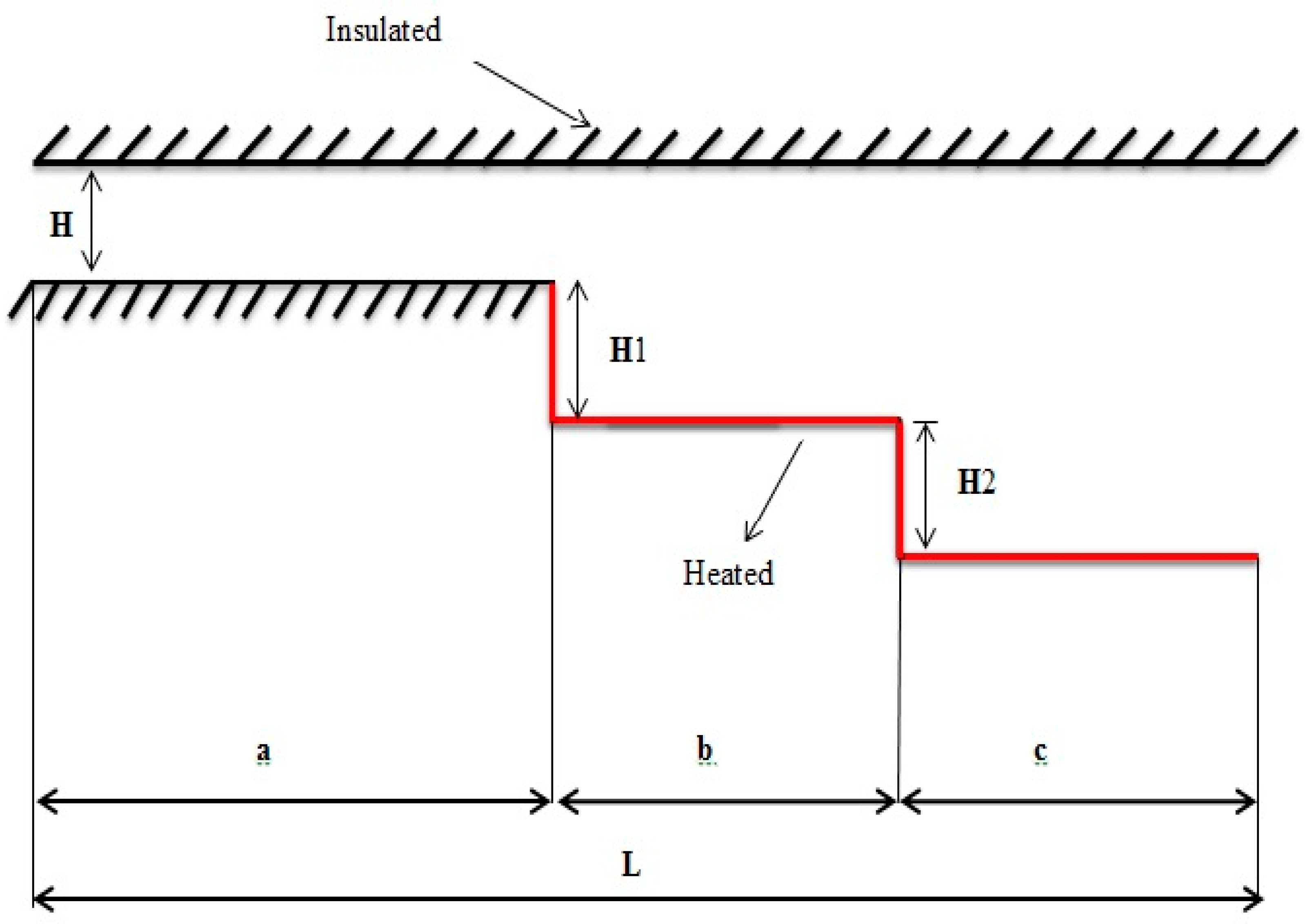


| Cases | H (cm) | H1 (cm) | H2 (cm) | a (cm) | b (cm) | c (cm) |
|---|---|---|---|---|---|---|
| 1 | 0.98 | 1 | 1 | 200 | 50 | 50 |
| 2 | 0.98 | 2 | 1 | 200 | 50 | 50 |
| 3 | 0.98 | 1 | 2 | 200 | 50 | 50 |
| Fluid Type | ρ (kg/m3) | μ (N s/m2) | k (W/m K) | Cp (J/kg K) |
|---|---|---|---|---|
| Ammonia (liquid) | 650 | 0.000152 | 0.493 | 4758 |
| EG | 1111.4 | 0.0157 | 0.252 | 2415 |
| Water | 998.2 | 0.001003 | 0.6 | 4182 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulrazzaq, T.; Togun, H.; Alsulami, H.; Goodarzi, M.; Safaei, M.R. Heat Transfer Improvement in a Double Backward-Facing Expanding Channel Using Different Working Fluids. Symmetry 2020, 12, 1088. https://doi.org/10.3390/sym12071088
Abdulrazzaq T, Togun H, Alsulami H, Goodarzi M, Safaei MR. Heat Transfer Improvement in a Double Backward-Facing Expanding Channel Using Different Working Fluids. Symmetry. 2020; 12(7):1088. https://doi.org/10.3390/sym12071088
Chicago/Turabian StyleAbdulrazzaq, Tuqa, Hussein Togun, Hamed Alsulami, Marjan Goodarzi, and Mohammad Reza Safaei. 2020. "Heat Transfer Improvement in a Double Backward-Facing Expanding Channel Using Different Working Fluids" Symmetry 12, no. 7: 1088. https://doi.org/10.3390/sym12071088
APA StyleAbdulrazzaq, T., Togun, H., Alsulami, H., Goodarzi, M., & Safaei, M. R. (2020). Heat Transfer Improvement in a Double Backward-Facing Expanding Channel Using Different Working Fluids. Symmetry, 12(7), 1088. https://doi.org/10.3390/sym12071088







