Scattered Data Interpolation Using Quartic Triangular Patch for Shape-Preserving Interpolation and Comparison with Mesh-Free Methods
Abstract
1. Introduction
2. Materials and Methods
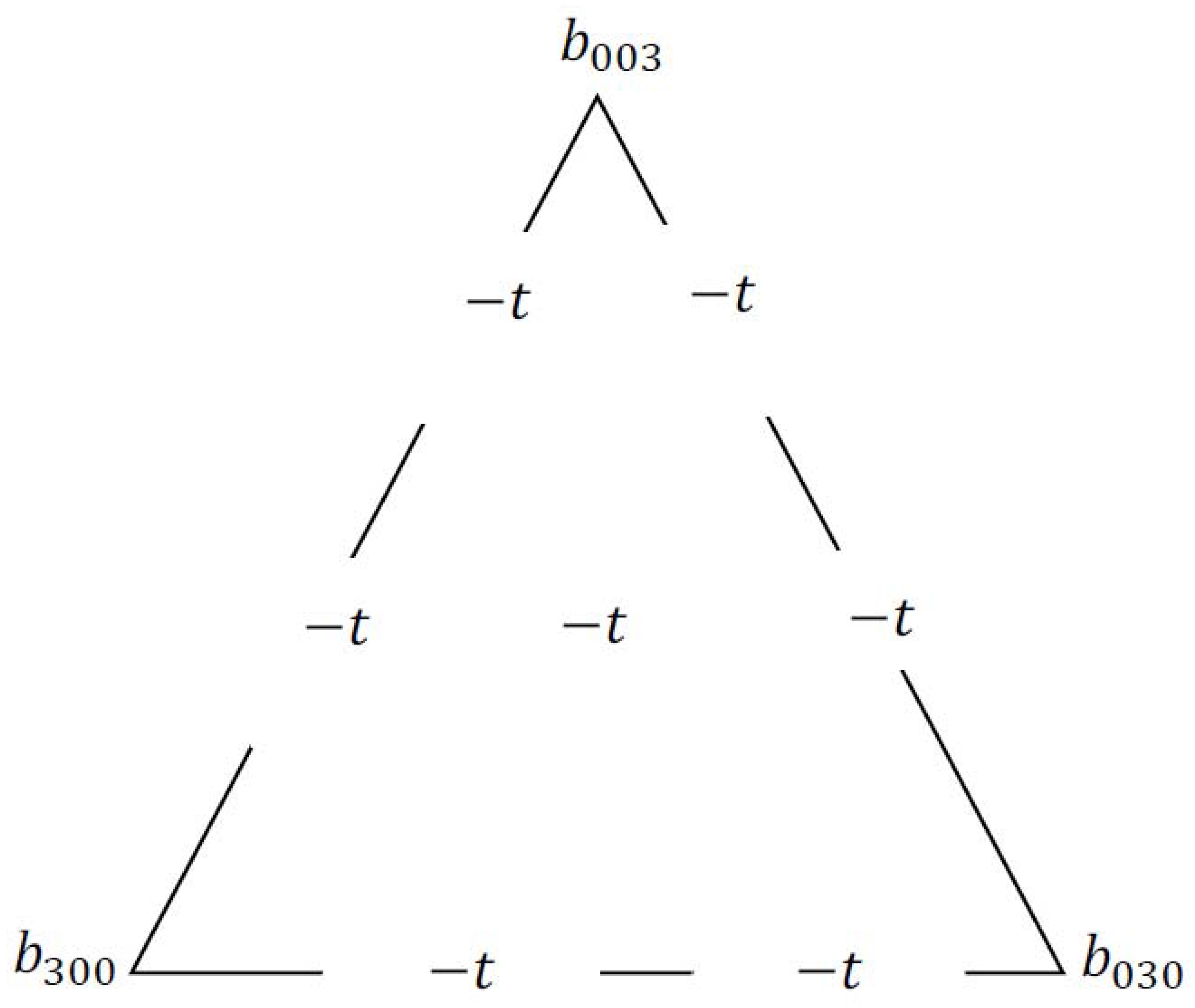
2.1. Review of the Cubic Triangular Bases of Zhu And Han
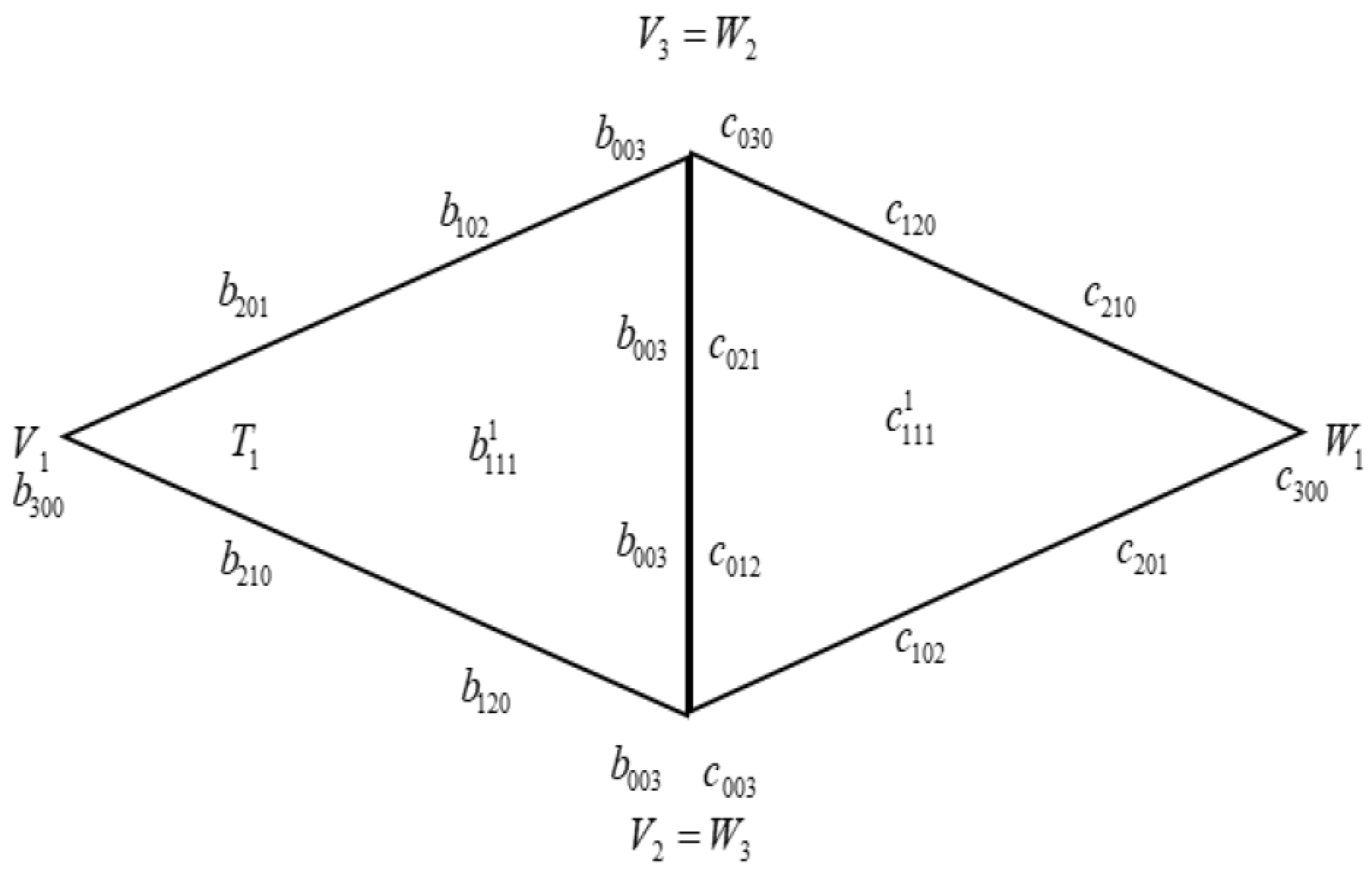
2.2. Quartic Zhu and Han Triangular Patches
2.3. Scattered Data Interpolation Using Quartic Zhu and Han Triangular Patches
| Algorithm 1 (Scattered Data Interpolation) |
| Step 1: Input scattered data points; Step 2: Estimate the partial derivative at the data points by using [25]; Step 3: Triangulate the domain of the data points; Step 4: Calculate the boundary control points using Equations (7)–(12); Step 5: Calculate inner control points for the local scheme, , by using the cubic precision method as in Foley and Opitz [30]; Step 6: Construct the interpolated surface using the convex combination method of three local schemes defined by (6); Step 7: Calculate CPU time (in seconds), R2, and maximum error. Repeat steps 1 through 6 for the other scattered data sets. |
3. Results and Discussion for Scattered Data Interpolation
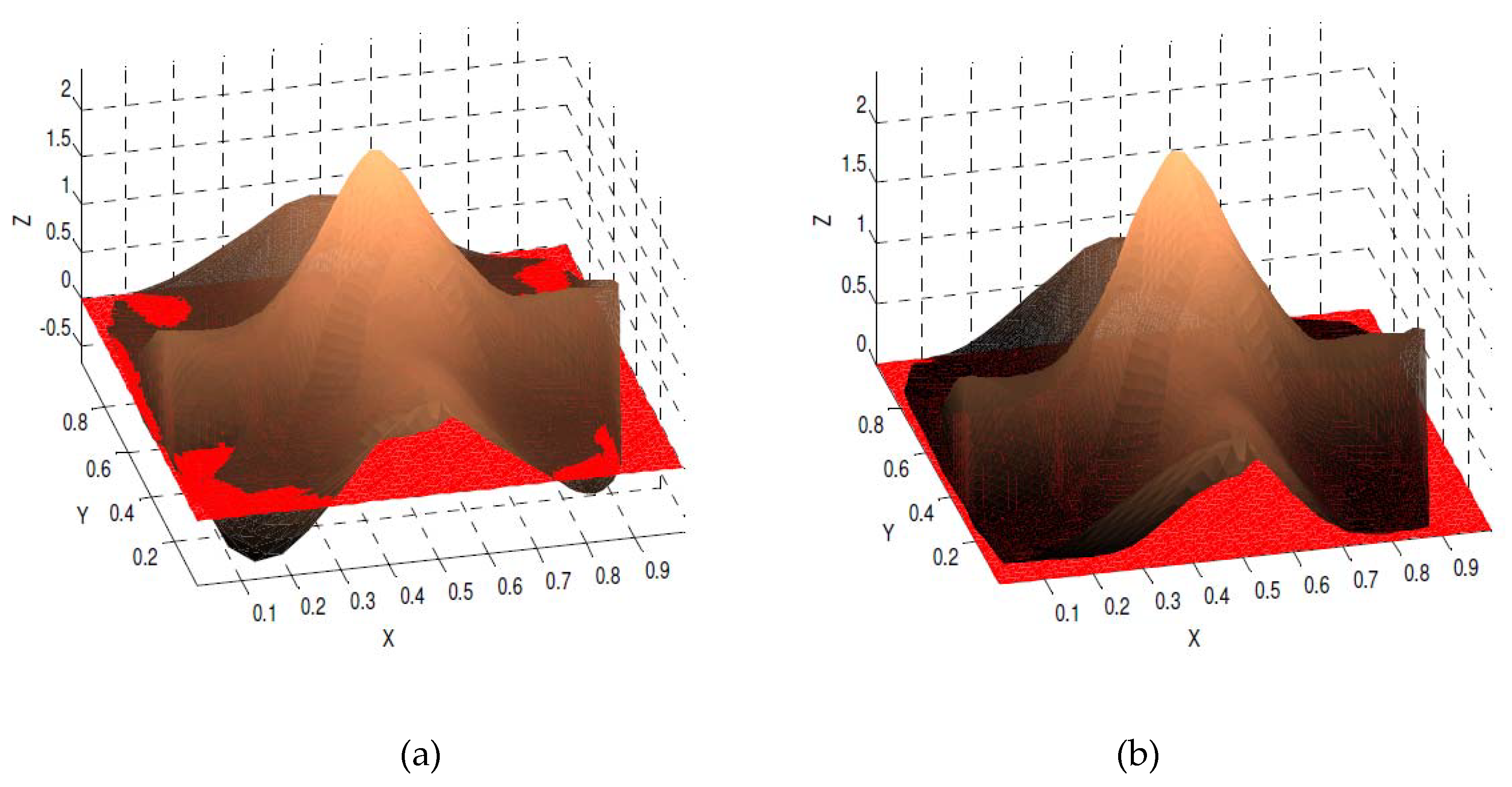
4. Positivity-Preserving Scattered Data Interpolation
5. Numerical Results and Discussion for Positivity-Preserving Scattered Data Interpolation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ali, F.A.M.; Karim, S.A.A.; Bin Saaban, A.; Hasan, M.K.; Ghaffar, A.; Nisar, K.S.; Baleanu, D. Construction of Cubic Timmer Triangular Patches and its Application in Scattered Data Interpolation. Mathematics 2020, 8, 159. [Google Scholar] [CrossRef]
- Bracco, C.; Gianelli, C.; Sestini, A. Adaptive scattered data fitting by extension of local approximations to hierachical splines. Comput. Aided Geom. Des. 2017, 52–53, 90–105. [Google Scholar] [CrossRef]
- Borne, S.L.; Wende, M. Domain decomposition methods in scattered data interpolation with conditionally positive definite radial basis functions. Comput. Math. Appl. 2018, 77, 1178–1196. [Google Scholar] [CrossRef]
- Bozzini, M.; Lenarduzzi, L.; Rossini, M. Polyharmonic splines: An approximation method for noisy scattered data of extra-large size. Appl. Math. Comput. 2010, 216, 317–331. [Google Scholar] [CrossRef]
- Brodlie, K.W.; Asim, M.R.; Unsworth, K. Constrained Visualization Using the Shepard Interpolation Family. Comput. Graph. Forum 2005, 24, 809–820. [Google Scholar] [CrossRef]
- Cavoretto, R.; De Rossi, A.; Dell’Accio, F.; Di Tommaso, F. Fast computation of triangular Shepard interpolants. J. Comput. Appl. Math. 2019, 354, 457–470. [Google Scholar] [CrossRef]
- Chan, E.; Ong, B. Range restricted scattered data interpolation using convex combination of cubic Bézier triangles. J. Comput. Appl. Math. 2001, 136, 135–147. [Google Scholar] [CrossRef][Green Version]
- Chang, L.; Said, H. A C2 triangular patch for the interpolation of functional scattered data. Comput. Des. 1997, 29, 407–412. [Google Scholar] [CrossRef]
- Draman, N.N.C.; Karim, S.A.A.; Hashim, I. Scattered Data Interpolation Using Rational Quartic Triangular Patches With Three Parameters. IEEE Access 2020, 8, 44239–44262. [Google Scholar] [CrossRef]
- Fasshauer, G.E. Meshfree Approximation Methods with Matlab; World Scientific Publishing Co Pte Ltd.: Singapore, 2007. [Google Scholar]
- Dell’Accio, F.; Di Tommaso, F. On the hexagonal Shepard method. Appl. Numer. Math. 2020, 150, 51–64. [Google Scholar] [CrossRef]
- Dell’Accio, F.; Di Tommaso, F.; Nouisser, O.; Zerroudi, B. Increasing the approximation order of the triangular Shepard method. Appl. Numer. Math. 2018, 126, 78–91. [Google Scholar] [CrossRef]
- Dell’Accio, F.; Di Tommaso, F.; Hormann, K. On the approximation order of triangular Shepard interpolation. IMA J. Numer. Anal. 2015, 36, 359–379. [Google Scholar] [CrossRef]
- Crivellaro, A.; Perotto, S.; Zonca, S. Reconstruction of 3D scattered data via radial basis functions by efficient and robust techniques. Appl. Numer. Math. 2017, 113, 93–108. [Google Scholar] [CrossRef]
- Chen, Z.; Cao, F. Scattered data approximation by neural networks operators. Neurocomputing 2016, 190, 237–242. [Google Scholar] [CrossRef]
- Zhou, T.; Li, Z. Scattered Noisy Data Fitting Using Bivariate Splines. Procedia Eng. 2011, 15, 1942–1946. [Google Scholar] [CrossRef][Green Version]
- Zhou, T.; Li, Z. Scattered noisy Hermite data fitting using an extension of the weighted least squares method. Comput. Math. Appl. 2013, 65, 1967–1977. [Google Scholar] [CrossRef]
- Qian, J.; Wang, F.; Zhu, C. Scattered data interpolation based upon bivariate recursive polynomials. J. Comput. Appl. Math. 2018, 329, 223–243. [Google Scholar] [CrossRef]
- Liu, Z. Local multilevel scattered data interpolation. Eng. Anal. Bound. Elements 2018, 92, 101–107. [Google Scholar] [CrossRef]
- Joldes, G.; Chowdhury, H.A.; Wittek, A.; Doyle, B.J.; Miller, K. Modified moving least squares with polynomial bases for scattered data approximation. Appl. Math. Comput. 2015, 266, 893–902. [Google Scholar] [CrossRef]
- Lai, M.-J.; Meile, C. Scattered data interpolation with nonnegative preservation using bivariate splines and its application. Comput. Aided Geom. Des. 2015, 34, 37–49. [Google Scholar] [CrossRef]
- Schumaker, L.L.; Speleers, H. Nonnegativity preserving macro-element interpolation of scattered data. Comput. Aided Geom. Des. 2010, 27, 245–261. [Google Scholar] [CrossRef][Green Version]
- Karim, S.A.A.; Saaban, A.; Hasan, M.K.; Sulaiman, J.; Hashim, I. Interpolation using cubic Bézier triangular patches. Int. J. Adv. Sci. Eng. Inf. Technol. 2018, 8, 1746–1752. [Google Scholar] [CrossRef]
- Karim, S.A.A.; Saaban, A.; Skala, V.; Ghaffar, A.; Nisar, K.S.; Baleanu, D. Construction of new cubic Bézier-like triangular patches with application in scattered data interpolation. Available online: https://link.springer.com/content/pdf/10.1186/s13662-020-02598-w.pdf (accessed on 29 March 2020).
- Karim, S.A.B.A.; Saaban, A. Visualization Terrain Data Using Cubic Ball Triangular Patches. MATEC Web Conf. 2018, 225, 06023. [Google Scholar] [CrossRef]
- Said, H.B.; Rahmat, R.W. A Cubic Ball Triangular Patch for Scattered Data Interpolation. J. Phys. Sci. 1995, 5, 89–101. [Google Scholar]
- Feng, R.; Zhang, Y. Piecewise Bivariate Hermite Interpolations for Large Sets of Scattered Data. J. Appl. Math. 2013, 2013, 1–10. [Google Scholar] [CrossRef]
- Sun, Q.; Bao, F.; Zhang, Y.; Duan, Q. A bivariate rational interpolation based on scattered data on parallel lines. J. Vis. Commun. Image Represent. 2013, 24, 75–80. [Google Scholar] [CrossRef]
- Goodman, T.N.T.; Said, H.B. A C1- triangular interpolation suitable for scattered data interpolation. Commun. Appl. Numer. Methods 1991, 7, 479–485. [Google Scholar] [CrossRef]
- Foley, T.A.; Opitz, K. Hybrid cubic Bézier triangle patches. In Mathematical Methods in Computer Aided Geometric Design II; Lyche, T., Schumaker, L.L., Eds.; Academic Press: Cambridge, MA, USA, 1992; pp. 275–286. [Google Scholar]
- Goodman, T.; Said, H. Shape preserving properties of the generalised ball basis. Comput. Aided Geom. Des. 1991, 8, 115–121. [Google Scholar] [CrossRef]
- Goodman, T.; Said, H. Properties of generalized Ball curves and surfaces. Comput. Aided Des. 1991, 23, 554–560. [Google Scholar] [CrossRef]
- Hussain, M.Z.; Hussain, M. C1 positivity preserving scattered data interpolation using rational Bernstein-Bézier triangular patch. J. Appl. Math. Comput. 2009, 35, 281–293. [Google Scholar] [CrossRef]
- Goodman, T.; Said, H.; Chang, L. Local derivative estimation for scattered data interpolation. Appl. Math. Comput. 1995, 68, 41–50. [Google Scholar] [CrossRef]
- Saaban, A.; Piah, A.R.M.; Majid, A.A.; Chang, L.H.T. G1 scattered data interpolation with minimized sum of squares of principle curvatures. In Proceedings of the International Conference on Computer Graphics, Imaging and Visualization (CGIV’05), Beijing, China, 26–29 July 2005; pp. 385–390. [Google Scholar]
- Piah, A.R.M.; Saaban, A.; Majid, A.A. Range restricted positivity-preserving scattered data interpolation. Malays. J. Fundam. Appl. Sci. 2014, 2, 63–75. [Google Scholar] [CrossRef]
- Hussain, M.; Majid, A.A.; Hussain, M.Z. Convexity-preserving Bernstein–Bézier quartic scheme. Egypt. Inform. J. 2014, 15, 89–95. [Google Scholar] [CrossRef]
- Hussain, M.; Hussain, M.Z.; Buttar, M. C1 Positive Bernstein-Bézier Rational Quartic Interpolation. Int. J. Math. Models Methods Appl. Sci. 2014, 8, 9–21. [Google Scholar]
- Farin, G. Curves and Surfaces for CAGD: A Practicle Guide, 5th ed.; Palmer, C., Ed.; Morgan Kaufmann: San Diego, CA, USA, 2001. [Google Scholar]
- Franke, R. Scattered Data Interpolation: Tests of Some Method. Math. Comput. 1982, 38, 181. [Google Scholar] [CrossRef]
- Franke, R.; Nielson, G.M. Scattered data interpolation of large Sets of scattered data. Int. J. Numer. Methods Eng. 1980, 15, 1691–1704. [Google Scholar] [CrossRef]
- Franke, R.; Nielson, G.M. Scattered Data Interpolation and Applications: A Tutorial and Survey; Scattered data interpolation and applications: A tutorial and survey. In Geometric Modelling: Methods and Applications; Hagen, H., Roller, D., Eds.; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 1991; pp. 131–160. [Google Scholar]
- Lodha, S.; Franke, R. Scattered Data Techniques for Surfaces. In Proceedings of the Scientific Visualization Conference (dagstuhl ’97), Dagstuhl, Germany, 9–13 June 1997; pp. 189–230. [Google Scholar]
- Zhu, Y.; Han, X. A class of αβγ-Bernstein–Bézier basis functions over triangular domain. Appl. Math. Comput. 2013, 220, 446–454. [Google Scholar] [CrossRef]
- Press statement by the Director-General of Health Malaysia, Ministry of Health Malaysia. Available online: https://kpkesihatan.com (accessed on 15 April 2020).
- Karim, S.A.A.; Saaban, A.; Skala, V. Range-Restricted Surface Interpolation Using Rational Bi-Cubic Spline Functions with 12 Parameters. IEEE Access 2019, 7, 104992–105007. [Google Scholar] [CrossRef]


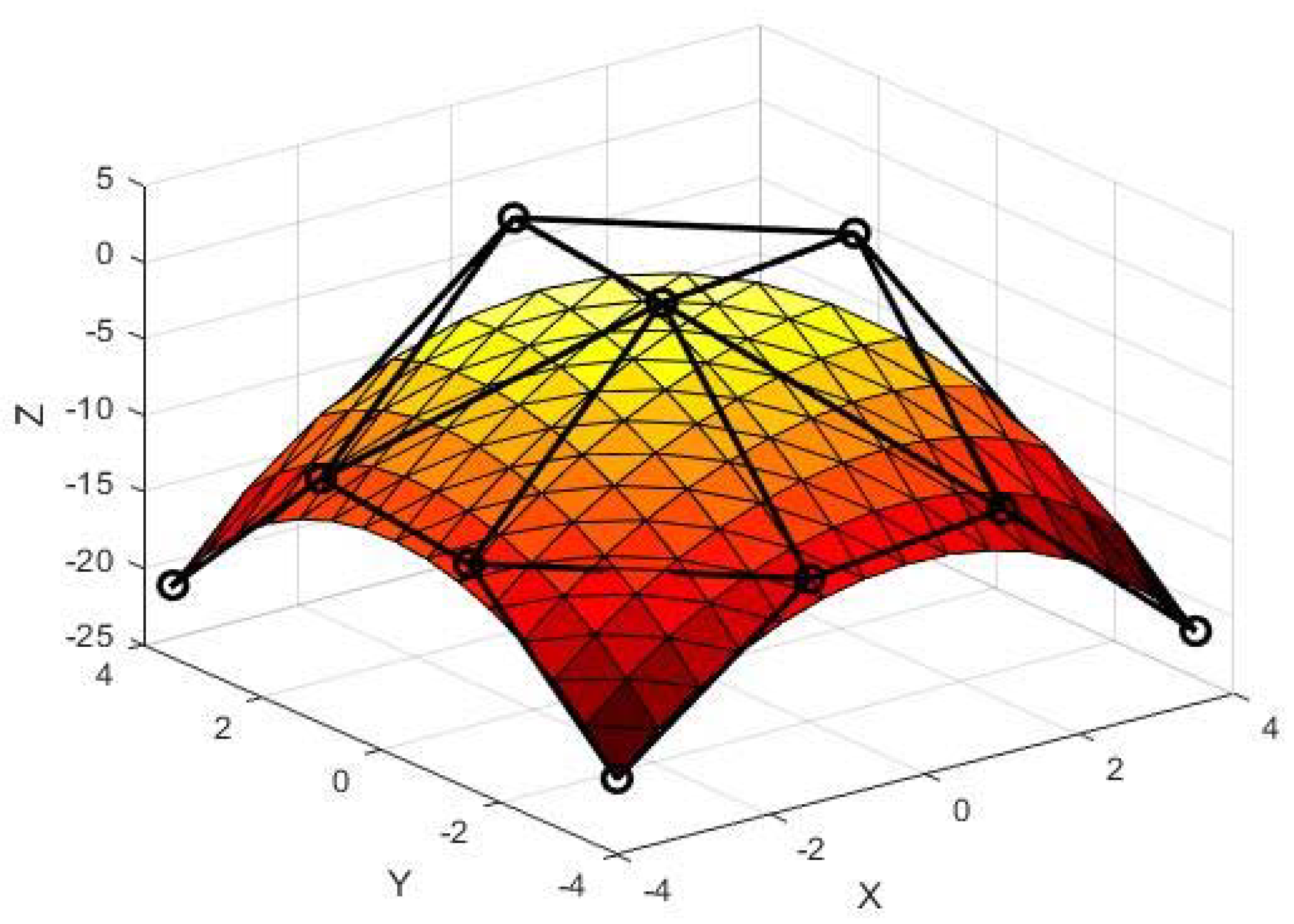
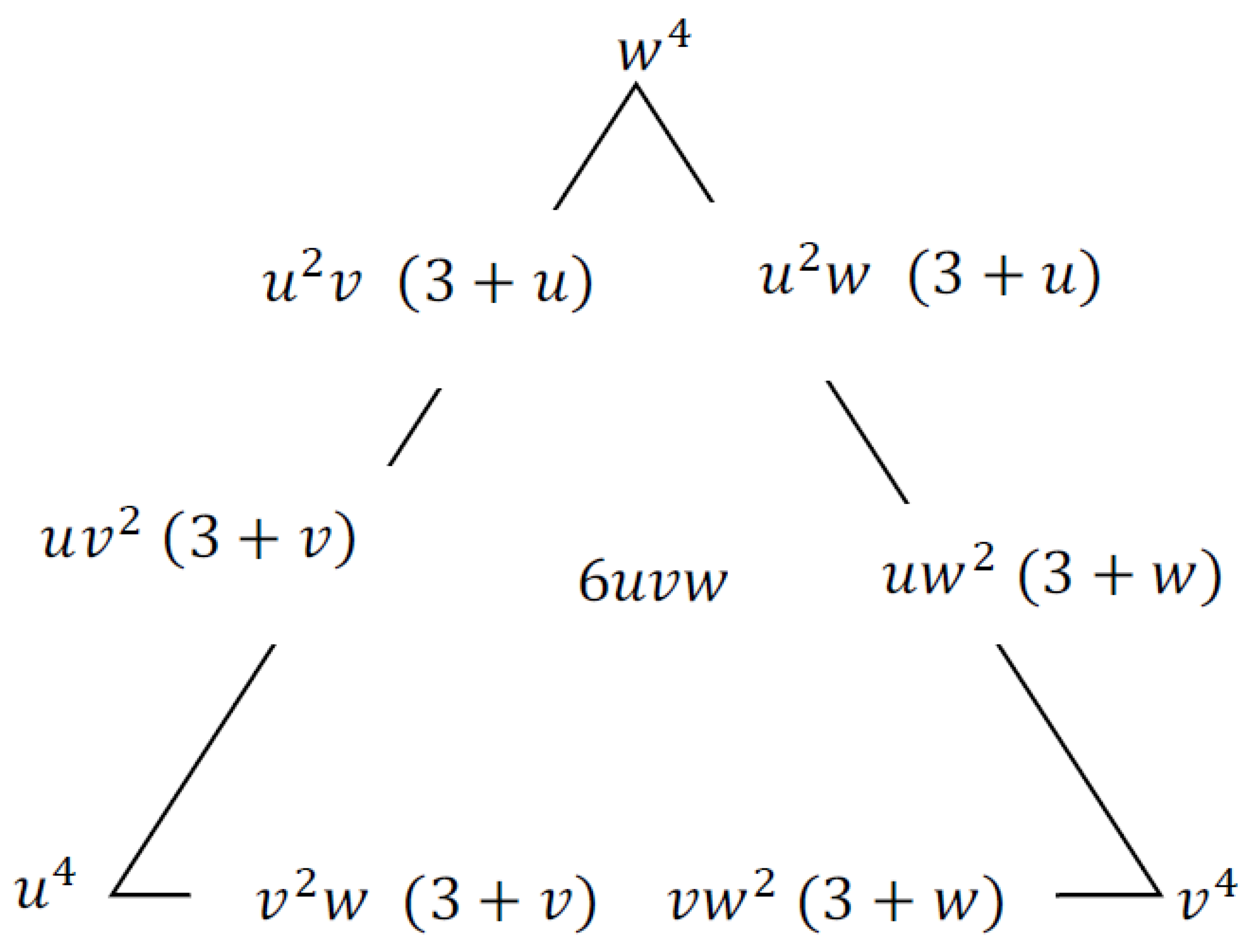
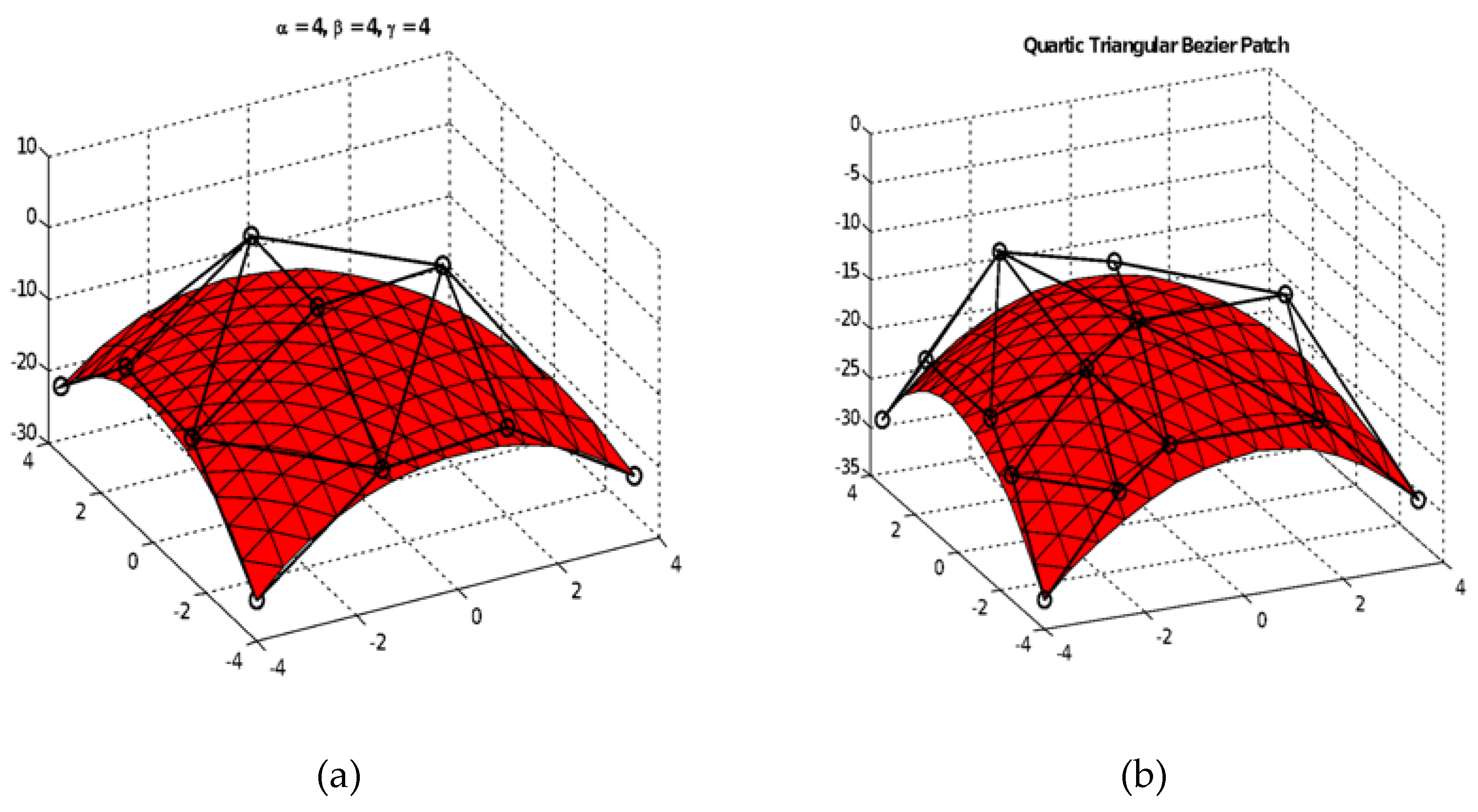
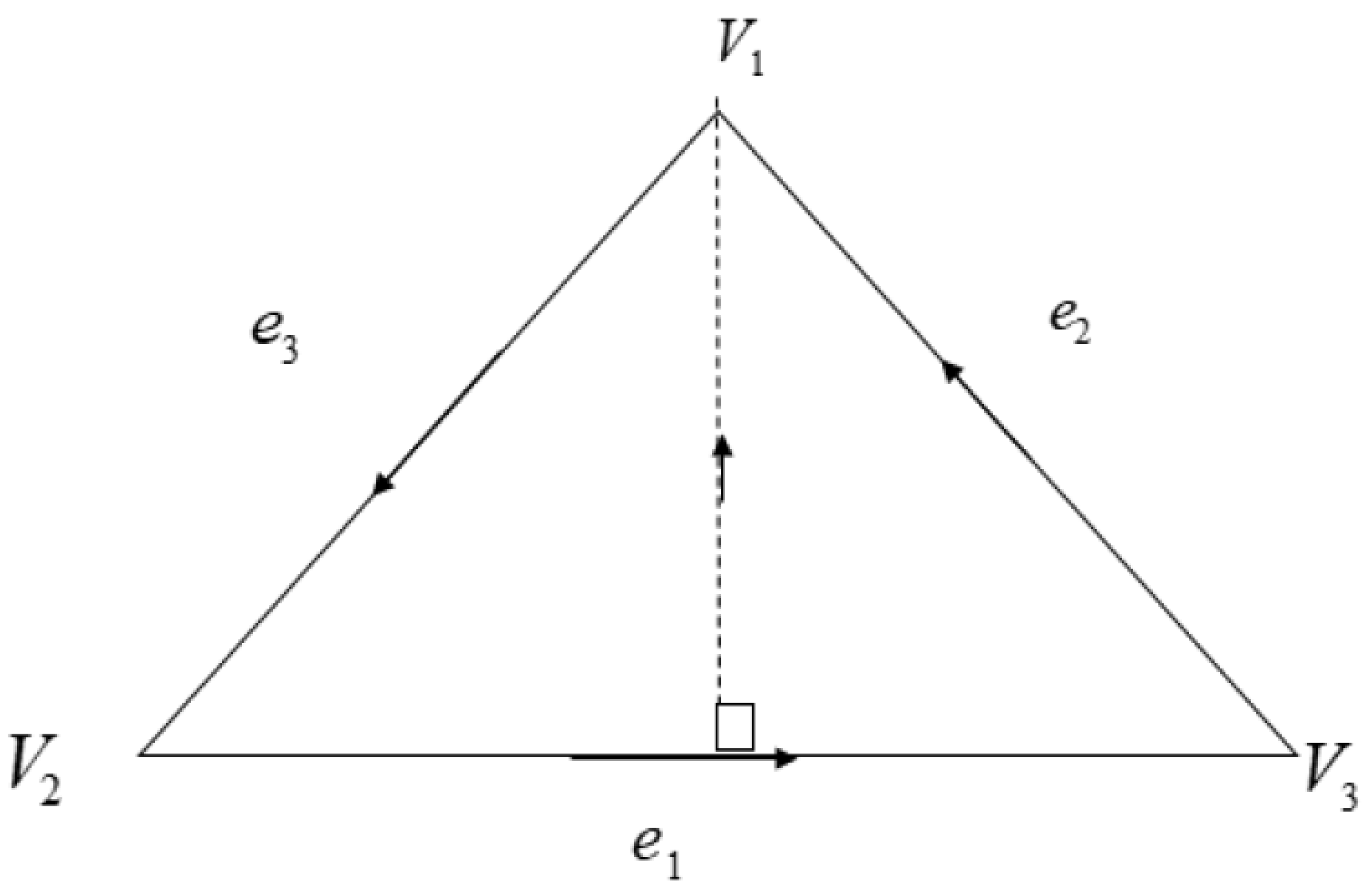

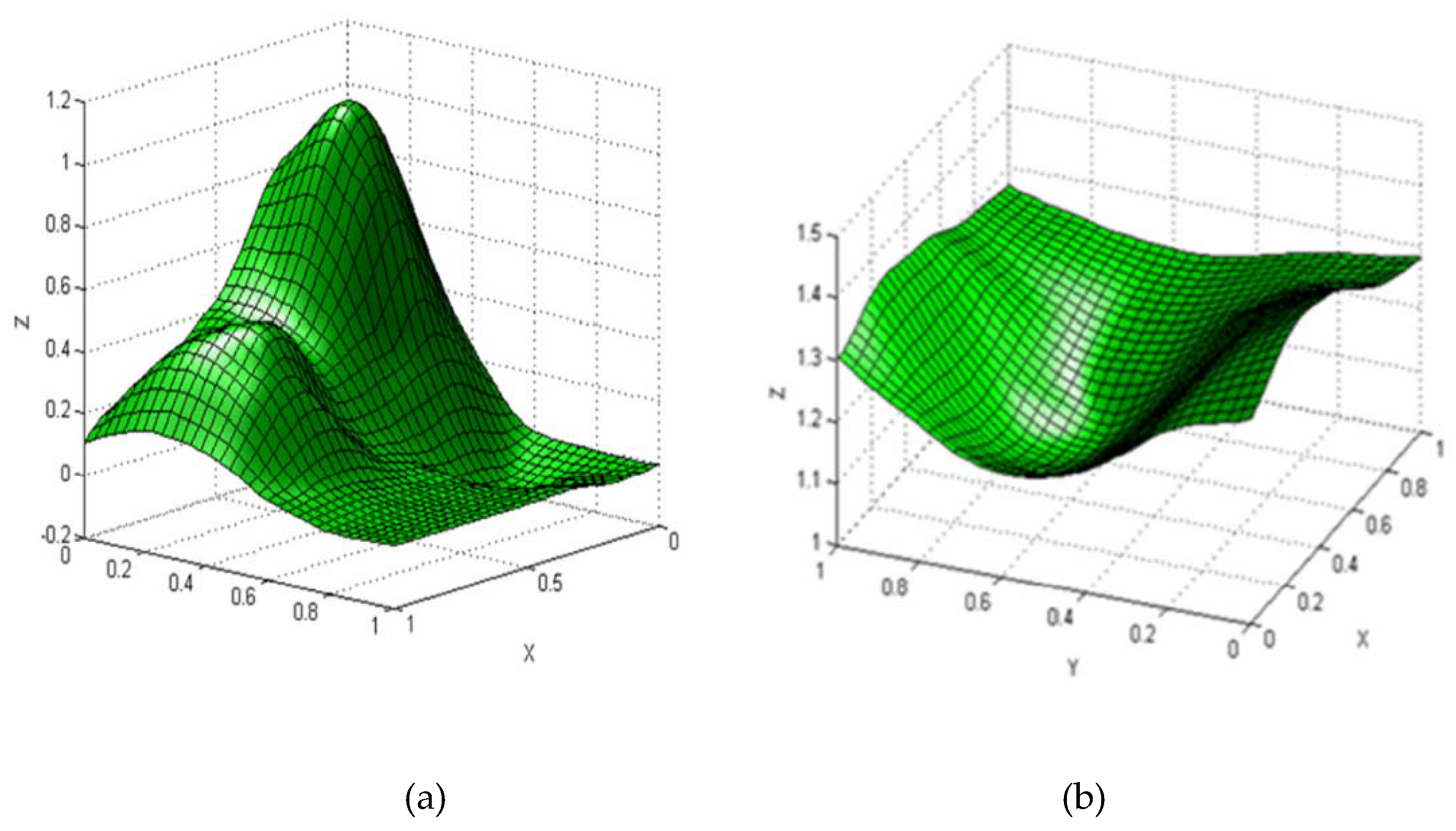
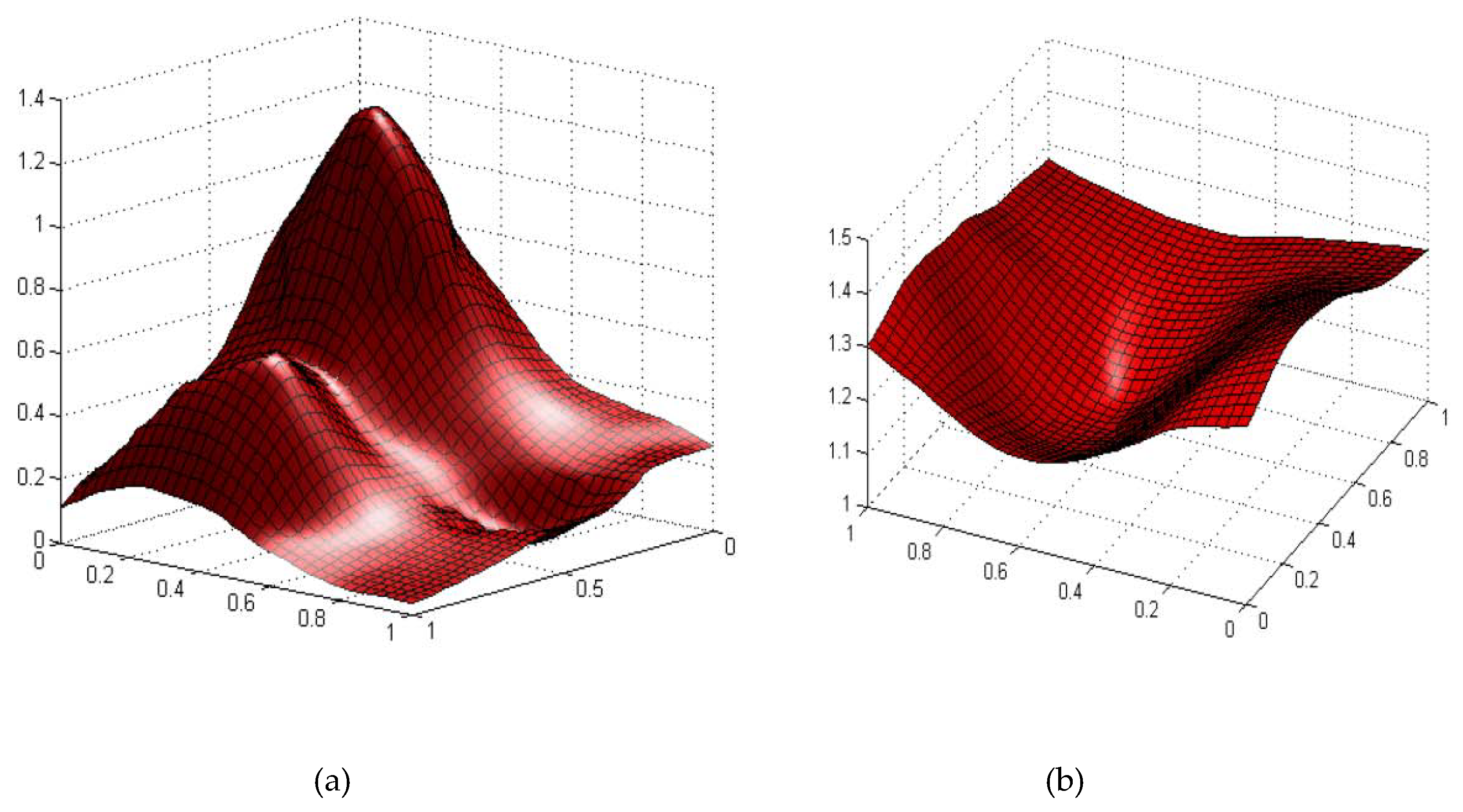
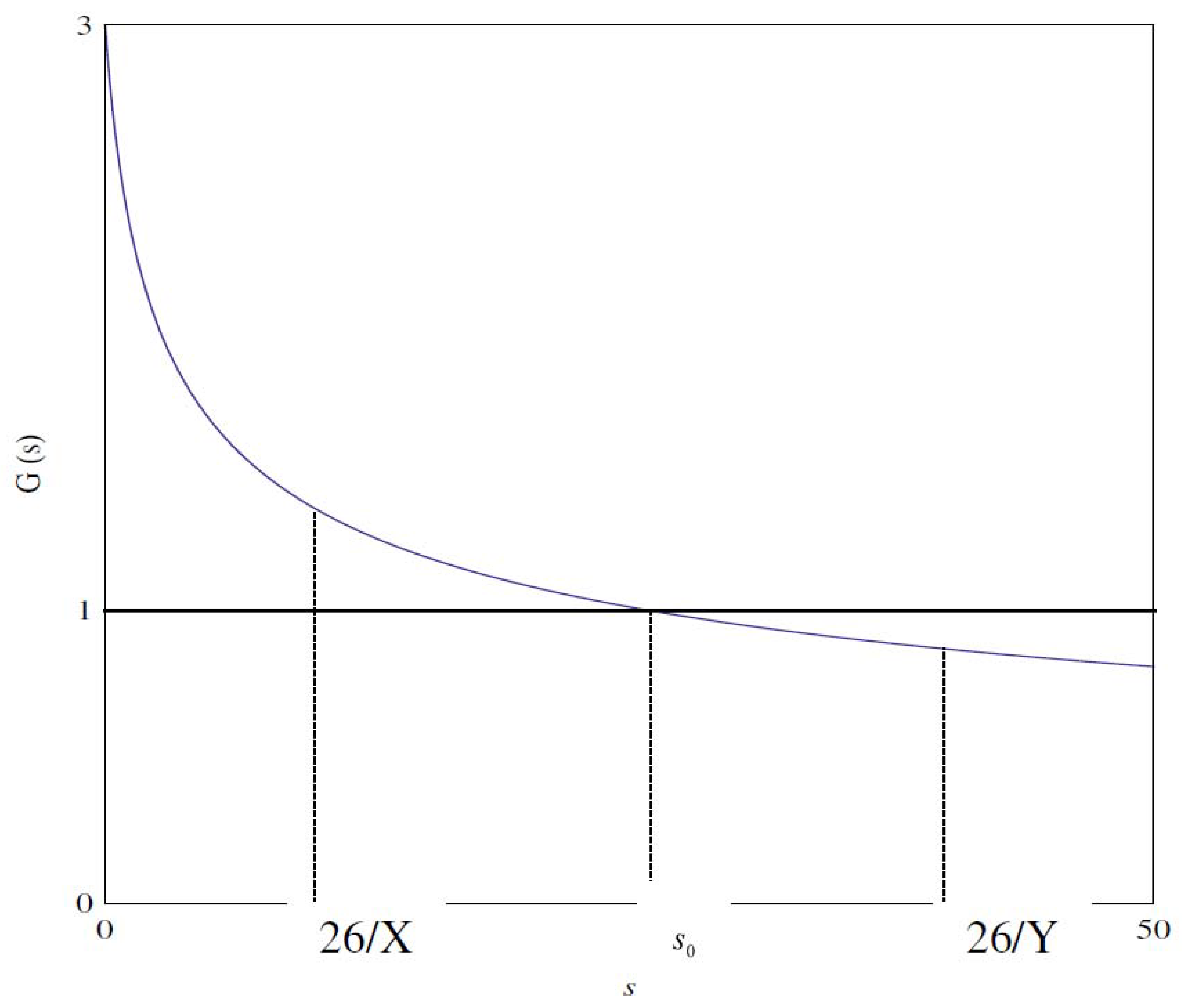
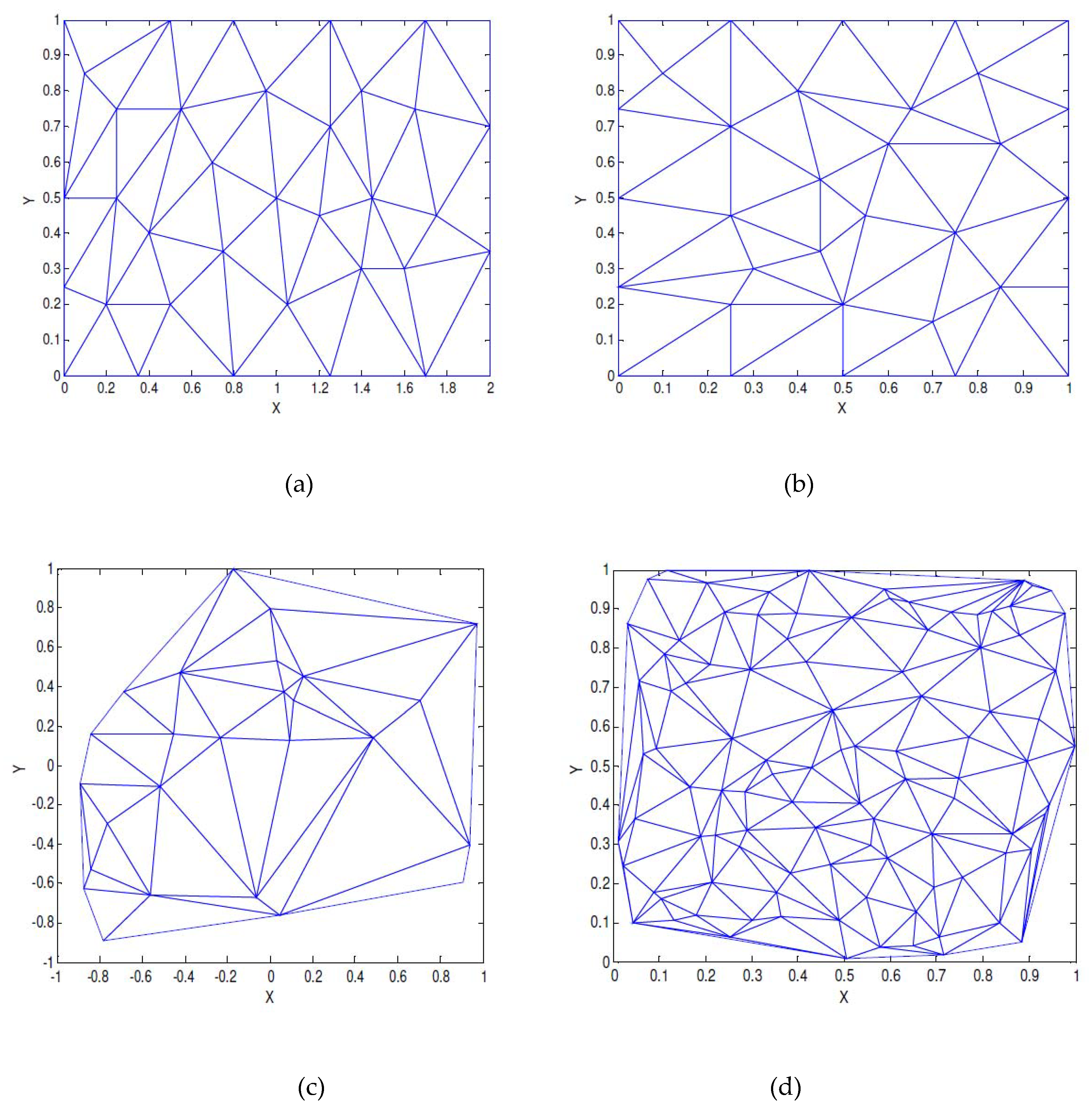
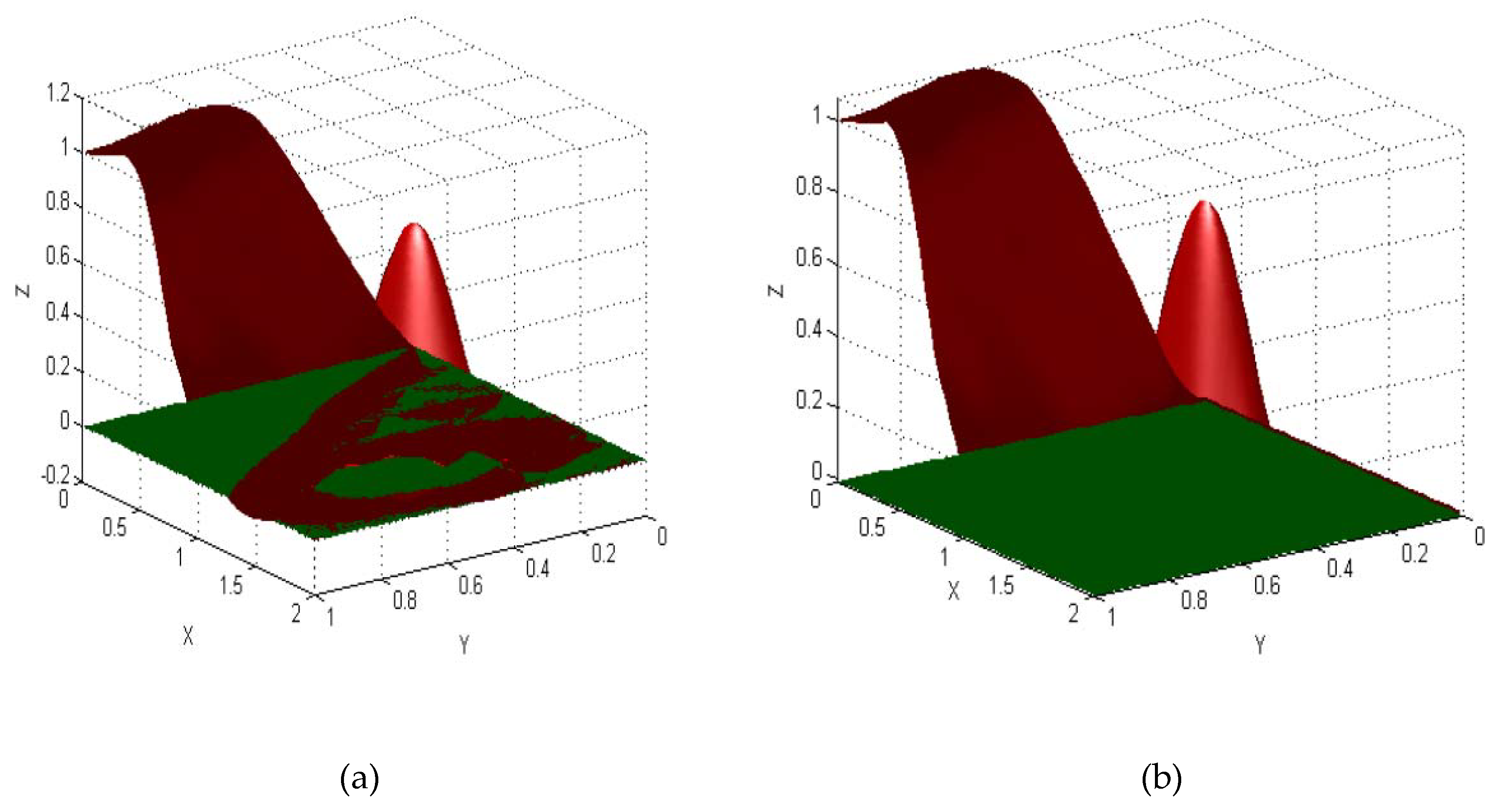
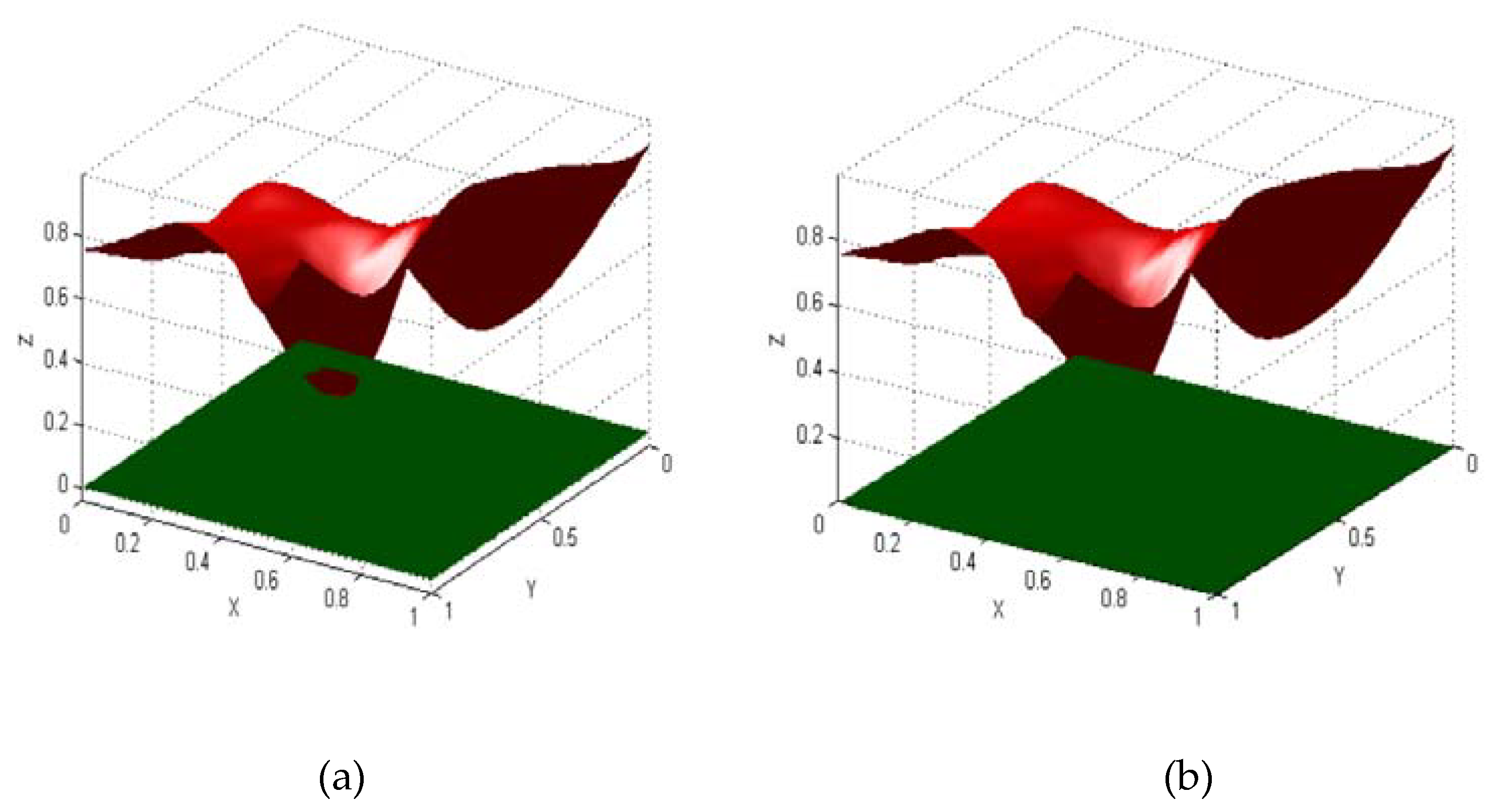

| x | y | F1(x,y) | F2(x,y) | x | y | F1(x,y) | F2(x,y) |
| 0 | 0 | 0.7664 | 1.3333 | 0.80 | 0.85 | 0.0823 | 1.2431 |
| 0.50 | 0 | 0.4349 | 1.3833 | 0.85 | 0.65 | 0.1412 | 1.2043 |
| 1.00 | 0 | 0.1076 | 1.2833 | 1.00 | 0.50 | 0.1610 | 1.2199 |
| 0.15 | 0.15 | 1.1370 | 1.3382 | 1.00 | 1.00 | 0.0359 | 1.2712 |
| 0.70 | 0.15 | 0.4304 | 1.3020 | 0.50 | 1.00 | 0.1460 | 1.3346 |
| 0.50 | 0.20 | 0.5345 | 1.3128 | 0.10 | 0.85 | 0.2935 | 1.2363 |
| 0.25 | 0.30 | 1.0726 | 1.2423 | 0 | 1.00 | 0.2703 | 1.3029 |
| 0.40 | 0.30 | 0.7134 | 1.2421 | 0.25 | 0 | 0.8189 | 1.4069 |
| 0.75 | 0.40 | 0.5903 | 1.2139 | 0.75 | 0 | 0.2521 | 1.3150 |
| 0.85 | 0.25 | 0.5088 | 1.2607 | 0.25 | 1.00 | 0.2222 | 1.3496 |
| 0.55 | 0.45 | 0.3823 | 1.1613 | 0 | 0.25 | 0.8026 | 1.2683 |
| 0 | 0.50 | 0.4818 | 1.1747 | 0.75 | 1.00 | 0.0810 | 1.2913 |
| 0.20 | 0.45 | 0.6458 | 1.1412 | 0 | 0.75 | 0.3395 | 1.1987 |
| 0.45 | 0.55 | 0.2946 | 1.1037 | 1.00 | 0.25 | 0.2302 | 1.2573 |
| 0.60 | 0.65 | 0.1920 | 1.1552 | 1.00 | 0.75 | 0.0504 | 1.2295 |
| 0.25 | 0.70 | 0.2930 | 1.1240 | 0.19 | 0.19 | 1.2118 | 1.3229 |
| 0.40 | 0.80 | 0.0515 | 1.1887 | 0.32 | 0.75 | 0.2029 | 1.1477 |
| 0.65 | 0.75 | 0.1372 | 1.1961 | 0.79 | 0.46 | 0.4777 | 1.2041 |
| Num. of Data Points | Function | Max Error | R2 | ||
|---|---|---|---|---|---|
| The Proposed Scheme | Quartic Bézier [35] | The Proposed Scheme | Quartic Bézier [35] | ||
| 100 | 1 | 3.436 × 10∧−2 | 3.598 × 10∧−2 | 0.99936 | 0.99934 |
| 2 | 4.500 × 10∧−2 | 7.61 × 10∧−2 | 0.99977 | 0.99967 | |
| 65 | 1 | 6.410 × 10∧−2 | 6.586 × 10∧−2 | 0.99720 | 0.99733 |
| 2 | 1.732 × 10∧−2 | 1.562 × 10∧−2 | 0.99796 | 0.99793 | |
| 36 | 1 | 9.740 × 10∧−2 | 9.973 × 10∧−2 | 0.99211 | 0.99256 |
| 2 | 2.675 × 10∧−2 | 2.762 × 10∧−2 | 0.99332 | 0.99208 | |
| Num. of Data Points | Function | CPU Time (in Seconds) | |
|---|---|---|---|
| The Proposed Scheme | Quartic Bézier [35] | ||
| 100 | 1 | 0.7097807844 | 5.6002481345 |
| 2 | 0.4234289196 | 3.5703151686 | |
| 65 | 1 | 0.2741610887 | 1.5474957467 |
| 2 | 0.2363209917 | 1.3271791002 | |
| 36 | 1 | 0.1298699059 | 0.5886074910 |
| 2 | 0.1163838547 | 0.4703613961 | |
| Num. of Data Points | Function | Max Err | ||||
|---|---|---|---|---|---|---|
| Dell’Accio et al. [12] | Dell’Accio and Di Tommaso [11] | Dell’Accio et al., [12] and Cavoretto et al. [6] | Dell’Accio et al. [12] | Dell’Accio et al. [13] and Cavoretto et al. [6] | ||
| 100 | 1 | 5.2990 × 10∧−2 | 8.6648 × 10∧−2 | 1.0970 × 10∧−1 | 6.2438 × 10∧−2 | 5.3936 × 10∧2 |
| 2 | 1.8617 × 10∧−2 | 5.0590 × 10∧−2 | 3.2842 × 10∧−2 | 1.5449 × 10∧−2 | 1.9619 × 10∧−2 | |
| 65 | 1 | 1.0147 × 10∧−1 | 1.1864 × 10∧−1 | 1.1221 × 10∧−1 | 7.6266 × 10∧−2 | 7.1704 × 10∧−2 |
| 2 | 6.4329 × 10∧−2 | 3.7704 × 10∧−2 | 3.5962 × 10∧−2 | 2.7322 × 10∧−2 | 2.8894 × 10∧−2 | |
| 36 | 1 | 1.2822 × 10∧−1 | 1.6219 × 10∧−1 | 1.3564 × 10∧−1 | 1.1371 × 10∧−1 | 9.8914 × 10∧−2 |
| 2 | 7.9686 × 10∧−2 | 5.6713 × 10∧−2 | 5.3611 × 10∧−2 | 5.1806 × 10∧−2 | 4.6253×10∧−2 | |
| Num. of Data Points | Function | CPU Time (Second) | ||||
|---|---|---|---|---|---|---|
| Dell’Accio et al. [12] | Dell’Accio and Di Tommaso [11] | Dell’Accio et al., [12] and Cavoretto et al. [6] | Dell’Accio et al. [12] | Dell’Accio et al. [13] and Cavoretto et al. [6] | ||
| 100 | 1 | 0.490380 | 1.894685 | 0.480296 | 0.423177 | 0.401825 |
| 2 | 0.502923 | 1.881019 | 0.501286 | 0.428949 | 0.417658 | |
| 65 | 1 | 0.486381 | 1.882420 | 0.478175 | 0.424583 | 0.424086 |
| 2 | 0.484984 | 1.849458 | 0.459517 | 0.424870 | 0.397832 | |
| 36 | 1 | 0.437090 | 1.707668 | 0.445523 | 0.415162 | 0.445566 |
| 2 | 0.448242 | 1.686242 | 0.448589 | 0.417875 | 0.421869 | |
| x | y | F1(x,y) | x | y | F1(x,y) | x | y | F1(x,y) |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0.35 | 0 | 0 | 1.4 | 0.8 | 0 |
| 0.2 | 0.2 | 0 | 0.8 | 0 | 0 | 1.65 | 0.75 | 0 |
| 0.5 | 0.2 | 0 | 0.1 | 0.85 | 1 | 2 | 1 | 0 |
| 0.4 | 0.4 | 0 | 0 | 0.25 | 0.5 | 1.25 | 0 | 0 |
| 0.75 | 0.35 | 0 | 0.8 | 1 | 0.4 | 1.7 | 0 | 0 |
| 0 | 0.5 | 1 | 2 | 0 | 0 | 1.25 | 1 | 0 |
| 0.25 | 0.5 | 0.5 | 1.4 | 0.3 | 0.0272 | 1.7 | 1 | 0 |
| 0.25 | 0.75 | 1 | 1.75 | 0.45 | 0 | 2 | 0.35 | 0 |
| 0.55 | 0.75 | 0.4 | 1.2 | 0.45 | 0 | 2 | 0.7 | 0 |
| 0.7 | 0.6 | 0 | 1.45 | 0.5 | 0.9045 | 1.05 | 0.2 | 0 |
| 0.5 | 1 | 1 | 1.6 | 0.3 | 0.0272 | 1 | 0.5 | 0 |
| 0 | 1 | 1 | 1.25 | 0.7 | 0 | 0.95 | 0.8 | 0 |
| x | y | F2(x,y) | x | y | F2(x,y) | x | y | F2(x,y) |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.2586 | 0 | 0.50 | 0.5960 | 0.50 | 1.00 | 0.8762 |
| 0.50 | 0 | 0.6429 | 0.25 | 0.45 | 0.6264 | 0.10 | 0.85 | 0.7316 |
| 1.00 | 0 | 0.9174 | 0.45 | 0.55 | 0.7981 | 0 | 1.00 | 0.7547 |
| 0.25 | 0.20 | 0.0056 | 0.60 | 0.65 | 0.8336 | 0.25 | 0 | 0.2629 |
| 0.70 | 0.15 | 0.6012 | 0.25 | 0.70 | 0.7862 | 0.75 | 0 | 0.7739 |
| 0.50 | 0.20 | 0.6329 | 0.40 | 0.80 | 0.9941 | 0.25 | 1.00 | 0.8026 |
| 0.30 | 0.30 | 0.4199 | 0.65 | 0.75 | 0.8825 | 0 | 0.25 | 0.2792 |
| 0.45 | 0.35 | 0.6618 | 0.80 | 0.85 | 0.9427 | 0.75 | 1.00 | 0.9440 |
| 0.75 | 0.40 | 0.4361 | 0.85 | 0.65 | 0.8838 | 0 | 0.75 | 0.6865 |
| 0.85 | 0.25 | 0.5164 | 1.00 | 0.50 | 0.8640 | 1.00 | 0.25 | 0.7948 |
| 0.55 | 0.45 | 0.6724 | 1.00 | 1.00 | 0.9891 | 1.00 | 0.75 | 0.9746 |
| x | y | F3(x,y) | x | y | F3(x,y) | x | y | F3(x,y) |
|---|---|---|---|---|---|---|---|---|
| 0.9375 | −0.4063 | 0.7997 | 0.0469 | −0.7656 | 0.3436 | −0.5156 | −0.1094 | 0.0708 |
| −0.1719 | 1.0000 | 1.0009 | −0.7813 | −0.8906 | 1.0017 | 0.4844 | 0.1406 | 0.0554 |
| −0.8906 | −0.0938 | 0.6292 | 0.0625 | 0.3750 | 0.0198 | −0.4531 | 0.1563 | 0.0427 |
| −0.0625 | −0.6719 | 0.2038 | −0.7656 | −0.2969 | 0.3513 | 0.7031 | 0.3281 | 0.2560 |
| −0.8750 | −0.6250 | 0.7388 | 0.0938 | 0.1250 | 0.0003 | −0.4219 | 0.4688 | 0.0800 |
| 0 | 0.7969 | 0.4033 | −0.6875 | 0.3750 | 0.2432 | 0.9063 | −0.5938 | 0.7990 |
| −0.8438 | −0.5313 | 0.5866 | 0.1094 | 0.3281 | 0.0117 | −0.2344 | 0.1406 | 0.0034 |
| 0.0313 | 0.5313 | 0.0797 | −0.5625 | −0.6563 | 0.2856 | 0.9688 | 0.7188 | 1.1476 |
| −0.8438 | 0.1563 | 0.5075 | 0.1563 | 0.4531 | 0.0427 |
| x | y | F4 (x,y) | x | y | F4 (x,y) | x | y | F4 (x,y) |
|---|---|---|---|---|---|---|---|---|
| 0.0096 | 0.3083 | 0.119425 | 0.3307 | 0.5159 | 1.155816 | 0.6677 | 0.6764 | 0.442125 |
| 0.0216 | 0.245 | 0.029055 | 0.3379 | 0.9426 | 0.268844 | 0.6814 | 0.8444 | 0.195332 |
| 0.0298 | 0.8614 | 0.00111 | 0.3439 | 0.48 | 1.248258 | 0.6888 | 0.3273 | 0.365476 |
| 0.0417 | 0.0978 | 0.000258 | 0.353 | 0.1783 | 0.345127 | 0.6941 | 0.1894 | 0.158965 |
| 0.047 | 0.3648 | 0.300748 | 0.3636 | 0.1147 | 0.395081 | 0.7062 | 0.0646 | 0.119387 |
| 0.0563 | 0.7156 | 0.073456 | 0.3766 | 0.8226 | 0.473071 | 0.7161 | 0.018 | 0.096822 |
| 0.0647 | 0.5311 | 0.714724 | 0.3822 | 0.2271 | 0.526808 | 0.7317 | 0.8905 | 0.068664 |
| 0.074 | 0.9756 | 0.000124 | 0.387 | 0.4074 | 1.274589 | 0.7371 | 0.4161 | 0.619367 |
| 0.0874 | 0.1781 | 0.004419 | 0.3973 | 0.8875 | 0.590813 | 0.7462 | 0.4689 | 0.797375 |
| 0.0935 | 0.5453 | 0.677296 | 0.4171 | 0.7632 | 0.749339 | 0.7567 | 0.2175 | 0.051462 |
| 0.1032 | 0.1604 | 0.00273 | 0.4256 | 0.9973 | 0.758236 | 0.77 | 0.5734 | 0.613977 |
| 0.111 | 0.7837 | 0.013932 | 0.4299 | 0.496 | 2.117705 | 0.7879 | 0.8853 | 0.016309 |
| 0.1181 | 0.9982 | 0.000684 | 0.4373 | 0.341 | 1.207499 | 0.7944 | 0.8018 | 0.021117 |
| 0.1252 | 0.6911 | 0.121795 | 0.4705 | 0.2498 | 1.021601 | 0.8164 | 0.6389 | 0.294451 |
| 0.1327 | 0.105 | 0.001483 | 0.4737 | 0.6409 | 1.512454 | 0.8193 | 0.8931 | 0.006444 |
| 0.144 | 0.8185 | 0.00648 | 0.4879 | 0.1059 | 0.99334 | 0.8368 | 0.1001 | 0.003695 |
| 0.1565 | 0.7086 | 0.088121 | 0.494 | 0.5412 | 2.374907 | 0.8501 | 0.279 | 0.067559 |
| 0.1651 | 0.4457 | 0.653239 | 0.5055 | 0.009 | 0.998497 | 0.8588 | 0.9083 | 0.001782 |
| 0.1786 | 0.1178 | 0.006221 | 0.5163 | 0.8784 | 0.987962 | 0.8646 | 0.3259 | 0.166279 |
| 0.1886 | 0.3189 | 0.154486 | 0.5219 | 0.5516 | 2.273778 | 0.8792 | 0.8319 | 0.003798 |
| 0.2017 | 0.9668 | 0.011703 | 0.5349 | 0.4039 | 1.858252 | 0.8838 | 0.0509 | 0.000664 |
| 0.21 | 0.7572 | 0.042784 | 0.5483 | 0.1654 | 0.895154 | 0.89 | 0.9708 | 0.000509 |
| 0.2147 | 0.2017 | 0.025997 | 0.557 | 0.2965 | 1.02504 | 0.897 | 0.5121 | 0.745189 |
| 0.2204 | 0.3232 | 0.180361 | 0.5639 | 0.366 | 1.370095 | 0.9045 | 0.286 | 0.076266 |
| 0.2344 | 0.4369 | 0.662063 | 0.5785 | 0.0367 | 0.734861 | 0.9084 | 0.9582 | 0.00026 |
| 0.241 | 0.8908 | 0.035317 | 0.5864 | 0.9502 | 0.688545 | 0.9204 | 0.6183 | 0.372734 |
| 0.2528 | 0.0647 | 0.047165 | 0.5929 | 0.2638 | 0.725544 | 0.9348 | 0.378 | 0.356442 |
| 0.2571 | 0.5693 | 0.673111 | 0.5988 | 0.9277 | 0.613938 | 0.9435 | 0.401 | 0.459525 |
| 0.2733 | 0.2947 | 0.174707 | 0.6118 | 0.5378 | 1.60735 | 0.949 | 0.9479 | 7.49E-05 |
| 0.2854 | 0.4332 | 0.760009 | 0.6252 | 0.7375 | 0.521789 | 0.957 | 0.7425 | 0.039667 |
| 0.2902 | 0.3347 | 0.323199 | 0.6331 | 0.4675 | 1.417194 | 0.9772 | 0.8883 | 0.00041 |
| 0.2965 | 0.7436 | 0.169566 | 0.6399 | 0.9186 | 0.375998 | 0.9983 | 0.5497 | 0.66287 |
| 0.302 | 0.1066 | 0.141203 | 0.6489 | 0.0417 | 0.330061 | |||
| 0.3126 | 0.8845 | 0.173287 | 0.6559 | 0.1291 | 0.29764 |
| Size Data | Interpolation Points | Function | CPU Time (in Seconds) | |
|---|---|---|---|---|
| The Proposed Scheme | Quartic Bézier [35] | |||
| 36 | 1296 | F1 | 0.6587 | 1.5653 |
| 33 | 1296 | F2 | 1.0159 | 2.6322 |
| 25 | 377 | F3 | 0.0935 | 1.1535 |
| 100 | 1697 | F4 | 0.5168 | 18.5996 |
| Number of Evaluation Points | Function | Max Error | R2 | ||
|---|---|---|---|---|---|
| The proposed scheme | Quartic Bézier [35] | The proposed scheme | Quartic Bézier [35] | ||
| 1296 | F1 | 0.2729197868113 | 0.282452475456 | 0.9800905 | 0.9760174674571 |
| 1296 | F2 | 0.6346772647732 | 0.633667822156 | 0.819140703 | 0.8244631293045 |
| 377 | F3 | 0.2716512377297 | 0.311611498819 | 0.93773671136 | 0.935885979498 |
| 1697 | F4 | 0.64080639264362 | 0.4808917225171 | 0.98734351099 | 0.988298717425 |
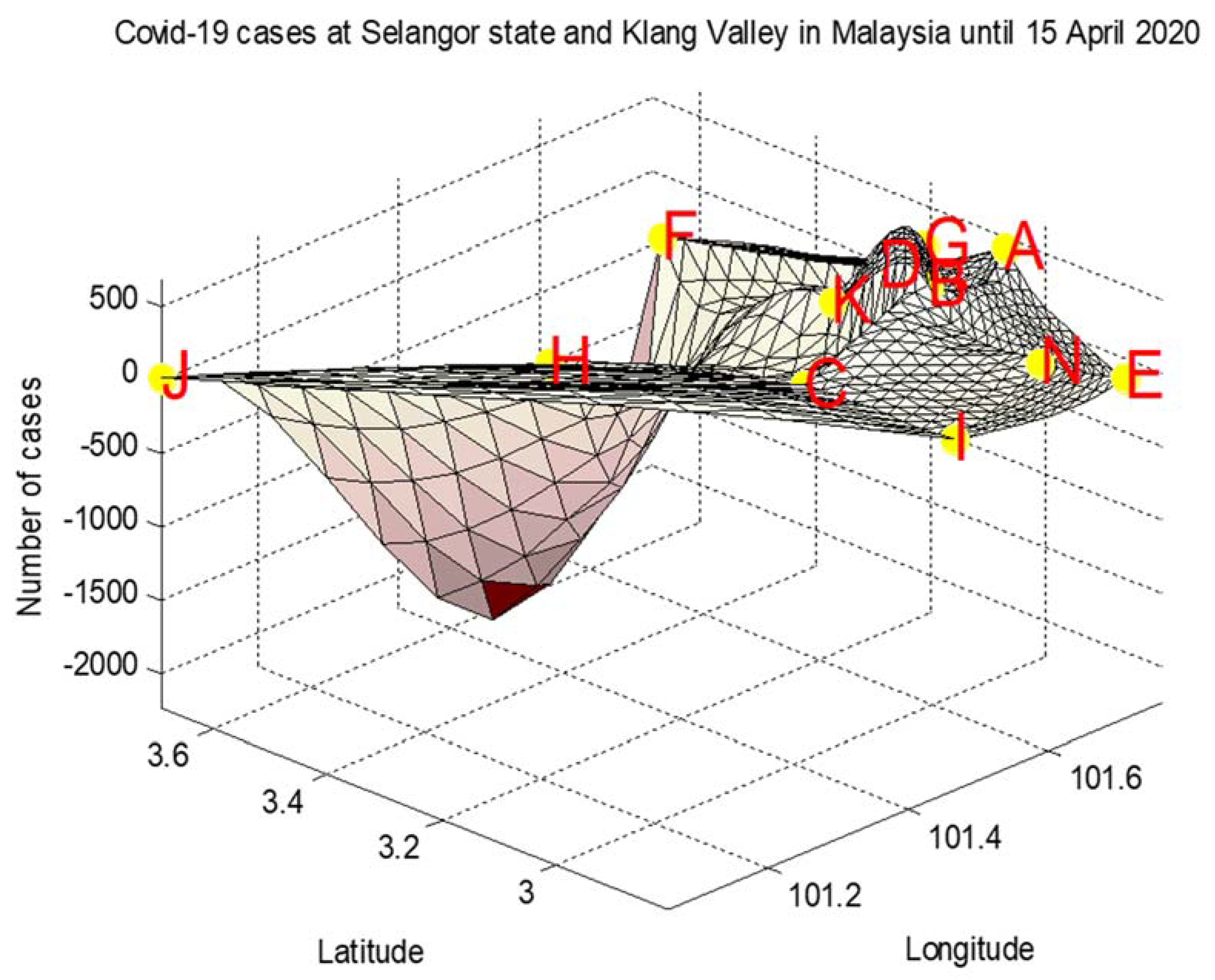
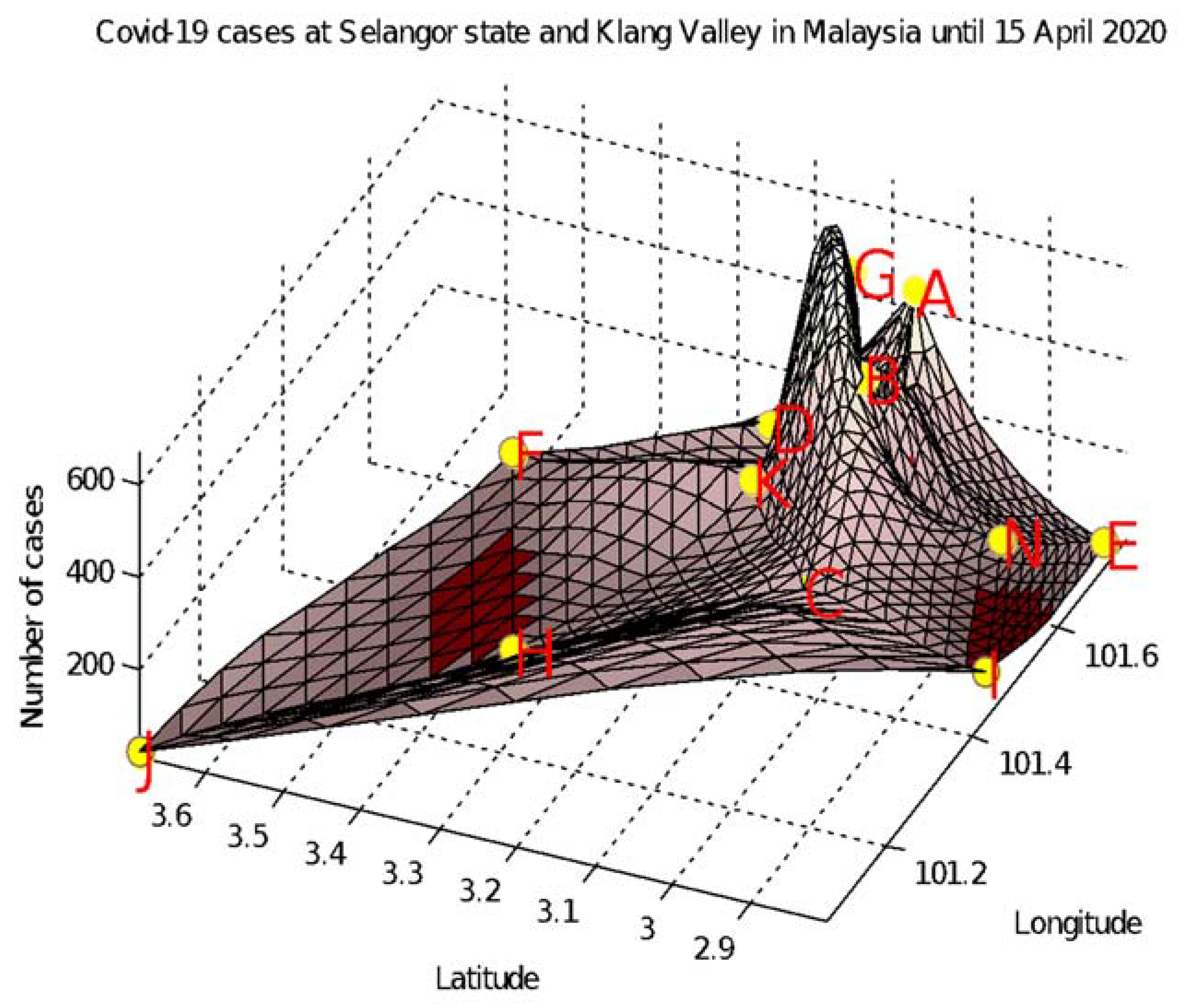
| Label | District | Longitude | Latitude | COVID-19 Cases |
|---|---|---|---|---|
| A | Hulu Langat | 101.7620249 | 3.0727692 | 440 |
| B | Petaling | 101.664208 | 3.086134 | 363 |
| C | Klang | 101.449611 | 3.043125 | 171 |
| D | Gombak | 101.714574 | 3.233044 | 142 |
| E | Sepang | 101.709401 | 2.800862 | 68 |
| F | Hulu Selangor | 101.641482 | 3.52361 | 49 |
| G | Lembah Pantai | 101.672189 | 3.104444 | 577 |
| H | Kuala Selangor | 101.34555 | 3.362102 | 35 |
| I | Kuala Langat | 101.496182 | 2.836562 | 25 |
| J | Sabak Bernam | 101.058059 | 3.687115 | 23 |
| K | Kepong | 101.623581 | 3.2059 | 142 |
| L | Titi Wangsa | 101.695278 | 3.173573 | 129 |
| M | Cheras | 101.71649 | 3.107178 | 78 |
| N | Putrajaya | 101.684046 | 2.918 | 54 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdul Karim, S.A.; Saaban, A.; Nguyen, V.T. Scattered Data Interpolation Using Quartic Triangular Patch for Shape-Preserving Interpolation and Comparison with Mesh-Free Methods. Symmetry 2020, 12, 1071. https://doi.org/10.3390/sym12071071
Abdul Karim SA, Saaban A, Nguyen VT. Scattered Data Interpolation Using Quartic Triangular Patch for Shape-Preserving Interpolation and Comparison with Mesh-Free Methods. Symmetry. 2020; 12(7):1071. https://doi.org/10.3390/sym12071071
Chicago/Turabian StyleAbdul Karim, Samsul Ariffin, Azizan Saaban, and Van Thien Nguyen. 2020. "Scattered Data Interpolation Using Quartic Triangular Patch for Shape-Preserving Interpolation and Comparison with Mesh-Free Methods" Symmetry 12, no. 7: 1071. https://doi.org/10.3390/sym12071071
APA StyleAbdul Karim, S. A., Saaban, A., & Nguyen, V. T. (2020). Scattered Data Interpolation Using Quartic Triangular Patch for Shape-Preserving Interpolation and Comparison with Mesh-Free Methods. Symmetry, 12(7), 1071. https://doi.org/10.3390/sym12071071





