A New Quasi Cubic Rational System with Two Parameters

Abstract

The purpose of this article is to develop a new system for the construction of curves and surfaces. Making the new system not only has excellent properties of the orthodox Bézier and the B-spline method but also has practical properties such as variation diminishing and local shape adjustability. First, a new set of the quasi-cubic rational (QCR) system with two parameters is given, which is verified on an optimal normalized totally positive system (B-system). The related QCR Bézier curve is defined, and the de Casteljau-type algorithm are given. Next, a group of non-uniform QCR B-spline system is shown based on the linear combination of the proposed QCR system, the relative properties of the B-spline system are analyzed. Then, the definition and properties of non-uniform QCR B-spline curves are discussed in detail. Finally, the proposed QCR system is extended to the triangular domain, which is called the quasi-cubic rational Bernstein-Bézier (QCR-BB) system, and its related definition and properties of patches are given at length. The experimental image obtained by using MATLAB shows that the newly constructed system has excellent properties such as symmetry, totally positive, and $C^2$ continuity, and its corresponding curve has the properties of local shape adjustability and $C^2$ continuity. These extended systems in the extended triangular domain have symmetry, linear independence, etc. Hence, the methods in this article are suitable for the modeling design of complex curves and surfaces.

1. Introduction

Bézier and B-spline methods are mainstream methods for computer-aided geometric design (CAGD). The Bézier and B-Spline method have good properties such as symmetry, continuity, convexity, and geometric invariance. Both methods are generally used in geometric design because they have some good properties. The rapid development of the modern geometric industry has led to the difficulty that traditional Bézier or B-spline curves and surfaces could not meet the requirements for geometric designers. Thus, several rationalizing Bézier curves have been proposed, but they have the problem of gradualness. Moreover, improper use of the weight factor would destroy geometric models which have been designed [1,2,3,4,5]. To overcome the above problems, scholars have proposed several Bernstein and B-spline systems with parameters [6,7,8,9,10,11,12,13,14].

The curves and surfaces constructed in the algebraic polynomial space have the advantages of simple and intuitive structure, few calculations, and low computational complexity. To increase the ability of geometric modeling of the traditional Bézier and B-spline methods, researchers have studied the key techniques of Bézier and B-spline curves in the algebraic polynomial space with parameters, such as shape adjustment, joining, and rotary surfaces. In reference [15], a set of Bernstein systems is based on the algebraic polynomial space $Span\{1,3t_{}^2-2t_{}^3,(1-\lambda t){(1-t)}_{}^3,(1-\lambda +\lambda t)t_{}^3\}$. The associated quasi-cubic Bézier curve that has been defined has geometric invariance and convexity. The authors of [16] combined the curve proposed in reference [15] with a rational interpolation function to design a class of geometric rotary surfaces with explicit expressions. Hu et al. [17] used the proposed system given in reference [15] to construct a quasi-cubic Bézier surface with multiple parameters. The resulting surface can be $G^1,G^2$ smoothly continuous joining, and its related system is the same as in reference [15] if its parameters values are equal. In reference [18,19], it can be seen from the system given by reference [15], that a new type of base with two parameters is proposed. Based on the new system, connection design, and rotary surface with parameters of the quasi-cubic Bézier surfaces are discussed, respectively. The authors of [20] monotonically increased the continuously differentiable nonlinear kernel function, and the concept of traditional normalized B-spline function is generalized.

The aim of this study, in the theoretical framework of blossom property of the quasi-expanded Chebyshev (QEC) space, is to propose a set of quasi-cubic rational Bernstein (QCR-B) system with $\alpha$ and $\beta$ in space $Span\{1,3t_{}^2-2t_{}^3,(1-\lambda t){(1-t)}_{}^3,(1-\lambda +\lambda t)t_{}^3\}$. Using the new system, a set of non-uniform QCR B-spline systems is constructed, and it is proved to be totally positive, linear independence, and $C^2$ continuity. Moreover, it is extended to the triangular domain to explore the properties of the triangular domain patches.

2. Preliminaries

To better understand this paper, we first introduce the knowledge with regard to the QEC space and the extended completed Chebyshev (ECC) space [21,22,23,24,25,26,27,28].

First, we suppose $I$ could be expressed by any closed interval $[a,b]$. Then, the following definitions of the ECC and QEC space can be shown.

Definition 1.

(see [21,22,23,24,25,26,27,28]). ECC space. If the $n+1$ positive weight functions $w_i\in C^{n-i}(I)(i=0,1,\cdots ,n)$ exist, it satisfies the canonical form:

$$\begin{array}{ccc}\hfill u_0(t)& =& w_0(t),\hfill \\ \hfill u_1(t)& =& w_0(t){\displaystyle {\int }_a^t{w}_1(t_1)d{t}_1},\hfill \\ \hfill u_2(t)& =& w_0(t){\displaystyle {\int }_a^t{w}_1(t_1){\displaystyle {\int }_a^{t_1}{w}_2(t_2)d{t}_2}d{t}_1,}\hfill \\ & ⋮& \\ \hfill u_n(t)& =& w_0(t){\displaystyle {\int }_a^t{w}_1(t_1)}{\displaystyle {\int }_a^{t_1}{w}_2(t_2)}\cdots {\displaystyle {\int }_a^{t_{n-1}}{w}_n(t_n)d{t}_n\cdots d{t}_1}.\hfill \end{array}$$

(1)

The function space$(u_0,u_1,\cdots ,u_n)$is called the$n+1$dimensional ECC space.

The adequate condition for the $n+1$ dimensional space $(u_0,u_1,\cdots ,u_n)\subset C^n(I)$ becoming an ECC space on the closed interval $I$ is that for any integer $k$, any linear combination of the function subspace $(u_0,u_1,\cdots ,u_k)$ has at most $k(0\le k\le n)$ zeros (including multiple zeros) on $I$.

Definition 2.

(see [21,22,23,24,25,26,27,28]). QEC space. If any linear combination in the space $(u_0,u_1,\cdots ,u_n)\subset C^{n-1}(I)$ has at most $n$ zeros on $I$, then the $n+1$ dimensional space $(u_0,u_1,\cdots ,u_n)$ is a QEC space.

Definition 3.

(see [21,22,23,24,25,26,27,28]). Totally positive system. The system $(u_0,u_1,\cdots ,u_n)$ is called a totally positive system on the closed interval $[a,b]$. If for any knot sequence $a\le t_0<t_1<\cdots <t_n\le b$, the configuration matrix ${(u_j(t_i))}_{0\le i,j\le n}$ of the system is the totally positive matrix, that is, the determinant of any submatrix of the configuration matrix is nonnegative.

3. Main Results

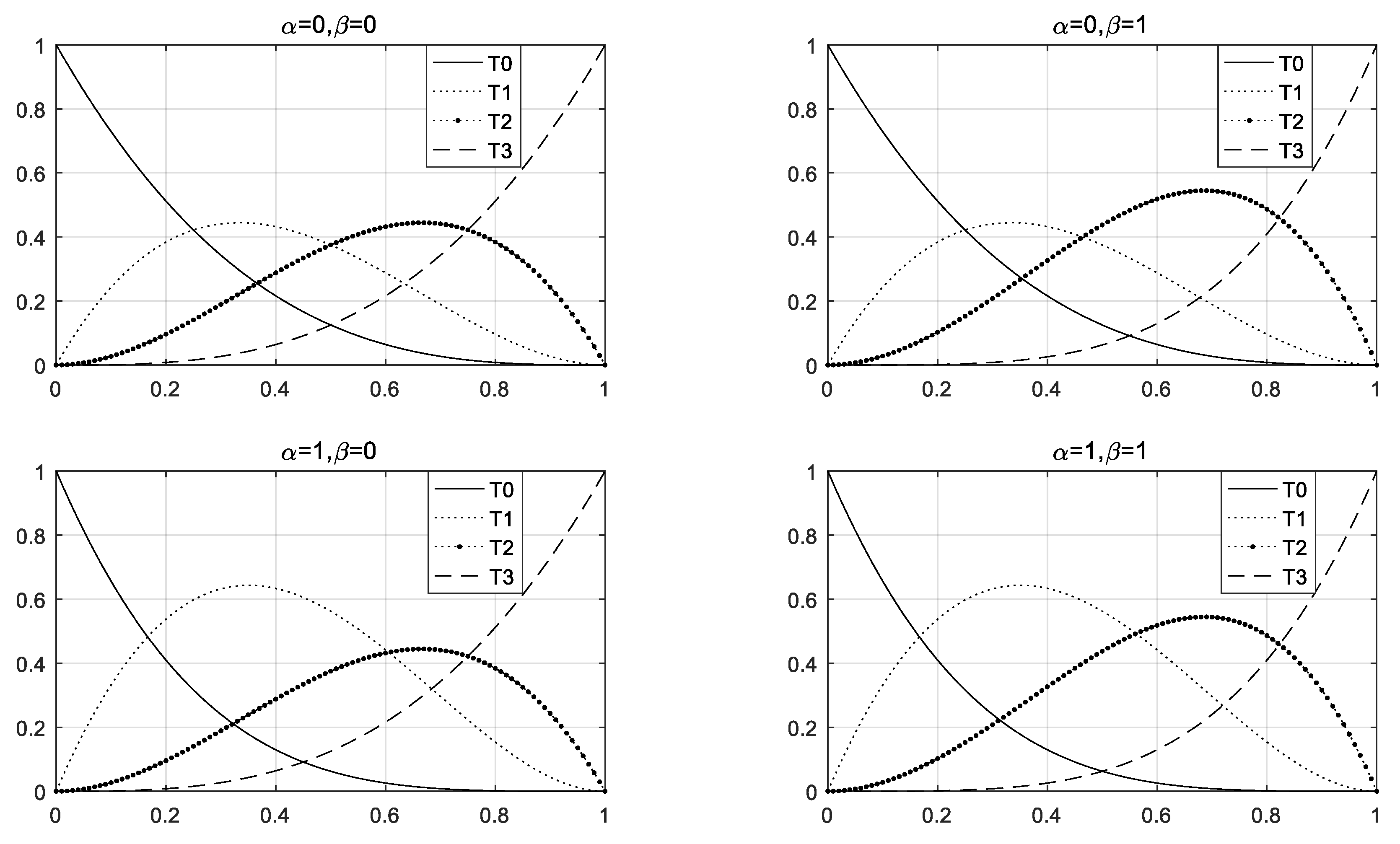
3.1. Construction of the QCR-B System

Yan et al. [14] describes a QCR-B system concerning parameters $\alpha$ and $\beta$, that is:

$$\{\begin{array}{l}{T}_0(t)=(1-\alpha t){(1-t)}^3,\\ T_1(t)=(3+\alpha -\alpha t){(1-t)}^{2}t,\\ T_2(t)=(3+\beta t)(1-t)t^2,\\ T_3(t)=(1-\beta +\beta t)t^3,\end{array}$$

where $\alpha ,\beta \in [0,1],t\in [0,1]$. The QCR-B system is constructed by a linear combination of the traditional Bernstein polynomials [29].

When $\alpha =\beta$, the QCR-B system has a similar form as the literature [15]. In particular, when $\alpha =\beta =0$, the QCR-B system would degenerate to the classical cubic Bernstein system. The definition and properties (such as nonnegativity, symmetry, and end-point properties) of the QCR-B system had already been discussed in [15] at length. However, the totally positive property is missed. Thus, we could use the theoretical knowledge of the ECC and QEC space to discuss the totally positive property of the QCR-B system.

Next, we discuss that the QCR-B system will form a set of B-systems in space $T_{\alpha ,\beta }$. For any $\alpha ,\beta \in [0,1],t\in [0,1]$, the related mother-functions of space $T_{\alpha ,\beta }$ is $\Phi (t)=\{3t_{}^2-2t_{}^3,(1-\alpha t){(1-t)}^3,(1-\beta +\beta t)t^3\}$. From Theorem 3.1 in reference [22], what we should do is to prove that the differential space $D{T}_{\alpha ,\beta }=\{6t(1-t),-(\alpha +3-4\alpha t){(1-t)}_{}^2,(3-3\beta +4\beta t)t_{}^2\}$ is a three-dimensional QEC space.

Theorem 1.

For any real number$\alpha ,\beta \in [0,1]$,$D{T}_{\alpha ,\beta }$is the QEC space on$[0,1]$.

Proof. 

Let

$$u(t)={\left[\frac{-(\alpha +3-4\alpha t){(1-t)}_{}^2}{6t(1-t)}\right]}^{\prime }=\frac{\alpha +3-4\alpha t_{}^2}{6t_{}^2}>0,$$

$$v(t)={\left[\frac{(3-3\beta +4\beta t)t_{}^2}{6t(1-t)}\right]}^{\prime }=\frac{3-3\beta +8\beta t-4\beta t_{}^2}{6{(1-t)}_{}^2}>0.$$

□

By directly differentiating on $u(t)$ and $v(t)$, it follows that:

$$u^{\prime }(t)=-\frac{\alpha +3}{3t_{}^3}<0\underset{}{},\underset{}{}{v}^{\prime }(t)=\frac{\beta +3}{3{(1-t)}_{}^3}>0.$$

Therefore, for any $t\in [a,b]$, the related Wronskian could be expressed as follows:

$$W(u,v)(t)=u(t)v^{\prime }(t)-u^{\prime }(t)v(t)>0.$$

Regarding any $t\in [a,b]\subset (0,1)$, define the weight functions as follows:

$$\begin{array}{l}{\omega }_0(t)=6t(1-t),\\ {\omega }_1(t)={\lambda }_{1}u(t)+{\lambda }_{2}v(t),\\ {\omega }_2(t)={\lambda }_3\frac{W(u,v)(t)}{{[{\lambda }_{1}u(t)+{\lambda }_{2}v(t)]}_{}^2},\end{array}$$

where ${\lambda }_i>0(i=1,2,3)$. Therefore, for $t\in [a,b]\subset (0,1)$, we have:

$${\omega }_i(t)>0,(i=0,1,2).$$

Then, we consider the following ECC spaces from Definition 1:

$$\begin{array}{l}{u}_0(t)={\omega }_0(t),\\ u_1(t)={\omega }_0(t){\displaystyle {\int }_a^t{\omega }_1(t_1)d{t}_1,}\\ u_2(t)={\omega }_0(t){\displaystyle {\int }_a^t{\omega }_1(t_1){\displaystyle {\int }_a^{t_1}{\omega }_2(t_2)d{t}_2}d{t}_1.}\end{array}$$

The formulas $u_0(t),u_1(t),u_2(t)$ that could be easily verified are linear combinations of the differential space $D{T}_{\alpha ,\beta }=\{6t(1-t),-{(1-t)}_{}^2(\alpha +3-4\alpha t),t_{}^2(3-3\beta +4\beta t)\}$. Thus, the differentiating space $D{\mathrm{T}}_{\alpha ,\beta }$ is an ECC space on the closed interval $[a,b]$. Moreover $[a,b]$ is any subset of $(0,1)$, so it is an ECC space on interval $(0,1)$. Therefore, any linear combinations of $D{\mathrm{T}}_{\alpha ,\beta }$ spaces have at most two zeros on interval $(0,1)$.

It is further proved that the differential space is the upper QEC space. Next, let us prove that the differentiating space $D{\mathrm{T}}_{\alpha ,\beta }$ is a QEC space on $[0,1]$. In this case, any linear combinations of $D{T}_{\alpha ,\beta }$ have at most two zeros on $[0,1]$. The linear function can be considered as:

$$F(t)={\mu }_0^{}6t(1-t)+{\mu }_1^{}[-{(1-t)}_{}^2(\alpha +3-4\alpha t)]+{\mu }_2^{}[t_{}^2(3-3\beta +4\beta t)],t\in [0,1].$$

Given that $D{T}_{\alpha ,\beta }$ is an ECC space on $(0,1)$. Hence, $F(t)$ has at the utmost two zeros on $(0,1)$.

If $F(t)$ has one zero at the point $t=0$, then ${\mu }_1=0$. Under this condition:

If ${\mu }_2=0$, then $F(t)$ has two zeros $t=0,t=1$.

If ${\mu }_0=0$, $F(t)=3-3\beta +4\beta t>0$, then $F(t)$ has only one zero on $[0,1]$.

If ${\mu }_0{\mu }_2>0$, then ${\mu }_0>0,{\mu }_2>0$ or ${\mu }_0<0,{\mu }_2<0$, then $F(t)$ has only one zero on $[0,1]$.

If ${\mu }_0{\mu }_2<0$, then ${\mu }_0>0,{\mu }_2<0$ or ${\mu }_0<0,{\mu }_2>0$, so we have:

$$F^{″}(t)=-12{\mu }_0+{\mu }_2[6-6\beta t+24\beta t].$$

Similarly, if $t=1$ is zero of $F(t)$, we can prove that $F(t)$ has at most two zeros on interval $[0,1]$. Thus, $F(t)$ monotonically increases or decreases the function on $(0,1)$; therefore, $F(t)$ has at the utmost two zeros on interval $[0,1]$. In summary, we could conclude that $D{\mathrm{T}}_{\alpha ,\beta }$ is a QEC space.

Theorem 2.

There exists a system$T_i(t),(i=0,1,2,3)$with one linear nontrivial identity providing a B-system of$T_{\alpha ,\beta }$on$t\in [0,1]$for each$\alpha ,\beta \in [0,1]$.

Proof. 

For any $\alpha ,\beta \in [0,1]$, according to the mother-function $\Phi (t)$, we have:

$$\begin{array}{ll}\Phi (0)=(0,1,0),\hfill & \Phi (1)=(1,0,1),\hfill \\ {\Phi }^{\prime }(0)=(0,-(\alpha +3),0),\hfill & {\Phi }^{\prime }(1)=(0,0,\beta +3),\hfill \\ {\Phi }^{″}(0)=(6,6(\alpha +1),0),\hfill & {\Phi }^{″}(1)=(-6,0,6(\beta +1)).\hfill \end{array}$$

From the blossom properties [28], by directly calculating, we have:

$${\Pi }_0=\Phi (0)=(0,1,0),$$

$${\Pi }_3=\Phi (1)=(1,0,1),$$

$$\left\{{\Pi }_1\right\}=Os{c}_1\Phi (0)\cap Os{c}_2\Phi (1)=(0,0,0),$$

$$\left\{{\Pi }_2\right\}=Os{c}_2\Phi (0)\cap Os{c}_1\Phi (1)=(1,0,0).$$

Therefore, $\Phi (t)={\displaystyle \sum _{i=0}^3{T}_i(t){\Pi }_i}$. For $t\in [0,1]$, we can easily get:

$$\{\begin{array}{l}{T}_2(t)+T_3(t)=3t^2-2t^3,\\ T_0(t)=(1-\alpha t){(1-t)}^3,\\ T_3(t)=(1-\beta +\beta t)t^3.\end{array}$$

From the above expression and ${\displaystyle {\sum }_{i=0}^3{T}_i(t)=1}$, we can easily find $T_1$ and Equation (1). Next, we verify that there exists a system $T_i(t),(i=0,1,2,3)$ with one linear nontrivial identity providing a B-system of $T_{\alpha ,\beta }$ on $[0,1]$ for each $\alpha ,\beta \in [0,1]$.

Firstly, we prove that $T_i(t)$ is a linear independence. For ${\xi }_i\in R(i=0,1,2,3)$, the following linear combination:

$${\displaystyle \sum _{i=0}^3{\xi }_i{T}_i(t)=0}.$$

(2)

By directly differentiating on both sides of the above expression, we have:

$${\displaystyle \sum _{i=0}^3{\xi }_i{T^{\prime }}_i(t)=0}.$$

(3)

When $t=0$, from Equations (2) and (3), we can easily get:

$$\{\begin{array}{l}{\xi }_0=0,\\ (\alpha +3)({\xi }_1-{\xi }_0)=0.\end{array}$$

Thus, we can get ${\xi }_0={\xi }_1=0$. When $t=1$, we can get ${\xi }_2={\xi }_3=0$ in the same way. Thus, the system $T_i(t)$ is linear independence.

When $t\in [0,1]$, $T_i(t)$ is nonnegative and when $t\in (0,1)$, $T_i(t)$ is totally positive. In addition, the following endpoint attributes are owned by $T_i(t)$:

$T_0(0)=1$ and $T_0(t)$ has triple zero at $t=1$;

$T_3(1)=1$ and $T_3(t)$ has triple zero at $t=0$.

For $i=1,2$, $T_1(t)$ and $T_2(t)$ have $i$ multiple zeros at $t=0$ and $3-i$ multiple zeros at $t=1$.

Therefore, when $t\in [0,1]$, $\alpha ,\beta \in [0,1]$, by Theorem 2.18 in reference [25], the system given in Equation (1) is a B-system of space $T_{\alpha ,\beta }$. □

For convenience, we define the corresponding QCR-B system as $T_i(\alpha ,\beta ;t)$. The images of the QCR-B system with different parameters are shown in Figure 1.

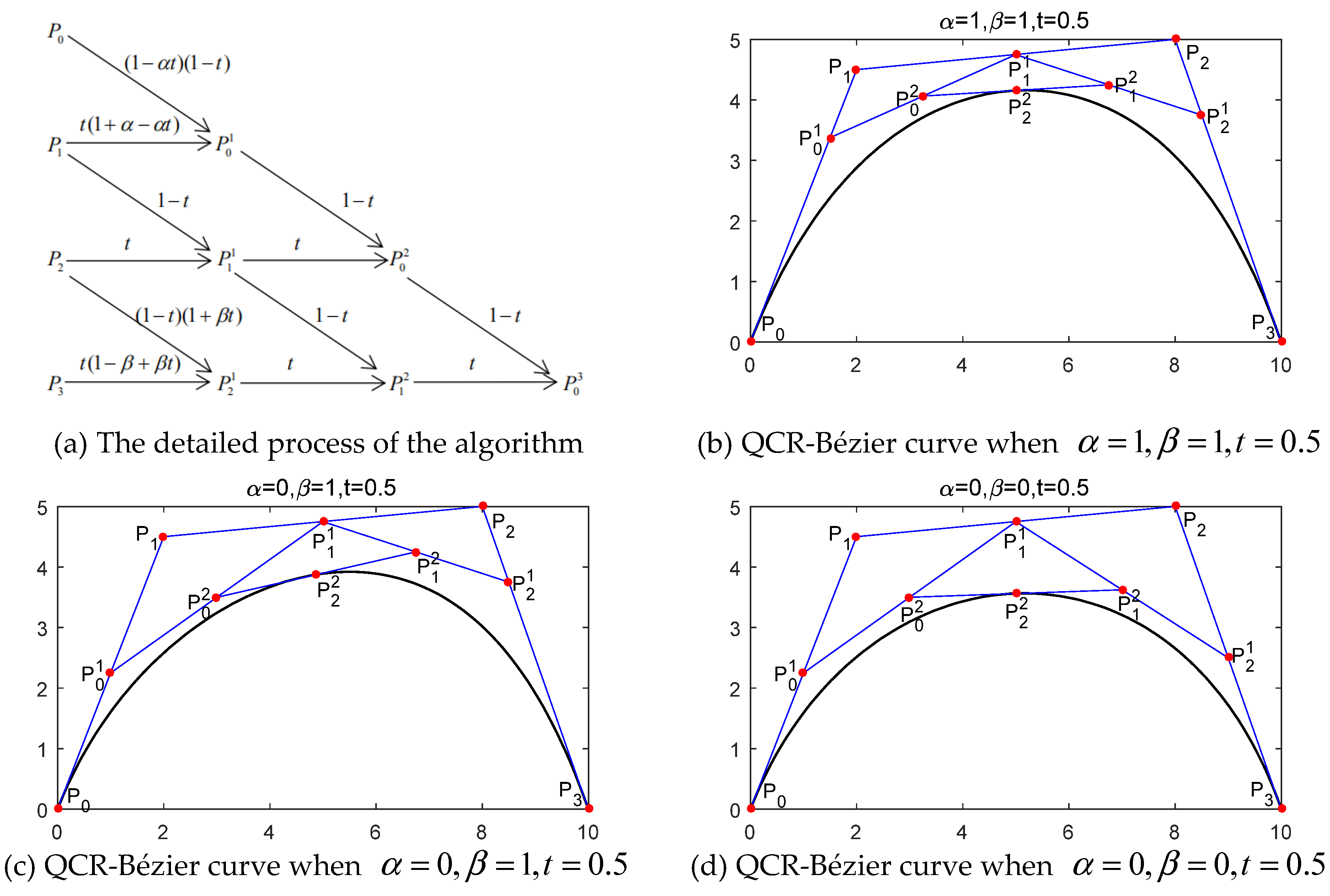
3.2. QCR-Bézier Curve

Definition 4.

For control points$P_i(i=0,1,2,3)\in R_{}^2/R_{}^3$, we call:

$$Q(\alpha ,\beta ;t)={\displaystyle \sum _{i=0}^3{T}_i(\alpha ,\beta ;t)P_i,t\in [0,1],\alpha ,\beta \in [0,1]},$$

(4)

as a QCR-Bézier curve with two parameters$\alpha ,\beta$.

When $\alpha ,\beta \in [0,1]$, the QCR-Bézier curve in reference [12] has proved to have convex hull, convexity, and end-point properties. Given that the system has the totally positive property, the related QCR-Bézier curve was variation diminishing as well.

Next, we give the de Casteljau-type algorithm of the QCR-Bézier curve, which is stable and efficient for computing each point of the QCR-Bézier curve. For any $t\in [0,1]$, let

$$\begin{array}{l}{P}_0^1=(1-t)(1-\alpha t)P_0+t(1+\alpha -\alpha t)P_1,\\ P_1^1=t{P}_2+(1-t)P_1,\\ P_2^1=t(1-\beta +\beta t)P_2+(1+\beta t)(1-t)P_3.\end{array}$$

Then, Equation (4) can be rewritten as follows:

$$Q(\alpha ,\beta ;t)=t[t{P}_2^1+(1-t)P_1^1]+(1-t)[t{P}_1^1+(1-t)P_0^1].$$

(5)

Moreover, let

$$\begin{array}{l}{P}_0^2=t{P}_{{}_1}^1+(1-t)P_{{}_0}^1,\\ P_1^2=t{P}_{{}_2}^1+(1-t)P_{{}_1}^1.\end{array}$$

Then, Equation (5) can be rewritten as follows:

$$Q(\alpha ,\beta ;t)=t{P}_1^2+(1-t)P_0^2=P_0^3.$$

(6)

Equations (5) and (6) are stable and efficient de Casteljau-type algorithms for generating the QCR-Bézier curve. For convenience, we also can rewrite Equation (4) as Equation (7). Figure 2a shows the detailed process of the algorithm, and Figure 2b–d shows the curve generated by the de Casteljau-type algorithm when taking different parametric values.

$$Q(t)=\left(\begin{array}{cc}1-t& t\end{array}\right)\times \left(\begin{array}{ccc}1-t& t& 0\\ 0& 1-t& t\end{array}\right)\times \left(\begin{array}{cccc}(1-t)(1-\alpha t)& t(1+\alpha -\alpha t)& 0& 0\\ 0& 1-t& t& 0\\ 0& 0& (1-t)(1+\beta t)& t(1-\beta +\beta t)\end{array}\right)\times \left(\begin{array}{c}{P}_0\\ P_1\\ P_2\\ P_3\end{array}\right).$$

(7)

3.3. Non-Uniform QCR-B Spline Curves and Their Applications

3.3.1. Structure of the Non-Uniform QCR-B Spline System

Given any knot sequence $u_0<u_1<\cdots <u_{n+4}$, let us write it down as $U=(u_0,u_1,\cdots ,u_{n+4})$. For ${\alpha }_i,{\beta }_i$, the non-uniform QCR-B spline system has the following form:

$$B_i(u)=\{\begin{array}{ll}{B}_{i,0}(t_i)=d_i{T}_3({\beta }_i;t_i),\hfill & u\in [u_i,u_{i+1}),\hfill \\ B_{i,1}(t_{i+1})={\displaystyle {\sum }_{j=0}^3{c}_{i+1,j}{T}_j({\alpha }_{i+1},{\beta }_{i+1};t_{i+1}),}\hfill & u\in [u_{i+1},u_{i+2}),\hfill \\ B_{i,2}(t_{i+2})={\displaystyle {\sum }_{j=0}^3{b}_{i+2,j}{T}_j({\alpha }_{i+2},{\beta }_{i+2};t_{i+2}),}\hfill & u\in [u_{i+2},u_{i+3}),\hfill \\ B_{i,3}(t_{i+3})=a_{i+3}{T}_0({\alpha }_{i+3};t_{i+3}),\hfill & u\in [u_{i+3},u_{i+4}),\hfill \\ 0,\hfill & u\notin [u_i,u_{i+4}),\hfill \end{array}$$

(8)

where $h_j=u_{j+1}-u_j$, $t_j(u)=(u-u_j)/h_j{}_{}^{}{,}_{}^{}j=0,1,2,\cdots ,n+3$; $T_j({\alpha }_i,{\beta }_i;t_i),j=0,1,2,3$ is given by Equation (1).

To determine the coefficient value $a_i,b_{i,j},c_{i,j},d_i$, two constraint conditions should be added: (1) $B_i(u)$ has $C^2$ continuity at each knot; (2) $B_i(u)$ has unity on $[u_3,u_{n+1}]$. By easily calculating, the related coefficient values are shown as follows:

$$\begin{array}{l}{\lambda }_i=3(1+{\alpha }_{i+1})(3+{\beta }_i)h_i+3(3+{\alpha }_{i+1})(1+{\beta }_i)h_{i+1},\\ {\mu }_i=(3+{\alpha }_{i+1})h_i+({\beta }_i+3)h_{i+1},\\ {\varphi }_i=\frac{{\lambda }_i}{3(3+{\beta }_i)h_{i+1}^2}{h}_i+\frac{{\mu }_i}{(3+{\beta }_i)h_{i+1}^{}},\\ {\phi }_i=\frac{{\lambda }_{i-1}}{3({\alpha }_i+3)h_{i-1}^2}{h}_i+\frac{{\mu }_{i-1}}{(3+{\alpha }_i)h_{i-1}^{}},\\ {\psi }_i=3{\lambda }_{i+1}{\mu }_i{h}_i+{\lambda }_i{\lambda }_{i+1}{h}_{i+1}+3{\lambda }_i{\mu }_{i+1}{h}_{i+2},\\ a_i=\frac{3({\beta }_{i-1}+3){\lambda }_{i-2}{h}_i^2}{{\psi }_{i-2}}\begin{array}{cc},& \end{array}{d}_i=\frac{3({\alpha }_{i+1}+3){\lambda }_{i+1}{h}_i^2}{{\psi }_i},\\ b_{i,0}=\frac{(3+{\alpha }_i){\varphi }_i{a}_{i+1}}{{\mu }_{i-1}}{h}_{i-1}+\frac{(3+{\beta }_{i-1})d_{i-2}{\phi }_{i-1}}{{\mu }_{i-1}}{h}_i,\\ b_{i,1}={\varphi }_i{a}_{i+1}\begin{array}{ccccc},& & & & \end{array}{c}_{i,0}=d_{i-1},\\ b_{i,2}=\frac{{\mu }_i}{(3+{\beta }_i)h_{i+1}}{a}_{i+1}\begin{array}{cc},& \end{array}{c}_{i,1}=\frac{{\mu }_{i-1}}{(3+{\alpha }_i)h_{i-1}}{d}_{i-1},\\ b_{i,3}=a_{i+1}\begin{array}{cccc},& & & \end{array}\begin{array}{cc}& \end{array}{c}_{i,2}={\phi }_i{d}_{i-1},\\ c_{i,3}=\frac{(3+{\alpha }_{i+1}){\varphi }_{i+1}{h}_i}{{\mu }_i}{a}_{i+2}+\frac{(3+{\beta }_i){\phi }_i{h}_{i+1}}{{\mu }_i}{d}_{i-1}.\end{array}$$

(9)

Definition 5.

For any${\alpha }_i,{\beta }_i\in [0,1]$and coefficients$a_i,b_{i,j},c_{i,j},d_i$, we call Equation (8) as a set of the QCR-B spline system concerning parameters$\alpha$and$\beta$.

The case of vector $U$ in equidistant node vectors is different from the case of vector $U$ in non-equidistant node vectors. In the former case, the QCR-B spline system is referred to as a uniform QCR-B spline system. Under the latter condition, the QCR-B spline system is referred to as a non-uniform QCR-B spline system. Figure 3 shows the images of the uniform QCR-B-spline system images under different parameters.

Direct calculations yield the following lemma, which will be very useful for subsequent discussion.

Lemma 1.

For any$i\in Z$, the following equations are true:

$$\begin{array}{ccc}(1)a_i+b_{i0}+c_{i0}=1,\hfill & (2)b_{i1}+c_{i1}=1,\hfill & (3)b_{i2}+c_{i2}=1,\hfill \end{array}$$

$$\begin{array}{ll}(4)b_{i3}+c_{i3}+d_i=1,\hfill & (5)d_i=c_{i+1,0},\hfill \\ (6)c_{i+1,3}=b_{i+2,0},\hfill & (7)b_{i+2,3}=a_{i+3,}\hfill \end{array}$$

$$(8)\frac{1}{h_i}\left({\beta }_i+3\right)d_i=\frac{1}{h_{i+1}}\left({\alpha }_{i+1}+3\right)\left(c_{i+1,1}-c_{i+1,0}\right),$$

$$(9)\frac{1}{h_{i+1}}\left(3+{\beta }_{i+1}\right)\left(c_{i+1,3}-c_{i+1,2}\right)=\frac{1}{h_{i+2}}\left(3+{\alpha }_{i+2}\right)\left(b_{i+2,1}-b_{i+2,0}\right),$$

$$(10)\frac{1}{h_{i+2}}\left(3+{\beta }_{i+2}\right)\left(b_{i+1,3}-b_{i+1,2}\right)=-\frac{1}{h_{i+3}}\left(3+{\alpha }_{i+3}\right)a_{i+3},$$

$$(11){\left(\frac{1}{h_i}\right)}^2\left(6{\beta }_i+6\right)d_i={\left(\frac{1}{h_{i+1}}\right)}^2\left[\left(6{\alpha }_{i+1}+6\right)c_{i+1,0}-(6{\alpha }_{i+1}+12)c_{i+1,1}+6c_{i+1,2}\right],$$

$$(12){\left(\frac{1}{h_{i+1}}\right)}^2\left[6c_{i+1,1}-(6{\beta }_{i+1}+12)c_{i+1,2}+(6{\beta }_{i+1}+6)c_{i+1,3}\right]={\left(\frac{1}{h_{i+2}}\right)}^2[\left(6{\alpha }_{i+2}+6\right)b_{i+2,0}-(6{\alpha }_{i+2}+12)b_{i+2,1}+6b_{i+2,2}],$$

$$(13){\left(\frac{1}{h_{i+2}}\right)}^2\left[6b_{i+2,1}-\left(6{\beta }_{i+2}+12\right)b_{i+2,2}+(6{\beta }_{i+2}+6)b_{i+2,3}\right]={\left(\frac{1}{h_{i+3}}\right)}^2\left(6{\alpha }_{i+3}+6\right)a_{i+3}.$$

In particular, when ${\alpha }_j=\alpha ,{\beta }_j=\beta ,j=i+1,i+2,i+3$, we have:

$$\begin{array}{l}{d}_i=\frac{\alpha +3}{2(\alpha \beta +3\alpha +3\beta +9)},\begin{array}{ccc}& & \end{array}{a}_{i+3}=\frac{\beta +3}{2(\alpha \beta +3\alpha +3\beta +9)},\\ c_{i+1,0}=\frac{\alpha +3}{2(\alpha \beta +3\alpha +3\beta +9)},\begin{array}{cc}& b_{i+2,0}=\frac{2\alpha \beta +5\alpha +5\beta +12}{2(\alpha \beta +3\alpha +3\beta +9)}\end{array},\\ c_{i+1,1}=\frac{\alpha +\beta +6}{2(\alpha \beta +3\alpha +3\beta +9)},\begin{array}{cc}& \end{array}{b}_{i+2,1}=\frac{2\alpha \beta +5\alpha +5\beta +12}{2(\alpha \beta +3\alpha +3\beta +9)},\\ c_{i+1,2}=\frac{2\alpha \beta +5\alpha +5\beta +12}{2(\alpha \beta +3\alpha +3\beta +9)},\begin{array}{cc}& \end{array}{b}_{i+2,2}=\frac{\alpha +\beta +6}{2(\alpha \beta +3\alpha +3\beta +9)},\\ c_{i+1,3}=\frac{2\alpha \beta +5\alpha +5\beta +12}{2(\alpha \beta +3\alpha +3\beta +9)},\begin{array}{cc}& \end{array}{b}_{i+2,3}=\frac{\beta +3}{2(\alpha \beta +3\alpha +3\beta +9)}.\end{array}$$

When $\alpha =\beta =0$, we have:

$$\begin{array}{lllll}{d}_i=\frac{1}{6},\hfill & c_{i+1,0}=\frac{1}{6},\hfill & c_{i+1,1}=\frac{1}{3},\hfill & c_{i+1,2}=\frac{2}{3},\hfill & c_{i+1,3}=\frac{2}{3},\hfill \\ b_{i+1,0}=\frac{2}{3},\hfill & b_{i+1,1}=\frac{2}{3},\hfill & b_{i+1,2}=\frac{1}{3},\hfill & b_{i+1,3}=\frac{1}{6},\hfill & a_{i+3}=\frac{1}{6}.\hfill \end{array}$$

3.3.2. Properties of the Non-Uniform QCR-B Spline System

(1)

Unity: For any $u\in [u_3,u_{n+1}]$, ${\displaystyle {\sum }_{i=0}^n{B}_i(u)=1}$.

Proof. 

For $u\in [u_i,u_{i+1}],\begin{array}{c}\end{array}i=3,4,\cdots ,n$, $B_j(u)=0,j\ne i-3,i-2,i-1,i$, from Equation (8) we get that:

$$\begin{array}{l}{B}_{i-3}(u)=a_i{T}_0({\alpha }_i;t_i),\begin{array}{ccc}& & \end{array}{B}_{i-2}(u)={\displaystyle \sum _{j=0}^3{b}_{i,j}{T}_j}({\alpha }_i,{\beta }_i;t_i),\\ B_{i-1}(u)={\displaystyle \sum _{j=0}^3{c}_{i,j}{T}_j}({\alpha }_i,{\beta }_i;t_i),\begin{array}{c}\end{array}{B}_i(u)=d_i{T}_3({\beta }_i;t_i).\end{array}$$

Therefore, from Lemma 1, we have:

$$\begin{array}{lll}{\displaystyle \sum _{i=0}^n{B}_i(u)}& =& a_i{T}_0(t_i;{\alpha }_i)+{\displaystyle \sum _{j=0}^3{b}_{i,j}{T}_j}(t_i;{\alpha }_i;{\beta }_i)+{\displaystyle \sum _{j=0}^3{c}_{i,j}{T}_j}(t_i;{\alpha }_i;{\beta }_i)+d_i{T}_3(t_i;{\beta }_i)\\ & =& \sum _{j=0}^3{T}_j(t_i;{\alpha }_i;{\beta }_i)=1.\hfill \end{array}\square$$

(2)

Nonnegativity: For any $u_i<u<u_{i+4}$, there is $B_i(u)>0$.

Proof. 

For any ${\alpha }_i,{\beta }_i$, from Equation (7), $a_i,b_{i,j},c_{i,j},d_i>0$, and from $T_j({\alpha }_i,{\beta }_i;t_i)\ge 0.$

(3)

Symmetry: For any ${\alpha }_i,{\beta }_i$, we have:

$$B_{i,n}(u)=B_{n-i,n}(1-u)$$

(4)

Linear independence: For any ${\alpha }_i,{\beta }_i\in [0,1]$, $\left\{B_0(u),B_1(u),\cdots ,B_n(u)\right\}$ is linear independence on interval $[u_3,u_{n+1}]$.

Proof. 

Let ${\xi }_i\in R(i=0,1,\cdots ,n)$, $u\in [u_3,u_{n+1}]$, and let for each:

$$B(u)={\displaystyle \sum _{i=0}^n{\xi }_i{B}_i(u)}=0.$$

For any ${\alpha }_i,{\beta }_i$,$i=3,4,\cdots ,n+1$,

$$\begin{array}{l}B(u_i)=a_i{\xi }_{i-3}+b_{i,0}{\xi }_{i-2}+c_{i,0}{\xi }_{i-1}=0,\\ B^{\prime }(u_i)=\frac{1}{h_i}[({\alpha }_i+3)a_i({\xi }_{i-2}-{\xi }_{i-3})+\frac{(3+{\beta }_{i-1})d_{i-1}{h}_i}{h_{i-1}}({\xi }_{i-1}-{\xi }_{i-2})]=0,\\ B^{″}(u_i)={\left(\frac{1}{h_i}\right)}^2[6({\alpha }_i+1)a_i({\xi }_{i-3}-{\xi }_{i-2})+\frac{6(1+{\beta }_i)d_{i-1}{h}_i^2}{h_{i-1}^2}({\xi }_{i-1}-{\xi }_{i-2})]=0.\end{array}$$

Therefore, we have the linear equations:

$$\{\begin{array}{l}{a}_i({\xi }_{i-3}-{\xi }_{i-2})+(a_i+b_{i,0}+c_{i,0}){\xi }_{i-2}+c_{i,0}({\xi }_{i-1}-{\xi }_{i-2})=0,\\ -({\alpha }_i+3)a_i({\xi }_{i-3}-{\xi }_{i-2})+\frac{({\beta }_{i-1}+3)d_{i-1}{h}_i}{h_i}({\xi }_{i-3}-{\xi }_{i-2})=0,\\ ({\alpha }_i+1)a_i({\xi }_{i-3}-{\xi }_{i-2})+\frac{({\beta }_{i-1}+1)d_{i-1}{h}_i^2}{h_{i-1}^2}({\xi }_{i-3}-{\xi }_{i-2})=0.\end{array}$$

(10)

From $a_i+b_{i0}+c_{i0}=1$, the related coefficient determinant with regard to Equation (10) could be concluded as follows:

$$\begin{array}{ccc}\hfill \left|A_i\right|& =& \left|\begin{array}{ccc}{a}_i& 1& c_{i,0}\\ -(3+{\alpha }_i)a_i& 0& (3+{\beta }_{i-1})d_{i-1}{h}_i/h_{i-1}\\ (1+{\alpha }_i)a_i& 0& (1+{\beta }_{i-1})d_{i-1}{h}_{{}_i}^2/h_{{}_{i-1}}^2\end{array}\right|\hfill \\ & =& \frac{a_i{d}_{i-1}{h}_i}{h_{{}_{i-1}}^2}[({\beta }_{i-1}+1)h_i({\alpha }_i+3)+({\beta }_{i-1}+3)({\alpha }_i+1)h_{i-1}]>0.\hfill \end{array}$$

Consequently, ${\xi }_{i-3}={\xi }_{i-2}={\xi }_{i-1}=0,i=3,4,\cdots ,n+1$. □

Totally positive: For $u\in [u_i,u_{i+1}],{\alpha }_i,{\beta }_i\in [0,1]$,$i=3,4,\dots ,n$, $(B_{i-3}(u),B_{i-2}(u),B_{i-1}(u),B_i(u))$ could form a set of normalized totally positive system of $T_{{\alpha }_i,{\beta }_i}$.

Proof. 

For $u\in [u_i,u_{i+1}],i=3,4,\cdots ,n$, we have:

$$(B_{i-3}(u),B_{i-2}(u),B_{i-1}(u),B_i(u))=(T_0({\alpha }_i;t_i),T_1({\alpha }_i;t_i),T_2({\beta }_i;t_i),T_3({\beta }_i;t_i))H_i,$$

(11)

where,

$$H_i=\left|\begin{array}{cccc}{a}_i& b_{i,0}& c_{i,0}& 0\\ 0& b_{i,1}& c_{i,1}& 0\\ 0& b_{i,2}& c_{i,2}& 0\\ 0& b_{i,3}& c_{i,3}& d_i\end{array}\right|,$$

and $t_i(u)=(u-u_i)/h_i,i=0,1,2,\cdots ,n+3$. From Theorem 2, $(T_0(t_{i;}{\alpha }_i),T_1(t_{i;}{\alpha }_i),T_2(t_{i;}{\beta }_i),T_3(t_{i;}{\beta }_i))$ is a B-system of space $T_{{\alpha }_i,{\beta }_i}$. By Theorem 4.2 in reference [27], $H_i$ is a non-singular random totally positive matrix. Thus, the system $(B_{i-3}(u),B_{i-2}(u),B_{i-1}(u),B_i(u))$ is from a totally positive system in space $T_{{\alpha }_i,{\beta }_i}$. □

For any ${\alpha }_i,{\beta }_i$, $a_i,b_{i,j},c_{i,j},d_i>0$ is evident. From Lemma 1, we can get that the sum of each row of the matric $H_i$ is $1$. That is, $H_i$ is a stochastic matrix. Moreover, by directly calculating, it follows that:

$$\left|\begin{array}{cc}{b}_{i,0}& c_{i,0}\\ b_{i,1}& c_{i,1}\end{array}\right|=\frac{{\phi }_{i-1}{d}_{i-1}{d}_{i-2}(3+{\beta }_{i-1})h_i}{(3+{\alpha }_i)h_{i-1}}>0,$$

$$\left|\begin{array}{cc}{b}_{i,0}& c_{i,0}\\ b_{i,2}& c_{i,2}\end{array}\right|=\frac{d_{i-1}{h}_i(a_{i+1}+3)({\lambda }_{i-1}{\mu }_i{h}_i+3{\lambda }_{i-1}{\mu }_i{h}_{i+1}+3{\lambda }_i{\mu }_{i-1}{h}_{i-1})}{9{\mu }_{i-1}(3+{\beta }_i)h_{i-1}{h}_{i+1}^2}+\frac{d_{i-2}{d}_{i-1}(3+{\beta }_{i-1}){\phi }_{i-1}{\phi }_i{h}_i}{{\mu }_{i-1}}>0,$$

$$\begin{array}{l}\left|\begin{array}{cc}{b}_{i,0}& c_{i,0}\\ b_{i,3}& c_{i,3}\end{array}\right|=\frac{a_{i+1}{a}_{i+2}({\alpha }_i+3)({\alpha }_{i+1}+3){\varphi }_i{\varphi }_{i+1}{h}_{i-1}{h}_i}{{\mu }_{i-1}{\mu }_i}+\frac{a_{i+1}{d}_{i-1}{h}_i({\lambda }_{i-1}{\mu }_i{h}_i+3{\lambda }_{i-1}{\mu }_i{h}_{i+1}+3{\lambda }_i{\mu }_{i-1}{h}_{i-1})}{9{\mu }_{i-1}{\mu }_i{h}_{i-1}{h}_{i+1}}+\\ \begin{array}{cccc}& & & \end{array}\frac{a_{i+2}{d}_{i-2}({\alpha }_{i+2}+3)({\beta }_{i-1}+3){\varphi }_{i+1}{\phi }_{i-1}{h}_i^2}{{\mu }_{i-1}{\mu }_i}+\frac{d_{i-2}{d}_{i-1}(3+{\beta }_{i-1})(3+{\beta }_i){\phi }_{i-1}{\phi }_i{h}_i{h}_{i+1}}{{\mu }_{i-1}{\mu }_i}>0,\end{array}$$

$$\left|\begin{array}{cc}{b}_{i,1}& c_{i,1}\\ b_{i,2}& c_{i,2}\end{array}\right|=\frac{h_i(3{\lambda }_{i-1}{\mu }_i{h}_{i+1}+{\lambda }_{i-1}{\mu }_i{h}_i+3{\lambda }_i{\mu }_{i-1}{h}_{i-1})}{9({\alpha }_i+3)({\beta }_i+3){\mu }_{i-1}{h}_{i-1}{h}_{i+1}^2}{a}_{i+1}{d}_{i-1}>0,$$

$$\left|\begin{array}{cc}{b}_{i,1}& c_{i,1}\\ b_{i,3}& c_{i,3}\end{array}\right|=\frac{h_i(3{\lambda }_{i-1}{\mu }_i{h}_{i+1}+{\lambda }_{i-1}{\mu }_i{h}_i+3{\lambda }_i{\mu }_{i-1}{h}_{i-1})}{9({\alpha }_i+3){\mu }_i{h}_{i-1}^2{h}_{i+1}^{}}{a}_{i+1}{d}_{i-1}+\frac{({\alpha }_i+3){\varphi }_i{\varphi }_{i+1}{h}_i}{{\mu }_i}{a}_{i+1}{a}_{i+2}>0,$$

$$\left|\begin{array}{cc}{b}_{i,2}& c_{i,2}\\ b_{i,3}& c_{i,3}\end{array}\right|=\frac{(3+{\alpha }_{i+1}){\varphi }_{i+1}{h}_i}{(3+{\beta }_i)h_{i+1}}{a}_{i+1}{a}_{i+2}>0.$$

Thus, the matrix $H_i$ is a non-singular random totally positive matrix.

(6)

Continuity: Given a non-uniform knot vector, for any ${\alpha }_i^{},{\beta }_i^{}\in [0,1]$, $B_i^{}(u)$ has $C_{}^2$ continuity at each knot.

Proof. 

For any ${\alpha }_i,{\beta }_i\in [0,1]$, it could conclude:

$$\begin{array}{l}{B}_i(u_{i+1}^{-})=d_i,\\ B_i(u_{i+1}^{+})=c_{i+1,0},\\ {B^{\prime }}_i(u_{i+1}^{-})=\frac{1}{h_i}({\beta }_i+3)d_i,\\ {B^{\prime }}_i(u_{i+1}^{+})=\frac{1}{h_{i+1}}(3+{\alpha }_{i+1})(c_{i+1,1}-c_{i+1,0}),\\ {B^{″}}_i(u_{i+1}^{-})={\left(\frac{1}{h_i}\right)}^2(6+6{\beta }_i)d_i,\\ {B^{″}}_i(u_{i+1}^{+})={\left(\frac{1}{h_{i+1}}\right)}^2[(6+6{\alpha }_{i+1})c_{i,0}-(12+6{\alpha }_{i+1})c_{i+1,1}+6c_{i+1,2}].\end{array}$$

From Lemma 1 and the above discussion, we have:

$$B_i(u_{i+1}^{+})=B_i(u_{i+1}^{-}),{B^{\prime }}_i(u_{i+1}^{+})={B^{\prime }}_i(u_{i+1}^{-}),{B^{″}}_i(u_{i+1}^{+})={B^{″}}_i(u_{i+1}^{-}).$$

(12)

□

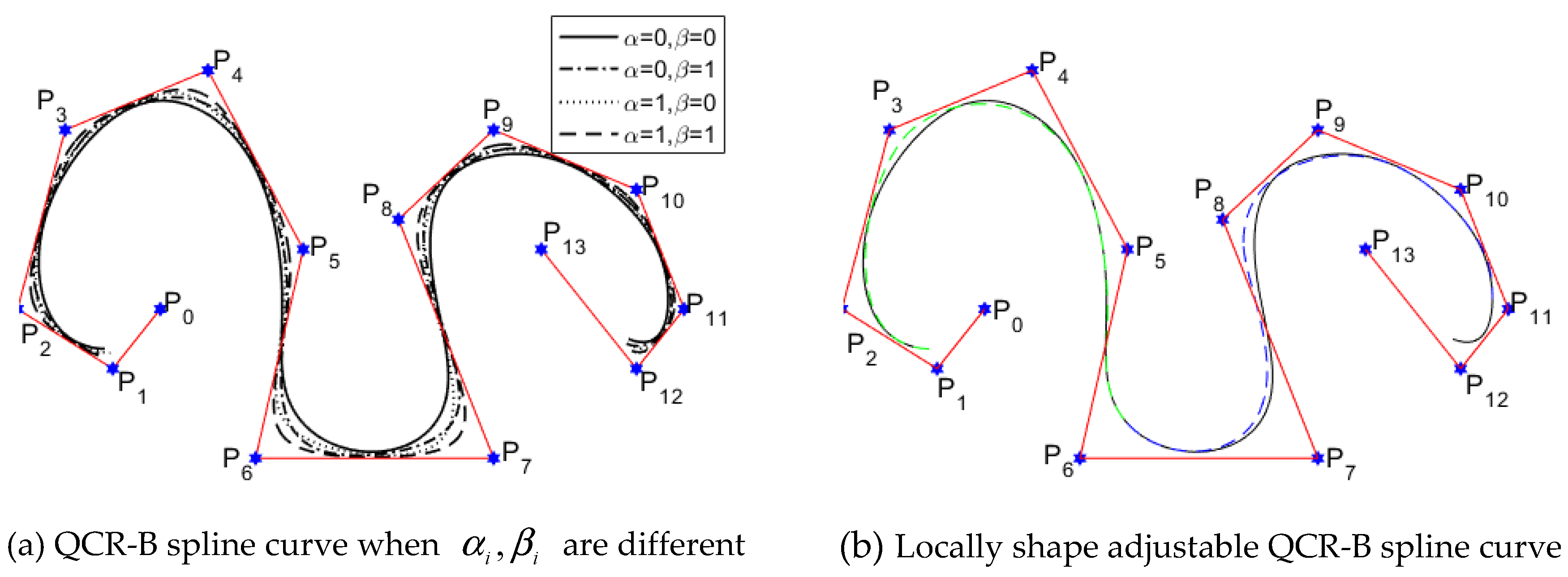
3.4. Non-Uniform QCR-B Spline Curve

3.4.1. Definition and Properties

Definition 6.

When the knot vector$U$and control points$P_i(i=0,1,\dots ,n)$ of non-uniform knots vector are given. A linear combination of the non-uniform QCR-B spline system and control front can generate the non-uniform QCR-B spline curve. For ${\alpha }_i,{\beta }_i\in [0,1],i\ge 3,u\in [u_3,u_{n+1}]$, we call:

$$Q(u)={\displaystyle \sum _{i=0}^n{B}_i(u)P_i}.$$

(13)

is the non-uniform QCR-B spline curve with parameters${\alpha }_i$and${\beta }_i$.

For $u\in [u_i,u_{i+1}]$, the non-uniform QCR-B spline segment of curve $Q_i(u)$ can be expressed as follows:

$$\begin{array}{cc}\hfill Q_i(u)& ={\displaystyle \sum _{i-3}^i{B}_j(u)P_j}=(a_i{P}_{i-3}+b_{i0}{P}_{i-2}+c_{i0}{P}_{i-1})T_0({\alpha }_i;t_i)+\hfill \\ & (b_{i1}{P}_{i-2}+c_{i1}{P}_{i-1})T_1({\alpha }_i;t_i)+(c_{i2}{P}_{i-1}+b_{i2}{P}_{i-2})T_2({\beta }_i;t_i)+\hfill \\ & (d_i{P}_i+c_{i3}{P}_{i-1}+b_{i3}{P}_{i-2})T_3({\beta }_i;t_i).\hfill \end{array}$$

(14)

From the properties of the non-uniform QCR-B spline system (1) and (2), for $u\in [u_i,u_{i+1}]$, the non-uniform QCR-B spline curve $Q_i(u)$ has affine invariance. Furthermore, from the properties of the non-uniform QCR-B spline system (6), the non-uniform QCR-B spline curve $Q_i(u)$ has variation diminishing. Therefore, the non-uniform QCR-B spline curve keeps all the essential properties of the traditional B-spline.

Theorem 3.

Given a non-uniform knot vector$U$, for any${\alpha }_i,{\beta }_i$the non-uniform QCR-B spline curve has$C^2$continuity at each control point.

Proof. 

First, we discuss the continuity of the non-uniform QCR-B spline curve $Q_i(u)$ at knot $u_{i+1}$. In intervals $[u_i,u_{i+1}]$ and $[u_{i+1},u_{i+2}]$, the non-uniform QCR-B spline segments can be separately shown as follows:

$$\begin{array}{l}{Q}_i(u)={\displaystyle \sum _{j=i-3}^i{B}_j(u)}{P}_j=(a_i{P}_{i-3}+b_{i,0}{P}_{i-2}+c_{i,0}{P}_{i-1})T_0({\alpha }_i;t_i)+\\ (b_{i,1}{P}_{i-2}+c_{i,1}{P}_{i-1})T_1({\alpha }_i;t_i)+(b_{i,2}{P}_{i-2}+c_{i,2}{P}_{i-1})T_2({\beta }_i;t_i)+\\ (b_{i,3}{P}_{i-2}+c_{i,3}{P}_{i-1}+d_i{P}_i)T_3({\beta }_i;t_i),\begin{array}{c}\end{array}u\in [u_i,u_{i+1}],\end{array}$$

and

$$\begin{array}{l}{Q}_{i+1}(u)={\displaystyle \sum _{j=i-2}^{i+1}{B}_j(u)}{P}_j=(a_{i+1}{P}_{i-1}+b_{i+1,0}{P}_{i-1}+c_{i+1,0}{P}_i)T_0({\alpha }_{i+1};t_{i+1})+\\ (b_{i+1,1}{P}_{i-1}+c_{i+1,1}{P}_i)T_1({\alpha }_{i+1};t_{i+1})+(b_{i+1,2}{P}_{i-1}+c_{i+1,2}{P}_i)T_2({\beta }_{i+1};t_{i+1})+\\ (b_{i+1,3}{P}_{i-1}+c_{i+1,3}{P}_i+d_{i+1}{P}_{i+1})T_3({\beta }_{i+1};t_{i+1}),\begin{array}{c}\end{array}u\in [u_{i+1},u_{i+2}].\end{array}$$

separately, therefore:

$$\begin{array}{l}{Q}_i(u_{i+1}^{+})=b_{i3}{P}_{i-2}+c_{i3}{P}_{i-1}+d_{i}P,\\ Q_{i+1}(u_{i+1}^{-})=a_{i+1}{P}_{i-2}+b_{i+1,0}{P}_{i-1}+c_{i+1,0}{P}_i,\\ {Q^{\prime }}_i(u_{i+1}^{+})=(b_{i3}{P}_{i-2}+c_{i3}{P}_{i-1}+d_i{P}_i)({\beta }_i+3)-(b_{i2}{P}_{i-2}+c_{i2}{P}_{i-1})({\beta }_i+3),\\ {Q^{\prime }}_{i+1}(u_{i+1}^{-})=(b_{i+1,1}{P}_{i-1}+c_{i+1,1}{P}_i)({\alpha }_{i+1}+3)-(a_{i+1}{P}_{i-2}+b_{i+1,0}{P}_{i-1}+c_{i+1,0}{P}_i)({\alpha }_{i+1}+3),\\ {Q^{″}}_i(u_{i+1}^{+})=6(b_{i1}{P}_{i-2}+c_{i1}{P}_{i-1})-6(b_{i2}{P}_{i-2}+c_{i2}{P}_{i-1})({\beta }_i+2)+6(b_{i3}{P}_{i-2}+c_{i3}{P}_{i-1}+d_i{P}_i)({\beta }_i+1),\\ {Q^{″}}_{i+1}(u_{i+1}^{-})=6(b_{i+1,2}{P}_{i-1}+c_{i+1,2}{P}_i)-6(b_{i+1,1}{P}_{i-1}+c_{i+1,1}{P}_i)({\alpha }_i+2)+6(a_{i+1}{P}_{i-2}+b_{i+1,0}{P}_{i-1}+c_{i+1,0}{P}_i)({\alpha }_i+1).\end{array}$$

□

Available from Lemma 1 and the above discussion, we can easily obtain that:

$$Q_i(u_{i+1}^{+})=Q_{i+1}(u_{i+1}^{-}),{Q^{\prime }}_i(u_{i+1}^{+})={Q^{\prime }}_{i+1}(u_{i+1}^{-}),{Q^{″}}_i(u_{i+1}^{+})={Q^{″}}_{i+1}(u_{i+1}^{-}).$$

Figure 4 shows the rotating surface of the vase obtained by the rotation of the $C^2$ continuous QCR-B spline curve, which provides a good tool for surface design.

3.4.2. Local Adjustment

Since the QCR-B spline curve $Q(u)$ has parameters ${\alpha }_i^{},{\beta }_i$. The shape of the $Q(u)$ could be locally modified by changing the value of ${\alpha }_i,{\beta }_i$ when keeping the control polygon fixed. From Equation (13), when $u\in [u_i,u_{i+1}]$, the shape of the $Q(u)$ could be affected by ${\alpha }_i^{},{\beta }_i^{}$. Moreover, ${\alpha }_i$ can control the shape of the four segments on $[u_{i-2},u_{i+2}]$, and ${\beta }_i$ can control the shape of the four segments on $[u_{i-1},u_{i+3}]$.

Trends of the QCR-B spline curve $Q(u)$ can be predicted by altering the values of the ${\alpha }_i,{\beta }_i$. When the value of ${\alpha }_i,{\beta }_i$ increases, the coefficient of $P_{i-3},P_i$ decreases and the coefficient of the $P_{i-2},P_{i-1}$ increases. Therefore, when ${\alpha }_i,{\beta }_i$ increases synchronously, the curve $Q(u)$ approaches to the edge $P_{i-2}{P}_{i-1}$. As ${\alpha }_i$ increases, the curve $Q(u)$ approaches to $P_{i-2}$. As ${\beta }_i$ increases, the curve $Q(u)$ approaches to $P_{i-1}$. Figure 5 shows the QCR-B spline curve. Figure 5a displays the case where the parameters ${\alpha }_i,{\beta }_i$ are different. Figure 5b displays that the curve has a locally adjustable property.

3.5. QCR-BB System over Triangular Domain

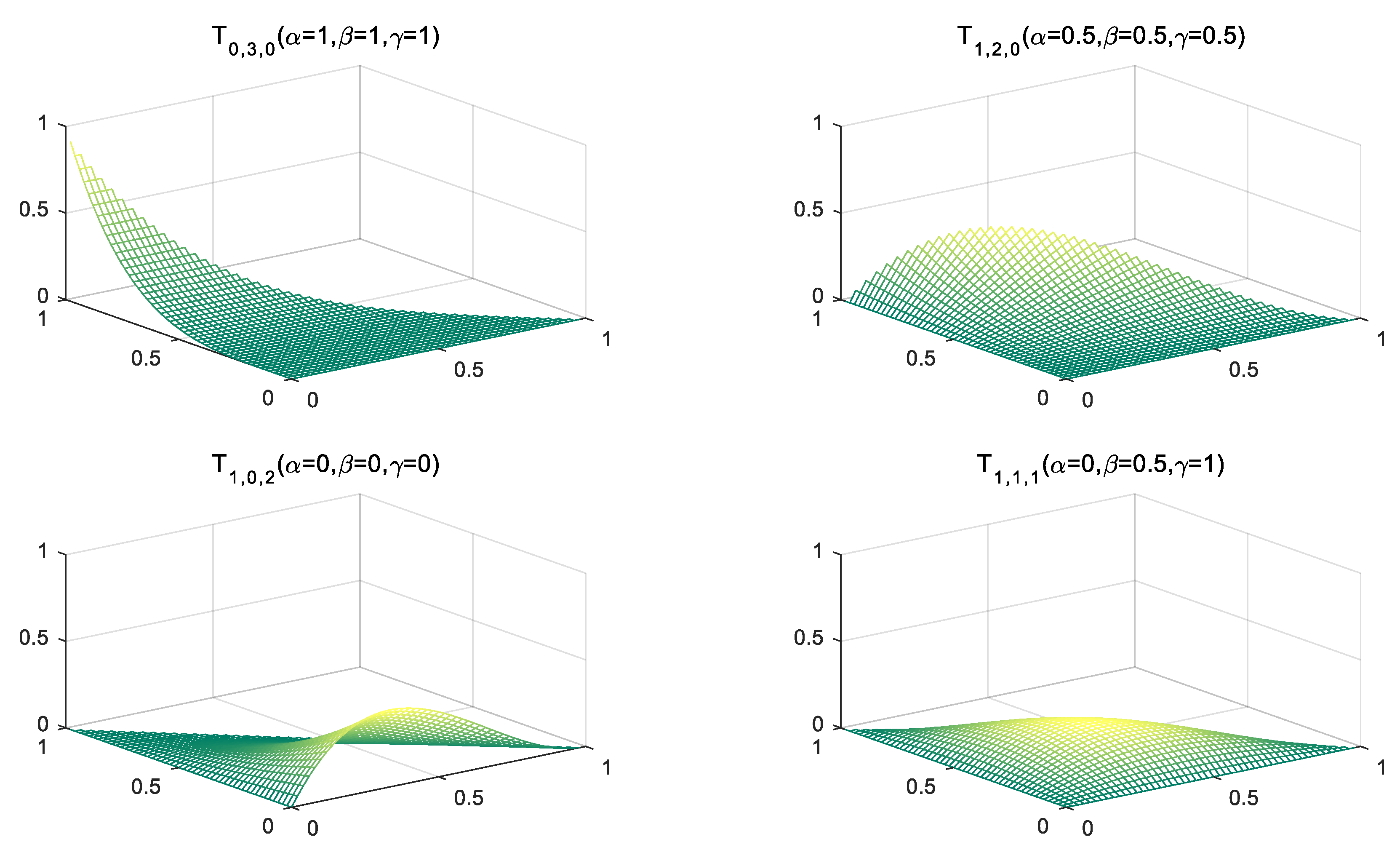
3.5.1. Construction of the QCR-BB System

Definition 7.

For$D=\{(u,v,w)|u+v+w=1,u\ge 0,v\ge 0,w\ge 0\}$, the ten polynomials are called a QCR-BB system concerning three parameters$\alpha ,\beta$, and$\gamma$over the triangular domain D:

$$\{\begin{array}{l}{T}_{3,0,0}^3(\alpha ,\beta ,\gamma ;u,v,w)=u^3(1-\alpha +\alpha u),\\ T_{0,3,0}^3(\alpha ,\beta ,\gamma ;u,v,w)=v^3(1-\beta +\beta v),\\ T_{0,0,3}^3(\alpha ,\beta ,\gamma ;u,v,w)=w^3(1-\gamma +\gamma w),\\ T_{2,1,0}^3(\alpha ,\beta ,\gamma ;u,v,w)=u^{2}v(3+\alpha u),\\ T_{2,0,1}^3(\alpha ,\beta ,\gamma ;u,v,w)=u^{2}w(3+\alpha u),\\ T_{1,2,0}^3(\alpha ,\beta ,\gamma ;u,v,w)=v^{2}u(3+\beta v),\\ T_{0,2,1}^3(\alpha ,\beta ,\gamma ;u,v,w)=v^{2}w(3+\beta v),\\ T_{1,0,2}^3(\alpha ,\beta ,\gamma ;u,v,w)=w^{2}u(3+\gamma w),\\ T_{0,1,2}^3(\alpha ,\beta ,\gamma ;u,v,w)=w^{2}v(3+\gamma w),\\ T_{1,1,1}^3=1-{\displaystyle \sum _{\begin{array}{l}i+j+k=3\\ i\cdot j\cdot k\ne 1\end{array}}{T}_{i,j,k}^3(\alpha ,\beta ,\gamma ;u,v,w).}\end{array}$$

Lemma 2.

For any$u,v,w\ge 0$, when$u+v+w=1$, it follows that:

$$1-[3(u^2+v^2+w^2)-2(u^3+v^3+w^3)]=6uvw.$$

Proof. 

For any $u,v,w\ge 0$, when $u+v+w=1$, by directly computing, we have:

$$\begin{array}{l}\begin{array}{c}\end{array}\begin{array}{c}\end{array}1-[3(u^2+v^2+w^2)-2(u^3+v^3+w^3)]\\ ={(u+v+w)}^3-[3(u^2+v^2+w^2)-2(u^3+v^3+w^3)]\\ =u^3+v^3+w^3+3u^{2}v+3u{v}^2+3u^{2}w+3u{w}^2+3v^{2}w\\ \begin{array}{c}\end{array}+3v{w}^2+6uvw-3u^2-3w^2-3v^2+2u^3+2w^3+2v^3\\ =u^2(3u+3v+3w)+v^2(3u+3v+3w)\\ \begin{array}{c}\end{array}+w^2(3u+3v+3w)+6uvw-3u^2-3v^2-3w^2\\ =6uvw.\end{array}$$

□

3.5.2. Properties of the QCR-BB System

From Equation (14), the following properties can be obtained:

(1)

Nonnegativity: For any $i,j,k\in N,i+j+k=3$, there are $T_{i,j,k}^3(\alpha ,\beta ,\gamma ;u,v,w)\ge 0.$

(2)

Unity:

$${\displaystyle {\sum }_{i+j+k=3}{T}_{i,j,k}^3}(\alpha ,\beta ,\gamma ;u,v,w)=1.$$

(3)

Symmetry:

$$\begin{array}{l}{T}_{i,j,k}^3(\alpha ,\beta ,\gamma ;u,v,w)=T_{i,k,j}^3(\alpha ,\gamma ,\beta ;u,w,v;)\\ =T_{j,k,i}^3(\beta ,\gamma ,\alpha ;v,w,u)=T_{j,i,k}^3(\beta ,\alpha ,\gamma ;v,u,w;)\\ =T_{k,j,i}^3(\gamma ,\beta ,\alpha ;w,v,u)=T_{k,i,j}^3(\gamma ,\alpha ,\beta ;w,u,v;).\end{array}$$

(4)

Boundary property:

If $w=0$, the ten system $T_{i,j,k}^3(\alpha ,\beta ,\gamma ;u,v,w)$ described in Equation (14) could degenerate to the QCR-Bernstein system given in Equation (1).

(5)

Linear independence: $T_{i,j,k}^3(\alpha ,\beta ,\gamma ;u,v,w)$ are linear independence.

Proof. 

We will proof properties (2) and (5) as follows, and the remaining properties are easy to be verified.

(2) For any $\alpha ,\beta ,\gamma$ and $i\cdot j\cdot k\ne 1$, we have $T_{i,j,k}^3(\alpha ,\beta ,\gamma ;u,v,w)\ge 0$. However, for $T_{i,j,k}^3(\alpha ,\beta ,\gamma ;u,v,w)$, from the Lemma 2, we have:

$$\begin{array}{ccc}\hfill T_{1,1,1}^3(\alpha ,\beta ,\gamma ;u,v,w)& =& 1-{\displaystyle \sum _{\begin{array}{l}i+j+k=3\\ i\cdot j\cdot k\ne 1\end{array}}\begin{array}{c}\begin{array}{c}\end{array}{T}_{i,j,k}^3(\alpha ,\beta ,\gamma ;u,v,w)\end{array}}\hfill \\ & =& {(u+v+w)}^3+2(u^3+v^3+w^3)-3(u^2+v^2+w^2)\hfill \\ & =& 6uvw\ge 0.\hfill \end{array}$$

□

(5) For any $\alpha ,\beta ,\gamma \in [0,1],{\xi }_{i,j,k}\in R$, the following linear combination is considered:

$${\displaystyle \sum _{i+j+k=3}\begin{array}{c}\end{array}{\xi }_{i.j.k}{T}_{i,j,k}^3(\alpha ,\beta ,\gamma ;u,v,w)=0}.$$

Let $w=0$, it can:

$${\displaystyle \sum _{i=0}^3{\xi }_{i,3-i,0}{T}_{i,j,k}^3(\alpha ,\beta ;u)}=0.$$

According to the linear independence of the $T_i^{}(t)$, we have ${\xi }_{i,(i-3),0}=0(i=0,1,2,3)$. Similarly, we have, ${\xi }_{i,0,(i-3)}=0,{\xi }_{i,(i-3),0}=0(i=0,1,2,3)$. Finally, we can easily get ${\xi }_{1,1,1}=0$. □

Figure 6 shows the images of the QCR-BB system.

3.5.3. The QCR-BB Patch

Definition 8.

For$D=\{(u,v,w)|u+v+w=1,u\ge 0,v\ge 0,w\ge 0\}$, we give the control mesh$P_{i,j,k}\in R^3$, a linear combination of the non-uniform QCR-BB system and the control mesh can generate a QCR-BB patch. We call:

$$R(u,v,w)={\displaystyle \sum _{i+j+k=3}\begin{array}{c}\end{array}{T}_{i,j,k}^3(u,v,w;\alpha ,\beta ,\gamma )P_{i,j,k}}(u,v,w)\in D,$$

as a non-uniform QCR-BB patch with$\alpha ,\beta$, and$\gamma$.

The properties of the related QCR-BB patches are as follows:

(1)

Convex hull and affine invariance: Given that the QCR-BB system has the unity and non-negativity, therefore, the QCR-BB patches have the property of convex hull and affine invariance.

(2)

Attribution of corner interpolation: By directly computing, that is:

$$\begin{array}{l}R(0,0,1)=P_{0,0,3},\\ R(0,1,0)=P_{0,3,0},\\ R(1,0,0)=P_{3,0,0}.\end{array}$$

The above expressions show that the $R(u,v,w)$ on the triangular domain has three interpolation corner points.

(3)

Corner point tangent plane: Let $w=1-u-v$, it can:

$$\begin{array}{l}{\frac{\delta R(u,v,w)}{\delta u}|}_{(1,0,0)}=(\alpha +3)(P_{3,0,0}-P_{2,0,1}),\\ {\frac{\delta R(u,v,w)}{\delta v}|}_{(1,0,0)}=(\alpha +3)(P_{2,1,0}-P_{2,0,1}),\\ {\frac{\delta R(u,v,w)}{\delta u}|}_{(0,1,0)}=(\beta +3)(P_{1,2,0}-P_{2,0,1}),\\ {\frac{\delta R(u,v,w)}{\delta v}|}_{(0,1,0)}=(\beta +3)(P_{0,3,0}-P_{2,0,1}),\\ {\frac{\delta R(u,v,w)}{\delta u}|}_{(0,0,1)}=(\gamma +3)(P_{1,0,2}-P_{0,0,3}),\\ {\frac{\delta R(u,v,w)}{\delta v}|}_{(0,0,1)}=(\gamma +3)(P_{0,1,2}-P_{0,0,3}).\end{array}$$

This indicates that the tangent planes of the QCR-BB patches on the triangular domain at the three corner points of $(1,0,0),(0,1,0),(0,0,1)$ are respectively generated by nine control points $P_{3,0,0},P_{0,3,0},P_{0,0,3},P_{2,1,0},P_{2,0,1},P_{1,2,0},P_{1,0,2},P_{0,1,2},P_{0,2,1}$.

(4)

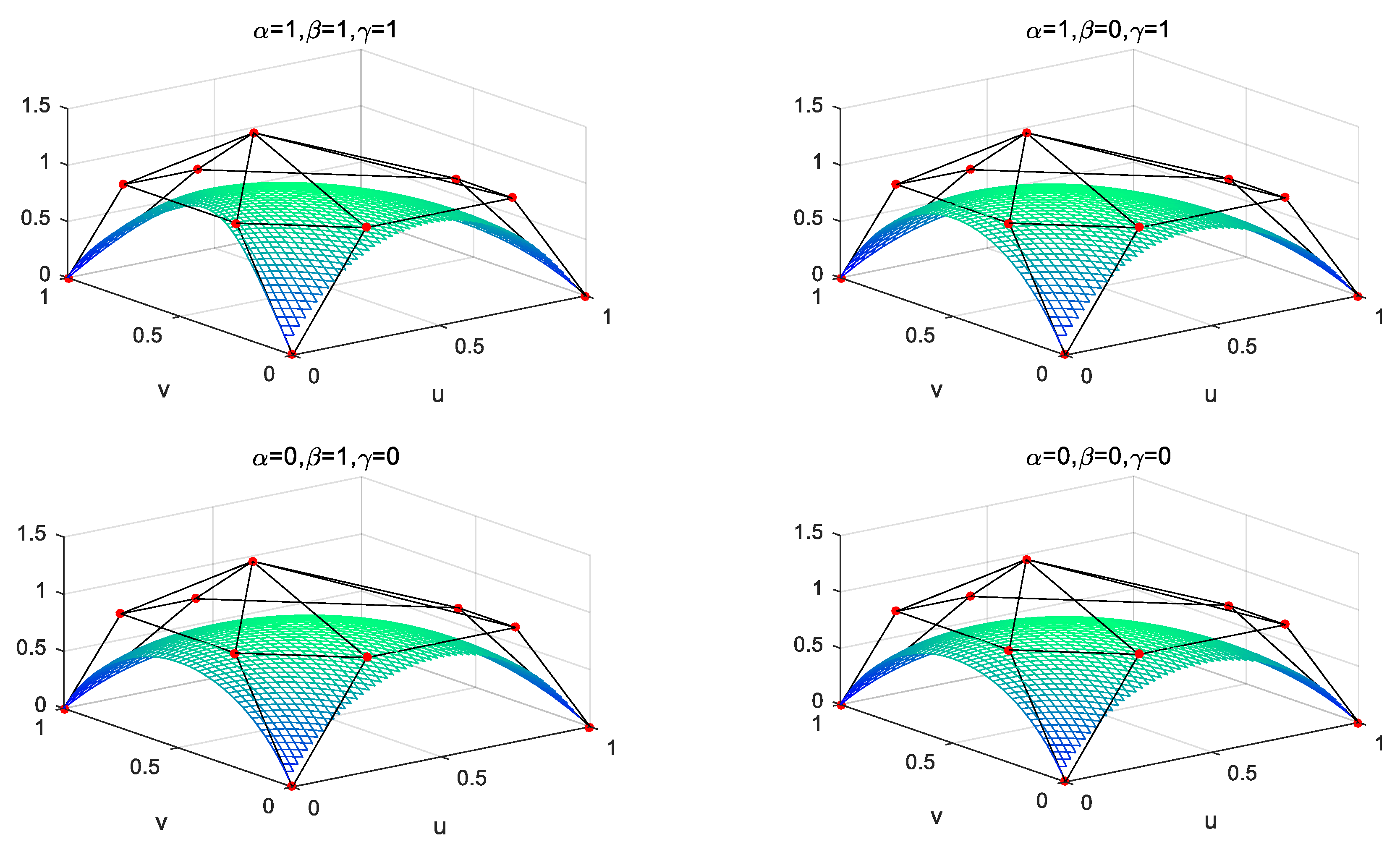
Boundary property: When $w=0$, $R(u,v,w)$ degenerated into a QCR-Bézier curve with two parameters $\alpha ,\beta$. When $u=0$, $R(u,v,w)$ degenerated into a QCR-Bézier curve with $\beta ,\gamma$. When $v=0$, $R(u,v,w)$ degenerated into a QCR-Bézier curve with $\alpha ,\gamma$. With the values of $\alpha ,\beta$, and $\gamma$ increasing, the QCR-BB patch will be approached to the control mesh. Hence, the parameters $\alpha ,\beta$, and $\gamma$ have a tension effect.

(5)

Shape adjustability: The shape of the $R(u,v,w)$ can be turned-up by modifying the value of the $\alpha ,\beta$, and $\gamma$ when the control mesh is stabled. With the values of $\alpha ,\beta$, and $\gamma$ increasing, the $R(u,v,w)$ would approach to the control mesh. Hence, it is easy for us to get the parameters $\alpha ,\beta$, and $\gamma$ to have a tension effect. According to the boundary property of the $R(u,v,w)$, each boundary curve $R(u,0,w),R(0,v,w)$, and $R(u,v,0)$ only have two related parameters. Thus, changing a parameter can only affect the shape of two boundary curves. Figure 7 shows the effects of different parameter values on the QCR-BB patch when the control mesh is fixed.

3.5.4. De Casteljau-Type Algorithm

Next, given is a high-efficiency de Casteljau-type algorithm for generating QCR-BB patches. For any $(u,v,w)\in D$, it can:

$$\begin{array}{l}R(u,v,w)=\\ u\left[u\left((1-\alpha +\alpha u)u{P}_{3,0,0}+\frac{3}{2}v{P}_{2,1,0}+\frac{3}{2}w{P}_{2,0,1}\right)+v(\alpha u^2{P}_{2,1,0}+\frac{3}{2}v{P}_{1,2,0}+w{P}_{1,1,1})+w(\alpha u^2{P}_{2,0,1}+v{P}_{1,1,1}+\frac{3}{2}w{P}_{1,0,2})\right]\\ +v\left[u(\frac{3}{2}u{P}_{2,1,0}+\beta v^2{P}_{1,2,0}+w{P}_{1,1,1})+v\left(\frac{3}{2}u{P}_{1,2,0}+(1-\beta +\beta v)v{P}_{0,3,0}+\frac{3}{2}w{P}_{0,2,1}\right)+w(u{P}_{1,1,1}+\beta v^2{P}_{0,2,1}+\frac{3}{2}w{P}_{0,1,2})\right]\\ +w\left[u(\frac{3}{2}u{P}_{2,0,1}+v{P}_{1,1,1}+\gamma w^2{P}_{1,0,2})+v(u{P}_{1,1,1}+\frac{3}{2}v{P}_{0,2,1}+\gamma w^2{P}_{0,1,2})+w\left(\frac{3}{2}u{P}_{1,0,2}+\frac{3}{2}v{P}_{0,1,2}+(1-\gamma +\gamma w)w{P}_{0,0,3}\right)\right]\\ =u(u{P}_{2,0,0}^1+v{P}_{0,1,0}^1+w{P}_{1,0,1}^1)+v(u{P}_{1,1,0}^1+v{P}_{0,2,0}^1+w{P}_{0,1,1}^1)+w(u{P}_{1,0,1}^1+v{P}_{0,1,1}^1+w{P}_{0,0,2}^1)\\ =u{P}_{1,0,0}^2+v{P}_{0,1,0}^2+w{P}_{0,0,1}^2\\ =P_{0,0,0}^3.\end{array}$$

From the above discussion, the following de Casteljau-type algorithm can be obtained:

$$P_{i,j,k}^m=f_{i+1,j,k}^{m-1}(u,v,w)P_{i+1,j,k}^{m-1}+g_{i,j+1,k}^{m-1}(u,v,w)P_{i,j+1,k}^{m-1}+h_{i,j,k+1}^{m-1}(u,v,w)P_{i,j,k+1}^{m-1},$$

where $P_{i+j+k}^0=P_{i+j+k},i,j,k>0,i+j+k=3-m,m=1,2,3,$

$$f_{i+1,j,k}^{m-1}(u,v,w)=\{\begin{array}{l}(1-\alpha +\alpha u)u,(i,j,k,m)=(2,0,0,1),\\ \frac{3}{2}u,(i,j,k,m)=(0,2,0,1),\\ \frac{3}{2}u,(i,j,k,m)=(0,0,2,1),\\ u,other,\end{array}$$

$$g_{i,j+1,k}^{m-1}(u,v,w)=\{\begin{array}{l}\frac{3}{2}v,(i,j,k,m)=(2,0,0,1),\\ (1-\beta +\beta v)v,(i,j,k,m)=(0,2,0,1),\\ \frac{3}{2}v,(i,j,k,m)=(0,0,2,1),\\ v,other.\end{array}$$

$$h_{i,j,k+1}^{m-1}(u,v,w)=\{\begin{array}{l}\frac{3}{2}w,(i,j,k,m)=(0,0,0,1),\\ \frac{3}{2}w,(i,j,k,m)=(0,2,0,1),\\ (1-\gamma +\gamma w)w,(i,j,k,m)=(0,0,2,1),\\ w,other.\end{array}$$

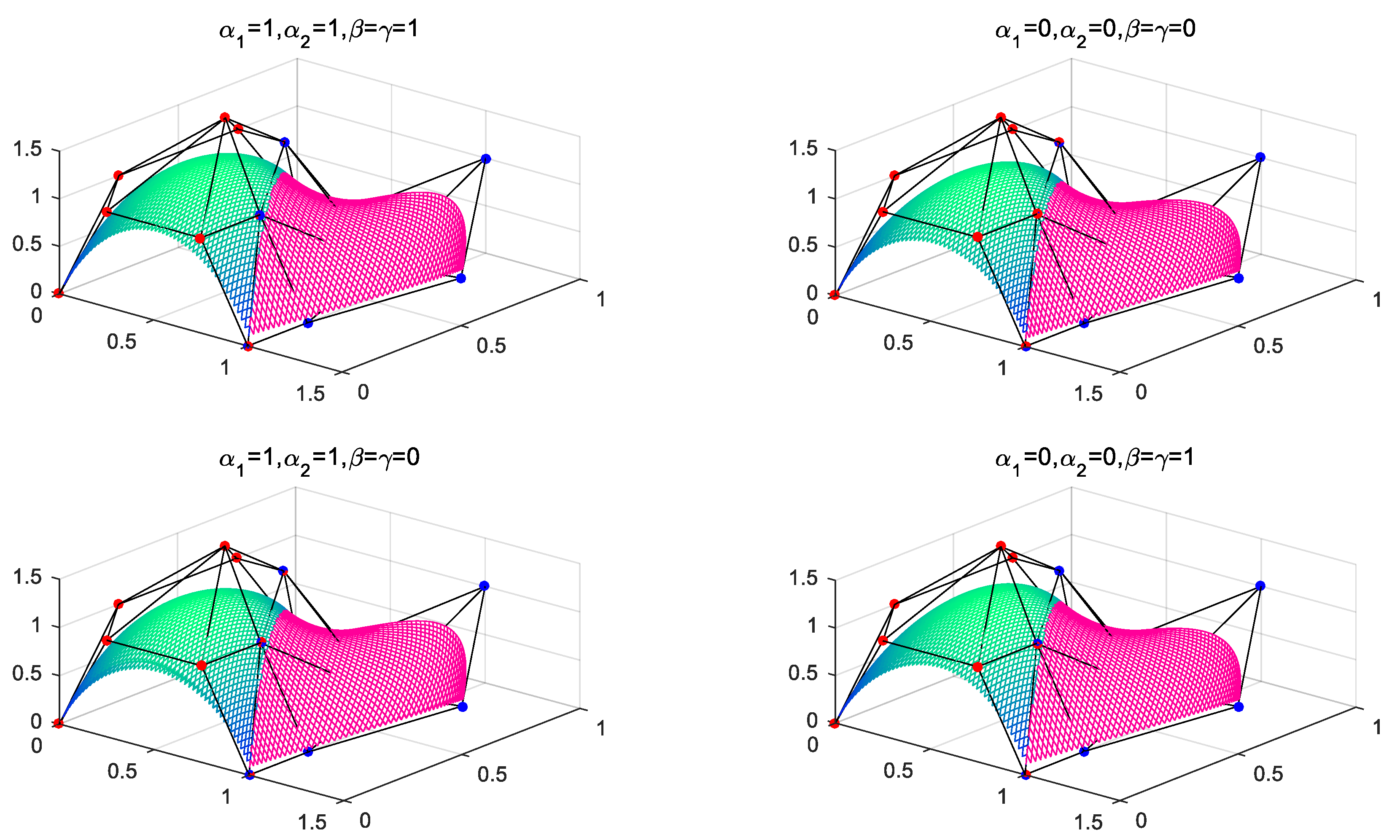
3.5.5. Joining of QCR-BB Patches

In the actual geometric design, a single patch is difficult to describe complex geometric shapes, so we will need to join two or more patches to meet complex geometric designs. Next, we will give the conditions of $G^1$ continuity of two QCR-BB patches as follows:

We give two QCR-BB patches as follows:

$$R_1(u,v,w)={\displaystyle \sum _{i+j+k=3}{T}_{i+j+k}^3({\alpha }_1,\beta ,\gamma ;u,v,w)P_{i,j,k}},(u,v,w)\in D,$$

$$R_2(u,v,w)={\displaystyle \sum _{i+j+k=3}{T}_{i+j+k}^3({\alpha }_2,\beta ,\gamma ;u,v,w)}{Q}_{i,j,k},(u,v,w)\in D.$$

If the control points meet the following conditions:

$$P_{0,j,k}=Q_{0,j,k},$$

(15)

we can obtain that $R_1(u,v,w)$ and $R_2(u,v,w)$ have a common boundary curve: $R_1(0,v,w)=R_2(0,v,w),v+w=1$. Under this occasion, the two QCR-BB patches are $C^0$ continuity.

We differentiate on $R_1(0,v,1-v)$ about variable $v$, and the following equation is obtained:

$$\begin{array}{c}\frac{d{R}_1(0,v,1-v)}{dv}=-(4\beta v^3+3v^2-3\beta v^2)(P_{0,2,1}-P_{0,3,0})-6v(1-v)(P_{0,1,2}-P_{0,2,1})\\ +[4\gamma {(1-v)}^3+3{(1-v)}^2-3\gamma {(1-v)}^2](P_{0,1,2}-P_{0,0,3}).\end{array}$$

(16)

Additionally, we will be differentiating on $R_1(0,v,1-v)$ and $R_2(u,v,1-u-v)$ about variable $u$:

$$\begin{array}{c}\frac{\partial R_1(u,v,1-u-v)}{\partial u}=(4\beta v^3+3v^2-3\beta v^2)(P_{1,0,2}-P_{0,2,1})+6v(1-v)(P_{1,1,1}-P_{0,1,2})\\ +[4\gamma {(1-v)}^3+3{(1-v)}^2-3\gamma {(1-v)}^2](P_{1,0,2}-P_{0,0,3}),\end{array}$$

(17)

$$\begin{array}{c}\frac{\partial R_2(u,v,1-u-v)}{\partial u}=(4\beta v^3+3v^2-3\beta v^2)(Q_{1,0,2}-Q_{0,2,1})+6v(1-v)(Q_{1,1,1}-Q_{0,1,2})\\ +[4\gamma {(1-v)}^3+3{(1-v)}^2-3\gamma {(1-v)}^2](Q_{1,0,2}-Q_{0,0,3}),\end{array}$$

(18)

The $G^1$ continuity condition of two QCR-BB patches $R_1(u,v,w)$ and $R_2(u,v,w)$ is that the two vectors given by Equation (16) to Equation (18) are collinear for any variable $v$ and can be shown as:

$${\frac{\partial R_2(u,v,1-u,v)}{\partial u}|}_{u=0}=\lambda \frac{d{R}_1(0,v,1-v)}{du}+\mu \frac{\partial R_1(u,v,1-u,v)}{\partial u}{|}_{u=0}.$$

where $\lambda$ and $\mu$ are arbitrary constants. Thus, the following conditions can be obtained:

$$\begin{array}{l}{Q}_{1,2,0}-Q_{0,2,1}=\lambda (P_{0,3,0}-P_{0,2,1})+\mu (P_{1,0,2}-P_{0,2,1}),\\ Q_{1,1,1}-Q_{0,1,2}=\lambda (P_{0,2,1}-P_{0,1,2})+\mu (P_{1,1,1}-P_{0,1,2}),\\ Q_{1,0,2}-Q_{0,0,3}=\lambda (P_{0,1,2}-P_{0,0,3})+\mu (P_{1,0,2}-P_{0,0,3}).\end{array}$$

(19)

From the above discussions, the following theorem can be obtained.

Theorem 4.

For any${\alpha }_i,\beta ,\gamma \in [0,1],i=1,2$, if the control points satisfy Equation (15) and Equation (19), simultaneously, then the two QCR-BB patches are$G^1$ continuity.

Figure 8 shows the $G^1$ continuity of two QCR-BB patches with different parameters.

4. Conclusions

Within the theoretical framework of the QEC space, a set of B-systems with two parameters was constructed. The novel system overcomes the shortcomings of the traditional literature that only discusses curve flexibility but neglects important properties (variation diminishing and totally positive). Based on the new system, the related QCR Bézier curves are constructed. A large experimental show of the non-uniform B-spline curves based on the B-system not only retains the excellent properties of the traditional B-spline method but also practical properties such as local shape adjustability and $C^2$ continuity. Moreover, the new system is also extended to the triangular domain, and the QCR-BB patches are defined, which is proved to have flexible shape adjustability. Under certain conditions, we give the conditions of the $G^1$ continuity joining patches of two QCR-BB patches. Thus, the curve and patch constructed in this work have a strong ability to geometric modeling. Our future work will pay attention to the precise quantitative analysis of the influence of parameters on a B-spline curve and the analysis of the cusps and inflection points of the proposed curve is necessary to meet the needs of complex modeling design.