Abstract
The apparel industry houses a huge amount and variety of data. At every step of the supply chain, data is collected and stored by each supply chain actor. This data, when used intelligently, can help with solving a good deal of problems for the industry. In this regard, this article is devoted to the application of data mining on the industry’s product data, i.e., data related to a garment, such as fabric, trim, print, shape, and form. The purpose of this article is to use data mining and symmetry-based learning techniques on product data to create a classification model that consists of two subsystems: (1) for predicting the garment category and (2) for predicting the garment sub-category. Classification techniques, such as Decision Trees, Naïve Bayes, Random Forest, and Bayesian Forest were applied to the ‘Deep Fashion’ open-source database. The data contain three garment categories, 50 garment sub-categories, and 1000 garment attributes. The two subsystems were first trained individually and then integrated using soft classification. It was observed that the performance of the random forest classifier was comparatively better, with an accuracy of 86%, 73%, 82%, and 90%, respectively, for the garment category, and sub-categories of upper body garment, lower body garment, and whole-body garment.
1. Introduction
Data mining and machine learning have been at the forefront of research, helping to solve analytical problems and overcoming business problems [1,2]. The power of data mining in analyzing big data has been proven in various studies [3,4]. The apparel industry is relatively new to the field of data mining and machine learning; however, it has a gamut of application areas in retail, production, and other business operations. Businesses, such as Myntra, Zalando, and StitchFix are trying to tap into the potential of data to gain deeper insight into their consumer bases [5,6,7]. They even provide smart recommendations based on customers’ past purchases. Some retailers gather data using machine learning models and then use it to make important business decisions [8]. For instance, with the information extracted from data, they can learn what products sell best and which ones need refining. Mined data can be of immense use to marketing teams in designing appealing and targeted promotions to attract more customers.
With the advent of the internet and massive technological developments, there has also been a rise in e-commerce in the apparel industry. The number of retail channels has increased, with customers buying products through different retail channels, such as mobile commerce, social media commerce, and retail shops [9]. Due to increasing web interactions, there are more ways for customers to leave their digital footprints and for businesses to collect data. These data, available from a multitude of sources and channels, necessitate the adoption of the latest technologies, such as artificial intelligence, big data analytics, and machine learning.
As the contemporary customer relies on online retail channels to make purchases, the need also arises for powerful and intelligent systems that can recommend, personalize, or help the customer in making purchasing decisions. Such models (decision support systems) can help customers in finding the right garments, according to their requirements. The first step towards achieving this is to make the models recognize the different garment categories and corresponding garment attributes. It is important to recommend the right garment to the customer as it directly impacts the customer’s shopping experience as well as the perception of the retailer itself [10]. Moreover, classifying products based on attributes can be beneficial for demand forecasting, as well as efficient assortment planning and comparison by retailers and producers [11]. In this context, this study proposes to utilize the big data available in the apparel industry to support the development of a classification framework by applying data mining and machine learning techniques.
Hence, the focus of this article is to build an integrated model that is capable of identifying garment attributes to predict garment type. Our approach applies data mining techniques to build an intelligent model, which learns from existing training dataset containing garment attributes, categories (upper wear, bottom wear, and whole-body wear garment), and sub-categories (shirt, jeans, dress, blouse, etc.). The classifiers are first individually trained to classify the garment categories (subsystem 1) and sub-categories (subsystem 2). After this, an integrated model is created that consists of both subsystems and provides a soft classification for any new instance that the model is provided with. Generally, this article is a preliminary attempt to use data mining and symmetry-based learning concepts, particularly classification, to support the decision-makers by evaluating product attribute data to identify the garment type.
The rest of the paper is structured as follows: Section 2 discusses the previous research carried in the field of data mining and machine learning in the apparel industry. Section 3 describes the data mining and machine learning algorithms used in this research. Section 4 briefly discusses the research framework adopted. Section 5 presents the results and findings and Section 6 provides the limitations, future scope, and conclusion.
2. Research Background
Even though the application of data mining and machine learning techniques are relatively new in the apparel industry, they have quickly gained popularity in related research. A considerable amount of work is done in improving various operations in the apparel production supply chain, with the help of data mining, which is discussed in the following section.
For instance, achieving a good garment fit has been a big issue in the apparel industry [12]. Nonetheless, attempts have been made to address the issue using various data mining techniques. There are a few sub-areas of research within this that are highly focused, including finding the most relevant body measurements to develop a new sizing system [13,14,15] and evaluating the fit of the garment using virtual try-on [16,17]. N. Zakaria et al. [18] employed principal component analysis, k-means clustering, and regression tree to address issues related to the identification of the most important body measurements. Similarly, Hsu and Wang [19] used Kaiser’s eigenvalue criteria along with the Classification and Regression Trees (CART) decision tree algorithm to identify and classify significant patterns in the body data.
On the other hand, forecasting is another popular research area, where data mining has been used for sales forecasting [20,21,22] and demand forecasting [23,24]. An application of time series on e-commerce to forecast sales trends has been discussed in the study by S.V. Kumar et al. [25]. With their proposed method, it is possible to achieve both short-term and long-term forecasting. The study by Z. Al-halah et al. [26] used fashion images to predict the popularity of styles in the future. They trained a forecasting model using these style images to represent the trend over time. Yet another application of data mining extensively worked upon is recommender systems [27,28]. An excellent overview of the existing apparel recommendation systems is presented in [29]. It highlights the improvement required in creating a comprehensive apparel and user profile to improve the existing recommendation systems and shows the need for long-term recommendations in design and manufacturing. On these lines, Z.H.U. Ming et al. [30] considered both user preference and behavioral data to design an online recommendation system aiming to provide increased relevance of the recommendations. In the study [31], C. Skiada et al. generated association rules using real Point-of-Sales (POS) data to provide recommendations and to understand the customer’s needs and behavior while shopping online or offline.
Furthermore, significant attention has been paid to utilizing image recognition and pattern recognition [32,33], and deep learning for classification of fashion images [34,35]. W. Surakarin et al. focused on classifying upper-body garments using Support Vector Machine (SVM) with a linear kernel to train the machine-learning model to classify clothing into sub-categories and realized an overall accuracy of 73.57%. On the other hand, C.-I. Cheng et al. [36] used neural network and fuzzy sets for garment characterization and measurements. More recently, generative adversarial networks were used by K.E.A. et al. [37] to translate target attributes into fashion images. This method has the advantage of working when the number of attributes to be manipulated in an image is large, which is usually the case with the data in the fashion and apparel industry [38]. This technique is still at a nascent stage, however, and holds immense potential to advance the task of automatic generation of fashion styles.
Classification techniques have also been used to categorize fabric and sewing defects in the industry using computer vision for different applications (e.g., see [39,40] for fabric defects and [41] for garment defects). It is interesting to note that the classification systems have also been employed in image retrieval systems. For example, A. Vuruskan et al. [42] created an intelligent system to select fashion for non-standard female bodies using a genetic algorithm and neural network. More recently, the convolutional neural network has become popular for the task of classification of clothing images. H. Tuinhof et al. [43] trained a convolutional neural network to classify images of fashion products and proposed a system that takes one image as input from the user and provides a range of similar recommendations. Luca Donati et al. [44] worked on automatic recognition and classification of various features of the garment, solely from rendering images of the products, and achieved an accuracy of 75%.
In some other works, Bossard et al. [45] focused on identifying the clothes worn by people in images by first locating the upper body in the image and then extracting the features for garment classification using Support Vector Machine and Random Forest with an accuracy of 35.03% and 38.29%, respectively. An interesting finding of this study was the different training accuracies between 38% and 71% for different garment categories. The study in [46] proposed a cross model search tool, which can do both image annotation and image search by training a neural network with fashion attributes.
When it comes to the classification of garments, most of the studies are associated with image recognition and computer vision. However, when a customer searches for a garment on an online retail channel, they often use certain keywords (garment attributes, categories, styles) while using a retailer’s website, or use ‘hashtags’ while searching on social media retail channels, such as Instagram. Classifying garments using text instead of images can be useful in this scenario. An efficient classification framework for categorizing garment categories according to their attributes can be useful for customers—as it provides better user experience when they receive the correct product suggestions—as well as businesses, as it directly influences sales. In this context, in a study by Hammar, K. et al. [47], they train a classifier using data from Instagram of clothing attributes and used it to predict the clothing with an f1 score of 0.60. The study in [48] trained a support vector machine by using the text representing product description to classify fashion styles by brand and achieved an accuracy of 56.25%.
As has been realized by examining the extant literature in the field of data mining and machine learning in the apparel industry, most of the research related to the classification of an apparel product has been focused on using visual features, while the research using attributes as ‘words’ to train the classification model is scant. Consequently, this study uses ‘words’ to build a classification framework that can predict the category and sub-category of garments, given their product attributes.
3. Machine Learning Algorithms for Garment Classification
Constructing precise and effectual classifiers for big databases is one of the basic tasks of data mining and machine learning algorithms. Typically, classification is one of the initial steps to inspect whether a set of observations can be grouped based on some similarity. A classifier aims to find predictor,, where represents the instance space, i.e., a feature vector of length constituting the features set of the object to be classified, and represents the object level denoting the classification into unique classes [49]. The classification predictor is often trained by training dataset , split from the original dataset of instances , where represents feature-label set of instance. Here, where is the feature set for object or instance and is the label assigned to object or instance. For the binary feature sets i.e., a set of binary variables if selected attributes are present is presented as , thus, .
Building these kinds of effective classification functions or systems is central to data mining. Provided a partial observation and a classification, a system can statistically identify the unobserved attribute. There are various kinds of techniques used for classification such as Decision Trees, Gradient Boost, Naïve Bayes, ensemble Learning methods, etc. However, this study employs four techniques: Decision Trees, Naïve Bayes, Random Forest, and Bayesian Forest, and are discussed in brief below.
3.1. Naïve Bayes (NB) Classification
Naïve Bayes classifier is a probabilistic machine-learning model, which is a collection of classification algorithms based on Bayes’ Theorem. It is considered fast, efficient, and easy to implement. It assumes that the predictive features are mutually independent given the class [50]. In this study, the Bernoulli Naïve Bayes algorithm is used, where each feature is supposed to be a binary-valued variable. Assuming that we have an object represented by a given feature vector of m-dimensions, i.e., , which is a Boolean expressing absence or presence of the ith feature. Based on the features, the object can be classified into a class in . Therefore, according to Bayes theorem [51],
where, is called a posterior probability, i.e., probability of class conditioned to a given feature vector , is known as the likelihood and defined as the probability of feature vector conditioned to class . The most common applications of the NB classifier include sentiment analysis, recommendation engines, and spam filtering, and is considered fast, efficient, and easy to implement [52].
3.2. Decision Trees (DT)
Decision trees are one of the most widely implemented supervised learning algorithms and are considered a structured approach for multiclass classification [53,54]. They are robust and can achieve high accuracy in various tasks while being accountable. The information gained by a decision tree during the training phase is formulated into a hierarchical structure. This structure is easy to interpret even by non-experts. The development of DT usually involves two steps—induction and pruning—in the formation of a tree-like structure. Induction involves tree building, i.e., the formation of nodes and branches of the decision tree. Each node (excluding the terminal nodes) splits the assigned attribute based on the magnitude or category and creates branching leading to nodes of the next attribute. A given node is divided into and such that the training set are classified into two subsets namely and based on the division of a particular feature into and and . The splitting of the feature at the node is carried out such that it creates the node, which is purer (i.e., homogenous in terms of their features) in the divided datasets. Therefore, a feature resulting in better segregation of the training data is placed near to the root node (first node of the tree hierarchy) and, subsequently, the other attributes are divided into an iterative process and placed in the tree hierarchy. In this context, Gini impurity or Gini index is used to determine the homogeneity or purity of the split data, based on the attribute, based on the following formulation [55],
where is the total number of classes, and is the fraction of objects labeled in class.
If the elements of or are of the same class label, no further splitting is done and that particular node is labeled as a terminal node. On the other hand, a node having a mixed labels dataset is further divided into two nodes based on another feature.
Pruning is the process where unnecessary structures are removed from the tree. This reduces the complexity and chances of overfitting making the tree easier to interpret. The basic algorithm iterates through the tree in the top to bottom approach, where the top node with no incoming branch is the root node, the nodes with outgoing branches are internal nodes and all others are leaves. The attributes of a model are depicted by the root and internal nodes, while the target class is depicted by the leaves. To decide the target class of a new instance, the decision tree algorithm begins at the root node, advancing towards the bottom through the internal nodes until it reaches a leaf node. At each node, an assessment is made to choose one of the branches. The new instance is labeled with the class of the concluding leaf node [56].
3.3. Random Forest (RF)
A random forest is an ensemble of multiple decision trees. It is a popular and highly efficient ensemble method for supervised learning algorithms and can be used for both regression and classification. Since the decision tree approach mentioned in Section 3.2 involves a single decision network, the main issue remains that the formed single decision tree may not be suitable for all data. In RF, bootstrap aggregating (bagging) technique is applied to a large set of decision tree learners [57]. Bagging is the process of creating sub-training datasets using the existing data with replacement [58]. Thus, there could be duplicate values in the sample datasets. As the name suggests, the random forest algorithm stochastically selects training sets to create decision trees. During the phase of testing, the RF receives predictions from each tree and then chooses the most efficient solution with the help of voting [59]. In a classification problem, every tree created provides a unit vote and assigns each input to the most probable target class. This collection of trees is also called the forest. It is comparatively a faster method that can identify non-linear patterns in data and is a good solution to a common problem with decision trees of overfitting. It works well for both numerical and categorical data.
3.4. Bayesian Forest (BF)
A Bayesian Forest is another ensemble learning method where the decision tree formation relies on the Bayesian statistics [60]. In RF, the training of the multiple random trees takes place and the appropriate tree configuration is selected, which results in the best classification. In a Bayesian-based random forest method, the Bayesian statistics are used for the selection of random decision trees from a collection of trees. As explained in Section 3.1, the Bayesian approach starts with a prior distribution. Subsequently, it estimates a likelihood function for each set of data in a decision tree. Bayesian forest draws the weights of the trees from an exponential distribution and the prediction is an approximate posterior mean. The mathematical formulation of the method and the computational steps followed can found in [60].
4. Research Methodology
Figure 1 shows an overview of the research framework. The research consists of three steps. The first step explains the dataset and tools used and provides details about the feature and target variables. Second is the data pre-processing step that includes data cleaning, data integration, feature selection, and data reduction. Lastly, the model-building step presents the development of the two subsystems, their integration, and the evaluation methods used.
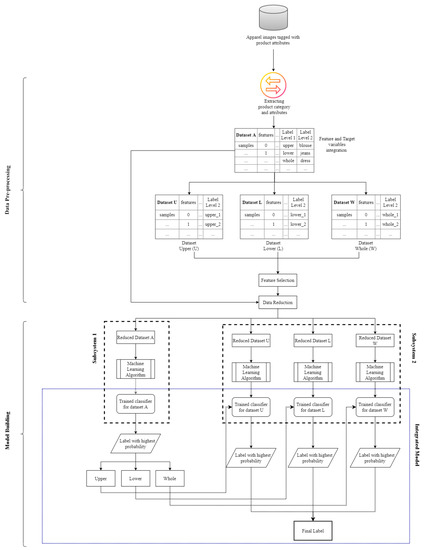
Figure 1.
Research framework.
Following the above-mentioned steps, the aim was to develop a classification model that can predict the garment types based on their attributes. The classification model consists of two-level hierarchy, the first level for classifying the garment category, and the other for classifying the garment sub-category. Hence, the classification system first gives an initial decision on whether a garment is for upper, lower or whole body and then based on this further provides a final class decision i.e., shirt, blouse, trousers, jeans, dress, kimono, and other garment sub-categories.
4.1. Tools and Dataset
The dataset used in this study is an open-source dataset named DeepFashion [61] The original dataset contains 289,222 images of apparel products tagged with 50 garment sub-categories (e.g., shirt, jeans, dresses, etc.) and 1000 garment attributes (A-line, long-sleeve, zipper, etc.). The tagged information was extracted from the dataset to build the classification model while the apparel product images were not used. The garment sub-categories are further grouped into three garment categories: upper wear, bottom wear, and whole-body wear (the list of garment sub-categories within each garment category is available in the Supplementary Materials as Table S1).
The open source dataset consists of different files, out of which four files were required to develop the classification model. The following files were used to extract information relevant to this study:
- List of garment sub-categories tagged in the images along with the corresponding garment categories.
- List of 289,222 image names with the corresponding garment category (upper, lower, whole).
- List of garment attributes containing the attribute name (A-line, long-sleeve, zipper, etc.) and the corresponding attribute type.
- List of 289,222 image names with 1000 columns for each garment attributes providing the presence or absence of the attribute in that image by (−1, 0, 1).
4.2. Data Preprocessing
This section briefly discusses data pre-processing carried out in two steps (data extraction and cleaning and integration) and features selection and data reduction. The following section describes these steps in detail.
4.2.1. Data Extraction, Cleaning, and Integration
As discussed in the previous section, it was important to extract information from different files and then integrate to create a dataset that can be provided as an input to the classification algorithm. The first and second files were used to get a list of image names with corresponding garment categories and sub-categories tagged in that image. As in the fourth file, the garment attributes were represented by numbers (1 to 1000), and the third file contained the attribute names corresponding to each number; the third file was used to replace these numbers by actual attribute names. The resulting dataset and integration of the first and second files were further integrated to get the final dataset.
Finally, this dataset was filtered at two levels. At the first level, dataset A was used that consisted three garment categories as the target variable, i.e., upper wear (referred as Upper or U), bottom wear (referred as Lower or L), and whole-body wear (referred as Whole or W). While at the second level, there were garment sub-categories for each category mentioned at the first level represented by dataset U, L, and W respectively, which included shirts, dresses, jeans, etc.
The resulting dataset was split and transformed to give a dataset for each garment category, as shown in Figure 1. This step was carried to develop the two subsystems of the classification model, discussed in detail in the sections to follow. After splitting, there were four datasets, the initial dataset A containing all the instances of the three garment categories, a dataset U containing instances of upper wear (U), a dataset L containing instances of bottom wear, and a dataset W containing instances of whole-body wear. The garment categories and sub-categories in each dataset were considered as target labels and the garment attributes as the feature variables.
4.2.2. Feature Selection and Data Reduction
For efficient training of the classifier, it was necessary to select the features that are most relevant for the target class. Since, dataset A has all three garment categories as the target classes, having all the garment attributes is understandable. However, after splitting the dataset for each garment category, not all garment attributes might be relevant. Therefore, this step illustrates feature selection for the datasets U, L, and W. This study uses tree-based feature importance measures. Due to the applicability of random forests to a wide range of problems, the capability to create accurate models, and provide variable importance measures, it was chosen as the preferred algorithm to implement the feature selection.
In case of this type of feature selection, the importance of feature in for predicting class in is calculated by adding weighted Gini decreases for the nodes where is used, averaged over all the trees in the forest. Therefore, the importance of each feature is calculated by [62]:
where,
- is the proportion of samples reaching .
- is the impurity function, i.e., Gini importance or mean decrease Gini.
- is the feature used in the split .
This method was chosen, as it is straightforward, fast, and the most accurate method for selecting suitable features for machine learning. Once the feature importance was calculated, the features with a threshold value above ‘1.25 * median’ were selected. The table of most relevant features can be found in the Supplementary Materials as Table S3. After the selection of the most important features for each dataset, the data reduction step was carried out by removing the rows in all four datasets that did not have any attribute tagged in the corresponding image. This resulted in reduced datasets A, U, L, and W; the final number of attributes and observations for these four reduced datasets are summarized in Table 1.

Table 1.
Number of observations and attributes after data reduction.
4.3. Model Building
The main objective of the proposed methodology is to build a classification that predicts the garment type based on its attributes. As depicted in Figure 1, to accomplish this, the model building process in itself was split into two phases—the development of subsystems and integration of the subsystems. In the first phase, the classifiers were trained individually for each dataset. The classifier trained with dataset A led to the formation of subsystem 1. While the classifiers trained with dataset U, L, and W led to the formation of subsystem 2. As discussed in Section 3, the chosen machine learning techniques for training the classifiers were Decision Trees, Naïve Bayes, Bayesian Forest, and Random Forest. The framework of the integrated system with an explanatory instance is depicted in Figure 2.
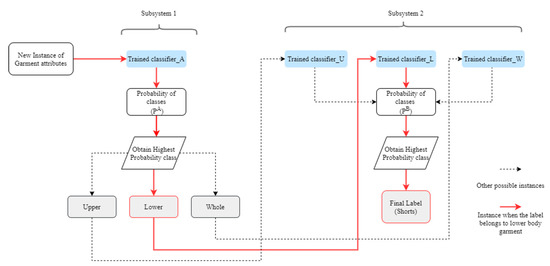
Figure 2.
Framework of the Integrated System.
4.3.1. Development of Subsystems
Model Development
In general, data classification is a two-step process. The first step indicates the learning or training phase, where a model is developed by providing a predetermined set of classes and the corresponding set of training instances. Each instance is assumed to represent a predefined class. The second step, the testing phase, uses a different set of data instances to estimate the classification accuracy of the model. If the model achieves acceptable accuracy, it can be used to classify future unlabeled data instances. Finally, the model acts as a classifier in the decision-making process. The primary focus of this study is the classification of garment attribute data. The process of testing and training is shown in Figure 3.
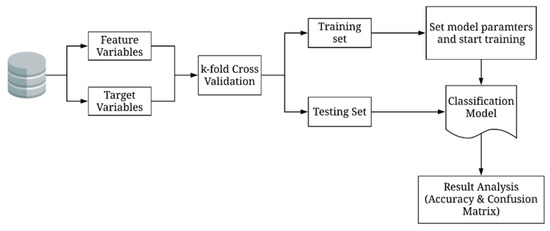
Figure 3.
General testing and training framework for building classifiers.
In order to create the classification models (i.e., ), the four datasets were first split into two parts, 80% used for building the model and the remaining 20% as the validation set for computing the performance of the integrated model. The dataset used for model building was further split into a set of features, , and target variables, . All of the garment attributes constitute the feature space, while the garment categories and sub-categories constitute the target space. Next, the target and feature datasets were split into train and test using stratified k (=10) fold cross-validation. The advantage of using stratified k-fold cross-validation is that it rearranges the data to ensure that each fold is a good representation of the entire dataset and, hence, is generally considered a good strategy for classification problems [63]. Stratified cross-validation is a common preference when dealing with multi-class classification problems, especially in the case of class imbalance [64]. A final evaluation was done using the test set. The following are the steps followed to accomplish stratified k-fold cross-validation:
- The dataset was randomly split into k (=10) equal size partitions.
- From the k partitions, one was reserved as the test dataset for the final evaluation of the model, while the other k-1 partitions were used to model training.
- The process was repeated for each model and machine learning technique k times with each of the k-partitions used exactly once as the test data.
- The k results acquired from each of the test partitions were combined by averaging them, to produce a single estimation.
Following this procedure, all four classifiers were trained separately for each dataset. The classifiers trained using dataset A belonged to subsystem 1, while all the other classifiers belonged to subsystem 2. These classifiers were further integrated into the next section to predict the label of new data instances.
Evaluation
Evaluation is one of the important steps in model building. With this, the accuracy of the classifier can be judged. There are many evaluation metrics available to determine the performance of a classification model. However, for a multiclass classifier, accuracy is the most widely used metric and is calculated as the number of correctly predicted labels divided by the total number of labels. [65]. Besides, a confusion matrix is widely adopted to measure the performance of a supervised machine-learning algorithm. The number of correct and incorrect predictions is aggregated by count values and broken down by category [66]. Hence, this study adopts accuracy and confusion matrix to assess the classification model. Moreover, the precision, recall, and f1-score of all the classifiers are also evaluated. The results from each evaluation metric are discussed in detail in Section 5.
4.3.2. Integration of Subsystems
Up to this point, the two subsystems trained independently, i.e., an instance can be classified into either a garment category or a garment sub-category, and each trained classifier, worked separately to give a prediction. Moreover, there was no way to handle ambiguous cases, where the classifier could not perform a hard classification and resulted in lower accuracy. To tackle these limitations, the concept of soft classification was adopted, which evaluates the conditional probabilities of each class and then realizes the classification based on the evaluated probabilities [67]. The two subsystems were combined by taking advantage of this characteristic. This section discusses the process of achieving the same in detail.
Model Development
Most classification algorithms compute the posterior probability of a class, given the learning data. In case of hard classification, the model directly yields the predicted class, while a soft classification yields a list of probabilities of all the classes in the form , where n is the number of data instances and is the number of classes [68]. Given the complexity of an apparel product, there are more chances of an ambiguous case occurring in the prediction phase of a classification model. Hence, the concept of soft classification was adopted, which indicates the confidence of a model in its prediction.
Thus, the test dataset from each dataset was used to compute the probability of the target classes. For every data instance, the classifier assigned an estimated posterior probability to each class. If the probability mass concentrates in one class, then it is very likely that the instance belongs to that class. However, if the probability mass is highly distributed, then that is considered as an ambiguous case, and making the final prediction using a threshold value becomes important. By using a threshold, a classifier considers the class with a probability above the given threshold and classifies the instance in question accordingly.
For the mathematical computation of this model, let us consider that the apparel product dataset X is represented by where being the total number of instances in the dataset. Each instance is of the form , where is a set of product attributes represented by and is a set of target classes represented by . The set of instances is divided into two sets, train set and test set . The instances in , i.e., are used to train the model , i.e., model to classify garment categories (upper, lower, and whole). Similarly, models, , and are trained to classify garment sub-categories belonging to upper, lower, and whole-body garments, respectively. The datasets used for training these models are explained in Section 4.2.2.
Following this, the test set was used to integrate the functionality of the trained models. In this case, the set of features from was used. When the first instance from is given to the model , it makes a decision among the class probabilities , and the final decision is made using the following formulation,
Depending on the decision , the instance passes through one of the classifiers from , , and , where signifies classifier, subscript indicates the respective dataset, or as described in Section 4.2.1. If is lower (L), then will be utilized for making further classification of the instance and make a decision from the class probabilities in , where is the number of target classes in lower body garment categories, as explained below,
where, represents the maximum in , and represents the second-highest in
The accuracy of the model is calculated by checking whether the final label is the same as the class in the test dataset, i.e., if Hence, the resultant class provided by the model will be given by . (a comprehensive table of the mathematical symbols used is available in the supplementary file as Table S2).
Evaluation
After integrating the two subsystems to create a single model, the validation dataset (not used during the model building process) was used to evaluate the model again to see if the accuracy of the classifiers changed positively, as discussed in detail in the next section.
5. Experimentation and Results
This section summarizes the results of the experiments. First, the results from the classification of the individual subsystems are discussed with a comparison between the performances of the four algorithms—Naïve Bayes, Decision Trees, Bayesian Forest, and Random Forest for each dataset. Further, the confusion matrix for each algorithm and subsystem is presented. Following this, the results from the integration of the two subsystems using soft classification are described. Finally, for better comprehension of the working of the entire system, a brief description is provided.
5.1. Analysis of Subsystems
In this study, four algorithms were used to classify the garment data—Naïve Bayes, Decision Trees, Bayesian Forest, and Random Forest. All the classifiers were provided with the same dataset and the model parameters of each classifier are presented in Table 2. As described in Section 4.3.2, the dataset was divided into training and testing data, using ten-fold cross-validation. Figure 4 shows the accuracy of the four classification models for each dataset (A, U, L, and W) as achieved during the k cross-validation implementation. The box plot represents the overall pattern of accuracies achieved by each classifier for each dataset. Further, the evaluation of this model is carried out with a validation dataset to calculate accuracy, precision, recall, and f-score as shown in Table 3. It should be noted that this validation dataset was not used during the model building process. As is evident in Figure 4 and Table 3, for all the datasets, RF achieved the highest performance in terms of accuracy, precision, and recall. The boxplot for RF is comparatively shorter for dataset A, indicating less variation in accuracy during the different training cycles. While for datasets U and W, this variation seems larger. This could correspond to the fact that there are a larger number of target classes for these two datasets. For dataset L, even though the box plot is short, the data is skewed towards the quartile 3 and 4. Besides, there is the presence of an outlier, which is also the case for DT and RF. An outlier can be seen in DT for all datasets, except dataset W. Apart from this, the boxplot for NB is comparatively consistent for all datasets, although the accuracy attained by this classifier is lowest amongst all the classifiers as resulted from the k cross-validation presented in the box plot in Figure 4.

Table 2.
Model Parameters for each classification algorithm.
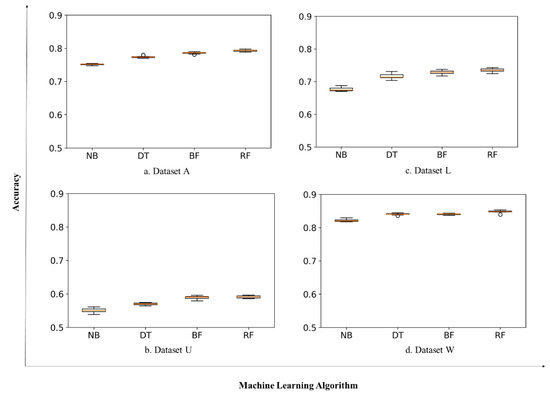
Figure 4.
Ten-fold cross validation results for (a) Dataset A, (b) Dataset U, (c) Dataset L, and (d) Dataset W.

Table 3.
Evaluation metrics for all classifiers and datasets.
As can be further analyzed from Figure 4, dataset U achieved the lowest accuracy for all the classifiers, while datasets A and W, the highest. One of the reasons for the low accuracy for dataset U could be more variation in the product types, i.e., the product attributes used in each upper body garment sub-category highly varied. This corresponds to the fact that in general, there is a higher number of styles available in the upper wear garment category.
To further validate the proposed method, a confusion matrix for all the classifiers and datasets was constructed using the validation dataset (data instances unseen by the model). As an example, Figure 5 shows the confusion matrix for the RF classifier (the confusion matrix for all of the other classifiers can be found in Supplementary Materials, Figures S1–S3). Each row represents the instances of the true label, while each column represents the instances of the predicted label. The diagonal represents the number of correct classifications and the off-diagonal instances represent the miss-classifications by the model.
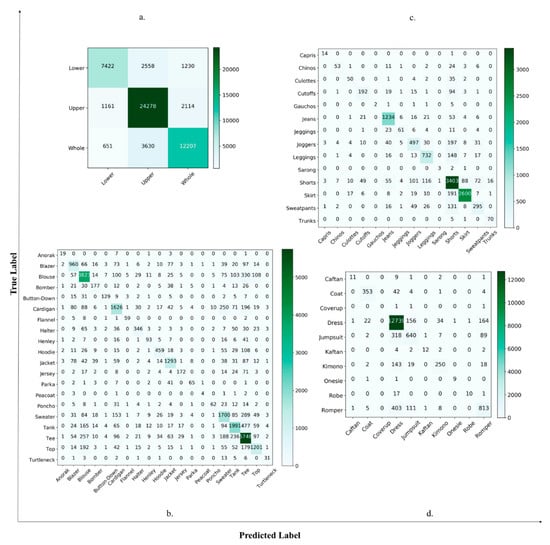
Figure 5.
Confusion Matrix for Random Forest Classifier for dataset (a) A, (b) U, (c) L, and (d) W.
As can be seen in Figure 5a, the number of correctly classified upper, lower, and whole-body garment categories are 35,402, 11,710, and 18,524, respectively, out of 39,486, 16,775, and 24,661. As in Figure 5b, the most correctly classified garment sub-categories (in lower) are shorts, skirts, and jeans. Similarly, in Figure 5d, tee, blouse, and tank, and Figure 5c, dress, romper, and jumpsuit, are the top three most correctly classified garment sub-categories.
5.2. Analysis of the Integrated System
Until this point, the two subsystems worked independently, with an average accuracy of 71%. To integrate the two subsystems and handle ambiguous cases and improve the accuracy of classification, the concept of soft classification was introduced, as discussed in Section 4.3.2. To do this, the pre-trained classifiers provided the probability of the classes instead of yielding the predicted class. Subsystem 1 predicted the probability of the garment categories (upper, lower, or whole-body garment), and subsystem 2 predicted the probability of garment sub-categories (dress, blouse, tee, capris, trousers, etc.). The integrated model was presented in Section 4.3 with an instance shown in Figure 2.
To present an overview of the working of the whole system, let us consider the following instance. When subsystem 1 receives a string of garment attributes, it will first try to label the data instance into one of the three target classes, upper, lower, or whole-body garments. The class with the highest probability will be considered as the resultant label from subsystem 1. If the label of the new set of data is lower body garment, the string of garment attributes will now pass through the second subsystem. Since it is already determined that it is a lower-body garment, the classifier trained with dataset L will get activated and further try to label the data instance into a specific lower garment sub-category. In this case, the classifier will compute the probabilities of all the lower garment sub-category classes and compare these values to a pre-set threshold value. Based on this value, subsystem 2 will decide the label of the new data instance based on the highest probability. In another case, where at subsystem 2, if two labels have equal or very close probabilities, if the classifier provides the class with the highest probability, even if the difference between the two values is as low as 0.1, the classification result can be considered biased. This would mean that even though the new data instance is close to more than one type of lower garment sub-category, the classifier does not handle this ambiguity well. Due to this reason, having subsystem 2 provide probabilities of these two classes, instead of a single predicted class, can help make an intelligent decision, in turn improving the model accuracy for future data instances. In this way, the system becomes equipped with handling ambiguous cases, which can occur frequently in a large dataset, given the complexity of an apparel product.
The change in classification accuracy due to the aforementioned algorithm can be seen in Figure 6. To compute the accuracy of the integrated model, the validation set (not used throughout the model building process) was used. As is visible, the accuracy for all the classifiers at different thresholds (0.1, 0.2, 0.3, and 0.4) for datasets U, L, and W improved considerably. In Figure 6d), the accuracy for dataset U increased from 75% to around 85%. A similar increment can be observed for this dataset for other classifiers as well. Dataset W reached an accuracy greater than 95% for random forest classifiers, which is considered as good performance for a classification model. For all the datasets, the accuracy is still the greatest with the random forest classifier, in correspondence to the results presented in Figure 4 and Figure 5.
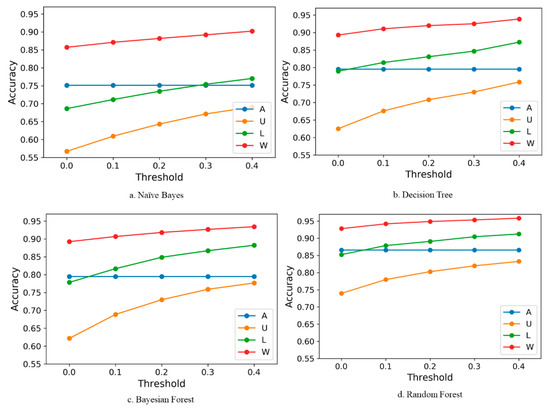
Figure 6.
Accuracies at different thresholds for (a) Naïve Bayes, (b) Decision Trees, (c) Bayesian Forest, and (d) Random Forest.
6. Conclusions
The term big data has become extremely prevalent in the business world, leading to an increase in the use of techniques, such as data mining, machine learning, and artificial intelligence. Businesses are excessively applying these techniques to help collect data on sales trends to understand, better, everything from marketing and inventory needs to acquiring new leads. Data mining is one of the most used techniques due to its ability to analyze a large amount of data for solving business problems. These problems can be targeted by focusing on the business database already present, of customer choices, past transactions, and product profiles.
This study recognizes the importance of product data and uses open-source product attribute data (namely Deep Fashion) from the apparel industry to create a classification model that can identify the garment category (upper, lower, or wholebody garment) and garment sub-category (dress, blouse, capris, trousers etc.). To do this, four classification algorithms were employed: Decision Trees, Naïve Bayes, Bayesian Forest, and Random Forest. The classification model consists of two individual subsystems: (1) to identify the garment category and (2) to identify the garment subcategory. After this, the two subsystems were integrated using soft computation to handle ambiguous cases and improve the overall accuracy of the classification model. It was observed that the performance of the Random Forest classifier was comparatively better with an accuracy of 86%, 73%, 82%, and 90%, respectively, for the garment category, and sub-categories of upper body garment, lower body garment, and whole-body garment. The reason behind a comparatively better performance of random forest classifiers lies in that it creates a large number of uncorrelated trees that are averaged to reduce bias and variance, and handles unbalanced data very well.
Every garment retailer and/or production house collects similar data related to the garment, i.e., the garment categories and attributes in the archive. In addition, these are also the details present on the product pages of the e-commerce websites. Hence, the data can be obtained from these sources and used to create a segmentation based on the attributes used in various garments. This segmentation can be used to classify the data based on the methodology described in this article. Such a classification can have various applications, such as in improving the existing recommendation algorithms by providing words instead of images, and enhancing the parsing algorithms, etc. In addition, as discussed in [69], living in a digital age, there is the availability of massive datasets in various formats, making it essential to design approaches to handle the access and integration of such data. The presented model can be trained with additional data formats and, hence, incorporate accessing and integrating data from multiple resources (especially data from the internet) as it provides a uniform terminology of garment categories, sub-categories, and their attributes.
This study presents a preliminary investigation and, hence, there are several potential avenues for future work, such as in-depth evaluation of why the upper body garment dataset exhibits the lowest classification accuracy for all the algorithms and how it can be improved. The threshold of the feature selection process can be varied to observe how it affects the model performance. The accuracy of the model can be further improved with the help of a richer dataset as the dataset employed in this study deals with a few limitations, such as data imbalance and the presence of too many negative attributes. Moreover, an application of the proposed model can be realized in a decision support system or a recommendation system that can support the customer in decision making during purchase. Additionally, the proposed framework can be tested with advanced techniques, such as deep learning, to enhance model performance. Further, with data growing at an unprecedented rate, its handling and management incur additional costs (especially when manually labeling data collected through the internet, it is not only expensive but labor-intensive). Hence, the proposed model can be utilized to support the transfer from manual labeling to automatic labeling of the internet data. In the future, we would also like to work on comparing the performance of algorithms based on the input being textual or visual.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-8994/12/6/984/s1. Figure S1. Confusion Matrix for Bayesian Forest Classifier for data set a) A, b) U, c) L and d) W. Figure S2: Confusion Matrix for Naïve Bayes Classifier for data set a) A, b) U, c) L and d) W. Figure S3: Confusion Matrix for Decision Tree Classifier for data set a) A, b) U, c) L and d) W, Table S1. List of Clothing sub-categories, Table S2. Table of Mathematical Symbols Used. Table S3. Table of most relevant features for dataset upper, lower and whole body garments.
Author Contributions
Conceptualization, S.J. and V.K.; Formal analysis, S.J.; Investigation, S.J.; Methodology, S.J.; Writing—original draft, S.J.; Writing—review and editing, V.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Education, Audiovisual and Culture Executive Agency, grant number 532704.
Acknowledgments
This work was conducted under the framework of SMDTex, which is financially supported by the European Commission.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guleria, P.; Sood, M. Big data analytics: Predicting academic course preference using hadoop inspired mapreduce. In Proceedings of the 2017 4th International Conference on Image Information Processing, ICIIP 2017, Shimla, India, 21–23 December 2017; pp. 328–331. [Google Scholar]
- Hsu, C.-H. Data mining to improve industrial standards and enhance production and marketing: An empirical study in apparel industry. Expert Syst. Appl. 2009, 36, 4185–4191. [Google Scholar] [CrossRef]
- Lu, Q.; Lyu, Z.-J.; Xiang, Q.; Zhou, Y.; Bao, J. Research on data mining service and its application case in complex industrial process. In Proceedings of the IEEE International Conference on Automation Science and Engineering, Xi’an, China, 20–23 August 2017; pp. 1124–1129. [Google Scholar]
- Buluswar, M.; Campisi, V.; Gupta, A.; Karu, Z.; Nilson, V.; Sigala, R. How Companies are Using Big Data and Analytics; McKinsey & Company: San Francisco, CA, USA, 2016. [Google Scholar]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Adhikari, S.S.; Singh, S.; Rajagopal, A.; Rajan, A. Progressive Fashion Attribute Extraction. arXiv 2019, arXiv:1907.00157. [Google Scholar]
- Zielnicki, K. Simulacra and Selection: Clothing Set Recommendation at Stitch Fix. In Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval, Paris, France, 18 July 2019; pp. 1379–1380. [Google Scholar]
- Griva, A.; Bardaki, C.; Pramatari, K.; Papakiriakopoulos, D. Retail business analytics: Customer visit segmentation using market basket data. Expert Syst. Appl. 2018, 100, 1–16. [Google Scholar] [CrossRef]
- Juaneda-Ayensa, E.; Mosquera, A.; Murillo, Y.S. Omnichannel Customer Behavior: Key Drivers of Technology Acceptance and Use and Their Effects on Purchase Intention. Front. Psychol. 2016, 7, 1117. [Google Scholar] [CrossRef]
- Manfredi, M.; Grana, C.; Calderara, S.; Cucchiara, R. A complete system for garment segmentation and color classification. Mach. Vis. Appl. 2014, 25, 955–969. [Google Scholar] [CrossRef]
- Ghani, R.; Probst, K.; Liu, Y.; Krema, M.; Fano, A. Text mining for product attribute extraction. ACM SIGKDD Explor. Newsl. 2006, 8, 41–48. [Google Scholar] [CrossRef]
- Gill, S. A review of research and innovation in garment sizing, prototyping and fitting A review of research and innovation in garment sizing, prototyping and fitting. Text. Prog. 2015, 47, 1–85. [Google Scholar] [CrossRef]
- Kausher, H.; Srivastava, S. Developing Structured Sizing Systems for Manufacturing Ready-Made Garments of Indian Females Using Decision Tree-Based Data Mining. Int. J. Mater. Text. Eng. 2019, 13, 571–575. [Google Scholar]
- Zakaria, N.; Ruznan, W.S. Developing apparel sizing system using anthropometric data: Body size and shape analysis, key dimensions, and data segmentation. In Anthropometry, Apparel Sizing and Design; Elsevier: Amsterdam, The Netherlands, 2020; pp. 91–121. [Google Scholar]
- Pei, J.; Park, H.; Ashdown, S.P. Female breast shape categorization based on analysis of CAESAR 3D body scan data. Text. Res. J. 2019, 89, 590–611. [Google Scholar] [CrossRef]
- Liu, K.; Zeng, X.; Bruniaux, P.; Wang, J.; Kamalha, E.; Tao, X. Fit evaluation of virtual garment try-on by learning from digital pressure data. Knowl.-Based Syst. 2017, 133, 174–182. [Google Scholar] [CrossRef]
- Lagė, A.; Ancutienė, K. Virtual try-on technologies in the clothing industry: Basic block pattern modification. Int. J. Cloth. Sci. Technol. 2019, 31, 729–740. [Google Scholar] [CrossRef]
- Zakaria, N.; Taib, J.S.M.N.; Tan, Y.Y.; Wah, Y.B. Using data mining technique to explore anthropometric data towards the development of sizing system. In Proceedings of the Proceedings—International Symposium on Information Technology, Kuala Lumpur, Malaysia, 26–28 August 2008; Volume 2. [Google Scholar]
- Hsu, C.H.; Wang, M.J.J. Using decision tree-based data mining to establish a sizing system for the manufacture of garments. Int. J. Adv. Manuf. Technol. 2005, 26, 669–674. [Google Scholar] [CrossRef]
- Thomassey, S. Sales forecasts in clothing industry: The key success factor of the supply chain management. Int. J. Prod. Econ. 2010, 128, 470–483. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, C.; Liu, Y. An AHP-Based Scheme for Sales Forecasting in the Fashion Industry. In Analytical Modeling Research in Fashion Business; Springer: Singapore, 2016; pp. 251–267. [Google Scholar]
- Craparotta, G.; Thomassey, S. A Siamese Neural Network Application for Sales Forecasting of New Fashion Products Using Heterogeneous Data. Int. J. Comput. Intell. Syst. 2019, 12, 1537–1546. [Google Scholar] [CrossRef]
- Beheshti-Kashi, S.; Thoben, K.-D. The Usage of Social Media Text Data for the Demand Forecasting in the Fashion Industry. In Dynamics in Logistics; Springer: Cham, Switzerland, 2016; pp. 723–727. [Google Scholar]
- Yang, S.J.; Jang, S. Fashion trend forecasting using ARIMA and RNN: Application of tensorflow to retailers’ websites. Asia Life Sci. 2019, 18, 407–418. [Google Scholar]
- Kumar, S.V.; Poonkuzhali, S. Improvising the Sales of Garments by Forecasting Market Trends using Data Mining Techniques. Int. J. Pure Appl. Math. 2018, 119, 797–805. [Google Scholar]
- Al-halah, Z.; Stiefelhagen, R.; Grauman, K. Fashion Forward: Forecasting Visual Style in Fashion Supplementary Material. In Proceeding of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 388–397. [Google Scholar]
- Stan, I.; Mocanu, C. An Intelligent Personalized Fashion Recommendation System. In Proceedings of the 2019 22nd International Conference on Control Systems and Computer Science (CSCS), Bucharest, Romania, 28–30 May 2019; pp. 210–215. [Google Scholar]
- Sugumaran, P.; Sukumaran, V. Recommendations to improve dead stock management in garment industry using data analytics. Math. Biosci. Eng. 2019, 16, 8121–8133. [Google Scholar] [CrossRef]
- Guan, C.; Qin, S.; Ling, W.; Ding, G. Apparel Recommendation System Evolution: An empirical review. Int. J. Cloth. Sci. Technol. 2016, 28, 854–879. [Google Scholar] [CrossRef]
- Sun, W.; Lin, H.; Li, C.; Wang, T.; Zhou, K. Research and Application of Clothing Recommendation System Combining Explicit Data and Implicit Data. In Proceedings of the International Conference on Artificial Intelligence and Computing Science (ICAICS 2019), Wuhan, China, 24–25 March 2019. [Google Scholar]
- Skiada, M.; Lekakos, G.; Gkika, S.; Bardaki, C. Garment Recommendations for Online and Offline Consumers. In Proceedings of the MCIS 2016 Proceedings, Paphos, Cyprus, 2016. [Google Scholar]
- Chen, Y.; Qin, M.; Qi, Y.; Sun, L. Improving Fashion Landmark Detection by Dual Attention Feature Enhancement. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Seoul, Korea, 27–28 October 2019. [Google Scholar]
- Karessli, N.; Guigourès, R.; Shirvany, R. SizeNet: Weakly Supervised Learning of Visual Size and Fit in Fashion Images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Surakarin, W.; Chongstitvatana, P. Classification of clothing with weighted SURF and local binary patterns. In Proceedings of the ICSEC 2015—19th International Computer Science and Engineering Conference: Hybrid Cloud Computing: A New Approach for Big Data Era, Chiang Mai, Thailand, 23–26 November 2015. [Google Scholar]
- Bhimani, H.; Kaimaparambil, K.; Papan, V.; Chaurasia, H.; Kukreja, A. Web-Based Model for Apparel Classification. 2nd International Conference on Advances in Science & Technology (ICAST) 2019 on 8th, 9th April 2019 by K J Somaiya Institute of Engineering & Information Technology, Mumbai, India. 2019. Available online: https://ssrn.com/abstract=3367732 (accessed on 2 June 2020).
- Cheng, C.-I.; Liu, D.S.-M. An intelligent clothes search system based on fashion styles. In Proceedings of the International Conference on Machine Learning and Cybernetics, Kunming, China, 12–15 July 2008; Volume 3, pp. 1592–1597. [Google Scholar]
- Ak, K.E.; Lim, J.H.; Tham, J.Y.; Kassim, A.A. Attribute Manipulation Generative Adversarial Networks for Fashion Images. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 10541–10550. [Google Scholar]
- Yildirim, P.; Birant, D.; Alpyildiz, T. Data mining and machine learning in textile industry. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1228. [Google Scholar] [CrossRef]
- Tong, L.; Wong, W.K.; Kwong, C.K. Fabric Defect Detection for Apparel Industry: A Nonlocal Sparse Representation Approach. IEEE Access 2017, 5, 5947–5964. [Google Scholar] [CrossRef]
- Wei, B.; Hao, K.; Tang, X.S.; Ren, L. Fabric defect detection based on faster RCNN. In Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2019; Volume 849, pp. 45–51. [Google Scholar]
- Gries, T.; Lutz, V.; Niebel, V.; Saggiomo, M.; Simonis, K. Automation in quality monitoring of fabrics and garment seams. In Automation in Garment Manufacturing; Elsevier Inc.: Amsterdam, The Netherlands, 2017; pp. 353–376. [Google Scholar]
- Vuruskan, A.; Ince, T.; Bulgun, E.; Guzelis, C. Intelligent fashion styling using genetic search and neural classification. Int. J. Cloth. Sci. Technol. 2015, 27, 283–301. [Google Scholar] [CrossRef]
- Tuinhof, H.; Pirker, C.; Haltmeier, M. Image-based fashion product recommendation with deep learning. In International Conference on Machine Learning, Optimization, and Data Science; Springer: Cham, 2019; pp. 472–481. [Google Scholar]
- Donati, L.; Iotti, E.; Mordonini, G.; Prati, A. Fashion product classification through deep learning and computer vision. Appl. Sci. 2019, 9, 1385. [Google Scholar] [CrossRef]
- Bossard, L.; Dantone, M.; Leistner, C.; Wengert, C.; Quack, T.; van Gool, L. Apparel classification with style. In Asian conference on computer vision; Springer: Berlin/Heidelberg, Germany, 2012; pp. 321–335. [Google Scholar]
- Laenen, K.; Zoghbi, S.; Moens, M.-F. Cross-modal Search for Fashion Attributes. In Proceedings of the KDD 2017 Workshop on Machine Learning Meets Fashion, Halifax, NS, Canada, 14 August 2017. [Google Scholar]
- Hammar, K.; Jaradat, S.; Dokoohaki, N.; Matskin, M. Deep Text Mining of Instagram Data Without Strong Supervision 4 th Mihhail Matskin. In Proceedings of the 2018 IEEE/WIC/ACM International Conference on Web Intelligence (WI), Santiago, Chile, 3–6 December 2018; pp. 158–165. [Google Scholar]
- Kreyenhagen, C.D.; Aleshin, T.I.; Bouchard, J.E.; Wise, A.M.I.; Zalegowski, R.K. Using supervised learning to classify clothing brand styles. In Proceedings of the 2014 IEEE Systems and Information Engineering Design Symposium (SIEDS), Charlottesville, VA, USA, 25 April 2014; pp. 239–243. [Google Scholar]
- Rutkowski, L.; Jaworski, M.; Pietruczuk, L.; Duda, P. The CART decision tree for mining data streams. Inf. Sci. 2014, 266, 1–15. [Google Scholar] [CrossRef]
- Fuster-Parra, P.; García-Mas, A.; Cantallops, J.; Ponseti, F.J.; Luo, Y. Ranking Features on Psychological Dynamics of Cooperative Team Work through Bayesian Networks. Symmetry 2016, 8, 34. [Google Scholar] [CrossRef]
- Mccallum, A.; Nigam, K. A Comparison of Event Models for Naive Bayes Text Classification. In AAAI-98 Workshop on Learning for Text Categorization; Madison, Wisconsin, 1998; pp. 41–48. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.65.9324&rep=rep1&type=pdf (accessed on 2 June 2020).
- Cheng, J.; Greiner, R. Comparing Bayesian network classifiers. In Proceedings of the Fifteenth Conference on Uncertainty in Artificial Intelligence, Stockholm, Sweden, 30–31 July 1999; pp. 101–108. [Google Scholar]
- Liu, L.; Su, J.; Zhao, B.; Wang, Q.; Chen, J.; Luo, Y. Towards an Efficient Privacy-Preserving Decision Tree Evaluation Service in the Internet of Things. Symmetry 2020, 12, 103. [Google Scholar] [CrossRef]
- Song, Y.Y.; Lu, Y. Decision tree methods: Applications for classification and prediction. Shanghai Arch. Psychiatry 2015, 27, 130–135. [Google Scholar]
- Farid, D.; Zhang, L.; Rahman, C.; Hossain, M.A.; Strachan, R. systems with, and U. 2014, “Hybrid decision tree and naïve Bayes classifiers for multi-class classification tasks. Expert Syst. Appl. 2014, 41, 1937–1946. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Ben-David, S. Understanding Machine Learning: From Theory to Algorithms; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Siddiqui, M.F.; Mujtaba, G.; Reza, A.W.; Shuib, L. Multi-Class Disease Classification in Brain MRIs Using a Computer-Aided Diagnostic System. Symmetry 2017, 9, 37. [Google Scholar] [CrossRef]
- Aggarwal, C. Data Classification: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Mao, W.; Wang, F.-Y. Cultural Modeling for Behavior Analysis and Prediction. In Advances in Intelligence and Security Informatics; Elsevier: Amsterdam, The Netherlands, 2012; pp. 91–102. [Google Scholar]
- Taddy, M.; Chen, C.-S.; Yu, J. Bayesian and Empirical Bayesian Forests. arXiv 2015, arXiv:1502.02312. [Google Scholar]
- Liu, Z.; Luo, P.; Qiu, S.; Wang, X.; Tang, X. DeepFashion: Powering Robust Clothes Recognition and Retrieval with Rich Annotations. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1096–1104. [Google Scholar]
- Louppe, G.; Wehenkel, L.; Sutera, A.; Geurts, P. Understanding variable importances in forests of randomized trees. In Advances in Neural Iinformation Processing Systems; Neural Information Processing Systems Foundation, Inc.: La Jolla, CA, USA, 2013; pp. 431–439. [Google Scholar]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. IJCAI 1995, 14, 1137–1145. [Google Scholar]
- Sechidis, K.; Tsoumakas, G.; Vlahavas, I. On the stratification of multi-label data. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases; Springer: Berlin/Heidelberg, Germany, 2011; pp. 145–158. [Google Scholar]
- Hossin, M.; Sulaiman, M. A review on evaluation metrics for data classification evaluations. Int. J. Data Min. Knowl. Manag. Process 2015, 5, 1. [Google Scholar]
- Gupta, D.L.; Malviya, A.K.; Singh, S. Performance analysis of classification tree learning algorithms. Int. J. Comput. Appl. 2012, 55. [Google Scholar]
- Liu, Y.; Zhang, H.H.; Wu, Y. Hard or soft classification? large-margin unified machines. J. Am. Stat. Assoc. 2011, 106, 166–177. [Google Scholar] [CrossRef] [PubMed]
- Wahba, G. Soft and hard classification by reproducing kernel Hilbert space methods. Proc. Natl. Acad. Sci. USA 2002, 99, 16524–16530. [Google Scholar] [CrossRef]
- Tu, D.Q.; Kayes, A.S.M.; Rahayu, W.; Nguyen, K. ISDI: A New Window-Based Framework for Integrating IoT Streaming Data from Multiple Sources. In Advanced Information Networking and Applications; AINA 2019. Advances in Intelligent Systems and Computing; Barolli, L., Takizawa, M., Xhafa, F., Enokido, T., Eds.; Springer: Cham, Switzerland, 2020; Volume 926, pp. 498–511. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).