Graphical Modeling and Simulation for a Multi-Aircraft Collision Avoidance Algorithm based on Collaborative Decisions
Abstract
1. Introduction
2. Improved TCAS Model
3. Conflict Detection Algorithm
3.1. Trajectory Prediction Algorithm
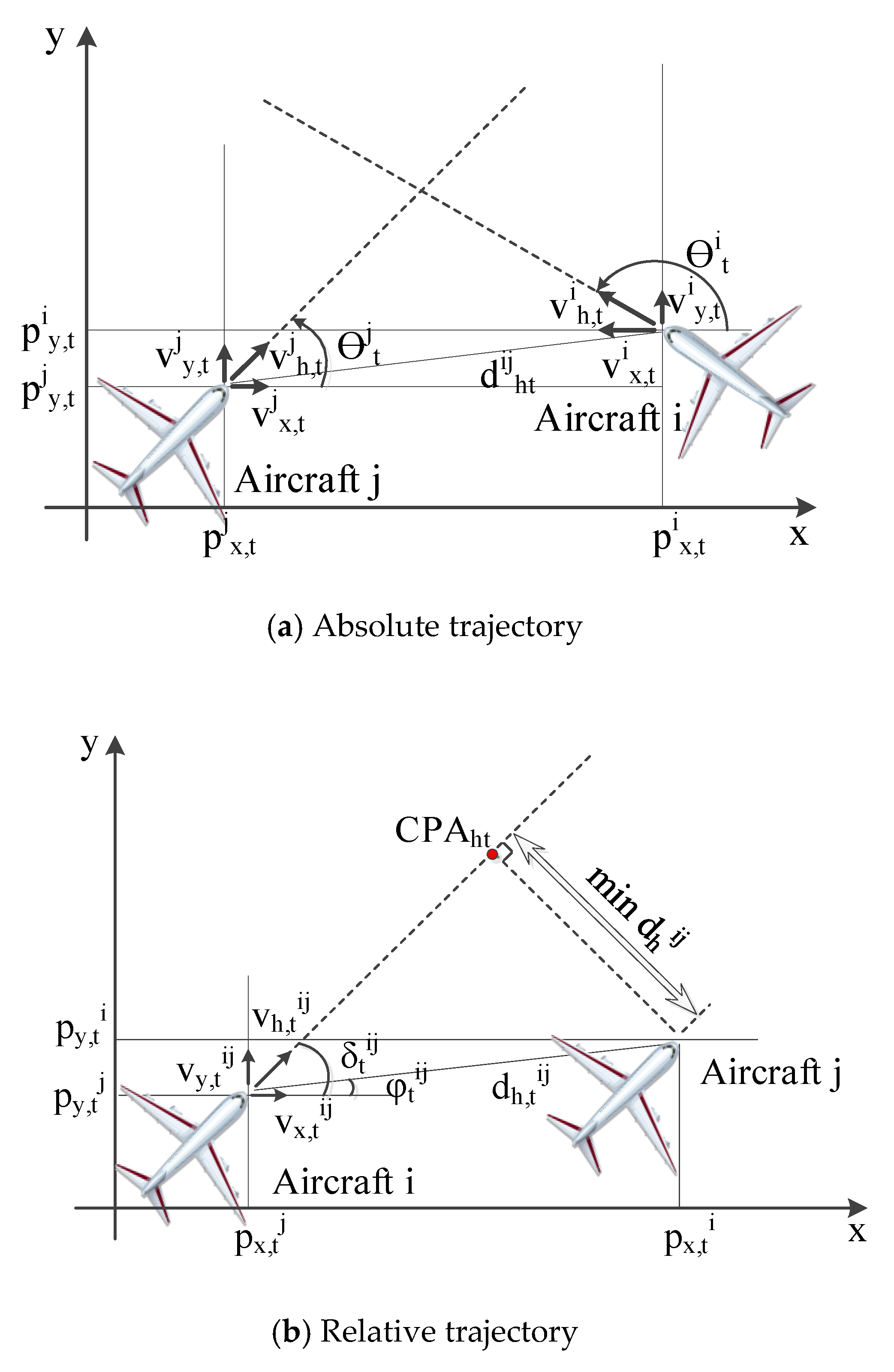
3.2. Pairwise Conflict Detection Algorithm
- 1.
- Time spent for aircraft i and j to reach CPAh and CPAz ( and ) are both less than the time threshold TimeRA, and horizontal distance when they reach CPAh is smaller than distance modification (DMOD), and vertical distance when they reach CPAZ is smaller than the vertical threshold value (ZTHR). The time and space thresholds used to define whether a collision will occur vary with different sensitivity levels (SLs) based on altitude [23].
- 2.
- Horizontal and vertical distance between aircraft i and j ( and ) are less than the threshold separately.
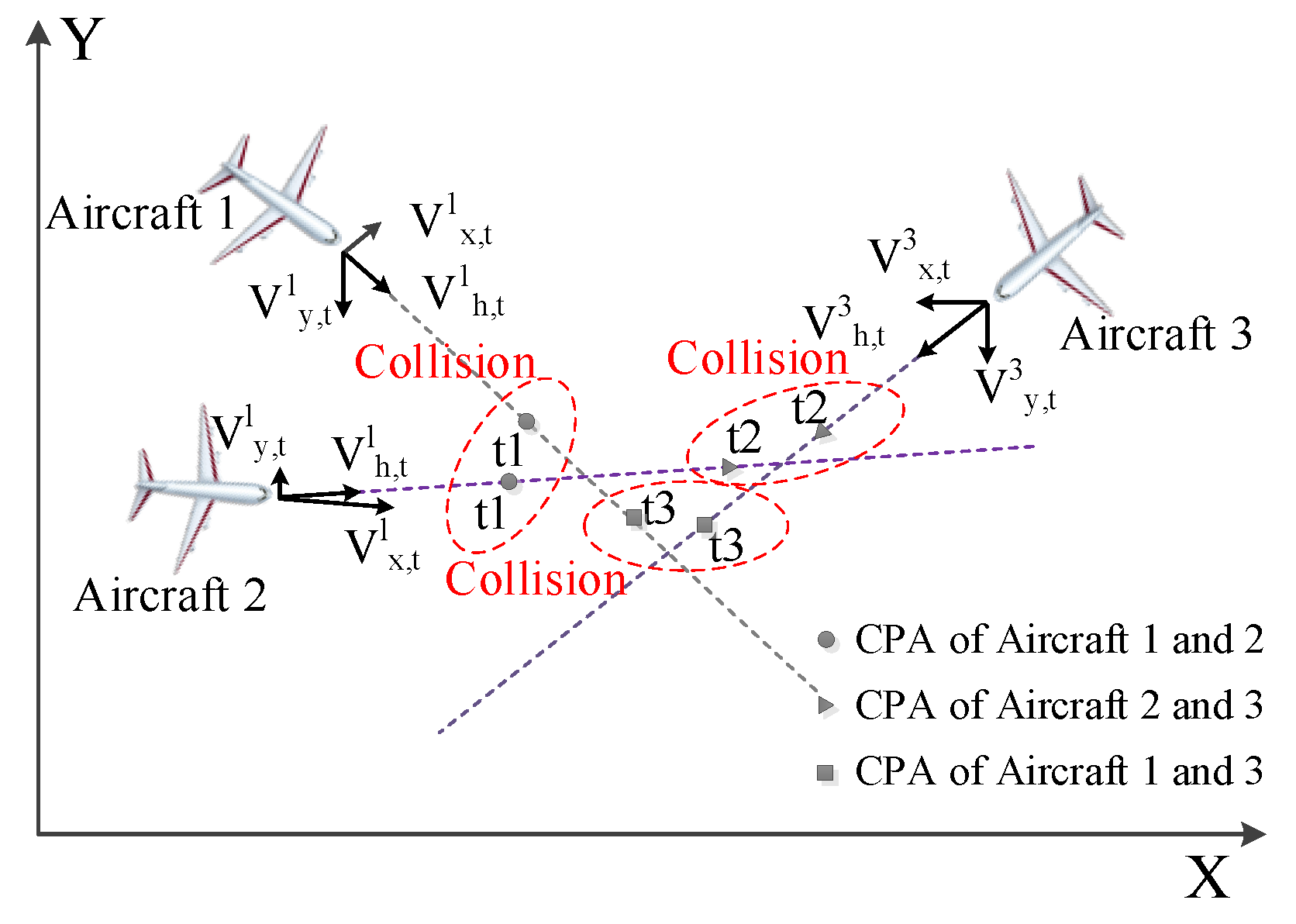
3.3. Multi-Aircraft Conflict Detection Algorithm
- (1)
- At moment t, there are two aircraft among aircraft i, j, m coming into conflict firstly.
- (2)
- Before moment , the third aircraft will come into conflict with either of the first two aircraft (supposing aircraft i and aircraft j come into conflict at moment t first, then aircraft m and aircraft i come into conflict).
4. Collaborative Conflict Resolution Algorithm
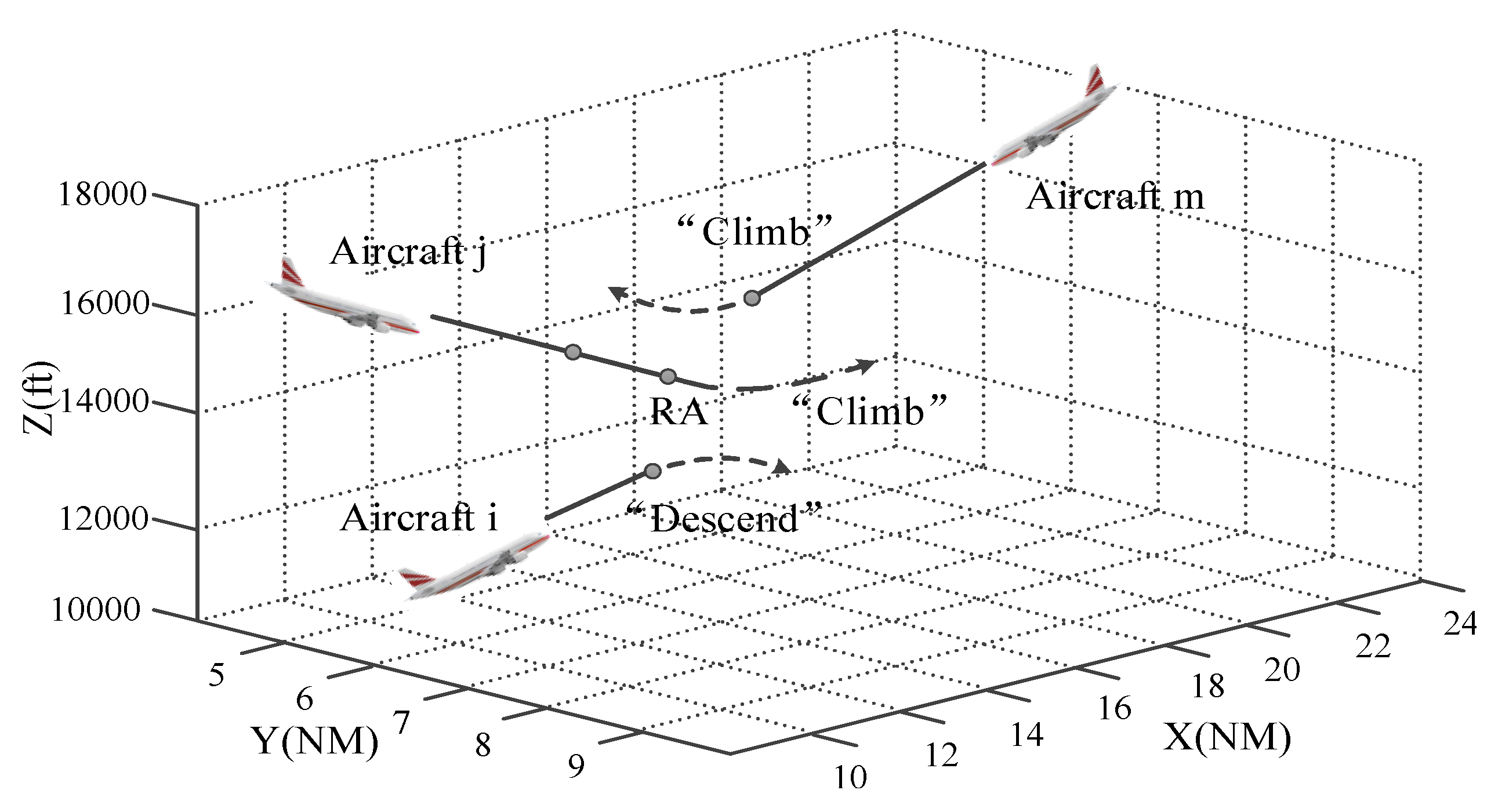
4.1. Pairwise Conflict Resolution Algorithm
4.1.1. Direction Choosing
- (1)
- Maximum vertical separation principle: The target aircraft needs to achieve maximum vertical separation from the intruder aircraft at CPAh in the case of the same intensity of speed change.
- (2)
- Noncrossing principle in the vertical direction: When maneuvering upwards or downwards, target aircraft should achieve the goal of not-crossing with the invader aircraft in the vertical direction as much as possible [24].
4.1.2. Intensity Choosing
4.1.3. Original Trajectory Recovery Algorithm
- At moment , target aircraft i is at CPAh. Through a change of vertical speed, target aircraft i has achieved adequate vertical separation from the invader aircraft at CPAh. After being cleared of conflict, the target aircraft adjusts vertical speed to return to its original altitude. is the speed of the target aircraft before adjustment, is the vertical speed after adjustment, time of adjustment is .
- At moment , target aircraft i will have returned to its original altitude, then it adjusts to its original speed.
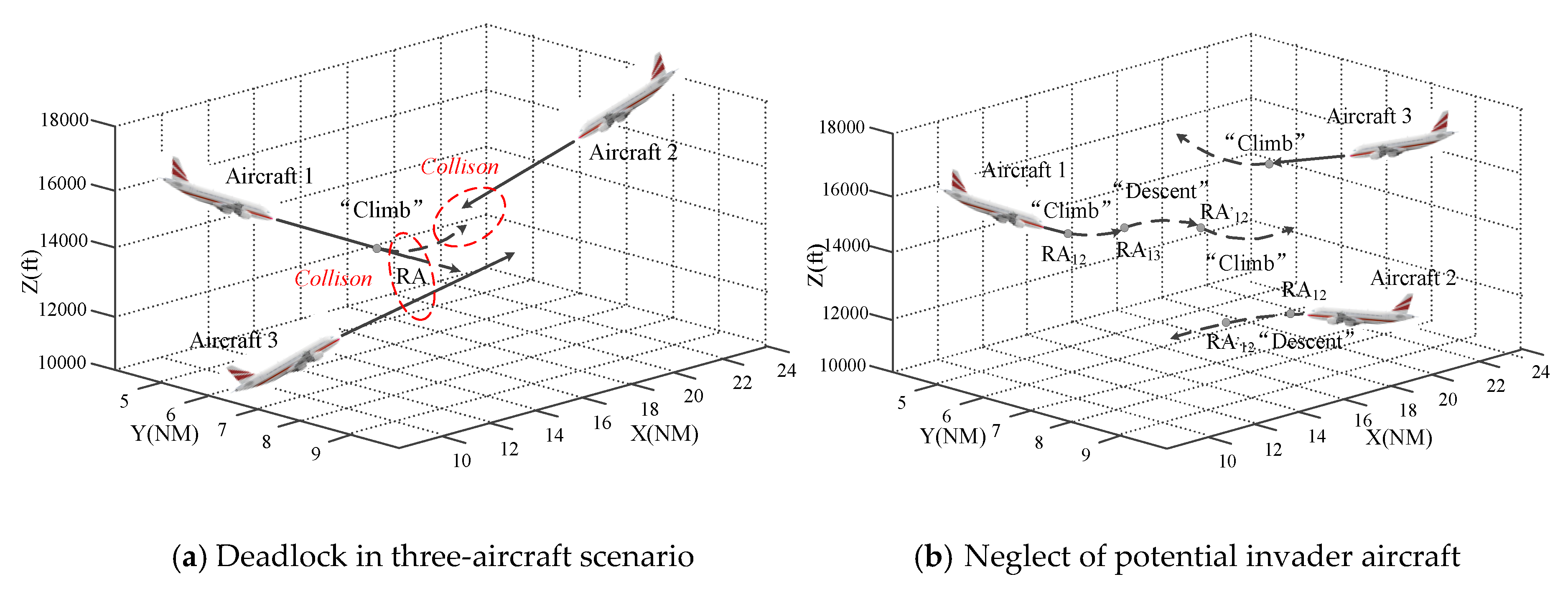
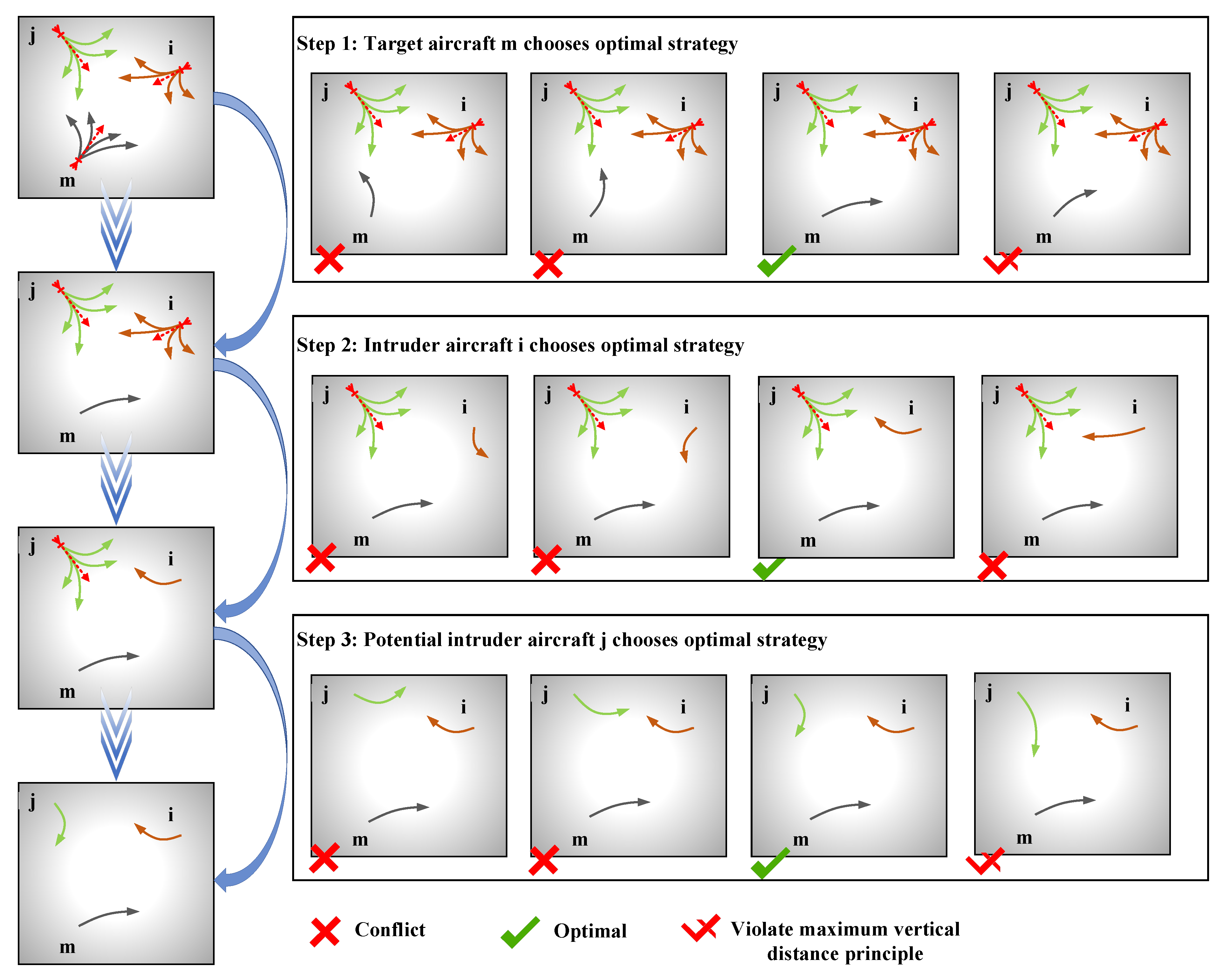
4.2. Multi-Aircraft Conflict Resolution Algorithm
4.2.1. Candidate-Strategies-Generating Module
4.2.2. Collaborative Decision-Making Module
5. Simulation
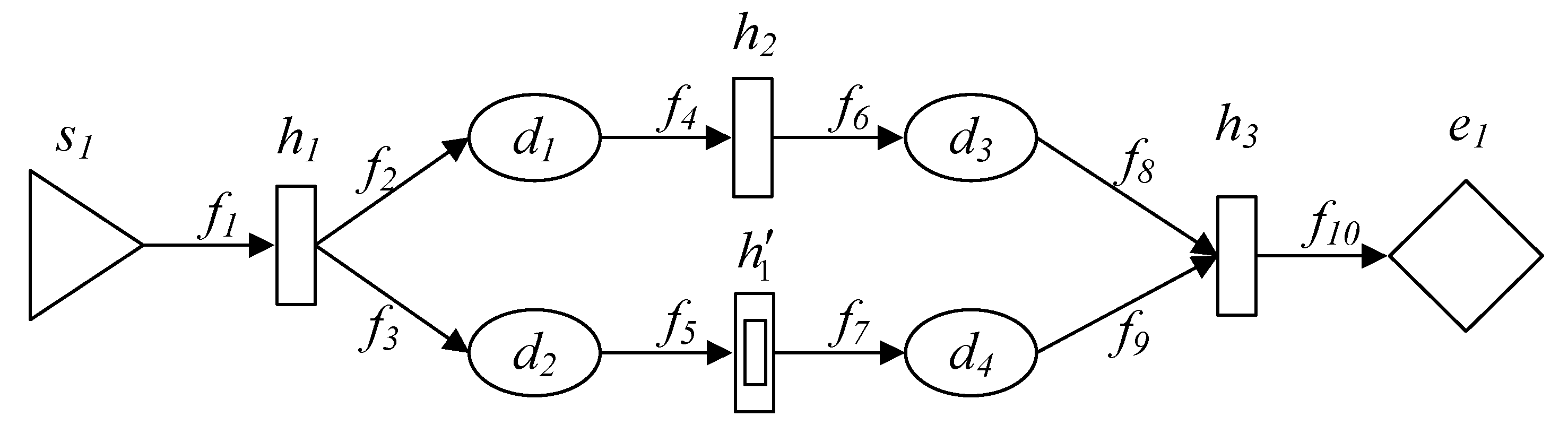
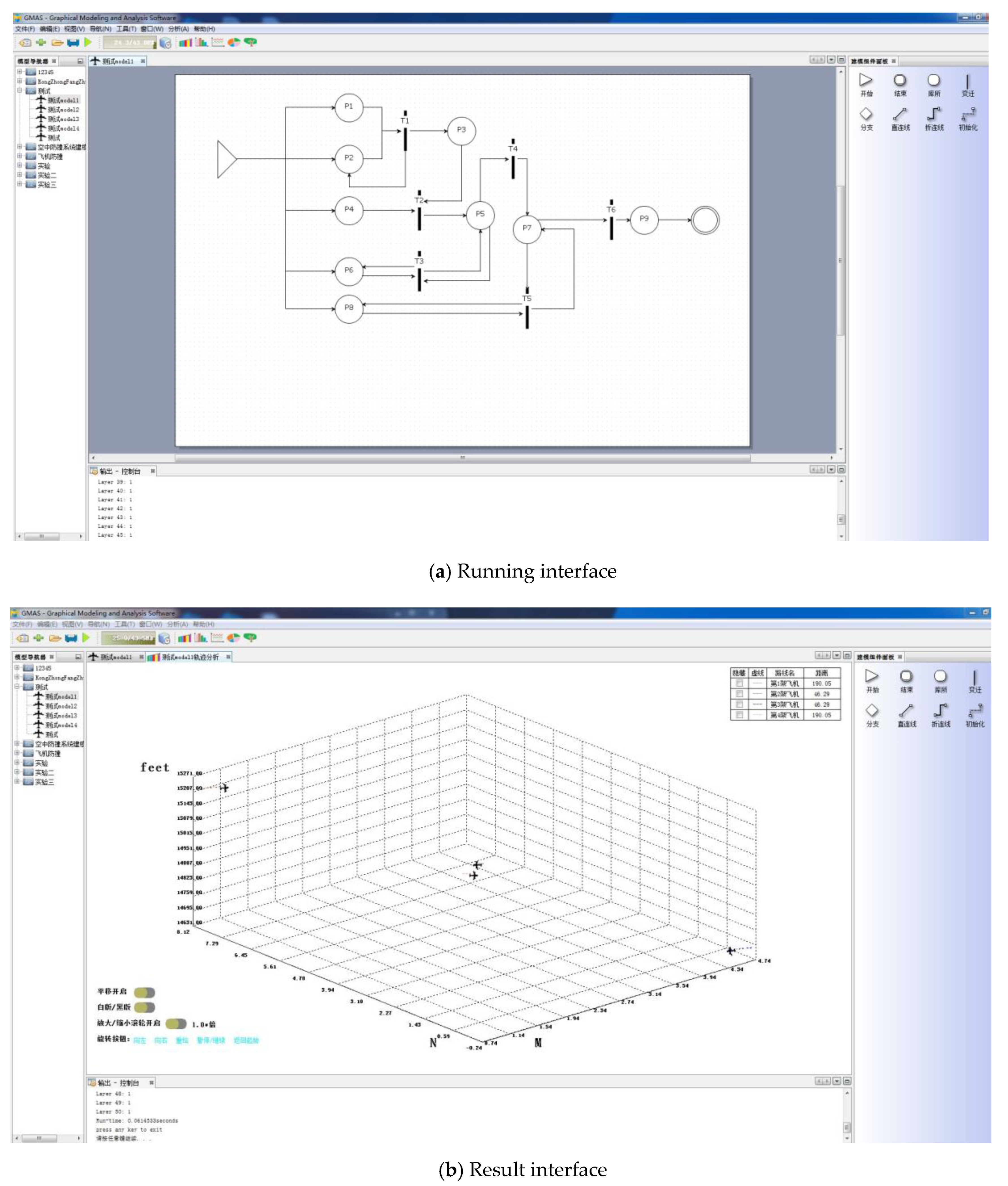
5.1. Introduction of Simulation Software
5.2. Simulation Modeling
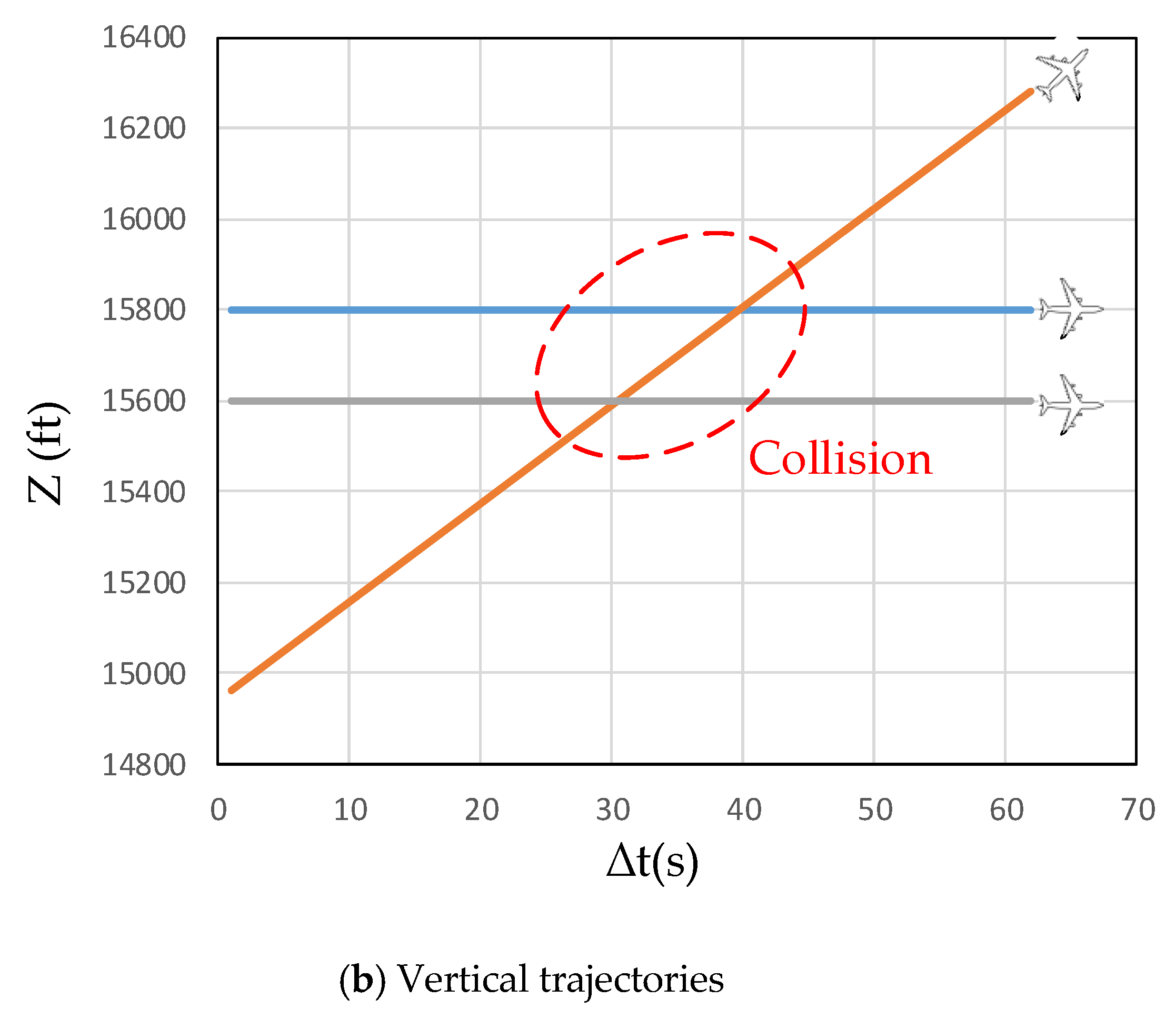
5.3. Result Analysis
6. Conclusions
- This paper studies the collision avoidance of multi-aircraft conflict and innovatively proposes a collaborative optimization CAS strategy based on the state prediction of invading aircraft and potential invading aircraft under complex conditions. The simulation performed on the relevant case study shows that the proposed algorithm effectively compensates the existing research gap on multi-aircraft conflict resolution.
- This paper improves the ability and efficiency of TCAS in solving multi-aircraft conflicts, especially three-aircraft conflict. In the collaborative decision-making algorithm proposed in this paper, the target aircraft takes into account the potential invader aircraft that poses a threat during the process of collision avoidance. It can avoid situations where target aircraft come into conflict with another aircraft when avoiding an invader aircraft. Through contrast experiments, the result shows that the proposed collaborative multi-aircraft CAS is better than TCAS in dealing with three-aircraft conflict.
Author Contributions
Funding
Conflicts of Interest
References
- Kuchar, J.; Andrews, J.; Drumm, A.; Hall, T.; Heinz, V.; Thompson, S.; Welch, J. A safety analysis process for the traffic alert and collision avoidance system (TCAS) and see-and-avoid systems on remotely piloted vehicles. In Proceedings of the AIAA 3rd “Unmanned Unlimited” Technical Conference, Workshop and Exhibit, Chicago, IL, USA, 20–23 September 2004; p. 6423. [Google Scholar]
- Billingsley, T.B.; Espindle, L.; Griffith, J.D. TCAS Multiple Threat Encounter Analysis. Available online: https://archive.ll.mit.edu/mission/aviation/publications/publication-files/atc-reports/Billingsley_2009_ATC-359_WW-18718.pdf (accessed on 7 April 2020).
- Kuchar, J.; Drumm, A.C. The traffic alert and collision avoidance system. Linc. Lab. J. 2007, 16, 277. [Google Scholar]
- Tang, J. Conflict Detection and Resolution for Civil Aviation: A Literature Survey. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 20–35. [Google Scholar] [CrossRef]
- Garcia-Chico, J.L. A Human Factors Analysis of Operational Errors in ATC: The TCAS Case Study. Available online: https://scholarworks.sjsu.edu/etd_theses/2999 (accessed on 7 April 2020).
- Kochenderfer, M.J.; Chryssanthacopoulos, J.P. A decision-theoretic approach to developing robust collision avoidance logic. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, Funchal, Portugal, 19–22 September 2010; pp. 1837–1842. [Google Scholar]
- Jun, B.-K.; Lim, S.-S. Improvement of the avoidance performance of TCAS-II by employing Kalman filter. J. Adv. Navig. Technol. 2011, 15, 986–993. [Google Scholar]
- Peng, L.; Lin, Y. Study on the model for horizontal escape maneuvers in TCAS. IEEE Trans. Intell. Transp. Syst. 2010, 11, 392–398. [Google Scholar] [CrossRef]
- Romli, F.; King, J.; Li, L.; Clarke, J.-P. Impact of automatic dependent surveillance-broadcast (ADS-B) on traffic alert and collision avoidance system (TCAS) performance. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; p. 6971. [Google Scholar]
- Woodell, D.L.; Smoak, G.M. Radar Augmented TCAS. U.S. Patent Application No. 620,828,4B1, 27 March 2001. [Google Scholar]
- Tang, J.; Piera, M.A.; Guasch, T. Coloured Petri net-based traffic collision avoidance system encounter model for the analysis of potential induced collisions. Transp. Res. Part C Emerg. Technol. 2016, 67, 357–377. [Google Scholar] [CrossRef]
- Tang, J. Analysis and improvement of traffic alert and collision avoidance system. IEEE Access 2017, 5, 21419–21429. [Google Scholar] [CrossRef]
- Munoz, C.; Narkawicz, A.; Chamberlain, J. A TCAS-II resolution advisory detection algorithm. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013; p. 4622. [Google Scholar]
- Otto, A.; Agatz, N.; Campbell, J.; Golden, B.; Pesch, E. Optimization approaches for civil applications of unmanned aerial vehicles (UAVs) or aerial drones: A survey. Networks 2018, 72, 411–458. [Google Scholar] [CrossRef]
- Mahjri, I.; Dhraief, A.; Belghith, A. A Review on Collision Avoidance Systems for Unmanned Aerial Vehicles. Available online: https://link.springer.com/chapter/10.1007/978-3-319-17765-6_18 (accessed on 7 April 2020).
- Sun, J.; Tang, J.; Lao, S. Collision avoidance for cooperative UAVs with optimized artificial potential field algorithm. IEEE Access 2017, 5, 18382–18390. [Google Scholar] [CrossRef]
- Liangfu, P. Influence of turning time and response delay on the horizontal collision avoidance for UAVs. In Proceedings of the 2013 Third International Conference on Intelligent System Design and Engineering Applications, Hong Kong, China, 16–18 January 2013; pp. 878–883. [Google Scholar]
- Yang, J.; Yin, D.; Shen, L.; Cheng, Q.; Xie, X. Cooperative deconflicting heading maneuvers applied to unmanned aerial vehicles in Non-Segregated airspace. J. Intell. Robot. Syst. 2018, 92, 187–201. [Google Scholar] [CrossRef]
- Yang, J.; Yin, D.; Cheng, Q.; Shen, L.; Tan, Z. Decentralized cooperative unmanned aerial vehicles conflict resolution by neural network-based tree search method. Int. J. Adv. Robot. Syst. 2016, 13, 1729881416663371. [Google Scholar] [CrossRef]
- Pérez-Castán, J.; Comendador, F.G.; Rodríguez-Sanz, A.; Cabrera, I.A.; Torrecilla, J. RPAS conflict-risk assessment in non-segregated airspace. Saf. Sci. 2019, 111, 7–16. [Google Scholar] [CrossRef]
- Pérez-Castán, J.A.; Comendador, F.G.; Rodríguez-Sanz, Á.; Valdés, R.M.A.; Alonso-Alarcon, J.F. Safe RPAS integration in non-segregated airspace. Aircr. Eng. Aerosp. Technol. 2020. [Google Scholar] [CrossRef]
- Billingsley, T.B. Safety Analysis of TCAS on Global Hawk Using Airspace Encounter Models. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2006. [Google Scholar]
- Tang, J.; Zhu, F.; Piera, M.A. A causal encounter model of traffic collision avoidance system operations for safety assessment and advisory optimization in high-density airspace. Transp. Res. Part C Emerg. Technol. 2018, 96, 347–365. [Google Scholar] [CrossRef]
- Netjasov, F.; Vidosavljevic, A.; Tosic, V.; Everdij, M.H.; Blom, H.A. Development, validation and application of stochastically and dynamically coloured Petri net model of ACAS operations for safety assessment purposes. Transp. Res. Part C Emerg. Technol. 2013, 33, 167–195. [Google Scholar] [CrossRef]
- Tang, J.; Zhu, F. Graphical modeling and analysis software for state space-based optimization of discrete event systems. IEEE Access 2018, 6, 38385–38398. [Google Scholar] [CrossRef]
- Kochenderfer, M.J.; Holland, J.E.; Chryssanthacopoulos, J.P. Next-Generation Airborne Collision Avoidance System; Massachusetts Institute of Technology-Lincoln Laboratory Lexington: Lexington, MA, USA, 2012. [Google Scholar]
- Jun, T.; Piera, M.A.; Ruiz, S. A causal model to explore the ACAS induced collisions. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 228, 1735–1748. [Google Scholar] [CrossRef]
- GitHub. Available online: https://github.com/Airspace-Encounter-Models (accessed on 20 May 2020).








| Methods | Strategy | Communication | Number of Aircraft | Logic and Algorithm | Other Equipment | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pilots | Robustness | Sensor Error | Others | ADS-B /GPSLE | ADS-B | Radar | ||||
| [6] | C(V,S) | √ | 4 | √ | ||||||
| [7] | C(V,S) | √ | 2 | √ | ||||||
| [8] | C(V,S) | √ | 2 | √ | ||||||
| [9] | C(T,S) | √ | 2 | √ | √ | |||||
| [10] | C(V,S) | √ | 2 | √ | ||||||
| [11] | C(V,S) | √ | 2 | √ | ||||||
| [12] | C(V,S) | √ | 4 | √ | √ | |||||
| [13] | C(V,S) | √ | 2 | √ | ||||||
| [15] | C(V,S) | √ | Multiple | √ | ||||||
| [16] | C(V,S) | √ | Multiple | √ | ||||||
| [17] | C(V,S) | √ | Multiple | √ | ||||||
| Aircraft | Candidate Strategies | |
|---|---|---|
| Direction of Speed Change | Intensity of Speed Change | |
| m | Climb () | |
| Descend () | ||
| Climb () | ||
| Descend () | ||
| i | Climb () | |
| Descend () | ||
| Climb () | ||
| Descend () | ||
| j | Climb () | |
| Descend () | ||
| Climb () | ||
| Descend () | ||
| Num | Places | Definition | Instruction |
|---|---|---|---|
| P1 | tra | t | |
| P2 | ALIM | ALIM | |
| P3 | DMOD | DMOD | |
| P4 | Aircraft 1,2,3 | cid*ac*x*y*z*vx*vy*vz | Situation |
| P5 | ZTHR | ZTHR | |
| P6 | Aircraft 1 CPA | AC1 | CPA |
| P7 | Aircraft 2 CPA | AC2 | |
| P8 | Aircraft 3 CPA | AC3 | |
| P9 | Aircraft 1,2,3 | cid*ac*x*y*z*vx*vy*vz | |
| P10 | Δt 1,2,3 | Δt | Time of conflict relieving |
| P11 | Δvz∆vz 1,2,3 | Δvz | Vertical speed change |
| P12 | Aircraft 1,2,3 | cid*ac*x*y*z*vx*vy*vz | |
| P13 | Aircraft 1,2,3 | cid*ac*x*y*z*vx*vy*vz | |
| P14 | Aircraft 1,2,3 | cid*ac*x*y*z*vx*vy*vz | |
| P15 | Aircraft 1,2,3 | cid*ac*x*y*z*vx*vy*vz |
| Altitude (ft) | Sensitivity Level | Time (s) | DMOD (NM) | ZTHR (ft) | ALIM (ft) |
|---|---|---|---|---|---|
| 1000–2350 | 3 | 15 | 0.20 | 600 | 300 |
| 2350–5000 | 4 | 20 | 0.35 | 600 | 300 |
| 5000–10,000 | 5 | 25 | 0.55 | 600 | 350 |
| 10,000–20,000 | 6 | 30 | 0.80 | 600 | 400 |
| 20,000–42,000 | 7 | 35 | 1.10 | 700 | 600 |
| >42,000 | 7 | 35 | 1.10 | 800 | 700 |
| Time | Aircraft | X(NM) | Y(NM) | Z(ft) (Gmas) | Z(ft) (InCAS) | Time | Aircraft | X(NM) | Y(NM) | Z(ft)(Gmas) | Z(ft)(InCAS) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 20:14:52 | 1 | −2.94101 | −25.6996 | 15,800 | 15,800 | 20:15:18 | 1 | −0.49181 | −26.9593 | 16,330.15 | 16,222 |
| 20:14:52 | 2 | −1.30919 | −22.9531 | 14,961.98 | 14,961.98 | 20:15:18 | 2 | −0.54999 | −25.492 | 15,017.92 | 15,077 |
| 20:14:52 | 3 | −1.91927 | −29.1889 | 15,600 | 15,600 | 20:15:18 | 3 | −0.47081 | −26.8489 | 15,600 | 15,205 |
| 20:14:54 | 1 | −2.75261 | −25.7965 | 15,800 | 15,808 | 20:15:20 | 1 | −0.30341 | −27.0562 | 16,378.35 | 16,226 |
| 20:14:54 | 2 | −1.25079 | −23.1484 | 15,017.98 | 15,005.26 | 20:15:20 | 2 | −0.49159 | −25.6873 | 15,012.82 | 15,071 |
| 20:14:54 | 3 | −1.80785 | −29.0089 | 15,600 | 15,592 | 20:15:20 | 3 | −0.35939 | −26.6689 | 15,600 | 15,209 |
| 20:14:56 | 1 | −2.56421 | −25.8934 | 15,800 | 15,848 | 20:15:22 | 1 | −0.11501 | −27.1531 | 16,426.54 | 16,230 |
| 20:14:56 | 2 | −1.19239 | −23.3437 | 15,073.98 | 15,047.84 | 20:15:22 | 2 | −0.43319 | −25.8826 | 15,007.72 | 15,065 |
| 20:14:56 | 3 | −1.69643 | −28.8289 | 15,600 | 15552 | 20:15:22 | 3 | −0.24797 | −26.4889 | 15,600 | 15,213 |
| 20:14:58 | 1 | −2.37581 | −25.9903 | 15,848.2 | 15,906 | 20:15:24 | 1 | 0.07339 | −27.25 | 16,474.74 | 16,234 |
| 20:14:58 | 2 | −1.13399 | −23.539 | 15,068.88 | 15,089.94 | 20:15:24 | 2 | −0.37479 | −26.0779 | 15,002.63 | 15,059 |
| 20:14:58 | 3 | −1.58501 | −28.6489 | 15,600 | 15,494 | 20:15:24 | 3 | −0.13655 | −26.3089 | 15,600 | 15,217 |
| 20:15:00 | 1 | −2.18741 | −26.0872 | 15,896.39 | 15,964 | 20:15:26 | 1 | 0.26179 | −27.3469 | 16,522.93 | 16,214 |
| 20:15:00 | 2 | −1.07559 | −23.7343 | 15,063.79 | 15,123 | 20:15:26 | 2 | −0.31639 | −26.2732 | 14,997.53 | 15,053 |
| 20:15:00 | 3 | −1.47359 | −28.4689 | 15,600 | 15,436 | 20:15:26 | 3 | −0.02513 | −26.1289 | 15,600 | 15,247 |
| 20:15:02 | 1 | −1.99901 | −26.1841 | 15,944.59 | 16,022 | 20:15:28 | 1 | 0.45019 | −27.4438 | 16,571.13 | 16,175 |
| 20:15:02 | 2 | −1.01719 | −23.9296 | 15,058.69 | 15,125 | 20:15:28 | 2 | −0.25799 | −26.4685 | 15,114.63 | 15,047 |
| 20:15:02 | 3 | −1.36217 | −28.2889 | 15,600 | 15,378 | 20:15:28 | 3 | 0.08629 | −25.9489 | 15,600 | 15,303 |
| 20:15:04 | 1 | −1.81061 | −26.281 | 15,992.78 | 16,080 | 20:15:30 | 1 | 0.63859 | −27.5407 | 16,571.13 | 16,138 |
| 20:15:04 | 2 | −0.95879 | −24.1249 | 15053.59 | 15,119 | 20:15:30 | 2 | −0.19959 | −26.6638 | 15,231.72 | 15,041 |
| 20:15:04 | 3 | −1.25075 | −28.1089 | 15,600 | 15,320 | 20:15:30 | 3 | 0.19771 | −25.7689 | 15,600 | 15,361 |
| 20:15:06 | 1 | −1.62221 | −26.3779 | 16,040.98 | 16,138 | 20:15:32 | 1 | 0.82699 | −27.6376 | 16,522.93 | 16,104 |
| 20:15:06 | 2 | −0.90039 | −24.3202 | 15,048.5 | 15,113 | 20:15:32 | 2 | −0.14119 | −26.8591 | 15,348.82 | 15,044 |
| 20:15:06 | 3 | −1.13933 | −27.9289 | 15,600 | 15,262 | 20:15:32 | 3 | 0.30913 | −25.5889 | 15,600 | 15,403 |
| 20:15:08 | 1 | −1.43381 | −26.4748 | 16,089.17 | 16,188 | 20:15:34 | 1 | 1.01539 | −27.7345 | 16,474.74 | 16,072 |
| 20:15:08 | 2 | −0.84199 | −24.5155 | 15,043.4 | 15,107 | 20:15:34 | 2 | −0.08279 | −27.0544 | 15,465.92 | 15,080 |
| 20:15:08 | 3 | −1.02791 | −27.7489 | 15,600 | 15,212 | 20:15:34 | 3 | 0.42055 | −25.4089 | 15,600 | 15,428 |
| 20:15:10 | 1 | −1.24541 | −26.5717 | 16,137.37 | 16,206 | 20:15:36 | 1 | 1.20379 | −27.8314 | 16,426.54 | 16,042 |
| 20:15:10 | 2 | −0.78359 | −24.7108 | 15,038.3 | 15,101 | 20:15:36 | 2 | −0.02439 | −27.2497 | 15,583.01 | 15,141 |
| 20:15:10 | 3 | −0.91649 | −27.5689 | 15,600 | 15,194 | 20:15:36 | 3 | 0.53197 | −25.2289 | 15600 | 15452 |
| 20:15:12 | 1 | −1.05701 | −26.6686 | 16,185.56 | 16,210 | 20:15:38 | 1 | 1.39219 | 27.92835 | 16378.34 | 16014 |
| 20:15:12 | 2 | −0.72519 | −24.9061 | 15,033.21 | 15,095 | 20:15:38 | 2 | 0.03401 | 27.44503 | 15,700.105 | 15,200 |
| 20:15:12 | 3 | −0.80507 | −27.3889 | 15,600 | 15,193 | 20:15:38 | 3 | 0.64339 | −25.0489 | 15,600 | 15,474 |
| 20:15:14 | 1 | −0.86861 | −26.7655 | 16,233.76 | 16,214 | 20:15:40 | 1 | 1.58059 | 28.02527 | 16,330.14 | 15,988 |
| 20:15:14 | 2 | −0.66679 | −25.1014 | 15,028.11 | 15,089 | 20:15:40 | 2 | 0.09241 | 27.64033 | 15,817.197 | 15,256 |
| 20:15:14 | 3 | −0.69365 | −27.2089 | 15,600 | 15,197 | 20:15:40 | 3 | 0.75481 | −24.8689 | 15,600 | 15,494 |
| 20:15:16 | 1 | −0.68021 | −26.8624 | 16,281.95 | 16,218 | 20:15:42 | 1 | 1.76899 | 28.12219 | 16,281.94 | 15,963 |
| 20:15:16 | 2 | −0.60839 | −25.2967 | 15,023.01 | 15,083 | 20:15:42 | 2 | 0.15081 | 27.83563 | 15,934.289 | 15,310 |
| 20:15:16 | 3 | −0.58223 | −27.0289 | 15,600 | 15,201 | 20:15:42 | 3 | 0.86623 | −24.6889 | 15,600 | 15,514 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Wan, Y.; Lao, S. Graphical Modeling and Simulation for a Multi-Aircraft Collision Avoidance Algorithm based on Collaborative Decisions. Symmetry 2020, 12, 985. https://doi.org/10.3390/sym12060985
Chen X, Wan Y, Lao S. Graphical Modeling and Simulation for a Multi-Aircraft Collision Avoidance Algorithm based on Collaborative Decisions. Symmetry. 2020; 12(6):985. https://doi.org/10.3390/sym12060985
Chicago/Turabian StyleChen, Xi, Yu Wan, and Songyang Lao. 2020. "Graphical Modeling and Simulation for a Multi-Aircraft Collision Avoidance Algorithm based on Collaborative Decisions" Symmetry 12, no. 6: 985. https://doi.org/10.3390/sym12060985
APA StyleChen, X., Wan, Y., & Lao, S. (2020). Graphical Modeling and Simulation for a Multi-Aircraft Collision Avoidance Algorithm based on Collaborative Decisions. Symmetry, 12(6), 985. https://doi.org/10.3390/sym12060985





