On M-Polynomials of Dunbar Graphs in Social Networks
Abstract
1. Introduction
2. Defining Network Structure as M-Polynomial
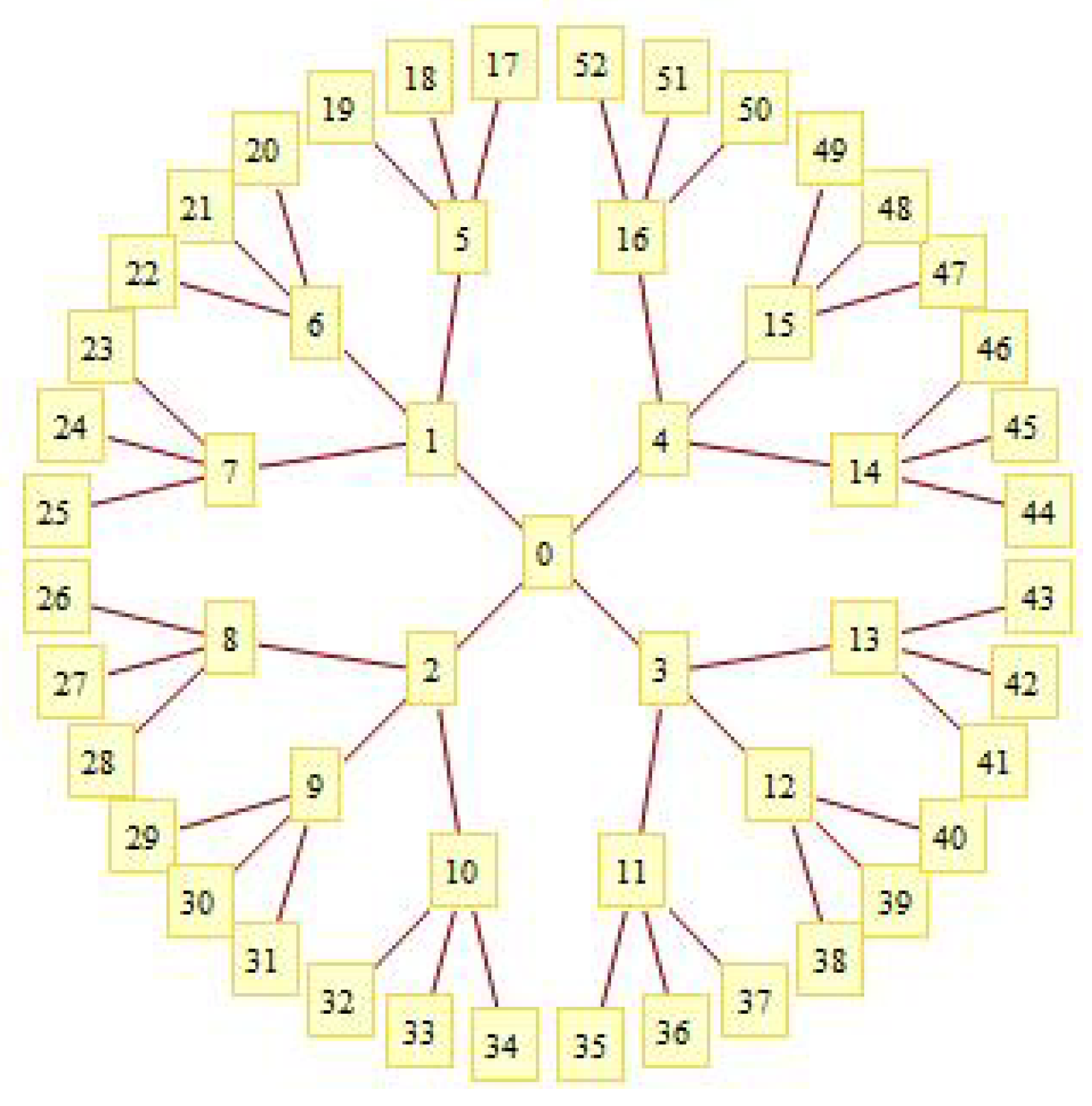
2.1. The -Agent Recruitment Graph
2.2. Topological Indices From The M-polynomial
3. Dunbar Graphs and Topological Indices
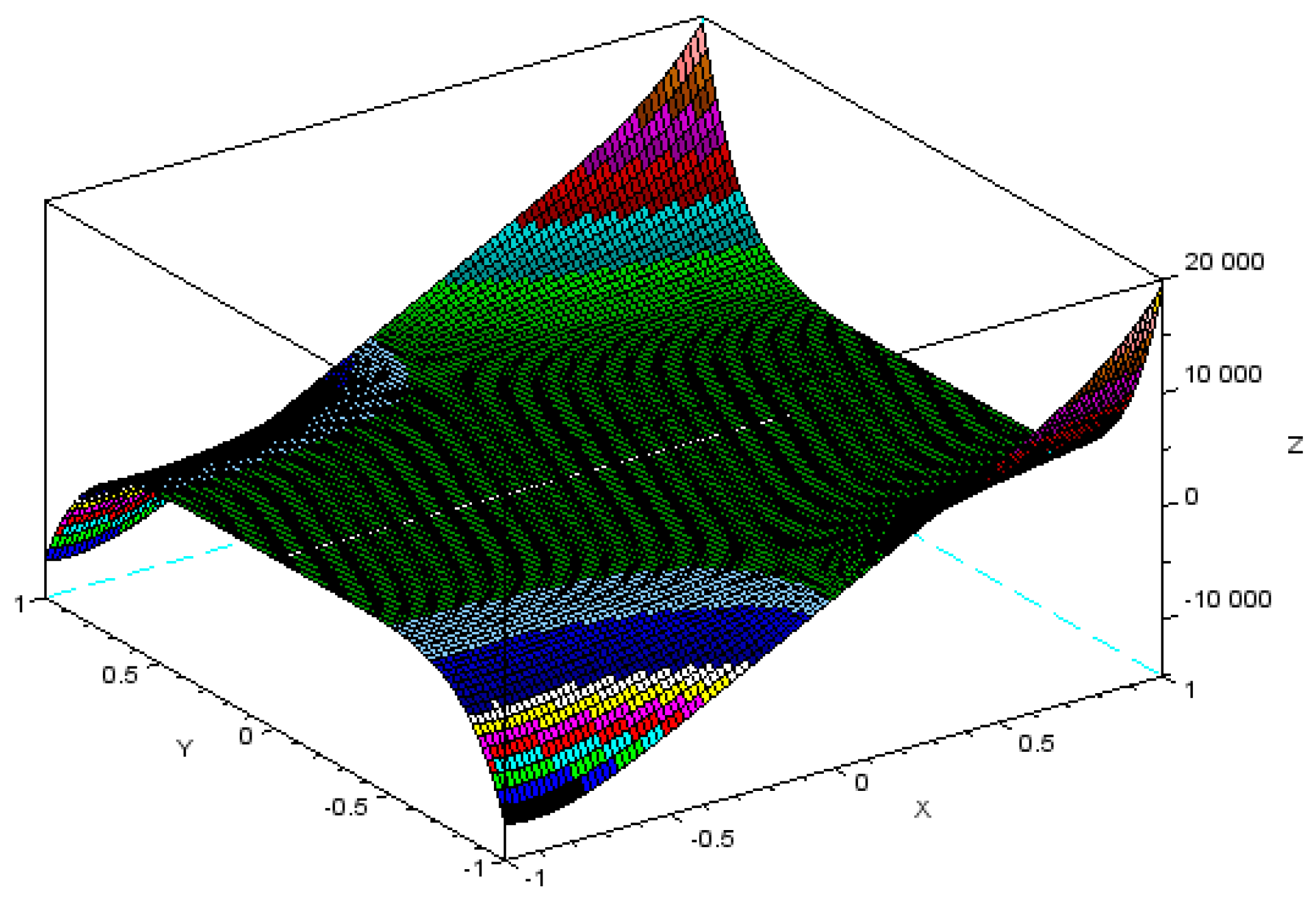
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- MacCarron, P.; Kaski, K.; Dunbar, R. Calling Dunbar’s number. Soc. Netw. 2016, 47, 151–155. [Google Scholar] [CrossRef]
- Zhou, W.X.; Sornette, D.; Hill, R.A.; Dunbar, R.I.M. Discrete hierarchical organization of social group sizes. Proc. R. Soc. B 2005, 272, 439–444. [Google Scholar] [CrossRef]
- Dunbar, R.I.M. The anatomy of friendship. Trends Cognit. Sci. 2018, 22, 32–50. [Google Scholar] [CrossRef]
- Hill, R.A.; Dunbar, R.I.M. Social network size in humans. Hum. Nat. 2003, 24, 53–72. [Google Scholar] [CrossRef] [PubMed]
- Arnaboldi, V.; Guazzini, A.; Passarella, A. Egocentric online social networks: Analysis of key features and prediction of tie strength in Facebook. Comput. Commun. 2013, 36, 1130–1144. [Google Scholar] [CrossRef]
- Chun, H.; Kwak, H.; Eom, Y.H.; Ahn, Y.Y.; Moon, S.; Jeong, H. Comparison of online social relations in terms of volume vs. interaction: A case study of Cyworld. In Proceedings of the IMC-2008, Blagoevgrad, Bulgaria, 25–31 July 2008; pp. 57–69. [Google Scholar]
- Dunbar, R.I.M. Sexual segregation in human conversations. Behaviour 2016, 153, 1–14. [Google Scholar] [CrossRef]
- Goncalves, B.; Perra, N.; Vespignani, A. Modeling users’ activity on Twitter networks: Validation. PLoS ONE 2011, 6, e22656. [Google Scholar] [CrossRef]
- Haerter, J.O.; Jamtveit, B.; Mathiesen, J. Communication dynamics in finite capacity social networks. Phys. Rev. Let. 2012, 109, 168701. [Google Scholar] [CrossRef]
- Wang, P.; Ma, J.C.; Jiang, Z.Q.; Zhou, W.X.; Sornette, D. Comparative analysis of layered structures in empirical investor networks and cellphone communication networks. EPJ Data 2020, 9, 11, in press. [Google Scholar] [CrossRef]
- Dunbar, R.I.M. The social brain hypothesis. Evol. Anthropol. 1988, 10, 142–149. [Google Scholar] [CrossRef]
- Dunbar, R.I.M. Co-evolution of neocortex size, group size and language in humans. Behav. Brain Sci. 1993, 16, 681–734. [Google Scholar] [CrossRef]
- Wilson, C.; Boe, B.; Sala, A.; Puttaswamy, K.P.N.; Zhao, B.Y. User interactions in social networks and their implications. In Proceedings of the 4th ACM European Conference on Computer Systems (EuroSys ’09), Nuremberg, Germany, 1–3 April 2009; 14p. [Google Scholar]
- Milgram, S. The small-world problem. Psychol. Today 1967, 1, 61–67. [Google Scholar]
- Barabási, A.L. Linked: The New Science of Networks; Perseus Publishing: Cambridge, MA, USA, 2007; pp. 25–40. [Google Scholar]
- Travers, J.; Milgram, S. An experimental study of the small-world problem. Sociometry 1969, 32, 425–443. [Google Scholar] [CrossRef]
- Dodds, P.S.; Muhamad, R.; Watts, D.J. An experimental study of search in global social networks. Science 2003, 301, 827–829. [Google Scholar] [CrossRef] [PubMed]
- Aylward, B.S.; Odar, C.C.; Kessler, E.D.; Canter, K.S.; Roberts, M.C. Six degrees of separation: An exploratory network analysis of mentoring relationships in pediatric psychology. J. Pediatr. Psychol. 2012, 37, 972–979. [Google Scholar] [CrossRef][Green Version]
- Backstrom, L.; Boldi, P.; Rosa, M.; Ugander, J.; Vigna, S. Four degrees of separation. In Proceedings of the 4th Annual ACM Web Science Conference, Evanston, IL, USA, 22–24 June 2012; pp. 33–42. [Google Scholar]
- Bhagat, S.; Burke, M.; Diuk, C.; Filiz, I.O.; Edunov, S. Three and a Half Degrees of Separation. Available online: https://research.fb.com/three-and-a-half-degrees-of-separation/ (accessed on 18 December 2019).
- Daraghmi, E.Y.; Yuan, S.M. We are so close, less than 4 degrees separating you and me! Comput. Hum. Behav. 2014, 30, 273–285. [Google Scholar] [CrossRef]
- Bakhshandeh, R.; Samadi, M.; Azimifar, Z.; Schaeffer, J. Degrees of separation in social networks. In Proceedings of the Symposium on Combinatorial Search, Barcelona, Spain, 15–16 July 2011; pp. 18–23. [Google Scholar]
- Kalish, Y.; Robins, G. Psychological predispositions and network structure: The relationship between individual predispositions, structural holes and network closure. Soc. Netw. 2006, 28, 56–84. [Google Scholar] [CrossRef]
- Roberts, S.G.B.; Wilson, R.; Fedurek, P.; Dunbar, R.I.M. Individual differences and personal social network size and structure. Personal. Individ. Differ. 2008, 44, 954–964. [Google Scholar] [CrossRef]
- Miritello, G.; Lara, R.; Cebrian, M.; Moro, E. Limited communication capacity unveils strategies for human interaction. Sci. Rep. 2013, 3, 1–7. [Google Scholar] [CrossRef]
- Burch, K.J. Chemical applications of graph theory. In Mathematical Physics in Theoretical Chemistry; Blinder, S.M., House, J.E., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; p. 261. [Google Scholar]
- Došlić, T. Planer polycyclic graphs and their Tutte polynomials. J. Math. Chem. 2013, 51, 1599–1607. [Google Scholar]
- Wiener, H.J. Structural Determination of Paraffin Boiling Points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef]
- Zanni, R.; Llompart, M.G.; Domenech, R.G.; Galvez, J. Latest advances in molecular topology applications for drug discovery. Expert Opin. Drug Discov. 2015, 10, 945–957. [Google Scholar] [CrossRef] [PubMed]
- Munir, M.; Nazeer, W.; Rafique, S.; Kang, S.M. M-polynomial and related topological indices of nanostar dendrimers. Symmetry 2016, 8, 97. [Google Scholar] [CrossRef]
- Randić, M. Characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Bollobas, B.; Erdos, P. Graphs of extremal weights. Ars Comb. 1988, 50, 225–233. [Google Scholar] [CrossRef]
- Balaban, A.T. Chemical graphs. Theor. Chem. Acta 1979, 53, 355–375. [Google Scholar] [CrossRef]
- Hosoya, H. On some counting polynomials in chemistry. Discret. Appl. Math. 1988, 19, 239–257. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, F. The clar covering polynomial of hexagonal systems I. Discret. Appl. Math. 1996, 69, 147–167. [Google Scholar] [CrossRef]
- Farrell, E.J. An introduction to matching polynomials. J. Comb. Theor. Ser. B 1979, 27, 75–86. [Google Scholar] [CrossRef]
- Hassani, F.; Iranmanesh, A.; Mirzaie, S. Schultz and modified Schultz polynomials of C100 fullerene. MATCH Commun. Math. Comput. Chem. 2013, 69, 87–92. [Google Scholar]
- Deutsch, E.; Klavžar, S. M-Polynomial and degree based topological indices. Iran. J. Math. Chem. 2015, 6, 93–102. [Google Scholar]
- Yang, H.; Baig, A.Q.; Khalid, W.; Farahani, M.R.; Zhang, X. M-Polynomial and Topological Indices of Benzene Ring Embedded in P-Type Surface Network. J. Chem. 2019, 9. [Google Scholar] [CrossRef]
- Webber, E.; Dunbar, R.I.M. The fractal structure of communities of practice: Implications for business organization. PLoS ONE 2020, 15, e0232204, in press. [Google Scholar] [CrossRef] [PubMed]
- Killworth, P.D.; Bernard, H.R.; McCarty, C. Measuring patterns of acquaintanceship. Curr. Anthropol. 1984, 25, 391–397. [Google Scholar] [CrossRef]
- Dezecache, G.; Dunbar, R. Sharing the joke: The size of natural laughter groups. Evol. Hum. Behav. 2012, 33, 775–779. [Google Scholar] [CrossRef]
- Dunbar, R.I.M. Constraints on the evolution of social institutions and their implications for information flow. J. Inst. Econ. 2011, 7, 345–371. [Google Scholar] [CrossRef]
- Dunbar, R.I.M. The social brain: Psychological underpinnings and implications for the structure of organizations. Curr. Dir. Psychol. Sci. 2014, 23, 109–114. [Google Scholar] [CrossRef]
- Dunbar, R.I.M. Do online social media cut through the constraints that limit the size of offline social networks? R. Soc. Open Sci. 2016, 3, 9. [Google Scholar] [CrossRef]
- Dunbar, R.I.M.; Duncan, N.D.C.; Nettle, D. Size and structure of freely forming conversational groups. Hum. Nat. 1995, 6, 67–78. [Google Scholar] [CrossRef]
- Krems, J.; Dunbar, R.I.M. Clique size and network characteristics in hyperlink cinema: Constraints of evolved psychology. Hum. Nat. 2013, 24, 414–429. [Google Scholar] [CrossRef]
- Krems, J.A.; Dunbar, R.I.M.; Neuberg, S.L. Something to talk about: Are conversation sizes constrained by mental modelling abilities? Evol. Hum. Behav. 2013, 37, 423–428. [Google Scholar] [CrossRef]
- KremMatthews, P.; Barrett, L. Small-screen social groups: Soap operas and social networks. J. Cult. Evol. Psychol. 2005, 3, 75–86. [Google Scholar]
- Kwun, Y.C.; Munir, M.; Nazeer, W.; Rafique, S.; Kang, S.M. M-polynomials and topological indices of V-phenylenic nanotubes and nanotori. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Stiller, J.; Nettle, D.; Dunbar, R.I.M. The small world of Shakespeare’s plays. Hum. Nat. 2004, 14, 397–408. [Google Scholar] [CrossRef] [PubMed]
| Topological Index | Notion for Topological Index | Derivation from or |
|---|---|---|
| First Zagreb | ||
| Second Zagreb | ( | |
| Second modified Zagreb | ||
| General Randi | ||
| General Inverse Randi | ||
| Symmetric Division Index | ||
| Harmonic Index | H(G) | 2 |
| Inverse sum Index | I(G) | |
| Augmented Zagreb Index | AZI(G) |
| 1 | m | ||
|---|---|---|---|
| Number of vertices | 1 |
| (1, ) | (m, ) | (, ) | |
|---|---|---|---|
| Number of edges | m |
| (5,5,6) | 156,230 | 234,300 | 2712.6667 | 96,364.333 | 5115.1948 | 5115.1948 | 13,406.494 |
| (5,150,6) | 5.848 | 1.154 | 2.515 | 5.734 | 5.013 | 3.772 | 3.873. |
| (5,5,4) | 6230 | 9300 | 108.5 | 3864.3333 | 204.48052 | 549.35065 | 1265.1852 |
| (5,150,4) | 2.599 | 5.130 | 111759.94 | 2.548 | 222,789.54 | 16,764,004 | 17,215,344 |
| (150,150,6) | 1.754 | 3.463 | 7.544 | 1.720 | 1.504 | 1.132 | 1.162 |
| (150,150,4) | 7.798 | 1.539 | 3352798 | 7.645 | 6,683,685.2 | 5.029 | 5.816 |
| (150,5,6) | 470,8650 | 715,9500 | 81,375.167 | 2,894,381 | 153,430.49 | 402,651.1 | 839,940.33 |
| (150,5,4) | 208,650 | 409,500 | 3250.1667 | 11,9381 | 6109.0659 | 16,936.813 | 62,340.333 |
| (5,15,6) | 73,225,380 | 1.302 | 238,364.12 | 60,987,322 | 463,641.65 | 357,3548.5 | 4,608,373.2 |
| (5,15,4) | 325,380 | 577,600 | 1059.4375 | 271,072 | 2060.7703 | 15,901.401 | 20,853.232 |
| (15,5,6) | 468,840 | 703,800 | 8137.6667 | 289,106 | 15,344.286 | 40,242.857 | 82,594.256 |
| (15,5,4) | 18,840 | 28,800 | 325.16667 | 11,606 | 612.14286 | 1671.4286 | 4834.2557 |
| (15,15,6) | 2.197 | 3.905 | 715,092.25 | 1.830 | 1,390,924.5 | 10,720,704 | 13,832,502 |
| (15,15,4) | 976,290 | 1,735,200 | 3178.1875 | 813,194.12 | 6181.8501 | 47,763.188 | 69,942.194 |
| (15,150,6) | 1.754 | 3.463 | 7.544 | 1.720 | 1.504 | 1.132 | 1.162. |
| (15,150,4) | 7.798 | 1.539 | 35,279.81 | 7.645 | 668,368.6 | 50,292,145 | 51,683,780 |
| 15,625 + 56 + 3900 | 15625 + 56 + 3900 | ||||||
| 3.797 + 5151 + 2.548 | 3.797 + 5151 + 2.548 | ||||||
| 625 + 56 + 150 | 625 + 56 + 150 | ||||||
| 16,875,000 + 5151 + 113,250 | 16,875,000 + 5151 + 113,250 | ||||||
| 1.139 + 150151 + 7.645 | 1.139 + 150151 + 7.645 | ||||||
| 5.062 + 150151 + 3,397,500 | 5.062 + 150151 + 3,397,500 | ||||||
| 468,750 + 1506 + 117,000 | 468,750 + 1506 + 117,000 | ||||||
| 18,750 + 1506 + 4500 | 18,750 + 1506 + 4500 | ||||||
| 3796875 + 516 + 271,200 | 3,796,875 + 516 + 271,200 | ||||||
| 16,875 + 516 + 1200 | 16,875 + 516 + 1200 | ||||||
| 46,875 + 156 + 11,700 | 46,875 + 156 + 11,700 | ||||||
| 1875 + 156 + 450 | 1875 + 156 + 450 | ||||||
| 11,390,625 + 1516 + 813,600 | 11,390,625 + 1516 + 813,600 | ||||||
| 50,625 + 1516 + 3600 | 50,625 + 1516 + 3600 | ||||||
| 1.139 + 15151 + 7.645 | 1.139 + 15151 + 7.645, | ||||||
| 50,625,000 + 15151 + 339,750 | 50,625,000 + 15151 + 339,750, | ||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acharjee, S.; Bora, B.; Dunbar, R.I.M. On M-Polynomials of Dunbar Graphs in Social Networks. Symmetry 2020, 12, 932. https://doi.org/10.3390/sym12060932
Acharjee S, Bora B, Dunbar RIM. On M-Polynomials of Dunbar Graphs in Social Networks. Symmetry. 2020; 12(6):932. https://doi.org/10.3390/sym12060932
Chicago/Turabian StyleAcharjee, Santanu, Bijit Bora, and Robin I. M. Dunbar. 2020. "On M-Polynomials of Dunbar Graphs in Social Networks" Symmetry 12, no. 6: 932. https://doi.org/10.3390/sym12060932
APA StyleAcharjee, S., Bora, B., & Dunbar, R. I. M. (2020). On M-Polynomials of Dunbar Graphs in Social Networks. Symmetry, 12(6), 932. https://doi.org/10.3390/sym12060932





