New Numerical Results for the Time-Fractional Phi-Four Equation Using a Novel Analytical Approach
Abstract
1. Introduction
2. Preliminaries
3. Solution Procedure for Fractional Phi-Four Equation
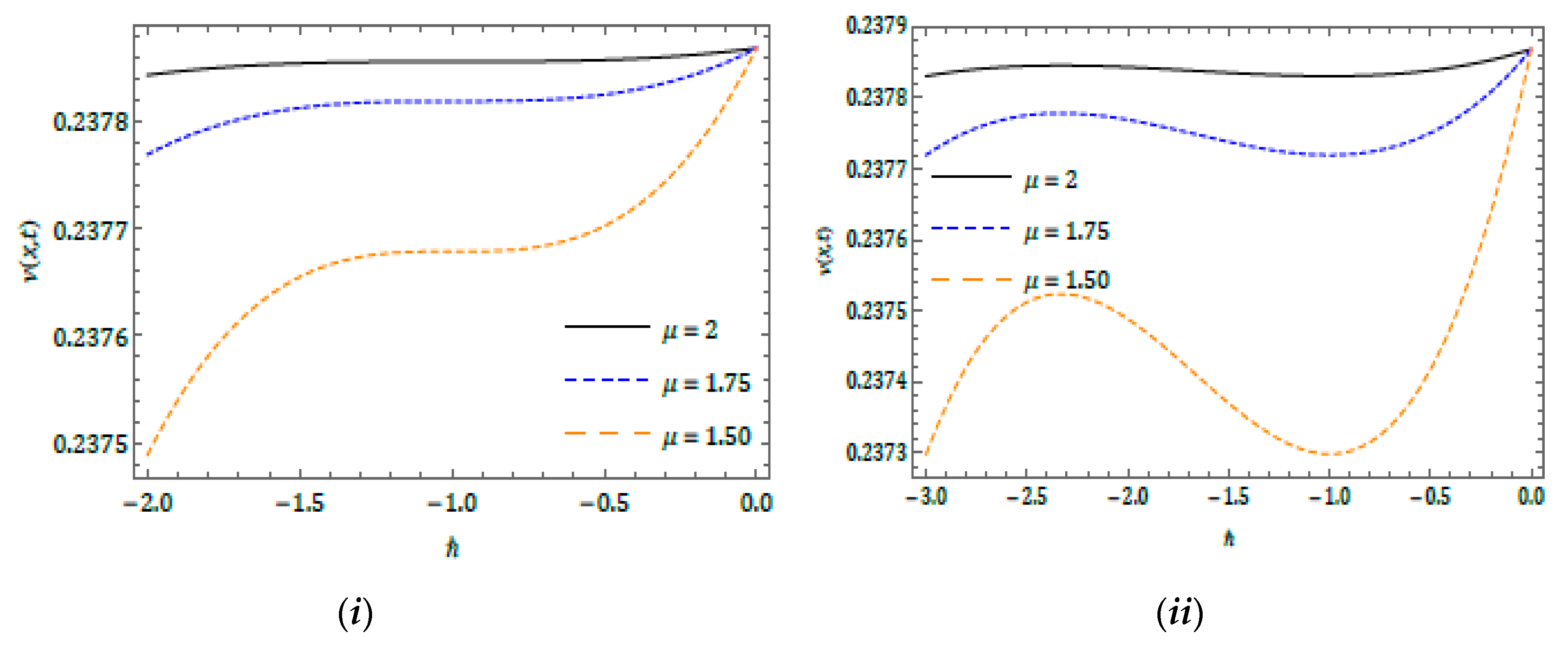
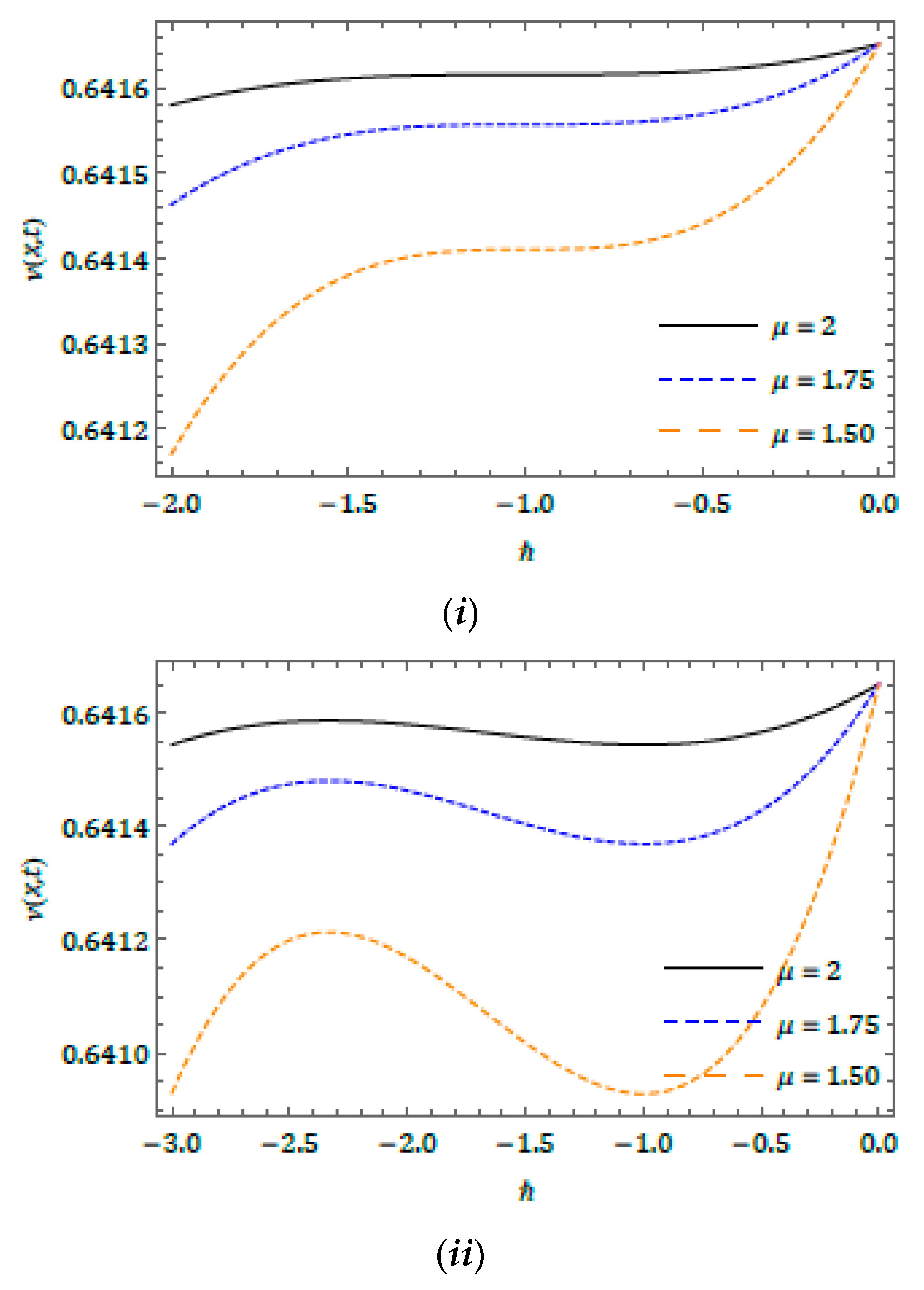
4. Convergence Analysis of the Proposed Method
5. Solution for Fractional PF Equation
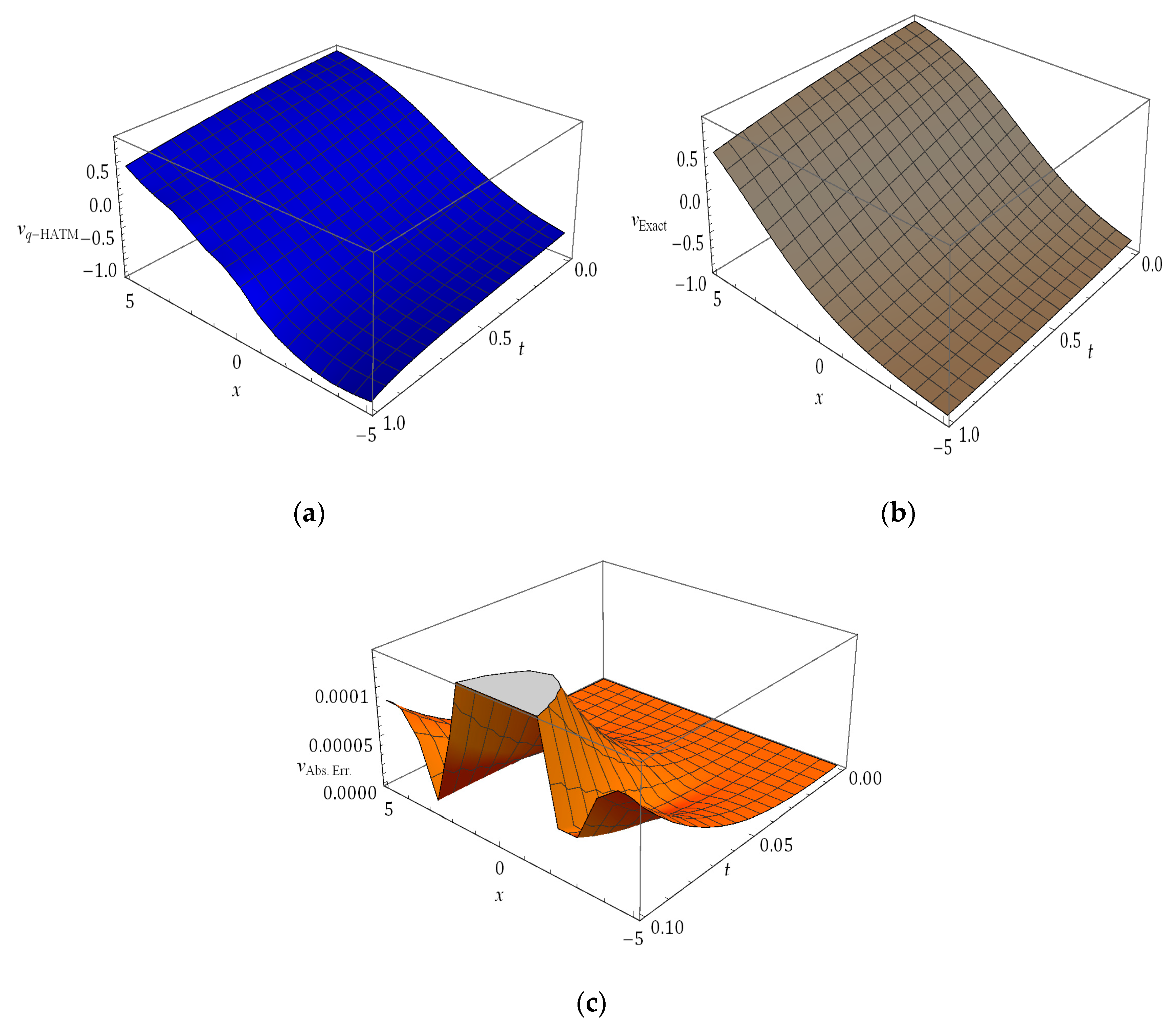
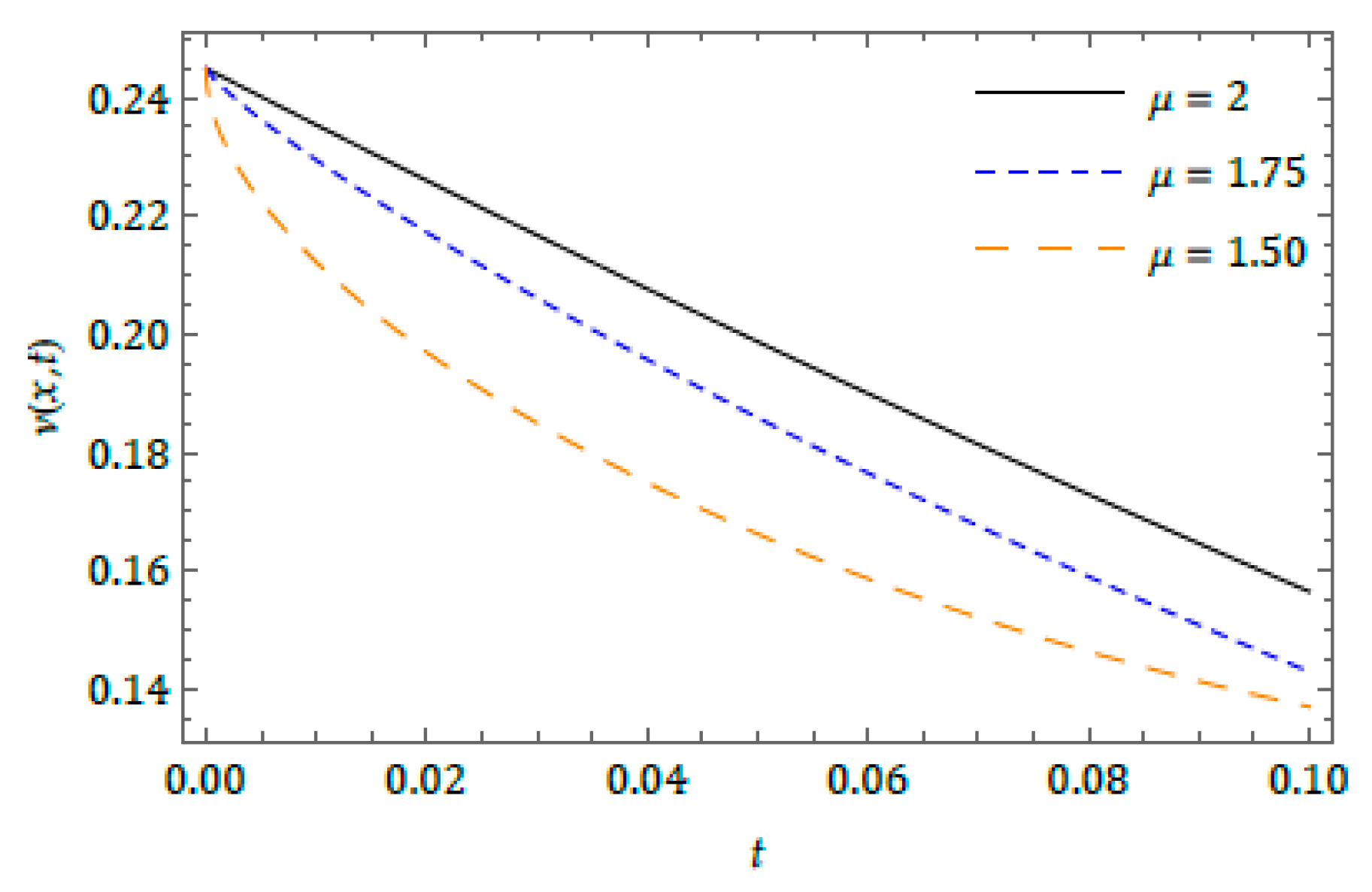
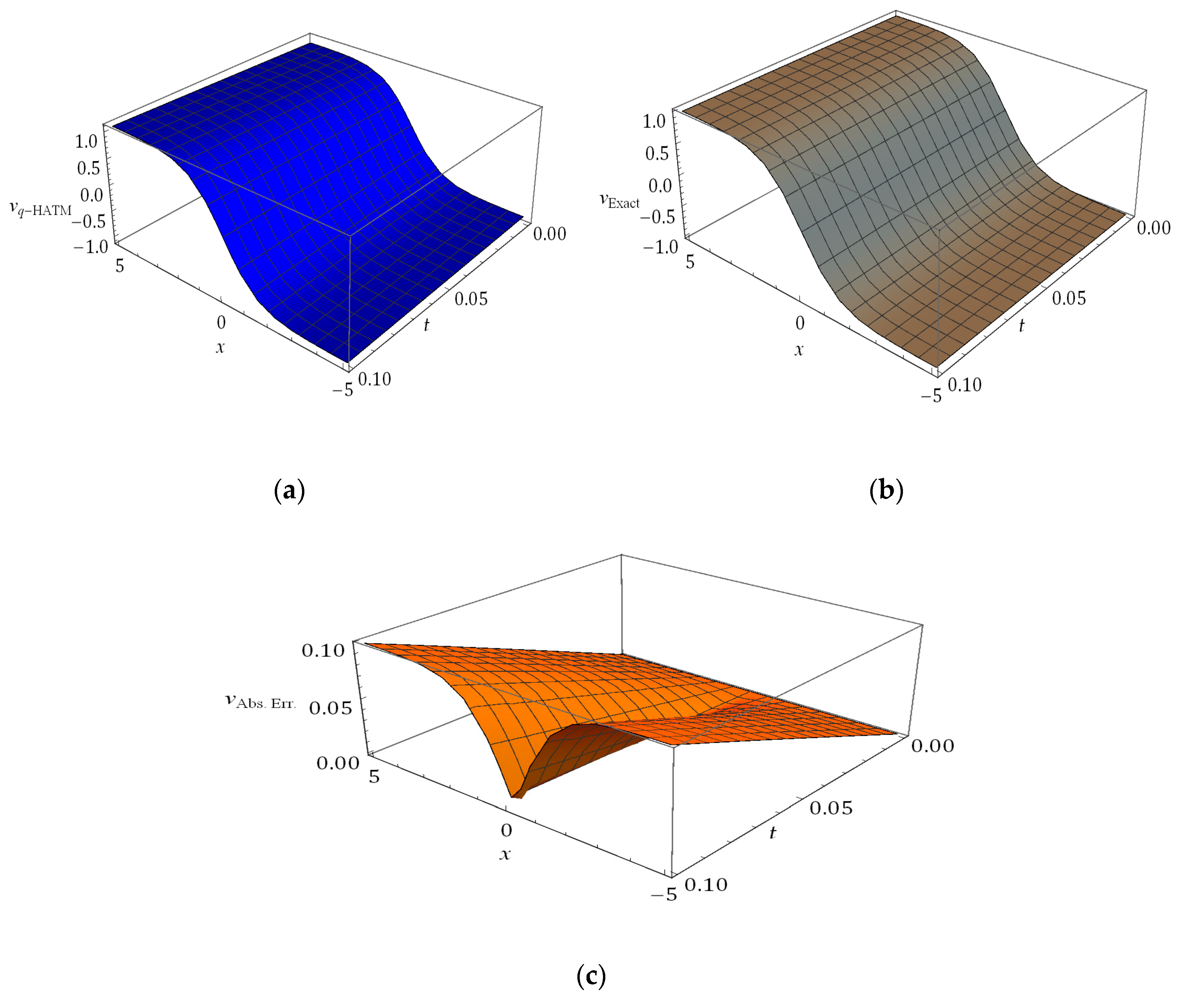
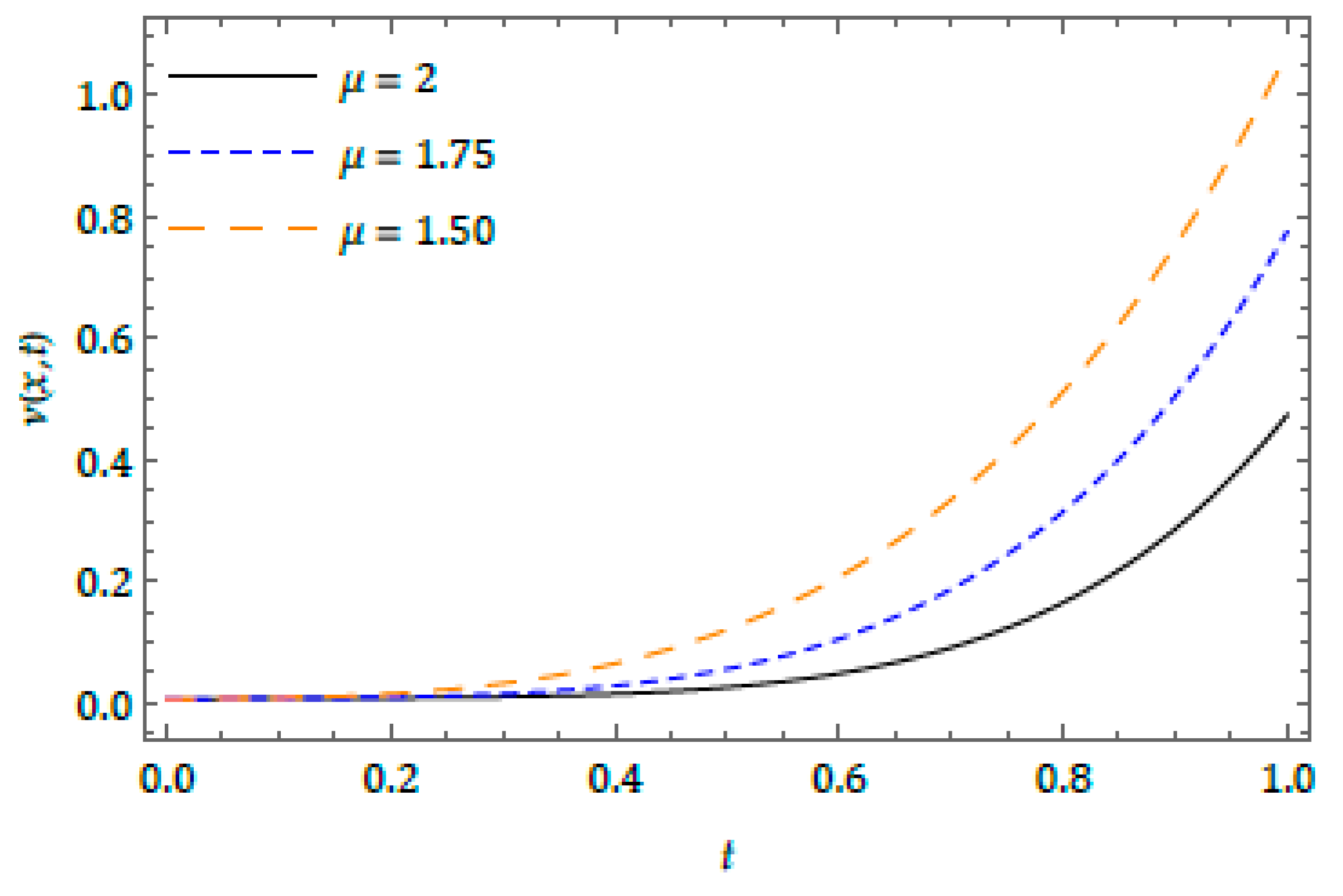
6. Numerical Results and Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liouville, J. Memoire surquelques questions de geometrieet de mecanique, etsurun nouveau genre de calcul pour resoudrecesquestions. J. Ecole Polytech. 1832, 13, 1–69. [Google Scholar]
- Riemann, G.F.B. Versuch Einer Allgemeinen Aufassung der Integration und Diferentiation; Gesammelte Mathematische Werke: Leipzig, Germany, 1896. [Google Scholar]
- Caputo, M. Elasticita e Dissipazione; Zanichelli: Bologna, Italy, 1969. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Cruz-Duarte, J.M.; Garcia, J.R.; Correa-Cely, C.R.; Perez, A.G.; Avina-Cervantes, J.G. A closed form expression for the Gaussian-based Caputo-Fabrizio fractional derivative for signal processing applications. Commun. Nonlinear Sci. Numer. Simul. 2018, 61, 138–148. [Google Scholar] [CrossRef]
- Esen, A.; Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. Optical solitons and other solutions to the conformable space–time fractional Fokas–Lenells equation. Optik 2018, 167, 150–156. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Hasan, M.M.A.; Baleanu, D. New studies for general fractional financial models of awareness and trial advertising decisions. Chaos Solitons Fractals 2017, 104, 772–784. [Google Scholar] [CrossRef]
- Baleanu, D.; Wu, G.C.; Zeng, S.D. Chaos analysis and asymptotic stability of generalized Caputo fractional differential equations. Chaos Solitons Fractals 2017, 102, 99–105. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. New numerical surfaces to the mathematical model of cancer chemotherapy effect in Caputo fractional derivatives. Chaos 2019, 29. [Google Scholar] [CrossRef]
- Atangana, A. Fractional discretization: The African’s tortoise walk. Chaos Solitons Fractals 2020, 130, 109399. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Hammouch, Z.; Atangana, A. A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl. Math. Comput. 2018, 316, 504–515. [Google Scholar]
- Kolade, O.M.; Hammouch, Z. Mathematical modeling and analysis of two-variable system with noninteger-order derivative. Chaos 2019, 29, 013145. [Google Scholar]
- Khan, M.A.; Hammouch, Z.; Baleanu, D. Modeling the dynamics of hepatitis E via the Caputo–Fabrizio derivative. Math. Model. Nat. Phenom. 2019, 14, 311. [Google Scholar] [CrossRef]
- Prakash, A.; Veeresha, P.; Prakasha, D.G.; Goyal, M. A homotopy technique for fractional order multi-dimensional telegraph equation via Laplace transform. Eur. Phys. J. Plus 2019, 134, 1–18. [Google Scholar] [CrossRef]
- Cattani, C.; Srivastava, H.M.; Yang, X.J. Fractional Dynamics; De Gruyter: Berlin, Germany, 2019; pp. 1–5. [Google Scholar]
- Zhang, Y.; Cattani, C.; Yang, X.J. Local fractional homotopy perturbation method for solving non-homogeneous heat conduction equations in fractal domains. Entropy 2015, 17, 6753–6764. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Solving smoking epidemic model of fractional order using a modified homotopy analysis transform method. Math. Sci. 2019, 13, 115–128. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Seadawy, A.R. Fractional solitary wave solutions of the nonlinear higher-order extended KdV equation in a stratified shear flow: Part I. Comp. Math. Appl. 2015, 70, 345–352. [Google Scholar] [CrossRef]
- Atangana, A.; Alkahtani, B.T. Analysis of the Keller-Segel model with a fractional derivative without singular kernel. Entropy 2015, 17, 4439–4453. [Google Scholar]
- Kaya, D.; Gulbahar, S.; Yokus, A.; Gulbahar, M. Solutions of the fractional combined kdv–mkdv equation with collocation method using radial basis function and their geometrical obstructions. Adv. Differ. Equ. 2018, 77, 2018. [Google Scholar] [CrossRef]
- Prakash, A.; Prakash, D.G.; Veeresha, P. A reliable algorithm for time-fractional Navier-Stokes equations via Laplace transforms. Nonlinear Eng. 2019, 8, 695–701. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. Analysis of regularized long-wave equation associated with a new fractional operator with Mittag-Leffler type kernel. Physica A 2018, 492, 155–167. [Google Scholar] [CrossRef]
- Brzeziński, D.W. Review of numerical methods for NumILPT with computational accuracy assessment for fractional calculus. Appl. Math. Nonlinear Sci. 2018, 3, 487–502. [Google Scholar] [CrossRef]
- Youssef, I.K.; Dewaik, M.H. Solving Poisson’s Equations with fractional order using Haarwavelet. Appl. Math. Nonlinear Sci. 2017, 2, 271–284. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Baleanu, D. New aspects of fractional Biswas-Milovic model with Mittag-Leffler law. Math. Modelling Nat. Phenomena 2019, 14, 303–310. [Google Scholar] [CrossRef]
- Cattani, C.; Ciancio. On the fractal distribution of primes and prime-indexed primes by the binary image analysis. Phys. A 2016, 460, 222–229. [Google Scholar] [CrossRef]
- Cattani, C. A review on Harmonic Wavelets and their fractional extension. J. Adv. Eng. Comput. 2018, 2, 224–238. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. An efficient technique for a fractional-order system of equations describing the unsteady flow of a polytropic gas. Pramana 2019, 93, 75. [Google Scholar] [CrossRef]
- Prakasha, D.G.; Veeresha, P.; Singh, J. Fractional approach for equation describing the water transport in unsaturated porous media with Mittag-Leffler kernel. Front. Phys. 2019, 7, 193. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Sajjadi, S.S.; Mozyrska, D. A new fractional model and optimal control of a tumor-immune surveillance with non-singular derivative operator. Chaos 2019, 29, 083127. [Google Scholar] [CrossRef]
- Jajarmi, A.; Arshad, S.; Baleanu, D. A new fractional modelling and control strategy for the outbreak of dengue fever. Phys. A 2019, 535. [Google Scholar] [CrossRef]
- Jajarmi, A.; Ghanbari, B.; Baleanu, D. A new and efficient numerical method for the fractional modeling and optimal control of diabetes and tuberculosis co-existence. Chaos 2019, 29. [Google Scholar] [CrossRef]
- Jajarmi, A.; Baleanu, D.; Sajjadi, S.S.; Asad, J.H. A new feature of the fractional Euler–Lagrange equations for a coupled oscillator using a nonsingular operator approach. Front. Phys. 2019, 7. [Google Scholar] [CrossRef]
- Baleanu, D.; Asad, J.H.; Jajarmi, A. New aspects of the motion of a particle in a circular cavity. Proc. Rom. Acad. Ser. A 2018, 19, 361–367. [Google Scholar]
- Veeresha, P.; Prakasha, D.G. Solution for fractional Zakharov-Kuznetsov equations by using two reliable techniques. Chin. J. Phys. 2019, 60, 313–330. [Google Scholar] [CrossRef]
- Baleanu, D.; Sajjadi, S.S.; Jajarmi, A.; Asad, J.H. New features of the fractional Euler-Lagrange equations for a physical system within non-singular derivative operator. Eur. Phys. J. Plus 2019, 134. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. Optical solitons to the fractional perturbed NLSE in nano-fibers. Discret. Contin. Dyn. Syst. Ser. S 2019, 13, 925–936. [Google Scholar]
- Dashen, R.F.; Hasslacher, B.; Neveu, A. Particle spectrum in model field theories from semi-classical functional integral technique. Phys. Rev. D. 1975, 11, 3424–3450. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Generalized forms of the phi-four equation with compactons, solitons and periodic solutions. Math. Comput. Simul. 2005, 69, 580–588. [Google Scholar] [CrossRef]
- Liao, S.J. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Liao, S.J. Homotopy analysis method and its applications in mathematics. J. Basic Sci. Eng. 1997, 5, 111–125. [Google Scholar]
- Singh, J.; Kumar, D.; Swroop, R. Numerical solution of time- and space-fractional coupled Burgers’ equations via homotopy algorithm. Alex. Eng. J. 2016, 55, 1753–1763. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Kumar, D.; Singh, J. An efficient analytical technique for fractional model of vibration equation. Appl. Math. Model. 2017, 45, 192–204. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. A New Numerical Algorithm for Fractional Fitzhugh-Nagumo Equation Arising in Transmission of Nerve Impulses. Nonlinear Dyn. 2018, 91, 307–317. [Google Scholar] [CrossRef]
- Singh, J.; Secer, A.; Swroop, R.; Kumar, D. A reliable analytical approach for a fractional model of advection-dispersion equation. Nonlinear Eng. 2019, 9, 107–116. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Novel simulations to the time-fractional Fisher’s equation. Math. Sci. 2019, 13, 33–42. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Swroop, R.; Kumar, S. An efficient computational approach for time-fractional Rosenau-Hyman equation. Neural Comput. Appl. 2018, 30, 3063–3070. [Google Scholar] [CrossRef]
- Prakasha, D.G.; Veeresha, P.; Baskonus, H.M. Two novel computational techniques for fractional Gardner and Cahn-Hilliard equations. Comput. Math. Methods 2019, 1, e1021. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Kumar, D. An efficient technique for nonlinear time-fractional Klein-Fock-Gordon equation. Appl. Math. Comput. 2020, 364, 124637. [Google Scholar] [CrossRef]
- Kumar, D.; Agarwal, R.P.; Singh, J. A modified numerical scheme and convergence analysis for fractional model of Lienard’s equation. J. Comput. Appl. Math. 2018, 399, 405–413. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baleanu, D. An efficient numerical technique for the nonlinear fractional Kolmogorov-Petrovskii-Piskunov equation. Mathematics 2019, 7, 365. [Google Scholar] [CrossRef]
- Prakash, A.; Veeresha, P.; Prakasha, D.G.; Goyal, M. A new efficient technique for solving fractional coupled Navier–Stokes equations using q-homotopy analysis transform method. Pramana 2019, 93, 6. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G. Solution for fractional generalized Zakharov equations with Mittag-Leffler function. Results Eng. 2020, 5, 100085. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Tariq, H.; Eslami, M.; Mirzazadeh, M.; Zhou, Q. New exact solutions of nonlinear conformable time-fractional Phi-4 equation. Chin. J. Phys. 2018, 56, 2805–2816. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Assas, L.M.; Alghamdi, M.A. An efficient spectral collocation algorithm for nonlinear Phi-four equations. Bound. Value Probl. 2013, 2013, 87. [Google Scholar] [CrossRef]
- Tariq, H.; Akram, G. New approach for exact solutions of time fractional Cahn–Allen equation and time fractional Phi-4 equation. Phys. A 2017, 473, 352–362. [Google Scholar] [CrossRef]
- Zahra, W.K. Trigonometric B-Spline collocation method for solving PHI-four and Allen–Cahn equations. Mediterr. J. Math. 2017, 14, 122. [Google Scholar] [CrossRef]
- Gao, W.; Ghanbari, B.; Baskonus, H.M. New numerical simulations for some real world problems with Atangana-Baleanu fractional derivative. Chaos Solitons Fractals 2019, 128, 34–43. [Google Scholar] [CrossRef]
- Mahmud, F.; Samsuzzoh, M.; Akbar, M.A. The generalized Kudryashov method to obtain exact traveling wave solutions of the PHI-four equation and the Fisher equation. Results Phys. 2017, 7, 4296–4302. [Google Scholar] [CrossRef]
- Gao, W.; Partohaghighi, M.; Baskonus, H.M.; Ghavi, S. Regarding the Group preserving scheme and method of line to the Numerical Simulations of Klein-Gordon Model. Results Phys. 2019, 15, 102555. [Google Scholar] [CrossRef]
- Gao, W.; Veeresha, P.; Prakasha, D.G.; Baskonus, H.M.; Yel, G. A powerful approach for fractional Drinfeld–Sokolov–Wilson equation with Mittag-Leffler law. Alex. Eng. J. 2019. [Google Scholar] [CrossRef]
- Gao, W.; Ismael, H.F.; Mohammed, S.A.; Baskonus, H.M.; Bulut, H. Complex and real optical soliton properties of the paraxial nonlinear Schrödinger equation in Kerr media with M-fractional. Front. Phys. 2019. [Google Scholar] [CrossRef]
- Yokus, A.; Gulbahar, S. Numerical Solutions with Linearization Techniques of the Fractional Harry Dym Equation. Appl. Math. Nonlinear Sci. 2019, 4, 35–42. [Google Scholar] [CrossRef]
- Gao, W.; Yel, G.; Baskonus, H.M.; Cattani, C. Complex Solitons in the Conformable (2+1)-dimensional Ablowitz-Kaup-Newell-Segur Equation. AIMS Math. 2020, 5, 507–521. [Google Scholar] [CrossRef]
- Al-Ghafri, K.S.; Rezazadeh, H. Solitons and other solutions of (3 + 1)-dimensional space–time fractional modified KdV–Zakharov–Kuznetsov equation. Appl. Math. Nonlinear Sci. 2019, 4, 289–304. [Google Scholar] [CrossRef]
- Ciancio, A.; Quartarone, A. A hybrid model for tumor-immune competition. UPB Sci. Bull. Ser. A 2013, 75, 125–136. [Google Scholar]
- Yel, G.; Baskonus, H.M. Solitons in Conformable Time-Fractional Wu-Zhang System Arising in Coastal Design. Pramana 2019, 93, 57. [Google Scholar] [CrossRef]
- Yang, X.J. New rheological problems involving general fractional derivatives with nonsingular power-law kernels. Proc. Rom. Acad. Ser. A Math. Phys. Tech. Sci. Inf. Sci. 2018, 19, 45–52. [Google Scholar]
- Baskonus, H.M. Complex Surfaces to the Fractional (2+1)-dimensional Boussinesq Dynamical Model with Local M-derivative. Eur. Phys. J. Plus 2019, 134, 322. [Google Scholar] [CrossRef]
- Lemkeddem, M.; Hammouch, Z.; Guerbati, K.; Benchohra, M. Impulsive partial functional fractional differential equations with non-local conditions. Nonlinear Stud. 2019, 10, 303–321. [Google Scholar]
- Ciancio, A. Analysis of time series with wavelets. Int. J. Wavelets Multiresolut. Inf. Process. 2007, 5, 241–256. [Google Scholar] [CrossRef]
- Yang, X.J. New general fractional-order rheological models with kernels of Mittag-Leffler functions. Rom. Rep. Phys. 2017, 69, 118. [Google Scholar]
- Tellab, B.; Haouam, K. Solvability of semilinear fractional differential equations with nonlocal and integral boundary conditions. Nonlinear Stud. 2019, 10, 341–356. [Google Scholar]
- Velioglu, Z. Soluble Product of Parafree Lie algebras and Its residual Properties. Appl. Math. Nonlinear Sci. 2019, 4, 1–5. [Google Scholar] [CrossRef]
- Kocak, Z.F.; Bulut, H.; Yel, G. The solution of fractional wave equation by using modified trial equation method and homotopy analysis method. AIP Conference Proceedings 2014, 1637, 504–512. [Google Scholar]
- Rani, D.; Mishra, V. Solving linear fractional order differential equations by Chebyshev polynomials based numerical inverse Laplace transform. Nonlinear Stud. 2019, 10, 781–791. [Google Scholar]
- Klimek, M.; Lupa, M. Reflection Symmetry in Fractional Calculus–Properties and Applications. In Advances in the Theory and Applications of Non-integer Order Systems; Springer: Heidelberg, Germany, 2013; pp. 201–211. [Google Scholar]
- Odibat, Z.M.; Shawagfeh, N.T. Generalized Taylor’s formula. Appl. Math. Comput. 2007, 186, 286–293. [Google Scholar] [CrossRef]
- Argyros, I.K. Convergence and Applications of Newton-Type Iterations; Springer: New York, NY, USA, 2008. [Google Scholar]
- Magrenan, A.A. A new tool to study real dynamics: The convergence plane. Appl. Math. Comput. 2014, 248, 215–224. [Google Scholar] [CrossRef]
- Alquran, M.; Jaradat, H.M.; Syam, M.I. Analytical solution of the time-fractional Phi-4 equation by using modified residual power series method. Nonlinear Dyn. 2017, 90, 2525–2529. [Google Scholar] [CrossRef]
- Zhou, H.; Shen, J. Bifurcations of travelling wave solutions for modified nonlinear dispersive phi-four equation. Appl. Math. Comput. 2010, 217, 1584–1597. [Google Scholar] [CrossRef]
- Deng, X.; Zhao, M.; Li, X. Travelling wave solutions for a nonlinear variant of the PHI-four equation. Math. Comput. Model. 2009, 49, 617–622. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Singh, J. Solution for fractional forced KdV equation using fractional natural decomposition method. AIMS Math. 2019, 5, 798–810. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G. An efficient technique for two-dimensional fractional order biological population model. Int. J. Model. Simul. Sci. Comput. 2020. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, W.; Veeresha, P.; Prakasha, D.G.; Baskonus, H.M.; Yel, G. New Numerical Results for the Time-Fractional Phi-Four Equation Using a Novel Analytical Approach. Symmetry 2020, 12, 478. https://doi.org/10.3390/sym12030478
Gao W, Veeresha P, Prakasha DG, Baskonus HM, Yel G. New Numerical Results for the Time-Fractional Phi-Four Equation Using a Novel Analytical Approach. Symmetry. 2020; 12(3):478. https://doi.org/10.3390/sym12030478
Chicago/Turabian StyleGao, Wei, Pundikala Veeresha, Doddabhadrappla Gowda Prakasha, Haci Mehmet Baskonus, and Gulnur Yel. 2020. "New Numerical Results for the Time-Fractional Phi-Four Equation Using a Novel Analytical Approach" Symmetry 12, no. 3: 478. https://doi.org/10.3390/sym12030478
APA StyleGao, W., Veeresha, P., Prakasha, D. G., Baskonus, H. M., & Yel, G. (2020). New Numerical Results for the Time-Fractional Phi-Four Equation Using a Novel Analytical Approach. Symmetry, 12(3), 478. https://doi.org/10.3390/sym12030478







