A Robust q-Rung Orthopair Fuzzy Einstein Prioritized Aggregation Operators with Application towards MCGDM

Abstract

A q-rung orthopair fuzzy set (q-ROFS) provides a significant mechanism for managing symmetrical aspects in real life circumstances. The renowned distinguishing feature of q-ROFS is that the sum of the qth powers to each membership degree (MD) and non-membership degree (NMD) is less than or equal 1, and therefore the comprehensive uncertain space for q-ROF information is broader. Numerous researchers have suggested several aggregation operators based on q-ROFSs. In order to discuss prioritized relationship in the criterion and a smooth approximation of q-ROF information, we introduced q-rung orthopair fuzzy Einstein prioritized weighted averaging (q-ROFEPWA) operator and q-rung orthopair fuzzy Einstein prioritized weighted geometric (q-ROFEPWG) operator. Additionally, we presented a multi-criteria group decision making (MCGDM) technique based on q-rung orthopair fuzzy Einstein prioritized aggregation operators. These operators can evaluate the possible symmetric roles of the criterion that express the real phenomena of the problem. In order to investigate characteristic of suggested operators regarding the symmetry of attributes and their symmetrical roles under q-ROF information, we presented an application of Einstein prioritized aggregation operators. Finally, by comparing it with some other established representative MCGDM models, an illustrative example is provided to check the feasibility, efficiency and supremacy of the proposed technique.

1. Introduction

Issues concerning unstable situations typically arise in decision-making, but they are demanding because of the complex and difficult situation of modeling and manipulation that emerges with such uncertainties. In an attempt to solve complex real-world problems, methods widely used in classical mathematics are often not useful due to the different kinds of complexity and lack of clarity in these important issues. To deal with uncertainties and vagueness. Zadeh initiated fuzzy set theory [1], Atanassov [2] introduced intuitionistic fuzzy sets (IFSs) and Yager [3,4,5] presented the notion of Pythagorean fuzzy sets. Zhang [6] introduced bipolar fuzzy sets and relations.

Several researchers have analyzed implementations of fuzzy sets; Ali et al. [7], Ali [8], Chen et al. [9], Chi and Lui [10], Çağman et al. [11], Eraslan and Karaaslan [12], Feng et al. [13,14,15,16] presented some work about soft sets combined with fuzzy sets and rough sets, Garg and Arora [17,18,19] introduced some aggregation operators (AOs) related to IFS, soft set and application related to MCDM, Kumar and Garg [20], Karaaslan [21], Liu et al. [22], Naeem et al. [23,24,25] introduced PFS with m-polar, Peng et al. [26,27,28,29] gave some results related to PFS, Riaz and Hashmi [30,31] presented a novel concept of linear diophantine fuzzy set, Riaz et al. [32], Riaz and Tehrim [33,34], Shabir and Naz [35], Wang et al. [36], Xu [37], Xu and Cai [38], Xu [39], Xu developed a number of AOs, based on IFSs [37], Ye [40,41], Zhang and Xu [42], Zhan et al. [43,44] presented some aggregation techniques and Zhang et al. [45,46,47] presented work of rough set, Riaz et al. [48,49] presented some AOs of q-ROFSs. Sharma et al. [50] and Sinani et al. [51] presented some work related to rough set theory.

Yager initiated the idea of q-ROFS as an extension of PFS [52], in which the sum of membership degree (MD) ${\check{\mathfrak{p}}}_A(\zeta )$ and non-membership degree (NMD) ${\overline{⨿}}_A(\zeta )$ satisfy the condition $0\le {\left({\check{\mathfrak{P}}}_A(\zeta )\right)}^q+{\left({\overline{⨿}}_A(\zeta )\right)}^q\le 1,(q\ge 1)$. The degree of indeterminacy (ID) is given by ${\pi }_A(\zeta )=\sqrt[q]{({\check{\mathfrak{P}}}_A^q(\zeta )+{\overline{⨿}}_A^q(\zeta )-{\check{\mathfrak{P}}}_A^q(\zeta ){\overline{⨿}}_A^q(\zeta ))}$. There is no condition on q other than $q\ge 1$. Although q is real number, but if q is integral value, it is also very easy to predict the area from which MD and NMD are selected. We can easily check that $99\%$ area is covered when we put $q=10$ of unit square $[0,1]\times [0,1]$.

Aggregation operators (AOs) are effective tools, particularly in the multi-criteria group decision making (MCGDM) analysis, to merge all input arguments into one completely integrated value. Since Yager introduced the classic OWA operator, different varieties of AOs were studied and applied to various decision-making issues [53]. Yager developed many weighted average, weighted geometric and ordered weighted AOs based on PFSs. Grag [54] and Rahmana et al. [55] introduced some Einstein AOs on PFS. Khan et al. [56] initiated the concept of prioritized AOs and also Einstein prioritized [57] on PFS. However, there has indeed been very few research on AOs in the context of q-ROF. In the available literature, relying on the proposed operation of q-rung orthopair fuzzy numbers (q-ROFNs). Liu and Wang [58] have established several more basic q-ROF AOs. Liu and Liu [59] drawn-out the Bonferroni mean AOs to q-ROF environment. Zhao [60] introduced some hammy mean AOs to aggregate the q-ROFNs. The AOs suggested above for q-ROFNs claiming that the parameters is of the same level of severity. Even so, this assumption may not always be usable in several practical issues. In this article we are specifically exploring the MCGDM issue where a priority relationship occurs over the parameters. The criteria are at different priority stages. Consider the issue in which we pick a new car on the basis of safeness, cost, presence and performance measures. We are not willing to sacrifice safeness for cost-effectiveness. First, we consider the safety requirements, then we consider the cost and finally, we consider appearance and performance. There is a prioritization relationship over the criteria in this situation. Protection has a greater priority than costs. Cost has a higher priority than appearance and performance.

About the question: why have we been developing all this research? If we consider existing aggregation operators, they have not provided us with a smooth approximation. There are several types of groups of t-norms and t-norms that can be chosen to construct intersections and unions. Einstein sums and Einstein products are good alternatives to algebraic sums and algebraic products because they provide a very smooth approximation. If we have a case in which we have a prioritized relationship in criteria and we also have a smooth approximation, we use the proposed aggregation operators.

In the rest of this paper: Section 2 consists of key characteristics for fuzzy sets, IFSs and q-ROFSs. Section 3 introduces some newly aggregation operators (AOs) based on q-ROFSs and their characteristics. Section 4 provides the proposed methodology to deal MCGDM problems. In Section 5 we give a concrete example of the effectiveness and viability of the suggested approach and also present comparison analysis with other techniques. Finally, whole paper is summarized in Section 6.

2. Preliminaries

In 1986, Atanassov developed the concept of IFS as a generalization of Zadeh’s fuzzy set, and it should be noted that IFS is an important way of dealing with vagueness and lack of consensus.

Definition 1.

Let$\breve{\Psi }=({\zeta }_1,{\zeta }_2,\dots {\zeta }_n)$be a finite set, then an IFS, $\breve{J}$ in$\breve{\Psi }$can described as follows:

$$\breve{J}=\{<\zeta ,{\check{\mathfrak{P}}}_{\breve{J}}(\zeta ),{\overline{⨿}}_{\breve{J}}(\zeta )>:\zeta \in \breve{\Psi }\}$$

(1)

where ${\check{\mathfrak{P}}}_{\breve{J}}(\zeta )$ and${\overline{⨿}}_{\breve{J}}(\zeta )$are mappings from$\breve{\Psi }$to $[0,1]$, ${\check{\mathfrak{P}}}_{\breve{J}}(\zeta )$ is called MD and${\overline{⨿}}_{\breve{J}}(\zeta )$is called NMD with conditions, $0\le {\check{\mathfrak{P}}}_{\breve{J}}(\zeta )\le 1$,$0\le {\overline{⨿}}_{\breve{J}}(\zeta )\le 1$and$0\le {\check{\mathfrak{P}}}_{\breve{J}}(\zeta )+{\overline{⨿}}_{\breve{J}}(\zeta )\le 1$,$\forall \zeta \in \breve{\Psi }$. ${\pi }_{\breve{J}}(\zeta )=1-({\check{\mathfrak{P}}}_{\breve{J}}(\zeta )+{\overline{⨿}}_{\breve{J}}(\zeta ))$is called ID of $\breve{J}$ in $\breve{\Psi }$. In addition,$0\le {\pi }_{\breve{J}}(\zeta )\le 1$$\forall \zeta \in \breve{\Psi }$.

Since IFS meets the limitations that the sum of its MD and NMD would be less than or equal to 1. Fortunately, the DM can handle the scenario in which the sum of MD and NMD is higher than unity in complex decision-making problem. Therefore, Yager introduced the concept of PFS to resolve this situation, which satisfies the constraints that the square sum of its MD and NMD should be less than or equal to 1.

Definition 2.

Let $\breve{\Psi }=({\zeta }_1,{\zeta }_2,\dots {\zeta }_n)$ be a finite set, then an PFS, $\breve{P}$ in $\breve{\Psi }$ can described as follows:

$$\breve{P}=\{<\zeta ,{\check{\mathfrak{P}}}_{\breve{P}}(\zeta ),{\overline{⨿}}_{\breve{P}}(\zeta )>:\zeta \in \breve{\Psi }\}$$

(2)

where ${\check{\mathfrak{P}}}_{\breve{P}}(\zeta )$ and ${\overline{⨿}}_{\breve{P}}(\zeta )$ are mappings from $\breve{\Psi }$ to $[0,1]$, ${\check{\mathfrak{P}}}_{\breve{P}}(\zeta )$ is called MD and ${\overline{⨿}}_{\breve{P}}(\zeta )$ is called NMD with conditions, $0\le {\check{\mathfrak{P}}}_{\breve{P}}(\zeta )\le 1$, $0\le {\overline{⨿}}_{\breve{P}}(\zeta )\le 1$ and $0\le {\check{\mathfrak{P}}}_{\breve{P}}^2(\zeta )+{\overline{⨿}}_{\breve{P}}^2(\zeta )\le 1$, $\forall \zeta \in \breve{\Psi }$. ${\pi }_{\breve{P}}(\zeta )=\sqrt{1-({\check{\mathfrak{P}}}_{\breve{P}}^2(\zeta )+{\overline{⨿}}_{\breve{P}}^2(\zeta ))}$ is called ID of $\breve{P}$ in $\breve{\Psi }$. In addition, $0\le {\pi }_{\breve{P}}(\zeta )\le 1$$\forall \zeta \in \breve{\Psi }$.

There is still a problem with DM’s question as to whether the square sum of MD and NMD is greater than one. To solve this problem, again Yager initiated the idea of q-ROFS in which the sum of $q^{th}$ power of MD and NMD is less or equal to 1.

Definition 3.

Let $\breve{\Psi }=({\zeta }_1,{\zeta }_2,\dots {\zeta }_n)$ be a finite universal set, then a q-ROFS, $\breve{H}$ in $\breve{\Psi }$ can described as follows:

$$\breve{H}=\{<\zeta ,{\check{\mathfrak{P}}}_{\breve{H}}(\zeta ),{\overline{⨿}}_{\breve{H}}(\zeta )>:\zeta \in \breve{\Psi }\}$$

(3)

where ${\check{\mathfrak{P}}}_{\breve{H}}(\zeta )$ and ${\overline{⨿}}_{\breve{H}}(\zeta )$ are mappings from $\breve{\Psi }$ to $[0,1]$, ${\check{\mathfrak{P}}}_{\breve{H}}(\zeta )$ is called MD and ${\overline{⨿}}_{\breve{H}}(\zeta )$ is called NMD with conditions, $0\le {\check{\mathfrak{P}}}_{\breve{H}}(\zeta )\le 1$, $0\le {\overline{⨿}}_{\breve{H}}(\zeta )\le 1$ and $0\le {\check{\mathfrak{P}}}_{\breve{H}}^q(\zeta )+{\overline{⨿}}_{\breve{H}}^q(\zeta )\le 1$$q\ge 1$, $\forall \zeta \in \breve{\Psi }$. ${\pi }_{\breve{H}}(\zeta )=\sqrt[q]{1-({\check{\mathfrak{P}}}_{\breve{H}}^q(\zeta )+{\overline{⨿}}_{\breve{H}}^q(\zeta ))}$ is called ID of $\breve{H}$ in $\breve{\Psi }$. In addition, $0\le {\pi }_{\breve{H}}(\zeta )\le 1$$\forall \zeta \in \breve{\Psi }$. For each $\zeta \in \breve{\Psi }$, a basic element of the form $\langle {\check{\mathfrak{P}}}_{\breve{H}}(\zeta ),{\overline{⨿}}_{\breve{H}}(\zeta )\rangle$ in a q-ROFS, denoted by $\ddot{\mathfrak{S}}$, is called q-ROFN. It could be given as $\ddot{\mathfrak{S}}=\langle {\check{\mathfrak{P}}}_{\breve{H}},{\overline{⨿}}_{\breve{H}}\rangle$.

Liu further suggested to aggregate the q-ROFN with the following operational rules.

Definition 4

([58]). Let ${\ddot{\mathfrak{S}}}_1=\langle {\check{\mathfrak{P}}}_1,{\overline{⨿}}_1\rangle$ and ${\ddot{\mathfrak{S}}}_2=\langle {\check{\mathfrak{P}}}_2,{\overline{⨿}}_2\rangle$ be q-ROFNs. Then

$$\overline{{\ddot{\mathfrak{S}}}_1}=\langle {\overline{⨿}}_1,{\check{\mathfrak{P}}}_1\rangle$$

(4)

$${\ddot{\mathfrak{S}}}_1\vee {\ddot{\mathfrak{S}}}_2=\langle max\{{\check{\mathfrak{P}}}_1,{\overline{⨿}}_1\},min\{{\check{\mathfrak{P}}}_2,{\overline{⨿}}_2\}\rangle$$

(5)

$${\ddot{\mathfrak{S}}}_1\wedge {\ddot{\mathfrak{S}}}_2=\langle min\{{\check{\mathfrak{P}}}_1,{\overline{⨿}}_1\},max\{{\check{\mathfrak{P}}}_2,{\overline{⨿}}_2\}\rangle$$

(6)

$${\ddot{\mathfrak{S}}}_1\oplus {\ddot{\mathfrak{S}}}_2=\langle \sqrt[q]{({\check{\mathfrak{P}}}_1^q+{\check{\mathfrak{P}}}_2^q-{\check{\mathfrak{P}}}_1^q{\check{\mathfrak{P}}}_2^q)},{\overline{⨿}}_1{\overline{⨿}}_2\rangle$$

(7)

$${\ddot{\mathfrak{S}}}_1\otimes {\ddot{\mathfrak{S}}}_2=\langle {\check{\mathfrak{P}}}_1{\check{\mathfrak{P}}}_2,\sqrt[q]{({\overline{⨿}}_1^q+{\overline{⨿}}_2^q-{\overline{⨿}}_1^q{\overline{⨿}}_2^q)}\rangle$$

(8)

$$\sigma {\ddot{\mathfrak{S}}}_1=\langle \sqrt[q]{1-{(1-{\check{\mathfrak{P}}}_1^q)}^{\sigma }},{\overline{⨿}}_1^{\sigma }\rangle$$

(9)

$${\ddot{\mathfrak{S}}}_1^{\sigma }=\langle {\check{\mathfrak{P}}}_1^{\sigma },\sqrt[q]{1-{(1-{\overline{⨿}}_1^q)}^{\sigma }}\rangle$$

(10)

Definition 5.

Suppose $\tilde{\Re }=\langle \check{\mathfrak{P}},\overline{⨿}\rangle$ is a q-ROFN, then a score function $\mathfrak{E}$ of $\tilde{\Re }$ is defined as

$$\mathfrak{E}(\tilde{\Re })={\check{\mathfrak{P}}}^q-{\overline{⨿}}^q$$

$\mathfrak{E}(\tilde{\Re })\in [-1,1]$. The score of a q-ROFN defines its ranking i.e., high score defines high preference of q-ROFN. However, score function is not useful in many cases of q-ROFN. For example, let us consider ${\ddot{\mathfrak{S}}}_1=\langle 0.6138,0.2534\rangle$ and ${\ddot{\mathfrak{S}}}_2=\langle 0.7147,0.4453\rangle$ are two q-ROFN, if we take value of q is 2. Then $\mathfrak{E}({\ddot{\mathfrak{S}}}_1)=0.3125=\mathfrak{E}({\ddot{\mathfrak{S}}}_2)$ i.e., score function of ${\ddot{\mathfrak{S}}}_1$ and ${\ddot{\mathfrak{S}}}_2$ are same. Therefore, to compare the q-ROFNs, it is not necessary to rely on the score function. We add a further method, the accuracy function, to solve this issue.

Definition 6.

Suppose $\tilde{\Re }=\langle \check{\mathfrak{P}},\overline{⨿}\rangle$ is a q-ROFN, then an accuracy function $\mathfrak{R}$ of $\tilde{\Re }$ is defined as

$$\mathfrak{R}(\tilde{\Re })={\check{\mathfrak{P}}}^q+{\overline{⨿}}^q$$

$\mathfrak{R}(\tilde{\Re })\in [0,1]$. The high value of accuracy degree $\mathfrak{R}(\tilde{\Re })$ defines high preference of $\tilde{\Re }$.

Again consider ${\ddot{\mathfrak{S}}}_1=\langle 0.6138,0.2534\rangle$ and ${\ddot{\mathfrak{S}}}_2=\langle 0.7147,0.4453\rangle$ two q-ROFNs. Then their accuracy functions are $\mathfrak{R}({\ddot{\mathfrak{S}}}_1)=0.4410$ and $\mathfrak{R}({\ddot{\mathfrak{S}}}_2)=0.4410$, so by accuracy function we have ${\ddot{\mathfrak{S}}}_1<{\ddot{\mathfrak{S}}}_2$.

Definition 7.

Let $\yen =\langle {\check{\mathfrak{P}}}_{\yen },{\overline{⨿}}_{\yen }\rangle$ and $\mathfrak{M}=\langle {\check{\mathfrak{P}}}_{\mathfrak{M}},{\overline{⨿}}_{\mathfrak{M}}\rangle$ are q-ROFNs, and $\mathfrak{E}(\yen ),\mathfrak{E}(\mathfrak{M})$ are the score function of ¥ and $\mathfrak{M}$, and $\mathfrak{R}(\yen ),\mathfrak{R}(\mathfrak{M})$ are the accuracy function of ¥ and $\mathfrak{M}$, then

 (1) 

If $\mathfrak{E}(\yen )>\mathfrak{E}(\mathfrak{M})$, then $\yen >\mathfrak{M}$

 (2) 

If $\mathfrak{E}(\yen )=\mathfrak{E}(\mathfrak{M})$, then

• if $\mathfrak{R}(\yen )>\mathfrak{R}(\mathfrak{M})$ then $\yen >\mathfrak{M}$,
• if $\mathfrak{R}(\yen )=\mathfrak{R}(\mathfrak{M})$, then $\yen =\mathfrak{M}$.

It should always be noticed that the value of score function is between –1 and 1. We introduce another score function, to support the following research, $\breve{\Xi }(\Re )=\frac{1+{\check{\mathfrak{P}}}_{\Re }^q-{\overline{⨿}}_{\Re }^q}{2}$. We can see that $0\le \breve{\Xi }(\Re )\le 1$. This new score function satisfies all properties of score function defined by Yager [52].

2.1. The Study’s Motivation and Intense Focus

In this subsection, we put a light on the scope, motivation and novelty of proposed work.

• This article covers two main issues: the theoretical model of the problem and the application of decision-making.
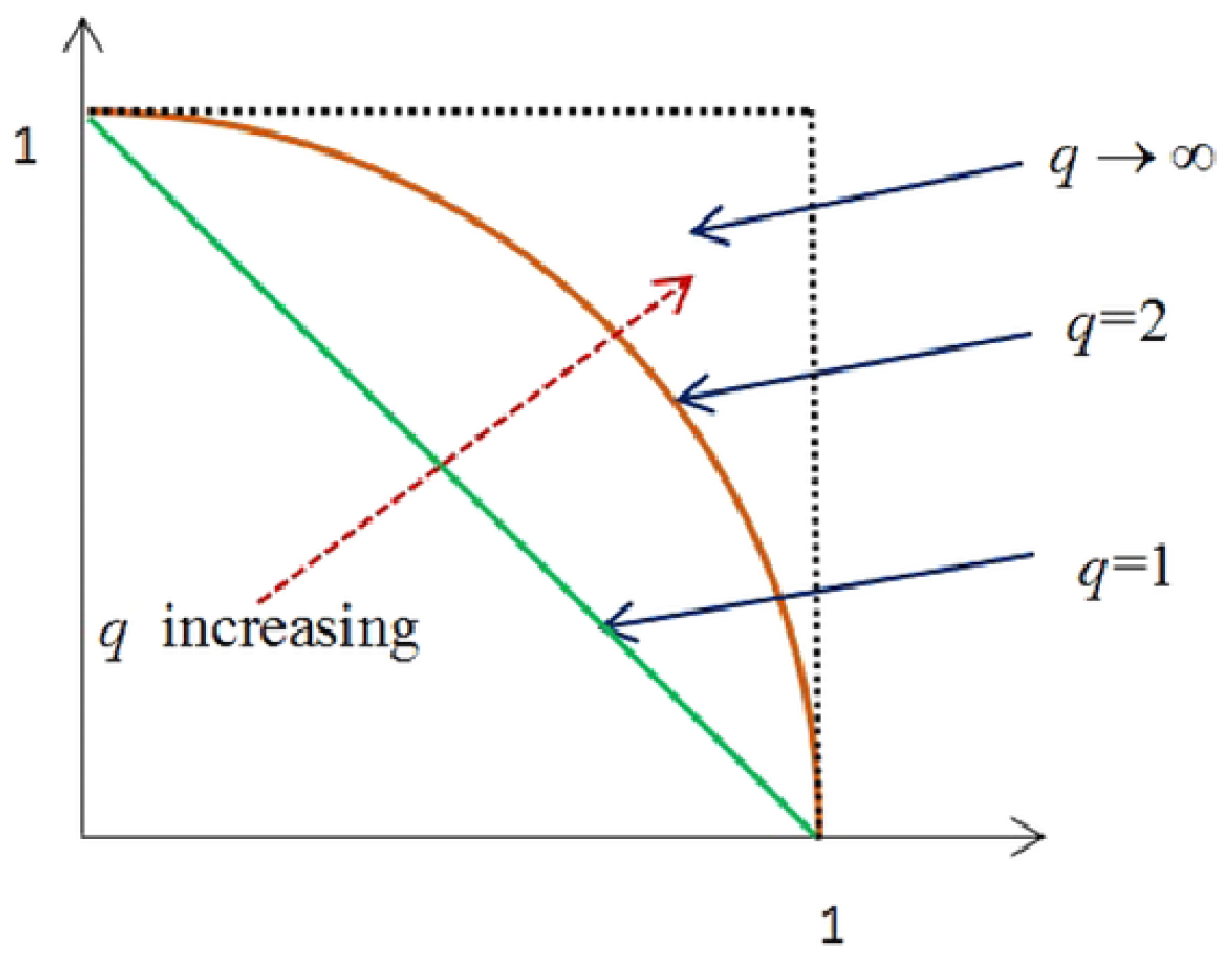
• The proposed models of aggregated operators are credible, valid, versatile and better than the rest to others because they will be based on the generalized q-ROFN structure. If the suggested operators are used in the context of IFNs or PFNs, the results will be ambiguous leading to the decrease of information in the inputs. This loss is due to restrictions on membership and non-membership of IFNs and PFNs. (see Figure 1). The IFNs and PFNs become special cases of q-ROFNs when $q=1$ and $q=2$ respectively.
• The main objective is to establish strong relationships with the multi-criteria decision-making issues between the proposed operators. The application shall communicate the effectiveness, interpretation and motivation of the proposed aggregated operators.
• This research fills the research gap and provides us a wide domain for the input data selection in medical, business, artificial intelligence, agriculture, and engineering. We can tackle those problems which contain ambiguity and uncertainty due to its limitations. The results obtained by using proposed operators and q-ROFNs will be superior and profitable in decision-making techniques.

For q-ROFNs, Riaz et al. [48] introduced the Einstein operation and studied the desirable properties of these operations. with the help of these operation they developed q-ROFEWA and q-ROFEWG operators.

Definition 8

([48]). Let ${\ddot{\mathfrak{S}}}_1=\langle {\check{\mathfrak{P}}}_1,{\overline{⨿}}_1\rangle$ and ${\ddot{\mathfrak{S}}}_2=\langle {\check{\mathfrak{P}}}_2,{\overline{⨿}}_2\rangle$ be q-ROFNs, $\mathfrak{w}>0$ be real number, then

$$\overline{{\ddot{\mathfrak{S}}}_1}=\langle {\overline{⨿}}_1,{\check{\mathfrak{P}}}_1\rangle$$

(11)

$${\ddot{\mathfrak{S}}}_1{\vee }_{ϵ}{\ddot{\mathfrak{S}}}_2=\langle \mathit{max}\{{\check{\mathfrak{P}}}_1,{\check{\mathfrak{P}}}_2\},\mathit{min}\{{\overline{⨿}}_1,{\overline{⨿}}_2\}\rangle$$

(12)

$${\ddot{\mathfrak{S}}}_1{\wedge }_{ϵ}{\ddot{\mathfrak{S}}}_2=\langle \mathit{min}\{{\check{\mathfrak{P}}}_1,{\check{\mathfrak{P}}}_2\},\mathit{max}\{{\overline{⨿}}_1,{\overline{⨿}}_2\}\rangle$$

(13)

$${\ddot{\mathfrak{S}}}_1{\otimes }_{ϵ}{\ddot{\mathfrak{S}}}_2=〈\frac{{\check{\mathfrak{P}}}_{1·ϵ}{\check{\mathfrak{P}}}_2}{\sqrt[q]{1+(1-{\check{\mathfrak{P}}}_1^q{)}_{·ϵ}(1-{\check{\mathfrak{P}}}_2^q)}},\sqrt[q]{\frac{{\overline{⨿}}_1^q+{\overline{⨿}}_2^q}{1+{\overline{⨿}}_{1·ϵ}^q{\overline{⨿}}_2^q}}〉$$

(14)

$${\ddot{\mathfrak{S}}}_1{\oplus }_{ϵ}{\ddot{\mathfrak{S}}}_2=〈\sqrt[q]{\frac{{\check{\mathfrak{P}}}_1^q+{\overline{⨿}}_2^q}{1+{{\check{\mathfrak{P}}}_1^q}_{·ϵ}{\check{\mathfrak{P}}}_2^q}},\frac{{\overline{⨿}}_{1·ϵ}{\overline{⨿}}_2}{\sqrt[q]{1+(1-{\overline{⨿}}_1^q{)}_{·ϵ}(1-{\overline{⨿}}_2^q)}}〉$$

(15)

$${\mathfrak{w}}_{·ϵ}{\ddot{\mathfrak{S}}}_1=〈\sqrt[q]{\frac{{(1+{({\check{\mathfrak{P}}}_1)}^q)}^{\mathfrak{w}}-{(1-{({\check{\mathfrak{P}}}_1)}^q)}^{\mathfrak{w}}}{{(1+{({\check{\mathfrak{P}}}_1)}^q)}^{\mathfrak{w}}+{(1-{({\check{\mathfrak{P}}}_1)}^q)}^{\mathfrak{w}}}},\frac{\sqrt[q]{2}{({\overline{⨿}}_1)}^{\mathfrak{w}}}{\sqrt[q]{{(2-{({\check{\mathfrak{P}}}_1)}^q)}^{\mathfrak{w}}+{({({\overline{⨿}}_1)}^q)}^{\mathfrak{w}}}}〉$$

(16)

$${\ddot{\mathfrak{S}}}_1^{\mathfrak{w}}=〈\frac{\sqrt[q]{2}{({\check{\mathfrak{P}}}_1)}^{\mathfrak{w}}}{\sqrt[q]{{(2-{({\check{\mathfrak{P}}}_1)}^q)}^{\mathfrak{w}}+{({({\check{\mathfrak{P}}}_1)}^q)}^{\mathfrak{w}}}},\sqrt[q]{\frac{{(1+{({\overline{⨿}}_1)}^q)}^{\mathfrak{w}}-{(1-{({\overline{⨿}}_1)}^q)}^{\mathfrak{w}}}{{(1+{({\overline{⨿}}_1)}^q)}^{\mathfrak{w}}+{(1-{({\overline{⨿}}_1)}^q)}^{\mathfrak{w}}}}〉$$

(17)

Theorem 1

([48]). Let ${\ddot{\mathfrak{S}}}_1$ and ${\ddot{\mathfrak{S}}}_2$ be q-ROFNs and $\mathfrak{w},{\mathfrak{w}}_1,{\mathfrak{w}}_2\ge 0$ be any real number, then

 (i) 

${\ddot{\mathfrak{S}}}_2{\otimes }_{ϵ}{\ddot{\mathfrak{S}}}_1={\ddot{\mathfrak{S}}}_1{\otimes }_{ϵ}{\ddot{\mathfrak{S}}}_2$

 (ii) 

${\ddot{\mathfrak{S}}}_2{\oplus }_{ϵ}{\ddot{\mathfrak{S}}}_1={\ddot{\mathfrak{S}}}_1{\oplus }_{ϵ}{\ddot{\mathfrak{S}}}_2$

 (iii) 

${({\ddot{\mathfrak{S}}}_2{\otimes }_{ϵ}{\ddot{\mathfrak{S}}}_1)}^{\mathfrak{w}}={\ddot{\mathfrak{S}}}_2^{\mathfrak{w}}{\otimes }_{ϵ}{\ddot{\mathfrak{S}}}_1^{\mathfrak{w}}$

 (iv) 

${\mathfrak{w}}_{·ϵ}({\ddot{\mathfrak{S}}}_1{\oplus }_{ϵ}{\ddot{\mathfrak{S}}}_2)={\mathfrak{w}}_{·ϵ}{\ddot{\mathfrak{S}}}_1{\oplus }_{ϵ}{\mathfrak{w}}_{·ϵ}{\ddot{\mathfrak{S}}}_2$

 (v) 

${\ddot{\mathfrak{S}}}_1^{{\mathfrak{w}}_1}{\otimes }_{ϵ}{\ddot{\mathfrak{S}}}_1^{{\mathfrak{w}}_2}={\ddot{\mathfrak{S}}}_1^{{\mathfrak{w}}_1+{\mathfrak{w}}_2}$

 (vi) 

${\mathfrak{w}}_{1·ϵ}({\mathfrak{w}}_{2·ϵ}{\ddot{\mathfrak{S}}}_1)=({\mathfrak{w}}_{1·ϵ}{\mathfrak{w}}_2{)}_{·ϵ}{\ddot{\mathfrak{S}}}_1$

 (vii) 

${({\ddot{\mathfrak{S}}}_1^{{\mathfrak{w}}_1})}^{{\mathfrak{w}}_2}={({\ddot{\mathfrak{S}}}_1)}^{{\mathfrak{w}}_{1·ϵ}{\mathfrak{w}}_2}$

 (viii) 

${\mathfrak{w}}_{1·ϵ}{\ddot{\mathfrak{S}}}_1{\oplus }_{ϵ}{\mathfrak{w}}_2=({\mathfrak{w}}_1+{\mathfrak{w}}_2{)}_{·ϵ}{\ddot{\mathfrak{S}}}_1$

Definition 9

([48]). Let ${\ddot{\mathfrak{S}}}_p=\langle {\check{\mathfrak{P}}}_p,{\overline{⨿}}_p\rangle$ be the family of q-ROFNs and (q-ROFEWA) $:{\Lambda }^n\to \Lambda$ if,

$$\begin{array}{cc}\hfill q-ROFEWA({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots ,{\ddot{\mathfrak{S}}}_n)& =\sum _{s=1}^n{\breve{\mathcal{Z}}}_s{\ddot{\mathfrak{S}}}_s\hfill \\ \hfill & ={\breve{\mathcal{Z}}}_{1·ϵ}{\ddot{\mathfrak{S}}}_1{\oplus }_{ϵ}{\breve{\mathcal{Z}}}_{2·ϵ}{\ddot{\mathfrak{S}}}_2{\oplus }_{ϵ}\dots {\oplus }_{ϵ}{\breve{\mathcal{Z}}}_{n·ϵ}{\ddot{\mathfrak{S}}}_n\hfill \end{array}$$

where Λ is the assemblage q-ROFNs, and $\breve{\mathcal{Z}}={({\breve{\mathcal{Z}}}_1,{\breve{\mathcal{Z}}}_2,\dots ,{\breve{\mathcal{Z}}}_n)}^T$ is weight vector (WV) of $({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots ,{\ddot{\mathfrak{S}}}_n)$, s.t $0⩽{\breve{\mathcal{Z}}}_s⩽1$ and ${\sum }_{s=1}^n$${\breve{\mathcal{Z}}}_s=1$. Then, the q-ROFEWA is called the q-rung orthopair fuzzy Einstein weighted averaging operator.

We can also consider q-ROFEWA by the following theorem by Einstein’s operational laws of q-ROFNs.

Theorem 2

([48]). Let ${\ddot{\mathfrak{S}}}_p=\langle {\check{\mathfrak{P}}}_p,{\overline{⨿}}_p\rangle$ be the family of q-ROFNs, we can also find q-ROFEWA by

$$\begin{array}{ccc}\hfill q-ROFEWA({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots ,{\ddot{\mathfrak{S}}}_n)& =& \left(\sqrt[q]{\frac{{\prod }_{s=1}^n{(1+{({\check{\mathfrak{P}}}_s)}^q)}^{{\breve{\mathcal{Z}}}_s}-{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{{\breve{\mathcal{Z}}}_s}}{{\prod }_{s=1}^n{(1+{({\check{\mathfrak{P}}}_s)}^q)}^{{\breve{\mathcal{Z}}}_s}+{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{{\breve{\mathcal{Z}}}_s}}},\frac{\sqrt[q]{2}{\prod }_{s=1}^n{\overline{⨿}}_s^{{\breve{\mathcal{Z}}}_s}}{\sqrt[q]{{\prod }_{s=1}^n{(2-{({\overline{⨿}}_s)}^q)}^{{\breve{\mathcal{Z}}}_s}+{\prod }_{s=1}^n{({({\overline{⨿}}_s)}^q)}^{{\breve{\mathcal{Z}}}_s}}}\right)\hfill \end{array}$$

(18)

where $\breve{\mathcal{Z}}={({\breve{\mathcal{Z}}}_1,{\breve{\mathcal{Z}}}_2,\dots ,{\breve{\mathcal{Z}}}_n)}^T$ is WV of $({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots ,{\ddot{\mathfrak{S}}}_n)$, s.t $0⩽{\breve{\mathcal{Z}}}_s⩽1$ and ${\sum }_{s=1}^n$${\breve{\mathcal{Z}}}_s=1$.

Definition 10

([48]). Let ${\ddot{\mathfrak{S}}}_p=\langle {\check{\mathfrak{P}}}_p,{\overline{⨿}}_p\rangle$ be the family of q-ROFNs and (q-ROFEWG)$:{\Lambda }^n\to \Lambda$ if,

$$\begin{array}{cc}\hfill q-ROFEWG({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots ,{\ddot{\mathfrak{S}}}_n)& =\sum _{s=1}^n{\ddot{\mathfrak{S}}}_s^{{\breve{\mathcal{Z}}}_s}\hfill \\ \hfill & ={\ddot{\mathfrak{S}}}_1^{{\breve{\mathcal{Z}}}_1}{\otimes }_{ϵ}{\ddot{\mathfrak{S}}}_2^{{\breve{\mathcal{Z}}}_2}{\otimes }_{ϵ}\dots {\otimes }_{ϵ}{\ddot{\mathfrak{S}}}_n^{{\breve{\mathcal{Z}}}_n}\hfill \end{array}$$

where Λ is the set of q-ROFNs, and $\breve{\mathcal{Z}}={({\breve{\mathcal{Z}}}_1,{\breve{\mathcal{Z}}}_2,\dots ,{\breve{\mathcal{Z}}}_n)}^T$ is WV of $({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots ,{\ddot{\mathfrak{S}}}_n)$, s.t $0⩽{\breve{\mathcal{Z}}}_s⩽1$ and ${\sum }_{s=1}^n{\breve{\mathcal{Z}}}_s=1$. Then, the q-ROFEWG is called the q-rung orthopair fuzzy Einstein weighted geometric operator.

We can also consider q-ROFEWG by the following theorem by Einstein’s operational laws of q-ROFNs.

Theorem 3

([48]). Let ${\ddot{\mathfrak{S}}}_p=\langle {\check{\mathfrak{P}}}_p,{\overline{⨿}}_p\rangle$ be the family of q-ROFNs. Then

$$\begin{array}{ccc}\hfill q-ROFEWG({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots ,{\ddot{\mathfrak{S}}}_n)& =& \left(\frac{\sqrt[q]{2}{\prod }_{s=1}^n{\check{\mathfrak{P}}}_s^{{\breve{\mathcal{Z}}}_s}}{\sqrt[q]{{\prod }_{s=1}^n{(2-{({\check{\mathfrak{P}}}_s)}^q)}^{{\breve{\mathcal{Z}}}_s}+{\prod }_{s=1}^n{({({\check{\mathfrak{P}}}_s)}^q)}^{{\breve{\mathcal{Z}}}_s}}},\sqrt[q]{\frac{{\prod }_{s=1}^n{(1+{({\overline{⨿}}_s)}^q)}^{{\breve{\mathcal{Z}}}_s}-{\prod }_{s=1}^n{(1-{({\overline{⨿}}_s)}^q)}^{{\breve{\mathcal{Z}}}_s}}{{\prod }_{s=1}^n{(1+{({\overline{⨿}}_s)}^q)}^{{\breve{\mathcal{Z}}}_s}+{\prod }_{s=1}^n{(1-{({\overline{⨿}}_s)}^q)}^{{\breve{\mathcal{Z}}}_s}}}\right)\hfill \end{array}$$

(19)

where $\breve{\mathcal{Z}}={({\breve{\mathcal{Z}}}_1,{\breve{\mathcal{Z}}}_2,\dots ,{\breve{\mathcal{Z}}}_n)}^T$ is WV of $({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots ,{\ddot{\mathfrak{S}}}_n)$, s.t $0⩽{\breve{\mathcal{Z}}}_s⩽1$ and ${\sum }_{s=1}^n$${\breve{\mathcal{Z}}}_s=1$.

Definition 11

([49]). Let ${\ddot{\mathfrak{S}}}_p=\langle {\check{\mathfrak{P}}}_p,{\overline{⨿}}_p\rangle$ be the family of q-ROFNs, and $q-ROFPWA:{\Lambda }^n\to \Lambda$, be an n dimension mapping. If

$$\mathrm{q}-\mathrm{ROFPWA}({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots {\ddot{\mathfrak{S}}}_n)=\left(\frac{{\breve{\beth }}_1}{{\sum }_{s=1}^n{\breve{\beth }}_s}{\ddot{\mathfrak{S}}}_1\oplus \frac{{\breve{\beth }}_2}{{\sum }_{s=1}^n{\breve{\beth }}_s}{\ddot{\mathfrak{S}}}_2\oplus \dots ,\oplus \frac{{\breve{\beth }}_n}{{\sum }_{s=1}^n{\breve{\beth }}_s}{\ddot{\mathfrak{S}}}_n\right)$$

(20)

then the mapping q-ROFPWA is called q-rung orthopair fuzzy prioritized weighted averaging (q-ROFPWA) operator, where ${\breve{\beth }}_j={\prod }_{k=1}^{j-1}\breve{\Xi }({\ddot{\mathfrak{S}}}_k)$$(j=2\dots ,n)$, ${\breve{\beth }}_1=1$ and $\breve{\Xi }({\ddot{\mathfrak{S}}}_k)$ is the score of $k^{th}$ q-ROFN.

Definition 12

([49]). Let ${\ddot{\mathfrak{S}}}_p=\langle {\check{\mathfrak{P}}}_p,{\overline{⨿}}_p\rangle$ be the family of q-ROFNs, and $q-ROFPWG:{\Lambda }^n\to \Lambda$, be an n dimension mapping. If

$$\mathrm{q}-\mathrm{ROFPWG}({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots {\ddot{\mathfrak{S}}}_n)=\left({\ddot{\mathfrak{S}}}_1^{\frac{{\breve{\beth }}_1}{{\sum }_{s=1}^n{\breve{\beth }}_s}}\otimes {\ddot{\mathfrak{S}}}_2^{\frac{{\breve{\beth }}_2}{{\sum }_{s=1}^n{\breve{\beth }}_s}}\otimes \dots ,\otimes {\ddot{\mathfrak{S}}}_n^{\frac{{\breve{\beth }}_n}{{\sum }_{s=1}^n{\breve{\beth }}_s}}\right)$$

(21)

then the mapping q-ROFPWG is called q-rung orthopair fuzzy prioritized weighted geometric (q-ROFPWG) operator, where ${\breve{\beth }}_j={\prod }_{k=1}^{j-1}\breve{\Xi }({\ddot{\mathfrak{S}}}_k)$$(j=2\dots ,n)$, ${\breve{\beth }}_1=1$ and $\breve{\Xi }({\ddot{\mathfrak{S}}}_k)$ is the score of $k^{th}$ q-ROFN.

2.2. Superiority and Comparison of q-ROFNs with Some Existing Theories

In this section, we discuss the supremacy and comparative analysis of q-ROFNs with several existing systems, such as fuzzy numbers (FNs), IFNs and PFNs. In the decision-making problem of using input data using FNs, we could never talk about the dissatisfaction of part of the alternative or DM’s opinion. If we use IFNs and PFNs, then we can not take the MD and NMD with an open choice of the actual working situation. Constraints restricted them to limited criteria. For example $0.75+0.85=1.60>1$ and ${0.75}^2+{0.85}^2=1.285>1$, which contradicts the conditions of IFNs and PFNs. If we select $q=3$ then for 3-ROFN the constraint implies that ${0.75}^3+{0.85}^3=0.614<1$. This criteria satisfy the fuzzy criteria and we can handle the decision-making input with wide domain. The Table 1 represents the brief comparison with advantages and limitations of q-ROFN with some exiting theories.

3. q-Rung Orthopair Fuzzy Einstein Prioritized Aggregation Operators

Within this section, we present the notion of q-rung orthopair fuzzy Einstein prioritized weighted average (q-ROFEPWA) operator and q-rung orthopair fuzzy Einstein prioritized weighted geometric (q-ROFEPWG) operator. Then we discuss other attractive properties of proposed operators.

3.1. q-ROFEPWA Operator

Definition 13.

Let ${\ddot{\mathfrak{S}}}_p=\langle {\check{\mathfrak{P}}}_p,{\overline{⨿}}_p\rangle$ be the family of q-ROFNs, and q-ROFEPWA: ${\Lambda }^n\to \Lambda$, be an n dimension mapping. If

$$\mathrm{q}-\mathrm{ROFEPWA}({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots {\ddot{\mathfrak{S}}}_n)=\left(\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\ddot{\mathfrak{S}}}_1{\oplus }_{ϵ}\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\ddot{\mathfrak{S}}}_2{\oplus }_{ϵ}\dots ,{\oplus }_{ϵ}\frac{{\breve{\beth }}_n}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\ddot{\mathfrak{S}}}_n\right)$$

(22)

then the mapping q-ROFEPWA is called q-rung orthopair fuzzy Einstein prioritized weighted averaging (q-ROFEPWA) operator, where ${\breve{\beth }}_j={\prod }_{k=1}^{j-1}\breve{\Xi }({\ddot{\mathfrak{S}}}_k)$$(j=2\dots ,n)$, ${\breve{\beth }}_1=1$ and $\breve{\Xi }({\ddot{\mathfrak{S}}}_k)$ is the score of $k^{th}$ q-ROFN.

Based on Einstein operational rules, we can also consider q-ROFEPWA by the theorem below.

Theorem 4.

Let ${\ddot{\mathfrak{S}}}_p=\langle {\check{\mathfrak{P}}}_p,{\overline{⨿}}_p\rangle$ be the family of q-ROFNs, we can also find q-ROFEPWA by

$$\begin{array}{c}\hfill q-ROFEPWA({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots ,{\ddot{\mathfrak{S}}}_n)=\left(\sqrt[q]{\frac{{\prod }_{j=1}^n{(1+{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}-{\prod }_{j=1}^n{(1-{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{\prod }_{j=1}^n{(1+{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{\prod }_{j=1}^n{(1-{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}},\frac{\sqrt[q]{2}{\prod }_{j=1}^n{\overline{⨿}}_j^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{\sqrt[q]{{\prod }_{j=1}^n{(2-{({\overline{⨿}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{\prod }_{j=1}^n{({({\overline{⨿}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}}\right)\end{array}$$

(23)

where ${\breve{\beth }}_j={\prod }_{k=1}^{j-1}\breve{\Xi }({\breve{\ddot{\mathfrak{S}}}}_k)$$(j=2\dots ,n)$, ${\breve{\beth }}_1=1$ and $\breve{\Xi }({\breve{\ddot{\mathfrak{S}}}}_k)$ is the score of $k^{th}$ q-ROFN.

Proof. 

This theorem is proven using mathematical induction.

For $n=2$

$$\mathrm{q}-\mathrm{ROFEPWA}({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2)=\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\ddot{\mathfrak{S}}}_1{\oplus }_{ϵ}\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\ddot{\mathfrak{S}}}_2$$

As we know that both $\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\ddot{\mathfrak{S}}}_1$ and $\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\ddot{\mathfrak{S}}}_2$ are q-ROFNs, and also $\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\ddot{\mathfrak{S}}}_1{\oplus }_{ϵ}\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\ddot{\mathfrak{S}}}_2$ is q-ROFN.

$$\begin{array}{ccc}\hfill \frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\ddot{\mathfrak{S}}}_1& =& \left(\sqrt[q]{\frac{{(1+{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}-{(1-{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{(1+{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{(1-{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}},\frac{\sqrt[q]{2}{({\overline{⨿}}_1)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{\sqrt[q]{{(2-{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{({({\overline{⨿}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}}\right)\hfill \\ \hfill \frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\ddot{\mathfrak{S}}}_2& =& \left(\sqrt[q]{\frac{{(1+{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}-{(1-{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{(1+{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{(1-{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}},\frac{\sqrt[q]{2}{({\overline{⨿}}_2)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{\sqrt[q]{{(2-{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{({({\overline{⨿}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}}\right)\hfill \end{array}$$

Then $\mathrm{q}-\mathrm{ROFEPWA}({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2)$

$$\begin{array}{cc}=\hfill & \frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\ddot{\mathfrak{S}}}_1{\oplus }_{ϵ}\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\ddot{\mathfrak{S}}}_2\hfill \\ =\hfill & \left(\sqrt[q]{\frac{{(1+{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}-{(1-{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{(1+{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{(1-{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}},\frac{\sqrt[q]{2}{({\overline{⨿}}_1)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{\sqrt[q]{{(2-{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{({({\overline{⨿}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}}\right)\hfill \\ \hfill & {\oplus }_{ϵ}\left(\sqrt[q]{\frac{{(1+{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}-{(1-{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{(1+{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{(1-{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}},\frac{\sqrt[q]{2}{({\overline{⨿}}_2)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{\sqrt[q]{{(2-{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{({({\overline{⨿}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}}\right)\hfill \\ =\hfill & \left(\sqrt[q]{\frac{\frac{{(1+{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}-{(1-{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{(1+{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{(1-{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}+\frac{{(1+{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}-{(1-{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{(1+{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{(1-{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}}{1+\left(\frac{{(1+{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}-{(1-{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{(1+{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{(1-{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}\right){·}_{ϵ}\left(\frac{{(1+{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}-{(1-{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{(1+{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{(1-{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}\right)}},\right.\hfill \\ \hfill & \left.\frac{\left(\frac{\sqrt[q]{2}{({\overline{⨿}}_1)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{\sqrt[q]{{(2-{({\overline{⨿}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{({({\overline{⨿}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}}\right){·}_{ϵ}\left(\frac{\sqrt[q]{2}{({\overline{⨿}}_2)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{\sqrt[q]{{(2-{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{({({\overline{⨿}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}}\right)}{\sqrt[q]{1+\left(1-\frac{2{({({\overline{⨿}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{(2-{({\overline{⨿}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{({({\overline{⨿}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}\right){·}_{ϵ}\left(1-\frac{2{({({\overline{⨿}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{(2-{({\overline{⨿}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{({({\overline{⨿}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}\right)}}\right)\hfill \\ =& \left(\sqrt[q]{\frac{{(1+{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}{·}_{ϵ}{(1+{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}-{(1-{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}{·}_{ϵ}{(1-{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{(1+{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}{·}_{ϵ}{(1+{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{(1-{({\check{\mathfrak{P}}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}{·}_{ϵ}{(1-{({\check{\mathfrak{P}}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}},\right.\hfill \\ \hfill & \left.\frac{\sqrt[q]{2}({\overline{⨿}}_1^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}{\overline{⨿}}_2^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}})}{\sqrt[q]{{(2-{({\overline{⨿}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}{·}_{ϵ}{(2-{({\overline{⨿}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{({({\overline{⨿}}_1)}^q)}^{\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{·}_{ϵ}{({({\overline{⨿}}_2)}^q)}^{\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}\right)\hfill \end{array}$$

which proves for $n=2$.

Suppose the result is true for $n=k$, we have

$$\begin{array}{ccc}\hfill q-ROFEWA({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots ,{\ddot{\mathfrak{S}}}_k)& =& \left(\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\breve{\ddot{\mathfrak{S}}}}_1{\oplus }_{ϵ}\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\breve{\ddot{\mathfrak{S}}}}_2{\oplus }_{ϵ}\dots ,{\oplus }_{ϵ}\frac{{\breve{\beth }}_k}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\breve{\ddot{\mathfrak{S}}}}_k\right)\hfill \\ \hfill & =& \left(\sqrt[q]{\frac{{\prod }_{j=1}^k{(1+{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}-{\prod }_{j=1}^k{(1-{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{\prod }_{j=1}^k{(1+{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{\prod }_{j=1}^k{(1-{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}},\frac{\sqrt[q]{2}{\prod }_{j=1}^k{\overline{⨿}}_j^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{\sqrt[q]{{\prod }_{j=1}^k{(2-{({\overline{⨿}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{\prod }_{j=1}^k{({({\overline{⨿}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}}\right)\hfill \end{array}$$

Now we will prove for $n=k+1$,

$$\begin{array}{ccc}\hfill q-ROFEPWA({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots ,{\ddot{\mathfrak{S}}}_{k+1})& =& q-ROFEPWA({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots ,{\ddot{\mathfrak{S}}}_k){\oplus }_{ϵ}\frac{{\breve{\beth }}_{k+1}}{{\sum }_{j=1}^{k+1}{\breve{\beth }}_j}{·}_{ϵ}{\ddot{\mathfrak{S}}}_{k+1}\hfill \\ \hfill & =& \left(\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\breve{\ddot{\mathfrak{S}}}}_1{\oplus }_{ϵ}\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\breve{\ddot{\mathfrak{S}}}}_2{\oplus }_{ϵ}\dots ,{\oplus }_{ϵ}\frac{{\breve{\beth }}_k}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}{\breve{\ddot{\mathfrak{S}}}}_k\right){\oplus }_{ϵ}\frac{{\breve{\beth }}_{k+1}}{{\sum }_{j=1}^{k+1}{\breve{\beth }}_j}{·}_{ϵ}{\ddot{\mathfrak{S}}}_{k+1}\hfill \\ \hfill & =& \left(\sqrt[q]{\frac{{\prod }_{j=1}^k{(1+{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}-{\prod }_{j=1}^k{(1-{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{\prod }_{j=1}^k{(1+{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{\prod }_{j=1}^k{(1-{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}},\frac{\sqrt[q]{2}{\prod }_{j=1}^k{\overline{⨿}}_j^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{\sqrt[q]{{\prod }_{j=1}^k{(2-{({\overline{⨿}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{\prod }_{j=1}^k{({({\overline{⨿}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}}\right)\hfill \\ \hfill & & {\oplus }_{ϵ}\left(\sqrt[q]{\frac{{(1+{({\check{\mathfrak{P}}}_{k+1})}^q)}^{\frac{{\breve{\beth }}_{k+1}}{{\sum }_{j=1}^{k+1}{\breve{\beth }}_j}}-{(1-{({\check{\mathfrak{P}}}_{k+1})}^q)}^{\frac{{\breve{\beth }}_{k+1}}{{\sum }_{j=1}^{k+1}{\breve{\beth }}_j}}}{{(1+{({\check{\mathfrak{P}}}_{k+1})}^q)}^{\frac{{\breve{\beth }}_{k+1}}{{\sum }_{j=1}^{k+1}{\breve{\beth }}_j}}+{(1-{({\check{\mathfrak{P}}}_{k+1})}^q)}^{\frac{{\breve{\beth }}_{k+1}}{{\sum }_{j=1}^{k+1}{\breve{\beth }}_j}}}},\frac{\sqrt[q]{2}{({\overline{⨿}}_{k+1})}^{\frac{{\breve{\beth }}_{k+1}}{{\sum }_{j=1}^{k+1}{\breve{\beth }}_j}}}{\sqrt[q]{{(2-{({\check{\mathfrak{P}}}_{k+1})}^q)}^{\frac{{\breve{\beth }}_{k+1}}{{\sum }_{j=1}^{k+1}{\breve{\beth }}_j}}+{({({\overline{⨿}}_{k+1})}^q)}^{\frac{{\breve{\beth }}_{k+1}}{{\sum }_{j=1}^{k+1}{\breve{\beth }}_j}}}}\right)\hfill \\ \hfill & =& \left(\sqrt[q]{\frac{{\prod }_{j=1}^k{(1+{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}{(1+{({\check{\mathfrak{P}}}_{k+1})}^q)}^{\frac{{\breve{\beth }}_{k+1}}{{\sum }_{j=1}^{k+1}{\breve{\beth }}_j}}-{\prod }_{j=1}^k{(1-{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}{(1-{({\check{\mathfrak{P}}}_{k+1})}^q)}^{\frac{{\breve{\beth }}_{k+1}}{{\sum }_{j=1}^{k+1}{\breve{\beth }}_j}}}{{\prod }_{j=1}^k{(1+{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}{(1+{({\check{\mathfrak{P}}}_{k+1})}^q)}^{\frac{{\breve{\beth }}_{k+1}}{{\sum }_{j=1}^{k+1}{\breve{\beth }}_j}}+{\prod }_{j=1}^k{(1-{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}{(1-{({\check{\mathfrak{P}}}_{k+1})}^q)}^{\frac{{\breve{\beth }}_{k+1}}{{\sum }_{j=1}^{k+1}{\breve{\beth }}_j}}}},\right.\hfill \\ \hfill & & \left.\frac{\sqrt[q]{2}{\prod }_{j=1}^k{\overline{⨿}}_j^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}{({\overline{⨿}}_{k+1})}^{\frac{{\breve{\beth }}_{k+1}}{{\sum }_{j=1}^{k+1}{\breve{\beth }}_j}}}{\sqrt[q]{{\prod }_{j=1}^k{(2-{({\overline{⨿}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}{(2-{({\overline{⨿}}_j)}^q)}^{\frac{{\breve{\beth }}_{k+1}}{{\sum }_{j=1}^{k+1}{\breve{\beth }}_j}}+{\prod }_{j=1}^k{({({\overline{⨿}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}{({({\overline{⨿}}_j)}^q)}^{\frac{{\breve{\beth }}_{k+1}}{{\sum }_{j=1}^{k+1}{\breve{\beth }}_j}}}}\right)\hfill \\ \hfill & =& \left(\sqrt[q]{\frac{{\prod }_{j=1}^{k+1}{(1+{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}-{\prod }_{j=1}^{k+1}{(1-{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{\prod }_{j=1}^{k+1}{(1+{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{\prod }_{j=1}^{k+1}{(1-{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}},\frac{\sqrt[q]{2}{\prod }_{j=1}^{k+1}{\overline{⨿}}_j^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{\sqrt[q]{{\prod }_{j=1}^{k+1}{(2-{({\overline{⨿}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{\prod }_{j=1}^{k+1}{({({\overline{⨿}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}}\right)\hfill \end{array}$$

thus the result holds for $s=k+1$. This proves the required result. □

Theorem 5.

Let ${\ddot{\mathfrak{S}}}_p=\langle {\check{\mathfrak{P}}}_p,{\overline{⨿}}_p\rangle$ be the family of q-ROFNs. Aggregated value using q-ROFEPWA operator is q-ROFN.

Proof. 

Suppose ${\mathcal{G}}_s=\langle {\check{\mathfrak{P}}}_s,{\overline{⨿}}_s\rangle$ family of q-ROFNs. By definition of q-ROFN,

$$0\le {({\check{\mathfrak{P}}}_s)}^q+{({\overline{⨿}}_s)}^q\le 1·$$

Therefore,

$$\begin{array}{cc}\hfill \frac{{\prod }_{s=1}^n{(1+{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}-{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}{{\prod }_{s=1}^n{(1+{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}& =1-\frac{2{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}{{\prod }_{s=1}^n{(1+{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}\hfill \\ \hfill & \le 1-\prod _{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}\le 1\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {(1+{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}& \ge {(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}\hfill \\ \hfill \prod _{s=1}^n{(1+{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}& \ge \prod _{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}\hfill \\ \hfill \prod _{s=1}^n{(1+{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}-\prod _{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}& \ge 0\hfill \\ \hfill \frac{{\prod }_{s=1}^n{(1+{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}-{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}{{\prod }_{s=1}^n{(1+{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}& \ge 0\hfill \end{array}$$

So, we get $0\le {\check{\mathfrak{P}}}_{\mathrm{q}-\mathrm{ROFEPWA}}\le 1$.

For ${\overline{⨿}}_{\mathrm{q}-\mathrm{ROFEPWA}}$, we have

$$\begin{array}{cc}\hfill \frac{2{\prod }_{s=1}^n{({({\overline{⨿}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}{{\prod }_{s=1}^n{(1+{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}& \le \frac{2{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}{{\prod }_{s=1}^n{(1+{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}\hfill \\ \hfill & \le \prod _{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}\hfill \\ \hfill & \le 1\hfill \end{array}$$

Also,

$$\frac{2{\prod }_{s=1}^n{({({\overline{⨿}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}{{\prod }_{s=1}^n{(1+{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}\ge 0⟺\prod _{s=1}^n{({({\overline{⨿}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}\ge 0$$

Moreover,

$$\begin{array}{cc}\hfill {\check{\mathfrak{P}}}_{\mathrm{q}-\mathrm{ROFEPWA}}^q+{\overline{⨿}}_{\mathrm{q}-\mathrm{ROFEPWA}}^q& =\frac{{\prod }_{s=1}^n{(1+{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}-{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}{{\prod }_{s=1}^n{(1+{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}+\hfill \\ \hfill & \frac{2{\prod }_{s=1}^n{({({\overline{⨿}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}{{\prod }_{s=1}^n{(2-{({\overline{⨿}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{({({\overline{⨿}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}\hfill \\ \hfill & \le 1-\frac{2{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}{{\prod }_{s=1}^n{(1+{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}+\hfill \\ \hfill & \frac{2{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}{{\prod }_{s=1}^n{(1+{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{(1-{({\check{\mathfrak{P}}}_s)}^q)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}\hfill \\ \hfill & \le 1\hfill \end{array}$$

Thus, $\mathrm{q}-\mathrm{ROFEPWA}\in [0,1]$. Consequently, q-ROFNs gathered by the q-ROFEPWA operator also are q-ROFNs. □

Theorem 6.

Let ${\ddot{\mathfrak{S}}}_p=\langle {\check{\mathfrak{P}}}_p,{\overline{⨿}}_p\rangle$ be the family of q-ROFNs and let

$$\begin{array}{ccc}\hfill \breve{\mathcal{Z}}& =& {\left(\frac{{\breve{\beth }}_1}{{\sum }_{s=1}^n{\breve{\beth }}_s},\frac{{\breve{\beth }}_2}{{\sum }_{s=1}^n{\breve{\beth }}_s},\dots ,\frac{{\breve{\beth }}_n}{{\sum }_{s=1}^n{\breve{\beth }}_s}\right)}^T\hfill \end{array}$$

(24)

be the WV of ${\ddot{\mathfrak{S}}}_p=\langle {\check{\mathfrak{P}}}_p,{\overline{⨿}}_p\rangle$. Then,

$$\begin{array}{ccc}\hfill q-ROFEPWA({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots ,{\ddot{\mathfrak{S}}}_n)& \le & q-ROFPWA({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots ,{\ddot{\mathfrak{S}}}_n)\hfill \end{array}$$

(25)

where ${\breve{\beth }}_j={\prod }_{k=1}^{j-1}\breve{\Xi }({\breve{\ddot{\mathfrak{S}}}}_k)$$(j=2\dots ,n)$, ${\breve{\beth }}_1=1$ and $\breve{\Xi }({\breve{\ddot{\mathfrak{S}}}}_k)$ is the score of $k^{th}$ q-ROFN.

Proof. 

Let $\mathrm{q}-\mathrm{ROFEPWA}({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots ,{\ddot{\mathfrak{S}}}_n)=({\mathfrak{Y}}_p^E,{\mathcal{F}}_p^E)$ and $\mathrm{q}-\mathrm{ROFPWA}({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots ,{\ddot{\mathfrak{S}}}_n)=({\mathfrak{Y}}_p,{\mathcal{F}}_p)$, we have

$$\begin{array}{cc}\hfill \sqrt[q]{\prod _{s=1}^n{\left(1-{({\check{\mathfrak{P}}}_s)}^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+\prod _{s=1}^n{\left({({\check{\mathfrak{P}}}_s)}^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}& \le \sqrt[q]{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}\prod _{s=1}^n\left(1-{({\check{\mathfrak{P}}}_s)}^q\right)+\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}\prod _{s=1}^n\left({({\check{\mathfrak{P}}}_s)}^q\right)}\hfill \\ \hfill & =\sqrt[q]{2}\hfill \end{array}$$

From above theorem,

$$\begin{array}{ccc}\hfill \sqrt[q]{\frac{{\prod }_{s=1}^n{\left(1+{({\check{\mathfrak{P}}}_s)}^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}-{\prod }_{s=1}^n{\left(1-{({\check{\mathfrak{P}}}_s)}^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}{{\prod }_{s=1}^n{\left(1+{({\check{\mathfrak{P}}}_s)}^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{\left(1-{({\check{\mathfrak{P}}}_s)}^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}}& \le & \sqrt[q]{1-\prod _{s=1}^n{\left(1-{({\check{\mathfrak{P}}}_s)}^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}\hfill \end{array}$$

(26)

$$\leftrightarrow {\check{\mathfrak{P}}}_p\ge {\check{\mathfrak{P}}}_p^E$$

These are equal iff ${\check{\mathfrak{P}}}_1={\check{\mathfrak{P}}}_2=\dots ={\check{\mathfrak{P}}}_n$

Additionally,

$$\begin{array}{cc}\hfill \sqrt[q]{\prod _{s=1}^n{\left(2-{({\overline{⨿}}_s)}^q\right)}^{{\breve{\mathcal{Z}}}_s}+\prod _{s=1}^n{\left({({\overline{⨿}}_s)}^q\right)}^{{\breve{\mathcal{Z}}}_s}}& \le \sqrt[q]{{\breve{\mathcal{Z}}}_s\prod _{s=1}^n\left(2-{({\overline{⨿}}_s)}^q\right)+{\breve{\mathcal{Z}}}_s\prod _{s=1}^n\left({({\overline{⨿}}_s)}^q\right)}=\sqrt[q]{2}\hfill \end{array}$$

Thus,

$$\begin{array}{ccc}\hfill \frac{\sqrt[q]{2{\prod }_{s=1}^n{\left({({\overline{⨿}}_s)}^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}}{\sqrt[q]{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}{\prod }_{s=1}^n\left(2-{({\overline{⨿}}_s)}^q\right)+\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}{\prod }_{s=1}^n\left({({\overline{⨿}}_s)}^q\right)}}& \ge & \frac{\sqrt[q]{2{\prod }_{s=1}^n{\left({({\overline{⨿}}_s)}^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}}{\sqrt[q]{{\prod }_{s=1}^n{\left(2-{({\overline{⨿}}_s)}^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{\left({({\overline{⨿}}_s)}^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}}\hfill \\ \hfill & \ge & \prod _{s=1}^n{\left({({\overline{⨿}}_s)}^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}\hfill \end{array}$$

$$\leftrightarrow {\overline{⨿}}_p\le {\overline{⨿}}_p^E$$

(27)

These are equal iff ${\overline{⨿}}_1={\overline{⨿}}_2=\dots ={\overline{⨿}}_n$.

Equations (26) and (27) imply,

$$\begin{array}{cc}\hfill {\check{\mathfrak{P}}}_p^E-{\overline{⨿}}_p^E& \le {\check{\mathfrak{P}}}_p-{\overline{⨿}}_p\hfill \\ \hfill \mathfrak{E}({\check{\mathfrak{P}}}_p^E,{\overline{⨿}}_p^E)& \le \mathfrak{E}({\check{\mathfrak{P}}}_p,{\overline{⨿}}_p)\hfill \end{array}$$

Thus we have the following relationship by defining the score function of q-ROFS.

$$q-ROFEPWA({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)\le q-ROFPWA({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)$$

 □

Example 1.

Let ${\ddot{\mathfrak{S}}}_1=(0.7908,0.2786)$, ${\ddot{\mathfrak{S}}}_2=(0.2086,0.6315)$, ${\ddot{\mathfrak{S}}}_3=(0.4966,0.2182)$, ${\ddot{\mathfrak{S}}}_4=(0.3298,0.5559)$, ${\ddot{\mathfrak{S}}}_5=(0.6107,0.2364)$ and ${\ddot{\mathfrak{S}}}_6=(0.3797,0.4850)$ be the q-ROFNs $q=3$ then we have,

$$\begin{array}{cc}\hfill \sqrt[q]{\frac{{\prod }_{j=1}^6{(1+{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}-{\prod }_{j=1}^6{(1-{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{\prod }_{j=1}^6{(1+{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{\prod }_{j=1}^6{(1-{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}}& =0.638318\\ \hfill \frac{\sqrt[q]{2}{\prod }_{j=1}^6{\overline{⨿}}_j^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{\sqrt[q]{{\prod }_{j=1}^6{(2-{({\overline{⨿}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{\prod }_{j=1}^6{({({\overline{⨿}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}}& =0.373708\end{array}$$

and

$$\begin{array}{ccc}\hfill q-ROFEPWA({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,{\ddot{\mathfrak{S}}}_3,{\ddot{\mathfrak{S}}}_4,{\ddot{\mathfrak{S}}}_5,{\ddot{\mathfrak{S}}}_6)& =& \left(\sqrt[q]{\frac{{\prod }_{j=1}^6{(1+{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}-{\prod }_{j=1}^6{(1-{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{\prod }_{j=1}^6{(1+{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{\prod }_{j=1}^6{(1-{({\check{\mathfrak{P}}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}},\right.\hfill \\ & & \left.\frac{\sqrt[q]{2}{\prod }_{j=1}^6{\overline{⨿}}_j^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{\sqrt[q]{{\prod }_{j=1}^6{(2-{({\overline{⨿}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{\prod }_{j=1}^6{({({\overline{⨿}}_j)}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}}\right)\hfill \\ & =& (0.638318,0.373708)\hfill \end{array}$$

Below we define some of q-ROFEPWA operator’s appealing properties.

Theorem 7.

(Idempotency) Assume that ${\ddot{\mathfrak{S}}}_j=\langle {\check{\mathfrak{P}}}_j,{\overline{⨿}}_j\rangle$ is the family of q-ROFNs, where ${\breve{\beth }}_j={\prod }_{k=1}^{j-1}\breve{\Xi }({\ddot{\mathfrak{S}}}_k)$$(j=2\dots ,n)$, ${\breve{\beth }}_1=1$ and $\breve{\Xi }({\ddot{\mathfrak{S}}}_k)$ is the score of $k^{th}$ q-ROFN. If all ${\ddot{\mathfrak{S}}}_j$ are equal, i.e., ${\ddot{\mathfrak{S}}}_j=\ddot{\mathfrak{S}}$ for all j, then

$$\mathrm{q}-\mathrm{ROFEPWA}({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots {\ddot{\mathfrak{S}}}_n)=\ddot{\mathfrak{S}}$$

Proof. 

$$\begin{array}{ccc}\hfill \mathrm{q}-\mathrm{ROFEPWA}({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots {\ddot{\mathfrak{S}}}_n)& =& \mathrm{q}-\mathrm{ROFEPWA}(\ddot{\mathfrak{S}},\ddot{\mathfrak{S}},\dots \ddot{\mathfrak{S}})\hfill \\ & =& \left(\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}\ddot{\mathfrak{S}}{\oplus }_{ϵ}\frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}\ddot{\mathfrak{S}}{\oplus }_{ϵ}\dots ,{\oplus }_{ϵ}\frac{{\breve{\beth }}_n}{{\sum }_{j=1}^n{\breve{\beth }}_j}{·}_{ϵ}\ddot{\mathfrak{S}}\right)\hfill \\ & =& \left(\sqrt[q]{\frac{{\prod }_{j=1}^n{(1+{(\check{\mathfrak{P}})}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}-{\prod }_{j=1}^n{(1-{(\check{\mathfrak{P}})}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{{\prod }_{j=1}^n{(1+{(\check{\mathfrak{P}})}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{\prod }_{j=1}^n{(1-{(\check{\mathfrak{P}})}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}}\right.,\hfill \\ & & \left.\frac{\sqrt[q]{2}{\prod }_{j=1}^n{\overline{⨿}}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}{\sqrt[q]{{\prod }_{j=1}^n{(2-{(\overline{⨿})}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}+{\prod }_{j=1}^n{({(\overline{⨿})}^q)}^{\frac{{\breve{\beth }}_j}{{\sum }_{j=1}^n{\breve{\beth }}_j}}}}\right)\hfill \\ & =& \left(\sqrt[q]{\frac{(1+{(\check{\mathfrak{P}})}^q)-(1-{(\check{\mathfrak{P}})}^q)}{(1+{(\check{\mathfrak{P}})}^q)+(1-{(\check{\mathfrak{P}})}^q)}},\frac{\sqrt[q]{2}\overline{⨿}}{\sqrt[q]{2}}\right)=(\check{\mathfrak{P}},\overline{⨿})=\ddot{\mathfrak{S}}\hfill \end{array}$$

 □

Corollary 1.

If ${\ddot{\mathfrak{S}}}_j=\langle {\check{\mathfrak{P}}}_j,{\overline{⨿}}_j\rangle$ is the family of largest q-ROFNs, i.e., ${\ddot{\mathfrak{S}}}_j=(1,0)$ $\forall j$, then

$$\mathrm{q}-\mathrm{ROFEPWA}({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots {\ddot{\mathfrak{S}}}_n)=(1,0)$$

Proof. 

We can easily obtain a Corollary similar to the Theorem 7. □

Corollary 2.

(Non-compensatory) If ${\ddot{\mathfrak{S}}}_1=\langle {\check{\mathfrak{P}}}_1,{\overline{⨿}}_1\rangle$ is the smallest q-ROFN, i.e., ${\ddot{\mathfrak{S}}}_1=(0,1)$, then

$$\mathrm{q}-\mathrm{ROFEPWA}({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots {\ddot{\mathfrak{S}}}_n)=(0,1)$$

Proof. 

Here, ${\ddot{\mathfrak{S}}}_1=(0,1)$ then by implication of the score function, we have got,

$$\breve{\Xi }({\ddot{\mathfrak{S}}}_1)=0$$

Since,

$${\breve{\beth }}_j=\prod _{k=1}^{j-1}\breve{\Xi }({\ddot{\mathfrak{S}}}_k)(j=2\dots ,n),\mathrm{and}{\breve{\beth }}_1=1$$

$\breve{\Xi }({\ddot{\mathfrak{S}}}_k)$ is the score of $k^{th}$ q-ROFN.

We have,

$${\breve{\beth }}_j={\prod }_{k=1}^{j-1}\breve{\Xi }({\ddot{\mathfrak{S}}}_k)=\breve{\Xi }({\ddot{\mathfrak{S}}}_1)\times \breve{\Xi }({\ddot{\mathfrak{S}}}_2)\times \dots \times \breve{\Xi }({\ddot{\mathfrak{S}}}_{j-1})=0\times \breve{\Xi }({\ddot{\mathfrak{S}}}_2)\times \dots \times \breve{\Xi }({\ddot{\mathfrak{S}}}_{j-1})(j=2\dots ,n)$$

$$\prod _{k=1}^j{\breve{\beth }}_j=1$$

From Definition 14, we have

$$\begin{array}{cc}\hfill \mathrm{q}-\mathrm{ROFEPWA}({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots {\ddot{\mathfrak{S}}}_n)& =\frac{{\breve{\beth }}_1}{{\sum }_{j=1}^n{\breve{\beth }}_j}{\ddot{\mathfrak{S}}}_1\oplus \frac{{\breve{\beth }}_2}{{\sum }_{j=1}^n{\breve{\beth }}_j}{\ddot{\mathfrak{S}}}_2\oplus \dots ,\oplus \frac{{\breve{\beth }}_n}{{\sum }_{j=1}^n{\breve{\beth }}_j}{\ddot{\mathfrak{S}}}_n\hfill \\ \hfill & =\frac{1}{1}{\ddot{\mathfrak{S}}}_1\oplus \frac{0}{1}{\ddot{\mathfrak{S}}}_2\oplus \dots \frac{0}{1}{\ddot{\mathfrak{S}}}_n\hfill \\ \hfill & ={\ddot{\mathfrak{S}}}_1=(0,1)\hfill \end{array}$$

 □

Corollary 2 meant that, if the higher priority criteria are met by the smallest q-ROFN, rewards will not be received by other criteria even though they are fulfilled.

Theorem 8.

(Monotonicity) Assume that ${\ddot{\mathfrak{S}}}_j=\langle {\check{\mathfrak{P}}}_j,{\overline{⨿}}_j\rangle$ and ${\ddot{\mathfrak{S}}}_{j^{*}}=\langle {\check{\mathfrak{P}}}_{j^{*}},{\overline{⨿}}_{j^{*}}\rangle$ are the families of q-ROFNs, where ${\breve{\beth }}_j={\prod }_{k=1}^{j-1}\breve{\Xi }({\ddot{\mathfrak{S}}}_k)$, ${\breve{\beth }}_{j^{*}}={\prod }_{k=1}^{j-1}\breve{\Xi }({\ddot{\mathfrak{S}}}_{k^{*}})$$(j=2\dots ,n)$, ${\breve{\beth }}_1=1$, ${\breve{\beth }}_{1^{*}}=1$, $\breve{\Xi }({\ddot{\mathfrak{S}}}_k)$ is the score of ${\ddot{\mathfrak{S}}}_k$ q-ROFN, and $\breve{\Xi }({\ddot{\mathfrak{S}}}_{k^{*}})$ is the score of ${\ddot{\mathfrak{S}}}_{k^{*}}$ q-ROFN. If ${\check{\mathfrak{P}}}_{j^{*}}\ge {\check{\mathfrak{P}}}_j$ and ${\overline{⨿}}_{j^{*}}\le {\overline{⨿}}_j$ for all j, then

$$\mathrm{q}-\mathrm{ROFPWA}({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots {\ddot{\mathfrak{S}}}_n)\le \mathrm{q}-\mathrm{ROFPWA}({\ddot{\mathfrak{S}}}_{1^{*}},{\ddot{\mathfrak{S}}}_{2^{*}},\dots {\ddot{\mathfrak{S}}}_{n^{*}})$$

Proof. 

Let $f(y)=\sqrt[q]{\frac{2-y^q}{y^q}}$, $y\in (0,1]$ and $q\ge 1$. Then $f^{\prime }(y)<0$. So, $f(y)$ is a decreasing function on $(0,1]$. If ${\check{\mathfrak{P}}}_j^{*}\ge {\check{\mathfrak{P}}}_j$ for all j. Then $f({\check{\mathfrak{P}}}_j^{*})\le f({\check{\mathfrak{P}}}_j)$, i.e.,

$$\sqrt[q]{\frac{2-{\check{\mathfrak{P}}}_{s^{*}}^q}{{\check{\mathfrak{P}}}_{s^{*}}^q}}\le \sqrt[q]{\frac{2-{\check{\mathfrak{P}}}_s^q}{{\check{\mathfrak{P}}}_s^q}}(j=1,2,\dots ,n)$$

Let

$$\begin{array}{ccc}\hfill \breve{\mathcal{Z}}& =& {\left(\frac{{\breve{\beth }}_1}{{\sum }_{s=1}^n{\breve{\beth }}_s},\frac{{\breve{\beth }}_2}{{\sum }_{s=1}^n{\breve{\beth }}_s},\dots ,\frac{{\breve{\beth }}_n}{{\sum }_{s=1}^n{\breve{\beth }}_s}\right)}^T\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\breve{\mathcal{Z}}}_{*}& =& {\left(\frac{{\breve{\beth }}_{1^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}},\frac{{\breve{\beth }}_{2^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}},\dots ,\frac{{\breve{\beth }}_{n^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}\right)}^T\hfill \end{array}$$

be the prioritized WVs of ${\ddot{\mathfrak{S}}}_j=\langle {\check{\mathfrak{P}}}_j,{\overline{⨿}}_j\rangle$ and ${\ddot{\mathfrak{S}}}_{j^{*}}=\langle {\check{\mathfrak{P}}}_{j^{*}},{\overline{⨿}}_{j^{*}}\rangle$ respectively, s.t

$$\sum _{s=1}^n\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}=1$$

and

$$\sum _{s=1}^n\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}=1$$

Now,

$$\begin{array}{ccc}\hfill \leftrightarrow \sqrt[q]{{\left(\frac{2-{\check{\mathfrak{P}}}_{s^{*}}^q}{{\check{\mathfrak{P}}}_{s^{*}}^q}\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}& \le & \sqrt[q]{{\left(\frac{2-{\check{\mathfrak{P}}}_s^q}{{\check{\mathfrak{P}}}_s^q}\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}\hfill \\ \hfill \leftrightarrow \sqrt[q]{{\prod }_{s=1}^n{\left(\frac{2-{\check{\mathfrak{P}}}_{s^{*}}^q}{{\check{\mathfrak{P}}}_{s^{*}}^q}\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}& \le & \sqrt[q]{{\prod }_{s=1}^n{\left(\frac{2-{\check{\mathfrak{P}}}_s^q}{{\check{\mathfrak{P}}}_s^q}\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}\hfill \\ \hfill \leftrightarrow \sqrt[q]{{\prod }_{s=1}^n{\left(\frac{2-{\check{\mathfrak{P}}}_{s^{*}}^q}{{\check{\mathfrak{P}}}_{s^{*}}^q}\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}+1}& \le & \sqrt[q]{{\prod }_{s=1}^n{\left(\frac{2-{\check{\mathfrak{P}}}_s^q}{{\check{\mathfrak{P}}}_s^q}\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+1}\hfill \\ \hfill \leftrightarrow \frac{1}{\sqrt[q]{{\prod }_{s=1}^n{\left(\frac{2-{\check{\mathfrak{P}}}_s^q}{{\check{\mathfrak{P}}}_s^q}\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+1}}& \le & \frac{1}{\sqrt[q]{{\prod }_{s=1}^n{\left(\frac{2-{\check{\mathfrak{P}}}_{s^{*}}^q}{{\check{\mathfrak{P}}}_{s^{*}}^q}\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}+1}}\hfill \\ \hfill \leftrightarrow \frac{\sqrt[q]{2}}{\sqrt[q]{{\prod }_{s=1}^n{\left(\frac{2-{\check{\mathfrak{P}}}_s^q}{{\check{\mathfrak{P}}}_s^q}\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+1}}& \le & \frac{\sqrt[q]{2}}{\sqrt[q]{{\prod }_{s=1}^n{\left(\frac{2-{\check{\mathfrak{P}}}_{s^{*}}^q}{{\check{\mathfrak{P}}}_{s^{*}}^q}\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}+1}}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \leftrightarrow \frac{\sqrt[q]{2}}{\sqrt[q]{\frac{{\prod }_{s=1}^n{\left(2-{\check{\mathfrak{P}}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}{{\prod }_{s=1}^n{\left({\check{\mathfrak{P}}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}}+1}& \le & \frac{\sqrt[q]{2}}{\sqrt[q]{\frac{{\prod }_{s=1}^n{\left(2-{\check{\mathfrak{P}}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}{{\prod }_{s=1}^n{\left({\check{\mathfrak{P}}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}}+1}\hfill \\ \hfill \leftrightarrow \frac{\sqrt[q]{2}}{\sqrt[q]{\frac{{\prod }_{s=1}^n{\left(2-{\check{\mathfrak{P}}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{\left({\check{\mathfrak{P}}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}{{\prod }_{s=1}^n{\left({\check{\mathfrak{P}}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}}}& \le & \frac{\sqrt[q]{2}}{\sqrt[q]{\frac{{\prod }_{s=1}^n{\left(2-{\check{\mathfrak{P}}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}+{\prod }_{s=1}^n{\left({\check{\mathfrak{P}}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}{{\prod }_{s=1}^n{\left({\check{\mathfrak{P}}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}}}\hfill \\ \hfill \leftrightarrow \frac{\sqrt[q]{2}\sqrt[q]{{\prod }_{s=1}^n{\left({\check{\mathfrak{P}}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}}{\sqrt[q]{{\prod }_{s=1}^n{\left(2-{\check{\mathfrak{P}}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{\left({\check{\mathfrak{P}}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}}& \le & \frac{\sqrt[q]{2}\sqrt[q]{{\prod }_{s=1}^n{\left({\check{\mathfrak{P}}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}}{\sqrt[q]{{\prod }_{s=1}^n{\left(2-{\check{\mathfrak{P}}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}+{\prod }_{s=1}^n{\left({\check{\mathfrak{P}}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}}\hfill \\ \hfill \leftrightarrow \frac{\sqrt[q]{2{\prod }_{s=1}^n{\left({\check{\mathfrak{P}}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}}{\sqrt[q]{{\prod }_{s=1}^n{\left(2-{\check{\mathfrak{P}}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{\left({\check{\mathfrak{P}}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}}& \le & \frac{\sqrt[q]{2{\prod }_{s=1}^n{\left({\check{\mathfrak{P}}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}}{\sqrt[q]{{\prod }_{s=1}^n{\left(2-{\check{\mathfrak{P}}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}+{\prod }_{s=1}^n{\left({\check{\mathfrak{P}}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}}\hfill \end{array}$$

(28)

Again, let $q(t)=\sqrt[q]{\frac{(1-t^q)}{(1+t^q)}}$, $t\in [0,1]$ and $q\ge 1$. Then $q^{\prime }(y)<0$. So, $q(y)$ is a decreasing function on $(0,1]$. If ${\overline{⨿}}_j^{*}\le {\overline{⨿}}_j$ for all j. Then $f({\overline{⨿}}_j^{*})\ge f({\overline{⨿}}_j)$, i.e.,

$$\sqrt[q]{\frac{1-{\overline{⨿}}_{s^{*}}^q}{1+{\overline{⨿}}_{s^{*}}^q}}\ge \sqrt[q]{\frac{1-{\overline{⨿}}_s^q}{1+{\overline{⨿}}_s^q}}(j=1,2,\dots ,n)$$

Let

$$\begin{array}{ccc}\hfill \breve{\mathcal{Z}}& =& {\left(\frac{{\breve{\beth }}_1}{{\sum }_{s=1}^n{\breve{\beth }}_s},\frac{{\breve{\beth }}_2}{{\sum }_{s=1}^n{\breve{\beth }}_s},\dots ,\frac{{\breve{\beth }}_n}{{\sum }_{s=1}^n{\breve{\beth }}_s}\right)}^T\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\breve{\mathcal{Z}}}_{*}& =& {\left(\frac{{\breve{\beth }}_{1^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}},\frac{{\breve{\beth }}_{2^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}},\dots ,\frac{{\breve{\beth }}_{n^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}\right)}^T\hfill \end{array}$$

be the prioritized WVs of ${\ddot{\mathfrak{S}}}_j=\langle {\check{\mathfrak{P}}}_j,{\overline{⨿}}_j\rangle$ and ${\ddot{\mathfrak{S}}}_{j^{*}}=\langle {\check{\mathfrak{P}}}_{j^{*}},{\overline{⨿}}_{j^{*}}\rangle$, respectively, s.t

$$\sum _{s=1}^n\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}=1$$

and

$$\sum _{s=1}^n\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}=1$$

Now,

$$\begin{array}{ccc}\hfill \leftrightarrow \sqrt[q]{{\left(\frac{1-{\overline{⨿}}_{s^{*}}^q}{1+{\overline{⨿}}_{s^{*}}^q}\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}& \ge & \sqrt[q]{{\left(\frac{1-{\overline{⨿}}_s^q}{1+{\overline{⨿}}_s^q}\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}\hfill \\ \hfill \leftrightarrow \sqrt[q]{{\prod }_{s=1}^n{\left(\frac{1-{\overline{⨿}}_{s^{*}}^q}{1+{\overline{⨿}}_{s^{*}}^q}\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}& \le & \sqrt[q]{{\prod }_{s=1}^n{\left(\frac{1-{\overline{⨿}}_s^q}{1+{\overline{⨿}}_s^q}\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}\hfill \\ \hfill \leftrightarrow \sqrt[q]{1+{\prod }_{s=1}^n{\left(\frac{1-{\overline{⨿}}_{s^{*}}^q}{1+{\overline{⨿}}_{s^{*}}^q}\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}& \ge & \sqrt[q]{1+{\prod }_{s=1}^n{\left(\frac{1-{\overline{⨿}}_s^q}{1+{\overline{⨿}}_s^q}\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}\hfill \\ \hfill \leftrightarrow \frac{1}{\sqrt[q]{1+{\prod }_{s=1}^n{\left(\frac{1-{\overline{⨿}}_{s^{*}}^q}{1+{\overline{⨿}}_{s^{*}}^q}\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}}& \le & \frac{1}{\sqrt[q]{1+{\prod }_{s=1}^n{\left(\frac{1-{\overline{⨿}}_s^q}{1+{\overline{⨿}}_s^q}\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}}\hfill \\ \hfill \leftrightarrow \frac{\sqrt[q]{2}}{\sqrt[q]{1+{\prod }_{s=1}^n{\left(\frac{1-{\overline{⨿}}_{s^{*}}^q}{1+{\overline{⨿}}_{s^{*}}^q}\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}}& \le & \frac{\sqrt[q]{2}}{\sqrt[q]{1+{\prod }_{s=1}^n{\left(\frac{1-{\overline{⨿}}_s^q}{1+{\overline{⨿}}_s^q}\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}}\hfill \\ \hfill \leftrightarrow \frac{\sqrt[q]{2}}{\sqrt[q]{1+\frac{{\prod }_{s=1}^n{\left(1-{\overline{⨿}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}{{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}}}& \le & \frac{\sqrt[q]{2}}{\sqrt[q]{1+\frac{{\prod }_{s=1}^n{\left(1-{\overline{⨿}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}{{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}}}\hfill \\ \hfill \leftrightarrow \frac{\sqrt[q]{2}}{\sqrt[q]{\frac{{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}+{\prod }_{s=1}^n{\left(1-{\overline{⨿}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}{{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}}}& \le & \frac{\sqrt[q]{2}}{\sqrt[q]{\frac{{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{\left(1-{\overline{⨿}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}{{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}}}\hfill \\ \hfill \leftrightarrow \frac{\sqrt[q]{2{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}}{\sqrt[q]{{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}+{\prod }_{s=1}^n{\left(1-{\overline{⨿}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}}& \le & \frac{\sqrt[q]{2{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}}{\sqrt[q]{{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{\left(1-{\overline{⨿}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}}\hfill \\ \hfill \leftrightarrow \sqrt[q]{\frac{2{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}{{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}+{\prod }_{s=1}^n{\left(1-{\overline{⨿}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}-1}& \le & \sqrt[q]{\frac{2{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}{{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{\left(1-{\overline{⨿}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}-1}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill & \leftrightarrow & \sqrt[q]{\frac{{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}-{\prod }_{s=1}^n{\left(1-{\overline{⨿}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}{{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}+{\prod }_{s=1}^n{\left(1-{\overline{⨿}}_{s^{*}}^q\right)}^{\frac{{\breve{\beth }}_{s^{*}}}{{\sum }_{s=1}^n{\breve{\beth }}_{s^{*}}}}}}\le \sqrt[q]{\frac{{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}-{\prod }_{s=1}^n{\left(1-{\overline{⨿}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}{{\prod }_{s=1}^n{\left(1+{\overline{⨿}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}+{\prod }_{s=1}^n{\left(1-{\overline{⨿}}_s^q\right)}^{\frac{{\breve{\beth }}_s}{{\sum }_{s=1}^n{\breve{\beth }}_s}}}}\hfill \end{array}$$

(29)

Let,

$$\mathrm{q}-\mathrm{ROFPWA}({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots {\ddot{\mathfrak{S}}}_n)=\ddot{\mathfrak{S}}$$

and

$$\mathrm{q}-\mathrm{ROFPWA}({\ddot{\mathfrak{S}}}_{1^{*}},{\ddot{\mathfrak{S}}}_{2^{*}},\dots {\ddot{\mathfrak{S}}}_{n^{*}})={\ddot{\mathfrak{S}}}_{{}^{*}}$$

Equations (28) and (29) can be written as ${\check{\mathfrak{P}}}_{\ddot{\mathfrak{S}}}\le {\check{\mathfrak{P}}}_{{\ddot{\mathfrak{S}}}_{{}^{*}}}$ and ${\overline{⨿}}_{\ddot{\mathfrak{S}}}\ge {\overline{⨿}}_{{\ddot{\mathfrak{S}}}_{{}^{*}}}$. Thus $\mathfrak{E}(\ddot{\mathfrak{S}})={({\check{\mathfrak{P}}}_{\ddot{\mathfrak{S}}})}^q-{({\overline{⨿}}_{\ddot{\mathfrak{S}}})}^q$$\le {({\check{\mathfrak{P}}}_{{\ddot{\mathfrak{S}}}_{{}^{*}}})}^q-{({\overline{⨿}}_{{\ddot{\mathfrak{S}}}_{{}^{*}}})}^q=\mathfrak{E}({\ddot{\mathfrak{S}}}_{{}^{*}})$ Therefore, $\mathfrak{E}(\ddot{\mathfrak{S}})\le \mathfrak{E}({\ddot{\mathfrak{S}}}_{{}^{*}})$. If $\mathfrak{E}(\ddot{\mathfrak{S}})<\mathfrak{E}({\ddot{\mathfrak{S}}}_{{}^{*}})$ then

$$\mathrm{q}-\mathrm{ROFPWA}({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots {\ddot{\mathfrak{S}}}_n)<\mathrm{q}-\mathrm{ROFPWA}({\ddot{\mathfrak{S}}}_{1^{*}},{\ddot{\mathfrak{S}}}_{2^{*}},\dots {\ddot{\mathfrak{S}}}_{n^{*}})$$

(30)

If $\mathfrak{E}(\ddot{\mathfrak{S}})=\mathfrak{E}({\ddot{\mathfrak{S}}}_{{}^{*}})$, i.e., ${({\check{\mathfrak{P}}}_{\ddot{\mathfrak{S}}})}^q-{({\overline{⨿}}_{\ddot{\mathfrak{S}}})}^q$$={({\check{\mathfrak{P}}}_{{\ddot{\mathfrak{S}}}_{{}^{*}}})}^q-{({\overline{⨿}}_{{\ddot{\mathfrak{S}}}_{{}^{*}}})}^q$, then we get, ${({\check{\mathfrak{P}}}_{\ddot{\mathfrak{S}}})}^q={({\check{\mathfrak{P}}}_{{\ddot{\mathfrak{S}}}_{{}^{*}}})}^q$ and ${({\overline{⨿}}_{\ddot{\mathfrak{S}}})}^q={({\overline{⨿}}_{{\ddot{\mathfrak{S}}}_{{}^{*}}})}^q$.

$\mathfrak{R}(\ddot{\mathfrak{S}})={({\check{\mathfrak{P}}}_{\ddot{\mathfrak{S}}})}^q+{({\overline{⨿}}_{\ddot{\mathfrak{S}}})}^q={({\check{\mathfrak{P}}}_{{\ddot{\mathfrak{S}}}_{{}^{*}}})}^q+{({\overline{⨿}}_{{\ddot{\mathfrak{S}}}_{{}^{*}}})}^q=\mathfrak{R}({\ddot{\mathfrak{S}}}_{{}^{*}})$. So we have

$$\mathrm{q}-\mathrm{ROFPWA}({\ddot{\mathfrak{S}}}_1,{\ddot{\mathfrak{S}}}_2,\dots {\ddot{\mathfrak{S}}}_n)=\mathrm{q}-\mathrm{ROFPWA}({\ddot{\mathfrak{S}}}_{1^{*}},{\ddot{\mathfrak{S}}}_{2^{*}}$$